2022届新高考版数学小题狂练03(含解析)

小题专练09解析几何(A)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(考点:直线的斜率与倾斜角的关系,★)下列命题中,正确的是( ). A .若直线的倾斜角越大,则直线的斜率就越大 B .若直线的倾斜角为α,则直线的斜率为tan α C .若直线的斜率为tan α,则直线的倾斜角是αD .当直线的倾斜角α∈[0,π2)∪(π2,π)时,直线的斜率分别在这两个区间上单调递增2.(考点:求直线的方程,★)已知直线l 过点(-1,2)且与直线2x-3y+4=0垂直,则直线l 的方程是( ). A .3x+2y-1=0 B .3x+2y+7=0 C .2x-3y+5=0 D .2x-3y+8=03.(考点:椭圆的标准方程,★)“-1<m<3”是“方程x 2m+1+y 27-m =1表示椭圆”的( ). A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件4.(考点:求双曲线的渐近线方程,★)若双曲线x 2a2-y 2b2=1(a>0,b>0)的离心率为53,则该双曲线的渐近线方程为( ). A .y=±45x B .y=±54xC .y=±43xD .y=±34x5.(考点:求双曲线的方程,★★)已知双曲线x 2a 2-y 2b 2=1(a>0,b>0)的一条渐近线过点(2,√3),且双曲线的一个焦点在抛物线y 2=4√7x 的准线上,则该双曲线的方程为( ). A .x 221-y 228=1 B .x 228-y 221=1 C .x 23-y 24=1 D .x 24-y 23=16.(考点:求双曲线的离心率,★★)已知双曲线C :x 2a 2-y 2b 2=1(a>0,b>0),以点P (b ,0)为圆心,a 为半径作圆P ,圆P 与双曲线C 的一条渐近线交于M ,N 两点,若∠MPN=90°,则双曲线C 的离心率为( ). A .√2B .√3C .√52 D .√727.(考点:抛物线定义的应用,★★)已知F 是抛物线x 2=6y 的焦点,A ,B 是该抛物线上的两点,|AF|+|BF|=9,则线段AB 的中点到x 轴的距离为( ).A .3B .92C .4D .328.(考点:点差法的应用,★★★)已知椭圆x 236+y 29=1的一条弦被点A (4,2)平分,则此弦所在的直线方程是( ).A .x-2y=0B .x+2y=4C .2x+3y=14D .x+2y=8二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分. 9.(考点:直线方程的应用,★★)下列说法正确的是( ). A .当x 1≠x 2,y 1≠y 2时,过(x 1,y 1),(x 2,y 2)两点的直线方程为y -y 1y 2-y 1=x -x 1x2-x 1B .点(0,2)关于直线y=x+1的对称点为(1,1)C .直线x-y-2=0与两坐标轴围成的三角形的面积是2D .经过点(1,1)且在x 轴和y 轴上截距都相等的直线方程为x+y-2=010.(考点:圆的对称性的应用,★★)已知圆O 的方程为x 2+y 2-4x-1=0,则圆O ( ). A .关于点(2,0)对称 B .关于直线y=0对称 C .关于直线x+3y-2=0对称 D .关于直线x-y+2=0对称11.(考点:双曲线的简单几何性质的应用,★★)已知双曲线E :x 24-y 212=1的左、右焦点分别为F 1,F 2,P 是双曲线右支上的一点,则下列结论正确的是( ). A .|PF 1|-|PF 2|=4B .双曲线E 的离心率是√3C .|PF 1|的最小值是6D .点P 到两渐近线的距离的乘积是312.(考点:抛物线定义的应用,★★★)已知抛物线C :y 2=2px (p>0)的焦点为F ,经过点F 且斜率为√3的直线l 与抛物线C 交于A ,B 两点(点A 在第一象限),与抛物线的准线交于点D ,若|AF|=8,则下列结论正确的是( ). A .p=4B .DF ⃗⃗⃗⃗⃗ =FA⃗⃗⃗⃗⃗ C .|BD|=2|BF| D .|BF|=4三、填空题:本题共4小题,每小题5分,共20分.13.(考点:抛物线的应用,★)已知抛物线y 2=2px (p>0)的准线与圆(x-3)2+y 2=16相切,则p 的值为 . 14.(考点:直线与圆的位置关系,★★)已知a ,b 为正实数,直线x+y+1=0截圆(x-a )2+(y-b )2=4所得的弦长为2√2,则ab 的最大值为 .15.(考点:双曲线性质的应用,★★)已知双曲线C :x 24-y 2b 2=1(b>0)的左、右顶点分别为A ,B ,点P 在双曲线C 上,且直线PA 与直线PB 的斜率之积为1,则该双曲线C 的焦距为 .16.(考点:抛物线定义的应用,★★★)已知过抛物线C :y 2=2px (p>0)的焦点F 的直线l :y=4x+b 截抛物线C 所得的弦长为17,设点A 为抛物线C 上的动点,点B (2,6),过点A 作抛物线C 的准线l 1的垂线,垂足为D ,则p 的值为 ,|AB|+|AD|的最小值为 .答案解析：1.(考点:直线的斜率与倾斜角的关系,★)下列命题中,正确的是( ). A .若直线的倾斜角越大,则直线的斜率就越大 B .若直线的倾斜角为α,则直线的斜率为tan α C .若直线的斜率为tan α,则直线的倾斜角是αD .当直线的倾斜角α∈[0,π2)∪(π2,π)时,直线的斜率分别在这两个区间上单调递增【解析】当直线的倾斜角α∈[0,π2)∪(π2,π)时,直线的斜率分别在这两个区间上单调递增,故A 错误,D 正确;当α=π2时,斜率不存在,故B 错误;只有当α∈[0,π2)∪(π2,π)时,直线的倾斜角才是α,故C 错误.故选D . 【答案】D2.(考点:求直线的方程,★)已知直线l 过点(-1,2)且与直线2x-3y+4=0垂直,则直线l 的方程是( ). A .3x+2y-1=0 B .3x+2y+7=0 C .2x-3y+5=0 D .2x-3y+8=0【解析】因为直线2x-3y+4=0的斜率为23,所以直线l 的斜率为-32,所以直线l 的方程为y-2=-32(x+1),即3x+2y-1=0. 【答案】A3.(考点:椭圆的标准方程,★)“-1<m<3”是“方程x 2m+1+y 27-m =1表示椭圆”的( ). A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【解析】因为方程x 2m+1+y 27-m =1表示椭圆,所以{m +1>0,7-m >0,m +1≠7-m ,解得-1<m<3或3<m<7.故“-1<m<3”是“方程x 2m+1+y 27-m =1表示椭圆”的充分不必要条件. 【答案】A4.(考点:求双曲线的渐近线方程,★)若双曲线x 2a2-y 2b2=1(a>0,b>0)的离心率为53,则该双曲线的渐近线方程为( ). A .y=±45x B .y=±54x C .y=±43x D .y=±34x【解析】因为双曲线的离心率为53,即e=c a =53, 所以c=53a ,又c 2=a 2+b 2,所以b=43a ,所以b a =43,所以该双曲线的渐近线方程为y=±43x. 【答案】C5.(考点:求双曲线的方程,★★)已知双曲线x 2a 2-y 2b 2=1(a>0,b>0)的一条渐近线过点(2,√3),且双曲线的一个焦点在抛物线y 2=4√7x 的准线上,则该双曲线的方程为( ). A .x 221-y 228=1 B .x 228-y 221=1C .x 23-y 24=1D .x 24-y 23=1【解析】由题意可得√3=2ba . ①因为抛物线y 2=4√7x 的准线是x=-√7,所以c=√7,即a 2+b 2=c 2=7. ② 联立①②,解得{a =2,b =√3,所以双曲线的方程为x 24-y 23=1. 【答案】D6.(考点:求双曲线的离心率,★★)已知双曲线C :x 2a 2-y 2b 2=1(a>0,b>0),以点P (b ,0)为圆心,a 为半径作圆P ,圆P 与双曲线C 的一条渐近线交于M ,N 两点,若∠MPN=90°,则双曲线C 的离心率为( ).A .√2B .√3C .√52 D .√72【解析】设双曲线C 的一条渐近线为bx-ay=0,且与圆P 交于M ,N 两点,因为∠MPN=90°,所以圆心P 到直线bx-ay=0的距离为2√a 2+b2=b 2c =√22a ,即2c 2-2a 2=√2ac ,因为e=ca >1,解得e=√2.【答案】A7.(考点:抛物线定义的应用,★★)已知F 是抛物线x 2=6y 的焦点,A ,B 是该抛物线上的两点,|AF|+|BF|=9,则线段AB 的中点到x 轴的距离为( ). A .3 B .92 C .4 D .32【解析】由题意可得F (0,32),抛物线的准线方程为y=-32.设A (x 1,y 1),B (x 2,y 2),根据抛物线的定义可得|AF|+|BF|=y 1+y 2+3=9,解得y 1+y 2=6,∴线段AB 中点的纵坐标为3,即线段AB 的中点到x 轴的距离为3. 【答案】A8.(考点:点差法的应用,★★★)已知椭圆x 236+y 29=1的一条弦被点A (4,2)平分,则此弦所在的直线方程是( ).A .x-2y=0B .x+2y=4C .2x+3y=14D .x+2y=8【解析】设过点A 的直线与椭圆相交于E (x 1,y 1),F (x 2,y 2)两点,则有x 1236+y 129=1,x 2236+y 229=1,两式相减得(x 1-x 2)(x 1+x 2)36+(y 1-y 2)(y 1+y 2)9=0.又∵A 为弦EF 的中点,且A (4,2),∴x 1+x 2=8,y 1+y 2=4,∴836(x 1-x 2)+49(y 1-y 2)=0, ∴k EF =y 1-y 2x 1-x 2=-12,∴过点A 且被该点平分的弦所在直线的方程是y-2=-12(x-4),即x+2y-8=0.【答案】D二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分. 9.(考点:直线方程的应用,★★)下列说法正确的是( ). A .当x 1≠x 2,y 1≠y 2时,过(x 1,y 1),(x 2,y 2)两点的直线方程为y -y 1y 2-y 1=x -x 1x2-x 1B .点(0,2)关于直线y=x+1的对称点为(1,1)C .直线x-y-2=0与两坐标轴围成的三角形的面积是2D .经过点(1,1)且在x 轴和y 轴上截距都相等的直线方程为x+y-2=0 【解析】对于A,当x 1≠x 2,y 1≠y 2时,过(x 1,y 1),(x 2,y 2)两点的直线方程为y -y 1y2-y 1=x -x 1x2-x 1,故A 正确;对于B项,点(0,2)与(1,1)的中点坐标为(12,32),满足直线方程y=x+1,并且两点连线的斜率为-1,所以点(0,2)关于直线y=x+1的对称点为(1,1),所以B正确;对于C项,直线x-y-2=0在两坐标轴上的截距分别为2,-2,故直线x-y-2=0与两坐标轴围成的三角形的面积是12×2×2=2,所以C正确;对于D项,经过点(1,1),且在x轴和y轴上截距都相等的直线方程为x+y-2=0或y=x,所以D不正确.【答案】ABC10.(考点:圆的对称性的应用,★★)已知圆O的方程为x2+y2-4x-1=0,则圆O().A.关于点(2,0)对称B.关于直线y=0对称C.关于直线x+3y-2=0对称D.关于直线x-y+2=0对称【解析】x2+y2-4x-1=0⇒(x-2)2+y2=5,所以圆心O的坐标为(2,0).对于A项,圆是关于圆心对称的中心对称图形,而点(2,0)是圆心,所以A选项正确;对于B项,圆是关于直径对称的轴对称图形,直线y=0过圆心,所以B选项正确;对于C项,圆是关于直径对称的轴对称图形,直线x+3y-2=0过圆心,所以C选项正确;对于D项,圆是关于直径对称的轴对称图形,直线x-y+2=0不过圆心,所以D选项不正确.【答案】ABC11.(考点:双曲线的简单几何性质的应用,★★)已知双曲线E:x24-y212=1的左、右焦点分别为F1,F2,P是双曲线右支上的一点,则下列结论正确的是().A.|PF1|-|PF2|=4B.双曲线E的离心率是√3C.|PF1|的最小值是6D.点P到两渐近线的距离的乘积是3【解析】由双曲线E:x 24-y212=1,得a2=4,b2=12,c2=a2+b2=16,解得a=2,b=2√3,c=4,由双曲线的定义得|PF1|-|PF2|=2a=4,所以A正确;离心率e=ca =42=2,所以B错误;当点P在右顶点时,|PF1|取得最小值,即|PF1|min=a+c=6,所以C正确;因为双曲线的渐近线方程为y=±bax=±√3x,设点P(x0,y0),则x024-y0212=1,即3x02-y02=12,则点P 到直线y=√3x 和y=-√3x 的距离的乘积为|√3x 0-y 0|2×|√3x 0+y 0|2=|3x 02-y 02|4=124=3,所以D 正确.【答案】ACD12.(考点:抛物线定义的应用,★★★)已知抛物线C :y 2=2px (p>0)的焦点为F ,经过点F 且斜率为√3的直线l 与抛物线C 交于A ,B 两点(点A 在第一象限),与抛物线的准线交于点D ,若|AF|=8,则下列结论正确的是( ). A .p=4B .DF ⃗⃗⃗⃗⃗ =FA⃗⃗⃗⃗⃗ C .|BD|=2|BF| D .|BF|=4 【解析】如图所示,分别过点A ,B 作抛物线C 的准线m 的垂线,垂足分别为点E ,M.抛物线C 的准线m 交x 轴于点P ,则|PF|=p ,由于直线l 的斜率为√3,其倾斜角为60°,又∵AE ∥x 轴,∴∠EAF=60°,由抛物线的定义可知,|AE|=|AF|,则△AEF 为等边三角形,∴∠EFP=∠AEF=60°,则∠PEF=30°,∴|AF|=|EF|=2|PF|=2p=8,解得p=4,故A 选项正确;∵|AE|=|EF|=2|PF|,又PF ∥AE ,∴F 为AD 的中点,则DF ⃗⃗⃗⃗⃗ =FA⃗⃗⃗⃗⃗ ,故B 选项正确; ∵∠DAE=60°,∴∠ADE=30°,∴|BD|=2|BM|=2|BF|,故C 选项正确; ∵|BD|=2|BF|,∴|BF|=13|DF|=13|AF|=83,故D 选项错误.【答案】ABC三、填空题:本题共4小题,每小题5分,共20分.13.(考点:抛物线的应用,★)已知抛物线y 2=2px (p>0)的准线与圆(x-3)2+y 2=16相切,则p 的值为 . 【解析】抛物线的准线方程为x=-p2,准线与圆相切,则3+p2=4,解得p=2.【答案】214.(考点:直线与圆的位置关系,★★)已知a ,b 为正实数,直线x+y+1=0截圆(x-a )2+(y-b )2=4所得的弦长为2√2,则ab 的最大值为 .【解析】由题意可得圆心(a ,b )到直线x+y+1=0的距离d=√22-(2√22)2=√2,故√2=√2.又a ,b 为正实数,故a+b=1,所以ab ≤(a+b 2)2=14,当且仅当a=b=12时取等号.【答案】1415.(考点:双曲线性质的应用,★★)已知双曲线C :x 24-y 2b2=1(b>0)的左、右顶点分别为A ,B ,点P 在双曲线C 上,且直线PA 与直线PB 的斜率之积为1,则该双曲线C 的焦距为 . 【解析】由双曲线方程可知A (-2,0),B (2,0), 设P (x 0,y 0),则k PA ·k PB =y 0x+2·y 0x-2=y 02x 02-4=1,即x 02-y 02=4. 又x 024-y 02b 2=1,∴b 2=4,∴c 2=a 2+b 2=8,∴双曲线C 的焦距2c=4√2. 【答案】4√216.(考点:抛物线定义的应用,★★★)已知过抛物线C :y 2=2px (p>0)的焦点F 的直线l :y=4x+b 截抛物线C 所得的弦长为17,设点A 为抛物线C 上的动点,点B (2,6),过点A 作抛物线C 的准线l 1的垂线,垂足为D ,则p 的值为 ,|AB|+|AD|的最小值为 .【解析】抛物线C :y 2=2px (p>0)的焦点为(p2,0),直线l 过焦点,故b=-2p ,即直线l :y=4x-2p.设直线l 与抛物线C 交点的横坐标分别为x 1,x 2,联立{y 2=2px ,y =4x -2p ,得8x 2-9px+2p 2=0,所以x 1+x 2=98p ,故x 1+x 2+p=178p=17,解得p=8,所以y 2=16x.易知点B (2,6)在抛物线外,所以|AB|+|AD|=|AB|+|AF|≥|BF|=2√10,当B ,A ,F 三点共线时等号成立. 【答案】8 2√10。

小题专练02函数、导数与不等式(B)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(考点:分段函数求值,★)设函数f (x )={32-x ,x ≤0,5-log 3x ,x >0,则f (f (-2))=( ).A .-1B .1C .2D .32.(考点:函数的奇偶性,★★)已知函数f (x )是定义域为R 的奇函数,当x ≥0时,f (x )=-x 2+x+b ,则当x<0时,f (x )的解析式为( ). A .f (x )=x 2+x B .f (x )=x 2-x C .f (x )=-x 2+xD .f (x )=-x 2-x3.(考点:函数值比较大小,★★)已知a=(1e )-4,b=332,c=log 0.25,则a ,b ,c 的大小关系是( ).A .a<c<bB .c<b<aC .b<c<aD .c<a<b4.(考点:函数单调性的应用,★★)若函数f (x )={(5-a )x +2,x ≤2,a x -1,x >2在定义域内单调递增,则实数a 的取值范围是( ). A .[4,5) B .(4,5) C .(3,5)D .(2,5)5.(考点:均值不等式,★★)设a>0,b>0,lg 4是lg 2a 与lg 8b 的等差中项,则1a +1b 的最小值为( ). A .2√2B .2+√32C .√32 D .96.(考点:利用导数研究函数的极值,★★★)若x=1是函数f (x )=(12x 2+2ax -2)e x-1的极值点,则f (x )的极小值为( ). A .2e -3B .-2e -3C .-54 D .547.(考点:函数的零点及应用,★★★)已知函数f (x )={3x +4,x ≤0,|22-x -2|,x >0,若函数y=f (x )-a 有三个零点,则实数a 的取值范围是( ). A .[0,2] B .(0,2)C .(-∞,0]∪[2,+∞)D .(-∞,0)∪(2,+∞)8.(考点:导数的综合应用,★★★)已知定义在R 上的奇函数f (x )满足f (-1)=1.若f (x )的导函数f'(x )满足f'(x )<x 3+2x ,则不等式f (x )+94<x 44+x 2的解集为( ).A .(0,+∞)B .(0,1)C .(1,+∞)D .(-∞,1)二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.(考点:不等式的综合应用,★★)若a ,b 为正实数,则a>b 的充要条件可以为( ). A .1a <1bB .ln a<ln bC .a ln a<b ln bD .a-b<e a -e b10.(考点:函数的基本性质,★★)下列命题正确的是( ). A .若函数f (x )在(2020,2021)上有零点,则一定有f (2020)·f (2021)<0 B .函数y=√16-x 2是偶函数C .若函数f (x )=lg(ax 2+5x+5)的值域为R,则实数a 的取值范围是[0,54] D .若函数f (x )满足条件f (x )-4f (1x )=x ,(x ∈R,x ≠0),则f (x )=-115(x +4x )(x ≠0)11.(考点:均值不等式,★★)下列说法正确的是( ). A .若x ,y>0,x+y=4,则2x +2y 的最小值为8 B .若x<12,则函数y=2x+12x -1的最大值为-2 C .若x ,y>0,x+y+xy=3,则xy 的最小值为1 D .函数y=2√x 2+2的最小值为412.(考点:导数的综合应用,★★★)已知函数f (x )=x 2+x -1e x,则下列结论正确的是( ).A .函数f (x )只有一个零点B .函数f (x )只有极大值而无极小值C .当-e <k<0时,方程f (x )=k 有且只有两个实根D .若当x ∈[t ,+∞)时,f (x )max =5e 2,则t 的最大值为2三、填空题:本题共4小题,每小题5分,共20分.13.(考点:不等式的解法,★)若关于x 的不等式ax 2+bx+4>0的解集为{x |-2<x <1},则2a-b= . 14.(考点:导数的几何意义,★★)若函数f (x )=ax+ln x 的图象在点(12,f (12))处的切线与直线x-3y+1=0垂直,则实数a= .15.(考点:不等式的综合应用,★★★)已知x>0,y>0,且1x +4y =2,若x+y ≥m 2+32m 恒成立,则实数m 的取值范围是 .16.(考点:导数的综合应用,★★★)设函数f (x )=x 2+1x,g (x )=x ex ,则函数g (x )=xex (x>0)的最大值为 ;若对任意x 1,x 2∈(0,+∞),不等式g (x 1)k≤f (x 2)k+1恒成立,则正数k 的最小值是 .答案解析：函数、导数与不等式(B)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(考点:分段函数求值,★)设函数f (x )={32-x ,x ≤0,5-log 3x ,x >0,则f (f (-2))=( ).A .-1B .1C .2D .3【解析】f (f (-2))=f (32-(-2))=f (34)=5-log 334=1.故选B . 【答案】B2.(考点:函数的奇偶性,★★)已知函数f (x )是定义域为R 的奇函数,当x ≥0时,f (x )=-x 2+x+b ,则当x<0时,f (x )的解析式为( ). A .f (x )=x 2+x B .f (x )=x 2-x C .f (x )=-x 2+xD .f (x )=-x 2-x【解析】由题意可得,当x=0时,f (0)=b=0,因为当x<0时,-x>0,所以f (-x )=-(-x )2-x=-x 2-x , 所以当x<0时,f (x )=-f (-x )=-(-x 2-x )=x 2+x. 故选A . 【答案】A3.(考点:函数值比较大小,★★)已知a=(1e )-4,b=332,c=log 0.25,则a ,b ,c 的大小关系是( ).A .a<c<bB .c<b<aC .b<c<aD .c<a<b【解析】∵1<b=332<e 4=a ,c=log 0.25<0,∴c<b<a.故选B .【答案】B4.(考点:函数单调性的应用,★★)若函数f (x )={(5-a )x +2,x ≤2,a x -1,x >2在定义域内单调递增,则实数a 的取值范围是( ). A .[4,5) B .(4,5) C .(3,5)D .(2,5)【解析】由题意可得{5-a >0,a >1,(5-a )×2+2≤a ,解得4≤a<5,所以实数a 的取值范围是[4,5). 故选A . 【答案】A5.(考点:均值不等式,★★)设a>0,b>0,lg 4是lg 2a 与lg 8b 的等差中项,则1a +1b 的最小值为( ). A .2√2B .2+√32C .√32D .9【解析】∵lg 4是lg 2a 与lg 8b 的等差中项,∴2lg 4=lg 2a +lg 8b ,即lg 16=lg(2a ·8b )=lg 2a+3b ,∴a+3b=4.∴1a +1b =(1a +1b )(a+3b )×14=1+14×(ab +3ba)≥1+√32=2+√32,当且仅当a b =3b a,即a=2√3-2,b=6-2√33时取等号.∴1a +1b 的最小值为2+√32.【答案】B6.(考点:利用导数研究函数的极值,★★★)若x=1是函数f (x )=(12x 2+2ax -2)e x-1的极值点,则f (x )的极小值为( ). A .2e -3B .-2e -3C .-54 D .54【解析】由题意可得f'(x )=(x+2a )e x-1+12x 2+2ax-2e x-1=[12x 2+(2a +1)x +2a -2]e x-1,因为f'(1)=0,所以a=18,f (x )=12x 2+14x-2e x-1,f'(x )=(12x 2+54x -74)e x-1.令f'(x )>0,解得x<-72或x>1;令f'(x )<0,解得-72<x<1.所以f (x )在(-∞,-72),(1,+∞)上单调递增,在(-72,1)上单调递减,所以f (x )的极小值为f (1)=(12+14-2)e 1-1=-54.故选C . 【答案】C7.(考点:函数的零点及应用,★★★)已知函数f (x )={3x +4,x ≤0,|22-x -2|,x >0,若函数y=f (x )-a 有三个零点,则实数a 的取值范围是( ).A .[0,2]B .(0,2)C .(-∞,0]∪[2,+∞)D .(-∞,0)∪(2,+∞) 【解析】画出f (x )的图象如图所示.要使函数y=f (x )-a 有三个零点,则函数f (x )的图象与直线y=a 有三个交点,结合图象可知实数a 的取值范围是(0,2). 【答案】B8.(考点:导数的综合应用,★★★)已知定义在R 上的奇函数f (x )满足f (-1)=1.若f (x )的导函数f'(x )满足f'(x )<x 3+2x ,则不等式f (x )+94<x 44+x 2的解集为( ).A .(0,+∞)B .(0,1)C .(1,+∞)D .(-∞,1)【解析】设g (x )=x 44+x 2-f (x ),则g'(x )=x 3+2x-f'(x ).因为f'(x )<x 3+2x ,所以g'(x )>0, 所以g (x )在R 上单调递增.又f (x )是定义在R 上的奇函数,则f (1)=-f (-1)=-1, 所以g (1)=14+1+1=94,所以不等式f (x )+94<x 44+x 2等价于不等式g (x )>g (1),解得x>1. 故选C . 【答案】C二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.(考点:不等式的综合应用,★★)若a ,b 为正实数,则a>b 的充要条件可以为( ). A .1a <1bB .ln a<ln bC .a ln a<b ln bD .a-b<e a -e b【解析】对于A 选项,因为a ,b 为正实数,所以1a <1b ⇔a>b ,故A 选项符合题意; 对于B 选项,因为a ,b 为正实数,所以ln a<ln b ⇔a<b ,故B 选项不符合题意;对于C 选项,取a=e 2>b=e,则e 2ln e 2=2e 2,eln e =e,即a ln a<b ln b 不成立,故C 选项不符合题意;对于D 选项,令y=e x -x ,因为y'=e x -1,当x>0时,y'>0,所以y=e x -x 在(0,+∞)上单调递增,即a>b ⇔e a -a>e b -b ⇔a-b<e a -e b ,故D 选项符合题意.故选AD . 【答案】AD10.(考点:函数的基本性质,★★)下列命题正确的是( ). A .若函数f (x )在(2020,2021)上有零点,则一定有f (2020)·f (2021)<0 B .函数y=2是偶函数C .若函数f (x )=lg(ax 2+5x+5)的值域为R,则实数a 的取值范围是[0,54] D .若函数f (x )满足条件f (x )-4f (1x )=x ,(x ∈R,x ≠0),则f (x )=-115(x +4x)(x ≠0)【解析】对于选项A,函数f (x )在(2020,2021)上有零点,不一定有f (2020)·f (2021)<0,选项A 错误; 对于选项B,函数y=√16-x2的定义域为(-4,4),且f (x )=√16-x2=√16-x2=√16-x 2,满足f (-x )=f (x ),所以f (x )是偶函数,选项B 正确;对于选项C,函数f (x )=lg(ax 2+5x+5)的值域为R,当a=0时,满足条件, 当a ≠0时,由{a >0,Δ=25-20a ≥0,解得0<a ≤54,综上,实数a 的取值范围是[0,54],选项C 正确;对于选项D,函数f (x )满足条件f (x )-4f (1x )=x (x ∈R,x ≠0), 则f (1x )-4f (x )=1x ,解得f (x )=-115(x +4x )(x ≠0),选项D 正确. 故选BCD . 【答案】BCD11.(考点:均值不等式,★★)下列说法正确的是( ). A .若x ,y>0,x+y=4,则2x +2y 的最小值为8B .若x<12,则函数y=2x+12x -1的最大值为-2C .若x ,y>0,x+y+xy=3,则xy 的最小值为1D .函数y=22的最小值为4【解析】对于选项A,x ,y>0,x+y=4,则2x +2y ≥2√2x+y =8,当且仅当2x =2y ,即x=y 时取等号,所以2x +2y 的最小值为8,故选项A 正确;对于选项B,当x<12时,函数y=2x+12x -1=-(1-2x +11-2x )+1≤-2√(1-2x )·11-2x +1=-1,当且仅当1-2x=11-2x ,即x=0时取等号,故选项B 错误;对于选项C,若x ,y>0,x+y+xy=3,则xy+2√xy ≤3,即0<√xy ≤1,故xy ≤1,所以xy 的最大值为1,故选项C 错误; 对于选项D,函数y=2√x 2+2=√x 2+2+√x 2+2≥2√√x 2+2·√x 2+2=4,当且仅当√x 2+2=√x 2+2,即x=±√2时取等号,故选项D 正确. 故选AD . 【答案】AD12.(考点:导数的综合应用,★★★)已知函数f (x )=x 2+x -1e x,则下列结论正确的是( ).A .函数f (x )只有一个零点B .函数f (x )只有极大值而无极小值C .当-e <k<0时,方程f (x )=k 有且只有两个实根D .若当x ∈[t ,+∞)时,f (x )max =5e 2,则t 的最大值为2 【解析】对于选项A,f (x )=0⇒x 2+x-1=0,解得x=-1±√52,所以A 选项错误;对于选项B,f'(x )=-x 2-x -2e x=-(x+1)(x -2)e x,令f'(x )>0,得-1<x<2;令f'(x )<0,得x<-1或x>2,所以函数f (x )的单调递减区间是(-∞,-1),(2,+∞),函数f (x )的单调递增区间是(-1,2),所以f (-1)是函数的极小值,f (2)是函数的极大值,所以B 选项错误;对于选项C,当x →+∞时,f (x )→0,根据选项B 可知,函数f (x )的最小值是f (-1)=-e,再根据单调性可知,当-e <k<0时,方程f (x )=k 有且只有两个实根,所以选C 项正确;对于选项D,因为f (2)=5e 2,结合图象可知,t 的最大值是2,所以D 选项正确.故选CD . 【答案】CD三、填空题:本题共4小题,每小题5分,共20分.13.(考点:不等式的解法,★)若关于x 的不等式ax 2+bx+4>0的解集为{x |-2<x <1},则2a-b= . 【解析】由题意可知-2和1是方程ax 2+bx+4=0的两根, 所以{4a =-2,-b a =-1,解得{a =-2,b =-2,所以2a-b=-2. 【答案】-214.(考点:导数的几何意义,★★)若函数f (x )=ax+ln x 的图象在点(12,f (12))处的切线与直线x-3y+1=0垂直,则实数a= .【解析】因为函数f (x )=ax+ln x 的导数为f'(x )=a+1x , 所以f (x )的图象在x=12处的切线斜率为a+2, 由该切线与直线x-3y+1=0垂直, 可得a+2=-3, 解得a=-5. 【答案】-515.(考点:不等式的综合应用,★★★)已知x>0,y>0,且1x +4y =2,若x+y ≥m 2+32m 恒成立,则实数m 的取值范围是 .【解析】由1x +4y =2可得x+y=(x+y )·(1x +4y )×12=52+12(yx +4x y)≥52+12×2√y x ·4x y =92,当且仅当y x =4x y ,即x=32,y=3时等号成立.又x+y ≥m 2+32m 恒成立,所以m 2+32m ≤(x +y )min , 故m 2+32m ≤92,即2m 2+3m-9≤0,解得-3≤m ≤32. 【答案】[-3,32]16.(考点:导数的综合应用,★★★)设函数f (x )=x 2+1x,g (x )=x e x ,则函数g (x )=xe x (x>0)的最大值为 ;若对任意x 1,x 2∈(0,+∞),不等式g (x 1)k≤f (x 2)k+1恒成立,则正数k 的最小值是 .【解析】∵g (x )=xex (x>0),∴g'(x )=e x -x ·e x (e x )2=1-x e x ,由g'(x )>0可得0<x<1,此时函数g (x )单调递增, 由g'(x )<0可得x>1,此时函数g (x )单调递减,∴g (x )的最大值为g (1)=1e .若对任意x 1,x 2∈(0,+∞),不等式g (x 1)k≤f (x 2)k+1恒成立,则等价为g (x 1)f (x 2)≤kk+1恒成立,f (x )=x 2+1x=x+1x ≥2√x ·1x =2,当且仅当x=1x ,即x=1时等号成立,故f (x )的最小值为2,且g (x )的最大值为g (1)=1e ,则g (x 1)f (x 2)的最大值为1e2=12e . 由k k+1≥12e ,得k (2e -1)≥1,即k ≥12e -1,所以k 的最小值为12e -1.【答案】1e 12e -1。

2021年高考理科数学小题狂练3（非新高考地区）解析版学校:___________姓名：___________班级：___________考号：___________注：满分80份，选择题12小题，填空题4小题，每小题5分。

限时：40分钟 一、单选题（每小题5分，共12小题，满分60分）1．已知全集U =R ，104x A x x ⎧⎫+=≥⎨⎬-⎩⎭，则UA（ ）A ．{}14x x -<< B ．{1x x ≤-或}4x ≥C ．{}14x x -≤≤D ．{}14x x -<≤【答案】D 【解析】 【分析】求出集合A ，利用补集的定义可求得集合UA .【详解】U R =，{1014x A xx x x ⎧⎫+=≥=≤-⎨⎬-⎩⎭或}4x >，{}14U A x x ∴=-<≤． 故选：D ． 【点睛】本题考查补集的计算，同时也考查了分式不等式的求解，考查计算能力，属于基础题. 2．i 是虚数单位，则231i i i +++=（ ） A ．1 B ．i C ．1-i D ．0【答案】D 【解析】试题分析：根据题意，2311+i-1-i=0i i i +++=,故可知答案为0，选D. 考点：复数的运算点评：主要是考查了虚数单位的运算，属于基础题3．某天的值日工作由4名同学负责，且其中1人负责清理讲台，另1人负责扫地，其余2人负责拖地，则不同的分工共有（ ） A ．6种 B ．12种 C ．18种 D ．24种【答案】B【解析】方法数有1134C C 12=种.故选B.4．函数()f x 的图象如图所示，则函数()f x 的解析式可能为（ ）A ．()22x xf x -=-B ．2()x e ef x x-= C ．31()f x x x =- D ．1()ln ||f x x x=-【答案】B 【解析】 【分析】由函数的定义域、奇偶性、单调性及函数图像的特点一一进行判断可得答案. 【详解】解：A 选项，由函数图像可得在0x =处没有定义，故排除A ； C 选项，由函数图像可得函数不为奇函数，故排除C ；D 选项，由函数图像可得当x →+∞时，函数变化趋势不符，1()ln ||f x x x=-越来越平（增加越来越慢），而不会向上扬起（增加越来越快）, 故排除D ； 故选：B. 【点睛】本题主要考查函数图像的识别及函数的定义域、单调性、奇偶性等基本性质，属于基础题型.5．设0.213a ⎛⎫= ⎪⎝⎭，131log 5b =，ln5c =，则a 、b 、c 的大小关系是（ ）A ．a b c >>B ．c b a >>C ．b c a >>D ．a c b >>【答案】B【解析】 【分析】利用指数函数和对数函数的单调性比较a 、b 、c 三个数与0和1的大小关系，利用换底公式和不等式的基本性质可得出b 、c 的大小关系，进而可得出这三个数的大小关系. 【详解】指数函数13x y ⎛⎫= ⎪⎝⎭在R 上为减函数，则0.2110133⎛⎫⎛⎫<<= ⎪⎪⎝⎭⎝⎭，即01a <<； 对数函数13log y x =在()0,∞+上为减函数，则113311log log 153b =>=； 对数函数ln y x =在()0,∞+上为增函数，则ln5ln 1c e =>=.1331ln 5log log 5ln 55ln 3b c ∴===<=. 因此，c b a >>. 故选：B. 【点睛】本题考查指数式和对数式的大小比较，一般利用指数函数和对数函数的单调性，结合中间值法来比较，考查推理能力，属于中等题.6．《周髀算经》有这样一个问题：从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸，雨水、惊蛰、春分、清明日影之和为三丈二尺，前七个节气日影之和为七丈三尺五寸，问立夏日影长为（ ） A ．七尺五寸 B ．六尺五寸 C ．五尺五寸 D ．四尺五寸【答案】D 【解析】 【分析】利用等差数列的通项公式以及求和公式列出方程组，求出首项和公差，由此可求得立夏日影长. 【详解】从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸，雨水、惊蛰、春分、清明日影之和为三丈二尺，前七个节气日影之和为七丈三尺五寸，设十二节气第()N n n *∈个节气的日影长为n a ，则数列{}n a 为等差数列，设其公差为d ，前n 项和为n S，则567817114223276772173.52a a a a a dS a d a d+++=+=⎧⎪⎨⨯=+=+=⎪⎩，解得12721ad⎧=⎪⎨⎪=-⎩，1012799922a a d∴=+=-=，因此，立夏日影长为四尺五寸.故选：D.【点睛】本题考查新文化中的等差数列问题，考查等差数列与前n项和中基本量的计算，考查计算能力，属于基础题.7．我们打印用的A4纸的长与宽的比约为2，之所以是这个比值，是因为把纸张对折，得到的新纸的长与宽之比仍约为2，纸张的形状不变．已知圆柱的母线长小于底面圆的直径长（如图所示），它的轴截面ABCD为一张A4纸，若点E为上底面圆上弧AB的中点，则异面直线DE与AB所成的角约为（）A．6πB．4πC．3πD．23π【答案】C【解析】【分析】设CD的中点为O，过E作EF⊥底面⊙O，连接OE，OF，证明OD⊥OE，计算tan∠EDO即可得出答案．【详解】∵AB//CD，∴∠EDC（或补角）为异面直线DE与AB所成的角，设CD的中点为O，过E作EF⊥底面⊙O，连接OE，OF，∵E是AB的中点，∴F是CD的中点，∴CD⊥OF，又EF⊥平面⊙O，∴EF⊥CD，EF OF F=∴CD ⊥平面OEF ，∴OD ⊥OE ． 设AD ＝1，则CD 2=，故OF 2=，EF ＝1， 于是OE 22261()22=+=， ∴tan ∠EDO 6232OEOD ===， ∴∠EDO 3π=．故选：C ． 【点睛】本题考查了异面直线所成的角，解题的关键是找出与异面直线所成角相等的相交直线所成的角，此题要求有一定的计算能力，属于中档题.8．已知向量(),12OA k =，()4,5OB =，(),10OC k =-，且A ，B ，C 三点共线，则k 的值是（ ） A ．23-B ．43C ．12D ．13【答案】A 【解析】 【分析】首先求向量AB 和AC ，再将三点共线转化成向量共线求参数的取值. 【详解】()4,7AB OB OA k =-=--，()2,2AC OC OA k =-=--.因为A ，B ，C 三点共线，所以,AB AC 共线， 所以()()2472k k -⨯-=-⨯-，解得23k =-.故选：A【点睛】本题考查根据三点共线求参数的取值范围，重点考查向量共线的公式，属于基础题型.9．《高中数学课程标准》(2017 版)规定了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平，现以六大素养为指标对二人进行了测验，根据测验结果绘制了雷达图(如图，每项指标值满分为5分，分值高者为优)，则下面叙述正确的是（）(注:雷达图(Radar Chart)，又可称为戴布拉图、蜘蛛网图(Spider Chart)，可用于对研究对象的多维分析)A．甲的数据分析素养高于乙B．甲的数学建模素养优于数学抽象素养C．乙的六大素养中逻辑推理最差D．乙的六大素养整体水平优于甲【答案】D【解析】【分析】根据雷达图，依次判断每个选项的正误得到答案.【详解】根据雷达图得甲的数据分析素养低于乙，所以A错误根据雷达图得甲的数学建模素养等于数学抽象素养，所以B错误根据雷达图得乙的六大素养中数学建模和数学抽象最差，所以C错误根据雷达图得乙整体为27分，甲整体为22分，乙的六大素养整体水平优于甲，所以D正确故答案选D【点睛】本题考查了雷达图，意在考查学生解决问题的能力.10．如图，矩形OABC内的阴影部分由曲线f(x)＝sin x(x∈(0，π))及直线x＝a(a∈(0，π))与x 轴围成，向矩形OABC内随机投掷一点，若该点落在阴影部分的概率为316，则a的值为( ) A．712πB．23πC．34πD．56π【答案】B【解析】依题意，阴影部分的面积为sinaxdx⎰＝(－cosx)|a＝－cosa＋cos0＝1－cosa，由几何概型知识得，1cos8aaa-⋅＝316，即cosa＝－12，而a∈(0，π)，故a＝23π．11．设1F和2F为双曲线()222210,0x ya ba b-=>>的两个焦点，若1F，2F，()0,2P b是正三角形的三个顶点，则双曲线的离心率为( )A．2 B．32C．52D．3【答案】A【解析】试题分析：如图，()2222211tan6034343PO POb c c a cFO FO=∴==∴-=222442c a e e ∴=∴=∴=考点：双曲线方程及性质 12．已知函数()()sin 06f x A x a a A ωπ⎛⎫=+-<< ⎪⎝⎭在区间70,3ωπ⎡⎤⎢⎥⎣⎦有三个零点1x ，2x ，3x ，且123x x x <<，若123523x x x π++=，则()f x 的最小正周期为（ ） A ．2πB ．23πC ．πD ．43π【答案】C 【解析】 【分析】根据题意，知当7π3x ω=时，π5π62x ω+=，由对称轴的性质可知122π3x x ω+=和238π3x x ω+=，即可求出w ，即可求出()f x 的最小正周期. 【详解】解：由于()()sin 06f x A x a a A ωπ⎛⎫=+-<< ⎪⎝⎭在区间70,3ωπ⎡⎤⎢⎥⎣⎦有三个零点1x ，2x ，3x ， 当7π3x ω=时，π5π62x ω+=， ∴由对称轴可知1x ，2x 满足12πππ2662x x ωω+++=⨯， 即122π3x x ω+=. 同理2x ，3x 满足23ππ3π2662x x ωω+++=⨯，即238π3x x ω+=， ∴12310π5π233x x x ω++==，2ω=， 所以最小正周期为：2ππ2T ==. 故选：C . 【点睛】本题考查正弦型函数的最小正周期，涉及函数的对称性的应用，考查计算能力.二、填空题（每小题5分，共4小题，满分20分） 13．已知α为锐角，且1cos 63πα⎛⎫+= ⎪⎝⎭，则cos α=_______． 322+【解析】 【分析】利用同角三角函数的基本关系可得22sin 63πα⎛⎫+= ⎪⎝⎭，再由cos 66ππαα⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦，利用两角差的余弦公式即可求解. 【详解】由α为锐角，且1cos 63πα⎛⎫+= ⎪⎝⎭， 所以222sin 1cos 663ππαα⎛⎫⎛⎫+=-+=⎪ ⎪⎝⎭⎝⎭， 所以cos cos cos cos sin sin 666666ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦1322132232+==322+【点睛】本题考查了两角差的余弦公式、同角三角函数的基本关系，需熟记公式，属于基础题． 14．如图的几何体，是在用密度等于38/g cm 的钢材铸成的底面直径和高都等于()221cm 的圆维内部挖去一个正方体后的剩余部分(正方体四个顶点在圆锥母线上，另四个顶点在圆锥底面上)，这个几何体的质量等于_____g (对小数部分四舍五入进行取整).【答案】172【解析】【分析】设被挖去的正方体的棱长为x cm，由（半）轴截面中的直角三角形相似，即PBF△相似于HBC，利用PF PBHC HB=，代入数据计算求得2x=.再利用体积公式求得最后结果.【详解】如图，设被挖去的正方体的棱长为x cm，由（半）轴截面中的直角三角形相似，即PBF△相似于HBC，由21HC=+，()221HB=+，2,2xHG PF HP x===，则PF PBHC HB=，得(()2221221221x x+-=++，解得：2x=.则该模型的体积()()2313.1421221221.453V≈⨯⨯+⨯+-≈，所以制作该模型所需材料质量约为21.458172m Vρ=≈⨯≈.故答案为：172.【点睛】本题考查立体几何的体积的求法，结合相似的知识点，考查运算求解能力，属于中档题. 15．设()f x是定义在R上的函数，其导函数为()'f x，若()()'1f x f x+>，()02020f=，则不等式()2019x xe f x e>+(其中e为自然对数的底数)的解集为__________.原创精品资源学科网独家享有版权，侵权必究！11【答案】()0,∞+【解析】【分析】构造函数()()2019x x g x e f x e =--，由题意，只需解()0>g x 即可，利用导数研究()g x 的单调性即可得到答案.【详解】设()()2019x x g x e f x e =--，不等式()2019x xe f x e >+的解等价于不等式()0>g x 的解， 因为''()(()()1)0x g x e f x f x =+->，所以()g x 在R 上单调递增，又(0)(0)120190g f =--=，所以()0(0)g x g >=，所以0x >，所以原不等式的解集为()0,∞+故答案为：()0,∞+【点睛】本题主要考查构造函数利用函数的单调性解不等式，考查学生转化与化归思想，是一道中档题. 16．已知抛物线2:4C y x =，其焦点为F ，准线为l ，P 为抛物线C 上第一象限内的点，过点P 作l 的垂线，垂足为Q .当PFQ △的周长为12时，PFQ △的面积为______. 【答案】43【解析】【分析】设||PQ a =，用a 表示出P ，Q 的坐标，根据PFQ △的周长为12，求得a ，判断PFQ ∆的形状，进而求PFQ △的面积.【详解】由24y x =得焦点(1,0)F ，准线:1l x =-.如图所示，试卷第12页，总12页设||||PQ PF a ==，由抛物线性质知||||1=PF OF ，即1a >， ∴(1,1)--P a a ，(1,1)--Q a . ∴2||4(21)2=+-=QF a a ∵PFQ △的周长为12，∴2212+=a a ，解得4a =.∴||4QF =，∴PFQ △是边长为4的等边三角形.∴PFQ △的面积为234434=故答案为：3【点睛】本题主要考查抛物线的方程及性质，还考查了数形结合的思想和运算求解的能力，属于中档题.。

2021-2022年（新课程）高中数学二轮复习 精选考前小题狂练3 理 新人教版一、选择题(本大题共12小题，每小题5分，共60分) 1．已知全集U ＝R ，集合A ＝{1,2,3,4,5}，B ＝[2，＋∞)， 则图中阴影部分所表示的集合为( )．A ．{0,1,2}B ．{0,1}C ．{1,2}D ．{1} 2．命题“∃x ∈R ，x 3－2x ＋1＝0”的否定是( )．A ．∃x ∈R ，x 3－2x ＋1≠0 B ．不存在x ∈R ，x 3－2x ＋1≠0 C ．∀x ∈R ，x 3－2x ＋1＝0 D ．∀x ∈R ，x 3－2x ＋1≠0 3．设i 是虚数单位，则i 1－i3＝( )．A.12－12i B ．1＋12iC.12＋12i D ．1－12i4．在等比数列{a n }中，a 1＝8，a 4＝a 3a 5，则a 7＝( )．A.116 B.18 C.14 D.125．要得到函数y ＝sin ⎝⎛⎭⎪⎫2x －π3的图象，只需将函数y ＝sin 2x 的图象 ( )．A ．向左平移π12个单位B ．向右平移π12个单位C ．向左平移π6个单位D ．向右平移π6个单位6．设随机变量X 服从正态分布N (0,1)，P (X >1)＝p ，则P (X >－1)＝( )．A ．pB ．1－pC ．1－2pD ．2p7．在△ABC 中，C ＝90°，且CA ＝CB ＝3，点M 满足BM →＝2MA →，则CM →·CB →等于( )．A ．2B ．3C ．4D ．68．某同学设计右面的程序框图用以计算 12＋22＋32＋…＋202的值，则在判断 框中应填写 ( )．A ．i ≤19B ．i ≥19C ．i ≤20D ．i ≤219．已知函数f (x )＝sin x －12x (x ∈[0，π])，那么下列结论正确的是( )．A ．f (x )在⎣⎢⎡⎦⎥⎤0，π2上是增函数B ．f (x )在⎣⎢⎡⎦⎥⎤π6，π上是减函数C ．∃x ∈[0，π]，f (x )>f ⎝ ⎛⎭⎪⎫π3D ．∀x ∈[0，π]，f (x )≤f ⎝ ⎛⎭⎪⎫π310．函数y ＝esin x(－π≤x ≤π)的大致图象为( )．11．过点(－2,0)且倾斜角为π4的直线l 与圆x 2＋y 2＝5相交于M 、N 两点，则线段MN 的长为( )．A ．2 2B ．3C ．2 3D ．612．已知抛物线y 2＝4x 的准线过双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左顶点，且此双曲线的一条渐近线方程为y ＝2x ，则双曲线的焦距等于( )．A. 5 B ．2 5 C. 3D ．2 3二、填空题(本大题共4小题，每小题4分，共16分)13．在区间[0,9]上随机取一实数x ，则该实数x 满足不等式1≤log 2x ≤2的概率为________． 14．一个棱锥的三视图如图所示， 则这个棱锥的体积为________．15．已知双曲线kx 2－y 2＝1的一条渐近线与直线2x ＋y ＋1＝0垂直，那么双曲线的离心率为________．16．已知函数f (x )＝3 sin ⎝⎛⎭⎪⎫ωx －π6(ω>0)和g (x )＝2 cos(2x ＋φ)＋1的图象的对称轴完全相同．若x ∈⎣⎢⎡⎦⎥⎤0，π2，则f (x )的取值范围是________． 参考答案【小题狂练(三)】1．D[阴影部分的元素x ∈A 且x ∉B ，即A ∩∁U B ，选项D 符合要求．] 2．D [根据含有量词的命题的否定知D 正确．] 3．C [i 1－i 3＝i 1＋i ＝i·1－i 1＋i 1－i ＝1＋i 2＝12＋i 2，故选C.] 4．B[由题意知，a 4＝1，所以q ＝12，故a 7＝a 1q 6＝18.]5．D [要得到函数y ＝sin ⎝⎛⎭⎪⎫2x －π3，只需将函数y ＝sin 2x 中的x 减去π6，即得到y ＝sin 2⎝ ⎛⎭⎪⎫x －π6＝sin ⎝⎛⎭⎪⎫2x －π3.]6．B [∵P (X <－1)＝P (X >1)，则P (X >－1)＝1－p .]7．B [CM →·CB →＝(CB →＋BM →)·CB →＝|CB →|2＋BM →·CB →＝9＋3×22×cos 135°＝3.] 8．C [由计算式可知程序到i ＝20终止，因此判断框中应填i ≤20.]9．D [注意到f ′(x )＝cos x －12，当x ∈⎝ ⎛⎭⎪⎫0，π3时，f ′(x )>0；当x ∈⎝ ⎛⎭⎪⎫π3，π时，f ′(x )<0，因此函数f (x )在⎝ ⎛⎭⎪⎫0，π3上是增函数，在⎝ ⎛⎭⎪⎫π3，π上是减函数，f (x )在[0，π]内的最大值是f ⎝ ⎛⎭⎪⎫π3，即∀x ∈[0，π]，都有f (x )≤f ⎝ ⎛⎭⎪⎫π3，因此D 正确．] 10．D [取x ＝－π，0，π这三个值，可得y 总是1，故排除A 、C ；当0<x <π2时，sinx 是增函数，e x 也是增函数，故y ＝e sin x也是增函数，故选D.]11．C [直线l 的方程为：x －y ＋2＝0，圆心(0,0)到直线l 的距离d ＝22＝ 2.则|MN |＝252－22＝2 3.]12．B [∵抛物线y 2＝4x 的淮线x ＝－1过双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左顶点，∴a＝1，∴双曲线的渐近线方程为y ＝±bax ＝±bx .∵双曲线的一条渐近线方程为y ＝2x ，∴b ＝2，∴c ＝a 2＋b 2＝5，∴双曲线的焦距为2 5.]13．解析 由1≤log 2x ≤2得：2≤x ≤4，故所求概率为29.答案 2914．解析 依题意得，该棱锥的体积等于13×(3×4)×3＝12.答案 1215．解析 双曲线kx 2－y 2＝1的渐近线方程为y ＝±kx ， 直线2x ＋y ＋1＝0的斜率为－2，∴k ×(－2)＝－1，即k ＝14.∴e ＝c a＝22＋124＝52. 答案5216．解析 由对称轴完全相同知两函数周期相同，∴ω＝2，∴f (x )＝3 sin ⎝⎛⎭⎪⎫2x －π6， 由x ∈⎣⎢⎡⎦⎥⎤0，π2，得－π6≤2x －π6≤56π，∴－32≤f (x )≤3.答案 ⎣⎢⎡⎦⎥⎤－32，3J35039 88DF 裟 30574 776E 睮~32722 7FD2 習A35932 8C5C 豜34955 888B 袋24854 6116 愖lI<22537 5809 堉28704 7020 瀠。

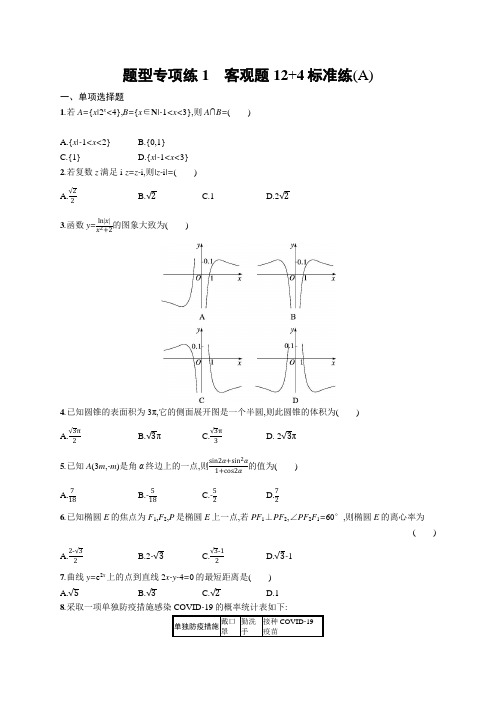
题型专项练1 客观题12+4标准练(A)一、单项选择题1.若A={x|2x <4},B={x ∈N |-1<x<3},则A ∩B=( )A.{x|-1<x<2}B.{0,1}C.{1}D.{x|-1<x<3}2.若复数z 满足i·z=z-i,则|z-i |=( ) A.√22 B.√2C.1D.2√23.函数y=ln |x |x 2+2的图象大致为( )4.已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的体积为( ) A.√3π2B.√3πC.√3π3D. 2√3π5.已知A (3m ,-m )是角α终边上的一点,则sin2α+sin 2α1+cos2α的值为( )A.718B.-518C.-52D.726.已知椭圆E 的焦点为F 1,F 2,P 是椭圆E 上一点,若PF 1⊥PF 2,∠PF 2F 1=60°,则椭圆E 的离心率为 ( )A.2-√32B.2-√3C.√3-12D.√3-17.曲线y=e 2x 上的点到直线2x-y-4=0的最短距离是( ) A.√5B.√3C.√2D.18.采取一项单独防疫措施感染COVID -19的概率统计表如下:一次核酸检测的准确率为1-10p.某家庭有3口人,他们每个人只戴口罩,没有做到勤洗手也没有接种COVID -19疫苗,感染COVID -19的概率都为0.01.这3个人不同人的核酸检测结果,以及其中任何一个人的不同次核酸检测结果都是互相独立的.他们3人都落实了表中的三项防疫措施,而且共做了10次核酸检测.以这家人的每个人每次核酸检测被确诊感染COVID -19的概率为依据,这10次核酸检测中,若有X 次结果为确诊,则X 的数学期望为( ) A.1.98×10-6 B.1.98×10-7C.1.8×10-7D.2.2×10-7二、多项选择题9.空气质量指数按大小分为五个等级,指数越大说明污染的情况越严重,对人体危害越大,指数范围在区间[0,50],[51,100],[101,200],[201,300],[301,500]上分别对应“优”“良”“轻度污染”“中度污染”“重度污染”五个等级,某市连续14天的空气质量指数变化趋势如图所示,下列说法正确的是( )A.从2日到5日空气质量越来越好B.这14天中空气质量指数的极差为195C.这14天中空气质量指数的中位数是103.5D.这14天中空气质量指数为“良”的频率为31410.已知△ABC 是边长为2的正三角形,该三角形重心为点G ,P 为△ABC 所在平面内任一点,则下列结论正确的是( ) A.|AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ |=2B.AB⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =2 C.PA⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =3PG ⃗⃗⃗⃗⃗D.|AB⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ |=|AB ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ | 11.已知点P (2,4),若过点Q (4,0)的直线l 交圆C :(x-6)2+y 2=9于A ,B 两点,R 是圆C 上一动点,则( ) A.|AB|的最小值为2√5 B.点P 到直线l 的距离的最大值为2√5C.PQ⃗⃗⃗⃗⃗ ·PR ⃗⃗⃗⃗⃗ 的最小值为12-2√5D.|PR|的最大值为4√2+312.已知三棱柱ABC-A 1B 1C 1为正三棱柱,且AA 1=2,AB=2√3,D 是B 1C 1的中点,点P 是线段A 1D 上的动点,则下列结论正确的是( )A.正三棱柱ABC-A 1B 1C 1外接球的表面积为20πB.若直线PB 与底面ABC 所成角为θ,则sin θ的取值范围为[√77,12] C.若A 1P=2,则异面直线AP 与BC 1所成的角为π4D.若过BC 且与AP 垂直的截面α与AP 交于点E ,则三棱锥P-BCE 的体积的最小值为√32三、填空题13.已知(√x 3-2a x)8的展开式中常数项为112,则实数a 的值为 .14.已知抛物线C :y 2=2px (p>0)的焦点为F ,A 为抛物线C 上一点,以F 为圆心,FA 为半径的圆交抛物线C 的准线于B ,D 两点,若A ,F ,B 三点共线,且|AF|=3,则抛物线C 的准线方程为 . 15.已知函数f (x )=ln(x 2+1)+e x +e -x ,则不等式f (x-2)-f (2x+1)≤0的解集为 . 16.定义在区间(0,+∞)上的函数y=f (x )满足:①当x ∈[1,3)时,f (x )={x -1,1≤x ≤2,3-x ,2<x <3;②f (3x )=3f (x ).(1)f (6)= ;(2)若函数F (x )=f (x )-a 的零点从小到大依次记为x 1,x 2,…,x n ,…,则当a ∈(1,3)时,x 1+x 2+…+x 2n-1+x 2n =.考前强化练题型专项练题型专项练1 客观题12+4标准练(A)1.B 解析 由2x <4,得x<2,所以A={x|x<2}.又B={0,1,2},所以A ∩B={0,1}.2.A 解析 因为i ·z=z-i,所以z=i1-i =i (1+i )(1-i )(1+i )=-1+i2,所以z-i =-1-i2=-12−12i .故|z-i |=√(-12)2+(-12)2=√22.3.B 解析 设y=f (x )=ln |x |x 2+2,则函数f (x )的定义域为{x|x ≠0},关于原点对称.又f (-x )=ln |-x |(-x )2+2=f (x ),所以函数f (x )为偶函数,排除AC;当x ∈(0,1)时,ln |x|<0,x 2+2>0 ,所以f (x )<0,排除D . 故选B .4.C解析设圆锥的底面半径为r(r>0),母线长为l(l>0),由于它的侧面展开图是一个半圆,所以2πr=πl,即l=2r,所以该圆锥的表面积S=πr2+πrl=3πr2=3π,解得r=1,所以圆锥的高h=√l2-r2=√3,所以圆锥的体积V=13S底·h=13×π×12×√3=√3π3.5.B解析因为A(3m,-m)是角α终边上的一点,所以tan α=-m3m =-13,所以sin2α+sin2α1+cos2α=2sinαcosα+sin2α2cos2α=tan α+12tan2α=-13+12×(-13)2=-518.6.D解析在△F1PF2中,∠F1PF2=90°,∠PF2F1=60°,设|PF2|=m(m>0),则2c=|F1F2|=2m,|PF1|=√3m,又由椭圆定义可知2a=|PF1|+|PF2|=(√3+1)m,则离心率e=ca=2c2a=(√3+1)m=√3+1=√3-1.7.A解析因为y=e2x,所以y'=2e2x,设曲线y=e2x在点P(x0,e2x0)处的切线与直线2x-y-4=0平行,则2e2x0=2,所以2x0=0,x0=0,切点P(0,1),曲线y=e2x上的点到直线2x-y-4=0的最短距离即为切点P到直线2x-y-4=0的距离d=√5=√5.8.B解析根据条件,p=0.01.一个人落实了表中三项防疫措施后,感染COVID-19的概率为145(1-p)p·p100=2.2×10-8,一次核酸检测的准确率为1-10×0.01=0.9,这个人再进行一次核酸检测,可知此人核酸检测被确诊感染COVID-19的概率为2.2×10-8×0.9=1.98×10-8.以这家人核酸检测确诊感染COVID-19的概率为依据,这家3口人10次核酸检测中被确诊感染COVID-19的次数为X~B(10,1.98×10-8),∴E(X)=10×1.98×10-8=1.98×10-7.9.BC解析从2日到5日空气质量指数越来越大,故空气质量越来越差,故A错误;这14天中空气质量指数的极差为220-25=195,故B正确;这14天空气质量指数由小到大排列,中间为86,121,故中位数为86+1212=103.5,故C正确;这14天中1日,3日,12日,13日空气质量指数为良,共4天,所以空气质量指数为“良”的频率为414=27,故D错误.10.BC解析因为△ABC是边长为2的正三角形,所以|AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ |=√(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )2=√AB ⃗⃗⃗⃗⃗ 2 +2AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗+AC⃗⃗⃗⃗⃗ 2=√4+2×2×2×12+4=2√3,故A 错误;AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =|AB ⃗⃗⃗⃗⃗ |·|AC⃗⃗⃗⃗⃗ |cos ∠BAC=2×2×12=2,故B 正确; 根据重心的性质可得AG ⃗⃗⃗⃗⃗ =23·12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=13(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ),所以3PG ⃗⃗⃗⃗⃗ -3PA ⃗⃗⃗⃗⃗ =PB⃗⃗⃗⃗⃗ −PA ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ −PA ⃗⃗⃗⃗⃗ ,所以3PG ⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ +PC⃗⃗⃗⃗⃗ ,故C 正确; 因为|AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ |=|AC⃗⃗⃗⃗⃗ |=2, |AB ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ |=√(AB ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗)2=√AB ⃗⃗⃗⃗⃗ 2 +CB⃗⃗⃗⃗⃗ 2+2AB ⃗⃗⃗⃗⃗ ·CB ⃗⃗⃗⃗⃗ =√4+4+2×2×2×12=2√3,故D 错误.11.ABD 解析 如图,当直线l 与x 轴垂直时,|AB|有最小值,且最小值为2√5,所以A 正确;当直线l 与PQ 垂直时,点P 到直线l 的距离有最大值,且最大值为|PQ|=2√5,所以B 正确;由题意,设R (6+3cos θ,3sin θ),则PQ ⃗⃗⃗⃗⃗ ·PR ⃗⃗⃗⃗⃗ =(2,-4)·(4+3cos θ,3sin θ-4)=6cos θ-12sin θ+24,所以PQ ⃗⃗⃗⃗⃗ ·PR ⃗⃗⃗⃗⃗ =6√5cos(θ+φ)+24,所以PQ ⃗⃗⃗⃗⃗ ·PR⃗⃗⃗⃗⃗ 的最小值为24-6√5,所以C 错误; 当P ,C ,R 三点共线时,|PR|分别取得最大、最小值,且最大值为|PC|+3=4√2+3,所以D 正确.12.AD 解析 选项A:设△ABC 外接圆的半径为r (r>0),则由正弦定理得2√3sin60°=2r ,所以r=√33×2√3=2.又AA 1=2,所以正三棱柱ABC-A 1B 1C 1外接球的半径R=√4+1=√5,所以外接球的表面积为4πR 2=20π,故A 项正确;选项B:取BC 的中点F ,连接DF ,AF ,BD ,A 1B ,由正三棱柱的性质可知平面AA 1DF ⊥平面ABC ,所以当点P 与A 1重合时,θ最小,当点P 与D 重合时,θ最大,所以sin θ∈[12,2√77],故B 错误;选项C:将正三棱柱补成如图所示的直四棱柱,则∠GAP (或其补角)为异面直线AP 与BC 1所成的角,易得AG=GP=4,AP=2√2,所以∠GAP ≠π4,故C 项错误;选项D:如图所示,因为V P-ABC =13×2×√34×(2√3)2=2√3,所以要使三棱锥P-BCE 的体积最小,则三棱锥E-ABC 的体积最大,设BC 的中点为F ,作出截面如图所示,因为AP ⊥α,所以点E 在以AF 为直径的圆上,所以点E 到底面ABC 距离的最大值为√32×2√3×12=32, 所以三棱锥P-BCE 的体积的最小值为2√3−13×32×√34×(2√3)2=√32,故D 项正确.13.±1 解析 由于(√x 3-2a x )8展开式中的通项公式为T r+1=C 8r (√x 3)8-r·(-2a x )r =C 8r (-2a )rx 8-r 3-r ,令8-r3-r=0,得r=2,可得它的展开式的常数项是C 82(-2a )2,再根据展开式中的常数项是112,可得C 82(-2a )2=112,得a=±1.14.x=-34 解析 如图,设线段BD 的中点为N ,因为A ,F ,B 三点共线,则AB 为圆的直径,即∠ADB=90°,所以AD ⊥BD.由抛物线的定义可得|AD|=|AF|=3,FN 为Rt △ADB 的中位线,所以|FN|=12|AD|=p=32,则抛物线C 的准线方程为x=-34.15.(-∞,-3]∪[13,+∞)解析由题意可得,f(x)的定义域为R.因为f(x)=ln(x2+1)+e x+e-x,所以f(-x)=ln(x2+1)+e-x+e x=f(x),所以f(x)是偶函数.因为f'(x)=2xx2+1+e x-e-x=2xx2+1+e2x-1e x,当x>0时,f'(x)>0,所以f(x)在区间(0,+∞)上单调递增.所以f(x-2)-f(2x+1)≤0,即f(x-2)≤f(2x+1),所以|x-2|≤|2x+1|,即3x2+8x-3≥0,解得x≤-3或x≥13.故所求不等式的解集为(-∞,-3]∪[13,+∞).16.(1)3(2)6(3n-1)解析(1)因为f(3x)=3f(x),所以f(6)=3f(2),当x=2时,f(2)=2-1=1,所以f(6)=3f(2)=3.(2)在同一平面直角坐标系内画出函数y=f(x)的图象和直线y=a如图所示.当a∈(1,3)时,利用对称性,依次有x1+x2=2×6=12,x3+x4=2×18=36,……x2n-1+x2n=2×2×3n,所以x1+x2+…+x2n-1+x2n=4×(3+32+…+3n)=4×3(1-3n)1-3=6(3n-1).题型专项练2客观题12+4标准练(B)一、单项选择题1.设集合M={x||x|≤2},N={x|x2-2x-3<0},则集合M∩N=()A.{x|-1≤x<2}B.{x|-1<x≤2}C.{x|-2<x≤3}D.{x|-2≤x<3}2.已知i为虚数单位,复数z=2-i1+i,则z的共轭复数在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.已知y=f(x)是定义在R上的周期为4的奇函数.若当x∈[0,1]时,f(x)=log2(x+a),则f(2 021)=()A.-1B.0C.1D.24.某工厂生产一批医疗器械的零件,每个零件生产成型后,得到合格零件的概率为0.7,得到的不合格零件可以进行一次技术精加工,技术精加工后得到合格零件的概率是0.3,而此时得到的不合格零件将不能再加工,只能成为废品,则生产时得到合格零件的概率是()A.0.49B.0.73C.0.79D.0.915.中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公式:C=W log2(1+SN).它表示:在受噪音干扰的信道中,最大信息传递速度C取决于信道带宽W,信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中SN叫做信噪比.当信噪比比较大时,公式中真数里面的1可以忽略不计.按照香农公式,若带宽W增大到原来的1.1倍,信噪比SN从1 000提升到16 000,则C大约增加了(附:lg 2≈0.3)()A.21%B.32%C.43%D.54%6.意大利数学家斐波那契的《算经》中记载了一个有趣的问题:已知一对兔子每个月可以生一对小兔子(一雄一雌),而每一对小兔子在它们出生后的第3个月里,又能生一对小兔子.假如没有发生死亡现象,那么从第1个月开始,每月末的兔子总对数依次为:1,1,2,3,5,8,13,21,34,55,89,144,…,如果用a n表示第n个月的兔子的总对数,那么a n=a n-1+a n-2(n∈N*,且n≥3),这就是著名的斐波那契数列,其中,a1=1,a2=1.若从该数列的前120项中随机地抽取一个数,则这个数是偶数的概率为()A.13B.2 3C.1 2D.347.《九章算术》是中国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.例如,堑堵指底面为直角三角形且侧棱垂直于底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若AA1=√2,AB=2,当阳马B-A1ACC1的体积最大时,堑堵ABC-A1B1C1中异面直线A1C与AB所成角的大小是()A.π6B.π4C.π3D.π28.已知拋物线y2=2px(p>0)上有两点A,B,O为坐标原点,以OA,OB为邻边的四边形为矩形,且点O到直线AB距离的最大值为4,则p=()A.1B.2C.3D.4二、多项选择题9.某教练组为了比较甲、乙两名篮球运动员的竞技状态,选取了他们最近10场常规赛得分如下,则从最近10场比赛的得分看()甲:8,12,15,21,23,25,26,28,30,34乙:7,13,15,18,22,24,29,30,36,38A.甲的中位数大于乙的中位数B.甲的平均数大于乙的平均数C.甲的竞技状态比乙的更稳定D.乙的竞技状态比甲的更稳定10.已知函数f(x)=sin ωx+√3cos ωx(ω>0)的零点构成一个公差为π2的等差数列,把函数f(x)的图象沿x轴向右平移π6个单位长度,得到函数g(x)的图象,关于函数g(x),下列说法正确的是()A.在区间[π4,π2]上单调递减B.其图象关于直线x=π2对称C.函数g(x)是偶函数D.当x∈[π6,2π3]时,g(x)∈[-√3,2]11.如图,在直角三角形ABC中,A=90°,|AB|=√5,|AC|=2√5,点P在以A为圆心且与边BC相切的圆上,则()A.点P 所在圆的半径为2B.点P 所在圆的面积为4πC.PB ⃗⃗⃗⃗⃗ ·PC⃗⃗⃗⃗⃗ 的最大值为14D.PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗⃗ 的最大值为16 12.已知a>0,b>0,且a+2b=2,则下列说法正确的是( )A.5a +25b ≥15B.4a+12b2≥6C.b+√a 2+b 2≥85D.b ln a 2+a ln(2b )≤0三、填空题13.已知双曲线x 2-y 2m=1的一个焦点与抛物线8x+y 2=0的焦点重合,则m 的值为 .14.有5名医生被安排到两个接种点进行新冠疫苗的接种工作,若每个接种点至少安排两名医生,且其中一名负责接种信息录入工作,则不同的安排方法有 种(数字作答).15.在△ABC 中,AB=AC ,BC=4,D 为BC 边的中点,沿中线AD 折起,使∠BDC=60°,连接BC ,所得四面体ABCD 的体积为√3,则此四面体内切球的表面积为 .16.在一个三角形中,到三个顶点距离之和最小的点叫做这个三角形的费马点.如图,在△ABC 中,P 为△ABC 的费马点,经证明它也满足∠APB=∠BPC=∠CPA=120°,因此费马点也称为三角形的等角中心.在△ABC 外作等边△ACD ,再作△ACD 的外接圆,则外接圆与线段BD 的交点P 即为费马点.若AB=1,BC=2,∠CAB=90°,则PA+PB+PC= .题型专项练2 客观题12+4标准练(B)1.B 解析 M={x||x|≤2}={x|-2≤x ≤2},N={x|x 2-2x-3<0}={x|-1<x<3},则M ∩N={x|-1<x ≤2}.2.A 解析 ∵z=2-i 1+i =(2-i )(1-i )(1+i )(1-i )=2-1-3i 2=12−32i,∴z =12+32i,故z 的共轭复数在复平面内对应的点位于第一象限.3.C 解析 因为y=f (x )是定义在R 上的奇函数,x ∈[0,1]时,f (x )=log 2(x+a ),所以f (0)=log 2(0+a )=0,所以a=1.又因为y=f (x )的周期为4,所以f (2 021)=f (4×505+1)=f (1)=1.4.C 解析 设事件A :“第一次就得到合格零件”,事件B : “第一次得到不合格零件,进行一次技术精加工后得到合格零件”,所以P (A )=0.7, P (B )=(1-0.7)×0.3=0.09,所以生产时得到合格零件的概率是P (A )+P (B )=0.7+0.09=0.79.5.D 解析 由题意1.1Wlog 216 000Wlog 21 000-1=1.1×lg16 000lg1 000-1=1.1×3+4lg23-1≈0.54,所以C 大约增加了54%.6.A 解析 因为奇数加奇数结果是偶数,奇数加偶数结果是奇数,偶数加奇数结果是奇数,所以数列中任意相邻的三项,其中一项为偶数,两项为奇数,所以前120项中偶数有40项,所以这个数是偶数的概率为40120=13.7.C 解析 在堑堵ABC-A 1B 1C 1中, AA 1⊥平面ABC ,BC ⊂平面ABC ,所以AA 1⊥BC.又AC ⊥BC ,且AA 1∩AC=A ,所以BC ⊥平面ACC 1A 1 ,所以阳马B-A 1ACC 1的体积V=13S 矩形ACC 1A 1·BC=13·AC·AA 1·BC=√23AC·BC , 在直角三角形ABC 中,4=AB 2=AC 2+BC 2≥2AC·BC , 即AC·BC ≤2,当且仅当AC=BC=√2时取得等号.所以当AC=BC=√2时,阳马B-A 1ACC 1的体积取得最大值2√23.又A 1B 1∥AB ,所以∠CA 1B 1(或其补角)为异面直线A 1C 与AB 所成的角,连接B 1C (图略),则B 1C=√BC 2+BB 12=√2+2=2,A 1C=√AC 2+AA 12=√2+2=2,即A 1B 1=B 1C=A 1C=2,所以∠CA 1B 1=π3,即异面直线A 1C 与AB 所成角为π3.8.B 解析 由题意,设直线AB 的方程为x=my+b (b ≠0),与抛物线方程联立,消去x 可得y 2-2pmy-2pb=0.设点A (x 1,y 1),B (x 2,y 2),则y 1+y 2=2pm ,y 1y 2=-2pb.由OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=(my 1+b )(my 2+b )+y 1y 2=(m 2+1)y 1y 2+mb (y 1+y 2)+b 2=(m 2+1)(-2pb )+2pm 2b+b 2=b 2-2pb=0,解得b=2p 或b=0(舍去),即直线AB 的方程为x=my+2p ,则原点O 到直线AB 的距离d=√1+m 2,当m=0时,d 取最大值,且d 最大值=2p=4.所以p=2. 9.AC 解析 由题意可得,甲、乙中位数分别为23+252=24,22+242=23,即甲的中位数大于乙的中位数,A 正确; 甲的平均数8+12+15+21+23+25+26+28+30+3410=22.2,乙的平均数7+13+15+18+22+24+29+30+36+3810=23.2,甲的平均数小于乙的平均数,B 错误;甲的方差s 12=110×[(8-22.2)2+(12-22.2)2+…+(34-22.2)2]=61.56,乙的方差s 22=110×[(7-23.2)2+(13-23.2)2+…+(38-23.2)2]=92.56,即s 12<s 22,甲的竞技状态比乙的更稳定,C 正确,D 错误.10.AD 解析 因为f (x )=sin ωx+√3cos ωx=2sin (ωx +π3),由于函数f (x )的零点构成一个公差为π2的等差数列, 则该函数的最小正周期为π.因为ω>0,所以ω=2ππ=2,所以f (x )=2sin (2x +π3). 将函数f (x )的图象沿x 轴向右平移π6个单位长度, 得到函数g (x )=2sin [2(x -π6)+π3]=2sin 2x 的图象.对于A 选项,当x ∈[π4,π2]时,π2≤2x ≤π,则函数g (x )在区间[π4,π2]上单调递减,A 选项正确;对于B 选项,g (π2)=2sin π=0≠±2,所以函数g (x )的图象不关于直线x=π2对称,B 选项错误;对于C 选项,函数g (x )的定义域为R ,g (-x )=2sin(-2x )=-2sin 2x=-g (x ),函数g (x )为奇函数,C 选项错误;对于D 选项,当π6≤x ≤2π3时,π3≤2x ≤4π3,则-√32≤sin 2x ≤1,所以-√3≤g (x )≤2. 所以当x ∈[π6,2π3]时,g (x )∈[-√3,2],D 选项正确.11.ABC 解析 如图,设BC 的中点为M ,过A 作AH ⊥BC 于点H ,连接PM ,PA ,AM.因为A=90°,|AB|=√5,|AC|=2√5,所以|BC|=5,|AM|=52,所以由12|AB||AC|=12|BC||AH|,得|AH|=|AB ||AC ||BC |=2,所以圆的半径为2,即点P 所在圆的半径为2,所以点P 所在圆的面积为4π,所以选项A 正确,B 正确;因为PB ⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ ,PC ⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ =0,所以PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗⃗ =(PA ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ )·(PA ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=PA ⃗⃗⃗⃗⃗ 2+PA ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ ·PA ⃗⃗⃗⃗⃗ =|PA ⃗⃗⃗⃗⃗ |2+PA ⃗⃗⃗⃗⃗ ·(AC ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ )=4+PA ⃗⃗⃗⃗⃗ ·2AM ⃗⃗⃗⃗⃗⃗ ,所以当P ,M ,A 三点共线,且P ,M 在点A 的两侧时,PA ⃗⃗⃗⃗⃗ ·2AM ⃗⃗⃗⃗⃗⃗ 取最大值,且(PA ⃗⃗⃗⃗⃗ ·2AM ⃗⃗⃗⃗⃗⃗ )max =2|PA ⃗⃗⃗⃗⃗ |·|AM ⃗⃗⃗⃗⃗⃗ |=2×2×52=10,所以PB ⃗⃗⃗⃗⃗ ·PC⃗⃗⃗⃗⃗ 的最大值为4+10=14,所以选项C 正确,D 错误.12.BCD 解析 因为a>0,b>0,且a+2b=2,对于A,5a +25b =5a +52b ≥2√5a ·52b =2√5a+2b =10,当且仅当5a =52b ,即a=1,b=12时取等号,故A 错误;对于B,因为a+2b=2,所以a=2-2b (0<b<1),所以4a +12b 2=42-2b +12b2=21-b +12b2,令f (b )=21-b +12b2,则f'(b )=2(1-b )2−1b3=2b 3-(1-b )2b 3(1-b )2,因为0<b<1,所以b 3(1-b )2>0,令g (b )=2b 3-(1-b )2,0<b<1,则g'(b )=6b 2-2b+2>0,所以g (b )在区间(0,1)上单调递增, 又g (12)=0,所以当b ∈(0,12)时,g (b )<0,即f'(b )<0,f (b )在区间(0,12)上单调递减,当b ∈(12,1)时,g (b )>0,即f'(b )>0,f (b )在区间(12,1)上单调递增,所以f (b )min =f (12)=6,故4a +12b2≥6,即B 正确;对于C,b+√a 2+b 2=b+√(2-2b )2+b 2=b+√5b 2-8b +4, 令h (b )=b+√5b 2-8b +4,则h'(b )=1+√5b -8b+4=1+√5(b -45)√(b -45)+425,当b>45时,h'(b )>0,所以h (b )在区间(45,+∞)上单调递增;当0<b<45时,h'(b )=1-√5√1+425·1(b -45)2,所以h'(b )在区间(0,45)上单调递增,又h'(35)=0,所以在区间(0,35)上,h'(b )<0,在区间(35,45)上,h'(b )>0,即在区间(0,35)上,h (b )单调递减,在区间(35,45)上,h (b )单调递增,所以b=35时h (b )取得最小值,且最小值为h (35)=85,所以b+√a 2+b 2≥85,故C 正确;对于D,b ln a 2+a ln(2b )=2b ln a+a ln(2b )=(2-a )ln a+a ln(2-a ), 令p (x )=(2-x )ln x+x ln(2-x ),0<x<2,则p (1)=0, p'(x )=-ln x+2x -1+ln(2-x )-x2-x =ln(2-x )-ln x+2-xx −x2-x , 当1<x<2时,ln(2-x )<0,-ln x<0,0<2-xx <1,x2-x >1,所以p'(x )<0,所以p (x )在区间(1,2)上单调递减,当0<x<1时,ln(2-x )>0,-ln x>0,2-xx >1,0<x2-x <1,所以p'(x )>0,所以p (x )在区间(0,1)上单调递增,所以x=1时p (x )有最大值,且p (x )max =p (1)=0,所以p (x )≤0在区间(0,2)上恒成立,所以p (a )≤0,故D 正确.13.3 解析 设抛物线的焦点为F ,由8x+y 2=0得y 2=-8x ,所以F (-2,0).由题意得m>0,所以1+m=22,得m=3. 14.120 解析 根据题意,分两步进行安排:第一步,将5名医生分为两组,一组3人,另一组2人,每一组选出1人,负责接种信息录入工作,有C 52·C 21·C 33·C 31=60种分组方法;第二步,将分好的2组,安排到两个接种点,有2种情况,则共有60×2=120种安排方法. 15.(84-48√3)π 解析 如图,由题意得BD=CD=2,AD ⊥平面BCD ,四面体A-BCD 的体积V A-BCD =13×(12×2×2sin60°)·AD=√3,得AD=3, 所以AB=√AD 2+BD 2=√32+22=√13, 设BC 的中点为E ,连接AE ,DE.因为BD=DC=2,∠BDC=60°,所以DE ⊥BC ,BC=BD=DC=2,DE=√3,所以AE ⊥BC. 所以AE=√AB 2-BE 2=√13-1=2√3.所以四面体A-BCD 的表面积S=(12×2×3)×2+12×2×√3+12×2×2√3=6+3√3. 设内切球的半径为R ,由V A-BCD =13×S·R=(2+√3)R=√3,得R=√32+√3=2√3-3,所以内切球的表面积为4πR 2=12(7-4√3)π=(84-48√3)π.16.√7 解析 根据题意有,∠APB=∠BPC=∠CPA=120°,则∠PAB+∠PBA=60°.因为AB=1,BC=2,∠CAB=90°,所以∠ABC=60°,即∠PBC+∠PBA=60°,所以∠PAB=∠PBC ,从而有△PAB ∽△PBC ,则PA PB =PB PC =AB BC =12,则PC=2PB=4PA ,在△PAB 中,由余弦定理,可得PA 2+PB 2-12=2PA·PB cos 120°,解得PB=2√77,PA=√77,则PC=4√77,故PA+PB+PC=√7.题型专项练3 客观题12+4标准练(C)一、单项选择题1.复数z=1-i 31+2i 的虚部为()A.-15iB.15iC.-15D.152.已知集合M={x|lg(x-1)≤0},N={x||x|<2},则M ∪N=( ) A.⌀ B.(1,2)C.(-2,2]D.{-1,0,1,2}3.4位优秀党务工作者到3个基层单位进行百年党史宣讲,每人宣讲1场,每个基层单位至少安排1人宣讲,则不同的安排方法数为()A.81B.72C.36D.64.若向量a,b满足|a|=2,|b|=√3,且(a-b)⊥(2a+3b),则a与b夹角的余弦值为()A.√112B.√336C.√215D.√365.核酸检测分析是用荧光定量PCR法,通过化学物质的荧光信号,对在PCR扩增进程中成指数级增加的靶标DNA实时监测,在PCR扩增的指数时期,荧光信号强度达到阈值时,DNA的数量X n与扩增次数n满足lg X n=n lg(1+p)+lg X0,其中p为扩增效率,X0为DNA的初始数量.已知某被测标本DNA扩增10次后,数量变为原来的100倍,则该样本的扩增效率p约为()(参考数据:100.2≈1.585,10-0.2≈0.631)A.0.369B.0.415C.0.585D.0.6316.某地区为落实乡村振兴战略,帮助农民脱贫致富,引入一种特色农产品种植,该农产品上市时间仅能维持5个月,预测上市初期和后期会因产品供应不足使价格持续上涨,而中期又将出现供大于求使价格连续下跌.经研究其价格模拟函数为f(t)=t(t-3)2+4(0≤t≤5,其中t=0表示5月1日,t=1表示6月1日,以此类推).为保护农户的经济效应,当地政府计划在价格下跌时积极拓宽外销,请你预测该农产品价格下跌的月份为()A.5月和6月B.6月和7月C.7月和8月D.8月和9月7.已知双曲线C:x 2a2−y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,若双曲线C上存在点P满足∠F2PO=2∠F1PO=π3,则该双曲线的离心率为()A.√3+1B.√2+1C.√3D.√28.已知函数f(x)的定义域为R,f(5)=4,f(x+3)是偶函数,任意x1,x2∈[3,+∞)满足f(x1)-f(x2)x1-x2>0,则不等式f(3x-1)<4的解集为()A.(23,3) B.(-∞,23)∪(2,+∞)C.(2,3)D.(23,2)二、多项选择题9.已知函数f(x)=cos(x+π6),则()A.2π为f(x)的一个周期B.f(x)的图象关于直线x=4π3对称C.f(x)在区间(π2,π)内单调递减D.f(x+π)的一个零点为π310.已知ln x>ln y>0,则下列结论正确的是()A.1x <1yB.(13)x>(13)yC.log y x>log x yD.x2+4y(x-y)>811.如图,在正方体ABCD-A1B1C1D1中,E,F,G分别为BC,CC1,BB1的中点,则()A.D1D⊥平面AEFB.A1G∥平面AEFC.异面直线A1G与EF所成角的余弦值为√1010D.点G到平面AEF的距离是点C到平面AEF的距离的2倍12.如图,在数表中,第1行是从1开始的正奇数,从第2行开始每个数是它肩上两个数之和,则下列说法正确的是()1 3 5 7 9 11…4 8121620…12202836……A.第6行第1个数为192B.第10行的数从左到右构成公差为210的等差数列C.第10行前10个数的和为95×29D.数表中第2 021行第2 021个数为6 061×22 020三、填空题13.在一次期中考试中某学校高三全部学生的数学成绩X服从正态分布N(μ,σ2),若P(X≥90)=0.5,且P(X≥110)=0.2,则P(X≤70)=.14.已知两条直线l1:y=2x+m,l2:y=2x+n与圆C:(x-1)2+(y-1)2=4交于A,B,C,D四点,且四边形ABCD为正方形,则|m-n|的值为.15.如图,O 是滑槽AB 的中点,短杆ON 可绕点O 转动,长杆MN 通过点N 处的铰链与ON 连接,MN 上的栓子D 可沿滑槽AB 滑动.当点D 在滑槽AB 内作往复移动时,带动点N 绕点O 转动,点M 也随之运动.记点N 的运动轨迹为C 1,点M 的运动轨迹为C 2.若ON=DN=1,MN=3,过轨迹C 2上的点P 向轨迹C 1作切线,则切线长的最大值为 .16.阿基米德在他的著作《论球和圆柱》中,证明了数学史上著名的圆柱容球定理:圆柱的内切球(与圆柱的两底面及侧面都相切的球)的体积与圆柱的体积之比等于它们的表面积之比.可证明该定理推广到圆锥容球也正确,即圆锥的内切球(与圆锥的底面及侧面都相切的球)的体积与圆锥体积之比等于它们的表面积之比,则该比值的最大值为 .题型专项练3 客观题12+4标准练(C)1.C 解析 因为z=1-i 31+2i=1+i 1+2i =(1+i )(1-2i )(1+2i )(1-2i )=35−15i,所以复数z 的虚部为-15.2.C 解析 根据题意,由lg(x-1)≤0,得0<x-1≤1,即1<x ≤2,则集合M={x|lg(x-1)≤0}={x|1<x ≤2}.由|x|<2,得-2<x<2,则N={x||x|<2}={x|-2<x<2}.故M ∪N={x|-2<x ≤2}=(-2,2].3.C 解析 根据题意,必有两人去同一个基层单位进行宣讲,故先从4位优秀党务工作者中选两人,有C 42=6种选法,将其看成整体,再和另外两人分配到3个基层单位,有A 33=6种分配方案,所以共有6×6=36种不同的安排方案.4.D 解析 由已知得(a -b )·(2a +3b )=2a 2+a ·b -3b 2=0,|a |=2,|b |=√3,则2√3cos <a ,b >-1=0,故cos <a ,b >=√36.5.C 解析 由题意知lg(100X 0)=10lg(1+p )+lg X 0,即2+lg X 0=10lg(1+p )+lg X 0,所以1+p=100.2≈1.585,解得p ≈0.585.6.B 解析 由f (t )=t (t-3)2+4(t ∈[0,5]),得f'(t )=(t-3)2+2t (t-3)=3(t-1)(t-3),当t ∈[0,1)时,f (t )单调递增;当t ∈(1,3)时,f (t )单调递减;当t ∈(3,5]时,f (t )单调递增.根据题意,可知该农产品价格下跌的月份为6月和7月. 7.A 解析 由∠F 2PO=2∠F 1PO=π3,可知∠F 1PF 2=π2,又O 为F 1F 2的中点,所以∠F 1F 2P=π3.根据题意可知|F 1F 2|=2c ,则|PF 2|=c ,|PF 1|=√3c ,所以√3c-c=2a ,所以e=ca =√3-1=√3+1.8.D解析因为f(x+3)是偶函数,所以f(x)的图象关于直线x=3对称,所以f(5)=f(1)=4.因为任意x1,x2∈[3,+∞)满足f(x1)-f(x2)x1-x2>0,所以f(x)在区间[3,+∞)内单调递增,在区间(-∞,3)内单调递减,所以f(3x-1)<4等价于1<3x-1<5,解得23<x<2.9.AD解析函数f(x)=cos(x+π6)的最小正周期为2π,故A正确;由x+π6=kπ,k∈Z,得x=-π6+kπ,k∈Z,无论k取何值,x≠4π3,故B错误;函数f(x)=cos(x+π6)在区间(π2,5π6)内单调递减,在区间(5π6,π)内单调递增,故C错误;∵f(x+π)=cos(x+7π6),∴f(π3+π)=cos7π6+π3=cos3π2=0,故D正确.10.ACD解析因为ln x>ln y>0,所以x>y>1,所以1x <1y,所以A正确;因为x>y>1,所以(13)x<(13)y,所以B错误;因为x>y>1,所以log y x>log y y=1,log x y<log x x=1, 所以log y x>log x y,所以C正确;因为x>y>1,所以0<y(x-y)≤[y+(x-y)2]2=x24,所以x2+4y(x-y)≥x2+16x2≥8,当且仅当x=2,y=1时,等号成立,又y>1,所以x2+4y(x-y)>8,所以D正确.11.BCD解析对于A,假设D1D⊥平面AEF,因为D1D∥A1A,所以AA1⊥平面AEF,显然不可能,所以假设不成立,故A错误;对于B,取B1C1的中点Q,连接GQ,A1Q(图略),则GQ∥EF,A1Q∥AE,可知GQ∥平面AEF,A1Q∥平面AEF,又GQ∩A1Q=Q,所以平面A1GQ∥平面AEF,又A1G⊂平面A1GQ,所以A1G∥平面AEF,故B正确;对于C,因为EF∥GQ,所以∠A1GQ或其补角为异面直线A1G与EF所成的角,设正方体的棱长为2,则A1G=A1Q=√5,QG=√2,由余弦定理得cos∠A1GQ=2×√5×√2=√1010,故C正确;对于D,连接GC,交FE于点O,连接GF(图略),则△OCE∽△OGF,所以OGOC=GFCE=2,所以点G到平面AEF的距离是点C到平面AEF的距离的2倍,故D正确.12.ABD 解析 数表中,每行是等差数列,且第1行的首项是1,公差为2,第2行的首项是4,公差为4,第3行的首项是12,公差为8,每行的第1个数满足a n =n×2n-1,每行的公差构成一个以2为首项,2为公比的等比数列,公差满足d n =2n .对于选项A,第6行第1个数为a 6=6×26-1=192,故A 正确;对于选项B,第10行的数从左到右构成公差为d 10=210的等差数列,故B 正确;对于选项C,第10行第1个数为a 10=10×210-1=10×29,公差为210,所以前10个数的和为10×10×29+10×92×210=190×29,故C 错误;对于选项D,数表中第2 021行第1个数为a 2 021=2 021×22 021-1=2 021×22 020,第2 021行的公差为22 021,故数表中第2 021行第2 021个数为2 021×22 020+(2 021-1)×22 021=6 061×22 020,故D 正确. 13.0.2 解析 由题意易得μ=90,所以P (X ≤70)=P (X ≥110)=0.2. 14.2√10 解析 由题意知l 1∥l 2,若四边形ABCD 为正方形,则正方形的边长等于直线l 1,l 2之间的距离d ,d=√5, 设圆C 的半径为r ,由正方形的性质知d=√2r=2√2, 即√5=2√2, 故|m-n|=2√10. 15.√15 解析 以滑槽AB 所在直线为x 轴,O 为坐标原点建立平面直角坐标系如图所示.因为|ON|=1,所以点N 的运动轨迹C 1是以O 为圆心,半径为1的圆,其方程为x 2+y 2=1.设点N 的坐标为(cos θ,sin θ),由于|ON|=|DN|=1,易得D (2cos θ,0),由|MN|=3,得NM ⃗⃗⃗⃗⃗⃗⃗ =3ND⃗⃗⃗⃗⃗⃗ ,设M (x ,y ),则(x-cos θ,y-sin θ)=3(cos θ,-sin θ),可得M (4cos θ,-2sin θ), 所以点M 的运动轨迹C 2是椭圆,其方程为x 216+y 24=1.设轨迹C 2上的点P (4cos α,2sin α),则|OP|2=16cos 2α+4sin 2α=4+12cos 2α≤16, 故切线长为√|OP |2-12≤√16-1=√15,即切线长的最大值为√15.16.12解析设圆锥的底面半径为r,母线长为l,圆锥内切球的半径为R,作出圆锥的轴截面如图所示.设∠OBC=θ,∵tan θ=Rr ,∴r=Rtanθ.∵OD⊥AB,OE⊥BC,∴∠DBE+∠DOE=π,又∠AOD+∠DOE=π,∴∠AOD=∠DBE=2θ,∴AD=R tan 2θ,∴l+r=AD+BD+r=AD+2r=R tan 2θ+2Rtanθ.又圆锥表面积S1=πr(l+r),圆锥内切球的表面积S2=4πR2,故所求比值为S2S1= 4πR2πR tanθ(2Rtanθ1-tan2θ+2Rtanθ)=2tan2θ(1-tan2θ).令t=tan2θ>0,则S2S1=2t(1-t)=-2t2+2t, 故当t=12时,S2S1取得最大值12.。

绝密★考试结束前2022年秋季高三开学摸底考试卷（新高考专用）03（试卷满分150分，考试用时120分钟）姓名___________ 班级_________ 考号_______________________注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效. 3．考试结束后，将本试卷和答题卡一并交回.一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求.1．已知集合{2,1,0,1,2}A =--，{|e ,}x B y y y N ==∈，则A B =（ ） A ．{1,0}- B ．{0,1} C ．{1,2} D ．{0,1,2} 【答案】C 【解析】【分析】由题可得，集合B 为正整数集，从而与集合A 求交集可得结果. 【详解】R x ∈时，e 0x >y=恒成立，又N y ， 故集合B 为正整数集，{1,2}A B ∴=.故选：C. 2．若12i z =-+，则i4z z z +=⋅-（ ） A ．13i -+ B ．13i -- C ．13i + D ．13i - 【答案】A 【解析】【分析】由共轭复数的概念与复数的四则运算法则求解即可 【详解】因为12i z =-+，所以()()412i 12i 41441z z ⋅-=-+---=+-=， 所以ii 13i 4z z zz +=+=-+-， 故选：A3．从2,4,6,8中任取2个不同的数,a b ，则4a b -=的概率是（ ） A ．12 B ．13 C ．14 D ．16【答案】B 【解析】 【分析】列举从2,4,6,8中任取2个不同的数,a b 的所有结果，共6个基本事件，符合条件的共2个基本事件，结合古典概型计算结果． 【详解】从2,4,6,8中任取2个不同的数,a b ，共有()()()()()()2,4,2,6,2,8,4,6,4,8,6,86个基本事件，取出的2个数之差的绝对值为4有()()2,6,4,82个基本事件，所以所求概率为2163P == 故选：B ．4．一种药在病人血液中的量不少于1500mg 才有效，而低于500mg 病人就有危险．现给某病人注射了这种药2500mg ，如果药在血液中以每小时20%的比例衰减，为了充分发挥药物的利用价值，那么从现在起经过 （ ）小时向病人的血液补充这种药，才能保持疗效．（附：lg 20.3010≈，lg30.4771≈，结果精确到0.1h ）A ．8.8小时B ．3.5小时C ．5.6小时D ． 2.3小时 【答案】D 【解析】【分析】根据已知关系式可得不等式()5002500120%1500x≤⨯-≤，结合对数运算法则解不等式即可求得结果.【详解】设应在病人注射这种药x 小时后再向病人的血液补充这种药， 则()5002500120%1500x≤⨯-≤，整理可得：0.20.80.6x ≤≤，0.80.8log 0.6log 0.2x ∴≤≤，0.8lg 0.6lg 61lg 2lg 31log 0.6 2.3lg 0.8lg813lg 21-+-===≈--，0.8lg 0.2lg 21log 0.27.2lg 0.83lg 21-==≈-， 2.37.2x ∴≤≤，即应在用药2.3小时后再向病人的血液补充这种药.故选：D.5．设函数()()3cos 0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭图象经过点3,38A π⎛⎫- ⎪⎝⎭，直线38x π=向左平移4π个单位长度后恰好经过函数()f x 的图象与x 轴的交点B ，若B 是()f x 的图象与x 轴的所有交点中距离点A 最近的点，则函数()f x 的一个单调递增区间为（ ）A ．,43ππ⎡⎤-⎢⎥⎣⎦ B ．,04π⎡⎤-⎢⎥⎣⎦C ．8,2ππ⎡⎤--⎢⎥⎣⎦D ．[],0π-【答案】C 【解析】【分析】根据()f x 最小正周期和338f π⎛⎫=-⎪⎝⎭可求得,ωϕ，进而得到()f x 解析式；利用余弦型函数单调区间的求法可求得()f x 的单调递增区间，验证选项即可得到结果.【详解】B 是()f x 的图象与x 轴的所有交点中距离点A 最近的点，A 为()f x 的最小值点，()f x ∴的最小正周期44T ππ=⨯=，即2ππω=，解得：2ω=，333cos 384f ππϕ⎛⎫⎛⎫∴=+=-⎪⎪⎝⎭⎝⎭，即3cos 14πϕ⎛⎫+=- ⎪⎝⎭， ()324k k πϕππ∴+=+∈Z ，解得：()24k k πϕπ=+∈Z ，又02πϕ<<，4πϕ∴=，()3cos 24f x x π⎛⎫∴=+ ⎪⎝⎭；令()2224k x k k ππππ-+≤+≤∈Z ，解得：()588k x k k ππππ-+≤≤-+∈Z ()f x ∴的单调递增区间为()5,88k k k ππππ⎡⎤-+-+∈⎢⎥⎣⎦Z ，令0k =，则5,88ππ⎡⎤--⎢⎥⎣⎦是()f x 的一个单调递增区间，5,,2888ππππ⎡⎤⎡⎤--⊆--⎢⎥⎢⎥⎣⎦⎣⎦，,28ππ⎡⎤∴--⎢⎥⎣⎦是()f x 的一个单调递增区间. 故选：C.6．已知6ln1.25a =，0.20.2e b =，13c =，则（ ）A ．a b c <<B ．c b a <<C ．c a b <<D ．a c b << 【答案】A 【解析】【分析】0.20.20.20.2e e ln e b ==，令()ln f x x x =，利用导数求出函数()f x 的单调区间，令()e 1x g x x =--，利用导数求出函数()g x 的单调区间，从而可得出0.2e 和1.2的大小，从而可得出,a b 的大小关系，将,b c 两边同时取对数，然后作差，从而可得出,b c 的大小关系，即可得出结论. 【详解】解：0.20.20.20.2e e ln e b ==，6ln1.2 1.2ln1.25a ==， 令()ln f x x x =，则()ln 1f x x '=+，当10e x <<时，()0f x '<，当1ex >时，()0f x '>， 所以函数()f x 在10,e ⎛⎫⎪⎝⎭上递减，在1,e⎛⎫+∞ ⎪⎝⎭上递增，令()e 1xg x x =--，则()e 1x g x '=-，当0x <时，()0g x '<，当0x >时，()0g x '>， 所以函数()g x 在(),0∞-上递减，在()0,∞+上递增， 所以()()0.200g g >=，即0.21e 10.2 1.2e>+=>，所以()()0.2e 1.2f f >，即0.20.2e e 1.22ln ln1.>，所以b a >， 由0.20.2e b =，得()0.211ln ln 0.2e ln 55b ==+， 由13c =，得1ln ln 3c =，11151ln ln ln ln ln 35535c b -=--=-，因为55625510e 3243⨯⎛⎫=>> ⎪⎝⎭， 所以155e 3>，所以51ln 35>，所以ln ln 0c b ->，即ln ln c b >， 所以c b >， 综上所述a b c <<. 故选：A.7．如图，在底面半径为1，高为6的圆柱内放置两个球，使得两个球与圆柱侧面相切，且分别与圆柱的上下底面相切．一个与两球均相切的平面斜截圆柱侧面，得到的截线是一个椭圆．则该椭圆的离心率为（ ）A ．2 B C D 【答案】D 【解析】 【分析】由题意如图所示，由球的半径可得|BF |，||BO 的值，进而可得BOF ODM ∠=∠的正弦值，求出||OD 的值，即求出a 的值，由圆柱的底面半径可得2b 的值，即求出b 的值，进而求出c 的值，再求出离心率的值．【详解】如图所示，1BF =，2BO =，1sin 2BOF ∠=，则11sin 2OM ODM OD OD∠===， 2OD ∴=，即2a =，而22b =，即1b =，所以c =所以离心率c e a = 故选：D ．8．已知定义在[1e ，e ]上的函数()f x 满足()1f x f x ⎛⎫= ⎪⎝⎭，且当x ∈[1e ，1]时，()ln 1f x x x =+，若方程()102f x x a --=有三个不同的实数根，则实数a 的取值范围是（ ） A ．(13e ，11e -] B ．(121e --，312e -] C ．(121e --，11e-] D ．(13e ，312e -] 【答案】B 【解析】 【分析】由题设，求分段函数()f x 的解析式并画出图像，将方程有三个不同实根转化为()f x 和12y x a =+有三个不同的交点问题，由数形结合思想结合导数研究函数的交点情况，进而求参数a 的范围. 【详解】∵当1,1x e ⎡⎤∈⎢⎥⎣⎦时，()ln 1f x x x =+， ∴当(]1,x e ∈时，()11ln 1f x f x x x ⎛⎫==-+ ⎪⎝⎭，综上，()(]11,,111,1,xlnx x e f x lnx x e x⎧⎡⎤+∈⎪⎢⎥⎪⎣⎦=⎨⎪-+∈⎪⎩，当1,1x e ⎡⎤∈⎢⎥⎣⎦时，()1ln 0f x x =+≥'，则()f x 在1,1e ⎡⎤⎢⎥⎣⎦上单调递增，当(]1,x e ∈时，()()21ln 10f x x x =-'≤，则()f x 在(]1,e上单调递减，∵()102f x x a --=有三个不同的实数根，∴()f x 的图像和直线12y x a =+有三个不同的交点， 作()f x 的大致图像如图所示，当直线12y x a =+和()f x 的图像相切时，设切点为()00,x y ，∴()0011ln 2f x x =='+，可得120x e -=，120112y e -=-⋅，代入12y x a =+，可得121a e -=-，当12y x a =+过点11,1e e ⎛⎫- ⎪⎝⎭时，312a e=-，由图知，实数a 的取值范围为1231,12e e -⎛⎤-- ⎥⎝⎦.故选：B.二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．已知由样本数据(i x ，)(1i y i =，2，3，⋯，10)组成的一个样本，得到回归直线方程为ˆ20.4yx =-，且2x =，去除两个样本点(2,1)-和(2,1)-后，得到新的回归直线的斜率为3.则下列说法正确的是（ ）A ．相关变量x ，y 具有正相关关系B ．去除两个样本点(2,1)-和(2,1)-后，回归直线方程为ˆ33yx =- C ．去除两个样本点(2,1)-和(2,1)-后，随x 值增加相关变量y 值增加速度变小 D ．去除两个样本点(2,1)-和(2,1)-后，样本(4,8.9)的残差为0.1 【答案】AB【解析】 【分析】对于A ，30>，则相关变量x ，y 具有正相关关系，故A 正确；对于B ，求出953322a =-⨯=-，故去除样本点后的回归直线方程为33y x =-，故B 正确； 对于C ，由于斜率为32>，随x 值增加相关变量y 值增加速度变大，故C 错误； 对于D,样本()4,8.9的残差为8.990.1-=-，故D 错误. 【详解】解：对于A ，去除两个样本点()2,1-和()2,1-后，得到新的回归直线的斜率为3，30>，则相关变量x ，y 具有正相关关系，故A 正确；对于B ，由2x =代入24y x =-得 3.6y =，则去除两个样本点()2,1-和()2,1-后，得到新的210582X ⨯==，3.610982Y ⨯==，953322a =-⨯=-，故去除样本点后的回归直线方程为33y x =-，故B 正确； 对于C ，由于斜率为32>，故相关变量x ，y 具有正相关关系且去除样本点后，随x 值增加相关变量y 值增加速度变大，故C 错误，对于D,当4x =时，3439y =⨯-=，则样本()4,8.9的残差为8.990.1-=-，故D 错误. 故选：AB.10．设正实数m 、n 满足2m n +=，则下列说法正确的是（ ） A ．2n m n+的最小值为3 B ．mn 的最大值为1C 的最小值为2D ．22m n +的最小值为2 【答案】ABD 【解析】 【分析】根据基本不等式判断． 【详解】因为正实数m 、n ，所以21213n n m n n m m n m n m n ++=+=++≥=+=，当且仅当n mm n=且m+n=2，即m=n=1时取等号，此时取得最小值3，A 正确； 由 2()12m n nm +≤=，当且仅当m=n=1时，mn 取得最大值1，B 正确；因为2224m n m n =+++≤++=，当且仅当m=n=1≤2即最大值为2，C 错误；2222()24242()22m n m n m n mn mn ++=+-=-≥-⨯=，当且仅当1m n ==时取等号，此处取得最小值2，故D 正确. 故选：ABD11．已知O 为坐标原点，过抛物线2:2(0)C y px p =>焦点F 的直线与C 交于A ，B 两点，其中A 在第一象限，点(,0)M p ，若||||AF AM =，则（ ） A ．直线AB的斜率为 B ．||||OB OF =C ．||4||AB OF >D ．180OAM OBM ∠+∠<︒ 【答案】ACD 【解析】 【分析】由AF AM =及抛物线方程求得3(4p A ，再由斜率公式即可判断A 选项；表示出直线AB 的方程，联立抛物线求得(,3pB ，即可求出OB 判断B 选项；由抛物线的定义求出2512p AB =即可判断C 选项；由0OA OB ⋅<，0MA MB ⋅<求得AOB ∠，AMB ∠为钝角即可判断D 选项. 【详解】对于A ，易得(,0)2p F ，由AF AM =可得点A 在FM 的垂直平分线上，则A 点横坐标为3224ppp +=， 代入抛物线可得2233242p y p p =⋅=，则3(4p A ，则直线AB的斜率为2342p p =-A 正确； 对于B，由斜率为AB的方程为2p x y =+，联立抛物线方程得220y py p -=， 设11(,)B x y1p y p +，则1y =，代入抛物线得212p x ⎛=⋅ ⎝⎭，解得13p x =，则(,3p B ，则2p OB OF =≠=，B 错误； 对于C ，由抛物线定义知：325244312p p pAB p p OF =++=>=，C 正确；对于D ，2333((,043434p p p p p OA OB ⎛⋅=⋅=⋅=-< ⎝⎭，则AOB ∠为钝角，又2225((,043436p p p p p MA MB ⎛⎛⎫⋅=-⋅-=-⋅-=-< ⎪ ⎝⎭⎝⎭，则AMB ∠为钝角， 又360AOB AMB OAM OBM ∠+∠+∠+∠=，则180OAM OBM ∠+∠<，D 正确. 故选：ACD.12．已知正方体1111ABCD A B C D -棱长为2，P 为空间中一点．下列论述正确的是（ ）A ．若112AP AD =，则异面直线BP 与1C D B ．若[]()10,1BP BC BB λλ=+∈，三棱锥1P A BC -的体积为定值C ．若[]()110,12BP BC BB λλ=+∈，有且仅有一个点P ，使得1AC ⊥平面1AB P D ．若[]()10,1AP AD λλ=∈，则异面直线BP 和1C D 所成角取值范围是,42ππ⎡⎤⎢⎥⎣⎦【答案】ABD 【解析】 【分析】根据向量关系式确定动点位置或轨迹，然后判断各个选项正误. 【详解】选项A ：由题，如下图，P 为1AD 中点，取11B D 的中点O ，连接,PO BO ，则1PO C D ∥，所以BPO ∠或其补角即为异面直线BP 与1C D 所成的角，易得BP PO BO ===，所以cos BPO ∠=A 正确；选项B ：由条件1([0,1])BP BC BB λλ=+∈，可知P 点的轨迹为线段11B C ，因为11B C BC ∥，故P 到平面1A BC 的距离为定值，且三角形1A BC 面积为定值，故三棱锥1P A BC -体积为定值43．故选项B 正确．选项C ：由11([0,1])2BP BC BB λλ=+∈可知点P 在线段EF 上（E 、F 分别为1BB 、1CC 中点），因为1AC ⊥平面11AB D ，所以平面1AB P 即为平面11AB D ，点P 即为平面1AB D 与直线EF 交点，此交点在FE 延长线上，故选项C 错误．选项D ：由1([0,1])AP AD λλ=∈可知点P 的轨迹为线段1AD ．建系如图，得1(2,0,2),(2,0,2)C D B =-，设(0,,2),[0,2]P a a a -∈，则(2,,)BP a a =--，所以1cos ,BP C D 〈〉==2[0,2]a x -=∈，当2a =，即0x =时，1cos ,0BP C D 〈〉=，此时直线BP 和1C D 所成角是2π；当2a ≠，即2(]0,x ∈时，则1cos ,BP C D 〉〈=令11,2t x ⎡⎫=∈+∞⎪⎢⎣⎭，1cos ,BP C D 〉〈=所以当112t x==，即0a =时，1cos ,BP C D 〈〉，直线BP 和1C D 所成角的最小值为4π，故选项D 正确． 故选：ABD.三、填空题：本题共4小题，每小题5分，共20分13．已知()5221ax x x ⎛⎫+- ⎪⎝⎭的展开式中各项系数的和为3-，则该展开式中x 的系数为_________【答案】120- 【解析】【分析】令1x =，求得a ，再利用通项公式求得x 项求解.【详解】因为()5221ax x x ⎛⎫+- ⎪⎝⎭的展开式中各项系数的和为3-，所以令1x =，得()13-+=-a ， 解得2a =，所以二项式为()52221x x x ⎛⎫+- ⎪⎝⎭，则展开式中含x 的项为322322355222C 1C 120⎛⎫⎛⎫⨯-+⨯-=- ⎪ ⎪⎝⎭⎝⎭x x x x x x ， 故x 的系数为-120， 故答案为：120-14．在边长为4的等边ABC 中，已知23AD AB =，点P 在线段CD 上，且12AP mAC AB =+，则AP =________.【解析】 【分析】根据题意得34AP mAC AD =+，求出14m =，所以1142AP AC AB =+，即21142AP AC AB ⎛⎫=+ ⎪，求解即可. 【详解】因为23AD AB =，所以32AB AD =，又12AP mAC AB =+， 即1324AP mAC AB mAC AD =+=+，因为点P 在线段CD 上，所以P ，C ，D 三点共线，由平面向量三点共线定理得，314m +=，即14m =， 所以1142AP AC AB =+，又ABC 是边长为4的等边三角形，所以222211111cos60421644AP AC AB AC AC AB AB ⎛⎫=+=++ ⎪⎝⎭1111164416716424=⨯+⨯⨯⨯+⨯=，故7AP =15．过点()1,0的直线l 截圆C ：22210x y x y +-+-=得到的最短弦长为___________.【答案】【解析】 【分析】由圆的一般方程求得圆的圆心和半径，设点P ()1,0，要使所得的弦长最短，则直线l 垂直于直线PC ，由点到直线的距离公式和勾股定理可求得答案. 【详解】由圆C ：22210x y x y +-+-=得()22191+24x y ⎛⎫-+= ⎪⎝⎭，所以圆心112C ⎛⎫- ⎪⎝⎭，，半径为32r =， 设点P ()1,0， 则11022PC =--=，要使过点()1,0的直线l 截圆C ：22210x y x y +-+-=得到的弦长最短，则直线l 垂直于直线PC ，此时最短弦长为=故答案为：16．已知函数()()2e ,xf xg x x a==，若存在一条直线同时与两个函数图象相切，则实数a 的取值范围__________．【答案】2e (,0),4∞∞⎡⎫-⋃+⎪⎢⎣⎭【解析】 【分析】分0a <与0a >两种情况进行讨论，当0a >时，转化为,()0x ∈+∞时，2exx a=有解，构造函数2(),(0,)ex x h x x ∞=∈+，求出单调性及极值，最值情况，求出a 的取值范围.【详解】数形结合可得：当0a <，存在一条直线同时与两函数图象相切；当0a >，若存在一条直线同时与两函数图象相切， 则,()0x ∈+∞时，2e xx a=有解， 所以21,(0,)ex x x a ∞=∈+，令2(),(0,)e x x h x x ∞=∈+，因为22(2)()e e x xx x x x h x --=='，则当(0,2)x ∈时，()0h x '>，()h x 为单调递增函数； 当(2,)x ∈+∞时，()0h x '<，()h x 为单调递减函数； 所以()h x 在2x =处取得极大值，也是最大值， 最大值为24(2)e h =，且()0h x >在,()0x ∈+∞上恒成立， 所以2140,e a ⎛⎤∈ ⎥⎝⎦，即2e (,0),4a ∞∞⎡⎫∈-⋃+⎪⎢⎣⎭． 故答案为：2e (,0),4a ∞∞⎡⎫∈-⋃+⎪⎢⎣⎭四．解答题：本小题共6小题，共70分。

2022年高考数学江苏卷必刷试卷三（带解析版）江苏卷03-2022年高考数学必刷试卷解析版（三）数学试题I一、填空题（共70分） 1.设全集U＝{x|x>1}，集合A⊆U.若∁UA＝{x|x>9}，则集合A＝________．答案：{x|1<x≤9}解析：因为∁UA＝{x|x>9}，U＝{x|x>1}，A⊆U，所以A＝{x|1<x≤9}．2.已知复数z满足z(1＋i)＝3－i，其中i为虚数单位，则复数z的模|z|＝________．答案：解析：由题意得z＝＝＝1－2i，所以＝.3.某时段内共有100辆汽车经过某一雷达测速区域，将测得的汽车时速绘制成如图所示的频率分布直方图．根据图形推断，该时段时速超过50km/h的汽车辆数为________辆．答案：77解析：由图可知时速超过50km/h的频率为0.039×10＋0.028×10＋0.01×10＝0.77，而共有100辆汽车经过雷达测速区域，所以速度超过50km/h的车辆为77辆．4.如图所示的流程图中，输出的S为________．答案：解析：S＝1＋＋＋＝.6.袋中有形状、大小都相同的4只球，其中1只白球，1只红球，2只黄球，从中一次随机摸出2只球，则这2只球颜色不同的概率为________．答案：解析：从4只球中一次性随机摸出2只球，共有6种情况，颜色相同的有1种，颜色不同的有5种，所以一次随机摸出2只球颜色相同的概率为.7已知正四棱锥的底面边长为4cm，高为cm，则该正四棱锥的侧面积是________cm2.答案：24解析：由题意得正四棱锥的侧面上的高为3，所以该正四棱锥的侧面积为4××4×3＝24.8.设函数f(x)＝－sin2ωx－sinωxcosωx(ω>0)，且y＝f(x)的图象的一个对称中心到最近的对称轴的距离为，则f(x)在区间上的最大值为________.答案：1 解析：f(x)＝－(1－cos2ωx)－sin2ωx＝cos2ωx－sin2ωx＝cos.由题意得＝，所以ω＝1，所以f(x)＝cos.因为x∈，所以∈，所以f(x)的最大值为1.9若b>a>1且3logab＋6logba＝11，则a3＋的最小值为________．答案：2＋1 解析：由3logab＋6logba＝11，可得logab＝3或logab＝.因为b>a>1，所以logab＝3，即b＝a3，所以a3＋＝b＋＝b－1＋＋1.因为b>1，所以b－1＋≥2，即a3＋≥2＋1，当且仅当b＝1＋时取等号．10已知P是圆x2＋y2＝1上一动点，AB是圆(x－5)2＋(y－12)2＝4的一条动弦(A，B是直径的两个端点)，则·的取值范围是________．答案：[140，192] 解析：设圆x2＋y2＝1的圆心为O1，圆(x－5)2＋(y－12)2＝4的圆心为O2，·＝(＋)·(＋)＝2－4，max＝＋1＝14，min＝－1＝12，所以·的最大值为192，最小值为140.13若a>0，b>0，且函数f(x)＝aex＋(b3－8)x在x＝0处取得极值，则a＋3b的取值范围是________．答案：(6，10] 解析：因为f′(x)＝aex＋(b3－8)，由题意得a＋(b3－8)＝0，所以a＝8－b3，所以a＋3b＝8－b3＋3b.令g(b)＝8－b3＋3b，g′(b)＝－3b2＋3＝－3(b＋1)(b－1)．因为a>0，所以8－b3>0.又b>0，所以0<b<2，所以g(b)在(0，1)上单调递增，在(1，2)上单调递减，所以g(b)∈(6，10]．14在△ABC中，边a，b，c所对应的角分别为A，B，C.若2sin2B＋3sin2C＝2sinAsinBsinC＋sin2A，则tanA＝________．答案：－1 解析：由2sin2B＋3sin2C＝2sinAsinBsinC＋sin2A及正弦定理，得2b2＋3c2＝2bcsinA＋a2，所以b2＋c2－a2＋b2＋2c2＝2bcsinA．由余弦定理得2bccosA＋b2＋2c2＝2bcsinA，即sinA－cosA＝≥，而sinA－cosA＝sin≤，所以sinA－cosA＝sin＝.因为0<A<π，所以A＝，所以tanA＝－1.二、解答题：本大题共6小题，共90分.解答时应写出必要的文字说明、证明过程或演算步骤．15.(本小题满分14分)在△ABC中，角A，B，C所对应的边分别为a，b，c.已知(sinC－sinA)＝sinB.(1)求的值；(2)若b＝，·＝，求△ABC的面积．解：(1)由正弦定理，(c－a)＝b⇒＝.(4分)(2)⇒⇒⇒(8分)∴cosB＝⇒sinB＝，(12分)∴△ABC的面积S＝acsinB＝.(14分)16.(本小题满分14分)如图，在四棱锥PABCD中，M是PA上的点，△ABD为正三角形，CB＝CD，PA⊥BD.(1)求证：平面MBD⊥平面PAC；(2)若∠BCD＝120°，DM∥平面BPC，求证：点M为线段PA的中点．证明：(1)取BD的中点O，连结OA，OC，∵△ABD为正三角形，∴OA⊥BD.∵CB＝CD，∴OC⊥BD.在平面ABCD内，过O点垂直于BD的直线有且只有一条，∴A，O，C三点共线，即AC⊥BD.(2分)∵PA⊥BD，AC，PA⊂平面PAC，AC∩PA＝A，∴BD⊥平面PAC.(4分)∵BD⊂平面MBD，∴平面MBD⊥平面PAC.(6分)(2)(证法1)延长BC，AD，交于Q点，连结PQ，∵DM∥平面BPC，DM⊂平面PAQ，平面BPC∩平面PAQ＝PQ，∴DM∥PQ.(8分)在△CBD中，∵CB＝CD，∠BCD＝120°，∴∠CBD＝30°，∴∠ABC＝30°＋60°＝90°，∴△ABO为直角三角形．∵在Rt△ABQ中，∠BAQ＝60°，∴AQ＝2AB＝2AD，∴点D是AQ的中点，(12分)∴点M为线段PA的中点．(14分)(证法2)取AB的中点N，连结MN和DN，易算得∠ABC＝90°，即AB⊥BC.∵△ABD为正三角形，∴DN⊥AB.又DN，BC，AB共面，∴DN∥CB.∵DN⊄平面BPC，CB⊂平面BPC，∴DN∥平面BPC.(8分)∵DM∥平面BPC，DN，DM⊂平面DMN，∴平面DMN∥平面BPC.(12分)∵MN⊂平面DMN，∴MN∥平面BPC.∵MN⊂平面PAB，平面PAB∩平面BPC＝PB，∴MN∥PB.∵N是AB的中点，∴M为线段PA的中点．(14分)17.(本小题满分14分)如图，一块地皮OAB，其中OA，AB是直线段，曲线段OB是抛物线的一部分，且点O是该抛物线的顶点，OA所在的直线是该抛物线的对称轴．经测量，OA＝2km，AB＝km，∠OAB＝.现要从这块地皮中划一个矩形CDEF来建造草坪，其中点C在曲线段OB上，点D，E在直线段OA上，点F在直线段AB上，设CD＝akm，矩形草坪CDEF的面积为f(a)km2.(1)求f(a)，并写出定义域；(2)当a为多少时，矩形草坪CDEF的面积最大？解：(1)以O点为原点，OA边所在直线为x轴，建立如图所示的平面直角坐标系，过点B作BG⊥OA于点G，在Rt△ABC中，AB＝，∠OAB＝，所以AG＝BG＝1.因为OA＝2，所以OG＝1，则B(1，1)．设抛物线OCB的标准方程为y2＝2px，代入点B的坐标，得p＝，所以抛物线OCB的方程为y2＝x.(4分)因为CD＝a，所以AE＝EF＝a，则DE＝2－a－a2，所以f(a)＝a(2－a－a2)＝－a3－a2＋2a，定义域为(0，1)．(8分)(2)由题意得f′(a)＝－3a2－2a＋2，令f′(a)＝0，得a＝或(舍)．(10分)当0<a<时，f′(a)>0，f(a)在上单调递增；当<a<1时，f′(a)<0，f(a)在上单调递减．所以当a＝时，f(a)取得极大值，也是最大值，此时矩形草坪CDEF的面积最大．(14分)18.(本小题满分16分)如图，在平面直角坐标系xOy中，A，B是圆O:x2＋y2＝1与x轴的两个交点(点B在点A右侧)，点Q(－2，0)，x轴上方的动点P使直线PA，PQ，PB的斜率存在且依次成等差数列．(1)求证：动点P的横坐标为定值；(2)设直线PA，PB与圆O的另一个交点分别为S，T，求证：点Q，S，T三点共线．证明：(1)由题设知A(－1，0)，B(1，0)．设P(x0，y0)(y0>0)，则kPQ＝，kPA ＝，kPB＝.(4分)因为直线PA，PQ，PB的斜率存在且依次成等差数列，所以2kPQ＝kPA＋kPB，即＝＋，解得x0＝－，即动点P的横坐标为定值．(8分)(2)由(1)知P，kPA＝2y0，kPB＝－y0，直线PA的方程为y＝2y0(x＋1)，代入x2＋y2＝1得(x＋1)[(1＋4y)x－(1－4y)]＝0，所以点S的横坐标xS＝，从而yS＝.同理：xT＝，yT＝，(12分)所以kQS＝＝，kQT＝＝，所以kQS＝kQT，所以点Q，S，T三点共线．(16分)19.(本小题满分16分)设f(x)＝ex·sinx＋ax(a为常数)，x∈[0，2π]．(1)当a＝0时，求f(x)的单调区间；(2)若f(x)在区间(0，2π)的极大值、极小值各有一个，求实数a的取值范围．解：(1)当a＝0时，f′(x)＝ex(sinx＋cosx)＝exsin.(2分)令f′(x)>0，则0<x<，<x<2π时，f(x)单调递增；(4分)令f′(x)<0，则<x<时，f(x)单调递减，所以f(x)的单调增区间为，，f(x)的单调减区间为.(6分)(2)设g(x)＝f′(x)＝ex(sinx＋cosx)＋a，则g′(x)＝2excosx.令g′(x)>0，则cosx>0，0<x<，<x<2π.令g′(x)<0，则cosx<0，<x<，所以g(x)的单调增区间为，，g(x)的单调减区间为，故g(x)在x＝处取得极大值，在x＝处取得极小值．(8分)g(0)＝a＋1，g＝a＋e，g＝a－e，g(2π)＝a＋e2π，所以g(2π)>g>g(0)>g.(10分)若g≥0恒成立，则f′(x)≥0，f(x)在(0，2π)上单调递增，故f(x)在(0，2π)内无极值，所以g<0.(12分)若g≤0，则f(x)在(0，2π)内至多有一个极值点，从而g>0，g(2π)>0，于是在区间，内f(x)分别有极大值、极小值各一个，则在内必无极值点，从而g(0)≥0.(14分)⇒⇒－1≤a<e，所以a的取值范围是[－1，e]．(16分)20.(本小题满分16分)设{an}为各项均不相等的数列，Sn为它的前n项和，且满足λnan＋1＝Sn＋1(n∈N*，λ∈R)．(1)若a1＝1，且a1，a2，a3成等差数列，求λ的值；(2)若数列{an}的各项均不为零，问当且仅当λ为何值时，a2，a3，a4，…，an，…成等差数列？试说明理由．解：(1)令n＝1，2，得又a1，a2，a3成等差数列，∴2a2＝a1＋a3＝1＋a3 ③.由①②③得λ＝.(3分)(2)当且仅当λ＝时，a2，a3，a4，…，an，…成等差数列．(5分)证明如下：λnan＋1＝Sn＋1 ①，n≥2时，λ(n－1)an＝Sn－1＋1 ②.①－②，得λnan＋1－λn an＋λan＝an，即λn(an＋1－an)＝(1－λ)an.由于{an}的各项均不相等，∴＝(n≥2)③.(7分)当n≥3时，＝④，③－④，得＝－⑤.(10分)(i)当λ＝时，由⑤得－＝1.当a≥3时，＝＋1＝.∵an≠0，∴an＋1－an＝an－an－1⇒2an＝an＋1＋an－1(a≥3)，故a2，a3，a4，…，an，…成等差数列．(12分)(ii)再证当a2，a3，a4，…，an，…成等差数列时，λ＝.∵a2，a3，a4，…，an，…成等差数列，∴an＋1－an＝an－an－1(n≥3)．由⑤得－＝－＝1＝，∴λ＝，∴当且仅当λ＝时，a2，a3，a4，…，an，…成等差数列．(16分)数学Ⅱ(附加题)21．【选做题】本题包括A、B、C三小题，请选定其中两小题，并在相应的答题区域内作答，若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．A.[选修4-2：矩阵与变换]（本小题满分10分）设矩阵A＝，若矩阵A的属于特征值1的一个特征向量为，属于特征值2的一个特征向量为，求矩阵A.解：由题意得＝1，＝2，(5分)所以故A＝.(10分)B(选修4-4：坐标系与参数方程)在极坐标系中，设直线l过点A(，)，B(a，0)，且直线l与曲线C：ρ＝cosθ有且仅有一个公共点，求正数a的值．解：依题意，A的直角坐标为A，(2分)曲线C：ρ＝cosθ的普通方程为2＋y2＝.(4分)因为直线l过点A且与曲线C有且只有一个公共点，设l：y－＝k，所以＝，解得k＝.(7分)令y＝0，所以a＝(另一解舍去)．(10分)C．(选修4-5：不等式选讲)已知a，b>0，且a＋b＝1，求证：＋≤2.证明：因为(＋)2≤(2a＋1＋2b＋1)(12＋12)＝8，所以＋≤2.(10分)【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．22.如图，在三棱锥ABCD中，已知△ABD，△BCD都是边长为2的等边三角形，点E为BD的中点，且AE⊥平面BCD，F为线段AB上一动点，记＝λ.(1)当λ＝时，求异面直线DF与BC所成角的余弦值；(2)当CF与平面ACD所成角的正弦值为时，求λ的值．解：连结CE,以E点为原点，以EB，EC，EA所在直线分别为x，y，z轴，建立如图空间直角坐标系，则A(0，0，)，B(1，0，0)，C(0，，0)，D(－1，0，0)．因为F为线段AB上一动点，且＝λ，则＝λ＝λ(－1，0，)＝(－λ，0，λ)，所以F(1－λ，0，λ)．(1)当λ＝时，F，＝，＝(1，－，0)，所以cos〈，〉＝＝.(4分)(2)＝(1－λ，－，λ)，设平面ACD的一个法向量为n＝(x，y，z)．由n⊥，n⊥得化简得令x＝，则y＝－1，z＝－1，取n＝(，－1，－1)．设CF与平面ACD所成角为θ，则sinθ＝|cos〈，n〉|＝＝，解得λ＝或λ＝2(舍)，所以λ＝.(10分)23.设(1＋2)2n＋1＝an＋bn(n∈N*，an∈Z，bn∈Z)．求证：(1)a－8b能被7整除；(2)bn不能被5整除．23.证明：(1)因为(1＋2)2n＋1＝C＋C(2)＋C(2)2＋…＋C(2)2n＋1，(1－2)2n＋1＝C－C(2)＋C(2)2＋…－C(2)2n＋1，又(1＋2)2n＋1＝an＋2bn，所以(1－2)2n＋1＝an－2bn，所以(1＋2)2n＋1(1－2)2n＋1＝(an＋2bn)(an－2bn)，即a－8b＝－72n＋1，所以a－8b能被7整除．(5分)(2)由a－8b＝－72n＋1得8b＝a＋72n＋1.因为72n＝49n＝(50－1)n＝C50n＋C50n－1(－1)＋…＋C50(－1)n－1＋C(－1)n除最后一项外都是5的倍数，所以72n＋1用5除所得的余数是2或－2.因为a是平方数，其末位数可能是0，1，4，5，6，9，所以a＋72n＋1末位数不可能是0或5，所以不能被5整除，即8b不能被5整除，从而b不能被5整除，所以bn不能被5整除．(10分)以下内容为“高中数学该怎么有效学习？”首先要做到以下两点：1、先把教材上的知识点、理论看明白。

2022年高考数学模拟卷（新高考专用）二轮拔高卷03(本试卷共6页，22小题，满分150分.考试用时120分钟)一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}sin ,M y y x x ==∈R ∣，{}2,x N y y x ==∈R ∣，则M N =（） A ．[)1,-+∞ B ．[)1,0-C ．[]0,1D ．(]0,12．已知12z i =-，则5iz=（） A ．2i -+ B ．2i - C ．105i -D ．105i -+3．，则该圆锥的体积为（）A B ．23πC D ．43π4．直线2x y +=与圆()()22236x y -+-=交于A 、B 两点，则AB =（）A ．BCD ．5．已知()f x 为偶函数，且函数()()g x xf x =在[)0,∞+上单调递减，则不等式()()11x f x --()220xf x +>的解集为（）A ．1,3⎛⎫-∞ ⎪⎝⎭B ．(),1-∞-C ．1,3⎛⎫+∞ ⎪⎝⎭D ．()1,-+∞6．假期里，有4名同学去社区做文明实践活动，根据需要，要安排这4名同学去甲、乙两个文明实践站，每个实践站至少去1名同学，则不同的安排方法共有（） A ．20种B ．14种C ．12种D ．10种7．长方体1111ABCD A B C D -中，11,2AB AD AA ===，E 为棱1AA 上的动点，平面1BED 交棱1CC 于F ，则四边形1BED F 的周长的最小值为（）A ．B ．C ．D ．2+8．已知()42e ,4(16)143,4x x f x x x -⎧≤=⎨-->⎩，则当0x ≥时，()2x f 与()2f x 的大小关系是（） A ．()()22x f f x ≤B ．()()22x f f x ≥C ．()()22x f f x =D ．不确定二､选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．若函数()cos2sin f x x x =+，则关于()f x 的性质说法正确的有（） A ．偶函数B ．最小正周期为πC ．既有最大值也有最小值D ．有无数个零点10．已知12,F F 为椭圆22:13xC y +=的左､右焦点，直线(0)y kx k =>与椭圆C 交于,A B 两点，过点A 向x 轴作垂线，垂足为E ，则（）A ．椭圆CB ．四边形12AF BF 的周长一定是C ．点E 与焦点重合时，四边形12AF BF 的面积最大D ．直线BE 的斜率为12k11．已知(),P x y 为曲线x =A 1B ．存在一个定点和一条定直线，使得P 到定点的距离等于P 到定直线的距离C ．P 到直线2y x =--D 612．对于正整数(),n n ϕ是小于或等于n 的正整数中与n 互质的数的数目.函数()n ϕ以其首名研究者欧拉命名，称为欧拉函数，例如()96ϕ=，则（）A ．()777log 76log 6ϕ=+B ．数列(){}3nϕ为等比数列C ．数列(){}2n ϕ单调递增D ．数列()2nnϕ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前n 项和恒小于4 三､填空题：本题共4小题，每小题5分，共20分.13．抛物线22(0)y px p =>上一点(3,)M t 与焦点F 的距离||MF p =，则M 到坐标原点的距离为___________.14．22244x x x+++的最小值为___________.15．已知向量()12,1a m =-，向量()31,2b m =+，若//a b ，则实数m =___________. 16．已知：若函数()(),f x g x 在R 上可导，()()f x g x =，则f x g x .又英国数学家泰勒发现了一个恒等式22012e xnn a a x a x a x =+++++，则0a =___________，1011n n na na +==∑___________.四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.17．从①sin sin D A =；②3ABCBCDS S=；③4DB DC ⋅=-这三个条件中任选一个，补充在下面的问题中，并完成解答.已知点D 在ABC 内，cos cos ,6,4,2A D AB AC BD CD >====，若___________，求ABC 的面积.注：如果选择多个条件分别解答，按第一个解答计分.18．已知n S 是数列{}n a 的前n 项和，2n S n =.(1)求数列{}n a 的通项公式； (2)求数列11n n a a +⎧⎫⎨⎬⋅⎩⎭的前n 项和n T .19．某车间打算购买2台设备，该设备有一个易损零件，在购买设备时可以额外购买这种易损零件作为备件，价格为每个100元.在设备使用期间，零件损坏，备件不足再临时购买该零件，价格为每个300元.在使用期间，每台设备需要更换的零件个数m 的分布列为X 表示2台设备使用期间需更换的零件数，n 代表购买2台设备的同时购买易损零件的个数. (1)求X 的分布列；(2)以购买易损零件所需费用的期望为决策依据，试问在11n =和12n =中，应选哪一个？20．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，AD BC ∥，90ABC ∠=︒，12BC AB AD ==，3PA PD ==，Q 为AD 的中点．(1)求证：AD PC ⊥；(2)若平面PAD ⊥底面ABCD ，点E 在棱PC 上，2PE EC =，且二面角E BQ C --的大小为45︒，求四棱锥P ABCD -的体积．21．已知双曲线C 的渐近线方程为y =，且过点P . (1)求C 的方程；(2)设(1,0)Q ，直线()x t t =∈R 不经过P 点且与C 相交于A ，B 两点，若直线BQ 与C 交于另一点D ，求证：直线AD 过定点.22．设函数()323ln 2,f x x x ax ax a =-++-∈R .(1)求函数()f x 在1x =处的切线方程；(2)若12,x x 为函数()f x 的两个不等于1的极值点，设()()()()1122,,,P x f x Q x f x ，记直线PQ 的斜率为k ，求证：122k x x +<+.2022年高考数学模拟卷（新高考专用）二轮拔高卷03(本试卷共6页，22小题，满分150分.考试用时120分钟)一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}sin ,M y y x x ==∈R ∣，{}2,x N y y x ==∈R ∣，则M N =（） A ．[)1,-+∞ B ．[)1,0-C ．[]0,1D ．(]0,1【答案】D 【详解】[]sin 1,1y x =∈-，所以[]1,1M =-，()0,2x y ∈=+∞，所以()0,N =+∞，故MN =(]0,1故选：D2．已知12z i =-，则5iz=（） A ．2i -+ B ．2i - C ．105i - D ．105i -+【答案】A()()()5i 12i 5i 5i2i 12i 12i 12i z +===-+--+， 故选：A.3．，则该圆锥的体积为（）A B ．23πC D ．43π【答案】D设圆锥的母线为l ，高为h ，由题意可知，圆锥的底面半径为r =圆锥的侧面积为2122S rl r π=⋅=侧，所以l =故2h =，所以该圆锥的体积为21433V r h ππ==，故选：D.4．直线2x y +=与圆()()22236x y -+-=交于A 、B 两点，则AB =（）A ．BCD ．【答案】B圆心()2,3到直线2x y +=的距离为d ==圆()()22236x y -+-=的半径为r =又2AB =，故AB 故选：B.5．已知()f x 为偶函数，且函数()()g x xf x =在[)0,∞+上单调递减，则不等式()()11x f x --()220xf x +>的解集为（）A ．1,3⎛⎫-∞ ⎪⎝⎭B ．(),1-∞-C ．1,3⎛⎫+∞ ⎪⎝⎭D ．()1,-+∞【答案】B 【解析】因为()f x 为偶函数，所以()()g x xf x =为奇函数，又()g x 在[)0,∞+上单调递减，所以()g x 在R 上单调递减，所以由()()()11220x f x xf x --+>，得()()()11220x f x xf x --+>， 即()()120g x g x -+>，()()()122g x g x g x ->-=-， 所以12x x -<-，得1x <-，即(),1x ∈-∞-. 故选：B.6．假期里，有4名同学去社区做文明实践活动，根据需要，要安排这4名同学去甲、乙两个文明实践站，每个实践站至少去1名同学，则不同的安排方法共有（） A ．20种 B ．14种 C ．12种 D ．10种【答案】B解：先将4名同学分为两组，两组人数为可能为1,3人或2,2人，当两组人数为1,3时，有13434C C =种方案，当两组人数为2,2时，有2242223=C CA 种方案，所以将4名同学分为两组，共有7种方案，再将两组同学分配到两个文明实践站，有222A =种，所以根据乘法原理得共有7214⨯=种不同的方法. 故选：B7．长方体1111ABCD A B C D -中，11,2AB AD AA ===，E 为棱1AA 上的动点，平面1BED 交棱1CC 于F ，则四边形1BED F 的周长的最小值为（）A ．B ．C ．D ．2+【答案】B解：将长方体展开，如图所示：当点E 为1BD 与1AA 的交点，F 为1BD 与1CC 的交点时，截面四边形1BED F 的周长最小，最小值为12BD == 故选：B ．8．已知()42e ,4(16)143,4x xf x x x -⎧≤=⎨-->⎩，则当0x ≥时，()2x f 与()2f x 的大小关系是（） A ．()()22x f f x ≤B ．()()22x f f x ≥C ．()()22x f f x =D ．不确定 【答案】B 【详解】解：由函数()42e ,4(16)143,4x x f x x x -⎧=⎨-->⎩， 得函数()f x 在(),4∞-上递增，在()4,16上递减，在()16,+∞上递增， 作出函数2x y =和2yx 的图像，如图所示，令22x x =，得2x =或4，结合图像可知，当02x ≤<时，2420x x >>≥，则()()22x f f x >，当24x ≤≤时，24216x x ≤≤≤，则()()22x f f x ≥， 当4x >时，2216x x >>，则()()22x f f x >，综上所述，当0x ≥时，()()22x f f x ≥.故选：B.二､选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．若函数()cos2sin f x x x =+，则关于()f x 的性质说法正确的有（） A ．偶函数B ．最小正周期为πC ．既有最大值也有最小值D ．有无数个零点【答案】CDA ：因为()()cos(2)sin()cos2sin f x x x x x f x -=-+-=-≠，所以该函数不是偶函数，因此本选项说法不正确；B ：因为()cos[2()]sin()cos2sin ()f x x x x x f x πππ+=+++=-≠，所以该函数最小正周期不是π，因此本选项说法不正确；C ：因为()2219cos2sin 12sin sin 2(sin )48f x x x x x x =+=-+=--+，当1sin 4x =时，该函数有最大值，当sin 1x =-时，该函数有最小值，因此本选项说法正确；D ：()cos2sin 0f x x x =+=，则有212sin sin 0x x -+=，解得sin 1x =，或1sin 2x =-，即()x k k Z π=∈，或72()6x k k Z ππ=+∈，或112()6x k k Z ππ=+∈，因此本选项说法正确， 故选：CD10．已知12,F F 为椭圆22:13x C y +=的左､右焦点，直线(0)y kx k =>与椭圆C 交于,A B 两点，过点A 向x 轴作垂线，垂足为E ，则（） A ．椭圆CB ．四边形12AF BF的周长一定是C ．点E 与焦点重合时，四边形12AF BF 的面积最大 D ．直线BE 的斜率为12k【答案】ABD由C的方程可得离心率为e =，故A 正确；由椭圆定义可知，122AF AF a +==122BF BF a +== 所以四边形12AF BF的周长一定是B 正确； 四边形12AF BF的面积12121212222AF F BF F AF F S SSScb =+=<⨯⨯=，当点E与焦点重合时，2b AE a ==此时四边形12AF BF的面积122AF F S S ==故C 错误；设()11,A x y ，故()11,B x y --，则()1111,0,22BE y E x k k x ==，故D 正确. 故选：ABD11．已知(),P x y为曲线x = A1B ．存在一个定点和一条定直线，使得P 到定点的距离等于P 到定直线的距离C ．P 到直线2y x =--D6【答案】ABD 【详解】由x =()240x y x =≥，则曲线x =24x y =的右半部分(含原点).因为抛物线24x y =的焦点为()0,1F ，准线为l ：1y =-，所以B 正确，1PF =≥，A 正确，原点到直线2y x =--2y x =--的距离是最短距离，C 错误.设点()1,5A 到准线l ：1y =-的距离为d ，P 到准线l ：1y =-的距离为1d ，PF PA =+1516d PA d =+≥=+=，D 正确. 故选：ABD12．对于正整数(),n n ϕ是小于或等于n 的正整数中与n 互质的数的数目.函数()n ϕ以其首名研究者欧拉命名，称为欧拉函数，例如()96ϕ=，则（）A ．()777log 76log 6ϕ=+B ．数列(){}3nϕ为等比数列C ．数列(){}2n ϕ单调递增D ．数列()2nnϕ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前n 项和恒小于4 【答案】ABD 【详解】因为7为质数，所以与77不互质的数为7，14，21，…，77，共有76777=个，所以()()776777log 7log 776log 6ϕ=-=+，故A 正确；因为与3n 互质的数为1，2，4，5，7，8，10，11，…，32n -，31n -，共有11(31)323n n ---⋅=⋅个，所以()1323n n ϕ-=⋅，则数列(){}3n ϕ为等比数列，故B 正确；因为()21ϕ=，()42ϕ=，()62ϕ=，所以数列(){}2n ϕ不是单调递增数列，故C 错误； 因为()122nn ϕ-=，所以()11122222nn ni i ii i i i i iϕ=====∑∑∑. 设21122222nn in i i n S ===+++∑，则231112122222nn n n nS +-=++++， 所以1231111111121222112222222212n n n n n n n n n S ++++-+=++++-=-=--，所以222n n n S +=-，从而数列()2nnϕ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前n 项和为122442n n n S -+=-<，故D 正确.故选：ABD三､填空题：本题共4小题，每小题5分，共20分.13．抛物线22(0)y px p =>上一点(3,)M t 与焦点F 的距离||MF p =，则M 到坐标原点的距离为___________. 【答案】 【详解】抛物线22y px =的准线为：2p x =-，由抛物线定义得：3()2pp --=，解得6p ， 抛物线方程为212y x =，而(3,)M t 在抛物线上，则236t =，原点为O ，即有||MO =所以M到坐标原点的距离为故答案为：14．22244x x x+++的最小值为___________.【答案】9 【详解】因为22222444559x x x x x+++=++≥=，当且仅当224x x =，即22x =时，等号成立，所以22244x x x+++的最小值为9.故答案为：915．已知向量()12,1a m =-，向量()31,2b m =+，若//a b ，则实数m =___________. 【答案】17因为//a b ，所以3124m m +=-，所以17m =. 故答案为：17.16．已知：若函数()(),f x g x 在R 上可导，()()f x g x =，则f x g x .又英国数学家泰勒发现了一个恒等式22012e xnn a a x a x a x =+++++，则0a =___________，1011n n na na +==∑___________. 【答案】 1 2011##9111【详解】解：因为22012e x n n a a x a x a x =+++++，令0x =，即00e a =，所以01a =；()()221121e 2e21xxn n n n a a x na x n a x -+'==++++++又220122e 2222x n n a a x a x a x =+++++，所以()121n n a n a +=+，所以121n n a a n +=+，所以()1211211n n a n n n n na +⎛⎫==- ⎪++⎝⎭所以10101111111120212231011121111n n n na n n na +==⎛⎫==--+-+ ⎛⎫+-⎪ =⎝⎝⎭⎪+⎭∑∑故答案为：1；2011四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.17．从①sin sin D A =；②3ABCBCDS S=；③4DB DC ⋅=-这三个条件中任选一个，补充在下面的问题中，并完成解答.已知点D 在ABC 内，cos cos ,6,4,2A D AB AC BD CD >====，若___________，求ABC 的面积.注：如果选择多个条件分别解答，按第一个解答计分.【答案】【详解】 解：选择①，因为点D 在ABC 内，sin sin D A =，cos cos A D >， 所以A D π+=，所以cos cos D A =-，由余弦定理得222222cos 2cos BC DB DC DB DC D AB AC AB AC A =+-⋅⋅=+-⋅⋅， 即16416cos 361648cos A A ++=+-，解得1cos 2A =， 又()0,A π∈，所以3A π=，所以1sin 2ABCSAB AC A =⋅⋅=选择②， 因为3ABCBCDSS=，所以11sin 3sin 22AB AC A DB DC D ⋅⋅=⨯⋅⋅， 所以sin sin D A =，又因为点D 在ABC 内，cos cos A D >， 所以所以A D π+=，所以cos cos D A =-，由余弦定理得222222cos 2cos BC DB DC DB DC D AB AC AB AC A =+-⋅⋅=+-⋅⋅， 即16416cos 361648cos A A ++=+-，解得1cos 2A =， 又()0,A π∈，所以3A π=，所以1sin 2ABCSAB AC A =⋅⋅=选择③，因为4cos D D D B DC B DC ⋅⋅=-=，所以1cos 2D =-，在BCD △中 ，22212cos 164242282BC DB DC DB DC D ⎛⎫=+-⋅⋅=+-⨯⨯⨯-= ⎪⎝⎭，在ABC 中，2223616281cos 22642AB AC BC A AB AC +-+-===⋅⨯⨯，又()0,A π∈，所以3A π=，所以1sin 2ABCSAB AC A =⋅⋅=18．已知n S 是数列{}n a 的前n 项和，2n S n =.(1)求数列{}n a 的通项公式； (2)求数列11n n a a +⎧⎫⎨⎬⋅⎩⎭的前n 项和n T .【答案】(1)21n a n =- (2)21n nT n =+ 【解析】 【分析】（1）利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩求得n a .（2）利用裂项求和法求得n T . (1)当2n 时，由2n S n =，得21(1)n S n -=-，则221(1)21n nn a S S n n n -=-=--=-.当1n =时，有111S a ==，符合上式. 综上，21n a n =-. (2)由（1）得，()()111111212122121n n a a n n n n +⎛⎫==- ⎪⋅-+-+⎝⎭，则11111111121335572121n T n n ⎛⎫=-+-+-++- ⎪-+⎝⎭11122121n n n ⎛⎫=-= ⎪++⎝⎭. 19．某车间打算购买2台设备，该设备有一个易损零件，在购买设备时可以额外购买这种易损零件作为备件，价格为每个100元.在设备使用期间，零件损坏，备件不足再临时购买该零件，价格为每个300元.在使用期间，每台设备需要更换的零件个数m 的分布列为X 表示2台设备使用期间需更换的零件数，n 代表购买2台设备的同时购买易损零件的个数. (1)求X 的分布列；(2)以购买易损零件所需费用的期望为决策依据，试问在11n =和12n =中，应选哪一个？ 【答案】(1)答案见解析； (2)应选择12n =. 【解析】 【分析】(1)由每台设备需更换零件个数的分布列求出X 的所有可能值，并求出对应的概率即可得解. (2)分别求出11n =和12n =时购买零件所需费用的期望，比较大小即可作答. (1)X 的可能取值为10，11，12，13，14，(10)0.30.30.09P X ==⨯=，(11)20.30.50.3P X ==⨯⨯=，(12)20.30.20.50.50.37P X ==⨯⨯+⨯=，(13)20.50.20.2P X ==⨯⨯=， (14)0.20.20.04P X ==⨯=，则X 的分布列为：(2)记1Y 为当11n =时购买零件所需费用，()11100(11)0.39P Y P X ==≤=元，()11400(12)0.37P Y P X ====元， ()11700(13)0.2P Y P X ====元，()12000(14)0.04P Y P X ====元， ()111000.3914000.3717000.220000.041367E Y =⨯+⨯+⨯+⨯=元，记2Y 为当12n =时购买零件所需费用，()21200(12)0.76P Y P X ==≤=元，()21500(13)0.2P Y P X ====元， ()21800(14)0.04P Y P X ====元，()212000.7615000.218000.041284E Y =⨯+⨯+⨯=元，显然()()12E Y E Y >，所以应选择12n =.20．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，AD BC ∥，90ABC ∠=︒，12BC AB AD ==，3PA PD ==，Q 为AD 的中点．(1)求证：AD PC ⊥；(2)若平面PAD ⊥底面ABCD ，点E 在棱PC 上，2PE EC =，且二面角E BQ C --的大小为45︒，求四棱锥P ABCD -的体积．【答案】(1)证明见解析【解析】 【分析】（1）连接QC ，可证得四边形BCQA 为平行四边形，进而证明CQ AD ⊥，又由等腰PAD △三线合一可证得PQ AD ⊥，则AD ⊥平面PCQ ，故AD PC ⊥得证.（2）几何法：作出二面角E BQ C --的平面角EGH ∠，由45EGH ∠=︒得等腰直角EGH ，将两直角边EH 和GH 分别用PQ 和AQ 表示，求出AB 的值，根据棱锥的体积公式，则可求出四棱锥P ABCD -的体积；向量法：根据题中的条件，建立空间直角坐标系，设BC a =，将相关点的坐标表示出来，求出平面EBQ 和平面BQC 的法向量，根据二面角的向量计算方法，求出a 的值，最后根据棱锥的体积公式，求出四棱锥P ABCD -的体积. (1)证明：连接QC ， 因为1,2AD BC BC AD =∥，Q 为AD 的中点， 所以四边形BCQA 为平行四边形，所以BC AQ ∥， 因为90ABC ∠=︒，所以90AQC ∠=︒，即CQ AD ⊥， 因为PA PD =，Q 为AD 的中点，所以PQ AD ⊥ 所以AD ⊥平面PCQ ，因为PC ⊂平面PCQ ，所以AD PC ⊥．(2)解：因为PA PD =，Q 为AD 的中点，所以PQ AD ⊥， 因为平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，所以PQ ⊥平面ABCD ，过点E 作EH PQ ∥交CQ 于点H ，过点H 作HG BQ ⊥交BQ 于点G ，连接EG ，则EGH ∠为二面角E BQ A --的平面角，由已知得45EGH ∠=︒， ∴在直角EHG 中，EH GH =，由于12,33EH PQ GH AQ AQ ===，故PQ =．设12BC AB AD a ====，所以a =故四棱锥P ABCD -的体积为1132V =⨯⨯．法2：因为PA PD =，Q 为AD 的中点，所以PQ AD ⊥， 因为平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =， 所以PQ ⊥平面ABCD ．所以以Q 为原点，以,,QA QC QP 所在直线分别为x 轴，y 轴，z 轴 建立空间直角坐标系，令BC a =，如图：2(0,0,0),(,0,0),0,,3Q A a E a ⎛ ⎝(,,0),(0,,0)B a a C a ，所以20,3QE a ⎛= ⎝，又(,,0)QB a a =，设平面EBQ 的法向量为(,,)m x y z =，则0,0,m QE m QB ⎧⋅=⎨⋅=⎩所以20,30,a y z a x a y ⎧⋅=⎪⎨⎪⋅+⋅=⎩ 所以平面MBQ的法向量为1,m ⎛=- ⎝，由题意知平面BQC 的法向量为(0,0,1)n =， 因为二面角M BQ C --为45︒，所以cos45||||m nm n⋅︒===⋅，解得a =12BC ABAD === 所以四棱锥P ABCD -的体积为1132V =⨯⨯． 21．已知双曲线C 的渐近线方程为y =，且过点P . (1)求C 的方程；(2)设(1,0)Q ，直线()x t t =∈R 不经过P 点且与C 相交于A ，B 两点，若直线BQ 与C 交于另一点D ，求证：直线AD 过定点.【答案】(1)2213x y -=(2)见解析 【解析】 【分析】（1）可设双曲线的方程为()22930x y λλ-=≠，将点P 代入求出λ，即可得解；（2）可设直线BQ 为1x my =+，()()()112211,,,,,B x y D x y A x y -，联立22131x y x my ⎧-=⎪⎨⎪=+⎩，消x ，利用韦达定理求得1212,y y y y +，然后求出直线AD 的方程，整理分析即可得出结论. (1)解：因为双曲线C的渐近线方程为y =， 则可设双曲线的方程为()22930x y λλ-=≠，将点P 代入得9293λ-=，解得13λ=，所以双曲线C 的方程为2213x y -=；(2)解：显然直线BQ 的斜率不为零，设直线BQ 为1x my =+，()()()112211,,,,,B x y D x y A x y -， 联立22131x y x my ⎧-=⎪⎨⎪=+⎩，消x 整理得()223220m y my -+-=，依题意得230m -≠且()224830m m ∆=+->，即22m >且23m ≠，12122222,33m y y y y m m +=-=---， 直线AD 的方程为()211121y y y y x x x x ++=--， 令0y =， 得()211121x x y x xy y -=++122121x y x y y y +=+()()12212111my y my y y y +++=+()1212212my y y y y y ++=+2222223323mm m m m m -⋅---=-- 226323m m m --=-- 3=.所以直线AD 过定点()3,0.22．设函数()323ln 2,f x x x ax ax a =-++-∈R .(1)求函数()f x 在1x =处的切线方程；(2)若12,x x 为函数()f x 的两个不等于1的极值点，设()()()()1122,,,P x f x Q x f x ，记直线PQ 的斜率为k ，求证：122k x x +<+. 【答案】(1)1y a =- (2)证明见解析 【解析】 【分析】（1）首先求出函数的导函数，即可求出切线的斜率，再求出()1f ，即可求出切点坐标，从而求出切线方程；（2）首先求出函数的导函数，依题意()233230x a x +++=在()0,∞+上有两个不等于1的正根，即可得到韦达定理，不妨设12x x <，所以1201x x <<<，根据两点斜率公式得到()()2212121213ln12232x x k x x x x x x =+++---+，即证()()2212121211403ln 122xx x x x x x x +++---+<，根据对数平均不等式可得212121l 63nx x x x x x -<-+-，只需证明()()22121216140221x x x x x x -+++++-<，令21x x t +=，依题意即证328120t t t ++-<-，()2,t ∈+∞，再构造函数利用导数说明函数的单调性，即可得证； (1)解：因为()323ln 2,f x x x ax ax a =-++-∈R ，所以()3213ln111211f a a a =-++⨯-⨯=-，()23322f x x ax a x'=-++-，所以()10f '=，所以切点为()1,1a -，切线的斜率0k =，所以切线方程为1y a =- (2)解：因为()()()23221332333223322x x a x x ax ax f x x ax a x x x ⎡⎤-++++--⎣⎦'=-++-==因为12,x x 为函数()f x 的两个不等于1的极值点，所以()233230x a x +++=在()0,∞+上有两个不等于1的正根，所以()21212Δ3236032031a a x x x x ⎧=+->⎪+⎪+=->⎨⎪⋅=⎪⎩，所以92<-a ，不妨设12x x <，所以1201x x <<<，所以()()()2323222211112121213ln 23ln 2x x x x x x x x f x f x k a x x x a a a x -++--+=+--=--- ()()()()()2222122112121211213ln 2a a x x x x x x x x x x x x x x x x -+=-+++-+---()()221212121213ln2a x x x x x x x x x x a =++-+---+ ()()()()222121212121213323ln3123x x x x x x x x x x x x =--++--+++-++ ()()2212121213ln12232x x x x x x x x =+++---+ 要证122k x x +<+即证()()222121211123ln122232x x x x x x x x x x -+--+<++++， 即()()2212121211403ln122x x x x x x x x +++---+<，令2(1)()ln ,(1)(1)x g x x x x -=->+，则22214(1)()(1)(1)x g x x x x x -'=-=++，所以当1x >时，()0g x '>，所以函数()g x 在(1,)+∞上单调递增，故()(1)0g x g >=，即2(1)ln 0(1)x x x -->+，所以ln 211x x x >-+在(1,)+∞上恒成立，因为1201x x <<<，所以211x x >，所以212211ln 211x x x x x x >-+，即21212111ln2x x x x x x x x >-+， 即212121l ln 2n x x x x x x ->-+，所以212121l 63n xx x x x x -<-+-， 下面只需证明()()22121216140221x x x x x x -+++++-<，令21x x t +=，因为211x x ⋅=，所以121x x =，所以122212x x x x +=+>，所以2t >， 即证21142260t t t --+<+，()2,t ∈+∞， 即证328120t t t ++-<-，()2,t ∈+∞，令()32812g t t t t =-++-，()2,t ∈+∞，()()()23283420g t t t t t '=-++=-+-<，所以()g t 在()2,+∞上单调递减，所以()()20g t g <=，得证；。

2022年普通高等学校招生全国统一考试新高考卷数学模拟测试(三)1. 集合Z 中元素的个数为A. 5 B. 4 C. 3D. 22. 若复数，则A. iB.C.D.3. 北京时间2021年6月17日9时22分，搭载神舟十二号载人飞船的长征二号F 遥十二运载火箭在酒泉卫星发射中心点火发射.此后，神舟十二号载人飞船与火箭成功分离，进入预定轨道，顺利将聂海胜、刘伯明、汤洪波3名航天员送入太空，飞行乘组状态良好，发射取得圆满成功.某校欲组建航空航天课外兴趣小组，现从甲、乙、丙、丁4位学生中任选2人去航空航天博物馆进行参观学习，则甲、乙两位学生至少有一位被选中的概率为( )A. B.C.D.4.A. 2B.C. 1D.5. 已知函数，若，则( )A.B.C. 2D.6. 如图，在四棱锥中，四边形ABCD 为正方形，，，E 、F分别是线段BC 、CD 的中点，若，，则直线PE 与AF 所成角的余弦值为A.B. C. D.7. 已知动点到直线的距离的平方比到坐标原点O 的距离的平方大4，若动点Q 满足，且存在定点P ，使得为定值s ，则 A. 1B. 2C. 3D. 48. 若关于x 的方程在内有两个不同的实数根，则实数a 的取值范围为( )A.B.C. D.9. 有一组样本数据，，，的平均数、众数和中位数均为3，方差为2，由这组数据得到新样本数据，，，的平均数、众数、中位数及方差分别为a、b、c及d，则( )A. B. C. D.10. 已知双曲线的离心率为e，则( )A. 双曲线C的焦点不可能在y轴上B. 是该双曲线的一个焦点C. 该双曲线的渐近线方程可能为D. e的最大值为11. 已知函数，直线为图象的一条对称轴，则下列说法错误的是A.B. 在区间上单调递增C. 在区间上的最大值为2D. 若为偶函数，则Z12. 若，则下列说法一定正确的是A. B.C. 若，则D. 若，则13. 已知向量，，，若，则实数________.14. 的展开式中，除常数项外，各项系数和为________.15. 已知的内角A，B，C所对的边分别为a，b，c，若，，则外接圆的半径为________.16. 如图所示，四边形ABCD为菱形，，，平面ABCD，M，P，Q分别为BG，BA，EF的中点，N为平面EFG内一点，且直线平面当的面积最小时，三棱锥的外接球的体积为________.17. 2021年8月5日，在东京奥运会乒乓球女团决赛中，中国队战胜日本队，获得金牌．2021年8月6日，在东京奥运会乒乓球男团决赛中，中国队战胜德国队，获得冠军．某乒乓球业余爱好者协会为了解某社区青少年喜欢打乒乓球是否与性别有关，做了相关调查，制成如下列联表．喜欢不喜欢总计男8020100女7030100总计15050200男、女青少年喜欢乒乓球的频率分别为多少？能否有的把握认为喜欢乒乓球与性别有关？附：，k18. 在中，内角A，B，C的对边分别为a，b，c，且求；若的面积，求a的最小值．19. 已知正项数列的前n项和为，且满足求数列的通项公式；若，求20. 如图，在圆锥PO中，A，B，C，D四点在底面积圆O上，且，证明：若平面PAB与平面PCD的交线为l，且二面角的余弦值为，求圆锥PO的体积．21. 已知直线是曲线在处的切线．求a，b的值；证明：22.已知椭圆C：的左、右焦点分别为、，点E为椭圆C上一动点，O 为坐标原点．若，求的面积；若过点E的斜率为k的直线l与椭圆C相交于另一点F，，M为线段EF的中点，射线OM与椭圆C相交于点N，与的面积分别为、，求的取值范围．答案和解析1.【答案】C【解析】【分析】本题考查集合中元素个数问题，属于基础题.利用列举法化简集合A，即可得到集合A中的元素个数.【解答】解：，所以集合A中的元素个数为故答案选：2.【答案】B【解析】【分析】本题考查了复数代数形式的乘除运算，共轭复数，属于基础题．直接利用复数代数形式的乘除运算化简复数z，则可求．【解答】解：，则故答案选：3.【答案】A【解析】【分析】本题考查古典概型的计算与应用，属于基础题.利用列举法列举基本事件，再求事件的概率.【解答】解：从甲、乙、丙、丁四人中任取两人，共有甲，乙，甲，丙，甲，丁，乙，丙，乙，丁，丙，丁种方法，其中甲、乙两位学生至少有一位被选中的有甲，乙，甲，丙，甲，丁，乙，丙，乙，丁种方法，故所求事件的概率为故选：4.【答案】C【解析】【分析】本题考查诱导公式、二倍角公式的应用，属于基础题.由二倍角公式以及诱导公式化简可得.【解答】解：故答案选：5.【答案】B【解析】【分析】本题考查对数函数的运算，属于基础题.由，则，根据，即可求出【解答】解：因为，故函数的定义域为R，因为，所以函数为奇函数，所以，又因为，所以，所以故选：6.【答案】A【解析】【分析】本题考查异面直线所成角的应用，考查余弦定理，属于中档题.在线段AB上取一点G，且连接GE，PG，由图可知，为异面直线PE与AF所成角，利用余弦定理即可得放入三角形中进行求解.【解答】解：在线段AB上取一点G，且连接GE，PG，如图所示，在四边形ABCD中，易证，所以为异面直线PE与AF所成角，因为，，所以，，所以，则异面直线PE与AF所成角的余弦值为故选：7.【答案】B【解析】【分析】本题考查抛物线的综合应用，要求考生掌握数形结合的思想，把动态问题借助于焦点或准线转移到静态问题上，属于中档题.根据已知条件，得到动点M的轨迹方程，即可求解.【解答】解：由题意可知，，解得，因此点M的轨迹是抛物线，该抛物线的焦点坐标为，准线方程为，过点M作准线的垂线，垂足为N，所以因为，即因为存在定点P，使得为定值，所以有，此时点P为抛物线的焦点，所以故选：8.【答案】D【解析】【分析】本题考查函数与方程的关系，考查利用导数研究函数的单调性，考查转化，构造函数，属于中档题.方程等价于，令，利用导数研究函数的单调性，可得，即可求解.【解答】解：方程等价于，令，则，令，则在内恒成立.所以在上单调递增，因为，所以当时，，时，所以函数在上单调递减，在上单调递增，因为，所以，故实数a的取值范围为故选：9.【答案】BC【解析】【分析】本题考查数字特征，考查处理前后数据的平均数、众数、中位数及方差之间的关系，属于基础题.根据前后样本数据之间的平均数、众数、中位数及方差之间的关系可得.【解答】解：因为，，，的平均数，众数和中位数均为3，方差为2，所以数据，，，的平均数、众数、中位数及方差分别为7、7、7及8，所以及，所以A，D项错误，B、C项正确.故选：10.【答案】AD【解析】【分析】本题考查双曲线的标准方程和性质，属于基础题.利用双曲线的标准方程和性质逐个判断即可.【解答】解：对于A，由题意知，则，所以双曲线的焦点在x轴上，故A项正确;对于B，焦距为，焦点坐标为，故B项错误;对于C，因为该双曲线的渐近线方程为，，所以C项错误.对于D，因为，又，则，则，所以，所以e的最大值为，故D项正确；故选：11.【答案】AC【解析】【分析】本题考查三角函数的综合应用，理解三角函数的对称性、单调性、周期性，属于中档题.根据题意，结合三角函数图象与性质，进而对选项进行一一验证即可.【解答】解：因为直线为函数图象的一条对称轴，所以，因为，所以，故A错误；所以，令，解得，所以函数的单调递增区间为，故B正确；当时，，则，所以在区间上的最大值为1，故C错误；，若函数为偶函数，则，解得，故D正确.故选：12.【答案】ACD【解析】【分析】本题考查不等式性质，要求考生理解对数的运算性质及指数函数的性质，属于中档题.利用函数单调性以及不等式性质逐项分析求解.【解答】解：因为，所以，所以，故选项A正确；令，，所以，故选项B不正确；因为，所以函数在区间上单调递增，所以，即，故选项C正确；因为，所以，所以，所以，即，故选项D正确.故选：13.【答案】【解析】【分析】本题考查平面向量的坐标运算，向量共线的坐标表示，属于基础题.由向量的坐标运算得，根据两向量共线的充要条件解答即可.【解答】解：向量，，，，，，解得14.【答案】49【解析】【分析】本题考查二项式定理，要求考生会用二项式定理解决与二项展开式有关的问题，属于中档题.利用二项式展开项通项公式，以及二项式定理即可求解【解答】解：的展开式的通项公式为，，1，2，，6，令，解得，所以展开式中的常数项为，令，得到所有项的系数之和为，所以除常数项外，各项系数的和为故答案为：15.【答案】5【解析】【分析】本题考查解三角形，要求考生掌握正、余弦定理及三角恒等变换，属于基础题.利用余弦定理及同角三角关系求得，即可利用正弦定理求解.【解答】解：，所以，因为，所以，因为，所以外接圆的半径为故答案为：16.【答案】【解析】【分析】本题考查球的体积公式、线面平行的性质、面面平行的判定、面面平行的性质，属于中档题.证出平面平面AEG，求出的面积最小时，三棱锥的外接球半径，即可求出结果.【解答】解：因为，，且平面ABCD，所以四边形GBCF，EDCF均为矩形，所以，，所以四边形APQE为平行四边形，所以，因为平面AEG，平面AEG，所以平面AEG，因为，且平面AEG，平面AEG，所以平面AEG，又，所以平面平面AEG，因为直线平面MPQ，所以点N在直线EG上，由题意易知，，因为，所以当FN最小时，的面积最小，因为四边形ABCD为菱形，所以，所以当N为EG中点时，FN最小，所以平面EGB，所以，所以，均是以BF为斜边的直角三角形，所以BF是三棱锥外接球的直径，又因为，所以，所以三棱锥外接球的半径为，故三棱锥外接球的体积为故答案为：17.【答案】解：男生喜欢乒乓球的频率为，女性喜欢乒乓球的频率为由题知，，所以没有的把握认为喜欢乒乓球与性别有关.【解析】本题主要考查以奥运会中国丘乓球女团、男团夺冠为情景，要求考生运用独立性检验等相关知识解答相关问题.要求考生有运用所学知识解决实际问题的能力，体现数学运算及数据分析的学科素养，突出基础性、应用性的考查要求.属于基础题.根据列联表即可求解；由计算可得.18.【答案】解：设R为三角形的外接圆的半径，所以因为，所以，所以，所以，所以，因为，且，所以因为，所以，所以，由易知，，因为，所以，即，当且仅当时等号成立，所以a的最小值为【解析】【分析】本题主要考查三角形的面积公式，考查正弦定理，考查同角三角函数的基本关系，考查余弦定理及基本不等式，属于中档题.设R为三角形的外接圆的半径，由正弦定理可得，利用同角三角函数的基本关系，求出即可;由易知，，利用余弦定理及基本不等式即可求出a的最小值.19.【答案】解：当时，，，，当时，，，两式作差得：，，即是以1为首项，1为公差的等差数列，由得，，，两式相减得：【解析】本题主要考查了数列的递推关系，等差数列的判定及通项公式，以及错位相减法求和，考查了推理能力与计算能力，属于中档题.利用数列的递推关系，根据与的关系，可推出是以1为首项，1为公差的等差数列，由此可得的通项公式；利用错位相减法求和可得.20.【答案】证明：因为，，所以，故线段AD为圆O的直径.连接OC，因为，所以，所以，又因为，且，PO、平面POC，所以平面POC，因为平面POC，所以；解：由题意，四边形ABCD是等腰梯形，以O为坐标原点，建立如图所示的空间直角坐标系，设，因为，，所以，，，，，所以，，，设平面PAB的法向量，所以，即，取，解得，，所以平面PAB的一个法向量设平面PCD的法向量，所以，即，取，解得，，所以平面PCD的一个法向量，因为二面角的余弦值为，所以，解得或经检验，不合题意，所以圆锥PO的体积为【解析】本题考查线面垂直的判定，线面垂直的性质，二面角，利用空间向量求面面的夹角，圆锥体积的计算，属于中档题.根据题意利用线面垂直的判定定理证明平面POC，再由平面POC，线面垂直的性质可得；以O为坐标原点，建立如图所示的空间直角坐标系，设，利用空间向量法求出，再由圆锥的体积公式可得.21.【答案】解：因为，所以，又因为，所以，综上知，证明：先证：，即，令，，由，解得，由，解得，所以函数在区间上单调递减，在区间上单调递增，所以，即，当且仅当时等号成立.再证：，即，令，，由，解得，由，解得，所以函数在区间上单调递增，在区间上单调递减，所以，即，当且仅当时等号成立.所以【解析】本题考查导数的几何意义，构造函数，考查利用导数研究函数的单调性，考查导数中的函数不等式，属于较难题.由题知，，将代入，可求出a，b；将问题转化为先证：，利用导数研究函数得单调性即可；再证，构造函数，利用导数研究函数得单调性即可得证.22.【答案】解：设，，所以，由于，，，所以所以的面积为因为M为线段EF的中点，所以与的面积之比；设直线，，，由，得，所以，，所以，因为，所以，；所以，，即；整理得：，满足；当时，，此时；当时，射线OM所在直线方程为，由，得；所以，；综上，的取值范围【解析】本题考查椭圆的性质，直线与椭圆的位置关系，属于难题；设，，运用余弦定理即可解决问题；直线与椭圆联立，韦达定理，求出斜率与截距的关系；根据点M为中点，表示出面积比值，结合前面所求解决问题.。