2020-2021学年浙江省金华市东阳中学高一(上)段考数学试卷(10月份)

2020-2021学年浙江省金华市某校高一（上）段考数学试卷（10月份）一、单项选择题（本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知全集U＝{1, 2, 3, 4, 5, 6}，集合A＝{2, 3, 5, 6}，集合B＝{1, 3, 4, 6}，则集合A∩(∁U B)＝（）A.{2, 5}B.{3, 6}C.{2, 5, 6}D.{2, 3, 5, 6}【答案】A【考点】交、并、补集的混合运算【解析】进行补集和交集的运算即可．【解答】∵U＝{1, 2, 3, 4, 5, 6}，A＝{2, 3, 5, 6}，B＝{1, 3, 4, 6}，∴∁U B＝{2, 5}，A∩(∁U B)＝{2, 5}．2. 下列函数中，是同一函数的是（）A.y＝x2与y＝x|x|B.y=√x2与y=(√x)2C.y=x2+xx与y＝x+1 D.y＝2x+1与y＝2t+1【答案】D【考点】判断两个函数是否为同一函数【解析】由题意利用函数的三要素得出结论．【解答】根据函数的三要素，函数y＝x2的值域为[0, +∞)，而函数y＝x|x|的值域为(−∞, +∞)，故它们不是同一个函数；函数y=√x2的定义域为(−∞, +∞)，而函数y=(√x)2的定义域为[0, +∞)，故它们不是同一个函数．函数y=x 2+xx=x+1(x≠0)的定义域为{x|x≠0}，而函数y＝x+1的定义域为(−∞, +∞)，故它们不是同一个函数．函数y＝2x+1与y＝2t+1具有相同的定义域为(−∞, +∞)，值域为(−∞, +∞)，对应关系都是乘以2再加上1，故它们为同一个函数．3. 已知函数f(x)={x2+1(x≥2)f(x+3)(x<2)，则f(1)＝（）A.2B.12C.7D.17【答案】 D【考点】 求函数的值 函数的求值【解析】由函数性质得f(1)＝f(4)，由此能求出结果． 【解答】∵ 函数f(x)={x 2+1(x ≥2)f(x +3)(x <2) ，∴ f(1)＝f(4)＝42+1＝17． 故选：D ．4. 下列函数中，值域是(0, +∞)的是( ) A.y =2x +1(x >0)B.y =x 2C.y =√x 2−1D.y =2x【答案】 C【考点】函数的值域及其求法 【解析】结合一次函数，二次函数，反比例函数的性质分别检验各选项即可判断． 【解答】解：A ，当x >0时，y =2x +1>1，即值域为(1, +∞)，不符合题意， B ，y =x 2≥0，即值域为[0, +∞)，不符合题意；C ，由√x 2−1>0，得y >0，即值域为(0, +∞)，符合题意；D ，由反比例函数的性质可知y =2x ≠0，即值域为(−∞,0)∪(0, +∞)，不符合题意.故选C .5. 若命题“存在x ∈R ，使得x 2+(a −1)x +1<0”是假命题，则实数a 的取值范围是（ ）A.[−1, 3]B.(−1, 3)C.(−∞, −1]∪[3, +∞)D.(−∞, −1)∪(3, +∞)【答案】 A【考点】全称命题与特称命题 全称量词与存在量词【解析】因为不等式对应的是二次函数，其开口向上，若“∃x ∈R ，使得x 2+(a −1)x +1<0”，则相应二次方程有重根或没有实根． 【解答】∵ “∃x∈R，使得x2+(a−1)x+1<0是假命题，∴x2+(a−1)x+1＝0没有实数根或有重根，∴△＝(a−1)2−4≤0∴−1≤a≤36. 设f(x)是奇函数且在(−∞, 0)上是减函数，f(−1)＝0，则不等式xf(x)<0的解集为（）A.(−∞, −1)∪(1, +∞)B.(−1, 0)∪(0, 1)C.(−1, 0)∪(1, +∞)D.(−∞, −1)∪(0, 1)【答案】A【考点】奇偶性与单调性的综合【解析】本题可以利用f(x)在(−∞, 0)上是减函数，f(−1)＝0，得到函数有y轴左侧的图象草图，得到f(x)的相应函数值的正负情况，再根据f(x)是奇函数，得到函数有y轴右侧的图象草图，得到f(x)的相应函数值的正负情况，通过分类讨论，将不等式xf(x)<0转化为不等式组，解不等式组，得到本题结论．【解答】∵f(x)在(−∞, 0)上是减函数，f(−1)＝0，∴当x<−1时，f(x)>0；当−1<x<0时，f(x)<0．又∵f(x)是奇函数，∴由图象的对称性知：当0<x<1时，f(x)>0；当x>1时，f(x)<0．若f(0)有意义，则f(0)＝0．∵不等式xf(x)<0，∴{x>0f(x)<0或{x<0f(x)>0，∴x>1或x<−1．7. 已知m>0，xy>0，当x+y＝2时，不等式4x +my≥92恒成立，则m的取值范围是（）A.[12,+∞) B.[1, +∞) C.(0, 1] D.(0,12]【答案】B【考点】基本不等式及其应用【解析】根据“乘1法”，可得4x +my=12(4x+my)(x+y)，展开后，结合基本不等式可推出4x+my≥1 2(4+m+2√4m)≥92，解此不等式即可．【解答】∵xy>0，且x+y＝2，∴x>0，y>0，∴4x +my=12(4x+my)(x+y)=12(4+m+4yx+mxy)≥12(4+m+2√4yx⋅mxy)=12(4+m+2√4m)，当且仅当4yx =mxy即√mx＝2y时，等号成立，∵不等式4x +my≥92恒成立，∴12(4+m+2√4m)≥92，化简得，m+4√m−5≥0，解得√m≥1，即m≥1，∴m的取值范围是[1, +∞)．8. 已知函数f(x)=2x2+(4−m)x+4−m，g(x)=mx，若对于任一实数x，f(x)与g(x)的值至少有一个为正数，则实数m的取值范围是（）A.[−4, 4]B.(−4, 4)C.(−∞, 4)D.(−∞, −4)【答案】C【考点】二次函数的性质二次函数的图象【解析】对函数f(x)判断△=m2−16<0时一定成立，可排除D，再对特殊值m=4和−4进行讨论可得答案．【解答】解：当△=m2−16<0时，即−4<m<4，显然成立，排除D当m=4，f(0)=g(0)=0时，显然不成立，排除A；当m=−4，f(x)=2(x+2)2，g(x)=−4x显然成立，排除B；故选C．二、多项选择题（本大题共4个小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求全部选对得5分，选对但不全的得3分，有选错的得0分）设A={x|x2−8x+15=0}，B={x|ax−1=0}，若A∩B=B，则实数a的值可以为( )A.1 5B.0C.3D.13【答案】A,B,D【考点】集合关系中的参数取值问题交集及其运算【解析】推导出B ⊆A ，从而B ＝⌀或B ＝{3}或B ＝{5}，进而1a不存在，或1a=3，或1a=5．由此能求出实数a 的值． 【解答】解：∵ A ={x|x 2−8x +15=0}={3, 5}，B ={x|ax −1=0}={1a }，A ∩B =B ，∴ B ⊆A ，∴ B =⌀或B ={3}或B ={5}， ∴ 1a不存在或1a=3或1a=5，解得a =0或a =13或a =15，∴ 实数a 的值可以为0，15，13． 故选ABD .设a >b ，c <0，则下列结论正确的是（ ） A.ca >cbB.ac <bcC.b a >b−ca−cD.ac 2>bc 2【答案】 B,D【考点】不等式的基本性质 【解析】根据特殊值法判断A ，C ，根据不等式的基本性质判断B ，D 即可． 【解答】对于A ：令a ＝1，b ＝−1，c ＝−1，显然错误；对于B ：∵ a >b ，c <0，∴ ac <bc ，故B 正确； 对于C ：令a ＝1，b ＝−1，c ＝−1，显然错误；对于D:a >b ，c <0，则c 2>0，故ac 2>bc 2，故D 正确；使不等式1+1x >0成立的一个充分不必要条件是( ) A.x >2B.x ≥0C.x <−1或x >1D.−1<x <0【答案】 A,C【考点】必要条件、充分条件与充要条件的判断 【解析】不等式1+1x >0，即x+1x>0，x(x +1)>0，解得x 范围，即可判断出结论．【解答】解：不等式1+1x >0，即x+1x>0，∴x(x+1)>0，解得x>0或x<−1．∴选项中满足不等式1+1x>0成立的充分不必要条件是：x>2，及x<−1或x>1，选项AC符合题意.故选AC.下列命题中是真命题的是（）A.y=√x2+2+√x2+2的最小值为2B.当a>0，b>0时，1a +1b+2√ab≥4C.若a2+b2＝2，则a+b的最大值为2D.若正数a，b满足a+b＝2，则14a+2+1b+2的最小值为12【答案】B,C,D【考点】命题的真假判断与应用【解析】可令t=√x2+2(t≥√2)，结合对勾函数的单调性可判断A；由基本不等式计算可得最小值，可判断B；运用不等式a+b≤2√a2+b22，计算可判断C；由(4a+2)+(4b+8)＝18，结合乘1法和基本不等式可判断D．【解答】对于A，令t=√x2+2(t≥√2)，y=√x2+2√x2+2=t+1t在[√2, +∞)递增，可得y min=√2√2=3√22，此时x＝0，故A错误；对于B，a>0，b>0时，1a +1b+2√ab≥2√1ab+2√ab≥2√2√1ab⋅2√ab=4，当且仅当a＝b＝1时取得等号，故B正确；对于C，若a2+b2＝2，则a+b≤2√a2+b22=2，当且仅当a＝b＝±1时，取得等号，故C正确；对于D，若正数a，b满足a+b＝2，即为(4a+2)+(4b+8)＝18，则14a+2+1b+2=118[(4a+2)+(4b+8)](14a+2+44b+8)=118(1+4+4b+84a+2+4a+2b+2)≥1 18×(5+4)=12，当且仅当a＝b＝1时，取得等号，故D正确．三、填空题（本大题共4个小题，每小题5分，共20分）已知f(√x−1)＝x+2√x，则f(x)________．【答案】x2+4x+3(x≥−1)【考点】函数解析式的求解及常用方法【解析】令t=√x−1，将已知等式中的x一律换为t，求出f(t)即得到f(x)．注意定义域．【解答】令t=√x−1(t≥−1)则x＝(t+1)2所以f(t)＝(t+1)2+2(t+1)＝t2+4t+3(t≥−1)所以f(x)＝x2+4x+3(x≥−1)已知−4≤a−c≤−1，−1≤4a−c≤5，则2a+c的取值范围________．【答案】[1, 13]【考点】简单线性规划【解析】设2a+c＝m(a−c)+n(4a−c)＝(m+4n)a−(m+n)c，解出m，n即可得出．【解答】设2a+c＝m(a−c)+n(4a−c)＝(m+4n)a−(m+n)c，∴{m+4n=2m+n=−1，解得m＝−2，n＝1，∵−4≤a−c≤−1，−1≤4a−c≤5，∴2≤−2(a−c)≤8，−1≤4a−c≤5，∴1≤2a+c≤13，∴2a+c的取值范围是[1, 13]．已知x，y∈R，x2−xy+9y2＝1，则x+3y的最大值为________2√155．【答案】2√155【考点】基本不等式及其应用【解析】由x2+9y2＝1+xy≥2⋅x⋅3y，可推出xy≤15，而(x+3y)2＝x2+6xy+9y2＝1+ 7xy，代入所得结论即可．【解答】∵x2−xy+9y2＝1，∴x2+9y2＝1+xy≥2√x2⋅9y2=6xy，即xy≤15，当且仅当x＝3y，即x=3√1511，y=√1515时，等号成立，∴(x+3y)2＝x2+6xy+9y2＝1+7xy≤1+7×15=125，∴ −2√155≤x +3y ≤2√155， ∴ x +3y 的最大值为2√155．若f(x)为偶函数，且当x ≤0时，f(x)＝2x −1，则不等式f(x)>f(2x −1)的解集________|________>1或________<13} ．【答案】 {x ,x ,x 【考点】奇偶性与单调性的综合 【解析】根据函数奇偶性和单调性之间的关系，即可得到结论． 【解答】因为f(x)为偶函数，且当x ≤0时，f(x)＝2x −1单调递增，根据偶函数的对称性可知，当x >0时，函数单调递减，距离对称轴越远，函数值越小， 则由不等式f(x)>f(2x −1)可得|x|<|2x −1|， 两边平方可得，x 2<4x 2−4x +1， 整理可得，(3x −1)(x −1)>0， 解可得，x >1或x <13．四、解答题（共6小题，共70分．解答题应写出文字说明，证明过程或演算步骤）已知集合A ＝{x|a <x <3a, a >0}，集合B ＝{x|2<x ≤3}． （1）当a ＝1时，求A ∩B ，A ∪B ；（2）若A ∩B ＝⌀，求实数a 的取值范围．【答案】当a ＝1时，集合A ＝{x|1<x <3}，集合B ＝{x|2<x ≤3}． ∴ A ∩B ＝{x|2<x <3}， A ∪B ＝{x|1<x ≤3}．∵ 集合A ＝{x|a <x <3a, a >0}，集合B ＝{x|2<x ≤3}． A ∩B ＝⌀，∴ 当A ＝⌀时，a ≥3a ，解得a ≤0，不合题意， 当A ≠⌀时，{a <3a a ≥3 或{a <3a3a ≤2 ，解得a ≥3或a ≤23．又∵ a >0，故实数a 的取值范围是(0, 23]∪[3, +∞)． 【考点】并集及其运算 交集及其运算【解析】（1）当a ＝1时，求出集合A ，由此能求出A ∩B ，A ∪B ．（2）当A ＝⌀时，a ≥3a ，当A ≠⌀时，{a <3a a ≥3 或{a <3a3a ≤2 ，由此能求出实数a 的取值范围．【解答】当a ＝1时，集合A ＝{x|1<x <3}，集合B ＝{x|2<x ≤3}． ∴ A ∩B ＝{x|2<x <3}， A ∪B ＝{x|1<x ≤3}．∵ 集合A ＝{x|a <x <3a, a >0}，集合B ＝{x|2<x ≤3}． A ∩B ＝⌀，∴ 当A ＝⌀时，a ≥3a ，解得a ≤0，不合题意， 当A ≠⌀时，{a <3a a ≥3 或{a <3a3a ≤2 ，解得a ≥3或a ≤23．又∵ a >0，故实数a 的取值范围是(0, 23]∪[3, +∞)．已知函数f(x)=x+a x−2，x ∈(2, +∞)．（1）若a ＝4，判断函数f(x)在定义域上的单调性，并利用单调性定义证明你的结论．（2）若函数f(x)在区间(2, +∞)上单调递减，写出a 的取值范围（无需证明）． 【答案】根据题意，若a ＝4，则f(x)=x+4x−2=x−2+6x−2=1+6x−2，在定义域上为减函数，设2<x 1<x 2， 则f(x 1)−f(x 2)＝(1+6x 1−2)−(1+6x 2−2)=6(x 2−x 1)(x 1−2)(x 2−2)，又由2<x 1<x 2，则(x 1−2)>0，(x 2−2)>0，(x 2−x 1)>0，则f(x 1)−f(x 2)>0，f(x)在定义域上为减函数， f(x)=x+a x−2=x−2+a+2x−2=1+a+2x−2，若函数f(x)在区间(2, +∞)上单调递减，必有a +2>0，即a >−2， a 的取值范围是(−2, +∞)． 【考点】函数单调性的性质与判断 【解析】（1）根据题意，将函数的解析式变形为f(x)＝1+6x−2，设2<x 1<x 2，由作差法分析可得结论，（2）根据题意，由反比例函数的性质以及函数平移的性质可得结论． 【解答】根据题意，若a ＝4，则f(x)=x+4x−2=x−2+6x−2=1+6x−2，在定义域上为减函数，设2<x 1<x 2， 则f(x 1)−f(x 2)＝(1+6x1−2)−(1+6x 2−2)=6(x 2−x 1)(x 1−2)(x 2−2)，又由2<x 1<x 2，则(x 1−2)>0，(x 2−2)>0，(x 2−x 1)>0， 则f(x 1)−f(x 2)>0，f(x)在定义域上为减函数， f(x)=x+ax−2=x−2+a+2x−2=1+a+2x−2，若函数f(x)在区间(2, +∞)上单调递减，必有a +2>0，即a >−2， a 的取值范围是(−2, +∞)．（1）解关于x 的不等式ax 2−(2a +3)x +6>0(a ≠0)；（2）若对任意a ∈[−1, 1]，ax 2−(2a +3)x +6>0恒成立，求实数x 的取值范围． 【答案】ax 2−(2a +3)x +6>0(a ≠0)， 即(ax −3)(x −2)>0，当a <0，(x −3a )(x −2)<0，即有3a <x <2； 当3a =2即a =32时，(x −2)2>0，即x ≠2；当3a >2即0<a <32时，(x −3a )(x −2)>0，可得x <2或x >3a ； 当0<3a <2即a >32时，(x −3a )(x −2)>0，可得x >2或x <3a ， 综上可得，当a <0，解集为{x|3a <x <2}；当a =32时，解集为{x|x ∈R 且x ≠2}；当0<a <32时，解集为{x|x <2或x >3a }； 当a >32时，解集为{x|x >2或x <3a}；对任意a ∈[−1, 1]，ax 2−(2a +3)x +6>0恒成立， 可得a(x 2−2x)+6−3x >0，设f(a)＝a(x 2−2x)+6−3x ，a ∈[−1, 1]，可得{f(−1)>0f(1)>0 即{−(x 2−2x)+6−3x >0x 2−2x +6−3x >0 ，即有{−3<x <2x >3x <2 ，可得−3<x <2． 【考点】不等式恒成立的问题 其他不等式的解法 【解析】（1）对a 讨论，分当a <0时，当a =32时，当0<a <32时，当a >32时，运用二次不等式的解法，可得所求解集；（2）a(x 2−2x)+6−3x >0，设f(a)＝a(x 2−2x)+6−3x ，a ∈[−1, 1]，由恒成立思想可得f(−1)>0，且f(1)>0，解不等式可得所求范围． 【解答】ax 2−(2a +3)x +6>0(a ≠0)， 即(ax −3)(x −2)>0，当a <0，(x −3a )(x −2)<0，即有3a <x <2； 当3a =2即a =32时，(x −2)2>0，即x ≠2；当3a>2即0<a <32时，(x −3a )(x −2)>0，可得x <2或x >3a ；当0<3a <2即a >32时，(x −3a )(x −2)>0，可得x >2或x <3a ， 综上可得，当a <0，解集为{x|3a <x <2}；当a =32时，解集为{x|x ∈R 且x ≠2}；当0<a <32时，解集为{x|x <2或x >3a }； 当a >32时，解集为{x|x >2或x <3a }；对任意a ∈[−1, 1]，ax 2−(2a +3)x +6>0恒成立， 可得a(x 2−2x)+6−3x >0，设f(a)＝a(x 2−2x)+6−3x ，a ∈[−1, 1]，可得{f(−1)>0f(1)>0 即{−(x 2−2x)+6−3x >0x 2−2x +6−3x >0 ，即有{−3<x <2x >3x <2 ，可得−3<x <2．（1）作出f(x)＝x|x −4|的图象，并讨论方程f(x)＝m 的实根的个数；（2）已知函数f(x)＝x|x −a|−a(a ∈R)，若存在x ∈[3, 5]，使f(x)<0成立，求实数a 的取值范围． 【答案】f(x)＝x|x −4|={x 2−4x,x ≥4−x 2+4x,x <4 ，其图象如图：由图可知，当m ∈(−∞, 0)∪(4, +∞)时，方程f(x)＝m 有1个实根， 当m ＝0或4时，方程f(x)＝m 有2个实根， 当m ∈(0, 4)时，方程f(x)＝m 有3个实根； 函数f(x)＝x|x −a|−a(a ∈R)，命题若存在x ∈[3, 5]，使f(x)<0成立的否定为∀x ∈[3, 5]，使f(x)≥0成立． 下面求使命题∀x ∈[3, 5]，使f(x)≥0成立的a 的范围．①若a <3，则x ＝3时，f(x)在[3, 5]上取得最小值，f(3)＝3(3−a)−a ＝9−4a ， ∴ 9−4a ≥0，即a ≤94；②若3≤a ≤5，则x ＝a 时，f(x)取得最小值为f(a)＝−a ，−a <0不满足f(x)≥0恒成立；③若a >5，f(x)min ＝min {f(3), f(5)}＝min {3(a −3)−a, 5(a −5)−a}≥0， 解得a ≥254．综上可得，∀x ∈[3, 5]，使f(x)≥0成立的a 的范围是(−∞, 94]∪[254,+∞)， 则存在x ∈[3, 5]，使f(x)<0成立的a 的取值范围为(94,254)．【考点】函数的零点与方程根的关系 【解析】（1）写出分段函数解析式，作出图象，数形结合得答案；（2）写出命题存在x ∈[3, 5]，使f(x)<0成立的否定，即∀x ∈[3, 5]，使f(x)≥0成立，分类求解a 的取值范围，再由补集思想得答案． 【解答】f(x)＝x|x −4|={x 2−4x,x ≥4−x 2+4x,x <4 ，其图象如图：由图可知，当m ∈(−∞, 0)∪(4, +∞)时，方程f(x)＝m 有1个实根， 当m ＝0或4时，方程f(x)＝m 有2个实根， 当m ∈(0, 4)时，方程f(x)＝m 有3个实根； 函数f(x)＝x|x −a|−a(a ∈R)，命题若存在x ∈[3, 5]，使f(x)<0成立的否定为∀x ∈[3, 5]，使f(x)≥0成立． 下面求使命题∀x ∈[3, 5]，使f(x)≥0成立的a 的范围．①若a <3，则x ＝3时，f(x)在[3, 5]上取得最小值，f(3)＝3(3−a)−a ＝9−4a ， ∴ 9−4a ≥0，即a ≤94；②若3≤a ≤5，则x ＝a 时，f(x)取得最小值为f(a)＝−a ，−a <0不满足f(x)≥0恒成立；③若a >5，f(x)min ＝min {f(3), f(5)}＝min {3(a −3)−a, 5(a −5)−a}≥0， 解得a ≥254．综上可得，∀x ∈[3, 5]，使f(x)≥0成立的a 的范围是(−∞, 94]∪[254,+∞)， 则存在x ∈[3, 5]，使f(x)<0成立的a 的取值范围为(94,254)．一种药在病人血液中的含量不低于2克时，它才能起到有效治疗的作用，已知每服用m(1≤m ≤4且m ∈R)个单位的药剂，药剂在血液中的含量y （克）随着时间x （小时）变化的函数关系式近似为y ＝m ⋅f(x)，其中f(x)={104+x,0≤x <64−x2,6≤x ≤8．（1）若病人一次服用3个单位的药剂，则有效治疗时间可达多少小时？（2）若病人第一次服用2个单位的药剂，6个小时后再服用m 个单位的药剂，要使接下来的2小时中能够持续有效治疗，试求m 的最小值． 【答案】∵ m ＝3，∴ y ={304+x,0≤x <612−3x2,6≤x ≤8； 当0≤x <6时，304+x >304+6=3>2； 当6≤x ≤8时，12−32x ≥2得，x ≤203；故若病人一次服用3个单位的药剂，则有效治疗时间可达203小时． 当6≤x ≤8时，y ＝2(4−12x)+m[104+x−6] ＝8−x +10m x−2，∵ 8−x +10mx−2≥2对6≤x ≤8恒成立， 故m ≥x 2−8x+1210对6≤x ≤8恒成立， 令g(x)=x 2−8x+1210，则g(x)在[6, 8]上是增函数， 故g max (x)=65； 故m ≥65； 故m 的最小值为65． 【考点】分段函数的应用根据实际问题选择函数类型函数恒成立问题【解析】(1将m＝3代入得y={304+x,0≤x<612−3x2,6≤x≤8；从而解不等式即可．（2）当6≤x≤8时，y＝2(4−12x)+m[104+x−6]＝8−x+10mx−2，即8−x+10mx−2≥2对6≤x≤8恒成立，即m≥x2−8x+1210对6≤x≤8恒成立，从而化为最值问题．【解答】∵m＝3，∴y={304+x,0≤x<612−3x2,6≤x≤8；当0≤x<6时，304+x >304+6=3>2；当6≤x≤8时，12−32x≥2得，x≤203；故若病人一次服用3个单位的药剂，则有效治疗时间可达203小时．当6≤x≤8时，y＝2(4−12x)+m[104+x−6]＝8−x+10mx−2，∵8−x+10mx−2≥2对6≤x≤8恒成立，故m≥x 2−8x+1210对6≤x≤8恒成立，令g(x)=x 2−8x+1210，则g(x)在[6, 8]上是增函数，故g max(x)=65；故m≥65；故m的最小值为65．已知函数y＝x+ax有如下性质：如果常数a>0，那么该函数在(0,√a]上是减函数，在[√a,+∞)上是增函数．（1）若函数ℎ(x)＝x+4x,x∈[1,3]，求ℎ(x)的最值；（2）已知f(x)=4x 2−12x−32x+1,x∈[0,1]，求函数f(x)的值域；（3）对于（2）中的函数f(x)和函数g(x)＝kx −2，若对任意x 1∈[0, 1]，总存在x 2∈[1, 2]，使得g(x 2)＝f(x 1)成立，求实数k 的值． 【答案】由题意知，函数ℎ(x)＝x +4x 在[1, 2)上单调递减, 在(2, 3]上单调递增，而ℎ(1)＝1+4＝5，ℎ(3)＝3+43=133，∴ ℎ(x)min ＝ℎ(2)＝2+2＝4， ℎ(x)max ＝ℎ(1)＝5． f(x)=4x 2−12x−32x+1=(2x+1)2−8(2x+1)+42x+1=(2x +1)+42x+1−8，∵ x ∈[0, 1]，∴ 2x +1∈[1, 3]， 由（1）可知，f(x)min ＝f(12)＝4−8＝−4，f(x)max ＝f(0)＝5−8＝−3， ∴ 函数f(x)的值域为[−4, −3]．对于函数g(x 2)＝kx 2−2，x 2∈[1, 2]，①当k >0时，g(x 2)单调递增，其值域为[k −2, 2k −2]，∵ 对任意x 1∈[0, 1]，总存在x 2∈[1, 2]，使得g(x 2)＝f(x 1)成立， ∴ [−4, −3]⊆[k −2, 2k −2]，即{k −2≤−42k −2≥−3 ，无解；②当k <0时，g(x 2)单调递减，其值域为[2k −2, k −2]，同理可得，[−4, −3]⊆[2k −2, k −2]，即{2k −2≤−4k −2≥−3 ，解得k ＝−1；③当k ＝0时，g(x 2)＝−2恒成立，g(x 2)的值域为{−2}， 而[−4, −3]⊈{−2}，不符合题意，舍去， 综上，实数k 的值为−1． 【考点】函数与方程的综合运用 函数单调性的性质与判断 【解析】（1）由题意知，函数ℎ(x)＝x +4x 在[1, 2)上单调递减, 在(2, 3]上单调递增，计算ℎ(1)，ℎ(2)，ℎ(3)的值，即可得解；（2）将f(x)化简成f(x)＝(2x +1)+42x+1−8，结合（1）的结论即可得解； （3）先将原问题转化为f(x)的值域是g(x)的值域的子集，再分k >0、k <0和k ＝0三种情况讨论函数g(x)的值域，然后针对每种情况列出关于k 的不等式组，解之即可． 【解答】由题意知，函数ℎ(x)＝x +4x 在[1, 2)上单调递减, 在(2, 3]上单调递增， 而ℎ(1)＝1+4＝5，ℎ(3)＝3+43=133，∴ ℎ(x)min ＝ℎ(2)＝2+2＝4，ℎ(x)max ＝ℎ(1)＝5． f(x)=4x 2−12x−32x+1=(2x+1)2−8(2x+1)+42x+1=(2x +1)+42x+1−8，∵ x ∈[0, 1]，∴ 2x +1∈[1, 3]， 由（1）可知，f(x)min ＝f(12)＝4−8＝−4，f(x)max ＝f(0)＝5−8＝−3， ∴ 函数f(x)的值域为[−4, −3]．对于函数g(x 2)＝kx 2−2，x 2∈[1, 2]，①当k >0时，g(x 2)单调递增，其值域为[k −2, 2k −2]，∵ 对任意x 1∈[0, 1]，总存在x 2∈[1, 2]，使得g(x 2)＝f(x 1)成立， ∴ [−4, −3]⊆[k −2, 2k −2]，即{k −2≤−42k −2≥−3 ，无解；②当k <0时，g(x 2)单调递减，其值域为[2k −2, k −2]，同理可得，[−4, −3]⊆[2k −2, k −2]，即{2k −2≤−4k −2≥−3 ，解得k ＝−1；③当k ＝0时，g(x 2)＝−2恒成立，g(x 2)的值域为{−2}， 而[−4, −3]⊈{−2}，不符合题意，舍去， 综上，实数k 的值为−1．。

浙江省东阳中学2020届高三数学10月月考试题一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{0,1,2}A =，{1,0,1}B =-，则A B =U （ ）A.{0,1}B. {1,0,1,2}-C. {0}D. {2}2 若(2)5i z +=,则z 的虚部为 （ ）A.1- B.1 C.i - D.i3. 已知双曲线:C )0(116222>=-a y ax 的一个焦点为)0,5(，则双曲线C 的渐近线方程为（ ） A.1234=±y x B.0414=±y x C.0916=±y x D.430x y ±=4.若实数,x y 满足约束条件2330233010x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩ ，则2z x y =+的最大值是 （ ）A.5-B. 9-C. 5D. 9 5.设,m n 是不同的直线，,αβ是不同的平面，且,m n α⊂ ，则“//m β 且//n β”是“//αβ”的 （ ） A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件6. 函数()(33)lg ||x x f x x -=+的图象大致为 （ ）A B C D7. 随机变量X 的取值为0,1,2，若10)=4P X =（，()1E X =，则()D X = （ ）A. 32B. 12C. 14D. 18.在四面体ABCD 中，二面角A BC D --的大小为60o ，点P 为直线BC 上一动点，记直线PA 与平面BCD 所成的角为θ，则 （ ）A. θ的最大值为60oB. θ的最小值为60oC. θ的最大值为30oD. θ的最小值为30o9. 已知数列{}n a 满足：*113,2()n n na a a n N a +==+∈，则使20204n a >成立的最小正整数为（ ）A.10B.11C. 12D. 1310.已知函数()ln f x x ax b =--，对于任意的0,a b R <∈，都存在[]01,x m ∈使得()01f x ≥成立，则实数m 的取值范围是 （ ） A.2[,)e +∞ B. [,)e +∞ C. 3[,]e e D. 2(1,]e 二、填空题：本大题共7小题，多空题每小题6分，单空题每小题4分，共36分. 11. 某几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该多面体的各条棱长中最长棱的长度为 ，体积为 .12. 6(2)(1)x x ++展开式中，3x 项的系数为_________；所有项系数的和为_________. 13. 已知()|22||1|f x x x =++-的最小值为t ，则t 的值为 ，若实数,a b 满足2222a b t +=，求22141a b ++的最小值为 . 14.安排甲、乙、丙、丁、戊5名大学生去杭州、宁波、金华三个城市进行暑期社会实践，每个城市至少安排一人，则不同的安排方式共有 种；其中学生甲被单独安排去金华的概率是 .15. 设椭圆C 的两个焦点是12,F F ，过点1F 的直线与椭圆C 交于点,P Q ，若212||||PF F F =，且113||4||PF QF =，则椭圆C 的离心率为 .16. 顶点为P 的圆锥的轴截面是等腰直角三角形，A 是底面圆周上的点，B 是底面圆内的点，O 为底面圆圆心，AB OB ⊥，垂足为B ，OH PB ⊥，垂足为H ，且4PA = ，C 是PA 的中点，则当三棱锥O HPC -的体积最大时，OB 的长为 .17.已知平面内非零向量,,a b c r r r ，满足||2,||3a b ==r r ，3a b ⋅=r r ，若2280c b c -⋅+=r r r ，则||c a -r r的取值范围是 .三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤. 18.（本小题满分14分）已知函数()(3cos )cos f x x x x ωωω=+，x R ∈，0ω>，若()f x 的最小正周期为4π. （1）求函数()f x 的单调递增区间；（2）在ABC ∆中，角,,A B C 对边分别是,,a b c ，且满足(2)cos cos a c B b C -=，求函数()f A 的取值范围.19.（本小题满分15分）如图，已知三棱柱111ABC A B C -，90ABC ∠=o ，1AB BC CC ==，平面1ABC ⊥平面11BCC B . （1）证明AB ⊥平面11BCC B ；（2）若11120BB C ∠=o ，Q 是1AC 上的一点，且1CQ AC ⊥，求直线CQ 与平面1ABC 所成角的正弦值.20.（本小题满分15分）若数列{}n a 是公差为2的等差数列，数列{}n b 满足121,2b b ==，且1n n n n a b b nb ++=.（1）求{}n a ，{}n b 数列的通项公式；（2）设数列{}n c 满足11n n n a c b ++=，数列{}n c 的前n 项和为n T ，若不等式1(1)2n n n nT λ--<+对一切*n N ∈恒成立，求实数λ的取值范围.21. （本小题满分15分）已知椭圆22122:1(0)x y C a b a b+=>>左右焦点分别为21F F 、，且其中一个焦点与抛物线x y C 4:22=的焦点重合，直线1-=my x 与椭圆交于B A 、两点，2ABF ∆的周长为8..（1）求椭圆的标准方程；（2）若直线2AF 与抛物线交于D C 、两点，直线2BF 与抛物线交于F E 、两点（D C 、与F E 、分别在2F 的两侧求116CD EF ⋅的最大值.22.（本小题满分15分）设a R ∈，函数()ln f x x ax =-.（1）若()f x 无零点，求实数a 的取值范围；（2）若()f x 有两个相异零点12,x x ，且12ln ln x x m +>恒成立，求实数m 的最大值.参考答案 1~10 BADCB DBACA11. 313 12. 55 192 13. 2 92 14. 150 775 15. 57 16.26 17.[71,71]-+18.解：（1）1()(3sin cos )cos sin(2)62f x x x x x πωωωω=+=++242T ππω==Q ，即14ω= ， 11()sin()262f x x π∴=++又1222262k x k πππππ-+≤+≤+Q∴ 增区间为42[4,4],33k k k Z ππππ-++∈（2）由正弦定理化简得1cos 2B =，所以3B π=.又11()sin()262f A A π=++，203A π<<Q 6262A πππ∴<+< ，1sin()1226A π∴<+< 即函数()f A 的取值范围为3(1,)2.19.……………… 6分所以27sin CH HQC CQ ∠==； 所以直线CQ 与平面1ABC 所成角的正弦值为27720.（1）因为121,2b b ==，且1n n n n a b b nb ++=， 所以112a +=，得11a =， 所以21n a n =-. …………………………………………………………………3分 所以12n n nb nb +=，12n n b b += 所以数列{}n b 是等比数列，公比为2，所以12n n b -= . …………………………………………………………………6分（2）因为112nn n n a nc b -+== 所以21231222n n n T -=++++L 21112122222n n n n n T --=++++L 所以211111212222222n n n n n n T -+=++++-=-L所以1242n n n T -+=- ……………………………………………………………11分所以不等式可化为1(1)2n n n n T λ--<+可化为12(1)42n n λ--<-当n 为偶数时，1242n λ-<-，所以212432λ-<-=；当n 为奇数时，1242n λ->-+，所以112422λ->-+=-；综上所述，实数λ的取值范围为(2,3)- .21. （1）22143x y +=（2）设直线21:(1)AF y k x =-：，直线22:(1)BF y k x =-，1122(,),(,)A x y B x y2213412x my x y =-⎧⎨+=⎩ 得22(34)690m y my +--=12122269,(34)(34)m y y y y m m -+==++ 又11111111(1)x y k x k y -=-⇒=，22222211(1)x y k x k y -=-⇒=12122112211212121211(1)(1)(2)(2)11x x x y x y my y my y k k y y y y y y ---+--+-∴+=+==21212122622()10(34)293(34)mmy y y y m m m y y m -++==-=-+ 22121212121212121211(2)(2)2()41169x x my my m y y m y y m k k y y y y y y -----++=⋅===-又||2C D CD x x =++，||2E F EF x x =++；122221112(1)(24)04y k x k x k x k y x=-⎧⇒-++=⎨=⎩2142C D x x k ∴+=+同理2242E Fx x k +=+ 2222121212121111111||||112116CD EF k k k k k k k k ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥∴⋅=++=++-+ ⎪⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦425062578498181m m ⎛⎫=++≤⎪⎝⎭ 22.。

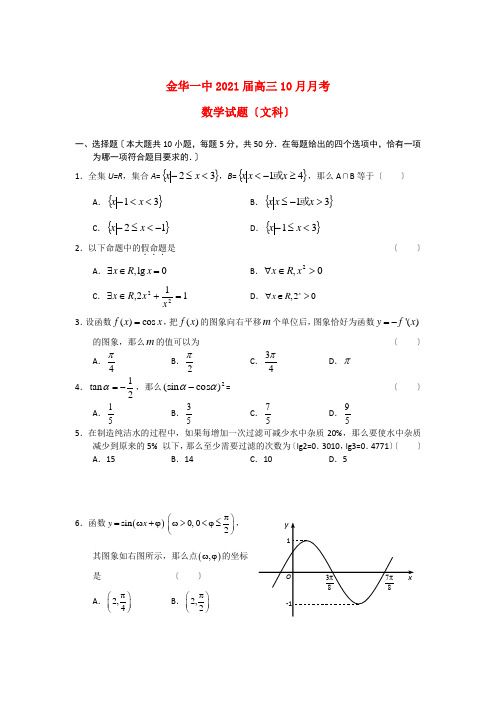
金华一中2021届高三10月月考数学试题〔文科〕一、选择题〔本大题共10小题，每题5分，共50分．在每题给出的四个选项中，恰有一项为哪一项符合题目要求的．〕 1．全集U=R ，集合A =}{32<≤-x x ，B ={}41≥-<x x x 或，那么A ∩B 等于〔 〕 A ．{}31<<-x x B ．{}31>-≤x x x 或C ．{}12-<≤-x xD ．{}31<≤-x x 2．以下命题中的假命题．．．是〔 〕A ．,lg 0x R x ∃∈=B ．0,2>∈∀x R xC ．112,22=+∈∃xx R x D ．,20x x R ∀∈>3．设函数()cos f x x =，把()f x 的图象向右平移m 个单位后，图象恰好为函数'()y f x =-的图象，那么m 的值可以为〔 〕A ．4π B ．2π C ．34πD ．π 4．1tan 2α=-，那么2)cos (sin αα-=〔 〕 A ．51 B ．53 C ．57D ．595．在制造纯洁水的过程中，如果每增加一次过滤可减少水中杂质20%，那么要使水中杂质减少到原来的5% 以下，那么至少需要过滤的次数为〔lg2=0．3010，lg3=0．4771〕〔 〕 A ．15 B ．14 C ．10 D ．56．函数()sin y x =ω+ϕ0,02π⎛⎫ω><ϕ≤ ⎪⎝⎭，其图象如右图所示，那么点(),ωϕ的坐标 是〔 〕A ．2,4π⎛⎫⎪⎝⎭B ．2,2π⎛⎫ ⎪⎝⎭C ．4,4π⎛⎫ ⎪⎝⎭D ．4,2π⎛⎫ ⎪⎝⎭7．函数22()2,()log ,()log 2x f x x g x x x h x x =+=+=-的零点依次为,,a b c ，那么〔 〕A ．a b c <<B ．c b a <<C ．c a b <<D ．b a c <<8．设==)21(,2cos )(sin f x x f 则〔 〕A ．-21B ．-23 C ．21 D ．239．数列{}n a 满足221221,2,(1cos )sin 22n n n n a a a a ππ+===++，那么该数列的前20项的和为〔 〕A ．2021B ．2056C ．2065D ．210110．假设x x x f λ+=2)(〔x ∈N*〕是单调增函数，那么实数λ的取值范围是 〔 〕A ．2->λB ．3->λC ．2-≥λD ．3-≥λ二、填空题〔本大题共7小题，每题4分，共28分．〕11．函数lg y x =的定义域为 ； 12．3(,0),sin ,25παα∈-=-那么=-)4cos(πα ；13．直线a x y -=与曲线x y ln =相切，那么a 的值为 ； 14．假设关于x 的方程01=+k x在]1,0(∈x 有实数根，那么k 的取值范围为 ； 15．整数以按如下规律排成一列：()1,1、()1,2、()2,1、()1,3、()2,2，()3,1，()1,4，()2,3，()3,2，()4,1，……，那么第60个数对是 ；16．对函数()sin f x x x =，现有以下命题：①函数()f x 是偶函数,②函数()f x 的最小正周期是2π,③函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递增，在区间,02π⎡⎤-⎢⎥⎣⎦上单调递减．其中是真命题的是 〔写出所有真命题的序号〕；17．不等式022<+-a x x 的整数解只有1，那么实数a 的取值范围是 ．三、解答题〔本大题共5小题共72分．解答时应写出文字说明、证明过程或演算步骤．〕 18．〔此题总分值12分〕函数2()sin cos2x f x x a =+，a 为常数，a R ∈，且2π=x 是方程0)(=x f 的解〔1〕求)611(πf 的值； 〔2〕当],0[π∈x 时，求函数)(x f 的值域．19．〔此题总分值14分〕等差数列}{n a 中，43=a ，其前10项和为65 〔1〕求数列}{n a 的通项公式； 〔2〕求数列}2{n na 的前n 项和n S ．20．〔此题总分值15分〕数列{}n a 中，11=a ，12n n n a a ++=〔n ∈N*〕，n n a b 3=〔1〕试证数列⎭⎬⎫⎩⎨⎧⨯-n n a 231是等比数列，并求数列{n b }的通项公式； 〔2〕在数列{n b }中，是否存在连续三项成等差数列的项，假设存在，求出所有这样的项，假设不存在，说明理由．21．〔此题总分值15分〕函数x ax x x f 54)(23+-=〔R ∈a 〕． 〔1〕 当a = 1时, 求函数在区间[0, 2]上的最大值;〔2〕 假设函数)(x f 在区间[0, 2]上无极值．．．, 求a 的取值范围．22．〔此题总分值16分〕函数x a x x f ln 2)(2-=〔0a >〕． 〔1〕讨论函数()f x 的单调性；〔2〕假设关于x 的方程()2f x ax =有唯一解，求a 的值．参考答案一、选择题〔每题5分，共50分〕二、填空题〔每题4分，共28分〕 11．(0,1] 12．10213．1 14．1-≤k 15．()5,7 16．①，③ 17．10<≤a 三、解答题〔共72分〕18．〔此题总分值12分〕函数2()sin cos2x f x x a =+，a 为常数，a R ∈，且2π=x 是方程0)(=x f 的解． 〔1〕求)611(πf 的值; 〔2〕当],0[π∈x 时，求函数)(x f 的值域．解：〔1〕2()sincos 0224f a πππ=+=，那么1102a +=，解得2a =-……………2分所以2()sin 2cossin cos 12xf x x x x =-=--…………………………………4分 所以233)611(-=πf ．……………………………………………………………6分〔2〕())14f x x π=--……………………………………………………8分由[0,]x π∈，得 3[,]444x πππ-∈-，那么sin()[42x π-∈-……………10分)14x π--∈[1]-所以()y f x =值域为[1]- ………12分19．〔此题总分值14分〕等差数列}{n a 中，43=a ，其前10项和为65 〔1〕求数列}{n a 的通项公式; 〔2〕求数列}2{n na 的前n 项和n S ．解：〔1〕 421=+d a ，652910101=⨯+d a ……………………4分得121==d a ， 1+=∴n a n …………………………………………………6分〔2〕2323412222n n n S +=++++ ① 23113412222n n n S ++=+++ ②①—②得23411111111222222n n n n S ++=+++++- ………………………………10分1121211)211(411++----+=n n n 1121)211(211+----+=n n n332n n n S +∴=-……………………………………………………14分20．〔此题总分值15分〕数列{}n a 中，11=a ，12n n n a a ++=〔n ∈N*〕，b n ＝3a n〔1〕试证数列⎭⎬⎫⎩⎨⎧⨯-n na 231是等比数列，并求数列{b n }的通项公式； 〔2〕在数列{b n }中，是否存在连续三项成等差数列的项，假设存在，求出所有这样的项，假设不存在，说明理由．解：〔1〕证明: 由12n n n a a ++=，得a n ＋1＝2n —a n ，∴nn n n nn n n n a a a a 2312312231231111⨯-⨯--=⨯-⨯-+++1231231-=⨯-⎪⎭⎫ ⎝⎛⨯--=n n n n a a ,∴数列⎭⎬⎫⎩⎨⎧⨯-n n a 231是首项为31321=-a ,公比为1-的等比数列．………………4分∴ ()1131231--⨯=⨯-n n n a , 即()[]nn n a 1231--=，∴()21nnn b =--………………………………………………………………………7分〔2〕解：假设在数列{b n }中，存在连续三项b k －1，b k ，b k ＋1〔k ∈N*, k ≥2〕成等差数列，那么b k －1＋b k ＋1＝2b k ，即()()()1111[21][21]2[21]k k kk k k -+-+--+--=--，即12k -＝41(1)k --……………………………………………………………10分假设k 为偶数，那么12k -＞0，41(1)k --＝－4＜0，所以，不存在偶数k ，使得b k －1，b k ，b k ＋1成等差数列。

浙江省金华市2020年高一上学期数学10月月考试卷C卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题；共16分)1. （2分）从集合的所有子集中任取一个，这个集合恰是集合的子集的概率是（）A .B .C .D .2. （2分）已知N为自然数集，集合P＝{1,4,7,10,13}，Q＝{2,4,6,8,10}，则P∩ 等于（）A . {1,7,13}B . {4,10}C . {1,7}D . {0,1,3}3. （2分）已知集合，则（）A . {0,x,1,2}B . {2,0,1,2}C . {0,1,2}D . 不能确定4. （2分） (2017高二上·景县月考) 集合A={x|﹣1≤x≤2}，集合B={x|x≤a}．若A∩B=∅，则实数a的取值范围是（）A . {a|a＜2}B . {a|a≥﹣1}C . {a|﹣1≤a＜2}D . {a|a＜﹣1}5. （2分） (2019高二上·诸暨月考) 已知，是平面内的两条直线，是空间中的一条直线.则“直线且”是“ ”的（）A . 充分而不必要条件B . 必要而不充分条件C . 充要条件D . 既不充分也不必要条件6. （2分） (2016高三上·宜春期中) 若集合M={y|y=3x}，N={x|y= }，则M∩N=（）A . [0， ]B . （0， ]C . （0，+∞）D . （﹣∞， ]7. （2分） (2019高一上·赣县月考) 已知全集，集合，，则图中阴影部分所表示的集合为（）A .B .C .D .8. （2分） (2019高一上·泉港月考) 对任意a [-1,1],函数的值恒大于零，则x的取值范围是（）A . 1<x<3B . x<1或x>3C . 1<x<2D . x<1或x>2二、多选题 (共4题；共12分)9. （3分） (2019高一上·如东月考) 已知集合中有且仅有一个元素，那么a的值为（）A . -1B . 1C .D . 010. （3分） (2020高一上·天门月考) 已知集合，集合，则（）A .B .C .D .11. （3分） (2020高一上·沧县月考) 设集合，若满足，则实数可以是（）A . 0B .C .D . 312. （3分） (2019高一上·滕州月考) 下列四个命题：其中不正确命题的是（）A . 函数在上单调递增，在上单调递增，则在R上是增函数B . 若函数与轴没有交点，则且C . 当时，则有成立D . 和表示同一个函数三、填空题 (共4题；共4分)13. （1分） (2019高三上·海淀月考) 已知函数f（x）为定义域为R，设Ff（x）= ．①若f（x）= ，则Ff（1）=________；②若f（x）=ea-|x|-1，且对任意x∈R，Ff（x）=f（x），则实数a的取值范围为________．14. （1分） (2018高二上·无锡期末) 命题“对任意的”的否定是________．15. （1分）如图，在△ABC中，MN∥DE∥BC，若AE：EC=7：3，则DB：AB的值为________ ．16. （1分）当x∈[﹣1，2]时，x3﹣x2﹣x＜m恒成立，则实数m的取值范围是________．四、解答题 (共6题；共60分)17. （5分） (2020高一下·隆化期中) 已知函数 .（1）当时，求不等式的解集；（2）当时，不等式恒成立，求m的取值范围.18. （10分） (2019高二上·滕州月考) 解关于的不等式: .19. （10分） (2016高一下·右玉期中) 已知集合A={x|x≤﹣1或x≥5}，集合B={x|2a≤x≤a+2}．（1）若a=﹣1，求A∩B和A∪B；（2）若A∩B=B，求实数a的取值范围．20. （10分） (2016高一上·南城期中) 已知二次函数f（x）的二次项系数为a（a＜0），且1和3是函数y=f （x）+2x的两个零点．若方程f（x）+6a=0有两个相等的根，求f（x）的解析式．21. （10分） (2020高一上·苏州期末) 已知 A = {x | (x−a)(x+a−2) < 0},B = {x | 0 < x < 4}.（1）若 a = 3, 求A∩B；（2）若A∪B = A，求实数 a 的取值范围.22. （15分） (2019高一上·镇海期中) 已知集合，，其中．（1）若，，求实数a的取值范围；（2）若，求实数a的取值范围．参考答案一、单选题 (共8题；共16分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：二、多选题 (共4题；共12分)答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：三、填空题 (共4题；共4分)答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：四、解答题 (共6题；共60分)答案：17-1、答案：17-2、考点：解析：答案：18-1、考点：解析：答案：19-1、答案：19-2、考点：解析：答案：20-1、考点：解析：答案：21-1、答案：21-2、考点：解析：答案：22-1、答案：22-2、考点：解析：。

东阳中学2017年高一下期第一次阶段性考试数学试卷命题：朱建华审题：吴再再提醒：答案全部写在答题卷上。

一、选择题：（5分⨯10=50分）1.设集合{|2}A x x =>，则A ．A φ∈B ．0A ∈C ．2A ∈D A 2.已知集合{3,2},{a,b}a A B ==，若{1}A B =，则a b +=A ．0B ．1C ．2D ．3 3.函数1()f x x x=-的图象关于下列那一个对称？ A ．关于x 轴对称 B ．关于y 对称 C ．关于原点对称 D ．关于直线y x =4.设0.21.60.22,2,0.4a b c ===，则,,a b c 的大小关系是A ．c a b <<B ．c b a <<C ．a b c <<D ．b a c <<5.设函数2,0(),0x x f x x x -≤⎧=⎨>⎩，若()4f a =，则实数a 的值为A ．2,4±±B ．2,4±-C ．2,4D ．2,4-6.设函数()f x 的图象是折线ABC ，其中A 、B 、C 的坐标分别为(0,4),(2,0),(6,4)，则((1))f f =A ．0B ．1C ．2D ．47.已知函数(2)75,1()1,1x a x a x f x a x -+-≤⎧=⎨+>⎩是R 上的增函数，则实数a 的取值范围是A ．1a >B ．12a <<C ．827a <<D ．827a ≤<8.在下列四个函数中，满足性质：“对于区间(1,2)上的任意1212,()x x x x ≠，不等式1212|()()|||f x f x x x -<-恒成立”的只有A ．1()f x x=B ．()||f x x =C ．()2x f x =D ．2()f x x = 9.已知集合A 、B 均为全集{1,2,3,4}U =的子集，且{2},(C )A {4}U A B B ==，则满足条件的集合B 的个数为A ．1个B ．2 个C ．4 个D ．8个10.对于任意实数,a b ，定义：1(,)(||)2F a b a b a b =++-。

东阳中学2020年下学期10月阶段考试卷（高三数学）一、选择题：本大题共10小题，每小题4分共40分在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合 {1,0,1,4,5},{2,3,4},{02},A B C x x =-==∈<<R ∣则 ()A C B = （ ）A. {4}B. {23}，C. {1,2,3,5}-D. {1,2,3,4} 2. 已知复数z = 3+i （i 为虚数单位）, 则2z = （ ） A. 106i - B. 106i + C. 86i - D. 86i + 3. 已知x 是实数，则“45x x+>”是 “4x >”的 （ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件4.若实数x ,y 满足条件2000x y x y x +-⎧⎪-⎨⎪⎩≥≤≥，则2z x y =- （ ）A.有最小值，无最大值B. 有最小值，有最大值C.无最小值，有最大值D. 无最小值，无最大值 5. 设函数21()ln(1||)1f x x x=+-+，则使得()(21)f x f x >-成立的x 的取值范围是（ ） A. 1,13⎛⎫⎪⎝⎭ B.1,3⎛⎫-∞ ⎪⎝⎭ C.11,33⎛⎫- ⎪⎝⎭ D. 11,,33⎛⎫⎛⎫-∞-+∞ ⎪⎪⎝⎭⎝⎭6. 在同一个直角坐标系中，函数a y x =，log a y x b =+（0a >且1a ≠）的图象如右图，则,a b 的取值可能是 （ ）A ．1,1a b >>B ．01,01a b <<<<C ．01,1a b <<>D ．1,01a b ><< 7. 已知函数()f x 满足()2()f x f x -=-，若函数1x y x+=与()y f x =图象的交点为11(,),x y 22(,),x y 1010,(,)x y ，则交点的所有横坐标和纵坐标之和为 （ ） A ．10 B ．10- C ．5 D ．208. 定义“规范01数列”{}n a 如下：{}n a 共有2m 项，其中m 项为0，m 项为1，且对任意2k m ≤，12,,,k a a a 中0的个数不少于1的个数，若4m =，则不同的“规范01数列”共有（ ）A. 12个B. 14个C. 16个D. 18个9. 已知x ∈R ，若函数2()||f x x x a =--有4个零点，则210ax x ++=的方程根个数为（ ） A. 0 B. 1 C. 2 D. 与a 的取值有关10. 设函数2,11()2,11x k x x f x kx x ⎧+-=⎨-<<⎩≤或≥，2()g x kx bx c =++，,,k b c 为实数，则 （ ）A ．若[()]f g x 的值域为[0,)+∞，则13k -≤；B ．若[()]f g x 的值域为[1,)-+∞，则0k ≥；C ．若1k ≥，则[()]f g x 的值域可能为[0,)+∞；D ．若0k ≤，则[()]f g x 的值域可能为(,0]-∞．二、填空题：本大题有7小题，多空题每题6分，单空题每题4分，共36分．11.已知函数2log ,0()21,0xx x f x x >⎧⎪=⎨-⎪⎩≤，则1(())2f f = ；若1()2f x = ，则x = ． 12. 在261(2)3x x-二项展开式的中，常数项是 ，其二项式系数之和为 ．13. 有9本不同的书，其中语文书2本，英语书3本，数学书4本，现随机拿出2本．两本书不同类的概率为 ；记拿出数学书的本数为X ，则()E X = ．14. 已知函数2()(3)1f x ax a x =+-+.若()f x 在区间上[1,)-+∞递减，则实数a 的取值范围是 ；若函数()f x 在[1,2]x ∈上的最小值为2，则a 的值为 ．15.把分别写有 1,2,3,4,5 的五张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张,则必须是连号,那么不同的分法种数为 .（用数字作答) 16. 已知实数0,0a b >>，且11=12a b +，则89211a b a b +--的最小值为 ． 17.若函数()|e |e xxaf x =+在区间(0,1)上存在最小值，则实数a 的取值范围是 . 三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18．已知函数()sin (sin 3cos )f x x x x =+. （1）求函数()f x 的最小正周期；（2）求函数()f x 在[0,]x ∈π上的单调增区间.19．如图，在四棱锥P ABCD -中，122PA PB AD CD BC =====，//AD BC ，AD CD ⊥，E 是PA的中点，平面PAB ⊥平面ABCD . （1）证明：PB CE ⊥；（2）求直线CE 与平面PBC 所成的角的正弦值.20.等差数列{}n a 满足13a =，2591,1,5a a a +++成等比数列，数列{}n b 满足11b =，1n n n b b a +=+. （1）求数列{}{},n n a b 的通项公式；（2）记数列1n n n a b b +⎧⎫⎨⎬⎩⎭的前n 项和n T ，求证1n T <．21．已知椭圆22221(0)x y a b a b +=>>的左焦点F在直线30x y -+=上，且2a b +=+（1）求椭圆的方程 ；（2）直线l 与椭圆交于A 、C 两点，线段AC 的中点为M ，射线MO 与椭圆交于点P ，点O 为PAC ∆的重心，探求PAC ∆面积S 是否为定值，若是，则求出这个值；若不是，则求S 的取值范围.22.已知函数2()ln ()2af x a x x ax a =+-+∈R .（1）当 a = 9时，求函数()f x 的单调递减区间；（2）若函数()f x 存在极大值点1x 与极小值点2x ，当21x x -()()12f x f x + (3ln6)λ-≤恒成立，求实数λ的取值范围.参考答案：1~10 DDBCA BABCC11. 12- 12.20,642713. 138,189 14. [3,0],2- 15. 36 16. 25 17.22(1,)(,1)e e --21.。

浙江省金华市东阳中学【精品】高一上学期10月月考数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知全集{}{}{}0,1,2,3,4,0,1,2,2,3U M N ===则U C M N ⋂= ( ) A ．{}2 B ．{}3 C ．{}2,3,4 D ．{}0,1,2,3,4 2．已知集合{}1,3M =，{}|03,N x x x Z =<<∈，又P MN =，那么集合P 的真子集共有（ ）A ．3个B ．7个C ．8个D ．9个 3．下列四组函数中，表示同一函数的是（ ）A ．1y x =-与y =B ．y =y =C ．0y x =与1y =D ．y x=与2y = 4．下列正确的是（ ）A ．log ()log log a a a x y x y ⋅=⋅B ．log ()log log a a a x y x y +=+C ．log ()log log a a a x y x y ÷=÷D ．1log log log ()a a a x y x y --=⋅ 5．函数3x y = 与3x y -=-的图象关于( )对称A ．x 轴B ．y 轴C ．直线y x =D ．原点中心对称 6．若32a =,则33log 82log 6-用含a 的代数式可表示为（ ）A ．2a -B ．()231a a -+C ．52a -D ．23a a - 7．已知奇函数()f x 的定义域为(,0)(0,)-∞+∞，且对任意正实数12,x x 12()x x ≠，恒有12)12()(f x f x x x --﹥0，则一定有（ ）A ．(3)(5)f f >-B ．(3)(5)f f -<-C ．(5)(3)f f ->D ．(3)(5)f f ->- 8．设f(x)＝()2,01,0x a x x a x x ⎧-≤⎪⎨++>⎪⎩若f(0)是f(x)的最小值，则a 的取值范围为( ) A ．[－1，2] B ．[－1，0]C ．[1，2]D ．[0，2]9．已知()538f x x ax bx =++-，且()lg210f =，那么1lg 2f ⎛⎫ ⎪⎝⎭等于（ ） A ．-26 B ．-18 C ．-10D ．10 10．已知函数()x F x e =满足()()()F x g x h x =+，且()g x ，()h x 分别是R 上的偶函数和奇函数，若(0,2]x ∀∈使得不等式(2)()0g x ah x -≥恒成立，则实数a 的取值范围是（ ）A．(,-∞B．(,-∞ C．(0,D．)+∞二、双空题11．31log 27=__________，1020.5312(0.01)54-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭=____________. 12．已知13x x -+=,则22x x -+=_________；1x x --=__________.13．函数21213x x y +-⎛⎫= ⎪⎝⎭的单调递减区间是_________；值域是_________.14．已知2(31)2f x x x +=-，则(4)f =______；()f x 的值域为_________.三、填空题15．函数1()2x f x a -=-（0a >且1 a ≠）的图象恒过定点____．16．若2()3f x x x =-在[]0,m 上的值域为9,04⎡⎤-⎢⎥⎣⎦，则m 的取值范围为_______. 17．若2()(1)3f x x m x m =+-+-在[]2,0x ∈-上是减函数，则m 的取值范围是________________.四、解答题18．已知全集U =R，集合R A x y x ⎧⎫⎪⎪==∈⎨⎬⎪⎪⎩⎭，{}2,R B x a x a a =≤≤+∈（1）当1a =时，求A B ；（2）当集合,A B 满足A B A ⋃=时，求实数a 的取值范围．19．已知函数f (x )是R 上的奇函数，当x >0时，1()1f x x=-+. （1）求函数f (x )的解析式；（2）证明函数f (x )在区间()0,∞+上是单调增函数． 20．设函数32()32x xx xf x -=+． （1）判断()f x 的奇偶性并证明；（2）当[)1,x ∈-+∞时，求()f x 的值域.21．已知函数111()32x f x +⎛⎫=- ⎪⎝⎭. (1)作出函数()f x 的图象,并写出其单调区间；(2)若关于x 的方程()f x m =有一正一负两个实根,求实数m 的取值范围.22．已知R m ∈，函数2()(32)2f x x m x m =-+-++．（1）若102m <≤，求()f x 在[1,1]-上的最大值()g m ； （2）对任意的(0,1]m ∈，若()f x 在[0,]m 上的最大值为()h m ，求()h m 的最大值．参考答案1．B【分析】先求M 的补集，再与N 求交集．【详解】∵全集U ＝{0，1，2，3，4}，M ＝{0，1，2}，∴∁U M ＝{3，4}．∵N ＝{2，3}，∴（∁U M ）∩N ＝{3}．故选B ．【点睛】本题考查了交、并、补集的混合运算，是基础题．2．B【详解】因为N={x|0＜x ＜3，x ∈Z}={1，2}，又M={1，3}，所以P=M ∪N={1，3}∪{1，2}={1，2，3}，所以集合{1，2，3}的真子集有：φ，{1}，{2}，{3}，{1，2}，{1，3}，{2，3}共7个．故选B ．3．A【分析】依次判断各个选项中两个函数的定义域和解析式，选择选项中定义域和解析式完全相同的两个函数，为同一函数.【详解】A 中，1y x =-定义域为R ；1y x ==-，且y =R1y x ∴=-与y =B 中，y =[)1,+∞；y =()1,+∞，两函数定义域不同y ∴=y = C 中，0y x =定义域为{}0x x ≠；1y =定义域为R ，两函数定义域不同0y x ∴=与1y =不是同一函数D 中，y x =定义域为R ；2y =定义域为[)0,+∞，两函数定义域不同y x ∴=与2y =不是同一函数 故选：A【点睛】 本题考查两函数表示同一函数的判断，关键是明确两函数如果是同一函数，则需两函数的定义域和解析式完全相同.4．D【分析】根据对数的运算公式，即可求解，得到答案.【详解】 根据对数的运算公式，可得1log log log log ()a a aa x x y x y y--==⋅. 故选：D.【点睛】本题主要考查了对数的运算的化简，其中解答中熟记对数的运算公式是解答的关键，着重考查了运算能力，属于基础题.5．D【分析】在函数3x y =的图象上任取一点(,3)a A a ，得到函数3x y -=-图象上点的坐标为(,3)a A a '--，结合点的对称关系，即可求解.【详解】在函数3x y =的图象上任取一点(,3)aA a ， 可得点A 对应函数3x y -=-图象上点的坐标为(,3)aA a '--，因为A 和点A '关于原点对称，所以可得函数3x y =与3xy -=-的图象关于原点对称.故选：D.【点睛】本题主要考查了指数函数的图象的应用，其中解答中熟记指数函数的图象与性质，合理利用点的对称关系是解答的关键，着重考查了推理与论证能力，属于基础题.6．A【解析】试题分析：由32a =得3log 2a =，所以()33333333log 82log 6log 22log 233log 22(log 2log 3)32(1)2a a a -=-⨯=-+=-+=-.考点：对数运算.7．D【分析】 根据不等式1212()()0f x f x x x ->-对任意两个不相等的正实数1x ，2x 都成立，得到()f x 在区间(0,)+∞单调递增，再根据()f x 为奇函数，根据对称性可知()f x 在(,0)-∞上也单调递增，从而求出答案．【详解】 解：对任意正实数1x 、212()x x x ≠，恒有不等式1212()()0f x f x x x ->-， ()f x ∴在区间(0,)+∞单调递增，又()f x 的定义域为(,0)(0,)-∞+∞且为奇函数，()f x ∴在区间(,0)-∞、(0,)+∞单调递增，(3)(5)f f ∴->-，故选：D ．【点睛】考查函数的单调性的定义及应用定义比较函数值的大小，属于基础题．8．D【分析】由分段函数可得当0x =时，2(0)f a =，由于(0)f 是()f x 的最小值，则(,0]-∞为减函数，即有0a ≥，当0x >时，1()f x x a x =++在1x =时取得最小值2a +，则有22a a ≤+，解不等式可得a 的取值范围.【详解】因为当x≤0时，f(x)＝()2x a -，f(0)是f(x)的最小值，所以a≥0.当x ＞0时，1()2f x x a a x =++≥+，当且仅当x ＝1时取“＝”． 要满足f(0)是f(x)的最小值，需22(0)a f a +>=，即220a a --≤，解得12a -≤≤，所以a 的取值范围是02a ≤≤，故选D.【点睛】该题考查的是有关分段函数的问题，涉及到的知识点有分段函数的最小值，利用函数的性质，建立不等关系，求出参数的取值范围，属于简单题目.9．A【分析】由解析式得到()f x -，可知()()16f x f x +-=-，得到()1lg16lg 22f f ⎛⎫=-- ⎪⎝⎭，进而求得结果.【详解】 ()538f x x ax bx =++- ()538f x x ax bx ∴-=----()()16f x f x ∴+-=-1lg lg 22=- ()()()1lg 2lg lg 2lg 2162f f f f ⎛⎫∴+=+-=- ⎪⎝⎭()1lg 16lg 21610262f f ⎛⎫∴=--=--=- ⎪⎝⎭故选A【点睛】本题考查根据函数的性质求解函数值的问题，关键是能够根据函数解析式得到()f x 与()f x -的关系.10．B【详解】试题分析：由已知可得()()()()()()()x x x F x g x h x e g x h x e g x h x e --=+=⇒-+-=⇒-=()2x xe e g x -+⇒=，2222()(2)()?0222x x x x x x x xx x e e e e e e e e h x g x ah x a a e e ------+-+=⇒-=-≥⇒≤-，(0,2]x ∀∈恒成立，又222()22()x x x x x x x x x x x x e e e e e e e e e e e e ------+-+==-+≥---(,a =∈-∞，故选B.考点：1、函数的奇偶性；2、函数与不等式.【方法点晴】本题考查导函数的奇偶性、函数与不等式，涉及函数与方程思想、数形结合思想和转化化归思想，考查逻辑思维能力、等价转化能力、运算求解能力，综合性较强，属于较难题型. 11．-3.4730. 【分析】根据指数幂和对数的运算公式，准确运算，即可求解，得到答案.【详解】由题意，根据对数的运算性质，可得33331log log 33log 3327-==-=-； 根据指数幂的运算性质，可得121020.520.52312(0.01)311[()][()]21054--⎛⎫⎛⎫+-= +-⎪ ⎪⎝⎭⎝⎭ 2147131030=+-=. 故答案为： 3-； 4730. 【点睛】 本题主要考查了对数的运算性质，以及指数幂的运算公式，其中解答中熟记指数幂的运算公式和对数的运算性质是解答的关键，着重考查了推理与运算能力，属于基础题.12．7.【分析】利用指数幂的运算性质，利用平方关系，即可求解，得到答案.【详解】由13x x -+=，可得1222()29x x x x--+=++=，所以227x x -+=，又由1222)2(725x x x x---=+-=-=，所以1x x --=故答案为：7，【点睛】本题主要考查了指数幂的运算性质的应用，其中解答中熟记指数幂的运算性质，合理利用平方关系求解是解答的关键，着重考查了推理与运算能力，属于基础题.13．(],1-∞. 1,9⎡⎫+∞⎪⎢⎣⎭. 【分析】令()2(1)2f x x =--+，根据二次函数的性质得到()f x 在(,1]-∞上单调递增，且()f x 的值域为(,2]-∞，再结合指数函数的性质及复合函数的单调性的判定方法，即可求解.【详解】由题意，令()2221(1)2f x x x x =-++=--+， 根据二次函数的性质，可得函数()f x 在(,1]-∞上单调递增，且()f x 的值域为(,2]-∞，又由1()3xy =在R 上为单调递减函数， 根据复合函数的单调性，可得函数21213x x y +-⎛⎫= ⎪⎝⎭的递增区间为(,1]-∞，且211()39y ≥=，即函数的值域为1[,)9+∞. 故答案为：(],1-∞，1,9⎡⎫+∞⎪⎢⎣⎭. 【点睛】本题主要考查了指数函数的图象与性质的应用，以及复合函数的单调性的判定，其中解答中熟记指数函数的图象与性质，以及熟练应用复合函数的单调性的判定方法是解答的关键，着重考查了推理与运算能力，属于中档试题. 14．-1. [)1,-+∞. 【分析】令1x =，可得(4)1f =-，再利用换元法求得21()(4)19f x x =⋅--，结合二次函数的性质，即可求得函数()f x 的值域. 【详解】由题意，函数2(31)2f x x x +=-，令1x =，可得2(4)1211f =-⨯=-， 令31t x =+，则13t x -=，可得22111()()2(4)1339t t f t t --=-⨯=⋅--， 21()(4)119f x x =--≥-，所以函数()f x 的值域为[)1,-+∞.故答案为：1-，[)1,-+∞. 【点睛】本题主要考查了函数值得求解，以及函数的解析式与函数的值域的求解，其中解答中熟记函数的解析式的求法，合理利用二次函数的性质求解是解答的关键，着重考查了推理与运算能力，属于基础题. 15．()1,1- 【分析】根据指数函数xy a =的平移，得到1()2x f x a -=-，从而得到其图象恒过的点，得到答案.【详解】将指数函数xy a =向右平移1个单位，再向下平移2个单位， 得到1()2x f x a -=-，而指数函数x y a =恒过点()0,1所以函数1()2x f x a -=-恒过点()1,1- 【点睛】本题考查指数函数平移后过定点问题，属于简单题. 16．3.32⎡⎤⎢⎥⎣⎦. 【分析】令(0)0f =，解得0x =或3x =，令9()4f x =-，解得32x =±，结合二次函数的性质，即可求解，得到答案. 【详解】由题意，函数2239()3()24f x x x x =-=--， 令(0)0f =，即230x x -=，解得0x =或3x =， 令9()4f x =-，即2399()244x --=，解得32x =±， 所以使得()f x 在[]0,m 上的值域为9,04⎡⎤-⎢⎥⎣⎦，结合二次函数的性质，可得332m ≤≤，即m 的取值范围为332⎡⎤⎢⎥⎣⎦，. 故答案为：332⎡⎤⎢⎥⎣⎦，【点睛】本题主要考查了二次函数的图象与性质的应用，其中解答中熟记二次函数的图象与性质，合理运算是解答的关键，着重考查了推理与运算能力，属于基础题. 17．(][),33,-∞-+∞.【分析】利用二次函数、带有绝对值的函数的图象和性质，结合函数()f x 的图象，即可求解. 【详解】由题意，函数2(1)3y x m x m =+-+-的判别式2(3)40m ∆=-=>， 所以方程2(1)30x m x m +-+-=有2个不等的实数根， 设两根分别为,a b ，且a b <，因为函数()f x 在[]2,0x ∈-上是减函数，如图（1）所示，可得0a ≥0≥，即22(1)(3)4m m -≥-+，解得3m ≥；如图（2）所示，可得0122b m ≥⎧⎪⎨-≤⎪⎩，即03m ≥⎪≤-⎩，解得3m ≤-， 综上可得，实数m 的取值范围是(][),33,-∞-+∞.故答案为：(][),33,-∞-+∞.【点睛】本题主要考查了二次函数，以及带有绝对值的函数的图象与性质的应用，其中解答中熟练应用二次函数的性质，得出带有绝对值函数的图象，结合图象列出不等式组是解答的关键，着重考查了数形结合思想，以及推理与计算能力，属于中档试题.若f(x)=|x 2+(1-m)x+m-3|在[-2,0]上是减函数，则m 的取值范围是________________. 18．(1),[)1,3A B ⋂=；(2) ()0,1. 【分析】（1）化简集合,A B ，根据交集的定义，即可求解；（2）由A B A ⋃=，得到B A ⊆，由此列出不等式组，即可求解实数a 的取值范围． 【详解】（1）由题意，集合{}2R 30{|03}A x y x x x x x x ⎧⎫⎪⎪==∈=-=<<⎨⎬⎪⎪⎩⎭，当1a =时，集合{}13B x x =≤≤，所以AB [){|13}1,3x x =≤<=.（2）由集合,A B 满足A B A ⋃=，即B A ⊆， 此时集合B φ≠，所以满足023a a >⎧⎨+<⎩，解得01a <<，即实数a 的取值范围()0,1 【点睛】本题主要考查了集合的交集运算，以及利用结合的包含关系求解参数的范围，其中解答中正确求解集合,A B ，熟记集合的交集运算，以及利用集合间的关系，列出不等式组是解答的关键，着重考查了推理与运算能力，属于基础题.19．(1)11,(0)()0,(0)11,(0)x x f x x x x⎧-+>⎪⎪==⎨⎪⎪--<⎩；(2)见解析.【分析】（1）设0x <，则0x ->，根据函数()f x 为奇函数，得到()00f =，且()()f x f x =--，即可求解函数的解析式；（2）根据函数的单调性性的定义，即可证明函数()f x 在()0,∞+上为单调递增函数. 【详解】（1）设0x <，则0x ->，因为函数()f x 为奇函数，则当0x =时，()00f =， 且()()11(1)1f x f x x x=--=--+=---， 所以函数()f x 的解析式为11,(0)()0,(0)11,(0)x x f x x x x⎧-+>⎪⎪==⎨⎪⎪--<⎩. （2）任取()12,0,x x ∈+∞，且12x x <， 则()12121221121111()1(1)x x f x f x x x x x x x --=-+--+=-=， 因为()12,0,x x ∈+∞，且12x x <，所以12120,0x x x x >-<， 所以()12()0f x f x -<，即()12()f x f x <， 所以函数()f x 在()0,∞+上为单调递增函数. 【点睛】本题主要考查了利用函数的奇偶性求解函数的解析式，以及利用函数的单调性的定义判定函数的单调性，其中解答中熟记函数的单调性的定义，以及合理应用函数的奇偶性，准确运算是解答的关键，着重考查了推理与运算能力，属于基础题. 20．(1)见解析；(2) 1[,1)5-. 【分析】（1）先求得函数的定义域，结合函数的解析式可得()f x -与()f x 的关系，即可求解；（2）将函数的解析式变形，可得31()21x y y+=-，结合x 的范围分析可得1213y y +≥-，即可求得x 的取值范围，得到答案. 【详解】（1）由题意，函数32()32x xx xf x -=+的定义域为R ，关于原点对称， 又由322332()()322332x x x x x xx x x x x xf x f x ------------===-=-+++，所以函数()f x 为定义域上的奇函数；（2）根据题意，函数3()1322()332()12x xxx xx y f x --===++，变形可得31()21x y y +=-， 又由[)1,x ∈-+∞，则1332()()223x -≥=，即1213y y +≥-， 解得115y -≤<，即函数()f x 的值域为1[,1)5-. 【点睛】本题主要考查了函数的奇偶性的判定与证明，以及函数值域的求解，其中解答中熟记函数的奇偶性的定义，以及合理变形，结合指数函数的性质求解函数的值域是解答的关键，着重考查了推理与运算能力，属于基础题.21．（1）递增区间(],1-∞-，递减区间[)1,-+∞（2）11(,)26--. 【分析】（1）把函数的解析式，分类讨论去掉绝对值，得到分段函数，作出函数的图象，结合图象，即可求解函数的单调区间；（2）转化成关于x 的方程()f x m =有一正一负两个实根，即函数()y f x =与直线y m =有2个交点，且两个交点位于y 轴的两侧，结合函数的图象，即可求解. 【详解】（1）由题意，函数可化为111()32x f x +⎛⎫=-⎪⎝⎭， 可得，当1x ≥-时，111()()32x f x +=-，当1x <-时11()32x f x +=-， 其图象如图所示：结合图象可得，函数()f x 的递增区间为(,1]-∞-，递减区间为[1,)-+∞.（2）根据题意，函数()111()32x f x +=-，则()1110326f =-=-， 若关于x 的方程()f x m =有一正一负两个实根，即函数()y f x =与直线y m =有2个交点，且两个交点位于y 轴的两侧，结合函数的图象可得1126m -<<-， 求实数m 的取值范围11(,)26--.【点睛】本题主要考查了分段函数的应用，以及函数与方程的综合应用，其中解答中根据函数的解析式，准确作出函数的图象，结合图象求解是解答的关键，着重考查了数形结合思想，以及推理与运算能力，属于基础题. 22．（1）()4g m m =-；（2）10.3【分析】（1）先判断函数()f x 在[1,1]-上的单调性，求出函数()f x 的最大值，即可求得函数()g m ； （2）求出m 与对称轴的关系，结合一元二次函数的性质，即可求解. 【详解】（1）由题意，函数2()(32)2f x x m x m =-+-++22223232324817()2()()2224m m m m m x m x ----+=--+++=--+， 则函数的对称轴为322mx -=， 若102m <≤，则021m <≤，则323122m -≤<， 则函数()f x 在区间[1,1]-为增函数，所以当1x =时，函数取得最大值，最大值为2(1)1(32)124f m m m =-+-⨯++=-， 即()4g m m =-.（2）由()22324817()24m m m f x x --+=--+，得函数的对称轴为322m x -=， 当(0,1]m ∈，则022m <≤，则1323222m -≤<，若322m m -≤，即304m <≤时，函数()f x 在[0,]m 上单调递增， 则最大值为()()22(32)234h m f m m m m m m m ==-+-++=-++2；若322m m ->，即314m <≤时，函数()f x 在[0,]m 上先增后减， 当322m m -=时，函数()f x 取得最大值，最大值为()2232481717()2244h m m m m m f m --+=-+==，所以223342,04()1732,144m m m h m m m m ⎧-++<≤⎪⎪=⎨⎪-+<≤⎪⎩，当304m <≤时，2()342h m m m =-++的对称轴为23m =， 当23m =时，函数()h m 取得最大值222210()3()423333h =-⨯+⨯+=；当314m <≤时，217()24h m m m =-+的对称轴为1m =，此时函数()h m 为减函数， 则函数23331753()()()2444416h m h <=-⨯+=，因为1053316>，所以()h m 的最大值为103. 【点睛】本题主要考查了一元二次函数的图象与性质的应用，以及一元二次函数在区间上的最值问题的求解，其中解答中熟记一元二次函数的图象与性质，合理根据函数的对称轴与区间的关系分类讨论求解是解答的关键，着重考查了分类讨论思想，以及推理与运算能力，属于中档试题.。

2024-2025学年浙江省金华市高三上学期10月联考数学检测试卷考生注意：1．本试卷满分150分，考试时间120分钟.2．考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色.墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效.一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，集合，则（）{}2450A x x x =--<∣{}2,0,2,4,10B =-A B = A .B.{}2,0,2,4-{}2,10-C.D.{}0,2,4{}2,42. 已知，则（）1i z =--()1i z -=A .B. 1D. 22-3. 已知非零向量，，则“”是“向量”的（）a b a b a b +=- a b ⊥ A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 若过点与圆相切的两条直线的夹角为，则（ ）()224xy +=αcos α=A. B. D. 35455. 二项式的展开式中的常数项为（ ）622x x ⎛⎫+ ⎪⎝⎭A. 480B. 240C. 120D. 156. 已知底面半径为2的圆锥，其轴截面是正三角形，它的一个内接圆柱的底面半径为SO 1，则此圆柱侧面积与圆锥侧面积的比值为（）SO A. 1D. 127. 函数在区间上的所有零点之和为（ ）()5πsin cos cos 24x f x x x ⎛⎫=-+ ⎪⎝⎭()π,2π-A .B. C. D. 4π2π3π8. 已知函数的定义域为，当或或是无理数时，；当()f x []0,10x =1x =x ()0f x =（，，是互质的正整数）时，．那么当，，，都n x m =n m <m n ()1f x m =a b a b +ab 属于时，下列选项恒成立的是（）[]0,1A. B. ()()()f a b f a f b +≤+()()()f a b f a f b +≥⋅C.D.()()()f ab f a f b ≥+()()()f ab f a f b ≥⋅二、多项选择题：本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9. 随机变量，分别服从正态分布和二项分布，且，，则（X Y ()2,1X N ()4,0.5Y B ~）A. B. ()()04P X P X ≤=≥()()04P Y P Y ≤=≥C.D.()()E X E Y =()()22P X P Y ≤=≤10. 在正四棱柱中，，点是棱上的动点（不含端点），1111ABCD A B C D -12AB AA =M 1DD 则（）A. 过点有且仅有一条直线与直线，都垂直M AC 11B DB. 过点有且仅有一条直线与直线，都相交M AC 11B DC. 有且仅有一个点满足和的面积相等M MAC △11MB D D. 有且仅有一个点满足平面平面M MAC ⊥11MB D 11. 已知是曲线上的一点，则下列选项中正确的是（ ）()00,P x y 33:C x y y x +=-A. 曲线的图象关于原点对称C B. 对任意，直线与曲线有唯一交点0x ∈R 0x x =C PC. 对任意，恒有[]01,1y ∈-012x <D. 曲线在的部分与轴围成图形的面积小于C 11y -≤≤y π4三、填空题：本大题共3小题，每小题5分，共15分．12. 已知椭圆的左、右焦点分别为，，椭圆上一点满足，则22143x y +=1F 2F P 212PF F F ⊥线段__________．2PF =13. 已知曲线在处的切线恰好与曲线相切，则实数的值为e xy =1x =l ln y a x =+a ______．14. 数学老师在黑板上写上一个实数，然后老师抛掷一枚质地均匀的硬币，如果正面向上，0x 就将黑板上的数乘以再加上3得到，并将擦掉后将写在黑板上；如果反面向上，0x 2-1x 0x 1x 就将黑板上的数除以再减去3得到，也将擦掉后将写在黑板上．然后老师再抛0x 2-1x 0x 1x 掷一次硬币重复刚才的操作得到黑板上的数为．现已知的概率为0.5，则实数的2x 20x x >0x 取值范围是__________．四、解答题：本大题共5小题，共77分．解答应写出必要的文字说明、证明过程及演算步骤．15. 在中，角的对边分别为，，，已知，ABC V ,,A B C a b c 222c a b ab =++．()sin cos C B A-=（1）求角和角．C B （2）若边的面积．BC ABC V 16. 已知双曲线与过点，的直线有且只2222:1(0,0)x y C a b ab -=>>A⎫⎪⎭(0,B有一个公共点，且双曲线的离心率．T C e =（1）求直线和双曲线的方程；AB C （2）设，为双曲线的左、右焦点，为线段的中点，求证：1F 2F C M 2AF ．21MTF TF A ∠=∠17. 如图，在四棱锥中，底面是菱形，，侧面是正三P ABCD -ABCD 60BAD ∠=PAD 角形，是棱的中点．M PC（1）证明：；AD DM ⊥（2）若二面角为，求直线与平面所成角的正弦值．P AD B --60oDM PAB 18. 已知函数．()()e xf x x a =-（1）若，求函数的单调区间和最值；2a =()f x （2）若，且一次函数的图象和曲线相切于处，求函数0a ≤()y g x =()y f x =1x =-的解析式并证明：恒成立．()g x ()()g x f x ≤（3）若，且函数在上有两个极值点，求实数的1a =()()()2h x f x t x x =--1,22x ⎛⎫∈ ⎪⎝⎭t 取值范围．19. 已知整数，数列是递增的整数数列，即4n …{}n a 且．数列满足，．若对于12,,,n a a a ∈Z12n a a a <<<{}n b 11b a =n n b a =，恒有等于同一个常数，则称数列为的“左型间隔数{}2,3,,1i n ∈- 1i i b a --k {}n b {}n a k 列”；若对于，恒有等于同一个常数，则称数列为的{}2,3,,1i n ∈- 1i i a b +-k {}n b {}n a “右型间隔数列”；若对于，恒有或者，则称数k {}2,3,,1i n ∈- 1i i a b k +-=1i i b a k --=列为的“左右型间隔数列”．{}n b {}n a k （1）写出数列的所有递增的“左右1型间隔数列”；{}:1,3,5,7,9n a （2）已知数列满足，数列是的“左型间隔数列”，数列{}n a ()81n a n n =-{}n b {}n a k 是的“右型间隔数列”，若，且有，求{}n c {}n a k 10n =1212n n b b b c c c +++=+++ 的值；k（3）数列是递增的整数数列，且，．若存在的一个递增的“右4型{}n a 10a =27a ={}n a 间隔数列”，使得对于任意的，都有，求的关于{}n b {},2,3,,1i j n ∈- i j i j a b b a +≠+n a 的最小值（即关于的最小值函数）．n n ()f n 2024-2025学年浙江省金华市高三上学期10月联考数学检测试卷考生注意：1．本试卷满分150分，考试时间120分钟.2．考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色.墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效.一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，集合，则（）{}2450A x x x =--<∣{}2,0,2,4,10B =-A B = A. B. {}2,0,2,4-{}2,10-C.D.{}0,2,4{}2,4【正确答案】C【分析】先求出集合A ，后根据交集概念计算即可.【详解】因为，{15}A x x =-<<∣{}2,0,2,4,10B =-所以．{}0,2,4A B ⋂=故选：C ．2. 已知，则（）1i z =--()1i z -=A. B. 1D. 22-【正确答案】A【分析】根据复数的乘法运算即可求解.【详解】因为．()()()21i 1i 1i (i)12z -=---=--=-故选：A ．3. 已知非零向量，，则“”是“向量”的（）a b a b a b +=- a b ⊥ A. 充分不必要条件 B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件【正确答案】C【分析】根据充分条件、必要条件的定义及数量积的运算律判断即可.【详解】因为，为非零向量，ab 若，则，则，a b a b+=-()()22a ba b+=- 222222aa b b a a b b +⋅+=-⋅+ 所以，所以，故充分性成立；40a b ⋅= a b ⊥若，则，所以，a b ⊥ 0a b ⋅= 222222a a b b a a b b +⋅+=-⋅+ 所以，则，故必要性成立；()()22a ba b+=- a b a b+=- 所以“”是“向量”的充要条件.a b a b+=-a b ⊥故选：C ．4. 若过点与圆相切的两条直线的夹角为，则（ ）()224xy+=αcos α=A. B.D. 3545【正确答案】A【分析】由题意求出点到圆心的距离为，进而可得，结合二倍角的余()d sin=2rd α弦公式计算即可求解.【详解】点到圆心的距离为，圆的半径为，()()0,0d =2r =所以，于是．sin 2r d α===223cos 12sin 1225αα=-=-=故选：A ．5. 二项式的展开式中的常数项为（ ）622x x ⎛⎫+ ⎪⎝⎭A. 480 B. 240C. 120D. 15【正确答案】B【分析】运用通项公式计算即可.【详解】因为得到常数项，则．()621231662C C 2,rrrr r rr T xxx --+⎛⎫== ⎪⎝⎭4r =.246C 21516240=⨯=故选:B．6. 已知底面半径为2的圆锥，其轴截面是正三角形，它的一个内接圆柱的底面半径为SO 1，则此圆柱侧面积与圆锥侧面积的比值为（）SO A. 1D.12【正确答案】C.【详解】作出轴截面，如图所示，由题意可得：，可知分别为的中点，4,2AB DE ==,D E ,SA SB 则分别为的中点，则，,M N ,OAOB 12DM SO ==可得；2πS ==圆柱侧面积π248πS =⨯⨯=圆锥侧面积故选：C ．7. 函数在区间上的所有零点之和为（ ）()5πsin cos cos 24x f x x x ⎛⎫=-+ ⎪⎝⎭()π,2π-A. B. C. D. 4π2π3π【正确答案】B【分析】根据函数零点个数与其对应方程的根、函数图象的交点个数之间的关系，作出函数和的图象，利用数形结合的思想即可求解.5πcos 24x y ⎛⎫=+ ⎪⎝⎭tan y x =【详解】由得，即，()0f x =sin 5πcos cos 24x x x⎛⎫=+ ⎪⎝⎭5πtan cos 24x x ⎛⎫=+ ⎪⎝⎭函数的零点即方程的根，()f x 5πtan cos 24x x ⎛⎫=+ ⎪⎝⎭作出函数和的图象，如图，5πcos 24x y ⎛⎫=+ ⎪⎝⎭tan y x =由图可知两个图均关于中心对称且在上有两个交点，π,02⎛⎫ ⎪⎝⎭π,2π2⎛⎫⎪⎝⎭故函数在区间上有4个零点，所以4个零点的和为．()f x ()π,2π-2π故选：B ．8. 已知函数的定义域为，当或或是无理数时，；当()f x []0,10x =1x =x ()0f x =（，，是互质的正整数）时，．那么当，，，都n x m =n m <m n ()1f x m =a b a b +ab 属于时，下列选项恒成立的是（）[]0,1A. B. ()()()f a b f a f b +≤+()()()f a b f a f b +≥⋅C.D.()()()f ab f a f b ≥+()()()f ab f a f b ≥⋅【正确答案】D【分析】使用特值法可排除A,B,C,据，的取值可分类讨论证明D 正确.a b 【详解】当时，，，12a b ==()()=1=0f a b f +()11==44f ab f⎛⎫ ⎪⎝⎭，()()11==()22f a f b f =所以，，故排除B 、C ；()()()f a b f a f b +<⋅()()()f ab f a f b <⋅当，时，，，，18a =38b =()11==22f a b f ⎛⎫+ ⎪⎝⎭()11==88f a f ⎛⎫ ⎪⎝⎭()31==88f b f ⎛⎫ ⎪⎝⎭所以，故排除A ．()()()f a b f a f b +>+下面证明D 的正确性：当，之一为无理数或者0或者1时，不等式右边为0，显然成立．a b 当，都是真分数时，不妨设，，a b n a m =q b p =则不等式右边为，显然有左边大于或等于．1mp 1mp 所以不等式成立．故选：D ．二、多项选择题：本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9. 随机变量，分别服从正态分布和二项分布，且，，则（X Y ()2,1X N ()4,0.5Y B ~）A .B. ()()04P X P X ≤=≥()()04P Y P Y ≤=≥C.D.()()E X E Y =()()22P X P Y ≤=≤【正确答案】ABC【分析】根据正态分布的性质和二项分布的性质计算即可.【详解】对A ，因为，根据对称性，知道，故A 正确；()2E X =对B ，因为，故B 正确；()()()()440411100C (()441622P Y P Y P Y P Y ≤=======≥对C ，因为，故C 正确；()()2,40.52E X E Y ==⨯=对D ，因为，，()122P X ≤=()004113222444111111112C (()C ()()C (()22222216P Y ≤=++=故D 错误.故选：ABC ．10. 在正四棱柱中，，点是棱上的动点（不含端点），1111ABCD A B C D -12AB AA =M 1DD 则（）A. 过点有且仅有一条直线与直线，都垂直M AC 11B DB. 过点有且仅有一条直线与直线，都相交M AC 11B DC. 有且仅有一个点满足和的面积相等M MAC △11MB D D. 有且仅有一个点满足平面平面M MAC ⊥11MB D 【正确答案】AB【分析】由空间线线、线面、面面的位置关系逐项判断即可.【详解】由图可知直线和直线异面，AC 11B D 则过空间中一点都是有且仅有一条直线与它们垂直，故A 正确；又易知与，都相交，且点在上，1DD AC 11B D M 1DD 所以过点有且仅有一条直线与直线，都相交，故B 正确；M AC 11B D 连接交于，易知，所以，BD AC O MA MC =MO AC ⊥可知到的距离大于，且，M AC DO 1AB A DO ==又到的距离小于，结合所以三角形面积不可能相等，故C 错误；M 11B D 1AA 11AC B D =由正四棱柱易得：平面，又平面，AC ⊥11MB D AC ⊂MAC 所以对任意恒有平面平面，故D 错误.M MAC ⊥11MB D 故选：AB.11. 已知是曲线上的一点，则下列选项中正确的是（ ）()00,P x y 33:C x y y x +=-A. 曲线的图象关于原点对称C B. 对任意，直线与曲线有唯一交点0x ∈R 0x x =C PC. 对任意，恒有[]01,1y ∈-012x <D. 曲线在的部分与轴围成图形的面积小于C 11y -≤≤y π4【正确答案】ACD【分析】将，替换为，计算即可判断A ；取，可判断有三个交点即可判断x y x -y -0x =B ；利用函数的单调性来得出的取值范围，再结合的单调性3y x x =-300y y -()3f x x x =+进行求解即可判断C ；利用图象的对称性和半圆的面积进行比较即可判断D ．【详解】A ．对于，将，替换为，，所得等式与原来等价，故A 33x y y x +=-x y x -y -正确；B ．取，可以求得，，均可，故B 错误；0x =0y =1y =1y =-C ．由，，函数，故，330000x x y y +=-[]01,1y ∈-3y x x =-213y x '=-令，解得：，在，时，，函数单调2130y x '=-=1x =1,x ⎡∈-⎢⎣⎤⎥⎦0'<y 递减，在时，，函数单调递增，所以，x ⎛∈ ⎝0'>y 300y y ⎡-∈⎢⎣又因为是增函数，，所以有，故C 正确；()3f x x x =+1528f ⎛⎫=> ⎪⎝⎭012x <D ．当时，，又，[]00,1y ∈3300000x x y y +=-≥320002x x x +≥，所以．32000022y y y y -≤-22000x y y ≤-曲线与轴围成半圆，又曲线的图象关于原点对称，22x y y =-y C 则曲线与轴围成图形的面积小于，故D 正确．C y π4故选：ACD ．三、填空题：本大题共3小题，每小题5分，共15分．12. 已知椭圆的左、右焦点分别为，，椭圆上一点满足，则22143x y +=1F 2F P 212PF F F ⊥线段__________．2PF =【正确答案】##32 1.5【分析】由已知可得点的横坐标为，代入椭圆方程即可求得点坐标，得出结果.P 1x =P 【详解】因为椭圆，则，所以，，22143xy +=2,1a b c ===()11,0F -()21,0F 因为,212PF F F ⊥所以点的横坐标为，代入求得纵坐标为，即．P 1x =32±232PF =故3213. 已知曲线在处的切线恰好与曲线相切，则实数的值为e xy =1x =l ln y a x =+a ______．【正确答案】2【分析】根据是曲线在处的切线求出的方程，再求出与曲线相l e xy =1x =l l ln y a x =+切的切点即可求解.【详解】由得，又切点为，故，切线为，e x y =e xy '=(1,e)e =k l e y x =设与曲线的切点为，，所以，解得切点为，l ln y a x =+()00,e x x 1y x '=01e x =1,1e ⎛⎫ ⎪⎝⎭所以，解得．1ln 11e a a +=-=2a =故2.14. 数学老师在黑板上写上一个实数，然后老师抛掷一枚质地均匀的硬币，如果正面向上，0x就将黑板上的数乘以再加上3得到，并将擦掉后将写在黑板上；如果反面向上，0x 2-1x 0x 1x 就将黑板上的数除以再减去3得到，也将擦掉后将写在黑板上．然后老师再抛0x 2-1x 0x 1x 掷一次硬币重复刚才的操作得到黑板上的数为．现已知的概率为0.5，则实数的2x 20x x >0x 取值范围是__________．【正确答案】()(),21,-∞-+∞ 【分析】构造函数，，由两次复合列出不等式求解即可.()23f x x =-+()32xg x =--【详解】由题意构造，，()23f x x =-+()32x g x =--则有，，，．()()43f f x x =-()()9f g x x =+()()92g f x x =-()()342x g g x =-因为，恒成立，()()f g x x>()()g f x x<又的概率为0.5，20x x >所以必有或者解得．43,3,42x x x x ->⎧⎪⎨-≤⎪⎩43,3,42x x x x -≤⎧⎪⎨->⎪⎩()(),21,x ∈-∞-⋃+∞故()(),21,-∞-+∞ 四、解答题：本大题共5小题，共77分．解答应写出必要的文字说明、证明过程及演算步骤．15. 在中，角的对边分别为，，，已知，ABC V ,,A B C a b c 222c a b ab =++．()sin cos C B A-=（1）求角和角．C B （2）若边的面积．BC ABC V 【正确答案】（1），2π3C =π4B =（2【分析】（1）根据余弦定理求出，再将化简为2π3C =()sin cos C B A -=，从而求出即可；2ππsin sin 36B B ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭π4B =（2）根据边求出，，利用求解即可.BC 2b =c =1sin 2S bc A =【小问1详解】由余弦定理知，故．2221cos 22a b c C ab +-==-2π3C =因为，所以，()sin cos C B A -=2πππsin cos sin 336B B B ⎛⎫⎛⎫⎛⎫-=-=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又，所以，故．π03B <<2ππ36B B -=+π4B =【小问2详解】因为边上的高，解得，，BC sin sin h b C c B ===2b=c =又，()sin sin sin cos sin cos A B C BC C B =+=+=所以的面积．ABC V 1sin 2S bc A ==16. 已知双曲线与过点，的直线有且只2222:1(0,0)x y C a b a b -=>>A ⎫⎪⎭(0,B 有一个公共点，且双曲线的离心率．T C e =（1）求直线和双曲线的方程；AB C （2）设，为双曲线的左、右焦点，为线段的中点，求证：1F 2F C M 2AF ．21MTF TF A ∠=∠【正确答案】（1），；:AB y =-2215y x -=（2）证明见解析【分析】（1）由离心率求出关系，并化简双曲线方程，再求出直线方程代入双曲线方程,a b 中，利用求解即可；Δ0=（2）求出点坐标，可进一步证明，进而证明.T 122F F T TF M ∽△△21MTF TF A ∠=∠【小问1详解】因为双曲线的离心率，e =所以，解得，2226a b a +=b =设双曲线方程.222215x y a a -=直线过点，，AB A ⎫⎪⎪⎭(0,B 所以直线，即，AB 1=:AB y =代入双曲线方程，得，22255x y a -=22220x a -+--=由题意，，解得()2Δ24820a =-+=21a =所以双曲线的方程：．C 2215y x -=【小问2详解】因为，于是即，21a =22220xa -+--=2230x -+=所以，代入x=y=y =则，又，所以，T 2F 224TF =因为为线段的中点，所以，M 2AF M ⎫⎪⎪⎭所以．222124F M F F F T ⋅===又，所以，故．122F F T TF M ∠=∠122F F T TF M ∽△△21MTF TF A∠=∠17. 如图，在四棱锥中，底面是菱形，，侧面是正三P ABCD -ABCD 60BAD ∠=PAD 角形，是棱的中点．M PC （1）证明：；AD DM ⊥（2）若二面角为，求直线与平面所成角的正弦值．P AD B --60oDM PAB 【正确答案】（1）证明见解析（2【分析】（1）取与中点，．连接，，，，证明四边形AD PB O N PO OB ON MN 是平行四边形．得到线面垂直，再用性质即可.ODMN （2）建立空间直角坐标系，求出平面的一个法向量为，再用向量夹角计算公式计算PAB n即可.【小问1详解】证明：分别取与中点，．连接，，，，AD PB O N PO OB ON MN 则运用中位线性质知且,则11//,22NM BC NM BC =11//,22OD BC OD BC =，//,OD MN OD MN =则四边形是平行四边形．ODMN 侧面是正三角形，易知，.PAD AD OP ⊥底面是菱形，，则底面是正三角形，则.ABCD 60BAD ∠=BAD AD OB ⊥平面， 平面，,,OP OB O OP OB =⊂ POB AD ∴⊥POB 平面，.ON ⊂ POB AD ON ∴⊥由于四边形是平行四边形．，．ODMN DM ON ∥AD DM ∴⊥【小问2详解】由（1）知为二面角的平面角，即，前面知道，POB ∠P AD B --60POB ∠=AD OB ⊥则过O 做AD 的垂线Oz ，以为坐标原点，为坐标轴，建立空间直角坐标系O ,,OA OB Oz 如图，O xyz -设，则，，，，，2AB =A (1,0,0)()1,0,0D-()C-()B 32P ⎛⎫⎪ ⎪⎝⎭，，，，34M ⎛⎫- ⎪ ⎪⎝⎭34DM ⎛⎫∴= ⎪ ⎪⎝⎭()AB =-32PB ⎛⎫=- ⎪ ⎪⎝⎭ 设平面的一个法向量为，PAB n =(x,y,z )则，进而求得一个法向量为．030x z ⎧-+=⎪-=()n = 设直线与平面所成角为，DM PAB α则．sin DM n DM n α⋅=== 18. 已知函数．()()e xf x x a =-（1）若，求函数的单调区间和最值；2a =()f x （2）若，且一次函数的图象和曲线相切于处，求函数0a ≤()y g x =()y f x =1x =-的解析式并证明：恒成立．()g x ()()g x f x ≤（3）若，且函数在上有两个极值点，求实数的1a =()()()2h x f x t x x =--1,22x ⎛⎫∈ ⎪⎝⎭t 取值范围．【正确答案】（1）单调递减区间为，单调递增区间为，最小值为，(),1-∞()1,+∞()1e f =-无最大值．（2），证明见解析()12e e a ag x x +=--（3）．22e e,3⎛⎫⎪⎝⎭【分析】（1）利用导数与单调性的关系求解单调区间，再结合单调性求解最值即可；（2）根据导数的几何意义求出；令12()e e a ag x x +=--，利用导数求出最小值为即()()()()12e e e x a a u x f x g x x a x +=-=-++()u x ()10u -=可；（3）因为函数在上有两个极值点，所以()()()21e xh x x t x x =---1,22⎛⎫⎪⎝⎭在上有两个变号零点，分离参数得，求解直线()()e 21x h x x t x -'=-1,22⎛⎫ ⎪⎝⎭121e x x t x -=与函数在上的图象有两个交点即可.1y t =()21e x x H x x -=1,22⎛⎫⎪⎝⎭【小问1详解】因为，所以，定义域为，求导得，2a =()()2e x f x x =-R ()()1e xf x x -'=故当时，；当时，，(),1x ∞∈-f '(x )<0x ∈(1,+∞)f '(x )>0所以函数的单调递减区间为，单调递增区间为，()f x (),1∞-(1,+∞)所以最小值为，无最大值．()1ef =-【小问2详解】，所以，又，()()1exf x x a =-+'()1e a f '-=-()11e af +-=-所以，即；()()11e e a ag x x +=-+-12()e e a a g x x +=--令，()()()()12e e e x a a u x f x g x x a x +=-=-++则，，这里表示的导函数．()()1e e x au x x a =-++'()()2e xu x x a =-+''()u x ''()u x '令，则，()0u x ''=2=-x a 当变化时，与的变化情况如下表：x ()u x ''()u x 'x(),2a ∞--2a -()2,a ∞-+()u x ''-+()u x '单调递减2e ea a --+单调递增所以当时，函数有极小值，极小值为，也是最小值，2=-x a ()u x '2e e a a--+因为当时，无限趋向于，所以当时，，x →-∞()u x '0e a ≤2x a <-()0u x '<又，此时，在上单调递减，在上单调递增，()10u '-=()u x (),1∞--()1,∞-+所以，即不等式恒成立．()()10u x u ≥-=g (x )≤f (x )【小问3详解】因为函数在上有两个极值点，()()()21e xh x x t x x =---1,22⎛⎫ ⎪⎝⎭所以在上有两个变号零点，()h x '1,22⎛⎫⎪⎝⎭因为，令，即，()()e 21x h x x t x -'=-()0h x '=()e 210x x t x --=因为不是的根，所以，0x =()e 210xx t x --=121e x x t x -=令，则，()2112e 2x x H x x x -⎛⎫=<< ⎪⎝⎭()()()()()()222e 121e 121e e x xxxx x x x x H x x x -+--+==-'当时，；当时，，112x <<()0H x '>12x <<()0H x '<所以函数在上单调递增，在上单调递减，()H x (12,1)()1,2又，，，作出函数在上的图象，102H ⎛⎫= ⎪⎝⎭()11e H =()2322e H =()H x 1,22⎛⎫ ⎪⎝⎭当，即时，直线与函数在上的图象有两个交点，23112e e t <<22e e 3t <<1y t =()H x 1,22⎛⎫ ⎪⎝⎭设两个交点的横坐标分别为，且，12,x x 12x x <由图可知，当或时，，此时，112x x <<22x x <<121e x x t x ->()121e 0e x x x h x tx t x -⎛⎫- ⎝'=>⎪⎭当时，，此时，12x x x <<121e x x t x -<()121e 0e x x x h x tx t x -⎛⎫- ⎝'=<⎪⎭所以函数在上单调递增，在上单调递减，在上单调递增，ℎ(x )11,2x ⎛⎫ ⎪⎝⎭()12,x x ()2,2x 此时，函数有两个极值点，合乎题意．()f x 因此，实数的取值范围为．t 22e e,3⎛⎫⎪⎝⎭19. 已知整数，数列是递增的整数数列，即4n …{}n a 且．数列满足，．若对于12,,,n a a a ∈Z12n a a a <<<{}n b 11b a =n n b a =，恒有等于同一个常数，则称数列为的“左型间隔数{}2,3,,1i n ∈- 1i i b a --k {}n b {}n a k 列”；若对于，恒有等于同一个常数，则称数列为的{}2,3,,1i n ∈- 1i i a b +-k {}n b {}n a “右型间隔数列”；若对于，恒有或者，则称数k {}2,3,,1i n ∈- 1i i a b k +-=1i i b a k --=列为的“左右型间隔数列”．{}n b {}n a k （1）写出数列的所有递增的“左右1型间隔数列”；{}:1,3,5,7,9n a （2）已知数列满足，数列是的“左型间隔数列”，数列{}n a ()81n a n n =-{}n b {}n a k 是的“右型间隔数列”，若，且有，求{}n c {}n a k 10n =1212n n b b b c c c +++=+++ 的值；k （3）数列是递增的整数数列，且，．若存在的一个递增的“右4型{}n a 10a =27a ={}n a 间隔数列”，使得对于任意的，都有，求的关于{}n b {},2,3,,1i j n ∈- i j i j a b b a +≠+n a 的最小值（即关于的最小值函数）．n n ()f n 【正确答案】（1）1，2，4，6，9或1，2，4，8，9或1，2，6，8，9或1，4，6，8，9． （2）80k =（3）()()382n n f n -=+【分析】（1）由“左右型间隔数列”的定义，求数列的所有递增的“左右1型k {}:1,3,5,7,9n a 间隔数列”；（2）根据“左型间隔数列”和“右型间隔数列”的定义，由k k，则有，代入通项计算即可；1212n n b b b c c c +++=+++ 1291016a a k a a ++=+（3）由“右4型间隔数列”的定义，有，可知，则144i i i b a a +=->-{}3i i b a n n -∈≥-∣有()()()232431n n n a a a a a a a a -=+-+-++- ，化简即可．()()()()413216n n ≥-+-+-+-++- 【小问1详解】数列的“左右1型间隔数列”为1，2，4，6，9或1，2，4，8，9或{}:1,3,5,7,9n a 1，2，6，8，9或1，4，6，8，9．【小问2详解】由，可得，12101210b b b c c c +++=+++ 239239b b b c c c +++=+++ 即，即，128341088a a a k a a a k ++++=+++- 1291016a a k a a ++=+即，所以．16168988109k +=⨯⨯+⨯⨯80k =【小问3详解】当时，由，可知．{}2,3,,1i n ∈- 144i i i b a a +=->-{}3i i b a n n -∈≥-∣又因为对任意，都有，{},2,3,,1i j n ∈- i j i ja b b a +≠+即当时，两两不相等．{}2,3,,1i n ∈- i i b a -因为()()()232431n n n a a a a a a a a -=+-+-++- ()()()2233117444n n b a b a b a --=++-++-+++- ()()()()223311742n n n b a b a b a --=+-+-+-++- ()()()()413216n n ≥-+-+-+-++- ．()382n n -=+所以的最小值函数．n a ()()382n n f n -=+另外，当数列的通项{a n }()0,1,38,2,2i i a i i i n =⎧⎪=⎨-+≤≤⎪⎩间隔数列的通项时也符合题意．{b n }(),1,13,21,2i i a i i n b i i i n ==⎧⎪=⎨-+≤≤-⎪⎩或方法点睛：在实际解决“新定义”问题时，关键是正确提取新定义中的新概念、新公式、新性质、新模式等信息，确定新定义的名称或符号、概念、法则等，并进行信息再加工，寻求相近知识点，明确它们的共同点和不同点，探求解决方法，在此基础上进行知识转换，有效输出，合理归纳，结合相关的数学技巧与方法来分析与解决!。

浙江省东阳中学2021-2022高一数学上学期10月月考试题（含解析）一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集U＝{0，1，2，3，4}，M＝{0，1，2}，N＝{2，3}，则（∁U M）∩N＝（）A．{2} B．{3} C．{2，3，4} D．{0，1，2，3，4} 2．已知集合M＝{1，3}，N＝{x|0＜x＜3，x∈Z}，又P＝M∪N，那么集合P的真子集共有（）A．3个B．7个C．8个D．9个3．下列四组函数中，表示同一函数的是（）A．B．C．y＝x0与y＝1 D．4．下列正确的是（）A．log a（x•y）＝log a x•log a yB．log a（x+y）＝log a x+log a yC．log a（x÷y）＝log a x÷log a yD．log a x﹣log a y＝log a（x•y﹣1）5．函数y＝3x与y＝﹣3﹣x的图象关于（）对称．A．x轴B．y轴C．直线y＝x D．原点6．已知3a＝2，那么log38﹣2log36用a表示是（）A．a﹣2 B．5a﹣2 C．3a﹣（1+a）2D．3a﹣a27．已知奇函数f（x）的定义域为（﹣∞，0）∪（0，+∞），且对任意正实数x1，x2（x1≠x2），恒有＞0，则一定有（）A．f（3）＞f（﹣5）B．f（﹣3）＜f（﹣5）C．f（﹣5）＞f（3）D．f（﹣3）＞f（﹣5）8．函数f（x）＝，若f（0）是f（x）的最小值，则a的取值范围为（）A．[﹣1，2] B．[﹣1，0] C．[1，2] D．[0，2]9．已知f（x）＝x5+ax3+bx﹣8，且f（lg2）＝10，那么等于（）A．﹣26 B．﹣18 C．﹣10 D．1010．已知函数F（x）＝e x满足F（x）＝g（x）+h（x），且g（x），h（x）分别是R上的偶函数和奇函数，若∀x∈（0，2]使得不等式g（2x）﹣ah（x）≥0恒成立，则实数a 的取值范围是（）A．B．C．D．二．填空题：本大题共7小题，前4题每空3分，后3题每空4分，共36分.11．＝，＝．12．已知x+x﹣1＝3，则x2+x﹣2＝；x﹣x﹣1＝．13．函数的单调递减区间是；值域是．14．已知f（3x+1）＝x2﹣2x，则f（4）＝；f（x）的值域为．15．当a＞0且a≠1时，函数f（x）＝a x﹣1﹣2的图象必过定点．16．若f（x）＝x2﹣3x在[0，m]上的值域为，则m的取值范围为．17．若f（x）＝|x2+（1﹣m）x+m﹣3|在x∈[﹣2，0]上是减函数，则m的取值范围是．三．解答题：本大题共5小题，18题14分，其余各题15分，共74分.18．已知全集U＝R，集合，B＝{x|a≤x≤a+2，a∈R} （1）当a＝1时，求A∩B；（2）当集合A，B满足A∪B＝A时，求实数a的取值范围．19．已知函数f（x）是R上的奇函数，当x＞0时，．（1）求函数f（x）的解析式；（2）用定义法证明函数f（x）在区间（0，+∞）上是单调增函数．20．设函数．（1）判断f（x）的奇偶性并证明；（2）当x∈[﹣1，+∞）时，求f（x）的值域．21．已知函数．（1）作出函数f（x）的图象，并写出其单调区间；（2）若关于x的方程f（x）＝m有一正一负两个实根，求实数m的取值范围．22．已知m∈R，函数f（x）＝﹣x2+（3﹣2m）x+2+m．（1）若0＜m≤，求|f（x）|在[﹣1，1]上的最大值g（m）；（2）对任意的m∈（0，1]，若f（x）在[0，m]上的最大值为h（m），求h（m）的最大值．2021-2022浙江省金华市东阳中学高一（上）10月月考数学试卷参考答案与试题解析一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集U＝{0，1，2，3，4}，M＝{0，1，2}，N＝{2，3}，则（∁U M）∩N＝（）A．{2} B．{3} C．{2，3，4} D．{0，1，2，3，4} 【解答】解：∵全集U＝{0，1，2，3，4}，M＝{0，1，2}，∴∁U M＝{3，4}．∵N＝{2，3}，∴（∁U M）∩N＝{3}．故选：B．2．已知集合M＝{1，3}，N＝{x|0＜x＜3，x∈Z}，又P＝M∪N，那么集合P的真子集共有（）A．3个B．7个C．8个D．9个【解答】解：∵集合M＝{1，3}，N＝{x|0＜x＜3，x∈Z}＝{1，2}，∴P＝M∪N＝{1，2，3}，则P真子集的个数为23﹣1＝7．故选：B．3．下列四组函数中，表示同一函数的是（）A．B．C．y＝x0与y＝1 D．【解答】解：对于A，函数y＝|x﹣1|（x∈R），与函数y＝＝|x﹣1|（x∈R）的定义域相同，对应关系也相同，是同一函数；对于B，函数y＝（x≥1），与函数y＝＝（x＞1）的定义域不同，不是同一函数；对于C，函数y＝x0＝1（x≠0），与函数y＝1（x∈R）的定义域不同，不是同一函数；对于D，函数y＝|x|（x∈R），与函数y＝＝x（x≥0）的定义域不同，对应关系也不同，不是同一函数．故选：A．4．下列正确的是（）A．log a（x•y）＝log a x•log a yB．log a（x+y）＝log a x+log a yC．log a（x÷y）＝log a x÷log a yD．log a x﹣log a y＝log a（x•y﹣1）【解答】解：log a（x•y）＝log a x+log a y≠log a x•log a y A错log a（x+y）＝log a x+log a y此式不成立B错log a（x÷y）＝log a x﹣log a y≠log a x÷log a y C错D对故选Dlog a x﹣log a y＝log a＝log a（x•y﹣1 ），D对故选D5．函数y＝3x与y＝﹣3﹣x的图象关于（）对称．A．x轴B．y轴C．直线y＝x D．原点【解答】解：在函数y＝3x的图象上取一点A（a，3a），可得点A对应函数y＝﹣3﹣x图象上的点A′（﹣a，﹣3a），∵A与A′关于原点对称，∴由点A的任意性，得函数y＝3x与y＝﹣3﹣x的图象关于原点对称，故选：D．6．已知3a＝2，那么log38﹣2log36用a表示是（）A．a﹣2 B．5a﹣2 C．3a﹣（1+a）2D．3a﹣a2【解答】解：∵3a＝2，∴a＝，∴﹣2＝3﹣2（+1）＝3a﹣2（a+1）＝a﹣2，故选：A．7．已知奇函数f（x）的定义域为（﹣∞，0）∪（0，+∞），且对任意正实数x1，x2（x1≠x2），恒有＞0，则一定有（）A．f（3）＞f（﹣5）B．f（﹣3）＜f（﹣5）C．f（﹣5）＞f（3）D．f（﹣3）＞f（﹣5）【解答】解：根据题意，对任意正实数x1，x2（x1≠x2），恒有＞0，则函数f（x）在（0，+∞）上为增函数，又由f（x）为奇函数，则f（x）在（﹣∞，0）上也为增函数，据此分析选项：对于选项A、C：不能判定f（3）与f（﹣5）的关系，则A、C不正确；对于选项B、D：f（x）在（﹣∞，0）上为增函数，则f（﹣3）＞f（﹣5），则D正确，B不正确；故选：D．8．函数f（x）＝，若f（0）是f（x）的最小值，则a的取值范围为（）A．[﹣1，2] B．[﹣1，0] C．[1，2] D．[0，2]【解答】解：由于f（x）＝，则当x＝0时，f（0）＝a2，由于f（0）是f（x）的最小值，则（﹣∞，0]为减区间，即有a≥0，则有a2≤x++a，x＞0恒成立，由x+≥2＝2，当且仅当x＝1取最小值2，则a2≤2+a，解得﹣1≤a≤2．综上，a的取值范围为[0，2]．故选：D．9．已知f（x）＝x5+ax3+bx﹣8，且f（lg2）＝10，那么等于（）A．﹣26 B．﹣18 C．﹣10 D．10【解答】解：根据题意，f（x）＝x5+ax3+bx﹣8，则f（﹣x）＝﹣（x5+ax3+bx）﹣8，则f（x）+f（﹣x）＝﹣16，又由lg＝﹣lg2，则f（lg2）+f（lg）＝f（lg2）+f（﹣lg2）＝﹣16，若f（lg2）＝10，则＝﹣16﹣10＝﹣26；故选：A．10．已知函数F（x）＝e x满足F（x）＝g（x）+h（x），且g（x），h（x）分别是R上的偶函数和奇函数，若∀x∈（0，2]使得不等式g（2x）﹣ah（x）≥0恒成立，则实数a 的取值范围是（）A．B．C．D．【解答】解：∵F（x）＝g（x）+h（x），且g（x），h（x）分别是R上的偶函数和奇函数，∴g（x）+h（x）＝e x，则g（﹣x）+h（﹣x）＝e﹣x，即g（x）﹣h（x）＝e﹣x，解得g（x）＝，h（x）＝，则∀x∈（0，2]使得不等式g（2x）﹣ah（x）≥0恒成立，等价为﹣a•≥0 恒成立，∴a≤＝＝（e x﹣e﹣x）+，设t＝e x﹣e﹣x，则函数t＝e x﹣e﹣x在（0，2]上单调递增，∴0＜t≤e2﹣e﹣2，此时不等式t+≥2，当且仅当t＝，即t＝时，取等号，∴a≤2，故选：B．二．填空题：本大题共7小题，前4题每空3分，后3题每空4分，共36分.11．＝﹣3 ，＝．【解答】解：＝＝﹣3，＝1+﹣0.12×0.5＝1+﹣＝．故答案为：﹣3，．12．已知x+x﹣1＝3，则x2+x﹣2＝7 ；x﹣x﹣1＝．【解答】解：∵x+x﹣1＝3，∴（x+x﹣1）2＝x2+2+x﹣2＝9，∴x2+x﹣2＝7，∴（x﹣x﹣1）2＝x2+x﹣2﹣2＝7﹣2＝5，∴．故答案为：．13．函数的单调递减区间是（﹣∞，1] ；值域是[，+∞）．【解答】解：令t＝1+2x﹣x2，该函数的对称轴方程为x＝1，图象是开口向下的抛物线，∴内层函数t＝1+2x﹣x2的增区间为（﹣∞，1]，又外层函数y＝为减函数，∴函数的单调递减区间是（﹣∞，1]；又t＝1+2x﹣x2＝﹣（x﹣1）2+2≤2，∴≥．即函数的值域是[，+∞）．故答案为：（﹣∞，1]；[，+∞）．14．已知f（3x+1）＝x2﹣2x，则f（4）＝﹣1 ；f（x）的值域为[﹣1，+∞）．【解答】解：令t＝3x+1，则，故，∴，∴f（4）＝﹣1，由二次函数的性质有，f（x）≥﹣1，即值域为[﹣1，+∞）．故答案为：﹣1，[﹣1，+∞）．15．当a＞0且a≠1时，函数f（x）＝a x﹣1﹣2的图象必过定点（1，﹣1）．【解答】解：∵a0＝1，∴令x﹣1＝0，则1﹣2＝﹣1，故x＝1，故函数f（x）＝a x﹣1﹣2的图象必过定点（1，﹣1）．故答案为（1，﹣1）．16．若f（x）＝x2﹣3x在[0，m]上的值域为，则m的取值范围为．【解答】解：作出函数f（x）的图象，如图所示，函数f（x）对称轴为x＝，f（）＝﹣，当y＝0时，x＝0或3，函数f（x）＝x2﹣2x+3在闭区间[0，m]上的值域是[﹣，0]，则实数m的取值范围是[，3]．故答案为：[，3]．17．若f（x）＝|x2+（1﹣m）x+m﹣3|在x∈[﹣2，0]上是减函数，则m的取值范围是（﹣∞，﹣3]∪[3，+∞）．【解答】解：函数y＝x2+（1﹣m）x+m﹣3的判别式△＝（m﹣3）2+4＞0，∴x2+（1﹣m）x+m﹣3＝0有2个不等实数根，设这两个根为a、b，且a＜b，∵f（x）在[﹣2，0]上是减函数，∴a≥0 ①，如图（1）所示：或②，如图（2）所示．由①可得，即（m﹣1）2≥（m﹣3）2+4，解得m≥3；由②可得，解得m≤﹣3．综上可得，m的取值范围为：（﹣∞，﹣3]∪[3，+∞），故答案为：（﹣∞，﹣3]∪[3，+∞）．三．解答题：本大题共5小题，18题14分，其余各题15分，共74分.18．已知全集U＝R，集合，B＝{x|a≤x≤a+2，a∈R} （1）当a＝1时，求A∩B；（2）当集合A，B满足A∪B＝A时，求实数a的取值范围．【解答】解：（1）集合＝{x|3x﹣x2＞0}＝{x|0＜x＜3}，a＝1时，集合B＝{x|a≤x≤a+2，a∈R}＝{x|1≤x≤3}；所以A∩B＝{x|1≤x＜3}；（2）当集合A，B满足A∪B＝A时，B⊆A，此时B≠∅，应满足，解得0＜a＜1；所以实数a的取值范围是0＜a＜1．19．已知函数f（x）是R上的奇函数，当x＞0时，．（1）求函数f（x）的解析式；（2）用定义法证明函数f（x）在区间（0，+∞）上是单调增函数．【解答】（1）解：设x＜0，则﹣x＞0，∴f（﹣x）＝﹣＝，∵f（x）是R上的奇函数，∴f（﹣x）＝﹣f（x），即﹣f（x）＝，∴，当x＝0时，f（﹣0）＝﹣f（0），∴f（0）＝0，∴（2）任取0＜x1＜x2，则＝＝∵0＜x1＜x2，∴x1﹣x2＜0，x1x2＞0，故f（x1）﹣f（x2）＜0，∴f（x1）＜f（x2），∴函数f（x）在区间（0，+∞）上是单调增函数．20．设函数．（1）判断f（x）的奇偶性并证明；（2）当x∈[﹣1，+∞）时，求f（x）的值域．【解答】解：（1）根据题意，函数为奇函数，证明：函数，其定义域为R，f（﹣x）＝＝＝﹣f（x），故f（x）为奇函数；（2）根据题意，y＝＝，变形可得：（）x＝，又由x∈[﹣1，+∞），则（）x≥（）（﹣1）＝，则有≥，解可得：﹣≤y＜1，即函数的值域为[﹣，1）．21．已知函数．（1）作出函数f（x）的图象，并写出其单调区间；（2）若关于x的方程f（x）＝m有一正一负两个实根，求实数m的取值范围．【解答】解：（1）根据题意，函数＝，其图象如图：则f（x）的递增区间为（﹣∞，﹣1]，递减区间为[﹣1，+∞）；（2）根据题意，函数，f（0）＝﹣＝﹣，若关于x的方程f（x）＝m有一正一负两个实根，即函数y＝f（x）与直线y＝m有2个交点，且两个交点位于y轴的两侧，必有，即m的取值范围为．22．已知m∈R，函数f（x）＝﹣x2+（3﹣2m）x+2+m．（1）若0＜m≤，求|f（x）|在[﹣1，1]上的最大值g（m）；（2）对任意的m∈（0，1]，若f（x）在[0，m]上的最大值为h（m），求h（m）的最大值．【解答】解：（1）f（x）＝﹣x2+（3﹣2m）x+2+m＝﹣（x﹣）2+2+m+（）2＝﹣（x﹣）2+，则对称轴为x＝，若0＜m≤，则0＜2m≤1，1≤＜，则函数f（x）在[﹣1，1]上为增函数，则当x＝1时，函数f（x）为最大值f（1）＝﹣1+3﹣2m+2+m＝4﹣m，当x＝﹣1时，函数f（x）为最小值f（﹣1）＝﹣1﹣3+2m+2+m＝3m﹣2，∵0＜m≤，∴0＜3m≤，﹣2＜3m﹣2≤﹣则|f（﹣1）|＝|3m﹣2|∈[，2），f（1）＝4﹣m∈[，4），则|f（1）|＞|f（﹣1）|，即|f（x）|在[﹣1，1]上的最大值g（m）＝f（1）＝4﹣m；（2）f（x）＝﹣x2+（3﹣2m）x+2+m＝﹣（x﹣）2+，则函数对称轴为x＝，若0＜m≤1，则0＜2m≤2，≤＜，若m≤，即0＜m≤时，函数f（x）在[0，m]上单调递增，则最大值为h（m）＝f （m）＝﹣m2+（3﹣2m）m+2+m＝﹣3m2+4m+2．若m＞，即＜m≤1时，函数f（x）在[0，m]上不单调，此时当x＝时，函数f（x）取得最大值h（m）＝＝m2﹣2m+即h（m）＝，当0＜m≤时，h（m）＝﹣3m2+4m+2的对称轴为m＝＝．即当m＝时，函数h（m）取得最大值h（）＝﹣3×（）2+4×+2＝．当＜m≤1时，h（m）＝m2﹣2m+的对称轴为m＝1，此时函数h（m）为减函数，则函数h（m）＜h（）＝（）2﹣2×+＝．∵＞．∴h（m）的最大值是．。