下载文档原格式
第7章 梁弯曲变形的计算§7-1 挠度与转角及梁的刚度条件梁变形前后形状的变化称为变形，一般用各段梁曲率的变化表示。
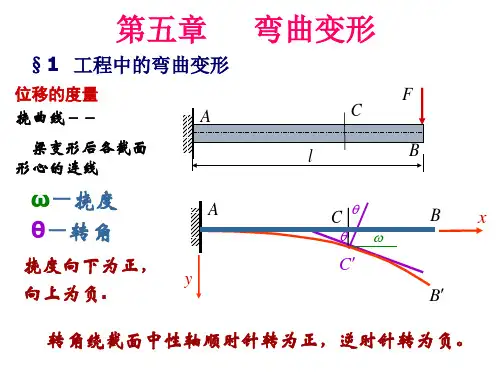
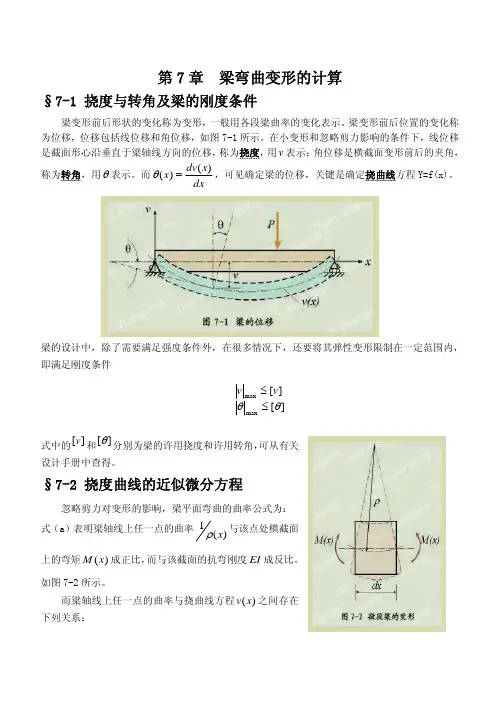
梁变形前后位置的变化称为位移，位移包括线位移和角位移，如图7-1所示。
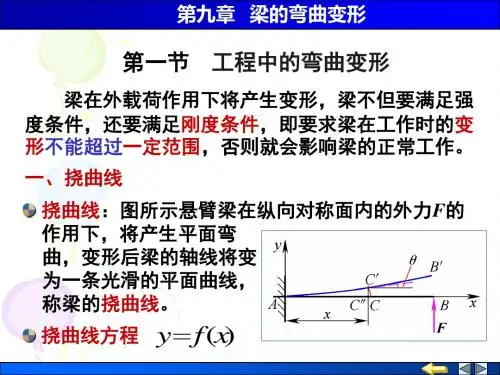
在小变形和忽略剪力影响的条件下，线位移是截面形心沿垂直于梁轴线方向的位移，称为挠度，用v 表示；角位移是横截面变形前后的夹角，称为转角，用θ表示。
而dxx dv x )()(=θ，可见确定梁的位移，关键是确定挠曲线方程Y=f(x)。
梁的设计中，除了需要满足强度条件外，在很多情况下，还要将其弹性变形限制在一定范围内，即满足刚度条件][][max max θθ≤≤v v式中的和][v ][θ分别为梁的许用挠度和许用转角，可从有关设计手册中查得。
§7-2 挠度曲线的近似微分方程忽略剪力对变形的影响，梁平面弯曲的曲率公式为： 式（a）表明梁轴线上任一点的曲率)(1x ρ与该点处横截面上的弯矩成正比，而与该截面的抗弯刚度)(x M EI 成反比。
如图7-2所示。
而梁轴线上任一点的曲率与挠曲线方程v 之间存在下列关系：)(xEIx M x )()(1=ρ （a） 232221)(1⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±dx dv dx vd x ρ （b）将上式代入式（a），得到EIx M dx dv dx v d )(12322=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±（c） 小挠度条件下，1<<=θdxdv，式（c）可简化为： EI x M dxv d )(22=±（d）在图7-3所示的坐标系中，正弯矩对应着22dx vd 的正值（图7-3a），负弯矩对应着22dxvd 的负值（图7-3b），故式（d）左边的符号取正值EI x M dx v d )(22= （8-1）式（7-1）称为小挠度曲线微分方程，简称小挠度微分方程。
显然，小挠度微分方程仅适用于线弹性范围内的平面弯曲问题。
