当前位置：文档之家 › 静电场二(场强计算)

静电场二(场强计算)

  • 格式：ppt
  • 大小：300.00 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

计算电场强度的基本方法

计算电场强度的基本方法

计算电场强度的基本方法电场强度是静电学中最基本最重要的概念之一，是历年高考考查的热点。

高考中将静电学与力学、磁学等问题放在一起作为综合题考查在每年是必不可少的。

这些题目中往往涉及有电场力、电势和电势能等参数，这些参数与静电场最基本的物理性质参数——电场强度是紧密相关的。

因此，要解决好这些问题，我们首先必须熟练掌握计算电场强度的方法。

在这里，我们首先介绍一下计算电场强度的基本方法。

结合所分析的静电场的特点，很多求解电场强度的问题都可以用它来解决。

对于一些比较特殊的电场，我们将在下一节介绍一些特殊的方法，那些特殊的方法也是由这些基本方法衍生而来的，因此，我们需要掌握好这些基本方法。

下面来看一看这些基本方法。

方法特点电场强度的定义是检验电荷在电场中某点受到的电场力F与电荷q的比值，用E表示。

因此，我们可以利用这一定义去求电场中某点的电场强度。

想办法求出电荷q在某点所受的电场力，使用公式FqE=，即可求出电场强度。

在这里需要注意两点：（1）这里q代表电量，如果带正电则值为正，此时E的方向与F相同；如果带负电则值为负，此时E的方向与F相反。

（2）由于E有方向，是矢量，因此我们可以使用矢量的运算法则（正交分解法、平行四边形法则、矢量三角形法则等）求几个不同的电场在某一点所产生的合场强。

根据这一定义，点电荷Q在周围某点所产生的场强为22QqF rqk QE kq r===。

根据这一定义以及匀强电场中电场力做功与电势能的关系有W F d qE d q U===，因此匀强电场的场强为UdE=。

从定义引出来的方法是最基本的方法，下面我们来看一看具体该怎么用。

经典体验（1）如图所示，带正电小球质量为m=1×10-2kg，带电量为q=1.6×10-6C。

置于光滑绝缘水平面上的A点，当空间存在着斜向上的匀强电场时，该小球从静止开始始终沿水平面做匀加速直线运动，当运动到B点时，测得速度v B=1.5m/s，此时小球的位移为s=0.15m，求此匀强电场的场强E的取值范围（g=10m/s2）。

静电场-2

静电场-2

解
E dE
由对称性有 E E i x
q ( ) 2π R
q R
y dq dl r
o
P
x
x
1 dl er 2 4π 0 r
z
dE
qx E 2 2 32 4π 0 ( x R )
讨论
q R
y dq dl r
o

P x
x
（1）q 0 , E 沿 x 正向 q 0 , E 沿 x 负向
根据数学中的高斯定理
dV
V
E dS EdV
S V
因此有
E ε0
(高斯定理的微分形式）
高斯定理的微分形式
E ε0

哈密顿算符
i j k x y z
E 称为矢量场 E 称为矢量场
F qE
3.场强叠加原理
q1
q2
合力 F Fi
i
r2
r1
总场强
Fi F E Ei q0 i q0 i
E Exi Ey j Ez k
qi
ri
q0
Fi F2 F 1
场强叠加原理: 电场中任意点的场强,等于空间各点电荷
4）仅高斯面内的电荷对高斯面的电通量有贡献.
5）静电场是有源场.
讨论
将 q2 从 A 移到
B
A q2 P*
q2 B
点
P 电场强度是否变化？ 穿过高斯面 的 Φ 有否变化？ e
s
q1
s
在点电荷 q 和 q 的静电场中，做如下的三 个闭合面 S1 , S 2 , S3 , 求: 通过各闭合面的电通量 .

第五章 电场强度

第五章 电场强度

第五章 静电场
例3 正电荷 q 均匀分布在半径为 R 的圆环上. 的圆环上. 的电场强度. 计算在环的轴线上任一点 P 的电场强度.
y dq = λdl
q R
o
r
q (λ = ) 2π R
x
P
v dE =
x
1 λdl v er 2 4π ε0 r
clc2000@
z
桂林电子科技大学十院
第五章 静电场
1 、点电荷产生的场强
点电荷产生的场强具有球 点电荷产生的场强具有球 面对称性， 面对称性，即在以点电荷为球 心的任意球面上， 心的任意球面上，场强的大小 均相等，方向均沿半径方向。 均相等，方向均沿半径方向。
r r F Q v ∴E = = e 2 r q 0 4πε 0 r
§5-1 电场强度
2 2 32
E=
由例3 由例 q x
y
r
dq = σ 2π rdr
(x + r )
2 2 1/2
o
R
v x P dE x
dr
q = σ πR
2
clc2000@
z
桂林电子科技大学十院
第五章 静电场
σx 1 1 E = ( − ) 2ε 0 x2 x2 + R2 σ x << R 无限大均匀带电平面 讨 论 （1） R → ∞ , E ≈ 2ε 0 σ <0 σ >0
几个常用的电场公式 (1)无限长均匀带电 无限长均匀带电 细棒的场强 (2)圆环在其中轴线上 圆环在其中轴线上 任意点产生的场强 (3)无限大均匀带电 无限大均匀带电 平面产生的场强
桂林电子科技大学十院
λ E = 2 πε 0 a

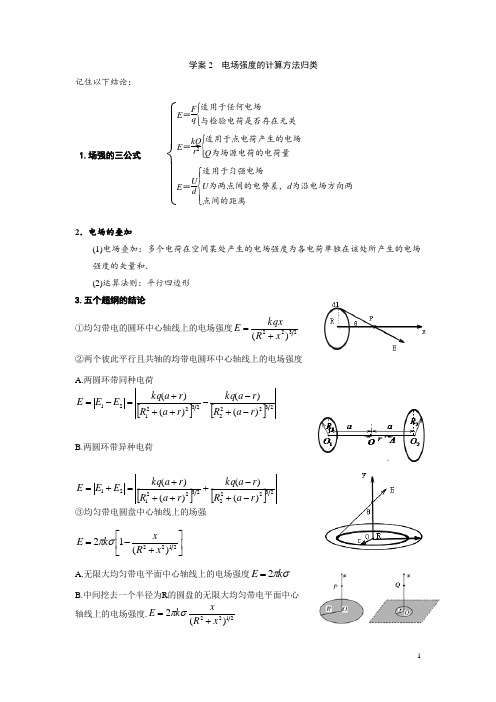
电场强度的计算打印

电场强度的计算打印

学案2 电场强度的计算方法归类 记住以下结论：1.场强的三公式 ⎩⎪⎪⎨⎪⎪⎧E ＝F q ⎩⎪⎨⎪⎧ 适用于任何电场与检验电荷是否存在无关E ＝kQr 2⎩⎪⎨⎪⎧ 适用于点电荷产生的电场Q 为场源电荷的电荷量E ＝U d ⎩⎪⎨⎪⎧适用于匀强电场U 为两点间的电势差，d 为沿电场方向两点间的距离2．电场的叠加(1)电场叠加：多个电荷在空间某处产生的电场强度为各电荷单独在该处所产生的电场强度的矢量和．(2)运算法则：平行四边形 3.五个超纲的结论①均匀带电的圆环中心轴线上的电场强度2322)(x R kqxE +=②两个彼此平行且共轴的均带电圆环中心轴线上的电场强度A.两圆环带同种电荷[][]232222322121)()()()(r a Rr a kq r a Rr a kq E E E -+--+++=-=B.两圆环带异种电荷[][]232222322121)()()()(r a Rr a kq r a Rr a kq E E E -+-++++=+=③均匀带电圆盘中心轴线上的场强⎥⎦⎤⎢⎣⎡+-=2122)(12x R xk E σπA.无限大均匀带电平面中心轴线上的电场强度σπk E 2=B.中间挖去一个半径为R 的圆盘的无限大均匀带电平面中心轴线上的电场强度.2122)(2x R xk E +=σπ0 )(R r ④均匀带电球壳的场强E=)(2R r rQk ≥ )(3R r RQrk⑤ 对称分布的带电球体的场强E=)(2R r r kQ≥ 二．电场强度的求解方法1.常规方法--直接用公式求解 ①定义式求解例.质量为m 、电荷量为q 的质点，在静电力作用下以恒定速率v 沿圆弧从A 点运动到B 点，其速度方向改变的角度为θ(弧度)，A 、B 弧长为s ，则A 、B 弧中点场强的大小E . ②点电荷公式求解 a.单个点电荷例：真空中，A 、B 两点与点电荷Q 的距离分别为r 和3r ，则A 、B 两点的电场强度大小之比为( )A ．3∶1 B ．1∶3 C ．9∶1 D ．1∶9b.点电荷系共线叠加例：如图，电荷量为q 1和q 2的两个点电荷分别位于P 点和Q 点。

静电场2

静电场2

8
3)求积分 3)求积分
E = Exi
y
dq Q
E x = ∫ dE x
R
r
o
θ
p
x
dEy
dEx dE
x
dEx = dE cos θ cos θ =
Ex = ∫ dEx =
z
2
x x +R
2
,
xλ
dE =
l 3
1
1
λ dl
2 2
4πε 0 x + R
0 2
1
4πε 0 ( x 2 + R 2 )
2
P
E
dS⊥
dN ∝ EdS⊥
静电场中电场线的性质: 静电场中电场线的性质: 中电场线的性质 有头(源)有尾, 由+(或∞)指向(或∞) 有头( 有尾, +(或 指向 无电荷处不中断 不闭合, 不相交 不闭合,
dN → E∝ dS⊥
18
线分布: 几种电荷的 E 线分布:
带正电的点电荷
电偶极子
均匀带电的直线段
一个点电荷所产生的电场, 一个点电荷所产生的电场,在以点电荷为 中心的任意球面的电通量等于 q
ε0
25
点电荷q被 点电荷 被 任意曲面 曲面包围 任意曲面包围
q dS ' q r dS q dΦE = = = d 2 2 4πε 0 r 4πε 0 r 4πε 0
对整个闭合面S有 对整个闭合面 有
p
dE x E
α
x
θ1
dE y
dE
λ Ex = 2πε 0 a
Ey = 0
θ2 → π , θ1 → 0 , 有
17

静电场的详细计算

静电场的详细计算

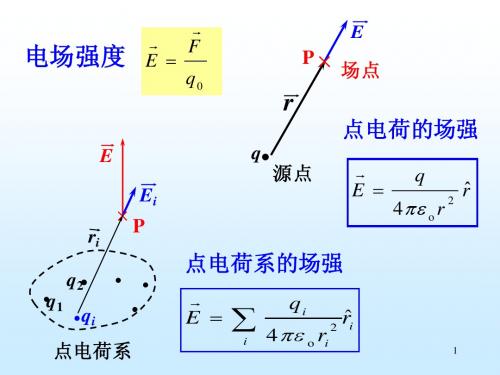
静电场定义由静止电荷(相对于观察者静止的电荷)激发的电场。

静电场性质根据静电场的高斯定理：静电场的电场线起于正电荷或无穷远,终止于负电荷或无穷远，故静电场是有源场．从安培环路定理来说它是一个无旋场．根据环量定理，静电场中环量恒等于零,表明静电场中沿任意闭合路径移动电荷，电场力所做的功都为零，因此静电场是保守场．根据库仑定律，两个点电荷之间的作用力跟它们的电荷量的乘积成正比，和它们距离的平方成反比，作用力的方向在它们的连线上，即F=（k·q1q2）/r²;,其中q1、q2为两电荷的电荷量（不计正负性）、k为静电力常量，约为9.0e+09（牛顿·米²）/（库伦²;），r为两电荷中心点连线的距离。

注意，点电荷是不考虑其尺寸、形状和电荷分布情况的带电体。

是实际带电体的理想化模型。

当带电体的距离比它们的大小大得多时，带电体的形状和大小可以忽略不计的点电荷。

静电场的泊松方程由于静电场是无旋场,故可用标量电位φ表征静电场（见电位）。

电位与电场强度的关系是式中Q点为电位参考点，可选在无穷远处；P点为观察点。

上式的微分形式为电场强度等于电位的负梯度，即E=-墷φ在ε为常数的区域，式中墷·墷可记作墷2，在直角坐标中分别为一阶与二阶微分算符。

这样,可得电位φ所满足的微分方程称为泊松方程。

如果观察点处自由电荷密度ρ为0，则墷2φ=0称为拉普拉斯方程。

泊松方程和拉普拉斯方程描述了静电场空间分布的规律性。

可以证明，当已知ρ、ε及边界条件时，泊松方程或拉普拉斯方程的解是惟一的，可以设法求解电位φ，再求出场中各处的E。

静电场知识点一、库仑定律①元电荷：元电荷是指最小的电荷量，用e表示，大小为②库仑定律：真空中两个静止点电荷之间的相互作用力，与它们的电荷量的乘积成正比，与它们的距离的二次方成反比，作用力的方向在它们的连线上。

表达式：，其中静电力常量二、电场①电场的产生：电荷的周围存在着电场，产生电场的电荷叫做源电荷。

第6章 静电场(2)高斯定理

S
0
q
S内
高斯面S上积分
S内一切电荷代数和
请思考：1）高斯面上的 E 与哪些电荷有关 ？
2）哪些电荷对闭合曲面 的 Φ e 有贡献 ？ （1）通过闭合曲面的总电通量只决定于它所包围的电荷，闭合曲面外部的电 荷对总电通量无贡献．
s
（2）虽然电场强度通量只与面内电荷有关，但高斯面上的电场强度是由全部 电荷（既包括闭合曲面内又包括闭合曲面外的电荷）共同产生的总电场强度，并 非只由闭合曲面内的电荷所产生。
四. 高斯定理应用
具有某种对称性的电场，可应用高斯定理求解静电场的场强分布。
1 用高斯定理直接求场强的条件： Φe E dS S
0
q
S内
电场（电荷）的分布具有某种对称性（球、面、轴对称性），使得高斯 面上的 E 为一常数，且 E 与d S 夹角 为一常数（为0、 2 或 ）这样E 才能由积分号中提出，将积分运算化为代数运算。
与球心相距r , 当 R a r R b 时， 该点的电场 强度的大小为： (D)
1 4
0
(A)

Qa Qb r
2
1
(B)
4

0
Qa Qb r
2
1
(C)
4
(
0
Qa r
2Qb Rb2来自1)(D)
4

0
Qa r
2
解：作半径为r的同心球面为高斯面，由高斯定理

Qa 2 E d S 4 r E

E dS
S
EdS
S
E 4π r
2

1
0

S内

静电场中电场强度的计算方法

静电场中电场强度的计算方法
静电场中电场强度的计算方法：E=F/q。

E表示电场中某点的场强，F表示放在这个点的电荷所受的电场力，q指的是这个电荷的电荷量。

这个公式中E与F和q无关，不存在E与F成正比，与q成反比关系。

场强方向判断方法：规定电场中某点的场强方向与放在该点的正电荷所受电场力方向相同，与负电荷所受电场力方向相反；在匀强电场中还可以利用电场线由高等势面指向低等势面，点电荷产生的电场也可以通过场源电荷的电性来判断。

电场 2

电场 考查点： 一、电场强度1．大小表达式：E ＝F/q 单位是：N/C 或V/m ；E=kQ/r 2（导出式，真空中的点电荷，其中Q 是产生该电场的电荷） E ＝U/d （导出式，仅适用于匀强电场，其中d 是沿电场线方向上的距离）常用判断法----①电场线分布疏密（至少两条）②等电势差等电势面分布疏密③电场力 2、方向判断①由电场线走向判断-----切向②由电场力方向 例题：电场强度E 的定义式为E ＝F /q ，根据此式，下列说法中正确的是①该式说明电场中某点的场强E 与F 成正比，与q 成反比，拿走q ，则E ＝0．②式中q 是放入电场中的点电荷的电量，F 是该点电荷在电场中某点受到的电场力，E 是该点的电场强度 ． ③式中q 是产生电场的点电荷的电量，F 是放在电场中的点电荷受到的电场力，E 是电场强度．④在库仑定律的表达式F ＝kq 1q 2/r 2中，可以把kq 2/r 2看作是点电荷q 2产生的电场在点电荷q 1处的场强大小，也可以把kq 1/r 2看作是点电荷q 1产生的电场在点电荷q 2处的场强大小．A ．只有①②B ．只有①③C ．只有②④D ．只有③④【解析】 E ＝qF 为电场强度的定义式，适用于各种电场，其中q 为检验电荷的电量，F 为其在电场中所受的电场力，电场强度E 由电场决定，与检验电荷及其受力无关，故①、③错，②对．由E ＝qF 和库仑定律F ＝221rq q k知，21rq k为q 1在q 2处产生电场的场强，22rq k为q 2在q 1处产生电场的场强，故④对，选C ．【答案】 C例题．在静电场中a 、b 、c 、d 四点分别放一检验电荷，其电量可变， 但很小，结果测出检验电荷所受电场力与电荷电量的关系如图所示， 由图线可知A ．a 、b 、c 、d 四点不可能在同一电场线上B ．四点场强关系是E c ＞E a ＞E b ＞E dC ．四点场强方向可能不相同D ．以上答案都不对【解析】 根据F ＝Eq 知，在F —q 图象中，E 为斜率，由此可得E c ＞E a ＞E b ＞E d ，选项B 正确．二、电场线是人们为了形象的描绘电场而想象出一些线，客观并不存在．1．切线方向表示该点场强的方向，也是正电荷的受力方向．2．从正电荷出发到负电荷终止，或从正电荷出发到无穷远处终止，或者从无穷远处出发到负电荷终止．3．疏密表示该处电场的强弱，也表示该处场强的大小．4．匀强电场的电场线平行且距离相等．5．没有画出电场线的地方不一定没有电场．6．顺着电场线方向，电势越来越低．7．电场线的方向是电势降落陡度最大的方向，电场线跟等势面垂直．8．电场线永不相交也不闭合，9．电场线不是电荷运动的轨迹．常见不同电场的电场线三、电场力做功特性及计算方法电场力做功与路径无关，只与初、末位置有关计算方法有：⑴由公式Ｗ＝ＦＳcosθ计算，此公式只适合于匀强电场中，可变形为Ｗ＝ＥqＳ，式中Ｓ为电荷初末位置在电场强度方向上的位移⑵由电场力做功与电势能改变关系计算，Ｗ＝Δε＝qＵ，对任何电场都适用⑶由动能定理计算Ｗ电场力＋Ｗ其它＝ΔＥＫ注意：只在电场力作用下运动的粒子，其任何位置的动能与电势能之和恒定四、电势差电荷从电场中的一点移到另一点，电场力做的功跟其电量的比值叫做这两点的电势差，U AB=W AB/q，是标量．五、电势某点相对零电势的电势差叫做该点的电势，是标量．在数值上等于单位正电荷由该点移到零电势点时电场力所做的功.由电场本身因素决定，与检验电荷无关。

电场强度的几种计算方法

电场强度的几种求法．公式法1．E F q是电场强度的定义式：适用于任何电场，电场中某点的场强是确定值，其大小和方向与试探电荷无关，试探电荷q 充当“测量工具”的作用。

2． E k r Q2 是真空中点电荷电场强度的决定r式，E 由场源电荷Q 和某点到场源电荷的距离r 决定。

3．E U d是场强与电势差的关系式，只适用于匀强电场，注意式中的d 为两点间的距离在场强方向的投影。

二．对称叠加法当空间的电场由几个点电荷共同激发的时候，空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和，其合成遵守矢量合成的平行四边形定则。

例：如图，带电量为+q 的点电荷与均匀带电。

例：如图，带电量为+q 的点电荷与均匀带电薄板相距为2d，点电荷到带电薄板的垂线通过板的几何中心，如图中a 点处的场强为零，求图中b 点处的场强多大b a + ddd 例：一均匀带负电的半球壳，球心为O 点，AB 为其对称轴，平面L垂直AB 把半球壳一分为二，L与AB 相交于M 点，对称轴AB上的N 点和M 点关于O点对称。

已知一均匀带电球壳内部任一点的电场强度为零，点电荷q 在距离其为r 处的电势为k q r。

假设左侧部分在M 点的电场强度为E1，电势为 1 ；右侧部分在M 点的电场强度为E2，电势为 2 ；整个半球壳在M 点的电场强度为E3，在N 点的电场强度为E4，下列说法中正确的是（）A．若左右两部分的表面积相等，有E1> E2，1 > 2B．若左右两部分的表面积相等，有E1<E2， 1 < 2C．只有左右两部分的表面积相等，才有E1>E2，E3=E4D．不论左右两部分的表面积是否相等，总有E1> E2，E3=E4答案：D例：ab 是长为L 的均匀带电细杆，P1、P2 是位于ab 所在直线上的两点，位置如图所示．ab 上电荷产生的静电场在P1 处的场强大小为E1，在P2 处的场强大小为E2。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例6、一玻璃棒被弯成半径为R的半圆型，沿其上半部分均匀分 布有电荷+Q，沿下半部分均匀分布有电荷-Q，求半圆中心处的 场强。
y
+ + o x

E E y j 2 dE cos j
0
2
Q
2 0 R2
j
E
x
解法2： 将带电圆形平面看成是许多圆环组成， 最小圆环半径为a，最大半径为R
qx 4 0 ( x R )
2 3 2 2
E 圆环 E x i
i
E
a
R
dqx 40 ( x 2 y 2 ) 3 / 2
1
例5、两无限大平行平板均匀带电，求1、2、3个区域的场强分布。 分别就两板均为 和一板为 ，一板为 两种情况讨论。
q 4 0 x 2
。（点电荷的场）
推广：均匀带电圆盘在垂直于盘面轴线上任一点P的场强。(带电面密 度σ，圆盘半径R,场点到盘心的距离为x) qx
E 圆环 E x i
y
ds 2ydy dq 2ydy
dE
4 0 ( x 2 R )
3 2 2
i
+ + o+ +
P dE
dqx 2yxdy 40 ( x 2 y 2 )3 / 2 4 0 ( x 2 y 2 )3 / 2
dE
x
xdy 2
4 0 ( x 2 y 2 )3 / 2
E
0
R
xdy 2
4 0 ( x 2 y 2 ) 3 / 2
x xd ( x 2 y 2 ) ( 1 ) 2 2 3/ 2 2 2 2 4 0 ( x y ) R x 0 0
dl Rd dq dl
y
dE
dl 4 0 R 2
Q R
dE x dE y
sin dl 4 0 R 2
cos dl 4 0 R 2
θ o
dEx
x

由对称性分析，Ey=0

dEy dE
E E x i dE x
0
R sin d Q i i 4 0 R 2 2 2 0 R 2
R
E
x (1 )i 2 2 2 0 R x
推广：无限大均匀带电平面的场强
带电圆盘在中心轴线上的场 E圆盘
x (1 ) 2 2 2 0 R x
E 圆盘
方向垂直于盘面
+ + 0+ +
x
当 R 时， E无 限 大
2 0
无限大均匀带电平面的场为匀强场
+σ + + + A B
-σ
-
E A EB
2 0
-
若无限大均匀带电平面处于介电系数为εr的电介质中
E无限大
2 0 r 2
求电荷是连续分布的带电体场强的基本步骤是：
1）将带电体分割成许多电荷元，使用点电荷的场强公式，在适 当的坐标系中写出某一电荷元的元场强。
2）根据场强叠加原理，将元场强进行矢量叠加。在这一过程中， 关于对称性的分析很重要，它可使计算大为简化。因此解此类 题的关键之一是如何灵活运用场的叠加原理。
P
(3)
a
+
1
2
+
x
+
无限长均匀带电直线外一点场强：
E 20a
(4)
+
-
E
+
E
+
+
-
例3、求均匀带电圆环在垂直于环面中心轴线上任一点P的场强(q,R)。
y
dq dl
坐标建立后，坐标原点0到场点P的距离x应为定值
+ + + x
+ o +
r

P
dEy
q 2R
dE
dEx
dl 40 r 2

E左

2 3
2 0 E右 2 0
E左

1
E1 0

2 3
0
E3 0
1 2 0
E右 2 0
E1
0
E左 2 0 E右 2 0
E2
E2 0
E3
0
Байду номын сангаас
大学物理练习题册静电场（二）第7题：设电量Q均匀分布在 半径为R的半圆周上，求圆心0处的电场强度。
x 各电荷元在P点产生的 d E 逆 dE 着X轴看，形成一锥形 由对称性分析，Ey=0
qx 4 0 ( x R )
2 3 2 2
cos dl dE x dE cos 4 0 r 2
x cos r
dE y
sindl 40 r 2
2R
Ex
cos dE x 4 0 r 2
第九章
静电场(二）
主讲 刘果红
回顾：
E的量值等于通过该点垂直于电力线的单位面积的电力线根数。
点电荷的场：
E
f q r0 （2） q0 40 r 2
4 0 ri2 qi ri 0
点电荷系的场：
E E1 E 2 E n
有限长均匀带电直线的场：
E
(cos1 cos 2 ) j (sin 2 sin1 )i 40a 40a
E Ex i
dl
0
2

答案：
qx 40 ( x R )
3 2 2
i
(5)
E Ex i
qx 40 ( x R )
2 3 2 2
i
(5)
对（5）式的讨论：
1）、由（5）式知：圆环轴线上每点E的大小是逐点不同的。
2）、在x=0 处，E0 =0
3）、当 x>>R时，E
例4、：一半径为R的均匀带电圆形平面，其电荷面密度为 ，在 圆平面的中心挖去小孔，其半径为a，求通过圆孔中心的轴线上与 圆心0相距为x处P点的场强。 解法1： E E大圆盘 E小圆盘 y
+ R + + o a + X
E
P
x x (1 ) (1 ) 2 0 2 0 a2 x2 R2 x 2