弹簧设计表ZYH

弹簧设计计算已知条件：弹簧自由长度H0=796.8mm弹簧安装长度L1=411mm 弹簧工作长度L2=227mm弹簧中径D=22.3mm弹簧直径d=3.2mm弹簧螺距P=12mm弹簧有效圈数n=66弹簧实际圈数n1=68计算步骤：（1）初步考虑采用油淬火-回火硅锰弹簧钢丝60Si2MnA C 类，抗拉强度1716-1863MPa ，切变模量G=79GPa ，弹性模量E=206GPa 。

取b σ=1716MPa 。

（2）压缩弹簧许用切应力p τ=(0.4~0.47) b σ=(0.4~0.47)*1716MPa=686.4~806.52MPa取p τ=686.4MPa 。

（3）由于弹簧刚度尚未可知，但是弹簧的中径、直径、有效圈数都已知。

2.33.22==d D C =6.9688（计算值在5~8之间） 6.9688615.046.9688416.96884615.04414+-⨯-⨯=+--=C C C K =1.2139 弹簧的最大工作压缩量Fn=795-227=568mm由公式348DP F Gd n n n =可得最大工作载荷34343.226685682.3798⨯⨯⨯⨯==nD F Gd P n n = 803.5758N 弹簧刚度663.2282.37983434'⨯⨯⨯==n D Gd P =1.4147N/mm 节距t=662.35.1795)2~1(0⨯-=-n d H =11.9727≈12 计算出来的自由高度H0=nt+1.5d=66*12+1.5*3.2=796.8mm压并高度Hb=(n+1.5)d=(66+1.5)*3.2=216mm弹簧最小工作载荷时的压缩量F1=795-411=384mm 则最小工作载荷3431413.226683842.3798⨯⨯⨯⨯==nD F Gd P =543.2625N 螺旋角α=arctan(t/πD )=arctan(12/(3.14*22.3))= 0.1696弧度= 9.7174°弹簧展开长度L=1696.0cos 683.22cos 1⨯⨯=παπDn = 4833.3mm ≈4833mm 弹簧压并高度H b ≤n 1*d max =68*（3.2+0.03）=219.64，取值216mm弹簧压并时的变形量为796.8-216=580.8mm弹簧压并时的载荷为Fa=580.8*1.4147=821.6578N（4）螺旋弹簧的稳定性、强度和共振的验算高径比b=H0/D=796.8/22.3=35.7309>0.4n B c P H P C P >=0' 不稳定系数C B =0.02==0'H P C P B c 0.02*1.4147*796.8=22.5447N<n P =803.5758N 所以必须设置导杆。

记号的含义螺旋弹簧的设计时候使用的记号如下表1所示。

横弹性系数G的值如表2所示。

螺旋弹簧的设计用基本计算公式螺旋弹簧的负荷和弹簧定数・弯曲的关系具有线性特征弹簧的负荷和弯曲是成比例的。

从螺旋弹簧的尺寸求弹簧的定数压缩螺旋弹簧的素線径因扭转而产生弯曲的弹簧定数K 螺旋弹簧的扭转应力螺旋弹簧的扭转修正应力螺旋弹簧试验载荷下高度（端面磨削的情况下）螺旋弹簧两端的各厚度之和不同材质螺旋弹簧在高温时的机械特性组合弹簧的计算公式螺旋弹簧的直列和并列弹簧在设计的时候，虽然应该尽可能设计一根弹簧，但是一根弹簧无法满足的情况下，也会对多根弹簧进行组合以满足设计要求。

弹簧的组合有纵向排列的直列法和横向排列的并列法两种模式。

这样的分类，不仅和螺旋弹簧有关，盘形弹簧等其他种类的弹簧也是一样，也会进行直列和并列组合来使用。

从负荷的观点来考虑的话，对各个弹簧作用相等的力的组合方式叫直列，各个弹簧变位相等的组合方式叫并列。

图1. 螺旋弹簧的直列组合和并列组合图示显示的是使用了3个弹簧的情况。

n个弹簧的各个定数就是k1 , k2 ,・・・, kn弹簧并列和直列组合时全部的定数K公式参照下列。

式1. 并列的弹簧定数计算公式式2. 直列的弹簧定数计算公式并列组合的螺旋弹簧的个数增加会导致全体弹簧定数变大，直列组合个数的增加会导致弹簧定数变小。

図2. 亲子弹簧并列的字面意思就是横向排列，但是单纯的排列空间上不好安排，所以像图3那样弹簧的内侧和弹簧组合，同心相排的情况下很多。

这样的排列一般被称作亲子弹簧。

但是，同心组合的情况下，为了弹簧不互相缠绕在一起，交替的改变弹簧卷的方向，或者确保弹簧和弹簧之间有一定的间隙是很有必要的。

另外，对弹簧的组合进行下功夫的话，像下图a,b那样，可以制作出不是直线的弹簧特性。

例如需要像图4那样特性弹簧的时候，需要对自由长或者不同密着负荷的弹簧进行组合。

图5的弹簧特性是在图6那样结构中加入弹簧，事先加上负荷，就会得到〔上段弹簧定数〕＜〔下段弹簧定数〕这样的组合。

已知条件：
F弹簧的工作荷载(N)：
1τp许用切应力（MPa）：查表16.1-10ƒ工作载荷下的变形量（mm）：
1τs试验切应力（MPa）：查表16.1-10C旋绕比，C=D/d：
8d材料直径（mm）：G切变模量（MPa）：查表16.1-4
79000D弹簧中径（mm）：
抗拉强度σb （MPa）：查表16.1-81540K曲度系数，由下式计算，或根据旋绕比查图16.1-4
压缩弹簧载荷-变形图： K = + = 1.18
κ弹簧刚度（N/mm）：
κ= =1
n弹簧的有效圈数：
n= =77.148τ切应力（MPa）：
τ= =≤τp
τ= = 1.5083图中f1、f2等是在F1、F2作用下的弹簧变形量（mm）；
H0是自由高度；p弹簧的节距（mm）；U弹簧变形量（N.mm）：
H1、H2等为F1、F2作用下的弹簧高度（长度）（mm）；
U= =0.5压缩弹簧，F 0=0
试验荷载为弹簧允许承受的最大荷载，其值按（1）中曲度系数K=1计算，即
F s = =664.9
但对于旋绕比C ≤的弹簧，如由于原材料和工艺的原因，仍可考虑加曲度系数K。

其中式中τs为最大载荷弹簧许用切应力。

对与I类和II类载荷的弹簧，在某种情况下可以取τs=（1.1~1.3）τp，或取Fs=（1.1~1.3）Fn。

但其值不得超过最大试验切应力值
设计计算书
4-4C 1-4C C 0.6153πd 8KDF 2πd 8KCF k
D Gd 34
8f F 3
πd 8KDF 2Ff
8D τπd s 3
539 847 4 32。

弹簧设计计算已知条件：弹簧自由长度H0=796.8mm弹簧安装长度L1=411mm弹簧工作长度L2=227mm弹簧中径D=22.3mm弹簧直径d=3.2mm弹簧螺距P=12mm弹簧有效圈数n=66弹簧实际圈数n1=68计算步骤：（1）初步考虑采取油淬火-回火硅锰弹簧钢丝60Si2MnA C 类，抗拉强度1716-1863MPa ，切变模量G=79GPa ，弹性模量E=206GPa 。

取b σ=1716MPa 。

（2）压缩弹簧许用切应力p τ=(0.4~0.47) b σ=(0.4~0.47)*1716MPa=686.4~806.52MPa取p τ=686.4MPa 。

（3）因为弹簧刚度还未可知，不过弹簧中径、直径、有效圈数全部已知。

2.33.22==d D C =6.9688（计算值在5~8之间） 6.9688615.046.9688416.96884615.04414+-⨯-⨯=+--=C C C K =1.2139 弹簧最大工作压缩量Fn=795-227=568mm由公式348DP F Gd n n n =可得最大工作载荷34343.226685682.3798⨯⨯⨯⨯==nD F Gd P n n = 803.5758N 弹簧刚度663.2282.37983434'⨯⨯⨯==n D Gd P =1.4147N/mm 节距t=662.35.1795)2~1(0⨯-=-n d H =11.9727≈12 计算出来自由高度H0=nt+1.5d=66*12+1.5*3.2=796.8mm 压并高度Hb=(n+1.5)d=(66+1.5)*3.2=216mm弹簧最小工作载荷时压缩量F1=795-411=384mm 则最小工作载荷3431413.226683842.3798⨯⨯⨯⨯==nD F Gd P =543.2625N 螺旋角α=arctan(t/πD )=arctan(12/(3.14*22.3))= 0.1696弧度= 9.7174° 弹簧展开长度L=1696.0cos 683.22cos 1⨯⨯=παπDn = 4833.3mm ≈4833mm 弹簧压并高度H b ≤n 1*d max =68*（3.2+0.03）=219.64，取值216mm弹簧压并时变形量为796.8-216=580.8mm弹簧压并时载荷为Fa=580.8*1.4147=821.6578N（4）螺旋弹簧稳定性、强度和共振验算高径比b=H0/D=796.8/22.3=35.7309>0.4n B c P H P C P >=0'不稳定系数C B =0.02==0'H P C P B c 0.02*1.4147*796.8=22.5447N<n P =803.5758N 所以必需设置导杆。

弹簧设计盘算已知前提：弹簧自由长度H0=mm弹簧装配长度L1=411mm弹簧工作长度L2=227mm弹簧中径D=mm弹簧直径d=3.2mm弹簧螺距P=12mm弹簧有用圈数n=66弹簧现实圈数n1=68盘算步调：（1）初步斟酌采取油淬火-回火硅锰弹簧钢丝60Si2MnA C 类,抗拉强度1716-1863MPa,切变模量G=79GPa,弹性模量E=206GPa. 取b σ=1716MPa.（2）紧缩弹簧许用切应力p τ=(0.4~0.47) b σ=(0.4~0.47)*1716MPa=~MPa取p τ.（3）因为弹簧刚度尚未可知,但是弹簧的中径.直径.有用圈数都已知.2.33.22==d D C =（盘算值在5~8之间） 6.9688615.046.9688416.96884615.04414+-⨯-⨯=+--=C C C K = 弹簧的最大工作紧缩量Fn=795-227=568mm由公式348D P F Gd n n n =可得最大工作载荷34343.226685682.3798⨯⨯⨯⨯==nD F Gd P n n = N 弹簧刚度663.2282.37983434'⨯⨯⨯==n D Gd P =N/mm 节距t=662.35.1795)2~1(0⨯-=-n d H =≈12 盘算出来的自由高度H0=nt+1.5d=66*12+1.5*3.2=mm 压并高度Hb=(n+1.5)d=(66+1.5)*3.2=216mm弹簧最小工作载荷时的紧缩量F1=795-411=384mm 则最小工作载荷3431413.226683842.3798⨯⨯⨯⨯==nD F Gd P =N螺旋角α=arctan(t/πD)=arctan(12/(3.14*2))= 弧度= ° 弹簧睁开长度L=1696.0cos 683.22cos 1⨯⨯=παπDn = mm ≈4833mm 弹簧压并高度H b ≤n 1*d max =68*（3.2+0.03）=,取值216mm 弹簧压并时的变形量为796.8-216=mm弹簧压并时的载荷为Fa=*=N（4）螺旋弹簧的稳固性.强度和共振的验算高径比b=H0/D==不稳固系数C B 2==0'H P C P B c 0.02**=N<n P =N所以必须设置导杆.导杆与弹簧的推举间隙为3~4毫米疲惫强度验算,安然系数p S S ≥+=maxmin 075.0τττ 0τb σ=0.35*1716MPa=MPa=⨯⨯⨯⨯==803.57582.33.221.21398833max ππτn P d KD MPa =⨯⨯⨯⨯==543.26252.33.221.213988313min ππτP d KD MPa 许用安然系数p S 取值1.3 5.16908.114275.06.60075.0max min 0⨯+=+=τττS =。

精心整理一. 弹簧按工作特点分为三组二. Ⅰ组：受动负荷(即受力忽伸忽缩,次数很多)的弹簧,而且当弹簧损坏后将引起整个机构发生故障.例如:发动机的阀门弹簧、摩擦离合器弹簧、电磁制动器弹簧等。

三. Ⅱ组：受静负荷或负荷均匀增加的弹簧，例如安全阀和减压阀的弹簧，制动器和传动装置的弹簧等。

四. Ⅲ组：不重要的弹簧，例如止回阀弹簧手动装置的弹簧，门弹簧和沙发弹簧等。

五. 按照制造精度分为三级 六. 1级精度：受力变形量偏差为±5%的弹簧，例如调速器和仪器等需要准确调整的弹簧。

七. 2级精度：受力变形量偏差为±10%的弹簧，例如安全阀、减压阀和止回阀弹簧，内燃机进气阀压、拉弹簧曲度系数C C C k 615.04414+--=； 扭转弹簧曲度系数44141--=C C k ；为了便于计算，根据上面两个公式算出K 和K 1值，列成表2：钢的E=4101.2⨯（公斤力/毫米2）；铜的E=41095.0⨯（公斤力/毫米2）。

6．计算压缩、拉伸弹簧时，主要是受剪切应力。

因此使用的是剪切弹性模数G 。

钢的剪切弹性模数G ≈8000（公斤力/毫米2）； 青铜的剪切弹性模数G ≈4000（公斤力/毫米2）。

7．工作圈数和支承圈工作圈的作用是使弹簧沿轴线伸缩，是实际参加工作的圈数，又叫“有效圈数”，用n来表示。

支承圈的功用，是用来保证压缩压缩弹簧在工作时轴线垂直于支承端面，但并不参加弹簧工作。

因此，压缩弹簧的两端至少各要3/4圈拼紧，并磨平作为支承面。

磨薄后的钢丝厚度约为1/4d ，n ≥7(1+=n n 81°相反的，中径D 229.单圈变形量在负荷P 作用下,压缩、拉伸弹簧一圈的变形量，叫“单圈变形量”，用f 表示。

如果已知单圈变形量f ，就可以求出总变形量F=fn 。

总变形量F 的计算公式是：4328GdnPD F =，（毫米）； 将n=1代入，便得压、拉弹簧的单圈变形量4328GdPD f =，（毫米）。

弹簧设计参考弹簧参考资料§12-1 概述弹簧是常用的弹性零件，它在受载后产生较大的弹性变形，吸收并储存能量。

弹簧有以下的主要功能：(1)减振和缓冲。

如缓冲器，车辆的缓冲弹簧等。

(2)控制运动。

如制动器、离合器以及内燃机气门控制弹簧。

(3)储存或释放能量。

如钟表发条，定位控制机构中的弹簧。

(4)测量力和力矩。

用于测力器、弹簧秤等。

按弹簧的受力性质不同，弹簧主要分为：拉伸弹簧，压缩弹簧，扭转弹簧和弯曲弹簧。

按弹簧的形状不同又可分为螺旋弹簧、板弹簧、环形弹簧、碟形弹簧等。

此外还有空气弹簧、橡胶弹簧等。

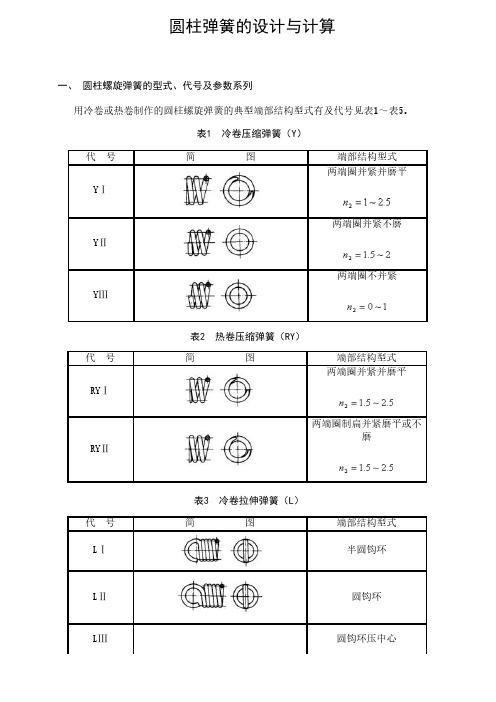
§12-2 圆柱拉、压螺旋弹簧的设计一、圆柱形拉、压螺旋弹簧的结构、几何尺寸和特性曲线1、弹簧的结构(1)压缩弹簧（图12－1）A、YI型：两端面圈并紧磨平B、YⅢ型：两端面圈并紧不磨平。

磨平部分不少于圆周长的3/4，端头厚度一般不少于d/8。

(a)YⅠ型(b)YⅡ型图12-1 压缩弹簧(2)拉伸弹簧（图12－2）A、LI型：半圆形钩B、LⅡ型：圆环钩C、LⅦ型：可调式挂钩，用于受力较大时图12-2 拉伸弹簧2、主要几何尺寸弹簧丝直径d、外径D、内径、中径、节距p、螺旋升角、自由高度(压缩弹簧)或长度(拉伸弹簧)，如图12-3。

此外还有有限圈数n，总圈数，几何尺寸计算公式见表12-1。

(a) (b)图12-3 圆柱形拉、压螺旋弹簧的参数表12-1 圆柱形压缩、拉伸螺旋弹簧的几何尺寸计算公式螺旋升角对压缩弹簧，推荐＝5°～9°间距 /mm＝p－d＝0L=D2n1/cos L=D2n+钩部展开长度弹簧指数C：弹簧中径D2和簧丝直径d的比值即：C=D2/d。

弹簧丝直径d相同时，C值小则弹簧中径D2也小，其刚度较大。

反之则刚度较小。

通常C值在4～16范围内，可按表12-2选取。

表12-2 圆柱螺旋弹簧常用弹簧指数C3、特性曲线弹簧所受载荷与其变形之间的关系曲线称为弹簧的特性曲线。