当前位置：文档之家 › 第二章立体表面交线投影2-4

第二章立体表面交线投影2-4

  • 格式：doc
  • 大小：2.03 MB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

2第二章：正投影法基础

2第二章：正投影法基础

• 如图所示，已切圆 锥体的三面投影以 及圆锥面上一点A 的正面投影a‘，求 作它的水平投影a 和侧面投影a”。 • 解１ • 解２
• 3、圆球体 • 球是由球面围成的。球面可看作是圆(母线) 绕其作为轴线的直径旋转180度而成。 球的投影特点： 圆球体的三个投影都是直径相等的圆。如图 所示，正面投影是平行于v面的圆素线的投影，该 素线的水平投影和圆球的水平投影的横向中心线 重合，侧面投影和圆球的侧面投影的竖向中心线 重合。 • 圆球的水平投影的轮廓线是平行于H面的圆 素线的投影。 • 圆球的侧面投影轮廓线是平行于w面的圆的 素线的投影。 • 例１ 例２
• 直线与平面、平面与平面的相对位置，除 了直线位于平面上或两平面位于同一平面 上的特例外，只可能是平行或相交。垂直 是相交中的一个特例。 • 一、平行 • 二、相交 • 三、垂直
• 一、平行 • 1、特殊情况 A、当平面为投影面的垂直面时，只要直线的 投影与平面的具有积聚性的投影平行时，或直线 也为该投影面的垂直线，则直线与平面必定平行。 B、当两平面同为某一投影面的垂直面，只要 它们的积聚投影平行，则两面必定平行。
• 一般位置平面 当平面与三个投影面均倾斜时，称为一般位置 ∆ABC 平面，如图。图中用∆ABC来表示平面，投影因 得到三个三角形的投影，均为封闭线框，与 ∆ABC类似，但不反映∆ABC的实形，面积均比 ∆ABC小。一般位置平面的投影特性是：三个投 影仍是平面图形，与空间平面图形类似，且面积 缩小。
2.3.2 曲面立体的投影
• 曲面立体由曲面或曲面和平面所围成，工 程上常用的曲面立体(如图)有圆锥、圆柱、 圆球 • １、圆柱 • ２、圆锥 • ３、圆球
圆柱 圆柱面可以看作直线绕与它平行的轴线旋转而成。 该直线称为“母线”，它的任何位置称为“素线” • 1．圆柱体的投影特点 如图所示，圆柱的轴线是一条铅垂线，则圆 柱面上所有直素线都是铅垂线：圆柱面的水平投 影为一圆周，有积聚性，这个圆周上的任意点， 是圆柱面上相应位置素线的水平投影： 圆柱正面投影中左、右两轮廊线是圆柱面上最左、 最右素线的投影。它们把圆柱面分为前后两半， 前半可见，而后半不可见，是可见和不对见的分 界线。 • 例１ • 例２

哈工大工程制图习题册答案_图文

哈工大工程制图习题册答案_图文
2-5 补画出三棱锥的侧面投影，并判断各棱线是什么位置直线
第二章 点、直线和平面
2-6 根据所给的条件作出直线的三面投影 已知线段点A（30,10,10），点B（10,20,25）。
点A（30,15,10）和线段AB的实长30, 的正平线。
过点A,作一侧垂线AB，长为30且与H,V面等距。
作侧平线AB,长为20，与V,H面倾角相等。
（1）
（2）
第七章 机件的表达方法
7-11 看懂主、俯视图，补出取半剖视图的左视图，并在主视图上取半剖视图，把不要的线打上×
第七章 机件的表达方法
7-12 根据轴测图把主、左视图画成半剖视图，并标注尺寸
第七章 机件的表达方法
7-13 在视图的适当位置上取局部剖视图
第七章 机件的表达方法
7-14 根据剖视规则，画出图中所漏的可见轮廓线
第四章 平面与曲面立体相交、两曲面立体相交
4-3 补画出立体的水平投影
第四章 平面与曲面立体相交、两曲面立体相交
4-4 完成圆锥被截切后的各投影
第四章 平面与曲面立体相交、两曲面立体相交
4-5 完成曲面立体被截切后的各投影
第四章 平面与曲面立体相交、两曲面立体相交
4-6 完成圆球被截切后的各投影
2. 在装配图上标注基本尺寸和配合代号，并说明其配合种类。
第九章 零件图
9-4 公差与配合 根据装配图中所注配合尺寸，分别在相应的零件图上注出基本尺寸 和偏差数值，并说明这两个配合尺寸的含义。
(1)外螺纹
(2)内螺纹
(3)外螺纹连接
(4)螺纹连接
第八章 标准件与常用件
8-2 不通孔螺纹画法及螺纹规定代号
第八章 标准件与常用件
8-3 在图中标出螺纹部分的尺寸

第2章 投影制图

第2章 投影制图

1
北
1
2
3
平面图1:50
2、 尺 寸 基 准
高度方向基准
定位的基准,即 定位尺寸的起点。
宽度方向基准
长度方向基准
3. 尺寸标注应注意的几个问题
• 尺寸标注要严格遵守国家制图标准的有关 规定。 • 尺寸标注要齐全，即所标注的尺寸完整、 不遗漏、不多于、不重复。 • 尺寸一般应尽量注在反映形体特征的投影 图上，布臵在图形轮廓线之外，但又应靠近 轮廓线，表示同一结构或形体的尺寸应尽量 布臵在同一个投影图上。
高
高
长
宽
长
形体的V面投影反映了形体的正面形状和形体的长度及高度，形体的H面投影反映了形体水平面 的形状和形体的长度及宽度，形体的W面投影反映了形体左侧面的形状和形体的高度及宽度。
宽
(4) 三面正投影的方位关系
上
上
上 后 右
左
前
右 后
左
前 下
下 后 左 下 前 左 上 右
前
V面投影图反映形体的上、下和左、右的情况，不反映前、后情况；H面投影图反 映形体的前、后和左、右的情况，不反映上、下情况；W面投影图反映形体的上、下 和前、后情况，不反映左、右情况。
由此可见形体分析法把形体分解、切割都是假想的。
2、形体分析的内容
1) 平面体相邻组成部分间的 表面衔接与投影图的关系
对齐共面衔接处无线
2)曲面体相邻组成部分间的表面衔接与投影图的关系
？
？
两表面相切时, 以切线位置分界光 滑过渡不能画线.
应注意的问题：形体分析法是
假想把形体分解为若干基本几何体
或简单形体，只是化繁为简的一种
• 用两个相交的剖切面剖切须标注。在剖切平面的 起止和转折处，标注剖切符号及剖面图编号。

(精品)机械制图第二版习题解答1

(精品)机械制图第二版习题解答1

5-6 根据两视图,参照轴测图补画第三视图 3.
5-6 根据两视图,参照轴测图补画第三视图 4.
5-7 根据两视图补画第三视图 1.
5-7 根据两视图补画第三视图 2.
5-7 根据两视图补画第三视图 3.
5-7 根据两视图补画第三视图 4.
5-8 根据两视图补画第三视图 1.
5-8 根据两视图补画第三视图 2.
1.根据主视图，补画俯、左视图（该体由三个几何体组成）。
3.根据俯视图，补画主、左视图（该体由五个几何体组成）。
2.根据左视图，补画主视图（该体由四个几何体组成）。
第三章 轴测图 3-1.根据平面体的两面视图补画第三视图，并补画轴测图。
1.
2.
3-2.补画第三视图,并画正等测 轴测图。
1.
2.
3-3.补画第三视图,并画斜二测 轴测图。
1.
2.
续5-2 根据轴测图画三视图,尺寸从图中量取(1:1)
1.
2.
5-3 参照轴测图补画图中的漏线 1.
5-3 参照轴测图补画图中的漏线 2.
5-3 参照轴测图补画图中的漏线 3.
5-3 参照轴测图补画图中的漏线 4.
5-6 根据两视图,参照轴测图补画第三视图 1.
5-6 根据两视图,参照轴测图补画第三视图 2.
(1)
(2)
(2)
(3)
(3)
(4)
(4)
(1)
(5)
(6)
(6)
(5)
2-3.由给出的两个视图,参照轴测图补画第三视图,
1.
2.
3.
4.
2-4.根据轴测图或模型画三视图.
1.
2.
续2-4.根据轴测图或模型画三视图.

02 正投影基础1-4

02 正投影基础1-4
2010-姚春东制作
(3)
点分线段之比不变
直线上的一点分线段之比是平行投影的不变量。
AC/BC = ac/bc
2010-姚春东制作
(4)
类似性
一般情况下，平面图形的投影都要发生变形， 但投影形状总与原形相类似。 即平面投影后，与原形的对应线段保持定比性， 表现为投影形状与原形的边数相同、平行性相同、 凸凹性相同及边的直线或曲线性质不变。
作图步骤：
a X
c
b
1）过a(或b)任作一直线aB1（或bB1) ； 2）在aB1上取C1， 使aC1∶C1B1＝1∶2； 3）连接B1、b； 4）过C1作C1c∥B1b，与ab交于c ；
c
a C1
b
B1
5）过c作X轴的垂线与a′b′交于c 。则 c 、c′即所求分点C 的投影。
分析：分点C 的投影，必在AB 线段的同面投影上，且
V c a
C A
b
B
b a c H
AC/CB=ac/cb= ac / cb
从属性 定比性
［例1］判断点C是否在线段AB上。
a c● b X o a c● b YH YW
Z
a
●
AB是什么位置直线？
b
c
因c不在a b上，故点C 不在AB上。
另一判断法?
应用定比性
2010-姚春东制作
2010-姚春东制作
2.2 点的投影(用正投影法)
一、点在一个投影面上的投影
过空间点A的投射线 与投影面P的交点即为点 A在P面上的投影a 。 点在一个投影面 上的投影不能确定点 的空间位置。
解决办法？ A
●
P
●
a
P
B2

建筑制图习题集

建筑制图习题集

建筑制图习题集
P8：
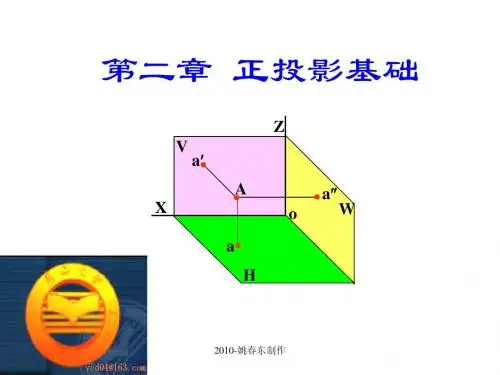
第二章正投影法基础
2-1 根据立体图找投影图
P9：
2-2 根据立体图画三面投影（尺寸从立体图上量取）
P11：
2-4 点的投影
P13：
2-6 直线的投影
P16：
2-9 平面的投影
P18：
2-11 补画立体的第三视图，并作出立体表面上个点的三面投影
P19：
2-12 根据给出的立体图，完成三面图投影（尺寸从立体图中量取）
P20：
2-13 由已知的投影补画另一投影
P21：
2-14 补画投影图中漏画的图线
P22：
2-15 根据给出的两投影补画另一投影（1~4）、补画正面投影中的漏线（5、6）
P24：
2-17 组合形体（2）
2-19 根据给定的正面和水平投影，补画侧面投影（有多种答案，至少画两个）
第三章建筑型体表面交线3-1根据给定的两个或一个投影，补画第三投影
3-4 根据给定的两个或一个投影，补全其他投影
3-6 两平面体的表面交线
P36：
3-9 分析曲面体表面交线，补全立体相贯或穿孔后的投影
P38：
第四章轴测图与透视图4-1 根据正投影图，画出正等轴测图
4-2 根据正投影图，画出正等轴测图
第五章建筑形体的表达方式5-2 剖面（2）
5-5 剖面（5）绘制1-1剖面图
5-6 断面（1）
第六章建筑施工图6-1 房屋的基本表达形式
6-2 建筑施工图——楼层平面图
6-3 建筑施工图——立面图
6-4建筑施工图——1-1剖面图
6——5 建筑施工图——2-2剖面图
6-6 建筑施工图——楼梯间平面详图
6-7 读图——住宅墙身剖视图。

第二章 正投影法基础


例题：判断下列直线的位置
a' b' a'
b' a b
b a
2、直线上点的投影
（1）点在直线上，则点的各个投影必定在该直 线的同面投影上；并且符合点的投影特性。 （2） 点在直线上，分割线段成定比。 ac:cb = a‘c‘:c‘b‘ = a‖c‖:c‖b‖ = AC:CB b‘ a‘
X Z
b‖
c‘
a
b
重影点：
A、C为H面的重影点
a
● ●
空间两点在某一投 影面上的投影重合为一 点时，则称此两点为该 投影面的重影点。
被挡住的投 影加( )
a c
c●
●
a (c )
●
A、C为哪个投 影面的重影点 呢？
二、直线的投影
1、各种位置直线的投影特性 作直线的投影实际上就是作直线两端点的投影。
正平线（∥Ｖ面）
●
O
X
ax
●
A
O
a
Y
●
H
Y
点的投影规律:
① aa⊥OX轴 ② aax=y=A到V面的距离 aax=z=A到H面的距离
4、点在三投影面体系中的投影
在V、H两面系基础上增加侧立投影面W，构成了三面投影系。 不动
Z
向右翻
Z
V
V
a
●
az
●
a
●
az
O
●
a
W
X
ax
A O
●
a W
X
ax a
●
ay
Y
a 向下翻
斜三棱锥
1.棱柱 ⑴ 棱柱的组成
由两个底面和若干侧棱面 组成。侧棱面与侧棱面的交线 叫侧棱线，侧棱线相互平行。

化工制图教案第二章4


画图步骤：

对组合体进行形体分解 — 分块
• •
弄清各部分的形状及相对位置关系。 按照各块的主次和相对位置关系， 逐个画出它们的投影。 分析及正确表示各部分形体之间 的表面过渡关系。 • 检查、加深 。
•
例1：画轴承座的三视图
套筒 支撑板
肋板 底板 ⒈ 分解形体 ⒉ 分析各部分间的相对位置及表面过渡关系 ⒊ 选择主视图 原则：较多地表达出物体的形状特征及各部分 间的相对位置关系。
已知视图
修正
物体形状
物体的视图
物体形状
二、看图的方法和步骤 看图的基本方法 ☆ 形体分析法
用“分线框、对投影”的方法分析出组合体由 几部分组成，从特征视图入手，想象出各部分的形 状、相对位置关系及组合方式，最后综合想象出整 体形状。
形体分析法 面形分析法
☆ 面形分析法
用“分线框、对投影”的方法分析物体各表面 的形状，从而想象出物体的整体形状。
☆ 作图步骤：
◆ 作辅助平面与相贯的两立体相交 ◆ 分别求出辅助平面与相贯的两立体表面的交线 ◆ 求出交线的交点（即相贯线上的点）

☆ 辅助平面的选择原则：
使辅助平面与两回转体表面的交线的投影简 单易画，例如直线或圆。 一般选择投影面平行面。
例4：圆柱与圆锥相贯，求其相贯线的投影。
P
假想用水平面P截切立体,P面与圆柱面的交线 为两条直线，与圆锥面的交线为圆，圆与两直线 的交点即为相贯线上的点。
⒋ 画底稿
⑴ 布置视图： 画对称中心线、轴线及定位基准线 ⑵ 逐个画各形体的三视图： 从反映形体特征 的视图开始画， 三个视图对照画。
● ● ●
先整体，后局部。 先定位置，后定形 状。
●

2-4 两回转体表面相交 机械制图课件

(2)利用辅助平面法 求相贯虚实依次将各点 的投影连接为光滑 曲线并擦去被相贯 掉的轮廓线，加深 其余图线。
四、小结： 求相贯线的一般步骤
(1) 根据二相贯立体的形状及位置分析相贯线的形状； (2) 求相贯线上特殊位置各点及一般位置点的投影； (3) 判别可见性后依次连接各点，擦去被相贯掉的轮
请点击鼠标左键显示后视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示仰视图形
请点击鼠标左键显示后视图形
第四节 两回转体表面相交
一、利用积聚性求相贯线 二、辅助平面法求相贯线 三、正交二圆柱相贯线分析 四、小结
一、利用积聚性求相贯线
相贯线的定义：二个回转体相互贯穿时， 表面的交线称为相贯线。
1. 相贯线的特性
相贯线是二立体表面上共有点的连线；
相贯线一般为一条封闭的空间曲线。
请点击鼠标左键显示后面内容
廓线，加深其余图线。
请点击鼠标左键显示后面内容
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示后视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示后视图形
请点击鼠标左键显示另一图形
请点击鼠标左键显示对比图形
请点击鼠标左键显示主视图形
一、利用积聚性求相贯线
2.相贯线的求法
利用圆柱的有积聚性的圆投影求相 贯线上各点的投影。
圆柱与圆柱（孔）的相贯线；
圆柱与圆锥的相贯线； 用积聚性法可求:

第二章投影法基本知识

真实性
积聚性：当一线段与投影面垂直时，其正投影积聚为一
点；当一平面图形与投影面垂直时，其正投影积聚为 一直线。
积聚性
类似性：当一线段与投影面倾斜时，其正投影为缩短
的线段； 当一平面图形与投影面倾斜时，其正投影 为缩小的类似图形。
类似性
§2-2 三视图的形成及其对应关系
根据国标规定，用正投影法绘制出物体的图形称为视图。 下图表示的是三个不同形体，在一个投影面上的视图却是完 全相同的。
1、主视图—从前向后投射，在V 面上所得的视图。
2、俯视图—从上向下投射，在H 面上所得的视图。
3、左视图—从左向右投射，在W 面上所得的视图。
三视图的形成
三投影面的展开
V面保持不动，H面绕OX轴向下旋转90°，W面绕 OZ轴向右旋转90°，这样V、H和W三个投影面就摊 平在了同一平面上。
水 平 投 影 面 和侧立投影 面旋转后，OY轴被分成两 条，分别用OYh和OYw 表 示 。
注意：
要细心，不要把点对错了。
§2-4 直线的投影
二、各种位置直线的投影
根据直线在三投影面体系中对投影面的相对位置不同，将
直线分为：
投影面平行线 投影面垂直线
特殊位置直线
投影面倾斜线
一般位置直线
1、一般位置直线 定义：与三个投影面均成倾斜的直线
直线与 H、V、W 投影面的倾角分别用 α、β、γ表示，见图 中的标注。
即 ac:cb=a'c':c'b'=a''c'':c''b''=k
例: 判断图中点是否在直线上。
作图分析： ⑴由于AB直线为一般位置。而给出 的C点的两投影分别在AB线的同面投 影上，故可认定C点从属于AB直线。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

教学环节教学过程及内容
方
法
经典诵读1.《弟子规》诵读。

2.强调课堂纪律及操作规程。

调动学生激情，调节课堂气氛。

学习任务
情境
公司的设计部门人员需要根据客户需求作图；公司的生产加工人员，也
需要读懂图纸、会作简单的零件图。

新课题
机器上的零件，不论形状多么复杂，都可以看作是由基本几何体按照不
同的方式组合而成的。

讲
授
法
学习任务
描述
以正六棱柱为例。

如图3－1（a）所示为一正六棱柱，由上、下两个底面
（正六边形）和六个棱面（长方形）组成。

设将其放置成上、下底面与水平
投影面平行，并有两个棱面平行于正投影面面。

讲
授
法
演
示
法
任务引入
基本几何体——表面规则而单一的几何体。

按其表面性质，可以分为平
面立体和曲面立体两类。

1、平面立体——立体表面全部由平面所围成的立体，如棱柱和棱锥等。

（出示模型给学生看）。

2、曲面立体——立体表面全部由曲面或曲面和平面所围成的立体，如圆
柱、圆锥、圆球等。

（出示模型给学生看）。

曲面立体也称为回转体。

问
题
引
入
任务分析
1、平面立体——立体表面全部由平面所围成的立体，如棱柱和棱锥等。

（出示模型给学生看）。

2、曲面立体——立体表面全部由曲面或曲面和平面所围成的立体，如圆柱、圆锥、圆球等。

（出示模型给学生看）。

曲面立体也称为回转体。

学习内容教学方法
任务实施（一）平面立体的投影及表面取点
1、棱柱
棱柱由两个底面和棱面组成，棱面与棱面的交线称为棱线，棱线互相平行。

棱线与
底面
垂直的棱柱称为正棱柱。

本节仅讨论正棱柱的投影。

（1）棱柱的投影
以正六棱柱为例。

如图3－1（a）所示为一正六棱柱，由上、下两个底面（正六边
形）和六个棱面（长方形）组成。

设将其放置成上、下底面与水平投影面平行，并有两
个棱面平行于正投影面面。

上、下两底面均为水平面，它们的水平投影重合并反映实形，正面及侧面投影积聚
为两条相互平行的直线。

六个棱面中的前、后两个为正平面，它们的正面投影反映实形，
水平投影及侧面投影积聚为一直线。

其他四个棱面均为铅垂面，其水平投影均积聚为直
线，正面投影和侧面投影均为类似形。

（a）立体图（b）投影图
图3－1正六棱柱的投影及表面上的点
边画图边讲解作图方法与步骤。

讲
授
法
演
示
法
任务实施
总结正棱柱的投影特征：当棱柱的底面平行某一个投影面时，则棱柱在该投影面上
投影的外轮廓为与其底面全等的正多边形，而另外两个投影则由若干个相邻的矩形线框
所组成。

（2）物体种类
2、棱锥
三棱锥三视图画法
棱锥的棱线交于一点，底面平行水平投影面，三个三角形侧面是一般位置面。

底面
的投影在水平面反映实际形状，侧面投影是三个相似的三角形。

画图时，先画水平面上投影，底面在正投影和测投影中积聚一条线段，可以按投影
规律分别画出。

讲
授
法
演
示
法
（a）立体图（b）投影图
图3－2正三棱锥的投影
边画图边讲解作图方法与步骤。

总结正棱锥的投影特征：当棱锥的底面平行某一个投影面时，则棱锥在该投影面上投影的外轮廓为与其底面全等的正多边形，而另外两个投影则由若干个相邻的三角形线框所组成。

检查请同学们做出五棱柱的三视图
4人一组，共分15组，一组选一位同学当组长。

组长负责查人数，纪律维持。

做好作业教师公布答案，组长检查。

评价
评价项目分值评价标准自评组评师评作图完整20 要求做完布置的项目
作图准确20 要求作图准确
作图规范20 要求作图规范
保留作图痕迹20 按正确方法保留作图痕迹
纪律良好20 服从组长安排，纪律良好
总结1、总结表扬课堂练习优秀的学生；
2、总结棱柱、棱锥、的投影分析和投影特征。

3、指出在学生在练习中共同出现的问题和个别存在的问题。

课后作业：习题集2-4（1）、（2）、（3）。