( yi(2) y(2) )2
i1
i1
Fisher判别法
第一Fisher判别函数的方 向和距离判别函数等于0的 直线或平面之间相互垂直
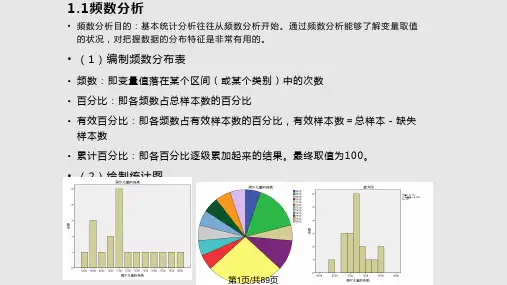
• 一般陈述:
• 点X在以a为法方向的投影为a’x,则各组数据的投
影为:
Gi
:
a'X1(i)
,.
..,
a X' (i) ni
,
i
1,2,...,k
x1,x2…为包 含p个元素 的列向量
W ( X ) ( X X )' 1( X (1) X (2) )
(X X )'a a'(X X )
判别函数为线性函数
单个判别变量时:判别函数等于0表示点X与两
类总中心重合(σ12 = σ22)
G2
G1
W(X)>0,则:X∈G1
如果W(X)<0,则:X∈G2
如果W(X)=0,则待判
距离判别法的特点
特点: 直观 若两类别的均值无显著差异,错判概率高
问题: 多个总体的均值是否存在显著差异 多个总体的协差阵是否存在显著差异
多个总体的均值检验:H0:(1)=…= (k) 单变量x均值检验中组间离差平方和与组内离差平 方和:
多变量的均值检验中计算平方和(p=2为例)
根据距离最近的原则,距离哪个中心近,则属于 哪个类
例:设(1), (2), (1), (2)分别为G1和G2的均值向量 和协差阵,则点X到Gi的距离定义为平方马氏距离为:
D2(X,Gi ) (X μ(i))'( (i))1(X μ(i)) i 1,2
u未知时用样本均值 替代
为什么采用马氏距离
为什么采用马氏距离