组合图形的面积计算练习课
- 格式:ppt
- 大小:232.50 KB
- 文档页数:21

人教版五年级数学上册第六单元《组合图形的面积》课时练习题(含答案)一、填空题1.如图,每个小格子的边长是1dm,阴影部分的面积约是( )dm2。
2.在下图中每个小方格的边长是1cm,写出每个图形的面积。
图①的面积是( )cm²。
图②的面积是( )cm²。
3.用图中方法估测不规则图形的面积,大约是________cm2。
4.上图每个小方格面积表示1cm2。
图形A的面积是( )cm2;图形B的面积是( )cm2;图形C的面积大约是( )cm2。
5.如图,在长方形ABCD中,AB长8厘米,BC长15厘米,四边形EFGH的面积是9平方厘米,则涂色部分的面积和为( )。
二、判断题6.用同样的小方块拼成和,它们的表面积相等。
( )7.都能密铺._____.(判断对错)8.不规则图形的面积可以转化为学过的图形来估算。
( )9.两个完全一样的梯形可以拼成一个平行四边形。
( )10.如图,每个小方格的面积是1cm2,草莓图的面积约是11cm2。
( )三、选择题11.如图,空白部分的面积()阴影部分的面积。
A.>B.<C.=12.图中每个小方格的面积是1平方厘米,下面图案的面积大约是()平方厘米。
A.17 B.18 C.19 D.2013.两个完全一样的直角三角形重叠成下图形状,形成两个梯形,这两个梯形的面积大小关系是()。
A.A大B.B大C.相等D.无法确定14.小明把一枚银杏树叶的轮廓描在方格纸上,如下图(图中每个小方格的面积是1cm2)。
这枚树叶的面积最接近()cm2。
A.19 B.32 C.45 D.5415.如下图,每个小正方形的面积是2cm2,涂色部分的面积是()cm2。
A.32 B.24 C.20 D.10时四、连线题16.将面积相等的图形连一连.五、解答题17.一块梯形菜地种了两种菜,如下图所示。
(1)已知平行四边形的面积是680平方米,它的高是多少米?(2)这块梯形菜地的面积是多少平方米?如果给整个梯形菜地施肥,每平方米施肥0.15千克,共施肥多少千克?18.乐山小学准备开辟一块地作为学生研学基地(如图),图中每个小方格的边长都是1m。
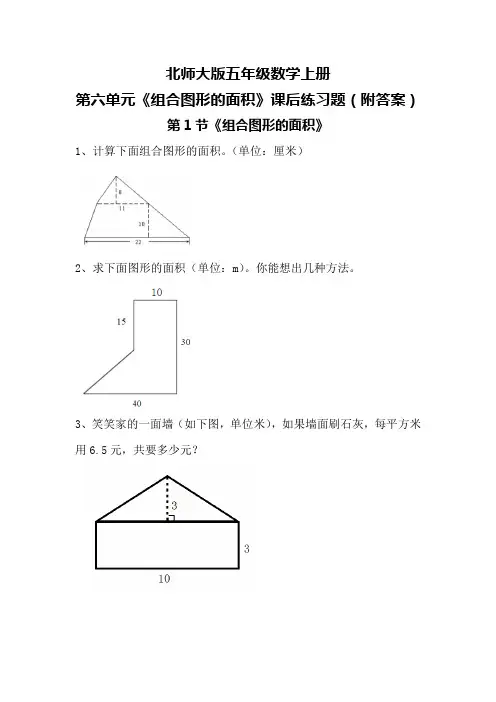
北师大版五年级数学上册第六单元《组合图形的面积》课后练习题(附答案)第1节《组合图形的面积》1、计算下面组合图形的面积。
(单位:厘米)2、求下面图形的面积(单位:m)。
你能想出几种方法。
3、笑笑家的一面墙(如下图,单位米),如果墙面刷石灰,每平方米用6.5元,共要多少元?参考答案:1、11×8÷2+22×10=264(平方厘米)2、方法一:分成三角形和长方形(40-10)×(30-15)÷2+10×30=525(平方米)方法二:分成长方形和梯形10×15+(40+10)×(30-15)÷2=525(平方米)方法三:从大长方形里减去一个梯形40×30-(30+15)×(40-10)÷2=525(平方米)3、(10×3+10×3÷2)×6.5=292.5(元)第2节《不规则图形的面积》课后练习题(附答案)1、写出下面图形的面积。
()平方厘米()平方厘米2、估一估,下面不规则土地的面积约是()平方米。
3、估一估,下面不规则土地的面积约是()平方米。
参考答案:1、16 212、26003.126第3节《面积单位的换算》课后练习题(附答案)1、填上适当的数。
12公顷=()平方米800000平方米=()公顷5000公顷=()平方千米4平方千米=()公顷3平方千米=()公顷=()平方米2、填上合适的单位名称。
餐桌的面积大约是44()。
教室的面积大约是48()。
一张1元的纸币的面积大约是44()。
我们校园的面积大约是1()。
中国的国土面积大约是960万()。
3、实际应用。
(1)一个长方形果园的长250米,宽120米,这个果园有多少公顷?(2)一块正方形地的周长是800米,每公顷收稻谷6.5吨,那么这块地收稻谷多少吨?参考答案:1、120000 80 50 400 300 30000002、平方分米平方米平方厘米公顷平方千米3.(1)250×120=30000(平方米)=3(公顷)(2)800÷4=200(米)200×200=40000(平方米)=4(公顷)4×6.5=26(吨)。

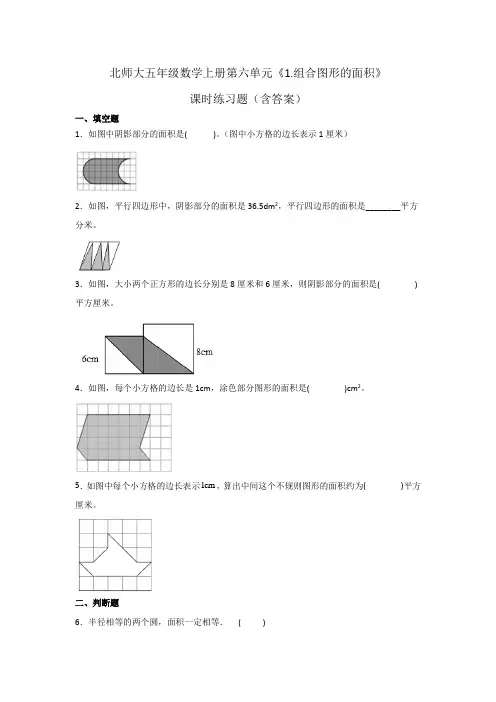
北师大五年级数学上册第六单元《1.组合图形的面积》课时练习题(含答案)一、填空题1.如图中阴影部分的面积是( )。
(图中小方格的边长表示1厘米)2.如图,平行四边形中,阴影部分的面积是36.5dm2,平行四边形的面积是________平方分米。
3.如图,大小两个正方形的边长分别是8厘米和6厘米,则阴影部分的面积是( )平方厘米。
4.如图,每个小方格的边长是1cm,涂色部分图形的面积是( )cm2。
5.如图中每个小方格的边长表示1cm,算出中间这个不规则图形的面积约为( )平方厘米。
二、判断题6.半径相等的两个圆,面积一定相等.( )7.只能分割成长方形和三角形.( )8.一个住宅小区的面积大约是2100m。
( )9.测量土地面积时只能用“2km”作单位。
( )10.一个组合图形可以由其他的基本图形组合而成。
( )三、选择题11.图①和图②的面积相比较()。
A.图①的面积大B.图②的面积大C.图①和图②相等12.图中阴影部分的面积是()平方厘米。
A.24 B.28 C.3213.比较图中阴影部分的面积,它们之间的大小关系是()A.①>②>③>④B.①<②<③<④C.①=②=③=④D.①=②<③=④14.如图,平行四边形的面积是484平方厘米,梯形(阴影)的面积是()平方厘米。
A.185 B.370 C.740 D.40715.请在下面图形中找出所有面积相等的图形()。
A.①②B.②③C.①②④D.①③④四、解决问题16.学校花园示意图如图所示,在灰色区域种植太阳花,算一算,太阳花的种植面积是多少平方米?(单位:米)17.下图是某山庄用木板制作的一个指示牌,现要给指示牌正反两面涂油漆。
若每平方厘米用油漆6克,制作50个这样的指示牌共需油漆多少千克?18.一块菜地(如图),如果每平方米收入30元,这块菜地一共收入多少元?19.实验小学每扇门上都有一块玻璃,整扇门的形状如下图。

五年级上册数学教案-5.4 组合图形面积的练习 -人教新课标教学内容本节课主要围绕组合图形的面积进行练习,学生将通过解决实际问题,加深对组合图形面积计算方法的理解。
课程内容将包括识别和分解组合图形,应用已学的面积计算公式,以及通过实际案例来应用这些技能。
教学目标1. 知识与技能:学生能够识别和分解组合图形,并应用相应的面积公式进行计算。
2. 过程与方法:学生将通过解决实际问题,培养逻辑思维能力和问题解决能力。
3. 情感态度价值观:培养学生对数学学习的兴趣,增强其自信心和团队合作精神。
教学难点1. 图形识别与分解:学生在识别和分解组合图形时可能会遇到困难,需要通过直观演示和实际操作来加深理解。
2. 面积公式的应用:学生需要熟练掌握各种基本图形的面积公式,并能灵活应用于组合图形的计算中。
教具学具准备1. 教具:组合图形模型、多媒体教学设备、教学课件。
2. 学具:学生自备的数学练习本、计算器(可选)。
教学过程1. 导入:通过回顾上节课的内容,引入组合图形的概念,激发学生的学习兴趣。
2. 新授:使用多媒体教学设备展示不同的组合图形,引导学生观察、识别并分解这些图形。
3. 实践:学生分组进行实际操作,通过合作解决实际问题,加深对组合图形面积计算方法的理解。
4. 讨论与分享:各小组分享解决问题的过程和结果,全班讨论不同方法的优势和局限。
5. 总结与反思:教师引导学生总结本节课的重点内容,并反思学习过程中的困难与收获。
板书设计板书设计将突出组合图形的识别、分解和面积计算方法,通过图表和公式来直观展示计算过程。
作业设计1. 必做题:学生完成教材上的相关练习题,巩固课堂所学。
2. 选做题:学生选择一道较难的组合图形面积计算题,尝试独立解决。
课后反思课后反思将重点关注学生对组合图形面积计算方法的掌握程度,以及在实际问题中的应用能力。
同时,教师也将反思教学过程中的不足之处,为下一节课的教学提供改进方向。
教学难点在以上教案中,教学难点是需要重点关注的细节。


《组合图形的面积》练习课教案【教学内容】:新课标人教版五年级上册第94--95页【教学目标】:1、使学生进一步认识组合图形,进一步掌握组合图形面积的计算方法,提高应用所学知识和解决问题的能力。
2、让学生在独立解决简单的实际问题及合作交流的过程中加深对所学知识的理解,提高掌握水平。
【教学准备】:多媒体课件,测试纸【教学过程】:一、问题引入,回顾再现。
师:同学们上一节课我们学习了组合图形的面积计算,并能解决生活中的一些实际问题,大家的表现都很棒,请同学们回想一下解决这一问题关键是什么?生:根据已知条件巧妙的分解。
师:真棒!老师还有一个问题,学校开运动会要制作一些锦旗,式样如图(出示课件)可是老师不知道需用多少布,想不想帮老师算出来?生:想!先让学生独立解决问题,再组织学生交流算法。
展示不同的风采:(说出自己的想法)生1把它分割成两个梯形,求这两个图形的面积和。
[(60+45)×(30÷2)÷2]×2生2把它分割成一个长方形和两个三角形,求这三个图形的面积和。
30×45+[30÷2×(60-45)÷2]×2生3:添上一个三角形,求长方形和三角形的面积差。
(30×60)-[30×(60-45)÷2师:这就是上节课我们学过的组合图形的面积解决生活中实际问题,这节课我们就来进行相关的练习。
二、分层练习,强化提高。
1、基本练习(1)师:老师先出道题考考你,看看你们对这部分知识掌握得怎么样?(课件出示) 考考你。
计算下面图形的面积。
你能想出几种方法?生独立完成。
师:先做完的同学可以互相交流你们的做题方法。
全班交流时,一生展示所做题汇报结果。
其余同学核对。
2综合练习(2)师:通过前面的练习,同学们的计算能力都有了提高,老师再出道题,有没有信心, (课件出示)生:有生独立完成,全班交流。
三、自主检测,评价完善。
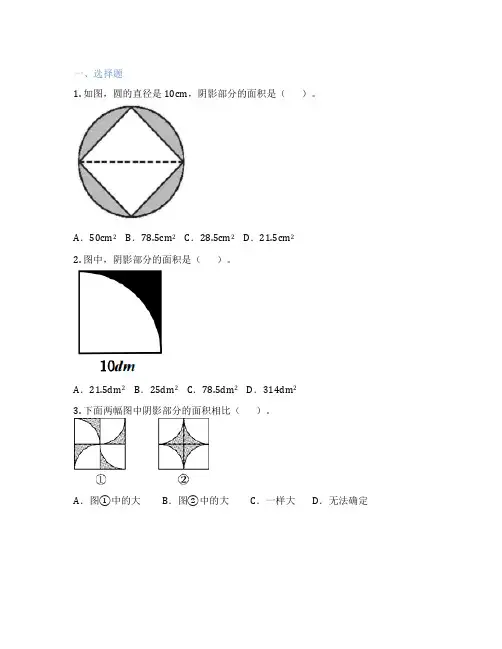
一、选择题1. 如图,圆的直径是10cm,阴影部分的面积是()。
A.50cm2B.78.5cm2C.28.5cm2D.21.5cm22. 图中,阴影部分的面积是()。
A.21.5dm2B.25dm2C.78.5dm2D.314dm23. 下面两幅图中阴影部分的面积相比()。
A.图①中的大B.图②中的大C.一样大D.无法确定4. 如图,两个正方形的边长相等,正方形中空白部分的面积相比较()。
A.①大B.②大C.同样大D.无法确定5. 如图是一个“禁止驶入”的交通标志,图中有一个70cm×12cm的白色长方形,其余部分为阴影(实际为红色)。
这个图形中阴影部分的面积是()cm2。
A.5024 B.20096 C.4184 D.19256二、填空题6. 如图,阴影部分的周长是________cm,面积是________cm2。
7. 如图,外侧大正方形的边长是10厘米,图中阴影部分的面积是27.5平方厘米,那么圆内大正方形面积是小正方形面积的________倍。
8. 如图所示,圆的直径是20cm,阴影部分的面积是( )cm²。
9. 如图,圆的面积等于长方形的面积。
如果圆的面积是,阴影部分的面积是( )。
10. 图中阴影部分的面积相当于正方形面积的%三、解答题11. 如下图,一个半圆中有一个直角三角形,直角三角形的顶点与圆心重合,求阴影部分的面积。
12. 如图,由以O1为圆心半圆和以O2为圆心的直角扇形重叠而成.线段AB=12厘米,三角形AO2B的面积是36平方厘米,求图中阴影部分的面积.(π取3.14)13. (1)如图1中,甲、乙两个图形重叠部分的面积相当于甲面积,相当于乙面积的.甲、乙两个图形的面积比是多少?(2)如图2,AO3= AB,AO2= AO3,阴影甲与阴影乙的面积的比多少?(3)如图3,AB= AD,EC= ED,图中阴影部分与空白部分面积的比多少?(4)如图4,S甲=16,S乙=12,S丙=10,阴影部分的面积是多少?14. 求下面操场的周长和面积.(单位:米)。

小学数学苏教版五年级上册第二单元第9课《组合图形面积计算练习》获奖教案公开课优质课教案观摩课讲课精品
教案
【省级获奖教案】
1教学目标
1、使学生进一步认识组合图形,进一步掌握组合图形面积的计算方法,提高应用所学知识和解决问题的能力。
2、让学生在独立解决简单的实际问题及合作交流的过程中加深对所学知识的理解,提高掌握水平。
3. 能运用方法解决生活中的一些综合性问题。
2学情分析
五年级学生活泼好动,精力旺盛,求知欲望、能力和好奇心都有所增强,对新鲜事物开始思考、追求、探索,学习兴趣更为广泛,自我意思有所发展,自主性要求日趋强烈,但仍缺乏自我约束能力、分析推理能力以及数学思想和方法。
本班学生还存在知识基础薄弱,理解能力偏低,注意力不稳定等因素。
3重点难点
教学重点:灵活运用知识解解决问题。
教学重难点:通过合作交流,评价与对比(比较)总结得出解决求组合图形面积的方法及最好的方法。
4教学过程
4.1第一学时
教学活动
1【导入】组合图形面积计算练习
1、师:你能说说我们学过哪些平面图形码?怎样计算各图形的面积?
2、出示上节课题目,让生说说都有哪些解题方法。
2【讲授】解决问题
先让学生独立解决问题,再组织学生交流算法。
汇报:1、添补法
添上一个正方形,求大梯形和正方形的面积差
2、分割法
A、把它分割成两个梯形,分析得出并不是很好算
B、把它分割成一个正方形和一个梯形,再求和。

6.4组合图形的面积(同步练习)一、填空题1.如图,AC长10厘米,BD长6厘米,且AC垂直BD,那么四边形ABCD的面积为平方厘米。
2.如下图所示的直角三角形ABC中,AB=6厘米,BC=8厘米,AC=10厘米,正方形BFGE的边长为1厘米,则GD=( )厘米。
3.图是一个长方形,长为10厘米,宽为6厘米,则阴影部分面积为( )平方厘米.4.如图,平行四边形ABCD的边长BC为10厘米,直角三角形BCE的直角边EC为8厘米,已知阴影部分的面积比三角形EFG的面积大4.8平方厘米,则CF的长是( ) 厘米.5.街心花园有一个正方形的花坛,四周有一条宽1.5米的甬道(如图),如果甬道的面积是27平方米,那么中间的花坛面积是( )平方米.二、判断题6.用正八边形可以密铺。
( )7.计算组合图形的面积也要用到基本图形的面积公式。
( )8.估算一片树叶的面积,可以先在方格纸上描出叶子的轮廓,再根据叶子轮廓的形状转化成近似的规则平面图形进行计算。
( )9.如图,阴影甲的面积大于阴影乙的面积.( )三、选择题10.如下图所示,每个小正方形面积是1cm²,阴影部分的面积是()cm².A.5.5B.7.5C.8D.8.511.比较下图中甲、乙阴影部分的面积,结果是( ).A.甲>乙B.甲<乙C.甲=乙D.不确定12.下图中每个小正方形的面积表示1平方厘米,芳芳2岁时脚印(阴影部分)的面积可能是()平方厘米。
A.20~25B.35~38C.40~45D.50~5513.如图所示,每个小方格的面积是1平方厘米,则阴影部分的面积大约是()平方厘米。
A.5B.8C.6D.20四、解答题14.如图,梯形的下底为8厘米,高为4厘米.阴影部分的面积是多少平方厘米?15.两个长12厘米、宽8厘米的长方形(如图)摆放后,组合图形的面积是多少?16.李叔叔准备在这块地里种郁金香(如图),每棵郁金香占地0.25平方米,这块地大约可种多少棵郁金香?17.下图是房屋的一面墙。
苏教版五年级上册《组合图形面积练习课》数学教案一、教学目标1.知识与技能目标:–认识组合图形的概念;–掌握组合图形面积的计算方法;–通过练习提高对组合图形面积的计算能力。
2.过程与方法目标:–注重启发式教学,让学生能够主动思考;–采用小组合作学习的方式,激发学生的合作意识和竞争意识;–引导学生运用已有知识解决新问题。
3.情感态度目标:–帮助学生树立自信心,在学习数学过程中发现自己的优势和潜力;–培养学生的空间想象能力,提高学生对数学的兴趣和热爱。
二、教学重点与难点1.教学重点:–认识组合图形的概念;–掌握组合图形面积的计算方法。
2.教学难点:–如何将已有的面积计算方法应用于组合图形的计算过程中。
三、教学内容与教学过程3.1 教学内容1.认识组合图形的概念;2.掌握组合图形面积的计算方法;3.通过练习提高对组合图形面积的计算能力。
3.2 教学过程3.2.1 导入首先,展示一些常见的组合图形,让学生描述每个图形的特点和面积计算方法。
1.认识组合图形的概念组合图形是由两个或以上的简单图形按照一定的方式组成的新图形,每个组成部分称为组合图形的构成部分。
2.掌握组合图形面积的计算方法计算组合图形的面积,可以将其划分成若干个简单的图形,然后将这些简单图形的面积相加即可得到组合图形的面积。
在计算面积时,可以采用如下方法:•将组合图形分解为简单图形,分别计算每个简单图形的面积,再将它们相加得到组合图形的面积。
•将组合图形分解为几个简单的图形,其中有部分图形可以合并为更简单的图形。
计算出合并后的简单图形的面积再减去重叠部分的面积即为组合图形的面积。
3.练习(1)将所给的图形分解为若干简单图形,并计算每个简单图形的面积,最后将它们相加得到组合图形的面积。
(2)通过练习,提高学生的对于组合图形面积计算方法的熟练度和速度。
3.2.3 辅导针对学生在练习过程中出现的问题,进行辅导解释,让学生理解并掌握所学知识。
3.2.4 小结对本课程所讲内容进行小结,强化学生的记忆和理解。