组合图形的面积计算

小学五年级数学《组合图形面积的计算》优秀教案三篇组合图形面积的计算是平面图形知识在小学阶段的综合应用。

计算一个组合图形的面积，有时可以有多种方法，下面就是我给大家带来的小学五年级数学《组合图形面积的计算》优秀教案三篇，希望能帮助到大家!小学五年级数学《组合图形面积的计算》优秀教案一教学目标：1、知道求组合图形的面积就是求几个图形面积的和(或差);能正确地进行组合图形面积计算，并能灵活思考解决实际问题。

2、注重对组合图形的分析方法与计算技巧，有利于提高学生的识图能力、分析综合能力与空间想象能力。

教学方法：讲解法、演示法教学过程：一、割补法这类方法一般是从组合图形中分割成几种不同的基本图形，这类图形的阴影部分面积就是求几个基本图形面积之和(或者差)。

Ppt演示变化过程，并出示解题过程。

二、等积变形法。

这类方法是将题中的条件或问题替换成面积相等的另外的条件或问题，使原来复杂的图形变为简单明了的图形。

Ppt演示变化过程，并出示解题过程。

三、旋转法。

这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图。

Ppt演示变化过程，并出示解题过程。

四、小结方法求组合图形面积可按以下步骤进行1、弄清组合图形所求的是哪些部分的面积。

2、根据图中条件联想各种简单图形的特征，看组合图形可以分成几块什么样的图形，能否通过割补、等积变形、旋转等方法使图形化繁为简。

小学五年级数学《组合图形面积的计算》优秀教案二教学内容：《义务教育课程标准实验教科书数学》(人教版)五年级上册“组合图形的面积”教学目标：1、明确组合图形的意义，掌握用分解法或添补法求组合图形的面积。

2、能根据各种组合图形的条件，有效地选择计算方法并进行正确的解答。

3、渗透转化的教学思想，提高学生运用新知识解决实际问题的能力，在自主探索活动中培养他们的创新精神。

教学重点：在探索活动中，理解组合图形面积计算的多种方法，会利用正方形、长方形、平行四边形、三角形、梯形这些平面图形面积来求组合图形的面积。

组合图形的面积（二）一.巩固旧知长方形面积= 正方形面积=平行四边形面积= 三角形面积=梯形的面积=二.当堂小启发组合图形多种多样、千变万化，求组合图形面积的方法也多种多样。

许多图形问题，只靠原图形上已有的线段很难发现解题思路，需要添加一条或几条原图形上没有的线段，在图形与图形之间搭起“桥梁”，这样就可以发现图形与图形之间、问题与条件之间的关系，从而找到解题的思路,这种求组合图形面积的方法我们称之为添辅助线求面积。

三. 经典例题例1：如右图，是由两个正方形组成的图形，求阴影部分的面积。

（单位：厘米）自我尝试老师解析小试牛刀如下图所示，阴影部分的面积比空白的直角三角形的面积大40平方厘米，求三角形的面积。

例2：正方形ABCD的边长是4厘米，长方形DEFG的长DG为5厘米，长方形的宽DE是多少厘米？自我尝试老师解析小试牛刀如图，E，F是平行四边形ABCD中BC，CD边的中点，求阴影部分的面积。

(单位:厘米)四. 举一反三1、有一个长方形，如果长增加8米，面积就增加64平方米；如果宽增加4米，面积也增加64平方米。

原来长方形的面积是多少平方米？2、一个正方形,一边截去6厘米，另一边截去2厘米，剩下的长方形面积比原正方形面积少68平方厘米，求原正方形的边长。

3、如图，三角形ABC的面积是24平方厘米，且BE=2EC，D，F分别是AB，CD的中点，那么阴影部分的面积是多少？4、平行四边形ABCD中，AE=EF=FB，AG=2CG，三角形GEF的面积是6平方厘米，平行四边形的面积是多少平方厘米？5、正方形ABCD的一条对角线BD被等分成三等份，每份长1厘米，E、F是等分点，AG和HC是平行线，求正方形ABCD的面积。

6、长方形ABCD的面积为36平方厘米，E、F、G分别是AB、BC、CD的中点，H 为AD边上任意一点，问：阴影部分的面积是多少？五.大显身手A：如右图，求四边形ABCD的面积。

（单位：厘米）B：求斜边是3厘米的等腰直角三角形的面积。

组合图形的面积公式许多天文学家和数学家经常发现，天文和数学形状的总体面积可以通过不同的图形组合而成。

经常的形状可以是三角形、正方形、圆形、多边形和椭圆形等。

为了计算组合图形的总体面积，我们需要知道每个组件面积的公式，以及它们如何组合在一起。

下面，我将介绍组合图形的常用面积公式。

1、三角形面积公式三角形的面积可以通过三角形的底边长与其高的乘积来确定。

如果三角形的底边长是a，其高为h，则可以通过以下公式确定三角形的面积：S = 1/2 a h2、正方形面积公式正方形的面积可以通过其边长乘积来确定。

如果正方形的边长是a，则可以通过以下公式确定正方形的面积：S = a a3、圆形面积公式圆形的面积可以通过圆形的半径乘以π来确定。

如果圆形的半径是r，则可以通过以下公式确定圆形的面积：S = r r4、多边形面积公式多边形的面积可以通过多边形的顶点与其中心的距离乘积来确定。

如果多边形的顶点是A，它的中心距离为d，则可以通过以下公式确定多边形的面积：S=1/2 A d5、椭圆形面积公式椭圆形的面积可以通过椭圆形的长轴与短轴的乘积来确定。

如果椭圆形的长轴是a，它的短轴是b，则可以通过以下公式确定椭圆形的面积：S = a b以上就是组合图形的常用面积公式。

当在计算更复杂的组合形状时，可以使用多边形分解法来计算总面积。

这种方法可以将复杂的多边形分解为若干较小的多边形，然后在每个小多边形上应用前面提到的面积公式，最后将每个小多边形的面积相加，从而获得总面积。

总之，组合图形的面积计算可以通过不同图形的面积公式进行计算，也可以通过多边形分解方法来计算总面积。

不同结构的图形可以有不同的面积计算方法，但基本思路都是将复杂的形状分成若干个简单的形状，以最简单的形状的面积公式为基础，求出复杂形状的面积值。

通过学习和研究以上计算面积的方法，可以帮助我们更好地解决天文学和数学中的组合图形的面积计算问题。

组合图形面积计算技巧“十法"一、相加相减法【点拨】：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，相加求出整个图形的面积.或者将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.【例题1】：求组合图形的面积。

（单位：厘米）【分析与解答】：上图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.4÷2=2（米）4×4+2×2×÷2=（平方厘米）【例题2】：长方形长6厘米，宽4厘米，求阴影部分的面积。

【分析与解答】：上图中，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.4÷2=2（米）6×4-2×2×÷（平方厘米）二、用比例知识求面积【点拨】：利用图形之间的比例关系解题。

【例题3】一块长方形耕地，它由四个小长方形拼合而成，其中三个小长方形的面积分别为15、18、30公顷，图中阴影部分的面积是多少？【分析与解答】：因为阴影部分也是一长方形，所以只要求出它的长、宽是多少就行，为此设它的长、宽分别为a、b，面积为18公顷的长方形的长、宽分别为c、d.直接按比例关系来理解。

因为（a×c）:(d×c)=(a×b):(d×b),a:d=15：18=阴影面积：30，阴影面积为15×30÷18＝25（公顷）。

三、等分法【点拨】：根据所求图形的对称性，将所求图形面积平均分成若干份，先求出其中的一份面积，然后求总面积。

【例题4】：求阴影部分的面积（单位：厘米）【分析与解答】：把原图平均分成八分，就得到下图，先求出每个小扇形面积中的阴影部分：×22÷4－2×2÷2=(平方厘米)阴影部分总面积为：×8=(平方厘米)四、等积变形【点拨】：将题中的条件或问题替换成面积相等的另外的条件或问题，使原来复杂的图形变为简单明了的图形。

组合图形面积6种办法组合图形面积是数学中一个重要的概念，它可以帮助我们计算复杂图形的面积。

组合图形面积的计算有很多种方法，下面我们就来介绍一下这六种计算组合图形面积的方法。

首先，我们可以使用分割法来计算组合图形的面积。

这种方法是将复杂图形分割成若干个简单图形，然后分别计算每个简单图形的面积，最后将这些简单图形的面积相加，就可以得到复杂图形的面积。

其次，我们可以使用三角形面积公式来计算组合图形的面积。

这种方法是将复杂图形分割成若干个三角形，然后分别计算每个三角形的面积，最后将这些三角形的面积相加，就可以得到复杂图形的面积。

第三，我们可以使用积分法来计算组合图形的面积。

这种方法是将复杂图形的面积看作一个函数，然后使用积分法来计算这个函数的积分，最后得到复杂图形的面积。

第四，我们可以使用梯形面积公式来计算组合图形的面积。

这种方法是将复杂图形分割成若干个梯形，然后分别计算每个梯形的面积，最后将这些梯形的面积相加，就可以得到复杂图形的面积。

第五，我们可以使用平行四边形面积公式来计算组合图形的面积。

这种方法是将复杂图形分割成若干个平行四边形，然后分别计算每个平行四边形的面积，最后将这些平行四边形的面积相加，就可以得到复杂图形的面积。

最后，我们可以使用椭圆面积公式来计算组合图形的面积。

这种方法是将复杂图形分割成若干个椭圆，然后分别计算每个椭圆的面积，最后将这些椭圆的面积相加，就可以得到复杂图形的面积。

以上就是六种计算组合图形面积的方法，它们都可以帮助我们计算复杂图形的面积，但是要根据实际情况选择合适的方法。

只有掌握了这些方法，才能更好地计算组合图形的面积。

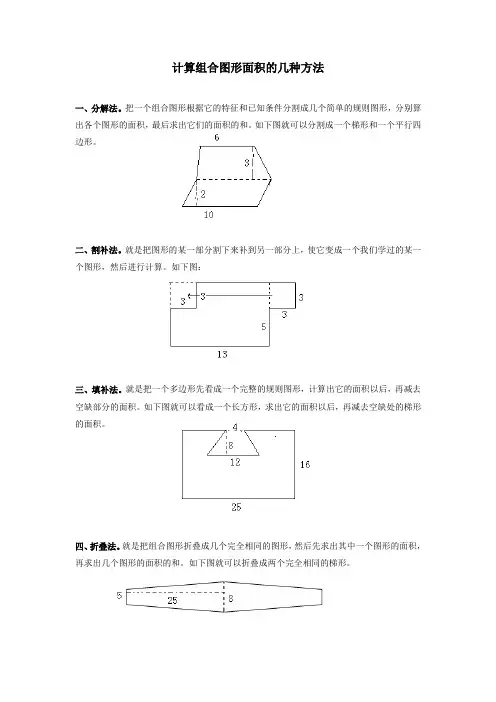
计算组合图形面积的几种方法
一、分解法。

把一个组合图形根据它的特征和已知条件分割成几个简单的规则图形，分别算出各个图形的面积，最后求出它们的面积的和。

如下图就可以分割成一个梯形和一个平行四边形。

二、割补法。

就是把图形的某一部分割下来补到另一部分上，使它变成一个我们学过的某一个图形，然后进行计算。

如下图：
三、填补法。

就是把一个多边形先看成一个完整的规则图形，计算出它的面积以后，再减去空缺部分的面积。

如下图就可以看成一个长方形，求出它的面积以后，再减去空缺处的梯形的面积。

四、折叠法。

就是把组合图形折叠成几个完全相同的图形，然后先求出其中一个图形的面积，再求出几个图形的面积的和。

如下图就可以折叠成两个完全相同的梯形。

五、旋转法。

就是把原来图形进行一次或几次旋转以后，使它变成我们熟悉的新图形，然后进行计算。

如下图就可以利用旋转法，使阴影部分变成一个三角形。

计算一个组合图形的面积，有时可以有多种方法，我们要根据图形的特征和已知条件以及整体与部分的关系，选择最佳的方法。

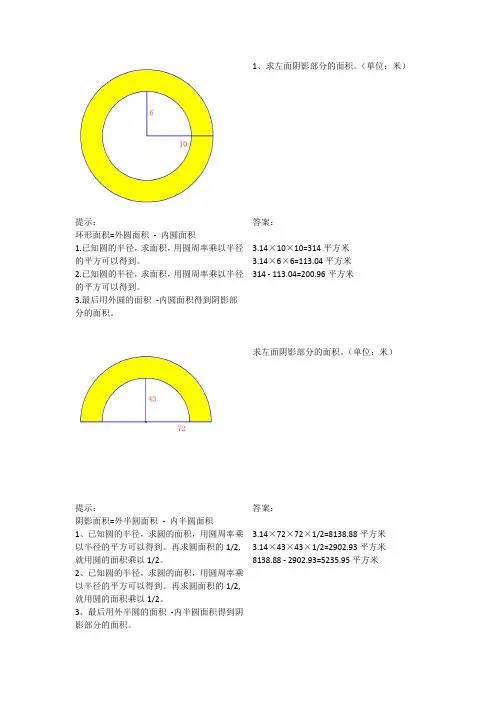
1、求左面阴影部分的面积。

（单位：米）提示：环形面积=外圆面积-内圆面积1.已知圆的半径，求面积，用圆周率乘以半径的平方可以得到。

2.已知圆的半径，求面积，用圆周率乘以半径的平方可以得到。

3.最后用外圆的面积-内圆面积得到阴影部分的面积。

答案：3.14×10×10=314平方米3.14×6×6=113.04平方米314 - 113.04=200.96平方米求左面阴影部分的面积。

（单位：米）提示：阴影面积=外半圆面积-内半圆面积1、已知圆的半径，求圆的面积，用圆周率乘以半径的平方可以得到。

再求圆面积的1/2,就用圆的面积乘以1/2。

2、已知圆的半径，求圆的面积，用圆周率乘以半径的平方可以得到。

再求圆面积的1/2,就用圆的面积乘以1/2。

3、最后用外半圆的面积-内半圆面积得到阴影部分的面积。

答案：3.14×72×72×1/2=8138.88平方米3.14×43×43×1/2=2902.93平方米8138.88 - 2902.93=5235.95平方米求左面阴影部分的面积。

（单位：米）提示：阴影部分面积可以用正方形的面积减去圆形的面积。

1、求正方形面积已知正方形的边长，求面积，用边长乘以边长可以得到。

2、求圆面积已知圆的直径，求面积，先用直径除以2得到半径，再用圆周率乘以半径的平方可以得到。

3、求阴影面积，用正方形面积减去圆的面积答案：1、正方形面积32×32=1024平方米2、圆面积32÷2=16米3.14×16×16=803.84平方米3、阴影面积1024- 803.84=220.16平方米求左面阴影部分的面积。

（单位：米）提示：阴影部分面积可以三角形面积减去右空白面积。

三角形面积是长方形面积的一半，右空白面积是长方形面积与半圆面积差的一半。

长方形的长就是圆的直径，宽是圆的半径。

组合图形的面积知识集结知识元组合图形的面积知识讲解1.1、各图形面积公式：2、组合图形：有几个简单的图形拼出来的图形，我们把它们叫做组合图形。

3、计算组合图形的面积：（1）分割法，即将这个图形分割成几个基本的图形。

分割图形越简洁，其解题的方法也将越简单，同时又要考虑分割的图形与所给条件的关系。

（2）添补法，即通过补上一个简单的图形，使整个图形变成一个大的规则图形。

5.计算组合图形阴影部分的面积：等于组合图形的面积减去空白部分的面积。

例题精讲组合图形的面积例1.'求下图中涂色部分的面积。

（单位：cm）求阴影部分面积。

如图，小正方形ABCD的边长是5cm，大正方形CEFG的边长是10cm，求图中阴影部分面积。

'例3.'在一块梯形菜地里，有一条宽约1m的小路（如图），每平方米产菜4.5kg，这块菜地共产菜多少千克？'例4.'如图是某工艺品的展开图。

它的面积是多少？（单位：cm）'例5.'图4由3个边长是6的正方形组成，则图中阴影部分的面积是________。

计算如图阴影部分的面积．（单位：厘米）'例7.'如图，2个大正方形、2个中正方形和1个小正方形紧挨着排在一起，其中大中小正方形的边长分别为3、2、1，那么阴影部分的面积是多少？'例8.'如图，三角形ABC的面积为10，AD与BF交于点E，且AE=ED，BD=CB，求图中阴影部分的面积和．'例9.'求图形中阴影部分的面积．（单位：dm）例10.'如图中，ADEF是一个长8CM，宽5CM的长方形，ABCD为直角梯形，BEF为直角三角形，图中阴影部分的面积是多少？'探索活动：成长的脚印知识讲解计算不规则图形的面积：估计、计算不规则图形面积的内容主要是以方格图作为背景进行估计与计算的，所以借助方格图能帮助建立估计与计算不规则图形面积的方法。

求组合图形面积的十种解法
求组合图形面积是一个典型的几何问题，为了解决这一问题，可以使用以下十种解法：
1、分法法：将复杂图形分解成若干简单图形，然后求其各自的面积，最后求总和即可。

2、叠加法：如果复杂图形与某一简单图形有公共部分，那么就可以把复杂图形和简单图
形叠加在一起，求出叠加图形的面积，然后用叠加图形的面积减去简单图形的面积即可求
得复杂图形的面积。

3、分数解法：如果复杂图形的面积太难求，可以采用分数解法，先把复杂图形分成若干
等份，每份更容易求面积，最后把求的的结果加起来即可。

4、数学公式法：如果复杂图形有相应的数学公式，可以利用这个公式来求复杂图形的面积。

5、经验法：一些规则复杂图形，有时候还可以借助经验法，比如正多边形，多个等腰三
角形等组合，通过一定的经验公式即可求得面积。

6、极限法：如果复杂图形不是太复杂，可以采用极限法，采用适当的空间坐标，把图形
分解成若干若干子图形，然后求得每个子图形的面积，把这些子图形的面积累加，最后就
可以求得复杂图形的面积。

7、计算机图形学法：使用计算机图形学的方法可以更准确快速地求组合图形面积。

利用
图形赋值法，先将要求面积的图形表示成点阵图，此时此刻，图形上面每个点对应着某个面积的的面积，然后将每个点的面积相加，就可以求出总的面积了。

8、三角函数法：如果所求复杂图形是圆形，那么可以采用三角函数法，根据圆心角的计
算公式，计算复杂图形的圆形面积。

9、渐近法：渐近法可以用来求一类复杂图形的面积，它将复杂图形分割为若干小正方形，再根据小正方形和图形的相似度，算出复杂图形面积接近的结果。

10、变换法：变换法是将复杂图形变换为简单图。

小学数学五年级上册
《组合图形的面积》资料计算公式
长方形：
{长方形面积=长×宽}
正方形：
{正方形面积=边长×边长}
平行四边形：
{平行四边形面积=底×高}
三角形：
{三角形面积=底×高÷2}
梯形：
{梯形面积=（上底+下底）×高÷2}
圆形（正圆）：
{圆形（正圆）面积=圆周率×半径×半径}
圆环：
{圆形（外环）面积={圆周率×（外环半径^2-内环半径^2）} 扇形：
{圆形（扇形）面积=圆周率×半径×半径×扇形角度/360}
长方体表面积：
{长方体表面积=（长×宽+长×高+宽×高）×2}
正方体表面积：
{正方体表面积=棱长×棱长×6}
球体（正球）表面积：
{球体（正球）表面积=圆周率×半径×半径×4}
椭圆
(其中π(圆周率，a,b分别是椭圆的长半轴，短半轴的长). 半圆：
(半圆形的面积公式=圆周率×半径的平方÷2）。

数学 - 组合图形面积的计算引言在数学中，组合图形是指由多个基本图形组合而成的复合图形。

而要计算组合图形的面积，需要先计算组合图形中各个基本图形的面积，然后将这些面积相加。

本文将介绍如何计算常见的组合图形的面积。

一、矩形和正方形的面积计算矩形和正方形是最简单的组合图形，其面积的计算公式分别为：•矩形的面积：$S = l \\times w$，其中l为矩形的长，w为矩形的宽。

•正方形的面积：$S = a \\times a$，其中a为正方形的边长。

示例：假设有一个矩形，长为 5，宽为 3，那么它的面积可以通过以下计算得到：S = 5 * 3 = 15因此，该矩形的面积为 15。

二、三角形的面积计算三角形是另一个常见的组合图形，其面积的计算公式为：$S = \\frac{1}{2} \\times b \\times h$，其中b为三角形的底边长，ℎ为三角形的高。

示例：假设有一个底边长为 4，高为 6 的三角形，那么它的面积可以通过以下计算得到：S = 0.5 * 4 * 6 = 12因此，该三角形的面积为 12。

三、圆的面积计算圆是另一种常见的组合图形，其面积的计算公式为：$S = \\pi \\times r^2$，其中r为圆的半径。

需要注意的是，计算圆的面积时，需要使用 $\\pi$（圆周率）的近似值，通常取 3.14 或更精确的值。

示例：假设有一个半径为 5 的圆，那么它的面积可以通过以下计算得到：S = 3.14 * (5^2) = 78.5因此，该圆的面积为 78.5。

四、组合图形的面积计算当组合图形由多个基本图形组合而成时，其面积的计算可以通过计算各个基本图形的面积，然后将这些面积相加得到。

示例：假设有一个由一个矩形和一个三角形组成的图形，如下图所示：---------------| ▲ || ╱╲ || ╱╲ || ╱╲ || ╱______╲ || ▔ |--------------矩形的长和宽分别为 6 和 4，三角形的底边长为 4，高为 3。