投影特性.
- 格式:doc
- 大小:1.89 MB
- 文档页数:13

2-2 点、线、面的投影特性一、点的投影1、点的三面投影点是组成物体最基本的几何元素。
如图2-9所示,在三投影面体系中,由空间点A(x,y,z)分别向三投影面作正投影,得其三面投影a(x,y)、a′(x,z)、a″(y,z),即过点A分别作三投影面的垂线,其垂足即为点A的三面投影;展开H面和W面,得到点A的三视图:a 、a′长对正,a′、a″高平齐,a 、a″宽相等,如图2-10所示。
图2-9 点的三面投影图2-10 点的三视图例1 :已知空间点B的两面投影b ,b′,如图2-11所示,求其第三面投影b″。
分析:空间点B的三面投影b 、b′、b″符合“长对正,高平齐,宽相等”的投影规律。
作图: b′与b″高平齐,b与b″宽相等,则其交点即为b″。
图2-11 求点的第三面投影图2-12 求点的三面投影例2 :已知空间点D(5,4,3),如图2-12所示,求其三面投影。
分析:空间点D的三面投影分别为d(x,y)、d′(x,z)、d″(y,z),且符合“长对正,高平齐,宽相等”的投影规律。
作图:分别在三投影轴上取x1=5,y1=4,z1=3,按“长对正,高平齐,宽相等”的投影规律分别作直线段,交点即为空间点D的三面投影(d 、d′、d″)。
2、两点的相对位置空间两点的相对位置是指空间两点间前后、左右、上下的位置关系。
两点在空间的相对位置可以根据两点的坐标值来判定,如图2-13所示。
X坐标确定两点的左右位置关系。
X坐标值大的点在左;Y坐标确定两点的前后位置关系。
Y坐标值大的点在前;Z坐标确定两点的上下位置关系。
Z坐标值大的点在上。
图2-13 两点的相对位置故A点在B点的右,后,上方,即B点在A点的左,前,下方。
3、重影点及其可见性判断若空间两点在某一投影面上的投影重合,则称这两点为该投影面的重影点。
此时,这两点位于同一投射线上,且有两个坐标的值分别相等,不等值的坐标之大小可以确定重影点的可见性,即X、Y、Z坐标值大的点分别位于左方、前方、上方,为可见点,如图2-14所示。

各种位置直线的投影特性按照直线对三个投影面的相对位置,可以把直线分为三类:一般位置直线、投影面平行线、投影面垂直线。
后两类直线又称为特殊位置直线。
1.一般位置直线—与三个投影面都倾斜的直线一般位置直线的投影特性如下(图3-10):1)三面投影都倾斜于投影轴。
2)投影长度均比实长短,且不能反映直线与投影面倾角的真实大小。
直线对H、V、W的倾角分别用α、β、γ表示。
投影面平行线——平行于一个投影面,倾斜于另外两个投影面的直线(1)投影面平行线又可分为三种:平行于V面的直线叫正平线;平行于H面的直线叫水平线;平行于W面的直线叫侧平线。
图3-11正平线的投影特性(2)正平线的投影特性(图3-11):1)直线平行于V面,则V面投影与直线本身平行且等长,a'b'=AB;2)正平线上各点到V面的距离即Y坐标都相等,则a b∥OX, a"b"∥OZ。
3)AB与H面的倾角为α,由于AB平行V面,所以AB与V面的倾角为0。
又因为AB ∥a'b',a b∥OX轴,所以,a'b'与OX轴的夹角为α,同理a'b'与OZ轴的夹角即为AB与W面的倾角γ。
表3-1为投影面平行线的投影特性。
表3-1 投影面平行线的投影特性名称轴测图投影图投影特性正平线(1)a'b'=AB, 反映α、γ角(2)a b//OX轴, a"b"//OZ轴水平线(1) cd=CD ,反映β、γ角(2)c'd'//OX轴, c"d"//O YW轴侧平线(1) e"f"=EF, 反映α、β角(2)e'f'//OZ轴,ef//O YH轴投影面平行线的投影特性:1.直线在与其平行的投影面上的投影,反映该线段的实长和与其他两个投影面的倾角2.直线在其他两个投影面上的投影分别平行于相应的投影轴,且比线段的实长短投影面垂直线——垂直于一个投影面,平行于另外两个投影面的直线1)投影面垂直线又可分为三种:垂直于V面的直线叫正垂线;垂直于H面的直线叫铅垂线;垂直于W面的直线叫侧垂线。

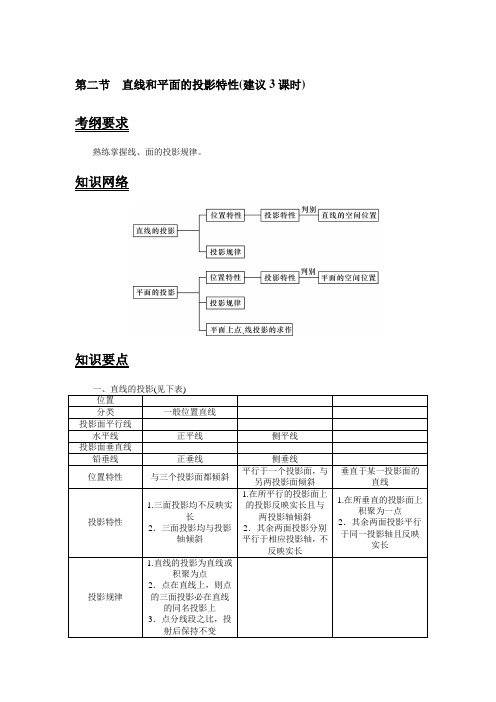
第二节直线和平面的投影特性(建议3课时) 考纲要求熟练掌握线、面的投影规律。
知识网络知识要点二、平面的投影(见表)典型例题【例1】 根据下图中直线的两面投影,判别直线的空间位置。
【解题指导】 (a )图中,直线EF 的正面投影平行OX 轴说明z E =z F ,水平投影也平行于OX 轴说明y E =y F ,则E 、F 两点的侧面投影e ″、f ″为一对重影,即E 、F 两点的侧面投影重合在一起,所以EF 为侧垂线。
同理,(d )图中直线GH 为铅垂线。
(b )图中,直线EF 的正面投影e ′f ′∥OX 轴,则e ′f ′上任一点到OX 轴的距离均相等,即e ′f ′上任一点的z 坐标都相等,所以EF 上任一点到H 面距离均相等,即EF ∥H 面。
由侧面投影及正面投影可知,EF 上任两点的x 、y 坐标值均不相等,所以EF 为水平线。
同理(c )图中直线GH 为一般位置直线。
【答案】 (a )EF 为侧垂线;(b )EF 为水平线;(c )GH 为一般位置直线;(d )GH 为铅垂线 【点评】 根据直线段的两面投影判别其空间位置,首先要熟练掌握各种位置直线的投影特性,其次要分析所给投影的特性,进而判别出直线的空间位置。
如果直线的两面投影都与投影轴平行且平行于同一个投影轴,则该直线为投影面垂直线;如果直线的两面投影平行于不同投影轴,则该直线为投影面平行线。
【例2】判断点M、N是否在平面ABC上。
【解题指导】线是由点构成的,面也是由点构成的。
某点是否在平面上,要先看点是否处于平面内的某一确定的直线上。
粗一看N点的两面投影都在平面的一条直线的投影上,其实N点正面投影与AC边上的1点是重影点,水平投影与BC边上的2点是重影点。
对于M点连接b′m′交a′c′于e′,通过投影关系,可以看出,M点的水平面投影m也在bc 上,所以M点在平面ABC上。
【答案】M点在平面ABC上,N点不在平面ABC上。
【例3】完成平面图形ABCDE的水平投影。


简述直线对于一个投影面的投影特性。
直线是几何学中最简单的一种形状,它是由两个点连接而成的无限长的线条,通常被用作画图和图表的基本线条。
在投影学中,直线对一个投影面的投影特性是非常重要的。
直线的投影是指,将物体的某个棱面的线投影到一个投影面上,形成的线段形式的影像。
在这种情况下,将物体的棱面直线投影到投影面上,得到的就是它的投影线。
投影线是一种现象,指将它所表示的直线投影到投影面后,形成一个投影面上沿着投影线方向滚动的直线。
投影面上的直线不会发生缩放和旋转,而是会沿着空间中的原生方向滚动,并保持原来的长度。
在平行投影法中,投影直线的作用就是保持元件的相对大小,保持它们的形状。
投影直线在投影面上所表示的图形,不会因为视点的变化而发生变化,体现出一个重要特征平行投影。
投影直线还有另一个重要特点透视投影。
当视点与物体之间有一定的位置关系时,投影线会形成一个透视投影。
在此情况下,投影直线会因视点的改变而发生变形,在投影面上形成一种新的形象远离视点的直线元件会更加细长,接近视点的元件则会更加宽大。
投影直线的起点和终点一般位于投影的点集上,从投影的点集的某点到另一个投影的点集的某点,即是投影直线。
由此,投影直线可以被用来表示一个物体中的某个棱面的形状,同时它也可以用来表示不同物体之间的联系,如物理学中的相关关系。
总之,直线对于一个投影面的投影特性非常重要,它可以保持物
体的相对大小和形状,可以用来表示物体中棱面的形状,也可以用来形象地表示不同物体之间的关系。
它所起的作用,是无可替代的。
正投影的投影特性有哪三种正投影的特点有真实性、积聚性和类似性。
正投影是指平行投射线垂直于投影面。
由一点放射的投射线所产生的投影称为中心投影,由相互平行的投射线所产生的投影称为平行投影。
特点1、真实性当直线段平行于投影面时,直线段与它的投影及过两端点的投影线组成一个
正投影的特点有真实性、积聚性和类似性。
正投影是指平行投射线垂直于投影面。
由一点放射的投射线所产生的投影称为中心投影,由相互平行的投射线所产生的投影称为平行投影。
特点
1、真实性
当直线段平行于投影面时,直线段与它的投影及过两端点的投影线组成一个矩形,因此,直线的投影反映直线的实长。
当平面图形平行与投影面时,不难得出,平面图形与它的投影为全等图形,即反映平面图形的实形。
2、积聚性
当直线垂直于投影面时,过直线上所有点的投影线都与直线本身重合,因此与投影面只有一个交点,即直线的投影积聚成一点。
当平面图形垂直于投影面时,过平面上所有点的投影线均与平面本身重合,与投影面交于一条直线,即投影为直线。
3、类似性
我们还看到,当直线倾斜于投影面时,直线的投影仍为直线,但不反映实长;当平面图形倾斜于投影面时,在该投影面上的投影为原图形的类似形。
3. 投影特性:(1)平面在它所垂直的投影面上的投影积聚为一斜直线,并且该投影与投影轴的夹角等于该平面与相应投影面的倾角;(2)平面的其它两个投影不是实形,但有相仿性。
4. 垂直面空间位置的判别:两框一斜线,定是垂直面;斜线在哪面,垂直哪个面。
3.3.2.3 一般位置平面1. 定义:与三个投影面均倾斜的平面,称为一般位置面。
2. 投影图:一般位置面的三个投影都呈倾斜位置,如图3-32所示。
图3-32 一般位置平面的投影因为一般位置平面与三个投影面都倾斜,所以平面图形的三个投影均不反映实形,也无积聚性,但具有原图形的相仿性。
在图3-31(b)中,三面投影Δa′b′c′、Δa bc、Δa″b″c″均比原几何图形ΔABC小。
3. 投影特性:平面的三个投影既没有积聚性,也不反映实形,而是原平面图形的类似形。
4. 一般位置线的判别:三个投影三个框,定是一般位置面。
3.3.3 平面上的点和直线3.3.3.1平面上的点3.3.3.2平面上的直线一直线若通过平面内的两点,则此直线必位于该平面上,由此可知,平面上直线的投影,必定是过平面上两已知点的同面投影的连线。
若点在直线上,直线在平面上,则点必定在平面上。
在平面上取点,首先要在平面上取线。
而在平面上取线,又离不开在平面上取点。
【例3-14】已知ΔABC平面上点M的正面投影m′,求它的水平投影图m(图3-33(a))。
分析:点M在ΔABC平面上,必然经过平面上一直线;m′和m应分别位于该直线的同名投影上。
因此,要补全点M的投影,需先在ΔABC内作出过点M的辅助线。
作图方法一:(a)已知条件(b)在正面投影上过a′和(c)自m′向下引OX轴的m′作辅助线a′m′,并延长垂线,与ad相交于m,与b′c′相交于d′;自d′向下m即为所求。
引OX轴的垂线,与bc相交于d,连ad;图3-33 补出平面上点M的水平投影作图方法一作图方法二(图3-35(c))(a)已知条件(b)过m′作辅助线e′f′,使(c)自m′向下引OX轴的e′f′∥a′c′;并与b′c′相交于垂线,与ef相交于m,me′;自e′向下引OX轴的垂即为所求。
线,与bc相交于e,作ef∥ac;;图3-34 补出平面上点M的水平投影作图方法二3.3.4 平面内的特殊位置直线平面内的直线,其位置各不相同。
其中常用的有平面上的正平线和水平线,以及与投影面成倾角最大的直线——最大斜度线,这些线统称为平面内投影面的特殊位置直线。
3.3.4.1平面内的正平线和正平线要在一般面ABC上作一条正平线,可根据正平线的H投影是水平的这个投影特点,先在ABC的水平投影上作一任意水平线,作为所求正平线的H投影,然后作出它的V投影,如图3-35所示。
在ABC上作水平线,也要抓住它的V投影一定水平的投影特点,作图步骤如图3-36所示。
图3-36 在平面上作水平线3.3.4.2平面内的最大斜度线平面上对某投影面的最大斜度线,就是在该面上对该投影面倾角最大的一条直线。
它必然垂直于平面上平行于该投影面的所有直线。
如图3.50(a)所示,平面P上的直线AB,是平面P上对H面倾角最大的直线。
图3-38 平面内对H面的最大斜度线要作△ABC对H面的最大斜度线,如图3-39 (a)所示。
图3-39 (b)中BK垂直于正平线AD,所以它就是面上对V面的最大斜度线。
(a)H面的最大斜度线(b)V面的最大斜度线图3-39 作平面上的最大斜度线3.3.5 直线与平面相交、平面与平面相交直线与平面相交有一个交点,交点是公共点,它即在直线上又在平面上;平面与平面相交有一条交线,交线是两平面的公共线,即同时位于两个平面上,求交点、交线,利用共有性求解。
3.3.5.1特殊情况相交特殊情况相交,是指参与相交的无论是直线还是平面,至少有一个元素对投影面处于特殊位置,它在该投影面上的投影有积聚性。
在投影作图中,则利用积聚性可以直接确定交点或交线的一个投影,而后再利用线上定点或面上定点的方法求交点的第二个投影,利用面上定线的方法求出交线的第二投影。
(1)直线与平面相交图3- 40所示为直线AB与铅垂面P相交。
铅垂面的水平投影具有积聚性,积聚投影与直线的水平投影的交点即为交点的投影,而交点的另一投影必在该直线的另一投影上。
图3-40 一般直线与铅垂面相交直线与平面相交后,直线便从平面的一侧到了平面的另一侧(以交点为分界)。
假定平面是不透明的,则沿投射方向观察直线时,位于平面两侧的直线,一侧直线看得见,另一侧直线则被平面遮挡而看不见,这就有判别可见性的问题。
在作图时,要把看得见的直线画成粗实线,把看不见的直线画成虚线,交点是可见与不可见的分界点。
【例3-17】求一般位置直线AB与铅垂面P的交点K。
分析:因为平面P是一铅垂面,其水平投影p有积聚性,所以的水平投影k在p上,而交点K又在直线AB上,所以K的水平投影应在直线AB的水平投影ab上。
因此,直线AB的水平投影ab与平面P的水平投影p的交点便是交点K的水平投影k。
根据点在直线上的投影特点,可在a′b′上求出k′。
作图方法(a)已知条件(b)在直线AB的水(c)自k向上作OX (c)判断可见性。
平投影ab和平面的轴垂线,与直线AB积聚投影p的交点的正面投影a′b′交于处标出交点的水平k′,k′为交点的正面投影k;投影。
图3-41 求作一般位置直线与铅垂面的交点因为平面P为铅垂面,所以看水平投影时直线都看得见(未被平面遮挡);从水平投影上可以看出,ak在p面之前,所以其正面投影a′k′为可见,b′k′与p′重影部分为不可见。
【例3-18】已知铅垂线MN和一般位置平面ΔABC相交,求它们的交点K。
分析:因为铅垂线MN的水平投影有积聚性,所以位于铅垂线MN上的交点K 的水平投影k必然与铅垂线的水平投影m(n)重合。
交点的水平投影的位置确定之后,就可以利用面上定点的方法求出交点的正面投影k′。
(a)已知条件(b)在铅垂线MN的水(c)在平面内过k点作(d)判断可见性平积聚投影m(n)上,辅助线ad,并作出它标出交点K的水平投影的正面投影a′d′,a′d′与k;m′n′的交点k′即为交点K的正面投影。
图3-42 求作铅垂线与一般位置平面的交点因为铅垂线MN的水平积聚为一个点,不判断可见性,只需判断V面投影的可见性。
利用两条直线交叉对V面的重影点,来判断其正面投影的可见性。
在V面投影上,直线上的点Ⅰ(1′,1)和AB上的点Ⅱ(2′,2),它们的正面投影重合,,从水平投影可以看出,ab上的点2在后,mn上的点1在前,故k′n′为可见,m′k′和Δa′b′c′的重影部分为不可见,画虚线。
(2)平面与平面相交图3- 43所示为铅垂面ΔABC与一般位置平面ΔEFG相交。
铅垂面ΔABC的水平投影具有积聚性,积聚投影与一般位置平面ΔEFG的水平投影重合部分,即为交线的投影,而交线的另一投影必在该平面的另一投影上。
图3-43 铅垂面与一般平面相交两平面相交后,假定两平面都是不透明的,则它们必定互相遮挡,而且不管对哪个平面来说,都是以交线为分界,被遮挡的部分看不见,未被遮挡的部分看得见。
交线是可见的。
【例3-19】求作铅垂面ΔABC与一般位置平面ΔEFG的交线MN。
分析:因为铅垂面ΔABC的水平投影具有积聚性,所以位于铅垂面上的交线其水平投影必定积聚在铅垂面的积聚投影上;交线的水平投影确定后,可利用一般位置平面上定线的方法作出交线的正面投影。
(a)已知条件(b)在铅垂面的积聚投影(c)自m和n分别向上(c)可见性的判断Δabc上标出交线MN 作OX轴的垂线,与g′f′的水平投影mn(端点和g′e′相交于m′和n′;M和N实际上是GF连接m′n′,m′n′即为交边和GE边与ΔABC线MN的正面投影。
平面的交点);图3-44 求作铅垂面与一般位置平面的交线因为ΔABC是铅垂面,所以看水平投影时,Δabc积聚成直线,Δefg平面都看得见;看正面投影时,以交线m′n′为分界,Δe′f′g′的g′m′n′部分在铅垂面的后面,被铅垂面遮挡的部分为看不见,Δe′f′g′的e′f′m′n′部分在铅垂面的前面,未被遮挡为看得见。
【例3-20】求作水平面ΔABC与正垂面P的线MN(图3-45(a))。
分析:由于水平面ΔABC与正垂面P的正面投影均具有积聚性,而交线又是两平面共有线,所以Δa′b′c′与p′的交点,即为交线的正面投影,故这两平面的交线是一条正垂线。
作图方法(a)已知条件(b)在水平面ΔABC的正(c)过m′(n′)向下作轴(d)可见性的判断面投影Δa′b′c′与正垂面的垂线,垂线在Δabc与P的正面投影p′的交点p的重影部分范围内的线处标注出两平面交线段mn,即是交线MN的MN的正面投影m′(n′);水平投影。
图3-45 求作水平面与正垂面的交线因为ΔABC是水平面,P是正垂面,所以V面投影不需判断可见性。
交线MN把平面ΔABC和P各分为两部分,从V面投影可以看出,MNAB在平面P的下方,MNC在平面P的上方,所以mnab与p重影部分为不可见,mnc和p重影部分为可见。
交线mn为可见当两个铅垂面相交,其交线为一铅垂线。
如图3-46所示,两铅垂面的水平投影有积聚性,而交线具有共有性,所以积聚投影的交点即为交线的水平投影,交线是一条铅垂线。
(a)直观图(b)投影图图3-46 两铅垂面相交同理,两个正垂面相交,交线为一条正垂线;两个侧垂面相交,交线为一条侧垂线。
学员可根据上图绘出这两种情况的投影图。
3.3.5.2一般情况相交一般情况相交,是指参与相交的无论是直线还是平面在投影体系中均处于一般位置。
可通过作辅助面的方法求出交点或交线的投影。
在这种情况下,它们的投影无积聚性,直线与平面交点投影、平面与平面交线的投影不能利用积聚性求出。
通常可通过作辅助面的方法求出交点或交线的投影。
下面我们讲一下利用辅助面法求交点和交线的作图方法。
(1)直线与平面相交图3-47(a)所示为一般位置直线EF和一般位置平面ΔABC相交。
为求EF和平面ΔABC交点的投影,见图3-47(b)所示,可通过直线EF作辅助平面P,与平面ΔABC的交于直线MN,同在平面P上的两直线EF和MN(MN 为ΔABC上的一条直线),必有一交点K,即为直线EF与平面ΔABC的交点。
因为K在EF上,又在MN上,所以必在EF和平面ΔABC,即K为EF与平面ΔABC的公有点,亦即所求的交点。
这种求交点的方法称为辅助平面法。
(a)(b)图3-47 一般直线与一般平面相交通过辅助平面法求交点,具体分为三个步骤:(1)过已知直线作一辅助平面。
为使作图简单,辅助平面应选择投影面的垂直面,如正垂面、铅垂面等;(2)求出辅助平面和已知平面的交线;(3)已知直线和上述交线的交点,即为直线与平面的交点。