2018考研数学重点：弧长曲线积分的计算

y O
1
x
高等数学
目录
上页
下页
返回
结束
二、对弧长的曲线积分的计算
基本思路: 求曲线积分

L
f ( x, y ) d s
转化
计算定积分 d s (d x) 2 (d y ) 2
x (t ) ( t ) (1)若L: y (t )
2 2 d s (t ) (t )dt
L
L1
xds xds
0 x
1
y x2 yx L1 (1,1) L2
x
0 x
1
O
L1 : y x, 0 x 1
2 1 (5 5 1) 2 12
高等数学
L2 : y x2 , 0 x 1
目录
上页
下页
返回
结束
补充: 设在 xoy 面上有一分布着质量的曲线弧 L, 其线密度为 ( x, y ), 用对弧长的曲线积分分别表达:
山东交通学院高等数学教研室
一、对弧长的曲线积分的概念与性质
1 引例: 曲线形构件的质量 假设曲线形细长构件在 xoy 面上对应 弧段为AB ,
其线密度为连续函数
求此构件的质量.
是常数, 且弧长为 s, 则其质量为 不是常数, 仍可采用 “分割, 作近似, 求和, 取极限”方法.
B
M n1
y
m

在 上的曲线积分:
连续
(3) 若 是空间光滑曲线弧， 类似可定义函数
L f ( x, y) ds存在.

L
f ( x, y, z ) d s lim f (i ,i , i ) si

则有
a
b
f ( x, ( x) ) 1 2 ( x) d x
如果方程为极坐标形式: L : r r ( ) ( ), 则



f ( r ( ) cos , r ( ) sin ) r 2 ( ) r 2 ( ) d
推广: 设空间曲线弧的参数方程为
Mk sk M k 1

如果 L 是 xoy 面上的曲线弧 , 则定义对弧长的曲线积
分为
lim L f ( x, y ) ds 0 f ( k ,k )sk
k 1 n
如果 L 是闭曲线 , 则记为 f ( x, y ) ds . L 思考: (1) 若在 L 上 f (x, y)≡1, 问 d s 表示什么?
L f ( x, y )ds


f ( r ( ) cos , r ( ) sin ) r 2 ( ) r 2 ( ) d
2. 性质
(1)


( 2)
L g ( x, y, z )ds ( , 为常数 )
2
f ( x, y , z ) d s
1
f ( x, y , z ) d s
f ( x, y , z ) d s
(3)
ds l
( l 曲线弧 的长度)
( 由1 , 2 组成)
例2. 计算曲线积分 线
其中为螺旋
的一段弧.
解:

( x y z ) ds
2
2
2

a k
2
2
0
2
[a k t ] d t
2
2 2

y
由曲线微元弧 ds (d x) 2 (d y ) 2
O
ds d y dx x x
因此
说明:
(1) sk 0, t k 0, 因此积分限必须满足 !
(2) 注意到
x ( t ) 因此上述计算公式相当于“换元法”. y (t )
d s (d x) 2 (d y) 2 dt
3
2
1
0
O
1x
例3. 计算
2 2 2 2
其中L为双 ) ( a 0 )
解: 在极坐标系下 它在第一象限部分为
y
(0 π ) 4
π 0 4 r cos
L1 : r a cos 2
4 4
π 0 4 a 2 cos
2xy ds 0
L
2 O
2x
x2 y2 原式 =12 ( )ds 12 ds 12a L 4 L 3
分析:
L
2 xy ds

2
2
2 xy 1 y2 dx
例７ 求圆 x 2 y 2 R 2 的周长。 解： 在第一象限， L: y
R x ds
2 2 2
其中 为球面
O1
y
与平面 x z 1 的交线 . x y z 9 2
2 1 2 1 1 ( x 2) 4 y 1 1 2 , 化为参数方程 解: : x z 1 x 1 x 2 cos 2 0 2π : y 2 sin z1 2 cos 2 则
( X 1) ds
2

利用形心公式

x
D
x ds l

L
L
从而
(x2 y)ds x2ds 1 (x2 y2 )ds ．
L
L
2L
因为点(x, y) 位于 L 上，所以 x, y 满足 L 的方程，即有 x2 y2 1，
故
(x2 y)ds 1 ds 1 L的周长 1 2 ．
L
2L 2
2
注：解法二表明在计算过程中，可将曲线方程直接代入被积函数中．
(11.1.4)
a
注：式(11.1.1),(11.1.2),(11.1.3) ，和 (11.1.4) 中，积分下限小于积分上限．
16-12
例 11.1.1 计算曲线积分 x2 y2ds ，其中 L 是由圆周x2 y2 a2(a 0) ， L
直线 y x 以及 x 轴在第一象限中所围平面图形的边界．
数，则
f (x, y)ds
b
f (x, y(x))
1 y2(x)dx ．
L
a
(11.1.2)
16-11
（续定理）如果曲线 L 的方程为 x x( y) (c y d ) ，且x( y) 在[c,d ] 上具有
连续导数，则
f (x, y)ds
d
f (x( y), y)
1 x2( y)dy ．
16-4
n
⑶ 求和：得柱面 面积的近似值S h(i ,i )si ． i1
⑷ 取极限：令 0，则有 的面积
n
S
lim
0
i1
h(i ,i )si
．
㈡ 曲线形物体的质量
设有平面上的曲线状物体，占有 xOy 坐标面上的
曲线段 L （见图 11-1-2），在 L 上任一点(x, y) 处，其线密

i 1
n
取极限
A
lim
0
i 1
h(i ,i
) si .
A
y
Mn
MnA1 i
Mi
Mi1 (i ,i )
2:非均匀平面曲线形构件的质量
均匀的质量 M s.
分割 M0 , M1,, Mn , 近似 取 (i ,i ) Mi1Mi ,
Mi (i ,i ) si .
y
M0
o
(x, y) Mn
则 f ( x, y, z)ds
0,
当 f ( x, y, z) 是x (或y) (或z) 的奇函数
2 f ( x, y)ds, 当 f ( x, y, z) 是x (或y) (或z)的偶函数 1
Γ1是曲线Γ落在yz (或xz) (或x y平) 面一侧的部分.
运用对称性简化第一类曲线积分计 算时, 应同时考虑被积函数 与积分曲线 的对称性.
A⌒B
BO
yB
OA : y 0, 0 x a,ds 1 02dx
O
Ax
e x2 y2ds a e xdx ea 1
OA
0
A⌒B : x a cos t, y a sint, 0 t
4
A⌒B e x2 y2ds
4 ea
0
(a sint)2 (a cos t)2 dt aea
解2 选 y 为积分变量
y2 2x x y2 2
(0 y 2)
2
1
I
y
0
1 y2dy 3 (5
5 1)
例 求I xyzds,其 中 : x a cos , y a sin ,
z k 的 一 段. (0 2 )

高等数学第一节 对弧长曲线积分
第十一章 曲线积分与曲面积分
*第一节 对弧长的曲线积分
一、对弧长曲线积分的概念 二、对弧长曲线积分的计算法
一、对弧长曲线积分的概念
引例 平面曲线的质量
若平面曲线 的线密度是常数 0，曲线长为 L， 则平面曲线的质量Ｍ = 0L．
若平面曲线 的线密度不是常数， 而是曲线上 点的位置的函数，设密度函数为 = f (x, y). 如何计算
f (x, y) —— 被积函数， f (x, y)dl —— 被积表达式，
dl —— 弧长元素， —— 积分路径.
如果 是封闭曲线，则曲线积分记为 f(x,y)dl. 设 由 1 与 2 组成，则
f(x, y)dl
f(x,y)d l f(x,y)d l.
1
2
由定义可知，对弧长的曲线积分与积分路径 的
f( x ,y ) d l a f [( t)( ,t)] 2 ( t) 2 ( t) d t.①
注意 由于dl > 0，故应保证 dt > 0， 因此公式 ① 右端对变量 t 的定积分中， 下限不超过上限.
上式可见，弧长的曲线积分化为定积分计算要 点是：
(1)被积函数定义在曲线 (或曲线 L)上，即 点 (x,y) 在曲线 上变化；
(2)弧长元素 dl (dx)2(dy)2;
(3)定积分的下限不超过上限.
例 1 试计算 (x y)dl, 其中 为 x 轴上直线 L
段 AB 与上半圆弧 BCA 组成的封闭曲线.
解 由曲线积分的性质，有
(xy)dl (x y )d l (x y )d l.
L
AB
BCA
y
由于直线段 AB 的参数式方程为
C

0 2
(2) L : x 2, 0 y 3
21 I (2 y) 0 1dy 0 2
3
x R cos (3) L : , 0 y R sin
I ( R cos R sin ) Rd 2 R 2
0

(4) L : y 1 x, 0 x 1
定理
设 f ( x , y )在曲线弧 L上有定义且连续, x ( t ), L的参数方程为 ( t )其中 y ( t ), ( t ), ( t )在[ , ]上具有一阶连续导数, 且
L
f ( x , y )ds f [ ( t ), ( t )] 2 ( t ) 2 ( t )dt
则

ds

( 2 sin )
2
( 2 sin ) d 2d
2
9 2 I 2 d 18 2 0
例6. 计算
其中L为双纽线
(x2 y2 ) 2 a2 (x2 y2 ) ( a 0 )
解: 在极坐标系下
它在第一象限部分为
y
(0
ab sin t cos t a 2 sin2 t b 2 cos 2 t dt
a ab 2 2 2 2 2 2 u du ( 令 u a sin t b cos t) 2 b a b
2 0
ab(a ab b ) . 3(a b)
2 2
例2.计算
其中(1) L 是抛物线
xds x , ds
L L
yds y . ds
L L
例7. 计算半径为 R ,中心角为 的圆弧 L 对于它的对 称轴的转动惯量I (设线密度 = 1). 解: 建立坐标系如图, 则

(1)若( x, y, z ) L, 都有f ( x, y, z ) f ( x, y, z ),
则 f ( x , y, z )ds 0;
L
(2)若( x , y , z ) L,都有f ( x , y , z ) f ( x , y , z ),
则 f ( x , y , z )ds 2 f ( x , y , z )ds ;
曲线积分与曲面积分
积分 定积分 二重积分 三重积分 曲线积分 曲面积分
积分范围 区间 平面区域 空间区域 曲线段 曲面域
曲线积分 曲面积分 对弧长的曲线积分
对坐标的曲线积分
对面积的曲面积分
对坐标的曲面积分
第十一章
第一节 对弧长的曲线积分
一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法
L
(2)若( x , y , z ) L,都有f ( x , y , z ) f ( x , y , z ),
则 f ( x , y , z )ds 2 f ( x , y , z )ds ;
L L1
机动 目录 上页 下页 返回 结束
对弧长的曲线积分的轮换对称性:
设空间曲线L关于平面y x对称,则有
如果方程为极坐标形式: L : r r ( ) ( ), 则
f (r ( ) cos , r ( ) sin ) r 2 ( ) r 2 ( ) d
推广: 设空间曲线弧的参数方程为

则

: x (t ), y (t ) , z (t ) ( t ) f ( x, y , z ) d s
L
机动
目录
上页
下页

B
Mk (ξk,ηk ) ∆s k Mk−1
∑
k= 1
机动
n
A
目录
上页
下页
返回
结束
2.定义 . 设 L 是平面上一条有限长的光滑曲线, 义在 L上的一个有界函数, 若对 L的任意分割 和对 的 (ξk,ηk ) 局部的任意取点 任意取点, 局部的任意取点 下列“乘积和式极限”
λ→ k= 0 1
lim ∑ f (ξk,ηk )∆sk
平 x 交 . +z2 = 9 与 面 +z =1的 线 2 1 (x − 1)2 + 1 y2 =1 2 2 4 解: L: , 化为参数方程 x + z =1 x = 2cosθ + 1 2 ( 0 ≤θ ≤ 2π ) L: y = 2sinθ z = 1 − 2cosθ 2 则
∫
机动
目录
上页
下页
返回
结束
例1. 计算
其中
①L是直线 y = x 上点 o ( 0,0 ) , A (1,1) 之间的一段 ②L是折线OBA，其中 o ( 0,0 ) , B (1,0 ) , A (1,1) ︵ ③L是上半圆周AB : x 2 + y 2 = R 2 ︵ 解: ① Q OA : y = x ( 0 ≤ x ≤ 1) , y A (1,1)
L
0
bt a 2 + b 2 dt = 2π 2 µb a 2 + b 2
2π 2 a 0
(
)
a 2 + b 2 dt = 2πµ a 2 a 2 + b 2
高斯 目录 上页 下页 返回 结束
内容小结
1. 定义
∫L f (x, y)ds

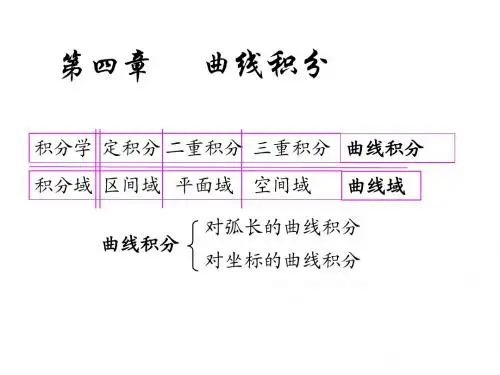
⾼等数学之曲线积分的计算⽅法总结
在考研数学中，曲线积分数学⼀重要考点之⼀，每年必考，并且时常考⼀道⼤题和⼀道⼩题，因此⼀定要掌握其基本计算⽅法和技巧。

下⾯我总结第⼀类曲线积分和第⼆类曲线积分的⼀些基本的计算⽅法，供各位考⽣参考。

对弧长的线积分计算常⽤的有以下两种⽅法：
（1）直接法：
（2）利⽤奇偶性和对称性
平⾯上对坐标的线积分（第⼆类线积分）计算常⽤有以下四种⽅法：
（1）直接法
（2）利⽤格林公式
注：应⽤格林公式⼀定要注意以下两点：
a.P(x,y),Q(x,y)在闭区间D上处处有连续⼀阶偏导数
b.积分曲线L为封闭曲线且取正向。

（3）补线后⽤格林公式
若要计算的线积分的积分曲线不封闭，但直接法计算不⽅便时，此时可补⼀条曲线，使原曲线变成封闭曲线。

（4）利⽤线积分与路径⽆关性
题型⼀：对弧长的线积分（第⼀类线积分）
例1：
解法⼀：利⽤直⾓坐标⽅程计算
解法⼆：利⽤参数⽅程计算
题型⼆：对坐标的线积分（第⼆类曲线积分）计算
例2：
解题思路：本题中积分路径L为封闭曲线，⾸先考虑格林公式，容易验证被积函数在L围成区域上满⾜格林公式条件。

解：。

定积分计算弧长公式弧长公式是计算曲线弧长的一种工具，通过定积分来求解。

弧长公式在多个领域应用广泛，如物理、数学、工程等。

在本文中，我们将介绍弧长公式的推导过程，并给出一些常见曲线的弧长计算示例。

我们首先考虑平面上的一条曲线，可以表示为y=f(x)。

我们的目标是计算曲线一段区间[a,b]的弧长。

我们将区间[a,b]等分成n个小区间，每个小区间的长度为Δx=(b-a)/n。

在每个小区间上，我们可以通过线段的长度来近似曲线上的弧长。

设曲线上一点(x,f(x))，它与相邻点(x+Δx,f(x+Δx))之间的线段长度为s。

根据勾股定理，我们有：s=√((Δx)²+(Δy)²)其中Δy=f(x+Δx)-f(x)为两个点在y轴上的纵向距离。

为了得到曲线上所有小线段的长度之和，我们要对每个小区间[x_i,x_i+1]上的线段长度进行求和。

我们可以将弧长公式表示为一个求和的形式：S=∑s_i其中s_i为小区间[x_i,x_i+1]上的线段长度。

现在我们来推导弧长公式的一般形式。

我们先对s进行平方，并展开成二项式的形式：s²=(Δx)²+(Δy)²=(Δx)²+(f(x+Δx)-f(x))²=(Δx)²+(f'(x)Δx+R(Δx))²其中f'(x)为f(x)的导数，R(Δx)为高阶无穷小。

将(s)²展开，得到：s²=(Δx)²+f'(x)²(Δx)²+2f'(x)R(Δx)Δx+R²(Δx)(Δx)²注意到R(Δx)是高阶无穷小，所以(R(Δx))²项可以忽略。

再次整理得：s²=(1+f'(x)²)(Δx)²+2f'(x)R(Δx)Δx将上述等式两边开平方，得到：s=√((1+f'(x)²)(Δx)²+2f'(x)R(Δx)Δx)现在我们要将s表示为x的函数。

∫
L
f ( x, y)ds
(化为定积分) 化为定积分)
x = ϕ(t ), 设曲线 L : (α ≤ t ≤ β ), y =ψ (t ), 且 其中 ϕ(t ),ψ (t ) 有连续的导数，
2 2
ϕ′ (t ) +ψ′ (t ) ≠ 0; f ( x, y) 在L上连续.
L : x = ϕ(t ), y =ψ (t ) (α ≤ t ≤ β ).
f ( x , y )ds;
∫
Γ
f ( x , y , z )ds
对面积的（第一类） 对面积的（第一类）曲面积分
∫∫
Σ
f ( x , y , z )dS
为平面或空间有限光滑(或分段光滑 当G为平面或空间有限光滑 或分段光滑 为平面或空间有限光滑 或分段光滑) 曲线(L或 时 积分称为对弧长的曲线积分 曲线 或 Γ)时，积分称为对弧长的曲线积分 或第一类曲线积分,即 第一类曲线积分 即
2 2
∆ x ds
dy
oa
x
x +∆x b
x
dy 2 ds = (dx) + (dy) = 1+ ( ) ⋅ dx, dx
弧长微分公式
ds = 1+ y′ dx,
2
(2) 参数方程情形
x = ϕ(t ), 曲线弧为 (α ≤ t ≤ β ). y =ψ (t ), 且在 [α, β ]上具有连续导数 ϕ′(t ),ψ ′(t ).
(1) 曲线弧为参数方程的计算 曲线弧为参数方程 参数方程的计算
L : x = ϕ(t ), y =ψ (t ) (α ≤ t ≤ β ).
β
∫
L
f ( x, y)ds= ∫α

∫α
于是
β
f [(t),ψ(t)] ′2(t)+ψ′2(t)dt .
β α
∫L
f (x, y)ds = ∫ f [(t),ψ(t)] ′2(t)+ψ′2(t)dt .
二、对弧长的曲线积分的计算
定理 设f(x, y)在曲线弧L上有定义且连续, L的参数方程为 x=(t), y=ψ(t) (α≤t≤β), 其中(t)、ψ(t)在[α, β]上具有一阶连续导数, 且′2(t)+ψ′2(t)≠0,
a
b
设曲线 L的参数方程为x=(t), y=ψ(t) (α≤t≤β), 则
∫L
讨论:
f (x, y)ds =∫ f [(t),ψ(t)] ′2(t)+ψ′2(t)dt (α<β).
α
β
(1)若曲线 L 的方程为 y=ψ(x)(a≤x≤b), 则∫ f (x, y)ds =？
L
(2)若曲线 L 的方程为 x=(y)(c≤y≤d), 则∫ f (x, y)ds =？
提示: 曲线形构件L的质量元素为
f (x, y)ds = f [(t),ψ(t)] ′2(t)+ψ′2(t)dt .
二、对弧长的曲线积分的计算
根据对弧长的曲线积分的定义, 如果曲线形构件L的线密 度为f(x, y), 则曲线形构件L的质量为
∫L f (x, y)ds .
另一方面, 如果曲线L是光滑的, 其参数方程为 x=(t), y=ψ (t) (α≤t≤β), 则曲线形构件L的质量为
α
β
(1)若曲线 L 的方程为 y=ψ(x)(a≤x≤b), 则∫ f (x, y)ds =？
L
(2)若曲线 L 的方程为 x=(y)(c≤y≤d), 则∫ f (x, y)ds =？

2018考研数学重点：弧长曲线积分的计算理解他的概念的主要的思想逻辑为分割，近似，求和，取极限。

对一条曲线进行分割，把每一段的长度记为ds，密度函数为f(x,y)，从而这一小段上的质量为f(x,y)*ds，从而整个曲线的质量为对f(x,y)*ds求和再取极限，极限过程就是每一小段的直径趋于0的过程。

他的物理意义为密度不均匀的曲线形物体的质量，从而对弧长的曲线积分的物理意义为密度不均匀的曲线形物体的质量，记作他的计算方法的总体思路就是把他化为定积分的形式，因为我们只会求定积分，那么怎样把他化成定积分呢?首先我们看到有ds，这个符号我们在定积分的应用里计算曲线的弧长中接触过，由微分法可得出以上我们可以总结出计算弧长曲线积分的一般思路：1.代入，2.把ds转化为dx(或者dy)，dt或，3.定限，数小的为下限，数大的为上限。

对于弧长的曲线积分大家主要理解以及掌握它的公式，会算即可。

倚窗远眺，目光目光尽处必有一座山，那影影绰绰的黛绿色的影，是春天的颜色。

周遭流岚升腾，没露出那真实的面孔。

面对那流转的薄雾，我会幻想，那里有一个世外桃源。

在天阶夜色凉如水的夏夜，我会静静地，静静地，等待一场流星雨的来临…许下一个愿望，不乞求去实现，至少，曾经，有那么一刻，我那还未枯萎的，青春的，诗意的心，在我最美的年华里，同星空做了一次灵魂的交流…秋日里，阳光并不刺眼，天空是一碧如洗的蓝，点缀着飘逸的流云。

偶尔，一片飞舞的落叶，会飘到我的窗前。

斑驳的印迹里，携刻着深秋的颜色。

在一个落雪的晨，这纷纷扬扬的雪，飘落着一如千年前的洁白。

窗外，是未被污染的银白色世界。

我会去迎接，这人间的圣洁。

在这流转的岁月里，有着流转的四季，还有一颗流转的心，亘古不变的心。

• 对光滑曲线弧 L :x ( t),y ( t),( t ) ,
L
f
(x,
y)ds


f[(t) , (t)]
2(t)2(t)dt
• 对光滑曲线弧 L :y ( x )( a x b ) ,
f(x,y)ds bf(x,(x)) 12(x)dx
解: 在极坐标系下 L:r2a2co2s,
y
它在第一象限部分为
L 1 :r a c2 o( 0 s 4 )
o
x
利用对称性 , 得

I
4 L1
xds
404rco sr2()r2()d

4 4a2cosd2
2a2
0
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
二、对弧长的曲线积分的计算法
基本思路: 求曲线积分 转 化 计算定积分
定理: 设f(x,y)是定义在光滑曲线弧
L:x(t),y (t)( t )
上的 L 连f 续( x 函,y 数) d ,s 则 曲 线f 积[ 分( t ) L,f(( xt) ,y)d] s2 存 ( t) 在 ,且2 ( t) d t
(2) kf(x,y,z)dsk f(x,y,z)ds （k 为常数)


(3) f(x,y,z)dsf(x ,y ,z )d s f(x ,y ,z )d s

1
2
( 由 1 , 2组成)
(4) ds l
( l 为曲线弧 的长度)
YANGZHOU UNIVERSITY
L
a
• 对光滑曲线弧 L :r r ()( ),

1.弧长公式积分公式是什么？
答：弧长公式积分公式：ds=√(1+y'^2)dx。

定积分作为积分的一种。

是函数f(x)在区间[a，b]上积分和的极限。

这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式）。

一个函数，可以存在不定积分，而不存在定积分：也可以存在定积分，而不存在不定积分。

一个连续函数，一定存在定积分和不定积分；若只有有限个间断点，则定积分存在：若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。