第一型曲线积分的计算

第一类曲线积分的计算第一类曲线积分的计算1、定义定义1 ：设L 为平面上可求长度的曲线段，)y ,x (f 为定义在L 上的函数．对曲线L 作分割T ，它把L 分成n 个可求长度的小曲线段)n ,,2,1i (L i ，i L 的弧长记为i s ，分割T 的细度为i ni 1s max T ，在i L 上任取一点(i ,).n ,,2,1i )(i 若存在极限J s ),(f lim i i n1i i 0T且J 的值与分割T 及点),(i i 的取法无关，则称此极限为)y ,x (f 在L 上的第一型曲线积分，记作 .ds )y ,x (f L （1） 定义2： 若L 为空间可求长曲线段，)y ,x (f 为定义在L 上的函数，则可类似地定义)z ,y ,x (f 在空间曲线L 上的第一型曲线积分为J s ),,(f lim i i i n1i i 0T ，(此处i s 为i L 的弧长,i n i 1s max T ,J 为一常数),并且记作 L .ds )z ,y ,x (f （2） 2、物理意义（1）设某物体的密度函数f （P ）是定义在 上的连续函数．当 是直线段时，应用定积分就能计算得该物体的质量。

现在研究当 是平面上某一可求长度的曲线段时物体的质量的计算问题．首先对 作分割,把 分成n 个可求长度的小曲线段i （i=1，2，…，n)，并在每一个i 上任取一点P i由于f （P ）为 上的连续函数,故当i 的弧长都很小时，每一小段i 的质量可近似地等于f （P i）i ,其中 i 为小曲线段i 的长度.于是在整个 上的质量就近似地等于和式i n1i i )P (f 当对 的分割越来越细密时,上述和式的极限就应是该物体的质量。

（2）空间曲线L 的重心坐标为(,,)(,,)yz LLx x y z dlM x Mx y z dl,(,,)(,,)zx LLy x y z dlM y Mx y z dl,(,,)(,,)xy LLz x y z dlM z Mx y z dl（3） 曲线L 的绕z 轴(x, y 轴)的转动惯量是22()(,,)z LJ x y x y z dl3、几何意义1） 当被积函数为1时, 积分的值恰为曲线的长度。

第一型曲线积分的定义第一型曲线积分，是微积分中的一种重要概念与计算方法，它涉及曲线和向量场之间的积分。

本文将介绍第一型曲线积分的定义、性质和计算方法。

一、第一型曲线积分的定义第一型曲线积分，也称为曲线的线积分，是指在曲线上某个有向长度元素$\mathrm{d}s$上的函数值与该长度元素的乘积$d\boldsymbol{s}$在整个曲线上的积分。

设$C$是曲线，其参数方程为$\boldsymbol{r}(t)=(x(t), y(t), z(t)), t\in[a,b]$，则$C$的长度由公式：$$ L(C)=\int_{C}\mathrm{d}s=\int_{a}^{b}\left[\ left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\r ight)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\f rac{1}{2}} \mathrm{d}t $$计算曲线$C$上的一个标量函数$f(x,y,z)$在曲线上的第一型曲线积分，即为：$$ \int_{C} f(x, y, z) \mathrm{d}s=\int_{a}^{b}f\left(\boldsymbol{r}(t)\right)\left[\left(x^{\prim e}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\frac{1}{2}}\mathrm{d}t $$若积分路径可以看成向量值函数$\boldsymbol{r}(t)$的积分，第一型曲线积分就可以写作：$$ \int_{\boldsymbol{r}}\boldsymbol{F}(\boldsymbol{r}) \cdot \mathrm{d}\boldsymbol{r}=\int_{a}^{b}\boldsymbol{F}\left(\boldsymbol{r}(t)\right) \cdot \boldsymbol{r}^{\prime}(t) \mathrm{d}t=\int_{a}^{b} \boldsymbol{F} \cdot \mathrm{d}\boldsymbol{s} $$其中$\boldsymbol{F}(\boldsymbol{r})$是向量场，$\mathrm{d}\boldsymbol{r}$表示一个有向长度元素，$\cdot$表示向量内积运算，$\mathrm{d}\boldsymbol{s}=\boldsymbol{r}^{\prime}(t ) \mathrm{d} t$表示线元素。

第一类曲线积分的极坐标形式曲线积分是微积分中的一个重要概念，它描述了沿着一条曲线的积分过程。

在曲线积分中，第一类曲线积分是最基本的一种类型，它描述了沿着曲线的标量场积分。

而在极坐标系下，第一类曲线积分的计算方法也有其独特的形式。

首先，我们来回顾一下第一类曲线积分的定义。

设曲线L为参数方程r(t)=(x(t),y(t))，其中a≤t≤b，f(x,y)为定义在曲线L上的标量场，则曲线L上f(x,y)的第一类曲线积分为：∫L f(x,y)ds = ∫b_a f(x(t),y(t))√[x'(t)²+y'(t)²]dt其中，ds表示曲线L上的弧长元素，x'(t)和y'(t)分别表示x(t)和y(t)对t 的导数。

接下来，我们来看第一类曲线积分在极坐标系下的形式。

在极坐标系下，曲线L可以表示为r(θ)=(r(θ)cosθ,r(θ)sinθ)，其中a≤θ≤b，r(θ)为极径函数。

此时，曲线L上f(x,y)的第一类曲线积分可以表示为：∫L f(x,y)ds = ∫b_a f(r(θ)cosθ,r(θ)sinθ)√[r'(θ)²+r(θ)²]dθ其中，ds表示曲线L上的弧长元素，r'(θ)表示r(θ)对θ的导数。

通过上述公式，我们可以看出，在极坐标系下，第一类曲线积分的计算方法与直角坐标系下有所不同。

在直角坐标系下，我们需要计算曲线L上的弧长元素ds，而在极坐标系下，我们需要计算曲线L上的弧度元素dθ。

此外，由于极坐标系下的曲线L是由极径函数r(θ)和极角θ共同确定的，因此在计算曲线积分时，我们需要将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。

总之，第一类曲线积分是微积分中的一个重要概念，它描述了沿着曲线的标量场积分。

在极坐标系下，第一类曲线积分的计算方法也有其独特的形式，需要注意弧度元素dθ的计算和将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。

第一型曲线积分的计算方法
1. 嘿，你知道直接法吗？就像我们要数清楚一堆糖果有多少颗一样直接！比如计算曲线 y=x^2 从 0 到 1 那一段的第一型曲线积分，咱就直接把函数的值代进去算，简单粗暴有木有！
2. 还有参数法呢！这就像给曲线找到一个特别的密码来解题呀！比如说一个圆的曲线，用参数表示出来再去计算积分，超有意思的咧！
3. 利用对称性来计算也很棒哦！这就好像发现了一个隐藏的小技巧。

像计算关于 x 轴对称的曲线的积分，有些部分咱直接就可以简化啦，多方便呀！
4. 想想看，换元法也不错呀！就如同给问题变个魔法一样。

比如把很难的式子通过换元变得简单易懂，然后轻松算出积分，多牛呀！
5. 哇塞，格林公式也能助力第一型曲线积分的计算哦！这就像是给我们开了一扇快捷之门呀。

特别是在一些复杂图形中，简直是救星呀！
6. 别忘了分块计算呀！这就好比把一个大难题拆分成好多小部分来解决。

遇到复杂的曲线，咱就一块块来，总能搞定的嘛！
总之，第一型曲线积分的计算方法多种多样，每一种都有它独特的魅力和用处，就看你怎么去运用啦！。

第一型曲线积分格林公式
曲线积分格林公式(Gauss Quadrature Formula)是一种高效的数值积
分的方法。

该方法可以有效的用有限的线性组合来近似曲线积分。

格林公式的一类是第一型格林公式，它提供一个比较容易实现的计算，有效的计算出一阶及二阶以上被积函数不论奇偶或异类在指定定积区
间的积分值。

这类公式可以用如下等式来描述：
$$
\int_{a}^{b}f(x)dx=\frac{b-a}{2}\sum_{k=1}^{n}w_{k}f\left(\frac{b-
a}{2}x_{k}+\frac{a+b}{2}\right)
$$
其中$w_{k}$和$x_{k}$分别为积分时要用到的权重及积分点。

使用第一型格林公式通常来说有以下优点：
- 可以完成计算可以使计算极为高效快速；
- 结果有更高的精确度，相比传统的梯形法与辛普森法有更优越准确的
结果；
- 第一型格林公式可以很容易的使用，不需要反复研究甚至编程就可以
实现曲线积分；
- 这类公式可以有效适用于一阶及二阶以上的被积函数；
- 其实现与容易计算使第一型格林公式在计算实数积分的应用很广泛。

曲线曲面积分公式(一)曲线曲面积分公式本文将介绍曲线曲面积分的相关公式，并通过举例进行解释说明。

一、曲线积分公式1. 第一型曲线积分第一型曲线积分表示对曲线上的函数在曲线长度方向上的积分，其公式为：(_C f(x, y, z) ds)其中，(C)为曲线，(f(x, y, z))为曲线上的函数，(ds)表示曲线微元的长度。

举例：考虑计算曲线(C: x = t, y = t^2, z = t^3)上函数(f(x, y, z) = x^2 + y + z)的第一型曲线积分。

首先需要计算曲线的参数方程可微分区间([a, b])上的导数：( = 1)( = 2t)( = 3t^2)曲线微元的长度(ds)可以表示为：(ds = dt = dt)因此，对函数(f(x, y, z) = x^2 + y + z)进行第一型曲线积分的结果为：(_C (x^2 + y + z) ds = _a^b (t^2 + t^2 + t^3) dt)2. 第二型曲线积分第二型曲线积分表示对曲线上的矢量场在曲线长度方向上的积分，其公式为：(_C d)其中，(C)为曲线，()为矢量场，(d)表示曲线微元的矢量。

举例：考虑计算曲线(C: x = t, y = t^2, z = t^3)上的矢量场( =(2xy, 3x^2, z))的第二型曲线积分。

首先需要计算曲线的参数方程可微分区间([a, b])上的导数：( = 1)( = 2t)( = 3t^2)曲线微元的矢量(d)可以表示为：(d = (, , ) dt = (1, 2t, 3t^2) dt)因此，对矢量场( = (2xy, 3x^2, z))进行第二型曲线积分的结果为：(_C (2xy, 3x^2, z) (1, 2t, 3t^2) dt = _a^b (2t(t^2),3(t2)2, t^3) (1, 2t, 3t^2) dt)二、曲面积分公式1. 第一型曲面积分第一型曲面积分表示对曲面上的函数在曲面面积方向上的积分，其公式为：(_S f(x, y, z) dS)其中，(S)为曲面，(f(x, y, z))为曲面上的函数，(dS)表示曲面微元的面积。

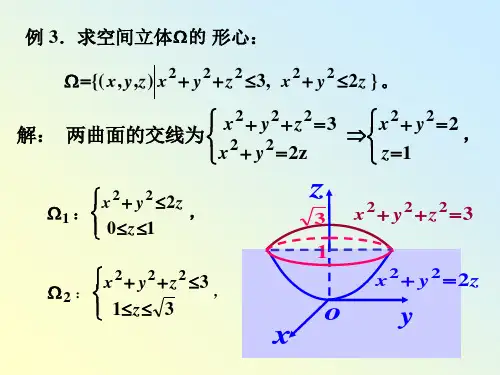
1. 计算第一型曲线积分:(1)⎰+Lds y x )(,其中L 是以)1,0(),0,1(),0,0(B A O 为顶点的三角形 分析：先将L 分段表示，在利用第一型曲线积分的性质。

L=OA+AB+BO ，又OA ：010x x x y =⎧≤≤⎨=⎩ AB ：011x xx y x =⎧≤≤⎨=-⎩BO ：001x y y y =⎧≤≤⎨=⎩ 解：⎰+Lds y x )(=⎰+OA ds y x )(+⎰+AB ds y x )(+⎰+BO ds y x )( =.212101010+=++⎰⎰⎰dy y dx dx x (2)⎰+L ds y x 2122)(,其中L 是以原点为中心,R 为半径的右半圆周; 分析：是以原点为中心,R 为半径的右半圆周的参数方程为：)22.(sin ,cos πθπθθ≤≤-==R y R x 解：⎰+L ds y x 2122)(=.2222R d R πθππ=⎰- .(3)⎰L xyds , 其中L 为椭圆12222=+by a x 在第一象限中的部分; 分析：先将椭圆12222=+by a x 在第一象限中的部分表示为:0y x a =≤≤ 解：因为,,2222x a bx y x a a b y --='-=从而 ⎰L xyds =dx y x a x a b a 2220)(1'+-⎰=dx x a a x b x a x a b a)(122222220-+-⎰ =⎰+-a dx x ab x a a b 02222222=⎰--a dx x b a a a b 0222242)(2 =)(3)(22b a b ab a ab +++. 此题也可将椭圆12222=+by a x 在第一象限中的部分表示为参数方程：cos 0sin 2x a y b θπθθ=⎧≤≤⎨=⎩ (4) ⎰L ds y ,其中L 为单位圆周122=+y x ;解：由于单位圆的参数方程为:cos ,sin (02)x y θθθπ==≤≤,从而⎰L ds y =4sin sin 20=-⎰⎰πππθθθθd d . (5) ⎰++L ds z y x )(222,其中L 为螺旋线)20(,sin ,cos π≤≤===t bt z t a y t a x 的一段;解：⎰++L ds z y x )(222=222222222202)43(32)(b a b a dt b a t b a ++=++⎰πππ. (6) ⎰L xyzds ,其中L 是曲线)10(21,232,23≤≤===t t z t y t x 的一段; 解：⎰L xyzds =dt t t t t t 223102121232++⋅⋅⎰ =.143216)1(32102/9=+⋅⎰dt t t (7)ds z y L ⎰+222,其中L 是2222a z y x =++与y x =相交的圆.分析：2222a z y x =++与y x =相交的圆⎩⎨⎧=+=2222a z y y x 的 其参数方程为)20(,cos ,sin 2π≤≤===t t a z t ay x 解：ds z y L ⎰+222=.2cos sin 2202222ππa dt t a t a a =+⎰注意：计算第一型曲线积分的关键是将L 的表达式正确的给出来。

第一类曲线积分的三种计算方式1.参数方程法参数方程法是最常用的计算第一类曲线积分的方法之一、它利用参数方程将曲线分成若干小段，然后计算每一小段上的积分，最后将所有小段上的积分相加得到整个曲线上的积分值。

具体步骤如下：1.将曲线的参数方程表示为x=f(t)，y=g(t)，z=h(t)，其中t的取值范围为[a,b]。

2.求出曲线的切线向量T(t)和曲率向量K(t)。

3.将向量场F(x,y,z)表示为F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k。

4. 计算曲线段的长度ds=sqrt(dx^2+dy^2+dz^2)，其中dx=f'(t)dt，dy=g'(t)dt，dz=h'(t)dt。

5.将向量场在曲线上的投影F·T计算出来。

6. 将F·T乘以ds，再积分得到曲线上的积分。

参数方程法的优点是适用于任意形状的曲线，缺点是当曲线的参数方程比较复杂时，计算较为繁琐。

2.向量场法向量场法是计算第一类曲线积分的另一种常见方法。

它直接利用向量场在曲线上的投影与曲线段的长度相乘然后积分，而无需转化为参数方程。

具体步骤如下：1.将向量场F(x,y,z)表示为F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k。

2.将曲线表示为r(t)=x(t)i+y(t)j+z(t)k，其中t的取值范围为[a,b]。

3. 计算向量场在曲线上的投影F·dr，其中dr=dx i+dy j+dz k，dx=x'(t)dt，dy=y'(t)dt，dz=z'(t)dt。

4. 将F·dr积分得到曲线上的积分。

向量场法的优点是计算较为简单直接，而无需转化为参数方程，缺点是不适用于复杂的曲线形状。

3.微积分基本定理法微积分基本定理法是计算第一类曲线积分的另一个重要方法。

它利用微积分基本定理将曲线积分转化为定积分，从而简化计算过程。

第一型曲线积分计算公式：第一型曲线积分也称为路径积分或弧长积分，用于计算向量场沿着曲线的积分。

其计算公式如下：∫C F · dr其中，C 是曲线，F 是向量场，dr 是曲线上的微元弧长向量。

以下是两个实例：实例1：考虑曲线C，由参数方程r(t) = (cos(t), sin(t))，其中0 ≤ t ≤ π/2。

向量场F(x, y) = (x, y)。

我们可以首先计算曲线的切向量r'(t) = (-sin(t), cos(t))。

然后计算F · dr：F · dr= (x, y) · (dx, dy) = (x, y) · (dx/dt, dy/dt) dt [使用链式法则将dr 转换为dt] = (cos(t), sin(t)) · (-sin(t), cos(t)) dt = -sin(t)cos(t) + sin(t)cos(t) dt = 0由于F · dr = 0，因此该曲线上的第一型曲线积分为0。

实例2：考虑曲线C，由参数方程r(t) = (t, t^2)，其中0 ≤ t ≤ 1。

向量场F(x, y) = (y, x)。

首先计算曲线的切向量r'(t) = (1, 2t)。

然后计算F · dr：F · dr = (y, x) · (dx, dy) = (y, x) · (dx/dt, dy/dt) dt = (t^2, t) · (1, 2t) dt = t^2 + 2t^2 dt = 3t^2 dt要计算第一型曲线积分，我们需要将积分限从参数t 转换为实际的曲线长度。

曲线长度由下式给出：s = ∫[a, b] ||r'(t)|| dt计算曲线长度：s = ∫[0, 1] ||r'(t)|| dt = ∫[0, 1] ||(1, 2t)|| dt = ∫[0, 1] sqrt(1^2 + (2t)^2) dt = ∫[0, 1] sqrt(1 + 4t^2) dt = ∫[0, 1] sqrt(4t^2 + 1) dt现在我们可以计算第一型曲线积分：∫C F · dr = ∫[0, 1] 3t^2 dt = 3∫[0, 1] t^2 dt = 3[t^3/3] [0, 1] = 1因此，该曲线上的第一型曲线积分为1。