当前位置：文档之家 › 静电学-环路定理电势能电势

静电学-环路定理电势能电势

  • 格式：pptx
  • 大小：1012.18 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

电势电势梯度

电势电势梯度
§ 5-4
静电场的环路定理
当带电体在静电场中移动时，静电场力对带电体要作 功，这说明静电场具有能量。
一、静电场力的功
d A = F . d l = q E .dl b r rb = q E .dl cosφ dl qq φ φ q = q E .dr = 4 r 2d r π ε ra q E q q rb d r qq 1 1 a A= 2 = r r 4π 4 π ra r b ε a ε
§5-5
等势面 电场强度与电势梯度的关系
注：相邻等势面之间的电势差相等。
一.等势面：在静电场中，电势相等的点所组成的面。
等势面的性质： （2）等势面与电场线处处正交 （3）电场线指向电势降低的方向 （4）等势面和电场线密集 处场强量值大，稀疏处场强 量值小
（1）在静电场中，沿等势面移动电荷时，电场力作功为零
=
q 4πε
o
[
x (x + R )
2 2 3 2
]
V dV
B2
n
B3
dn φ
B1
dV E dn
V
dl
II I
E
dV E dn
负号表示E与n的方向相反，正是E的方向
dV E n gradV dn
电场中各点的场强等于各点的电势 梯度矢量的
负值。
任一方向的电场强度的分量：
V dV
B3 II dn φ
B2
n
1. 点电荷的电势 Vp =
p
E .dl =
8
q 4 πε 0 r
2
8
p
d r cos 0
0
q 1 1 4o r r a

静电场环路定理

静电场环路定理

视dq为点电荷 dq
dU
4 0
dq U dU
Q 4 0r
4、电势迭加原理
r



L

s

V
dl
4 0r dS
4 0r dV
4 0r
dq
r P
Q
电场中任意一点的电势，等于各带电体单独存在
时在该点产生的电势的代数和
n
U ui
i 1
U
P
P
E
P
dl
E
dl
E
r

dr
பைடு நூலகம் q
4 0
1 r r2
dr

1
4 0
q r
例2 、求电偶极子电场中任一点P的电势
由叠加原理
Y
uP

u1
u2

q
4 0r1

q
4 0r2

q(r2 r1 )
4 0r1r2
P( x, y)
r l r2 r1 l cos

28.8 102V
q1
q2
O
r
q4
q3
②将 q0 1.0 109 c 从 0 电场力所作的功
A0 q0 (u u0 ) q0 (0 28.8 102 ) 28.8 107 J
③求该过程中电势能的改变
A0 W W0 28.8 107 0 电势能
x2
u
q
qx
E 4 0 ( x 2 R2 )32


qxdx
Edx
xp

静电场的环路定理 电势

静电场的环路定理 电势


· · a O
2
均匀带电球体内、外的场强： E内 r 3 0 均匀带电球体内某点的电势
2 腔内电势: U ( r ) U 1 U 2 [( 3 R12 r 2 ) ( 3 R2 r 2 )] 6 0
对O2点，r a, r 0
U r
(2) 点电荷系的电势
qi UA i 4 π ε0 ri
推广：
E Ei
A
U Ui
i
r1
q1
r2 ri
qi
rN
qN
电势叠加原理 （标量叠加）
q2
§3-1-4 静电场的环路定理 电势
(3) 有限连续带电体
【方法一】微元分割＋积分法
Q
dq
e
带电体
r
A
UA ? dU 4 0 r
但在工程技术中，取大地、仪器外壳等为电势零点； （2）电场的电势分布确定后，电场力做功
W AB q0 (U A U B )
§3-1-4 静电场的环路定理 电势
2、电势的计算 (1) 点电荷的电势
q
+
A
积分至无穷远
r
E
q U (r ) 4πε0 r
§3-1-4 静电场的环路定理 电势
3 解：取如图所示C点(0,3R/2) 0, R r 2 根据对称性 U B U C O A x C 补上下半球面成为完整球面后 y B Q R U A 4 0 R 0 R U U UC AC A 3 0 Q 2R UC 4 0 ( 3 R / 2) 3 0 1 R 再由根据对称性 U AB U AC U AC 2 6 0

09-4静电场的环路定理和电势

09-4静电场的环路定理和电势
P



r0

2 π 0r
dr
r
o VA 0 P r r0

2 π0
ln
r0 r
r
关于静电场的实验定律和定理的关系： 静电场 静止电荷
库仑定律
F12 q1q 2 4 π 0 r12
2
激发
高斯定理
e 12

1 E dS
S
0 （ S 内）

qi
平方反比律
-15
J C
1.6 10
-19
5 10 V
4
计算一个电子伏特（eV）的能量
一个电子在电场中经过电势差为1V的两点时，电 场力对它做的功
W qU
1.60 10
19
C 1V 1.60 10
19
J
一个电子伏特的能量
电子伏特是近代物理学中能量单位，虽然它也出现 “伏特”这个名称，但它并非电压的单位，而是能量 的单位
A B
A
AB两点之间的电势差等于场强由A点到B点的线积分
把电荷q从A点移动到B点，电场力做的功 B B WAB qE dl q E dl qU AB
A A
Wba 8 10
15
J
Wab qU ab q(Va Vb )
Vb 8 10
在负电荷形成的电场中，任 一点的电势均为负，且离点 电荷越远的点，电势越高
A A2 A3 1
点电荷系电场的电势 V A E dl
A
q1
q2 r2
r1
E3
场强的叠加原理


第10章静电学-3-静电场环路定理

第10章静电学-3-静电场环路定理

+q
11
(2)电荷分布如图所示, 将点电荷qo从a 经半圆b移到c的 过程中, 电场力对qo的功？
解 Aac qo (Ua Uc )
b
Ua
q
4o R
q
4o R
0
-q
a
+q R
o
c
Uc
q
4 o (3 R)
q
4o R
R
R
q
6o R
Aac
qqo
6o R
12
例10-14 一均匀带电直线段，长为L，电量为q ;取无穷远为电 势零点，求直线延长线上离一端距离为d 的P点的电势。
9
③对于电荷连续分布的带电体，可将其分割为无数多电荷元
dq，每个电荷元dq当作点电荷，其电势为
dU dq 4πε0r
根据电势叠加原理
U
V
dq
4 0r
dl dq dS
dV
积分遍及整个带电体，V是带电体的体积。
电势叠加原理也可以计算多个带电体所产生电场的总电 势，总电势应等于各带电体所产生电场的电势的代数和。
(3)电势差：
b
Uab Ua Ub E dl
a
静电场中a、b两点的电势差等于将单位正电荷由a沿任意路 径移至b过程中电场力做的功。
电势差是绝对量，与电势零点的选择无关。
6
由Wa
q
零势点 E
a
dl ,
得 Wa qUa
由Aab
q
b
E dl
a
Wa Wb ,
得 Aab q(Ua Ub )
(3)等于场强从该点沿任意路径到零势点的线积分。
说明：
(1)电势是相对量，要确定场中各点的电势必须选定电势零点。

09-4静电场的环路定理和电势

09-4静电场的环路定理和电势
电子伏特是近代物理学中能量单位
19
19
J
一个电子伏特的能量
9.4 静电场的环路定理和电势
9.4.3 电势的计算
一、点电荷q的电场中任一场点的电势
无穷远处为电势零点
V ( P)

P

E dl E dr P Edr P
q q dr 2 r 4 πε r 4πε 0 r 0
电场指向电势降落方向
沿电场线方向移动正电荷，电场力做正功， 正电荷的电势能减少，故电势减小。
9.4 静电场的环路定理和电势
我们的心脏附近 的等电势线（类似于 电偶极子）
9.4 静电场的环路定理和电势
电势差
9.5.2 电场强度与电势梯度 E
U AB VA VB V
U AB E l El cos
9.4 静电场的环路定理和电势
电势是相对的，电势差是绝对的
电势差 U V V PQ P Q
单位：1V＝1J/C
P
Q
E dl
二、电势零点 1、电荷只分布在有限区域时，电势零点通常选在无 穷远处。 VP E dl 设Q点在无限远，VQ=0
P
2、 电荷分布延伸到无限远；可选取场中任一点， 合理选择电势零点可使问题简化。
y
P( x, y)
p cos V 4 π 0 r 2
在图示的Oxy坐标系中
q
r
O
r

r
q
r x y
2 2
2
l
x
cos
x x2 y 2
px V 2 2 3/ 2 4 π 0 ( x y )
9.4 静电场的环路定理和电势

物理静电学3

物理静电学3

r dr dr E
1 .点电荷的场中电场力做的功： q q
r
q0
b
dW q0E dr q0Edr q0 40r2 dr
W
b
dW
a
b a
q0q
4 0 r
2
dr
q
q0q ( 1 1 )
rb
ra
a
q0
dr
4 0 ra rb
做功与路径无关
2. 任意静电场中电场力做的功：
b
b
Wab a q0E dl q0 a (E1 E2 En ) dl
2、利用电势定义
电势零点
V
E dl
任一位置
3、利用电场力做功（电势差）
U ab
Wab q0
例：已知某空间的电势函数V=x2+2xy，求(1)电场强度 函数；(2)坐标(2,2,3)点的电势及其与原点的电势差。
Ex
V x
2(x y)
Ey
V y
2x
E Exi Ey j 2(x y)i 2xj
若仍然选取无穷远为电势零点，则由积分可知各点电势将为 无限大而失去意义。此时，我们可以选取某一距带电直导线
p 为 r0的 p0 点为电势零点，则距带电直线为r 的 点的电势：
p'
p0
p0
V E dl E dl 0
dr
p
p'
p' 20r
rp
20 ln r 20 ln r0 20 ln r C
即 V (x, y, z) C的空间曲面称为等势面。
等势面的性质：
除电场强度为零处外，电场线与等势面正交。
证明： dWMN E dl Edl cos 0

【大学物理】静电场的环路定理 电势 等势面 电势梯度

【大学物理】静电场的环路定理 电势 等势面 电势梯度

r r r r－ r l cos
r

r
r+
q l
q+
3. 连续分布电荷电场中的电势 利用电势叠加原理：
dV
dq
dq VP 4 π 0 r
r
P
使用此公式的前提条件为有限大带电体且选无限远 处为电势零点；积分是对整个带电体的积分。 E 利用电势定义式： dl “ 0 ” P
qr E1 3 4 π 0 R
r
q E2 2 4 π 0 r
V1 E1dr E 2 dr
r R
R

q R

R
r
qr q dr dr 3 2 R 4 π r 4 π 0 R 0
2
q q q (3 R r ) 2 2 (R r ) 3 8 π 0 R 4 π 0 R 8 π 0 R
与路径无关
a
dr
任意带电体系产生的电场
任意带电体系都可以看成电荷系 q1、q2、…，移动q0， 静电力所作功为: b b q E •b dr W F dr 0
ab
q0 a• q0 ( E1 E 2 E n ) dr a( L) n b q 0 E i d r ＝ qi q0 ( 1 1 ) a( L) i 1 rbi i 4 0 rai
注意：
• 电势能的零点可以任意选取，但是在习惯上， 当场源电荷为有限带电体时，通常把电势能的零 点选取在无穷远处。 这时，空间a点的电势能：
E pa


a
q0 E dl
• 电势能为电场和位于电场中的电荷这个系统所 共有。

2023-2024学年高二下学期物理竞赛课件：静电场的环路定理和电势

2023-2024学年高二下学期物理竞赛课件：静电场的环路定理和电势

四、电势差
Q Aab qo
bv v a E dl Wa Wb
电势差：
b
E dl
Wa
Wb
a
qo b qvo v
Uab Va Vb
E dl
a
结论：静电场中a,b两点的电势差，在数值上等于 将单位正电荷从a点移至b点电场力所作的功。
Aab W Wa Wb qo (Va Vb )
二、电势能（W）
Wa q0
Wb
保守力作功等于势能的减少 a
b
b
Aab qo a E dl Wa Wb W
Wa,Wb的量值是相对的量；与零势能参考点的选取 有关，而势能的增量 W与零势能点选取无关是绝对
的量.
1、对有限的带电体选无限远处作为电势能零点，
Aa
qo
a
E dl
Wa W
1) rib
电场力是保守力
qi ria
qn a
qo
3、若q0在电场中沿L运动一周
A lqo E dl 0
q0
静电场的环路定理：
l
静电场中电场强度 E的环流为零。
l E dl 0
结论：一定量的电荷在静电场中移动时，电场力所作 的功只与电荷的起点和终点的位置有关，而与路径无 关。即电场力是保守力。静电场是保守场。
致冷系数：
Q2 Q2
A Q1 Q2
K‘系观察者测得相对他静止的棒的长度为：
l0 x2 ' x1 ' l0 称为固有长度
问：在K系中观察者（相对棒运动的观察者）测得
的棒的长度为多少？
他测得棒两端的坐标为x1和x2, t1=t2=t（同时测）
则棒长 l= x2-x1

华南师范大学电磁学第一章 静电学的基本规律(电势与静电能)

华南师范大学电磁学第一章 静电学的基本规律(电势与静电能)

因为各 E i q 0 dr 与路径无关，所以A与路径无关.
b a
a
a
a
结论：静电场力(库 仑力)是保守力！
2
2.静电场的环路定理
静电场中场强沿任意闭合环路的线积分恒 等于零.
E dr 0
L
证明: 将一点电荷q在静电场中沿任意闭合路径走一圈 静电场力是保守力
f dr qE dr 0

dq 4 0 r
d
Q
Q
dφ •P r
2）叠加 式中的 i 和d的物 理意义是 什么？
9
点电荷系的场
连续带电体的场
4. 电势的计算
（1）点电荷场电势公式
P E dr
P

Q
Q 4π 0 r
r
P dr E


dr
E dr
上式表明：当 p 与 E 方向相同时，电势能最小；当 p 与E 方向相反时，电势能最大.由于系统势能最小时的平衡 是稳定平衡，而势能最大时的平衡是不稳定平衡 ,所以 在外电场中，电偶极子总力求转到 p 与 E 方向相同30 .
W pE
五、电荷系的静电能 状态a时的静电能是什么？ 定义1：把系统从状态 a 无限 分散到彼此相距无限远的状态 中静电场力作的功 叫作系统 在状态a时的静电势能简称静 电能.也称为相互作用能(互能). 或:把这些带电体从无限远离 的状态聚合到状态a的过程中 外力克服静电力作的功
点电荷的电场线与等势面
+
19
电偶极子的电场线与等势面
+
20
平行板电容器的电场线与等势面

大学物理电场的环路定理及电势的计算

大学物理电场的环路定理及电势的计算

0
qr
3
(r R ) (r R )
4 0 r
E
令 U 0 ，沿径向积分

1 r
2

U外

P
E 外 d r q 1 r

o
4
r
qr dr
0
r
3
R
r
4 0 r
U外

q 4 0 r
E dr

R
1 r
R


a
E dl
零势点
Ecosdl
a
注意： • 选取零势点的原则：使场中电势分布有确定值 一般,场源电荷有限分布:选 U 0 场源电荷无限分布:不选 U 0 许多实际问题中选 U 地 球 0
[例一] 点电荷 q 场中的电势分布
r E
o
P
解： E
L L
静电场中任意闭合路径
静电场环路定理

E dl 0
L
路径上各点的总场强
静电场强沿任意闭合路径的线积分为零.反映了 静电场是保守力场.
凡保守力都有与其相关的势能，静电场是有势场.
三. 电势能 W
由 A保 E P W
b
A静 电 力 q 0
a
E dl (W b W a ) W a W b
dq 4 0 r
dU
4 r d r
2
4 0 r

rd r 0
R2

由叠加原理：
r
R2
R1
o P
U

dU

静电场的环路定理讲座

静电场的环路定理讲座
（点电荷电势）
例3：求一均匀带电球面的电势分布。
解：由高斯定理知，电场分布为
E
0
rR
1q
4o r 2
rR
当r<R 时
V


r
E

dr

R
E dr
r

E dr
R
1 q
R 4 0 r 2 dr
1
4 0
q R
R
r
.P
当r> R 时
V


r
E
dr
处,VP为正值。这个例题的结果再次表明，在静电
场中只有两点的电势差有绝对的意义，而各点的电
势值却只有相对的意义。
小结： 1.叠加法 (1) 将带电体划分为电荷元 dq。
(2) 选零势点，写出 dq 在场点的电势 dv 。
(3) 由叠加原理得 V Vi 或V dV。
2. 场强积分法(由定义求)
电势能不是点函数只能说电荷q在某位置的势能为多少电势静电场中某点电势等于单位正电荷在该点具有的电势能或将单位正电荷由该点移至零势点过程中静电力所做的功
同 学 们 好
§8-4 静电场的环路定理 电势
静电场对移动带电体要做功，说明静电场具有能量。 一、 静电场力的功
1.点电荷电场中
试探电荷q0从A点经任意路径到达B点。
r
2π R P
x
x
+
+
z +++
dVP

1
4π 0r
qd l 2π R
VP

1
4π 0r
qdl q
q

物理-环路定理

物理-环路定理

三、电势
1、定义
说明：
U E p
“0” E dr
q
A
（1）对有限带电体，通常 选 无限 远为电势零点
U A
E dl
A
但在工程技术中，取大地、仪器外壳等为电势零点；
（2）电场的电势分布确定后，电场力做功
W势
2、电势的计算 (1) 点电荷的电势
Q
dq
e
带电体
r
A
UdUA
? dq
4 0r
dq
U A Q 4πε0r
三、电势
例2 求一均匀带电细圆环，半径为R，带正电
荷量Q。求圆环轴线上任意点P 的电势。
dU p
z
r
O
R dl
三、电势
例3 求均匀带电薄圆盘轴线上任意点P 的电
势。设圆盘半径为R，盘上电荷面密度为 σ 。
dUp
dq 4πε0(r 2
即：静电场是无 旋场。 E 0
二、静电势能
(1) 电势能是电荷与静电场
B
所构成的系统共有的。
L1
(2) 某点电势能的大小与势
能零点的选取有关。
q
A
L2
E
但任意两点间的电势能差 与势能零点选取无关。
“0”
E pA A Fe dr
1E8pA11E年pB泊 松W把eA势B 能
(3) 库用 电仑于 学力静 的F电 解与e 学 析电， 理势发论能E展。p的了关静系：
q+
A
积分至无穷远
E
r
U(r) q
4πε0r
三、电势
(2) 点电荷系的电势
U A
推广：
i
qi 4 π ε0ri

22-场强环路定理、电势

22-场强环路定理、电势
O
2012年4月26日
∞
∞
q 4πε 0 r
2
dr =
q 4πε 0 r
11 11
r
大连理工大学 秦 颖
大连理 工大学
例 5 ：长为 l 的均匀带电直线，电荷线密度为 λ 。 求：图中 p 点的电势。 解：如图选取坐标系，
dU = dq 4π ε 0 r
l
dq = λd x
x
o
r
l
dx
dU
a
p
x
=
作功与检验电荷的电量和电场强度的线积分成正比。 ① 单位正电荷放在a点处， 系统的电势能。 ② 把单位正电荷从 a 点移 到0电势(无限远)处，电场 力所做的功。
2. 电势差：在电场中移动单位正电荷时电场作的功。
Ua − Ub =
∫
∞ a
E ⋅ dr −
∫
∞ b
E ⋅ dr =
∫
b a
E ⋅ dr 电 压
4πε 0 R 球面内 q U= 4πε 0 r 球面外
a
q
均匀带电 λ ln r 无限长直线 U =
2π ε 0
均匀带电 无限长直线
方向垂直于直线
λ E= 2πε 0 r
均匀带电 无限大平面
σ ⋅d U = Ed = 2ε 0
σ 均匀带电 E= 无限大平面 2ε 0
方向垂直于平面
秦 颖
17 17
2012年4月26日
∫
∞
r
qr ⋅ d r = 3 4π ε 0 r
∫
∞
r
dr
4π ε 0 r 4π ε 0 r r 例2 ：求一对正、负电荷连线中垂线上的电势。
O

环路定理

环路定理

电子伏特

电子伏特：能量单位

带有电量+e或-e的粒子飞跃一个电势差为1V的 区间，电场力对它作的功(从而粒子本身获得 这么多能量（动能）——1eV
19 19
1eV 1.6010 C 1V 1.6010
1keV 103 eV 千 1GeV 109 eV 吉
2005.2.
J
直角坐标系表示
E总是沿着指向电势减少的方向——E与Δn相反 在数学场论中把
U :
A:
A :
例题
2005.2.
称作梯度
称作散度
称作旋度
北京大学物理学院王稼军编写
静电场的基本方程的微分形式

数学场论公式
A dS AdV
S V
面积分 体积分
A dl ( A) dS
P
电势能的 改变量
q0在 P点 的电势能
q0在 Q点 的电势能
电势增量

可以与重力做功类比
电场力做正功，电势能将减少 电场力做负功，电势能将增加

2005.2.
北京大学物理学院王稼军编写
电势的定义
0 电 场 付 出 能 量 ， 能 量少 减 APQ WPQ (电 势 能 的 减 少 与 场 源 和 0均 有 关 ， q 电 场 吸 收 能 量 ， 能 量加 增 0
静电场的环路定理

静电场力做功与路径无关 等价 于静电场力沿任意闭合回路做功 恒等于零 E dl 0

在任意电场中取一闭合回路，将试探电荷沿路径 L从 p——Q——P，电场力所做的功为
Q P L
Q
A q0 E d l q0 E d l q0 E d l

静电场的环路定理

静电场的环路定理
a ( L2 )
b
a ( L1 )
v v b q0 E ⋅ dl − ∫
v v q0 E ⋅ dl
环路定理
=0
∫
L
v v E ⋅ dl = 0
该定理还可表达为：电场强度的环流等于零。 该定理还可表达为：电场强度的环流等于零。 根据保守力的定义，任何力场， 根据保守力的定义，任何力场，只要其场强的环流 为零，该力场就叫保守力场 势场。 保守力场或 为零，该力场就叫保守力场或势场。可以引入相应 的势能，即电势能。 的势能，即电势能。
q 4πε 0 x
•从电荷分布求场强，再由场强分布求电势 从电荷分布求场强， 从电荷分布求场强
U P = ∫ E • d r （场强积分法） 场强积分法）
P ∞
例4 求均匀带电球面的电场中电势的分布 解 由高斯定理可以求的球面内外的场强分布为
+ P1 + + + + +
2
r <R r ≥R
对球外一点P 对球外一点
二 电势
某点电势电W 之比只取决于电场， 某点电势电 a与q0之比只取决于电场，定义电该 点的电势 单位：伏特（ ） 电势. 点的电势. 单位：伏特（V） 电势电
W a = q0 ∫
"0"
a
v E ⋅ dl
电势
WA VA = q0
=∫
"0"
A
v E⋅ E⋅ dl
由上式可以看出, 由上式可以看出,静电场中某点的电势在数值上 等于单位正电荷放在该点处时的电势能, 等于单位正电荷放在该点处时的电势能,也等于单位 正电荷从该点经任意路径到电势零点处(无穷远处) 正电荷从该点经任意路径到电势零点处(无穷远处) 时电场力所做的功。 时电场力所做的功。

10静电场2(环路定理、电势)

10静电场2(环路定理、电势)
2
P 1
3.关系：E q V P 0
W EP1 EP2 q0U12
二、点电荷电场的电势 在点电荷的电场中任取一点P，由电势的定义来 计算P的电势：
V

P

E dr E dr
P
q
P

q 40 r
2
P
dr
q 40 r
r
E dr

积分路径选为沿径向的直线 在正点电荷的电场中，电势为正，随r的增大电 势逐渐减小；在负点电荷的电场中，电势为负，随 r的增大电势逐渐增大。并且，在点电荷的电场中， 电势也呈球对称分布。
2．在电场中任一点，电势沿不同方向的空间 变化率不相等。 当 0 时，l 沿着 E 的方向，变化率有最 大值： dV E max dl
即沿某一方向的电势的空间变化率最大， 此最大值称为该点的电势梯度，其方向是 该点附近电势升高最快的方向。
E
三、电势能 静电场力是保守力，可引入电势能的概念。 静电场力做功等于电势能的减少。 在静电场中，试验电荷由点 P 运动到点 P2， 1 则电场力做功为： P W q0 E dr EP EP
2
P 1
1
2
P E P1 、 P2 即分别为 q0 在 P 、 2 点的电势能。 E 1
则有： 1 V2 V
P2
P 1
E dr
1.单位：V， V 1J / C 1 2.通常选取无穷远处或大地为电势零点，则有： EP V E dr P q0
即P点的电势等于场强沿任意路径从P点到 无穷远处的线积分。
电势的值随电势零点选取的不同而不同， 是相对的；而两点的电势差是绝对的，与 电势零点无关。 P U12 V1 V2 E dr
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
P
Q
q0在 P点 的电势能 q0在 Q点 的电势能
WP q0 E d l q0 E d l
P P0
P0
P
电势能减小量
WQ q0 E d l q0 E d l
Q P0
P0
Q
P0 是电势能0点， 电势能等于把电荷从该点移动到电势0点处电场所作功
或，电势能等于把电荷从电势能0点移到该点外力所作功
静电势方程: Poisson Equation
E U
E
电场旋度为0, 有心力场的直接结果.
0
高斯定理:平方反比的直接结果
(U ) 0
电荷为0的地方:
U Poisson Equation 0
2
2U 0 Laplace Equation
有关电势的讨论
电势与场强一样是一个描述场本身性质的物理量，与试探 电荷无关，是标量,是电场理论中的一个重要物理量。 电场线的方向总是由高电势指向低电势 在实际问题中，常取大地或无限远处的电势为零。电势能 的零点是可以任意选取的，改变零点的位置，各点的电势 能和电势的数值将随之变化，但都改变一个相同量，以至 不会影响两点间的电势能差和电势差。 问题
• 把电荷从无穷远处移到该点外力克服电场力所做 的功= 把电荷从改点移到无穷远处 (外力对电场做工)
WP q0 E d l q0 E d l
P
P

电势能的差
电场力 的功
静电场与 q0有能量交换
APQ q0 E d l WPQ (WQ WP )
Q P0
P0
Q
P0 是电势能0点， 电势能等于把电荷从该点移动到电势0点处电场所作功
或，电势能等于把电荷从电势能0点移到该点外力所作功
• 可以与重力做功类比
– 电场力做正功，电势能将减少 – 电场力做负功，电势能将增加
电势的定义
从中扣除q0,即引入电势
P WP U P E d l P0 q0
电场的环量
电场的环量
A E dl
L
电场的环量的物理意义：
Aq Aq q E dl F dl A q L L
它说明静电场的环量表示静电场对沿该闭合路径 移动的单位正电荷所作的功。
电场的环量
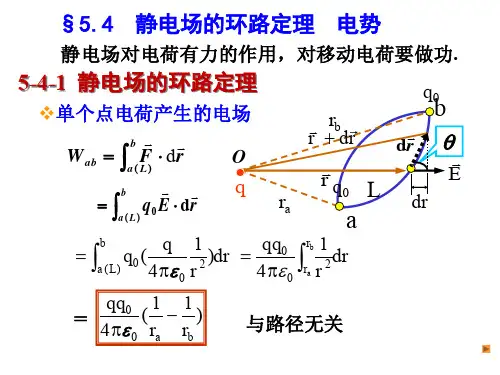
• 单个点电荷产生的场
– 把单位电荷从P移到Q E
如弹性力 f kr 也有类似性质/ 还有重力 F Mg

哪些力具有做功与路径无关这种性质？ 引力 引力势能 如何定义/衡量势能? 重力 重力势能 外力做功的多少, 弹性力 弹性势能 在这个过程中场所获得的能量多 少 静电力 静电势能
他们都是有心保守力
电势能的定义
• 势能产生的原因 (外力做功,静场,那能量哪里去了,什么东 西变化消耗了能量), 代表场潜在的做功的能力. (场里的能 量, 以重力场为例, 场物质的形变, 以弹簧为例,势能的绝对 大小没有实际意义) 物质组成: 物体+场; 场力对外做功, 势能减小, 反之增加.

电势能的差
电场力 的功
静电场与 q0有能量交换
APQ q0 E d l WPQ (WQ WP )
P
Q
q0在 P点 的电势能 q0在 Q点 的电势能
WP q0 E d l q0 E d l
P P0
P0
P
电势能减小量
WQ q0 E d l q0 E d l
静电场的总结(2): 三个基本量的关系
静电学: 库仑定律+叠加原理

U
E
电势能的定义
• 势能产生的原因 (外力做功,静场,那能量哪 里去了,什么东西变化消耗了能量), 场潜在 的做功的能力. (场里的能量, 以重力场为例, 场物质的形变, 一弹簧为例)
• 把电荷从无穷远处移到该点外力克服电场 力所做的功= 把电荷从改点移到无穷远处 P0 P ) (外力对电场做工 WP q0 E d l q0 E d l
• 把电荷从无穷远处移到该点外力克服电场力所做 的功= 把电荷从改点移到无穷远处 (外力对电场做工)
WP q0 E d l q0

P
P0

E dl
电势能的定义
• 势能产生的原因 (外力做功,静场,那能量哪里去了,什么东 西变化消耗了能量), 代表场潜在的做功的能力. (场里的能 量, 以重力场为例, 场物质的形变, 以弹簧为例,势能的绝对 大小没有实际意义) 物质组成: 物体+场; 场力对外做功, 势能减小, 反之增加.
•在材料/器件模拟中, 我们求解Poisson Equation(Poisson Solver), 得到电势,来得到体 系电荷的总能. •方法的变化: 1:从力出发来求解体系的状态2:把能量作为出发点来求解体系 两者等价, 但后者往往更加方便,因为前者是矢量运算,后者是标量运算.
静电场的总结(1): 基本定律
• 闭合面外的电荷虽然对通量没有贡献，但并不 意味着不影响闭合面上的电场，高斯面上的场 强是空间所有带电体所产生的 • 高斯定理是静电场的一条重要的定理，有其重 要的理论地位，是静电场基本方程之一 ，它 是由库仑定律导出的， 反映了电力平方反比 律 ，如果电力平方反比律不满足，则高斯定 理也不成立。
每项均与路径无关，只与位置有关
静电场力做功只与起点终点有关，与路径无关
静电场的环路定理（积分形式）
在任意电场中取一闭合回路，沿路径L 从 PQP，电场力所做的功为
W E dl E dl E dl
L P ( L1 ) Q ( L2 ) Q P
E dl E dl 0
APQ E d l E cosdl
P P
Q
Q
Edr
P
Q
rQ
rP
q Edr 4 0
rQ rP
dr rP r 2
rQ
APQ
q 4 0

dr q 1 1 r 2 4 0 r r p Q
静电场力做功只与起点终点有关，与路径无关
与q0的大小无关，只和位置有关系 (类似电场强度， 是场的一种特性)
• 为了确定某点的值，还需要选择零点 • 一般选择无穷远为势能零点。
U ( p) E d l E d l
P
P

P点电势值公式
有关电势的讨论
电势与场强一样是一个描述场本身性质的物理量，与试探 电荷无关，是标量,是电场理论中的一个重要物理量。 电场线的方向总是由高电势指向低电势 在实际问题中，常取大地或无限远处的电势为零。电势能 的零点是可以任意选取的，改变零点的位置，各点的电势 能和电势的数值将随之变化，但都改变一个相同量，以至 不会影响两点间的电势能差和电势差。 问题
1 E dS
S
0
q
S内
E
0
大家喜欢标量函数的运算. 简化计算. 探索更加简单的 方法
矢量运算, 多维微分或积分
高斯定理说明
• 闭合面内的电荷决定通过闭合面的电通量,只 要 S内电荷不为零 ，则通量不为零——有源
– 正电荷 —— 喷泉形成的流速场—— 源 – 负电荷 —— 有漏洞水池中的流速场——漏
• 静电力是有心力，但高斯定理只给出了源和通 量的关系，并没有反映静电场是有心力场这一 特性，它只反映静电场性质的一个侧面（下一 节还要讲另一个定理——环路定理）
– 一般不能直接说高斯定理与库仑定律完全等价 – 若不添加附加条件（如场的对称性等），无法从高 斯定理导出库仑定理 – 电力平方反比律 ——Gauss定理 – 电荷间的作用力是有心力 ——Stokes定理
U ( p) E d l E d l
P
P

P点电势值公式
电势的一般表达式
U (r ) E d l P
q1 (r ) d l 3 4 0 P r

1
q1 r cos( )dl 3 4 0 P r

1
q1 dr 2 4 0 P r
q r E 3 0 4 0 r
直接推导：可以从一个点电荷产生的场的旋度和叠加原理来获得一般 场的旋度为0的结论 q r E 4 0 r 3
静电场的环路定理(讨论)
• 环路定理表明，静电场是一个无旋场，静电场不会有闭合的电场线。 • 在证明Gauss定理中，说电力必须与r2成反比，由环路定理的证明过程可 以看出，它不要求库仑定律是严格的平方反比。
选无穷远为零点？选地为零点即地和无穷远等电势吗？
q0 4 0
q2 q2 qn qn q q 1 1 r r r r r r p 1 Q 1 p 2 Q 2 pn Qn
P 到 q1 的距离
Q 到 q1 的 距离
电场的环量
• 点电荷组产生的场
APQ
q1 , q2 ,, qn E E1 E2 En Q Q E dl E dl P P Q Q Q E1 dl E2 dl En dl P P P
• 电场力做正功，电势能将减少; 电场力做负功，电势能将增加
U U dl E dl
由于位移矢量的任意性:
E U
• 将电场强度矢量和静电势标量直接联系起来了. • 可以将复杂的3维矢量问题约化为一个标量问题. 为电场强度的求解 提供了第3种方法 (1,直接求解, 2,高斯定理). • 这个关系是电场是有心保守力场的直接结果, 与平方反比关系无关.