当前位置：文档之家 › 静电场高斯定理、环路定理

静电场高斯定理、环路定理

  • 格式：ppt
  • 大小：1.94 MB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

9-5-静电场的环路定理解析

9-5-静电场的环路定理解析

•电势是标量，有正有负； •电势的单位：伏特 1V=1J.C-1； •电势具有相对意义，它决定于电势零点的选择。 在理论计算中，通常选择无穷远处的电势为零；
•在实际工作中，通常选择地面的电势为零。 •但是对于“无限大”或“无限长”的带电体， 只能在有限的范围内选取某点为电势的零点。
3、电势差
在静电场中，任意两点A和点B之间的电势之差， 称为电势差，也叫电压。
步骤：
(1)先算场强 (2)选择合适的路径L
(3) 积分(计算)
•2、利用点电荷的电势公式和电势的叠加原理
dq dV
4 0r
dq
V 4 0r
要求电荷的分布区域是已知的；
当电荷分布在有限的区域内，可以选择无穷
远点作为电势的零点的；而当激发电场的电荷分
布延伸到无穷远时，只能根据具体问题的性质，
在场中选择某点为电势的零点。
E
1
4 0
Q r2
er
B
Q
rB
r
rA
dr C r
A
dl
er
E
dW
1
4 0
Qq0 r2
er
dl
1
4 0
Qq0 r2
dr
rB
W
Qq0
dr Qq0 ( 1 1 )
rA 40r 2
40 rA rB
在点电荷的静电场中，电场力对试验电荷所作
的功与其移动时起始位置与终了位置有关，与
其所经历的路径无关。
V
p 3xy
Ey
y
4 0
x2 y2 5/2
-q
+q
电偶极子的延长线上 y 0
2p 1
E x 4 0 x 3
10-4高斯定理和环路定理

10-4高斯定理和环路定理


B
o
R
B d l 0 I
l
dl
l
二、安培环路定理
1. 安培环路定理的表述
B dl 0 ?
l
表述: 在真空的稳恒磁场中，磁感应强度 B 沿任一
闭合路径的积分的值，等于 0 乘以该闭合路径所 包围的各电流的代数和. 表达式: 注意 电流 I 正负的规定 ： I 与 L 成右螺旋时， 为正；反之为负.
定理表达式中B是闭合积分环路上各点的
总磁感应强度,是由空间所有电流共同激发的
L
闭合环路不包围的电流对 B dl 没有贡献
该定理可用于求解对称性磁场的B分布
与静电场的高斯定理的应用相似
B dl 0 说明磁场不是保守场,而是非保守场,也叫涡旋场
L
定理只适用于稳恒电流的磁场
对称性分析 选择合适的高斯面 根据定理求解
二、安培环路定理的应用
1.分析磁场的对称性：根据电流的分布来分析；
一个重要结论: 若 Idl1 和 Idl2 关于某个面为镜象对称,则 此对对称电流元在该面上产生的合磁场 必与该面垂直
2. 选取合适的闭合积分路径和积分回路的绕向
过场点 积分路径上各点B大小相等, B//dl 规则曲线

m2 （2）计算 单位：韦伯(wb) 1Wb=1T·
a . dS垂 直B
b. dS跟B成角
d m B dS
d m B cosdS
c. 通过任一曲面的 磁通量
B dS
m B dS
S
B
dS dS n 源自B例 如图载流长直导线的电流为 I , 试求通过矩 形面积的磁通量.
关于静电场的高斯定理和静电场的环路定理

关于静电场的高斯定理和静电场的环路定理

关于静电场的高斯定理和静电场的环路定理静电场的高斯定理和静电场的环路定理是库仑定律的推论，所以称之为定理。

由于库仑定律是静电场的基本规律，适用于静电场，所以库仑定律的推论也适用于静电场。

电场有许多种：静电场（由静止电荷激发）、恒定电场（由运动然而空间分布不随时间改变的电荷体系激发的电场）、位电场（可以在其中建立电位函数的电场，位电场的电场强度等于电位的负梯度，分为恒定的与时变的，静电场和恒定电场就属于恒定的位电场）、涡旋电场。

静电场的高斯定理的文字表述是：静电场中，电场强度穿出闭合曲面的通量等于该闭合曲面所包围的总电量除以真空电容率。

静电场的高斯定理的数学表述式是：in 0d i S qE S ε⋅=∑⎰ 。

英国著名物理学家麦克斯韦首先假设静电场的高斯定理的数学表示式in 0d i S q E S ε⋅=∑⎰ 适用于一切电场，也就是说，实际的电场强度（即总电场强度）穿出闭合曲面的通量等于闭合曲面内的总电量除以真空电容率。

这个假设后来被实验证实了。

正因为这个原因，数学表示式in 0d i S qE S ε⋅=∑⎰ 也叫做高斯定律。

由于德国数学家高斯根据库仑定律推出的这个静电场规律的数学表示式是普遍适用的，这让高斯在电磁学中享有很高的声誉。

in 0d i S q E S ε⋅=∑⎰ 有好几个称谓：高斯定理、高斯通量定理、电场的高斯定理、电场的高斯通量定理、高斯定律、高斯通量定律、电场的高斯定律、电场的高斯通量定律。

对于静电场，这个规律叫做静电场的高斯定理，或者静电场的高斯通量定理。

高斯在数学方面有一项重要成就，叫做高斯公式（也可以叫做高斯通量公式或者高斯散度公式）。

高斯公式的数学表示式是d d S Vf S f V ⋅=∇⋅⎰⎰ 。

其含义是：矢量场穿出闭合曲面的通量等于矢量场的散度在闭合曲面所包围的空间区域内的体积分。

高斯定理是电（磁）学规律，高斯公式是纯粹数学规律，两者截然不同。

但是把两者结合起来，就可以推出0E ρε∇⋅= 。

高斯定理和环路定理

高斯定理和环路定理

高斯定理和环路定理高斯定理和环路定理是电磁学中两个重要的基本定律。

它们描述了电场和磁场的分布和变化规律，是理解电磁现象的基础。

本文将对高斯定理和环路定理进行详细介绍。

一、高斯定理高斯定理又称为高斯电场定理，它是描述电场分布的基本原理之一。

高斯定理表明，电场通过一个闭合曲面的通量等于该曲面内部电荷的代数和与真空介电常数的乘积。

具体来说，如果一个闭合曲面内部有正电荷和负电荷，那么通过这个曲面的电场通量将等于正电荷和负电荷的代数和除以真空介电常数。

高斯定理的数学表达式为：∮E·dA = Q/ε0其中，∮E·dA表示曲面上的电场通量，Q表示曲面内部的电荷总量，ε0为真空介电常数。

高斯定理的应用非常广泛。

例如，在计算电场分布时，可以通过选择适当的高斯曲面来简化计算。

通过高斯定理，可以快速得到电场在各个位置的大小和方向。

高斯定理也被用于推导其他电场分布的公式，如电偶极子和球壳电场的公式。

二、环路定理环路定理又称为安培环路定理，它是描述磁场分布的基本原理之一。

环路定理表明，磁场沿着一个闭合回路的线积分等于该回路内部电流的代数和乘以真空磁导率。

具体来说，如果一个闭合回路内部有电流通过，那么沿着这个回路的磁场线积分将等于电流的代数和除以真空磁导率。

环路定理的数学表达式为：∮B·dl = μ0I其中，∮B·dl表示回路上的磁场线积分，μ0为真空磁导率，I表示回路内部的电流。

环路定理的应用也非常广泛。

例如，在计算磁场分布时，可以通过选择适当的环路来简化计算。

通过环路定理，可以快速得到磁场在各个位置的大小和方向。

环路定理也被用于推导其他磁场分布的公式，如长直导线和环形线圈的磁场公式。

三、高斯定理与环路定理的关系高斯定理和环路定理是电磁学中两个基本定理，它们描述了电场和磁场的分布与变化规律。

虽然它们描述的是不同的物理量，但在某些情况下，它们是相互关联的。

例如，在静电场中，高斯定理可以推导出库仑定律，即电荷间的相互作用力与它们之间的距离成反比。

8-3-4静电场高斯定理、环路定理

8-3-4静电场高斯定理、环路定理


（3）无限大带电平面电场中的电场线
+
+ + + + + + + +
+
+
+++++++++
3、电场线（E）线的特点: （1）曲线上每一点的切线方向与该点的场强方向相一致； （2）电场线起始于正电荷，终止于负电荷，不形成闭合曲线； （3）任何两条电场线不会相交。 按照电场线的规定所作出的电场线只能定性描述电场的分布，而无法 反映场强的大小。 为了反映场强大小分布，可利用电场线的疏密程度来反映 。密、强； 疏、弱。 4、电场线数密度：垂直穿过单位面积的电场线数 N 均匀电场： 电场线数密度 S E dN N 非均匀电场： 电场线数密度 ds S 规定： 电场线数密度等于场强大小 即 均匀电场： E 非均匀电场：
S
＋
8.3.3 真空中的高斯定理 １、求几种情况下的电场强度通量
（１）包围点电荷球面的电场强度通量 通过
R S
球面上取面元 ds ,
∵球面上： E
ds 的电场强度通量为
d e E ds
q 方向：沿半径向外。 40 R 2 1 q d e E ds ds 2 40 R 1 通过球面的电场强度通量 e E ds
ra
r q0 q a 0
dl θ F q0 E
q0 q q0 q 1 q0 q 1 ( ) 4 0 ra rb 4 0 rb 4 0 ra
（2）任意静电场 元功： 总功：
dA F dl q0 E dl
（２）包围点电荷，任意闭合曲面Ｓ的电场强度通量
高斯定理和环路定理

高斯定理和环路定理


E
++
+ o+
++
P
dSE
S +e S
E S E dS 左 E dS 右 E dS 2ES
高斯面所包围的电量为
q eS
由高斯定理可知 2ES e S / 0
由此可知，电场强度为 电场强度的方向垂直于带电平面。
E e 2 0
e 0 电场强度方向离开平面 e 0 电场强度方向指向平面
（2）对于闭合曲面
约定：闭合曲面以向外为曲面法线的正方向。
出发点：一条穿过闭和曲 面的电场线对这个闭和曲

/2



n
面的电通量的贡献为零

E
电场线穿出闭合面为正通量，
电场线穿入闭合面为负通量。 n 0 / 2 E
二、高斯定理
1. 高斯定理的内容 在真空中的静电场内，通过任意闭合曲面的电通量，
3、关于高斯定理的说明
1、通过任意闭合曲面的电通量只决定于它所包围的电荷 的代数和，与闭合曲面内的电荷分布无关,闭合曲面外的电荷 对其电通量无贡献。但电荷的空间分布会影响闭合面上各点处 的场强大小和方向；
2、高斯面上电场强度是封闭曲面内和曲面外的电荷共同产 生的，并非只有曲面内的电荷确定；
3、 q 是电荷的代数和, qi 0 并非高斯面内一定无
电荷,E有d可s 能 是面内0正负电并荷非数高目斯相面同上;场强一qi 定处0处为也零只若是；表明,
s
e
Φ 0 4、 e
只能说明高斯面内电量的代数和为零,并非一定没
有电力线穿过;可能是穿进和穿出的一样多而以净电场线数目为零。
三、高斯定理的应用举例
静电场环路定理

静电场环路定理


视dq为点电荷 dq
dU
4 0
dq U dU
Q 4 0r
4、电势迭加原理
r



L

s

V
dl
4 0r dS
4 0r dV
4 0r
dq
r P
Q
电场中任意一点的电势，等于各带电体单独存在
时在该点产生的电势的代数和
n
U ui
i 1
U
P
P
E
P
dl
E
dl
E
r

dr
பைடு நூலகம் q
4 0
1 r r2
dr

1
4 0
q r
例2 、求电偶极子电场中任一点P的电势
由叠加原理
Y
uP

u1
u2

q
4 0r1

q
4 0r2

q(r2 r1 )
4 0r1r2
P( x, y)
r l r2 r1 l cos

28.8 102V
q1
q2
O
r
q4
q3
②将 q0 1.0 109 c 从 0 电场力所作的功
A0 q0 (u u0 ) q0 (0 28.8 102 ) 28.8 107 J
③求该过程中电势能的改变
A0 W W0 28.8 107 0 电势能
x2
u
q
qx
E 4 0 ( x 2 R2 )32


qxdx
Edx
xp
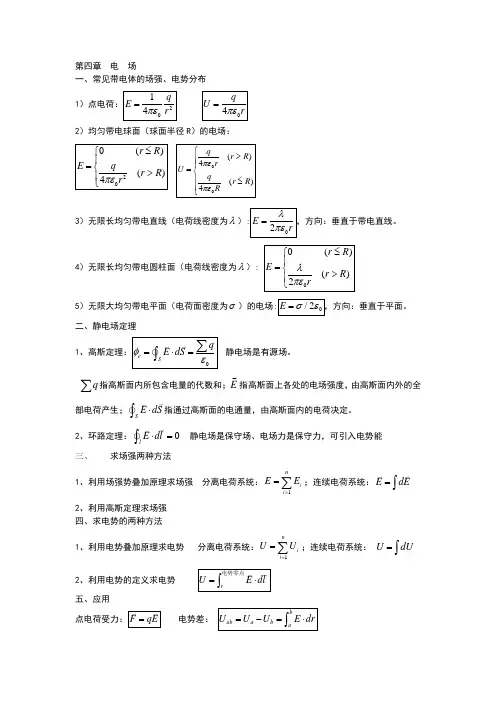
大学物理常用公式(电场磁场 热力学)

大学物理常用公式(电场磁场 热力学)

第四章 电 场一、常见带电体的场强、电势分布2）均匀带电球面（球面半径 ）的电场：3）无限长均匀带电直线（电荷线密度为）: E = ，方向：垂直于带电直线。

2r( rR ) 4）无限长均匀带电圆柱面（电荷线密度为）:E =2r (rR )5）无限大均匀带电平面（电荷面密度为）的电场: E =/20 ，方向：垂直于平面。

二、静电场定理 1、高斯定理：e = ÑE v dS v = q 静电场是有源场。

Sq 指高斯面内所包含电量的代数和；E 指高斯面上各处的电场强度，由高斯面内外的全 部电荷产生； Ñ E vdS v 指通过高斯面的电通量，由高斯面内的电荷决定。

2、环路定理： Ñ E v dl v =0 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统： E v = E v i ；连续电荷系统： E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统：U =U i ；连续电荷系统： U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力： F = qE电势差： U ab =U a -U b = b EdraE =1 qU =q4r 24r1）点电荷：E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能：W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -（W b -W a ）六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为 0，导体是一个等势体。

2）、导体表面的场强处处垂直于导体表面。

E v ⊥表面。

导体表面是等势面。

2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。

大学物理常用公式(电场磁场-热力学)

大学物理常用公式(电场磁场-热力学)

第四章 电 场一、常见带电体的场强、电势分布 1）点电荷：2014q E r πε=04q U rπε=2）均匀带电球面（球面半径R ）的电场：200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3）无限长均匀带电直线（电荷线密度为λ）:02E rλπε=，方向：垂直于带电直线。

4）无限长均匀带电圆柱面（电荷线密度为λ）: 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5）无限大均匀带电平面（电荷面密度为σ）的电场:0/2E σε=，方向：垂直于平面。

二、静电场定理 1、高斯定理：0e Sq E dS φε=⋅=∑⎰静电场是有源场。

q ∑指高斯面内所包含电量的代数和；E指高斯面上各处的电场强度，由高斯面内外的全部电荷产生；SE dS ⋅⎰指通过高斯面的电通量，由高斯面内的电荷决定。

2、环路定理：0lE dl⋅=⎰ 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统：1ni i E E ==∑；连续电荷系统：E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统：1nii U U==∑；连续电荷系统： U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力：F qE = 电势差： bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为0，导体是一个等势体。

2）、导体表面的场强处处垂直于导体表面。

E ⊥表表面。

导体表面是等势面。

2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。

2）导体腔内无电荷： 电荷都分布在导体外表面，空腔内表面无电荷。

3）导体腔内有电荷+q ，导体电量为Q ：静电平衡时，腔内表面有感应电荷-q ，外表面有电荷Q ＋q 。

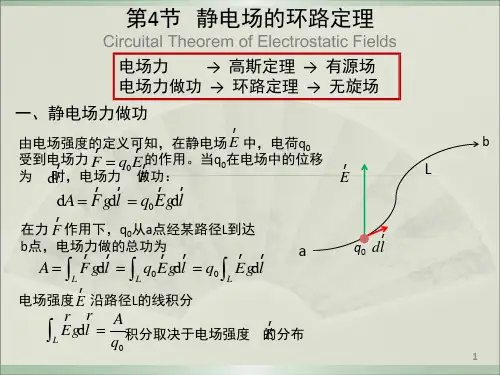
静电场的环路定理

静电场的环路定理


已知q的电场分布 E
根据定义, P点的电势为
4
q
0r
2
er
VP


P

E dl

r
q
40r
2Pdr4q04r2qe0rrP dl
q > 0时, VP为正, r V, r处V= 0 min q < 0时, VP为负, r V, r处V = 0 max
2.电场强度与电势梯度的关系
根据电势差的定义, 把单位正电荷从P1移到P2 电场力所作的功为：
dA E dn V (V dV )
r E
dn
n
P1
P2
V V dV
E dn dV
E


dV dn
grad V
E
ቤተ መጻሕፍቲ ባይዱ

dV dn
n
r E grad V
r 即:电场中某点的场强 E 等于该点电势梯度的负值
无意义
VP

P
E
dr
rP
2 0r
dr

2 0
ln
rP
r
P
P'
令某处 r = r0（有限值） V=0，则
VP

P0
P
E
dl

P
P
E dl

P0
P
E dl
r0 P0

P
P
2
0r
dr

2 0
ln
r0 r
可见：当电荷分布到无穷远时，
22
归纳 电场强度与电势的关系
积分关系：
4 静电场的环路定理

4 静电场的环路定理

B
高压发生器
静电力做正功， 电势能减少； 静电力做正功， ∆A > 0, WA > WB , 电势能减少； 静电力做负功， 电势能增加。 静电力做负功， ∆A < 0, WA < WB , 电势能增加。
电势能和重力势能一样，是一个相对量， 电势能和重力势能一样，是一个相对量，先要规定电 势能为0的参考点 如果参考点p0确定 的参考点。 确定， 势能为 的参考点。如果参考点 确定，则
R2 q1 R1 o Ⅰ Ⅱ
V=
1
r ≤ R1 R1 ≤ r ≤ R2
Ⅲ
r ≥ R2
无限长均匀带电圆柱面的电场。圆柱半径为R， 例6 无限长均匀带电圆柱面的电场。圆柱半径为 ，单 试求其电势分布。 位长度上的带电量为 + λ ，试求其电势分布。 解：电场分布也应有柱对称性 (1) r <R (2) r >R (2) r >R
∞ r r r r r r = ∫ E1 ⋅ dl + ∫ E2 ⋅ dl + ....... + ∫ En ⋅ dl P P
P ∞ P ∞ ∞
= u1 + u2 + ...... + un = ∑ ui = ∑
i =1
n
P
4πε 0 ri
qi
各点电荷单独存在时在该点电势的代数和 各点电荷单独存在时在该点电势的代数和, 代数和 注意(电势是一个标量) 电势是一个标量 注意 电势是一个标量
无旋场
2. 电势（Electric potential） ）
2.1 电势能
由环路定理知，静电场是保守场。 由环路定理知，静电场是保守场。 保守场必有相应的势能， 保守场必有相应的势能，对静电场 则为电势能。 则为电势能。 静电力的功，等于静电势能的减少。 静电力的功，等于静电势能的减少。

静电场的高斯定理和环路定理

静电场的高斯定理和环路定理
静电场是指电荷分布静止不动的情况下所产生的电场。

在静电场中，高斯定理和环路定理是两个非常重要的定理。

高斯定理是描述电场通量的定理，它表明：在任何闭合曲面内，电场的通量等于该曲面内的电荷总量除以介质常数。

即：ΦE = ∫E · dS = Q/ε0
其中，ΦE表示电场的通量，E表示电场强度，dS表示曲面元素的面积，Q表示该曲面内的电荷总量，ε0表示真空中的介电常数。

环路定理则是描述电场中电势的变化的定理，它表明：沿着任意闭合回路的线积分等于该回路内的电荷的代数和除以电容。

即：∮Edl = 0
其中，∮Edl表示沿着回路的电场强度的线积分，E表示电场强度，dl表示回路的微元长度，如果回路内有电荷则其代数和为Q。

电容则是电荷和电势之间的比值。

高斯定理和环路定理是静电学中的基本定理，对于研究静电场的性质和计算电场强度、电势等都具有重要的意义。

- 1 -。

5、电势


b rb q ra
r+dr
r
v dl
q a
0
r r r r dA = F ⋅ dl = q0 E ⋅ dl = q0 Edl cos θ = q0 Edr
第一章 静电场的基本规律 5
q0从a移动到 的过程中电场力做的总功为： 移动到b的过程中电场力做的总功为 移动到 的过程中电场力做的总功为：
A = ∫ dA = ∫ q0 Edr
r r r r
q 4πε 0 r
2
dr =
q
q 4πε 0 r
dr = q 4πε 0 R
16
2.当r<R 时 当
V =∫
∞ r r r r
r r ∞ r ∞ R ∞ r E ⋅ dl = ∫ E ⋅ dr = ∫ Edr = ∫ 0dr + ∫
R
4πε 0 r
2
第一章 静电场的基本规律
例2：求无限长均匀带电直线的电场中的电势分布。 求无限长均匀带电直线的电场中的电势分布。
b
= A1 + A2 + L + An
第一章 静电场的基本规律 7
qn qn q0 q1 q1 q2 q2 A= − + − + L + − 4πε 0 ra1 rb1 ra 2 rb 2 ran rbn
λ 由高斯定理知场强为： 解：由高斯定理知场强为： E = 2πε0r
方向垂直于带电直线。 方向垂直于带电直线。
若仍然选取无穷远为电势零点， 若仍然选取无穷远为电势零点，则由积分可知各点电势将 为无限大而失去意义。 为无限大而失去意义。 点为电势零点， 因此可以选取某一距带电直导线为r0的p0点为电势零点， 点的电势为： 则距带电直线为r 的p点的电势为： P v v P′ v v P v v 0 0 r P VP = E ⋅ dl = ∫ E ⋅ dl + ∫ E ⋅ dl P P P′ P0 P v v P 0 0 P′ = 0 + ∫ E ⋅ dl = ∫ Edl

静电场

静电场一个基本定律和一个叠加原理：库伦定律和电场强度叠加原理两个重要定理：高斯定理和静电场环路定理两个基本计算：电场强度和电势计算两个计算思路：定义式计算和特定情况下的简捷计算（高斯定理）一．知识点1. 库伦定律2. 静电场叠加原理3. 电偶极矩定义4. 电通量定义及其计算5. 高斯定理6. 静电场环路定理7. 电场力是保守力电势能概念掌握电场力做功和电势能的关系电势差8. 电势的定义及其含义二．基本计算1．电场强度计算1）根据静电场叠加原理，可以计算任意形状的带电体在空间激发的电场（1）点电荷点电荷系（2）连续带电体：1维、2维和3维体系熟悉简单带电体系在空间电场的分布电偶极子：均匀带点细棒：荷电圆环：荷电圆盘：2) 通过高斯定理，可以求解电荷分布对称体系的电场强度分布，如：均匀带电的无限长细棒：均匀带电球面：均匀带电球体：均匀带电的无限大平面薄板：均匀带电的无限长圆柱体：2. 电通量的计算，功、电势能的计算3. 电势的计算1）根据定义，可直接计算，计算中注意：积分上限为势能零点点电荷电势：点电荷系电势：均匀带正电圆环轴线上电势：2）如已知电场强度，可以通过电场强度对选择路径的积分得到均匀带电球体电场中的电势：均匀带电的无限长圆柱体：均匀带电的球面重点掌握利用高斯定理求解对称带电体系的电场强度分布，并进一步会计算电势。

注：以上知识点涉及到的例题和习题是复习重点。

三． 练习题1. 点电荷在真空中的分布如图所示，图中S 为闭合曲面，则通过闭合曲面的电通量⎰⋅sS d E = ，式中E是哪些点电荷在闭合曲面上任一点产生的场强的矢量和？答：是 。

题1图 题2图2. 如图所示，在场强为E 的均匀电场中，A,B 两点距离为d ，AB 连线方向与E方向一致，从A 点经任意路径到B 点的场强线积分l d E AB⋅⎰= 。

3. 有4个点电荷，电量都是Q ，分别放在边长为a 的正方形的四个顶点上，在中心放一点电荷q 0 ，当q 0= 时，各点电荷都处于平衡。

静电场高斯定理环路定理.pptx


e de E cosds
S
S
E
ds E n
S
E
若曲面S为闭合曲面,
则
e
E cosds
S
法线方向的规定：闭合曲面上各点的法线方向垂直
向外为正方向。
ds
B A
C
分析：
A点处，场线穿进， / 2, cos 0, de 0为负值。 B点处，场线穿出， / 2, cos 0, de 0为正值。 C点处，场线与表面向切， / 2, cos 0, de 0.
F dl
l
l q0E dl 0
说明静电场是保守
l E dl 0
场，是无旋场。
结论：静电场中，场强沿任意闭合路径的线积分（环流）等于零。该结论称 为静电场的环路定理（环流定理）。
或者说将单位正电荷绕任意闭合路径一周静电场力所作的功等于零。
第15页/共29页
8.4.2 电势能
静电场力作功与路径无关，仅与始末位置有关，位置确定做功本
（2）电场中a点的电势，等于将单位正电荷由a点移到无穷远点静电场力 所作的功。
电势的单位：
焦尔/库仑
伏特 V ,
第17页/共29页
1V=1JC-1
8.4.4
电势差
Ua
E dl
a
Ub b E dl
Ua a
E
Ub b
∴电势差 Uab=Ua - Ub E dl E dl
∴ 以柱体轴线为轴线，取以r为半径，高为h的闭合柱面S为高斯面。
根据高斯定理
S
E
dS
1
q
SE dS E ds E ds E ds
上底面 / 2 侧面 0 下底面 / 2
r S

物理-环路定理


三、电势
1、定义
说明：
U E p
“0” E dr
q
A
（1）对有限带电体，通常 选 无限 远为电势零点
U A
E dl
A
但在工程技术中，取大地、仪器外壳等为电势零点；
（2）电场的电势分布确定后，电场力做功
W势
2、电势的计算 (1) 点电荷的电势
Q
dq
e
带电体
r
A
UdUA
? dq
4 0r
dq
U A Q 4πε0r
三、电势
例2 求一均匀带电细圆环，半径为R，带正电
荷量Q。求圆环轴线上任意点P 的电势。
dU p
z
r
O
R dl
三、电势
例3 求均匀带电薄圆盘轴线上任意点P 的电
势。设圆盘半径为R，盘上电荷面密度为 σ 。
dUp
dq 4πε0(r 2
即：静电场是无 旋场。 E 0
二、静电势能
(1) 电势能是电荷与静电场
B
所构成的系统共有的。
L1
(2) 某点电势能的大小与势
能零点的选取有关。
q
A
L2
E
但任意两点间的电势能差 与势能零点选取无关。
“0”
E pA A Fe dr
1E8pA11E年pB泊 松W把eA势B 能
(3) 库用 电仑于 学力静 的F电 解与e 学 析电， 理势发论能E展。p的了关静系：
q+
A
积分至无穷远
E
r
U(r) q
4πε0r
三、电势
(2) 点电荷系的电势
U A
推广：
i
qi 4 π ε0ri

第10章2静电场的基本规律


面外电荷

S
Ek 1 dS En dS
S


i 1
k
qi
q 14 是指面内电荷代数和
0

q
0
右边
i 1
qi
k
0
左边=右边 证毕
连续带电体
q ρdV 或 q σdS 或 q λdl
V s l
1 e E dS S 0
E E1 Ek Ek 1 En
面内电荷
S
左边 e E dS

S S
E1 dS Ek dS

S
( E1 Ek Ek 1 En ) dS
q 左边 e E dS 0 右边 0 S 0
左边=右边
e 0
面外电荷对电通量无贡献
E
13
(3)点电荷系：设有 1、2、·· 个电荷在闭合面内， ·、k k+1、k+2、·· 个电荷在闭合面外 ·、n 由场叠加原理，高斯面上的场强为：
R n
E
高斯面
与电荷q全部集中在中心的场的分布相同（r>R）
4 3 r3 面内电荷代数和为 q V r q 3 4 33 R R 3 1 rq q
作半径为 r 的球面；
E
4 0 R 3
r
20
结论：球体内，E∝r; 球体外，E ~ q集中在球心的点电荷的电场。 r qr (r R) E (r ) 4 R 3 3 0 0 E (r ) q (r R) 2 4 0 r
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

de E ds
∵球面上：
q E 40R2
方向：沿半径向外。
1 q
de E ds 40 R2 ds
1q
通过球面的电场强度通量
e
E ds
S
S 4 0
R2 ds
6
通过球面的电场强度通量
e
E ds
S
1
S 4 0
q R2
ds
1
4
0
q R2
4R 2
q
0
即
E ds
ds
E n
S
e de E cosds
E
S
S
若曲面S为闭合曲面, 则
e
E cosds
S
法线方向的规定：闭合曲面上各点的法线方向
垂直向外为正方向。
ds
B A
C
分析：
A点处，场线穿进， / 2, cos 0, de 0为负值。
B点处，场线穿出， / 2, cos 0, de 0为正值。 C点处，场线与表面向切， / 2, cos 0, de 0.
在同一高度上移动物体。
20
2、电子伏：能量单位，电子经过1伏的电势差所获得的能量。
1eV=1.602×10-19（J）
3、电势的计算 电势叠加原理
E
p
（1） 点电荷的电势
r
上底面 / 2 侧面 0 下底面 / 2
S
h
0 E 2r h 0 E 2r h
E q
2 rh
（1）当r < R时，
q r2h
r 2h
E
r
2rh 2
均匀带电直圆柱体内的场强与半径 r 成正比。
12
E r
高斯面S
2
R
（2）当r > R时，
S
q R2h 0
E SdS
E4r 2
1
q
E
R
R
3 0
3
E 1 4
q
r2
均匀带电球体 内场强与半径 r 成正
比
O
R
r
当0< r < R时，
q 4 r3
3
E r 3
当R< r < ∞时，∑q=q
E 1 q R3 40 r 2 30r 2
0
讨论： r→0时，E→0 r R时，E R .
r R时，E R . 3 0
无限大均匀带电平面的电场是均匀场
求：两无限大均匀带电平面，带等量异号的电荷，平行放置时的电场。
两板之外： E = 0
记
-σ
+σ
两板之间： E 0
方向：正板指向负板
作业：8-2 8-3 8- 6 8-7
14
§8-4 静电场的环路定理 电势
8.4.1 静电场的环路定理
当带电体在静电场中移动时，静电场力对带电体要作功，说明静电 场具有能量。环路定理就是从能量的角度来讨论静电场的性质。
力所作的功。
17
若取b点为无穷远 ，则 Wb=W∞=0 , 则
Wa a q0 E dl
物理意义：电场中,q0 在a点的电势能，等于将q0由a点移到无穷远点静电
场力所作的功。
电势能的单位： 焦尔 J
当a点确定后,为恒量，恒量的大
8.4.3 电势
小反映了静电场做功的本领。从
由上式 Wa q0
5
３、电场强度通量的常用表示
大小：ds
引入面元矢量
ds dsn
方向： n 为面元法线方向
则
de
E cosds
E ds
e
E ds S
e
E ds
S
ds
n
E
q
＋
8.3.3 真空中的高斯定
RS
理 １、求几种情况下的电场强度通量
球（面１上）取包面围元点d电s荷, 球通面过的d电s场的强电度场通强量度通量为
∴ 垂直穿过带电平面底面为△S高为2r的闭合 柱面S为高斯面。
+σ
++
E dS E dS E dS E dS
S
左底
侧
右底
E
++
+ +
++
+ +
+ + ++
S
ES 0 ES 2ES
0
E
2 0
+ ++ + +
E
++
++Δ+S+
+ + +
+ ++
+
+ +
（3）高斯定理是电磁场的基本定理之一。说明静电场是有源场，发散场。
8.3.4 高斯定理的应用（求场强） 分析：
1、巧取高斯面（充分利用对称性）。 2、能方便的求出s内的电荷。
E
ds
S
1
0
qi
i( s内）
9
例8-5 求：均匀带电球面的电场。 解： ∵ 电场分布具有球对称性。
∴ 取以r为半径的球面S为高斯面
a
∵静电场力是保守力，保守力的功等于势能增量的负值。
若 Wa ―――q0 在a点的电势能;
Wb ―――q0 在b点的电势能。
则 A (Wb Wa ) 若取b点 Wb=0 , 则
b
a q0 E dl
b
Wa a q0 E dl
比较 EP=mgh
物理意义：q0 在电场中a点的电势能，等于将q0由a点移到零势能点静电场
E
结论：真空中穿过任意闭合曲面Ｓ的电场强度通量等于该闭合曲面内电
荷代数和的1/ε0倍。
8
即
E
ds
S
1
0
qi
i( s内）
记 真空中高斯定理的
若电荷连续分布，
数学表达式
则
E
ds
1
dV
S
0 V (S所围的带电体)
注意： （1）式中 E ，是所有电荷所产生。S内、S外。
（2）式中电荷求和（积分），只对s内的电荷求和（积分）。
根据高斯定理
S
E
dS
1
0
q
高斯面
+++ S
q+
+
+ + +
R
o
r S
+ + +
+
+
++ +
E
ds
E
dS E4r 2 1
q
S
S
0
E
E 1 q
4 0 r 2
均匀带电球面内 场强处处为零
0
R
r
与点电荷的电
当0< r < R时，∑q=0∴ E = 0
场分布相同
当R< r < ∞时，∑q=q
E
1 40
q r2
讨论：点电荷的电场 r →∞ E→0;
r →0 E→ ∞。 10
例题 半径为R 的介质球，均匀带电q (q > 0 ),电容率为ε，
求：此带电球的电场。 解： ∵ 电场分布具有球对称性。
q
4 R3
o
3
∴ 取以r为半径的球面S为高斯面
根据高斯定理
S
E dS
1
q
r
S R
SE ds
或者说将单位正电荷绕任意闭合路径一周静电场力所作的功等于零。
16
8.4.2 电势能
静电场力作功与路径无关，仅与始末位置有关，位置确定
做功本领确定，因此可以引入势能的概念，称为电势能。
1、电势能
电场中，将q0由a→b,电场力的功
为
b b
A
F dl
a
a q0 E dl
bE
dl
q0
F q0E
+ +
+
+
+
+ +
+ +
++
+++++++++
2
3、电场线（E）线的特点:
（1）曲线上每一点的切线方向与该点的场强方向相一致； （2）电场线起始于正电荷，终止于负电荷，不形成闭合曲线； （3）任何两条电场线不会相交。
按照电场线的规定所作出的电场线只能定性描述电场的分布，而无法 反映场强的大小。
为了反映场强大小分布，可利用电场线的疏密程度来反映 。密、强； 疏、弱。
§8-3 静电场中的高斯定理
8.3.1、电场线（E线、电力线）
1、电场的分布（1）点电荷；（2）电偶极子；（3）无限大带电平面 2、电场线：为了形象地描述电场的分布而引入的一系列 （曲1线），点曲电线荷上电各场点中的的切电线场方线向与该点的场E强a 方向相同。Eb
b a
+
1
（2）电偶极子电场中的电场线 （3）无限大带电平面电场中的电场线
n
E
S
说明: 通过s的电场强度通量等于s在垂直于场强方向上的投影面s’与场强的乘积。
或者说，通过s的电场强度通量等于场强在s法线方向上的分量与s的乘积4 。
2、在非均匀电场中，通过任意曲面S的电场强度通量。
(1) 取面元ds，通过ds的电场强度通量为
E
de E cosds
(2) 通过任意曲面S的电场强度通量为
4、电场线数密度：垂直穿过单位面积的电场线数