向量组的线性相关性(2)
- 格式:ppt
- 大小:1.59 MB
- 文档页数:58



⼤学数学基础(2)mooc-向量组的线性相关性(2)数学基础(2)第三章向量第三讲向量组的线性相关性(2)主讲教师王玮副教授⼆、线性相关的性质定理12(2)1.m m m ααα≥?-向量组,,,线性相关其中⾄少有⼀个向量可由其余个向量线定1性表⽰理12(2)1.m m m ααα≥?-向量组,,,线性⽆关其中任何⼀个向量不可由其余个向推量线性表⽰论121212.m m m ααααααββααα如果向量组,,,线性⽆关,⽽向量组,,,,线性相定关,则可由向量组,,,线性表⽰,且表2⽰式唯⼀理12(2)1.m m m ααα≥?-向量组,,,线性相关其中⾄少有⼀个向量可由其余个向量线定1性表⽰理必要性12121122(2)0m m m m m k k k k k k αααααα≥+++=若向量组,,,线性相关,则存在不全为零的数,,,,使得10k ≠不妨设,11.m α-即可由其余个向量线性表⽰32123111m mk k k k k k αααα=-+-+- ? ? ?则有找等式,看系数12(2)1.m m m ααα≥?-向量组,,,线性相关其中⾄少有⼀个向量可由其余个向量线定1性表⽰理充分性1m -设向量组中⾄少有⼀个向量可由其余个向量线性表⽰,1211122111(1)0m m m m k k k k k k αααα----++++-=因此存在⼀组不全为零的数,,,,,使得12m ααα故向量组,,,线性相关.1211122111m m m m m m k k k k k k ααααα----=+++不妨设可以由其余个向量线性表⽰,即存在⼀组数,,,,使得12(2)1.m m m ααα≥?-向量组,,,线性⽆关其中任何⼀个向量不可由其余个向推量线性表⽰论121212.m m m ααααααββααα如果向量组,,,线性⽆关,⽽向量组,,,,线性相定关,则可由向量组,,,线性表⽰,且表2⽰式唯⼀理121211220m m m m k k k k k k k k αααβαααβ++++=证由,,,,线性相关知:存在不全为零的数,,,,,使得①k ≠1211220m m m k k k k k k ααα+++=否则,①变为存在不全为零的数,,,,使得12m ααα这与向量组,,,线性⽆关⽭盾. 12120m mk k k k kkkβααα≠=----,12m βααα即可由向量组,,,线性表⽰.找等式,看系数下⾯证明表⽰法唯⼀121212.m m m ααααααββααα如果向量组,,,线性⽆关,⽽向量组,,,,线性相定关,则可由向量组,,,线性表⽰,且表2⽰式唯⼀理1122m m l l l βααα=+++假设,111222()()()0m m m l l l µαµαµα-+-++-=两式相减得121122m m ml l l αααµµµ===由向量组,,,线性⽆关知,,,得证1122m m βµαµαµα=+++,121211*********.,,,(3)(A ),,,0(B ),,,(C ),,,(D ),,,s s s ss s s n s n k k k k k k ααααααααααααααα≤≤+++≠维向量组线性⽆关的充要条件是存在⼀组不全为零的数,使中任意两个向量都线性⽆关中存在⼀个向量,它不能由其余向量线性表⽰中任意⼀个向量都不能⽤其余向量线性表⽰【典型例题】D(A )(B )(C ).、、是此向量组线性⽆关的必要条件,但不充分条件12112212,,,0,,,.(D ).s s ss k k k k k k αααααα+++=解向量组线性⽆关的定义是关系式,只能在全为零时才成⽴对照这⼀定义知,只有正确√1231232.(1,0,0),(1,1,0),(1,1,1),(,,).,,.a b c αααββααα====判断下列命题是否正确:设向量组则⼀定可由线性表⽰,且表达式唯⼀121212,,,,,,,,,,,,.m m m ααααααββααα向量组线性⽆关,⽽向量组线性相关则可由线性表⽰且表⽰法唯⼀数学基础(2)第三章向量第三讲向量组的线性相关性(2)END。






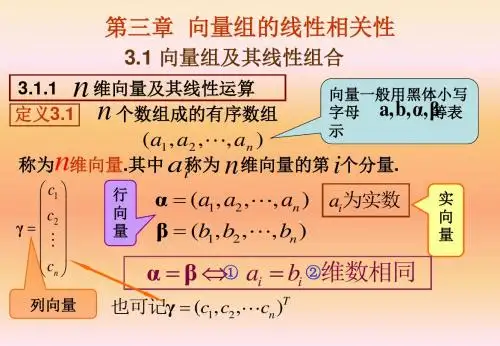
第四章 向量组的线性相关性§1 n 维向量概念一、向量的概念定义1 n 个有次序的数12,,,n a a a 所组成的数组称为n 维向量,这n 个数称为该向量的n 个分量,第i 个数i a 称为第i 个分量.注1分量全为实数的向量称为实向量.分量不全为实数的向量称为复向量. 注2 n 维向量可以写成一行的形式()12,,,n a a a a =,出可以写成一列的形式12n a a a a ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭,前者称为行向量,而后者称为列向量.行向量可看作是一个1n ⨯矩阵,故又称行矩阵;而列向量可看作一个1n ⨯矩阵,故又称作列矩阵.因此它们之间的运算就是矩阵之间的运算,从而符合矩阵运算的一切性质.向量之间的运算只涉及到线性运算和转置运算.为叙述方便,特别约定:在不特别声明时说到的向量均为列向量,行向量视为列向量的转置.注3 用小写黑体字母,,,a b αβ 等表示列向量,用,,,T T T T a b αβ表示行向量. 例1 设123(1,1,0),(0,1,1),(3,4,0)T T T v v v ===,求12v v -及12332v v v +-.解 12v v -(1,1,0)(0,1,1)T T =-(10,11,01)T =---(1,0,1)T =-12332v v v +-3(1,1,0)2(0,1,1)(3,4,0)T T T =+-(31203,31214,30210)T =⨯+⨯-⨯+⨯-⨯+⨯-(0,1,2)T =定义 设v 为n 维向量的集合,如果集合v 非空,且集合v 对于加法与数乘两种运算封闭(即若α∈v,β∈v ,有α+β∈v ;若α∈v, k ∈R ,有k α∈v ),称v 为向量空间。
§2 向量组的线性相关性一、向量组的线性组合 定义3 给定向量组A :12,,,m a a a ,对于任何一组实数12,,,m k k k ,称向量1122m m a a a k k k +++ 为向量组A 的一个线性组合,12,,,m k k k 称为这个线性组合的系数.定义4 给定向量组A :12,,,m a a a 和向量b ,若存在一组实数12,,,m λλλ,使得1122m m a a a b λλλ=+++则称向量b 是向量组A 的一个线性组合,或称向量b 可由向量组A 线性表示.注1任一个n 维向量12n a a a a ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭都可由n 维单位向量组12,,,n e e e 线性表示:1122n n a a a a e e e =+++ .注2向量b 可由向量组A :12,,,n a a a 线性表示(充要条件)⇔方程组1122n n a a a x x x b +++=有解m n A x b ⨯⇔=有解()(,)R A R A b ⇔=注3 由于线性方程组的解分为:无解,有唯一解,有无穷多解三种情况,所以向量β由向量12,,,n a a a 线性表示的情形也分为三种:不能线性表示,唯一线性表示,无穷多种线性表示,且线性表示式中的系数就是对应线性方程组的解。
