绳绕圆柱体的摩擦力分析

人教版物理高二选修2—2第一章第二节平动和转动同步练习一．选择题1．如图所示,AC 是上端带定滑轮的固定竖直杆，质量不计的轻杆AB 一端通过铰链固定在A 点，另一端B 悬挂一重为G 的物体，且B 端系有一根轻绳并绕过定滑轮C ,用力F 拉绳,开始时∠BAC ＞90°，现使∠BAC 缓慢变小，直到杆AB 接近竖直杆AC ．此过程中，轻杆B 端所受的力（ ）A ． 逐渐减小B ． 逐渐增大C ． 大小不变D ．先减小后增大答案:C解析：解答：A 、由于B 点始终处于平衡状态,故B 点受到的力的大小为各力的合力．故B 点在变化过程中受到的力始终为0．故大小不变．故A 错误B 、由对A 项的分析知B 点受到的力始终为0，不变．故B 错误．C 、由对A 项的分析知B 点受到的力始终为0，不变．故C 正确．D 、由对A 项的分析知B 点受到的力始终为0，不变．故D 错误．故选：C分析：以B 为研究对象，并受力分析．由题目中“缓慢”二字知整个变化过程中B 处于平衡态．2．如图,由两种材料做成的半球面固定在水平地面上,球右侧面是光滑的,左侧面粗糙，O 点为球心，A 、B 是两个相同的小物块（可视为质点)，物块A 静止在左侧面上，物块B 在图示水平力F 作用下静止在右侧面上，A 、B 处在同一高度，AO 、BO 与竖直方向的夹角均为θ,则A 、B 分别对球面的压力大小之比为（ ）A ． s in 2θ:1B ． s inθ:1C ． c os 2θ：1D ．cosθ：1答案:C解析:解答：分别对A 、B 两个相同的小物块受力分析如图，由平衡条件，得：N =mgcosθ 同理cos mg N θ'= 由牛顿第三定律,A 、B 分别对球面的压力大小为N 、N ′；则它们之比为2cos cos cos N mg mg N θθθ=='，故C 正确故选C分析：分别对A、B两个相同的小物块受力分析，由受力平衡,求得所受的弹力，再由牛顿第三定律，求A、B分别对球面的压力大小之比．3．如图所示，小车的质量为M，人的质量为m,人用恒力F拉绳，若人与车保持相对静止，且地面为光滑的，又不计滑轮与绳的质量,则车对人的摩擦力不可能是(）A．0B．m Mm M-+F,方向向右C．m Mm M-+F,方向向左D．m Mm M-+F，方向向右答案：B解析:解答：整体的加速度2FaM m=+，方向水平向左．隔离对人分析，人在水平方向上受拉力、摩擦力,根据牛顿第二定律有：设摩擦力方向水平向右．F﹣f=ma,解得f=F﹣ma=m MFm M-+．若M=m，摩擦力为零．若M＞m，摩擦力方向向右,大小为m MFm M-+．若M＜m,摩擦力方向向左,大小为m MFm M-+．故A、C、D正确，B错误．故选B．分析:对人和车整体分析，根据牛顿第二定律求出整体的加速度,再隔离对人分析,求出车对人的摩擦力大小．4．如图所示，质量为M、半径为R的半球形物体A放在水平地面上，通过最高点处的钉子用水平细线拉住一质量为m、半径为R的光滑球B．则（)A．A对地面的压力等于（M+m）g B．A对地面的摩擦力方向向左C ． B 对A 的压力大小为r r R +mgD ． 细线对小球的拉力大小为r Rmg 答案：A解析：解答：AB 、对AB 整体受力分析，受重力和支持力,相对地面无相对滑动趋势，故不受摩擦力，根据平衡条件，支持力等于整体的重力，为（M +m ）g ；根据牛顿第三定律，整体对地面的压力与地面对整体的支持力是相互作用力，大小相等，故对地面的压力等于(M +m ）g ,故A 正确，B 错误；CD 、对小球受力分析，如图所示：根据平衡条件,有：cos mg F θ=，T =mg t a n θ 其中cosθ=R r R +，22(r R)R tan Rθ+-=, 故:R r F mg R +=，22(r R)R T mg R+-= 故C 、D 错误；故选：A ．分析：先对整体受力分析，然后根据共点力平衡条件分析AB 选项，再隔离B 物体受力分析后根据平衡条件分析CD 选项．5．一倾角为30°的斜劈放在水平地面上，一物体沿斜劈匀速下滑．现给物体施加如图所示力F ，F 与竖直方向夹角为30°，斜劈仍静止,则此时地面对斜劈的摩擦力（ ）A ． 大小为零B ． 方向水平向右C ． 方向水平向左D ． 无法判断大小和方向答案：A解析：解答：物块匀速下滑时,受重力、支持力和摩擦力，三力平衡,故支持力和摩擦力的合力与重力平衡，竖直向上，根据牛顿第三定律得到滑块对斜面体的作用力方向竖直向下，等于mg ;当加推力F 后，根据滑动摩擦定律F =μN ,支持力和滑动摩擦力同比增加，故其合力的方向不变，根据牛顿第三定律,滑块对斜面体的压力和滑动摩擦力的合力方向也不变,竖直向下；故斜面体相对与地面无运动趋势，静摩擦力仍然为零；故选A ．分析：物块匀速下滑时,受重力、支持力和摩擦力，三力平衡,故支持力和摩擦力的合力与重力平衡,竖直向上，根据牛顿第三定律得到滑块对斜面体的作用力方向；当加推力F 后，滑块对斜面体的压力和滑动摩擦力同比增加，合力方向不变．6．如图所示，质量为m的小球，用OB和O′B两根轻绳吊着，两轻绳与水平天花板的夹角分别为30°和60°，这时OB绳的拉力大小为F1，若烧断O′B绳,当小球运动到最低点C时,OB绳的拉力大小为F2，则F1:F2等于(）A．1：1 B．1：2C．1:3 D．1：4答案:D解析：解答：烧断水平细线前，小球处于平衡状态，合力为零，根据几何关系得：F1=mgsin30°=12mg；烧断水平细线,设小球摆到最低点时速度为v，绳长为L．小球摆到最低点的过程中，由机械能守恒定律得：mgL（1﹣sin30°)=12mv2在最低点，有F2﹣mg=m2vL联立解得F2=2mg；故F1：F2等于1:4；故选：D．分析：烧断水平细线前，小球处于平衡状态，合力为零,根据平衡条件求F1．烧断水平细线，当小球摆到最低点时,由机械能守恒定律求出速度，再由牛顿牛顿第二定律求F2．7．有一个直角支架AOB，AO水平放置，表面粗糙，OB竖直向下,表面光滑．AO上套有小环P，OB上套有小环Q，两环质量均为m，两环由一根质量可忽略、不可伸长的细绳相连，并在某一位置平衡（如图所示）．现将P环向左移一小段距离,两环再次达到平衡，那么将移动后的平衡状态和原来的平衡状态比较，AO杆对P环的支持力F N和摩擦力F的变化情况是()A．F N不变，F变大B．F N不变，F变小C．F N变大，F变大D．F N变大，F变小答案：B解析：解答：对小环Q受力分析,受到重力、支持力和拉力,如图根据三力平衡条件，得到 cos mg T θ= N =mg t a n θ再对P 、Q 整体受力分析，受到总重力、OA 杆支持力、向右的静摩擦力、BO 杆的支持力，如图根据共点力平衡条件,有N =FF N =（m +m ）g =2mg故F =mg t a n θ当P 环向左移一小段距离，角度θ变小，故静摩擦力F 变小,支持力F N 不变；故选B ．分析：先对小环Q 受力分析，受到重力、支持力和拉力，跟三力平衡条件，求出拉力的表达式；在对P 、Q 两个小环的整体受力分析，根据平衡条件再次列式分析即可．8．如图所示,质量相同分布均匀的两个圆柱体a 、b 靠在一起,表面光滑，重力均为G ，其中b 的下一半刚好固定在水平面MN 的下方，上边露出另一半，a 静止在平面上，现过a 的轴心施以水平作用力F ,可缓慢的将a 拉离平面一直滑到b 的顶端,对该过程分析,应有（ )A ． 拉力F 先增大后减小，最大值是GB ． 开始时拉力F 3,以后逐渐减小为0C ． a 、b 间压力由0逐渐增大,最大为GD ． a 、b 间的压力开始最大为2G ，而后逐渐减小到0答案：B解析：解答：对于a 球：a 球受到重力G 、拉力F 和b 球的支持力N ，由平衡条件得:F =Ncosθ，Nsinθ=G则得 F =G c o t θ，sin G N θ= 根据数学知识可知，θ从30°增大到90°，F 和N 均逐渐减小，当θ=30°，F 有最大值为3G ，N 有最大值为2G ，故B 正确．故选B分析：a 球缓慢上升，合力近似为零，分析a 受力情况,由平衡条件得到F 以及b 球对a 的支持力与θ的关系式,即可分析其变化．9．如图所示，一个质量为m 的人站在台秤上，跨过光滑定滑轮将质量为m ′的重物从高处放下，设重物以加速度a 加速下降（a ＜g ），且m ′＜m ，则台秤上的示数为（ )A ． (m +m ′）g ﹣m ′aB ． （m ﹣m ′）g +m ′aC ． （m ﹣m ′）g ﹣m ′aD ．（m ﹣m ′）g答案：B解析:解答:对重物受力分析，受重力和拉力，加速下降,根据牛顿第二定律,有：m ′g ﹣T =m ′a ①再对人受力分析，受到重力、拉力和支持力，根据共点力平衡条件，有：N +T =mg ②由①②,解得N =（m ﹣m ′)g +m ′a故选B ．分析：先对重物受力分析，受重力和拉力,加速下降,然后根据牛顿第二定律列式求出绳子的拉力；再对人受力分析，受到重力、拉力和支持力，根据平衡条件求出支持力，而台秤读数等于支持力．10．如图所示，物体A 和B 质量均为m ，且分别与轻绳连接跨过光滑轻质定滑轮,B 放在水平面上,A 与悬绳竖直．用力F 拉B 沿水平面向左匀速运动的过程中,绳对A 的拉力的大小是( ）A．大于mg B．总等于mgC．一定小于mg D．以上三项都不正确答案:A解析:解答：将B的运动分解为沿绳子方向的运动，以及垂直绳子方向运动即绕滑轮的转动,如图解得v2=vcosθ由于θ不断变小,故v2不断变大；由于物体A的速度等于v2,故物体A加速上升，加速度向上，即物体A处于超重状态，故绳子的拉力大于mg；故选A．分析:由于B做匀速运动，将B的运动分解为沿绳子方向的运动,以及垂直绳子方向运动即绕滑轮的转动，得到沿绳子方向的运动速度，即物体A的速度表达式，得到A的运动规律，再根据牛顿第二定律判断绳子拉力的变化情况．11．如图所示，两梯形木块A、B叠放在水平地面上，A、B之间的接触面倾斜．A的左侧靠在光滑的竖直墙面上，关于两木块的受力,下列说法正确的是（）A．A、B之间一定存在摩擦力作用B．木块A可能受三个力作用C．木块A一定受四个力作用D．木块B受到地面的摩擦力作用方向向右答案：B解析：解答：A、由于AB间接触面情况未知，若AB接触面光滑，则AB间可以没有摩擦力；故A错误；B、对整体受力分析可知，A一定受向右的弹力；另外受重力和支持力；因为AB间可能没有摩擦力；故A可能只受三个力;故B正确；C错误；D、木块B受重力、压力、A对B的垂直于接触面的推力作用，若推力向右的分力等于F，则B可能不受摩擦力;故D错误;故选：B．分析：分别对AB及整体进行分析，由共点力的平衡条件可判断两物体可能的受力情况．12．如图所示，质量为m的物体A在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程斜面体B仍静止，斜面体的质量为M，则水平地面对斜面体（)A．无摩擦力B．有水平向右的摩擦力C．支持力为（m+M）g D．支持力小于（m+M）g答案：D解析：解答：以物体A和斜面体整体为研究对象，分析受力情况：重力（M+m）g、地面的支持力N，摩擦力F和拉力F，根据平衡条件得:F=Fcosθ,方向水平向左N=（M+m）g﹣Fsinθ＜(m+M）g故选D分析：物体A在沿斜面向上的拉力F作用下沿斜面匀速下滑，合力为零．斜面体B静止,合力也为零．以物体A和斜面体整体为研究对象，分析受力情况，根据平衡条件研究水平地面对斜面体的摩擦力和支持力．13．如图所示，用一轻绳将光滑小球P系于竖直墙壁上的O点，在墙壁和球P之间夹有一长方体物块Q，P、Q均处于静止状态,现有一铅笔紧贴墙壁从O点开始缓慢下移，则在铅笔缓慢下移的过程中(）A ． 细绳的拉力逐渐变小B ． Q 受到墙壁的弹力逐渐变大C ． Q 受到墙壁的摩擦力逐渐变大D ． Q 将从墙壁和小球之间滑落答案：B解析：解答：A 、对P 分析，P 受到重力、拉力和Q 对P 的弹力处于平衡，设拉力与竖直方向的夹角为θ，根据共点力平衡有：拉力cos mg F θ=，Q 对P 的支持力N =mgtanθ．铅笔缓慢下移的过程中,θ增大，则拉力F 增大，Q 对P 的支持力增大．故A 错误．B 、C 、D 、对Q 分析知，在水平方向上P 对A 的压力增大，则墙壁对Q 的弹力增大，在竖直方向上重力与摩擦力相等，所以A 受到的摩擦力不变,Q 不会从墙壁和小球之间滑落．故B 正确,C 、D 错误．故选:B ．分析：分别对P 、Q 受力分析，通过P 、Q 处于平衡判断各力的变化．14．如图所示,两个质量为m 1的小球套在竖直放置的光滑支架上，支架的夹角为120°，用轻绳将两球与质量为m 2的小球连接，绳与杆构成一个菱形，则m 1：m 2为（ ）A ． 1:1B ． 1：2C ． 1:3D ．3：2答案:A解析：解答:将小球m 2的重力按效果根据平行四边形定则进行分解如图，由几何知识得:T =m 2g ①对m 1受力分析，由平衡条件,在沿杆的方向有：m 1gsin 30°=Tsin 30° 得：T =m 1g ②可见m 1:m 2的=1：1；故选：A．分析：将小球m2的重力按效果根据平行四边形定则进行分解，由几何知识求出m2g与绳子拉力T的关系，对m1受力分析，由平衡条件求出m1g与T的关系，进而得到m1：m2的比值．15．图中弹簧秤、绳和滑轮的重量均不计，绳与滑轮间的摩擦力不计，物体的重力都是G，在图甲、乙、丙三种情况下，弹簧秤的读数分别是F1、F2、F3,则（）A．F1＞F2=F3B．F3=F1＞F2C．F1=F2=F3D．F1＞F2=F3答案：B解析：解答：甲图：物体静止，弹簧的拉力F1=mg；乙图：对物体为研究对象,作出力图如图．根据平衡条件有:F2=mgsin60°=0.866mg丙图：以动滑轮为研究对象,受力如图．由几何知识得F3=mg．故F3=F1＞F2故选B．分析：弹簧称的读数等于弹簧受到的拉力．甲图、乙图分别以物体为研究对象由平衡条件求解．丙图以动滑轮为研究对象分析受力情况，根据平衡条件求解．二．填空题16．如图所示，粗细和质量分布都均匀的呈直角的铁料aob质量为12k g,ao、ob两段长度相等,顶点o套在光滑固定轴上使直角铁料能绕o轴在竖直平面内转动,a端挂有质量为9k g的物体P，ao与竖直方向成37°角，则P对地面的压力大小是,要使P对地面的压力为零，至少在b端上施加力F= ．(g取10m/s2,sin37°=0。

双斜楔结构锁绳器各楔块角度及摩擦系数分析双楔复式机构已广泛应用于单纯锁绳的卡绳器和首绳调换装置中，其自动化程度高的优势普遍被市场所采纳。

以往的设计均参照《》进行，未曾精确计算，且在实际使用中也出现过不少问题。

本文以两斜楔之间滚动体（圆柱滚子）为受力分析的着力点，尝试为此种结构提供科学、可靠的理论依据，为广大同行带来便利，为多绳摩擦系统首绳的维护和更换工作的安全高效提供必要的技术支持。

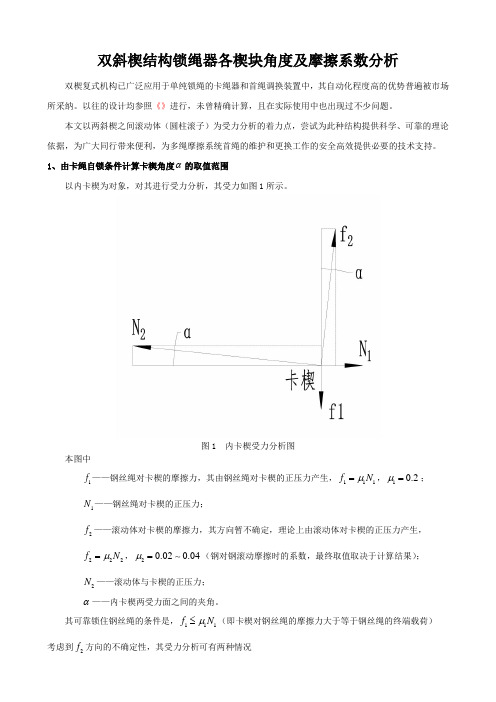
1、由卡绳自锁条件计算卡楔角度α的取值范围以内卡楔为对象，对其进行受力分析，其受力如图1所示。

图1 内卡楔受力分析图本图中1f ——钢丝绳对卡楔的摩擦力，其由钢丝绳对卡楔的正压力产生，111f N μ=，10.2μ=； 1N ——钢丝绳对卡楔的正压力；2f ——滚动体对卡楔的摩擦力，其方向暂不确定，理论上由滚动体对卡楔的正压力产生， 222f N μ=，20.020.04μ=（钢对钢滚动摩擦时的系数，最终取值取决于计算结果）； 2N ——滚动体与卡楔的正压力；α——内卡楔两受力面之间的夹角。

其可靠锁住钢丝绳的条件是，111f N μ≤（即卡楔对钢丝绳的摩擦力大于等于钢丝绳的终端载荷） 考虑到2f 方向的不确定性，其受力分析可有两种情况1）2f 方向与图中一致，则122122cos sin sin cos N N f f N f αααα=-=+，亦即121tan 1tan μαμμα-≤+…………………………（公式1） 2）2f 方向与图中方向相反，则 122122cos sin sin cos N N f f N f αααα=+=-，亦即121tan 1tan αμμμα-≥+…………………………（公式2） 欲使上列两式有合理的解，其必须满足条件1tan 0μα-≥，亦即1arctan 11.31αμ≤=︒。

2、根据自锁条件计算滚动体与卡楔和楔背之间的摩擦系数2μ的取值以滚动体（圆柱滚子）为对象，对其进行受力分析，其受力如图2所示。

柔韧体摩擦的欧拉公式(作者:赵夏云)[Abstract]Oula Formular in the Friction of Soft and Elastic Bodies are introduced.A main application of the Oula Formular in belt drive is discussed,as well as some interesting phenomenon in our real life .Key words: friction, Oula Formular, belt drive.(一)引例家在漓江边,小时候,常到河边码头玩耍,看一艘艘满载旅客的游船船头都有一缆柱,船靠岸时,船工就将一根很粗的缆绳抛到岸上系绳柱上,这样,挽了一个大圈的缆绳头就套住了岸上的柱子,而船工立即将绳的另一端缠绕在固定在船上的缆柱上,不一会,船稳稳的停在了岸边.一根缆绳绕几圈就拉住一艘船?自己也曾试过,直接拉住系在竹筏上的绳子,竹筏在水波中颠簸,要想拽住竹筏以防它漂离岸边,对小孩来说还得费一番功夫,但若将绳子在岸边柱子上绕几下,就轻而易举的拉住竹筏了,甚至只要在岸上用脚轻轻的踩住绳的一端,竹筏也会乖乖的靠在岸边.是什么魔力产生了这种”四两搏千斤”的”奇迹”?魔力就是”摩力”----缆绳和柱子间的摩擦力!再看一个有趣的例子来感受感受这种摩擦力的魅力吧.在儒尔·威廉的小说<<马迪亚思·山道尔>>中有那么一位大力士,叫马帝夫.他建立了许多功绩,其中有这么一件.一艘不大的双桅梯形帆船正在下水.帆船是用楔子固定在下水滑道上的,木匠们开始从龙骨下把楔子打掉.这时,一只快艇飞速驶进港来.可是帆船已经开始下水滑道向水中冲去.就要扎进快艇船舷了!说时迟,那时快!马帝夫从人群中跳出,抓住靠在帆船船头的绳索,用脚抵住地,开始将绳索往岸边的系绳柱绕,他以”超人”的臂力拽住绳子十来秒钟,绳索终于断了,但是,马帝夫为快艇赢得了宝贵的十秒钟!从以上几个例子都有一个共同点:套在(绕在)柱子上的绳子,一端是”四两”,一端是”千斤”.两者间的关系就是谈到摩擦时不能不提及的欧拉公式!(二)欧拉公式内容及推导如右图(1)示,假设一根绳绕在轮(柱)上,包角为a,绳的一端受力为F1,另一端受力为F2(F2>F1).F1式中 E–––自然对数的底（E≈2.718）；f–––带和轮缘间的摩擦系数；a–––传动带在带轮上的包角（rad）。

第19讲竖直面内圆周运动之绳”模型和“杆”模型及其临界问题1．（2022·江苏）在轨空间站中物体处于完全失重状态，对空间站的影响可忽略．空间站上操控货物的机械臂可简化为两根相连的等长轻质臂杆，每根臂杆长为L．如图1所示，机械臂一端固定在空间站上的O点，另一端抓住质量为m的货物．在机械臂的操控下，货物先绕O点做半径为2L、角速度为ω的匀速圆周运动，运动到A点停下．然后在机械臂操控下，货物从A点由静止开始做匀加速直线运动，经时间t到达B点，A、B间的距离为L。

（1）求货物做匀速圆周运动时受到的向心力大小F n。

（2）求货物运动到B点时机械臂对其做功的瞬时功率P。

（3）在机械臂作用下，货物、空间站和地球的位置如图2所示，它们在同一直线上．货物与空间站同步做匀速圆周运动．已知空间站轨道半径为r，货物与空间站中心的距离为d，忽略空间站对货物的引力，求货物所受的机械臂作用力与所受的地球引力之比F1：F2。

一.竖直面内的圆周运动——“绳”模型和“杆”模型1.在竖直平面内做圆周运动的物体，按运动到轨道最高点时的受力情况可分为两类：一是无支撑(如球与绳连接、沿内轨道运动的物体等)，称为“绳(环)约束模型”；二是有支撑(如球与杆连接、在弯管内的运动等)，称为“杆(管)约束模型”。

2．绳、杆模型涉及的临界问题绳模型杆模型常见类型均是没有支撑的小球均是有支撑的小球受力特征除重力外，物体受到的弹力向下或等于零除重力外，物体受到的弹力向下、等于零或向上受力示意图过最高点的临界条件由mg＝mv2r得v临＝gr由小球恰能做圆周运动得v临＝0讨论分析(1)过最高点时，v≥gr，F N＋mg＝mv2r，绳、圆轨道对球产生弹力F N(2)不能过最高点时，v<gr，在到达最高点前小球已经脱离了圆轨道(1)当v＝0时，F N＝mg，F N为支持力，沿半径背离圆心(2)当0<v<gr时，mg－F N＝mv2r，F N背离圆心，随v的增大而减小(3)当v＝gr时，F N＝0(4)当v>gr时，F N＋mg＝mv2r，F N指向圆心，并随v的增大而增大二. 例题精析题型一、杆球模型例1．一轻杆一端固定质量为m的小球，以另一端O为圆心，使小球在竖直面内做半径为R的圆周运动，如图所示，则下列说法正确的是（）A．小球过最高点时，杆所受到的弹力可以等于零B．小球过最高点的最小速度是√gRC．小球过最高点时，杆对球的作用力一定随速度增大而增大D．小球过最高点时，杆对球的作用力一定随速度增大而减小题型二、绳球模型例2．如图甲所示，轻绳一端固定在O点，另一端固定一小球（可看成质点），让小球在竖直平面内做圆周运动。

高中物理-摩擦力考点考点分类：考点分类见下表考点内容考点分析与常见题型对称法解决非共面力问题选择题摩擦与自锁现象选择题绳(杆)上的“死结”和“活结”模型选择题较多摩擦力方向与运动方向的关系选择题较多考点一对称法解决非共面力问题在力的合成与分解的实际问题中，经常遇到物体受多个非共面力作用处于平衡状态的情况，而在这类平衡问题中，又常有图形结构对称的特点，结构的对称性往往对应着物体受力的对称性．学%科网解决这类问题的方法是根据物体受力的对称性，结合力的合成与分解知识及平衡条件列出方程，求解结果．考点二摩擦与自锁现象1．力学中有一类现象，当物体的某一物理量满足一定条件时，无论施以多大的力都不可能让它与另一个物体之间发生相对运动，物理上称这种现象为“自锁”．生活中存在大量的自锁现象，例如维修汽车时所用的千斤顶就是根据自锁原理设计的．2．摩擦自锁现象是指当主动力合力的作用线位于摩擦角以内时，无论主动力合力多大，约束力都可与之平衡．摩擦自锁在生活中也大量的存在，并起着相当大的作用．3．最大静摩擦力Ffm与接触面的正压力FN之间的数量关系为Ffm＝μFN.其中，静摩擦系数μ取决于相互接触的两物体表面的材料性质及表面状况．考点三绳(杆)上的“死结”和“活结”模型1．绳模型(1)“死结”可理解为把绳子分成两段，且不可以沿绳子移动的结点．“死结”两侧的绳因结而变成了两根独立的绳，因此由“死结”分开的两段绳子上的弹力不一定相等．(2)“活结”可理解为把绳子分成两段，且可以沿绳子移动的结点．“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的．绳子虽然因“活结”而弯曲，但实际上是同一根绳，所以由“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线．2．杆模型杆可分为固定杆和活动杆．固定杆的弹力方向不一定沿杆，弹力方向视具体情况而定，活动杆只能起到“拉”和“推”的作用．一般情况下，插入墙中的杆属于固定杆(如甲、乙两图中的杆)，弹力方向不一定沿杆，而用铰链相连的杆属于活动杆(如丙图中的杆)，弹力方向一定沿杆．考点四摩擦力方向与运动方向的关系摩擦力的方向与物体间的相对运动或相对运动趋势方向相反,但与物体的实际运动方向(以地面为参考系)可能相同,可能相反,也可能不在同一直线上.典例精析★考点一：对称法解决非共面力问题◆典例一：（2018福建质检）课堂上，老师准备了“∟”型光滑木板和三个完全相同、外表面光滑的匀质圆柱形积木，要将三个积木按图示（截面图）方式堆放在木板上，则木板与水平面夹角θ的最大值为A．30°B．45°C．60°D．90°【参考答案】A【考查内容】本题是以三个圆柱形积木在“∟”型光滑木板上处于平衡状态为情境，主要考查共点力的平衡等知识。

一、选择题1．如图用同样的滑轮组分别提起质量相等的一个物体和两个物体，比较甲、乙两图，正确表示机械效率关系的是（）A．η甲=η乙B．η甲<η乙C．η甲>η乙D．无法比较2．用相同的滑轮和绳子分别组成如图所示的甲、乙两个滑轮组。

把相同的重物匀速提升相同的高度。

若不计绳重及摩擦，下列说法正确的是（）A．绳子受的拉力F1和F2大小相等，机械效率相同B．绳子受的拉力F1和F2大小不相等，机械效率不同C．绳子自由端移动的距离不相等，机械效率不同D．绳子自由端移动的距离不相等，机械效率相同3．某人用同一滑轮组分别将重100N和200N的物体匀速提升5m，动滑轮重20N，绳重及摩擦不计，则以下说法错误．．的是A．人做的额外功两次相等B．由于物体重量不同，因此两次滑轮组的机械效率不同C．两次人所做的总功相同D．前后两次绳自由移动的距离相等4．中国公路往往环绕山坡，盘山而上，人们称之为盘山公路．若一辆车在盘山公路上保持40千米/时的速度向山上行驶，则下列有关该汽车和盘山公路的说法正确的是A．汽车的运动状态没有发生改变B．汽车的牵引力与受到的摩擦力是一对平衡力C．盘山公路可以使汽车提高机械效率D．盘山公路可以使汽车减小所需的牵引力5．如图所示，甲、乙杠杆的质量和长度均相同，机械摩擦不计，分别使用甲、乙杠杆将物体A提升相同的高度，则在工作过程中，甲、乙杠杆的机械效率相比（）A．甲的大B．乙的大C．一样大D．无法确定6．如图所示，分别用一定滑轮和一动滑轮提起同一物体，利用定滑轮的拉力是F甲，对应的机械效率是η甲；利用动滑轮的拉力是F乙，对应的机械效率是η乙；（忽略机械摩擦和绳重，动滑轮重小于物重）下列说法正确的是（）A．F甲＞F乙η甲＜η乙B．F甲＞F乙η甲＞η乙C．F甲＜F乙η甲＞η乙D．F甲＜F乙η甲＜η乙7．用如图所示的滑轮组（甲）和（乙）提升重物，不计绳重和摩擦，下列说法正确的是（）A．若钩码重力和提升高度相同，则滑轮组的机械效率相同B．若滑轮重力和绳端拉力相同，则滑轮组的机械效率相同C．若钩码重力和绳端拉力相同，则滑轮组（甲）的机械效率高D．若滑轮重力和绳端拉力相同，则滑轮组（甲）的机械效率高8．电梯是高层住宅必备的交通工具。

软绳下滑问题的研究摘要：本文拟讨论软绳在非光滑面上下滑过程中转角处的摩擦力是否可以忽略, 经研究发现转角虽然很小但弹力并不小,所产生的摩擦力足可以与平面相比,摩擦力做功也不小，忽略转角处摩擦力做功，计算出的速度明显比实际速度大;另外在研究光滑面上软绳下滑过程中绳的长度与速度的关系时，根据所研究问题的侧重点不同，将面视为无摩擦力的完全理想化情况,本文运用微圆法、能量守恒定律和牛顿第二定律等对问题进行深入的分析。

关键词：摩擦力；桌面；软绳；速度引言：软绳下滑问题是力学研究中一种比较典型的问题。

软绳在下滑的问题中涉及的力学知识非常的广，其中有牛顿的三条定律（以牛顿第二定律运用最多），在物理问题中常常运用的微圆法，还有能量守恒定律等等。

从中学我们就开始接触软绳问题，如软绳连接着定滑轮的问题、软绳的自由落体运动、软绳的重心等等，再到大学中我们所学的软绳的一些例子，如阿特伍德机。

但我们很少单独的研究软绳的问题，本文就以软绳为研究对象，分析其在下滑过程中的一些情况。

1.软绳下滑转角处的摩擦力1.1软绳在光滑的桌面上下滑例1.如图1所示，一根长为1m软绳，一部分垂在桌沿下面，一部分放在桌面上，垂下部分最大长度0.2m，若保持静止求其在桌面上的摩擦因数为多少；若此时稍有扰动软绳就会滑离桌面，当软绳全部滑出桌面时速度为多少（g取10m/ ）解：据题对软绳受力分析，如图；图.2 在桌面上的绳受力分析Fig.2 on the desktop of the rope force analysis 图.3在沿桌面下滑的软绳Fig.3 Along the desktop in the rope of force analysis设软绳单位长度的质量为ρ，小绳的全长为s ，在桌沿下的长为l ，全部滑出桌面的速度为v 。

则有g l s G gl G )(,12-==ρρ(1)，g l s gl )(-=μρρ(2)，ls l -=μ(3)，根据能量守恒定律22212)()(21)(sv ls l s g l s g l s l ρρμρρ=--+---(4)，s m v22=，在上面的问题中没有考虑转角处的摩擦力情况，可能是考虑到转角非常的小，在此处的摩擦力所做的功可以忽略。