超静定问题及其解法

l1 F N 1l1 E 1 A1
FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程：由几何方程和物理方程得：
F N 1l1 E1 A1
2

cos a
(5)联解（1）、（2）、（3）式，得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力（支反 力、内力）的问题，称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力（支反 力、内力）的问题，称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固，角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa，弹性模量分别为E1=200GPa 和 E2 =10GPa；求许可载荷P。 解：（1）以压头为研究对象, 设每 个角钢受力为FN1，木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a

1.94
37
小 结
1、明确超静定、超静定次数、多余约束、 多余未知力、基本静定系等基本概念。 2、能判断超静定次数。 3、理解超静定问题的基本解法为考虑静 力平衡、变形相容和物理关系三个方面。 4、对于二次或二次以下的超静定问题， 能合理地选取基本静定系，正确地列出 变形几何方程。 5、初步学习利用对称性降低超静定次数、 选取基本静定系的技巧。
超静定次数： 未知力个数与独立平衡方程数之差，也等于多 余约束数。由于超静定结构能有效降低结构的内力 及变形，在工程上（如桥梁等）应用非常广泛。
4
二、求解超静定问题的基本方法
1.静定与超静定的辩证关系 多余约束的两种作用： 增加了未知力个数，同时增加对变形的限制与约束 前者使问题变为不可解；后者使问题变为可解。 2.超静定的处理方法 平衡方程
解除B端多余约束，代之以约束反力 R B
8
§6-2
拉压超静定问题
A
E1 A1
（2）建立变形协调方程。
AB BF BB 0
（3）物理方程。
F 1 BF AC () E1 A1 BB AB RB ( 1 2 )() E1 A1 E2 A2
目录
A
B FBy
C
(d)
3 FAy F ( ) 4
33
§6-4 简单超静定梁
例 8 梁AB 和BC 在B 处铰接，A、C 两端固定，梁的抗弯刚度 均为EI，F = 40kN，q = 20kN/m。画梁的剪力图和弯矩图。 解 从B 处拆开，使超静定结构变 成两个悬臂梁。 变形协调方程为： yB1 yB 2
(3)代入物理关系，建立补充方程
②
2
A
3

2.4m
l ＞
B端必接触
C
40kN 1.2m
静力平衡方程
RA RB 100kN
B
变形协调条件为 l
RB
RA
A
60kN 2.4m 1.2m
轴 力 图
15kN
85kN
⊕ 25kN
C
40kN 1.2m
B

RA 103 1.2 ( RA 60) 103 2.4 RB 103 1.2 l 9 6 9 6 9 6 210 10 600 10 210 10 600 10 210 10 300 10
3
FC
A
FC
C
L
2
L
B
2
P
例题 6.10
当系统的温度升高时,下列结构中的____不会 A 产生温度应力.
A
B
C
D
例题 6.11
图示静不定梁承受集中力F和集中力偶Me作用, 梁的两端铰支,中间截面C处有弹簧支座.在下列 关于该梁的多余约束力与变形协调条件的讨论 中,___是错误的. C
RB
RA 85kN
RB 15kN
三、扭转超静定问题 扭转变形计算公式
Tl GI p
T ( x) dx GI p l
例3.两端固定的圆截面等直杆AB，在截面
C受外力偶矩m作用，求杆两端的支座反力
偶矩。
m
A C B
a
b
解：
A
m
ɑ
mA
C
B
b
m
静力平衡方程为： m A mB m 变形协调条件为：
5 ql 8
B
L
q

FN1 cos FN2 cos FN3 F 0
FN1
FN 3
EA cos2
E3 A3
FN3 1 2
F EA
cos2
E3 A3
FN1
FN 2
1 2cos
F
E
E3 A3
A cos2
第13页/共59页
B 1
1
Δl3
D
3
C 2
A
3 F2
A
Δl1A' NhomakorabeaFA A C
F
B FB
14
b
a
l
第六章 简单的超静定问题
例题2 求图a所示等直杆AB上,下端的约束力， 并求C截面的位移。杆的拉压刚度为EA。
解: 1. 列平衡方程 有两个未知约束力FA , FB(见图a)，但只有一个独 立的平衡方程
FA+FB-F=0 为一次超静定问题。
第14页/共59页
2. 取固定端B为“多余”约束。相应 的相当系统如图b，它应满足相容条件 ΔBF+ΔBB=0，参见图c，d。
MA 0
F a F 2a 0
A
B
P
FN1 a
A
FN2 a
FN3 B
P
第17页/共59页
变形协调方程：
ΔL 1
L1 L3 2(L2 L3 ) （2）
物理方程：
l1
FN 1l EA
l2
FN 2l EA
l3
FN 3l EA
（3）
联解（1）（2）（3）式得：
F 5P 6
F
2
1 3
P
F
3
1 6
D
由位移相容条

( wB ) FBy
C C F F
8FBy a 3 3EI
(b) (b)
B B
所以
3 14 Fa 3 8FBy a 0 3EI 3EI
MA
MA MA
A A
B B (c) (c) B B B (d) (d) FBy FBy
FA y
A A A
C C
7 FBy F 4
4）由整体平衡条件求其他约束反力
第六章 简单的超静定问题
§6-1 超静定问题及其解法
§6-2 拉压超静定问题
§6-3 扭转超静定问题 §6-4 简单超静定梁
§6-1 超静定问题及其解法
超静定问题与超静定结构：未知力个数多于独立 的平衡方程数。 超静定次数：未知力个数与独立平衡方程数之差。 变形几何相容方程：有多余约束的存在，杆件（或 结构）的变形受到多于静定结构的附加限制。根据 变形的几何相容条件，建立附加的方程。
7-6
目录
采用超静定结构
MA MA FA y FA y
A A 2a 2a (a) (a) A A
B B a a
F F
C C
例 求梁的支反力，梁的抗弯 刚度为EI。 解：
1）判定超静定次数
(b) (b)
B B F F FBy FBy B B B
C C
2）解除多余约束，建立相当系统 3）进行变形比较，列出变形协调 条件
FN1 FN 2 33.3kN
FN 2 2 33.3MPa A2
FN 1 1 66.7MPa A1
例：设温度变化为t，1、2杆的膨胀系数为1， 3杆
的膨胀系数为3，由温差引起的变形为l= •t •l,
求各杆温度应力。

F3 b 3 EA
4. 变形几何协调条件
F1 A
F2
③
2 2 1
3 31
B
C
D F
位移法 1. 假设θ已知 2. 变形几何协调条件
θ
A
①
②
③ D F
1 l
2 2l
3 3l
3. 三杆轴力 EA EA F1 1 l b b
EA EA F2 2 2l b b EA EA F3 3 3l b b
3
A 0
ql 2 MA 8
§2 拉压超静定问题 例1. EA已知，求B处约束力。
A a C B F b
(1)
(2)求B处位移
AC
F FB a
EA EA
BC
FB b EA
A C B FB
B
F FB a FB b
EA
F
(3)变形协调
B 0
B
C
q
A B
C
C FCD
A
B
C
q
FCD C A B FCDl A B C
FCD
A
B
C
ql2/2
A B C q B C A FCDl
ql2/2 A
B
C
q A B C q B C A FCDl B
ql2/2 -FCDl
A
B
C
ql2/2 A
FCD C
q2l 3 ql 2 / 2 FCD l 2l ql 4 FCD l 3 C l 24 EI 3 EI 8 EI 3 EI
C
B1 B 2

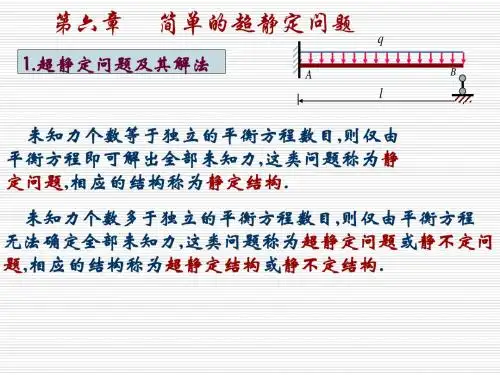
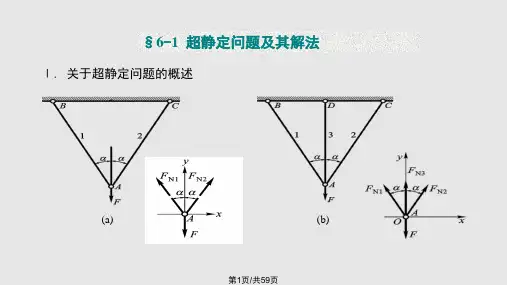
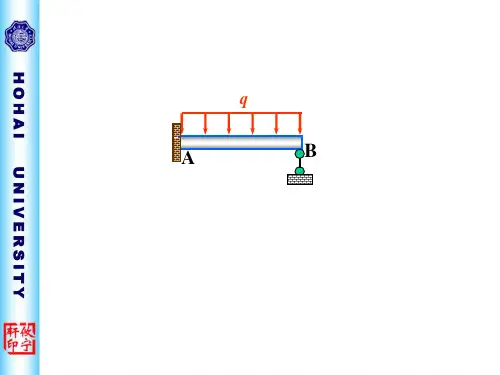
扭转超静定问题扭转的超静定问题 —— 受扭圆杆的未知反力偶或扭矩的数目超过独立的静力平衡方程数目。

静定轴 —— 由平衡条件就可确定全部未知力偶矩的轴。

超静定轴（静不定轴）—— 仅根据平衡条件不能确定全部未知力偶矩的轴。

La(a)M (b)AAAI M bM eeM BI BBBM ca b超静定问题的解法：（1）建立静力平衡方程，确定静不定次数； （2）由变形几何关系建立变形协调方程；（3）应用扭矩与相对扭转角之间的物理关系： 代入变形协调方程，得到补充方程；（4）补充方程与静力平衡方程联立，求解所有的未GI Tl =P知反力偶或扭矩。

有缘学习更多驾卫星ｙｇｄ３０７６或关注桃报：奉献教育（店铺）一组合杆由实心杆1和空心管2固接在一起所组成，杆和管的材料相同。

剪切弹性模量为G ，试求组合杆承受外力偶矩M 以后，杆和管内的最大切应力。

MM2d 1d 121 静力平衡关系2 变形几何关系 解：例1 3 物理关系1 T1 22T 1T （1） （2）（3）1141=π32T ld G ϕ12=T T T M+=12=ϕϕ224421=π-32T lG d d ϕ（）4 最大切应力计算杆1： 管2： 代入变形协调方程，得补充方程MM2d 1d （4）41124421=()d T T d d -41142=d T T d 4421242-=d d T T d （5）1111341P1216=ππ16T T Td d W d τ==（6） 2223341P222216=ππ[1()]16T T Td W d d d τ==-（7）。

M A Me M B 0
Me MB
A
C
B
2、变形协调方程
B 0
即
BM BM 0
e B
Me
MB
A
C
B
3、补充方程
BM
e
M e a GI p
BM
BM Bl GI p NhomakorabeaM e a M Bl 0 GI p GI p
M ea MB l

4、联立解得
3、物理方程
FN 1l l1 EA FN 3 l l 3 EA FN 2 l l 2 EA
得
FN 1 FN 2 FN 3
F 12 F 3
C′
补充方程 FN 1 FN 3 2FN 2
7F 12
例题3：如图所示结构，杆①、②的刚度为EA，梁BD 为刚体，载荷F=50kN，许用应力[s]160MPa。试确 定各杆的横截面积。 解： 1、确定各杆内力 取横梁为研究对象 平衡方程
FB aEAT
由平衡方程得 FA FB aEAT
例题5：如图所示结构，三杆的刚度均为EA，杆③的长 度比设计长度l短了d。试求装配后各杆的轴力。
A
D
① ③ a a C′ C l2 ②
B
解：对称结构，内力对称 变形协调方程
l1 d l 3 cos a
l
d
l3 l1
lt a1 T l1 a 2 T l 2
A
l1
C
l2
B
约束力产生的变形
l FB FB l1 F l B2 E1 A1 E2 A2
lt
FB
变形协调方程

5 Pa RD a RD a 6 EI 3EI 3EI
如何得到？
A D
P
B
自行完成
C D
RD
例题 6
图示结构AB梁的抗弯刚度为EI，CD杆的抗拉刚度为EA，
已知P、L、a。求CD杆所受的拉力。
D
a
A
C
L
2
L
B
2
P
解：变形协调条件为 wC lCD
D
a
C
FC
A
( P FC ) L wC 48EI FC L lCD EA
温度应力：
FB E t A
6 1 12 . 5 10 碳素钢线胀系数为 C0
温度应力：超静定结构中，由于温度变化，使构
件膨胀或收缩而产生的附加应力。
不容忽视！！！
路、桥、建筑物中的伸缩缝 高温管道间隔一定距离弯一个伸缩节
例题 11
图示阶梯形杆上端固定，下端与支座距离=1mm， 材料的弹性模量E=210GPa，上下两段杆的横截 面面积分别为600平方毫米和300平方毫米。试 作杆的轴力图。
C
A
FA
B
L2
FC
FA FB FC qL 0
L2
M
A
0
FB
变形协调方程
L qL2 FC FB L 0 2 2
3 FB qL 16
FA 3 qL 16
C q C FC 0
7.5kNm
5qL4 FC L3 5 0 FC qL 8 384 EI Z 48EI Z
由于超静定结构能有效降低结构的内力及变形，在 工程上（如桥梁等）应用非常广泛。
●超静定问题的解法：

第十一章
简单的超静定问题
超静定问题及其解法
❖ 静定问题：其约束力或构件内力可通过静力平衡方 程求解的问题
❖ 超静定问题：仅凭静力学平衡方程不能求解的问题 ❖ “多余约束”：在超静定问题中多于维持平衡所需
的约束，如支座、杆件等 ❖ 超静定次数：未知力超过平衡方程的数目（个数） ❖ 变形几何相容方程：根据多余约束处的几何相容条
件建立的构件变形关系。
超静定梁 基本静定系
静定梁 约束反力比平衡方程数多1
C点的变形状况： wC=0
❖ 超静定问题的解法
1、选定多余约束，解除多余约束，根据约束状况代 以约束反力，得到基本静定系。
2、建立平衡方程
3、由几何相容条件，建立补充方程。
(a) 确定被解除约束点的实际位移（角位移、线位 移）；
(b) 根据基本静定系计算各反力在该点的位移代数 和并让其等于实际位移值，得到该点的位移方程；
© 将物理方程带入该点的位移方程，从而得到有 约束反力表示的补充方程；
4、联立上述方程，从而解得该点约束反力。
11-1 拉压超静定问题
❖ 拉压超静定问题实例
已知l1＝l2＝l， E1＝E2＝E， A1=A2=A， l3 ，E3，A3 求P作用下结构各杆件的轴力
F
FN 3
1
2
EA E3 A3 cos3
11-2 装配应力、温度应力
一、装配应力 二、温度应力
11-3 扭转超静定问题
11-4 简单超静定 梁
未知反力的数目多于平衡方程的 数目，仅由静力平衡方程不能求 解的梁，称为超静定梁
例:已知q、l,求A、B支座反力。
解除B 处约束， 代之以约束反力
RB
存在变形协调条件

例1 木制短柱的四角用四个40404的等边角钢加固，角钢和 木材的许用应力分别为[]1=160M Fa和[]2=12MFa，弹性模
量分别为E1=200GFa 和 E2 =10GFa；求许可载荷P。 P 解：平衡方程: y Y 4F F P 0

N1
N2
4FN1
FN2
几何方程
2 FN1 FN3
X F
Y F
FN2
N1
N1
sin FN 2 sin 0

A P
cos FN 2 cos FN 3 P 0

A P
B 3
D
1

A
2
C 几何方程——变形协调方程： L1 L3 cos
物理方程——弹性定律：
L1 FN 1 L1 E1 A1 L3 FN 3 L3 E3 A3
(a)
Tb Ta
(b)
解: 1. 铜杆和钢管的横截面上各有一个未知内力矩 ── 扭矩Ta和Tb(图b)，但只有一个独立的静力平衡方程
Ta+Tb= Me，故为一次超静定问题。
2. 位移相容条件为
Ba Bb
Tb Ta
(b)
3. 利用物理关系得补充方程为
Ga I pa Tal Tbl ，即 Ta Tb Ga I pa Gb I pb Gb I pb
P1 A11 / 0.07 308.6 160/ 0.07 705.4kN
FN 2 0.72P A2 2
P2 A2 2 / 0.72 2502 12 / 0.72 1042kN
求结构的许可载荷： 方法2:
1 L1 / E1 0.8mm 2 L 2 / E2 1.2mm

结构与支承物的连接处只 能发生转动，不能发生刚 性位移。
按几何特征分类
连续性
Hale Waihona Puke 结构在各个方向上都是连 续的。非连续性
结构在某些方向上存在间 断，如梁的弯曲变形。
平面性
结构在某个平面内发生变 形，如薄板弯曲。
按求解方法分类
解析法
01
近似法
02
03
实验法
通过数学解析的方法求解超静定 问题，需要建立复杂的数学模型。
THANKS FOR WATCHING
感谢您的观看
解决超静定问题的技术和方法在工程 实践中具有广泛的应用价值，为复杂 结构的分析和设计提供重要的理论支 持和技术指导。
02 超静定问题的分类
按支承情况分类
01
02
03
固定支承
结构与支承物的连接处不 能发生任何方向的位移， 只能发生转动。
弹性支承
结构与支承物的连接处既 有刚性位移，又有弹性位 移。
铰支承
机械装置超静定问题分析
总结词
保障机械运转稳定性
详细描述
机械装置在运转过程中会受到各种外力和内 力的作用，导致其发生变形和位移。超静定 问题分析能够评估机械装置在不同工况下的 稳定性，预防因变形和位移引起的故障，提 高机械运转的可靠性和效率。
05 超静定问题的未来研究方 向
新型材料的超静定问题研究
详细描述
复杂结构如高层建筑、大跨度桥梁、空间结构等，其 超静定问题涉及到多个自由度和多种非线性因素，需 要深入研究其静力、动力和稳定性等问题。
多场耦合的超静定问题研究
要点一
总结词
要点二
详细描述
多场耦合的超静定问题研究将成为一个重要方向。

超静定问题的解法1. 画受力图,列平衡方程,判断静不定次数;2.根据结构的约束条件画变形图,找变形协调关系,列几何方程;3.由力与变形(或温度与变形)的物理关系, 列物理方程;4.联立几何方程与物理方程建立补充方程;5.补充方程与平衡方程联立解全部未知力.例2 求图示两端固定等直杆的约束反力AB 0A B P R R --=解：几何方程:(),B B P R R a b P al l E AE A+∆=∆=物理方程:代入平衡方程解得:A Pa R a b=+平衡方程:解除约束,以已知方向约束反力代替BP R l l ∆=∆为得到变形协调方程,解除多余约束，分别考虑外力和多余约束反力产生的位移叠加设B 为多余约束，此处的实际位移必须为0PRR B解得:B Pb R a b=+例8．例9．温度应力和装配应力练习题N EA l23=-δN EA l16=δ超静定问题求解原理：(1) 解除超静定结构的多余约束，以约束反力代替，使超静定结构变成静定结构。

多余约束反力的数目即为超静定次数，也是要寻找的补充方程数目；(2) 研究在外力和多余约束反力作用下的力的平衡条件。

(3) 研究在外力和多余约束反力作用下的结构的几何变形关系，列变形协调方程；(4) 由变形几何关系与物理方程联立得到 n 个补充方程，与平衡方程联立求解可得所有约束反力。

欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求。

例4 两铸件用两钢杆1、2连接如图，其间距为 l=200mm。现需 将制造得过长e=0.11mm的铜杆3装人铸件之间，并保持三杆 的轴线平行且有等间距a。试计算各杆内的装配应力。已知： 钢杆直径d=10mm，铜杆横截面为20mm 30mm的矩形，钢的 弹性模量E=210GPa，铜的弹性模量E=100GPa。铸件很厚，其 变形可略去不计。
最后，补充方程变为
7 qa4 FNa3 FNl 12 EI EI EA
解得
FN
7qa4 A 12(Il Aa3 )
B
D
在静定问题中，只会使结构的几 何形状略有改变，不会在杆中产生 附加的内力。如1杆较设计尺寸过长， C 仅是A点的移动。
3
1 aa
2
A''
A'
e
A
在超静定问题中，由于有了多余 约束，就将产生附加的内力。
附加的内力称为装配内力,与之相 应的应力则称为装配应力,装配应力 是杆在荷载作用以前已经具有的应 力，也称为初应力。
土建工程中的预应力钢筋混凝土构件，就是利 用装配应力来提高构件承载能力的例子。
(2)温度应力
静定问题：由于杆能自由变形，由温度所引起的变 形不会在杆中产生内力。
超静定问题：由于有了多余约束，杆由温度变化所 引起的变形受到限制，从而将在杆中产生内力。这 种内力称为温度内力。
与之相应的应力则称为温度应力。
M x 0, M A M B M e 0
变形协调条件：根据原超静定杆的约束情况，基 本静定系在B端的扭转角应等于零, 即补充方程为
B 0
按叠加原理：
B BB BM 0
BB、BM分别为MB、Me 引起的在杆端B的扭转角。
线弹性时，物理关系(胡克定理)为

对于一个平衡物体，若独立平衡方程数目与未知数的数目恰 好相等，则全部未知数可由平衡方程求出，这样的问题称为静 定问题。（图a） 但工程上有时为了增加结构的刚度或坚固性，常设置多余的 约束， 未知数的数目多于独立方程的数目，未知数不能由平 衡方程全部求出，这样的问题称为静不定问题或超静定问题。 （图b）
（3）本构方程
LT 2aT ;
FN 1a FN 2 a LN EA1 EA2
由变形和本构方程消除位移未知量
FN 1 FN 2 2T EA1 EA2
（4）联立求解得
FN 1 FN 2 33.3kN
（5）温度应力
FN 1 1 66.7MPa A1
FN 2 2 33.3MPa A2

A
2
1

A P
2
1、问题的提出
两杆桁架变成 三杆桁架，缺一个 方程，无法求解
P
F
x
FN 1 sin FN 2 sin 0
F
y
FN 1 cos FN 2 cos FN 3 P 0
三杆桁架是单靠静力方程求解不了的，称为 静不定（ Static indeterminate ）——静力不能确定 超静定问题（Hyperstatic ）——超出了静力范围 其实我们在拉压杆应力遇到过这类问题 拉压杆截面上有无穷个应力，单凭静力平衡方程 不能求解 —— 超静定问题： 补充变形协调方程 建立本构（或物理）方程予以沟通 结合平衡方程联立求解
q
1
2
3
如何求解？
1. 静力不定 2. 变形方程补充--------几何相容条件（不允许 一部分脱离另一部分，也不允许一部分嵌入 另一部分） 3. 物理方程在静力平衡与变形协调之间架桥

超静定问题的解题步骤概述说明以及解释1. 引言1.1 概述目前，超静定问题在工程设计和科学研究中扮演着至关重要的角色。

超静定问题是指那些具有多余约束条件的力学系统，在这种情况下，物体的运动过程不止一个可能的解。

解决超静定问题需要使用特定的数学工具和分析方法。

本文将介绍解题步骤，为读者提供一个清晰而简洁的指南。

1.2 文章结构本文分为五个主要部分。

在引言部分，我们将概述文章内容，并简要介绍超静定问题及其重要性。

第二部分将对超静定问题进行详细讨论，包括定义、背景知识以及实际应用场景。

接下来，第三部分将总结解题步骤，并概括每个步骤所需考虑的关键点。

第四部分则会更加详细地解释每个步骤，并提供具体操作步骤和示例。

最后，在结论与总结部分，我们将总结解题步骤，并讨论可能遇到的困难与挑战，以及其他相关问题和研究方向。

1.3 目的本文旨在帮助读者全面了解超静定问题和解题步骤。

通过详细讲解每个步骤的要点和操作方法，读者将能够更加轻松地解决超静定问题，并理解其在实际工程和科学领域的应用。

我们希望本文能成为读者解题过程中的有价值的参考资料，提供清晰而系统化的指导。

2. 超静定问题简介:2.1 定义和背景知识:超静定问题是指在静力学中，物体受到的约束超过了必要的约束数量。

这意味着通过仅使用平衡方程无法求解未知变量的值。

超静定问题在工程、建筑和力学领域中经常出现，并需要特殊的解题方法来找到合适的解决方案。

2.2 超静定问题的重要性:理解和解决超静定问题对于设计和分析结构非常重要。

一些实际应用场景中，超静定结构可以提供更高的刚度、稳定性和可持续性。

因此，研究人员和工程师需要掌握解决超静定问题的技巧。

2.3 实际应用场景:超静定问题广泛应用于建筑、土木工程、桥梁设计以及机械工程等领域。

例如，在建筑设计中，支撑柱或梁受到多个支点约束时可能会出现超静定问题。

在机械工程中，一些连接件或装配件也可能涉及到超静定问题。

了解超静定问题的定义、背景知识以及其在实际应用中的重要性对于理解本文后续将介绍的解题步骤至关重要。

wB wB q wB FBy wB M B
32
目录
I、超静定梁旳解法
q MA
A
l
B
q
MB
l
A或 B 0
A A q A M A A M B 0
33
目录
I、超静定梁旳解法
q
q FQc
MC q
A
l
B
C
l/2
M
C
l/2
C
利用对称性 FQc=0
FQc
再利用对称性 c=0
C C qC M C
, l2
l3
FN 2l2 E2 A2
8
目录
§6.2 拉压超静定问题
成果：由平衡方程、几何相容方程、物理 关系联立解出。
N1
1
FP 2E2 A2l1
,
E1 A1l2
E2 A2l1
FN2
FN3
E1 A1l2 1 2E2 A2l1
FP
E1 A1l2
9
目录
例题6-1
木制短柱旳4个角用4个40mm×40mm×4mm旳等边角
4 20 2 4 8.75 125 kN m
目录
例题6-2
B
1
C 2 30
30
3
D
列出变形几何关系，将A点旳位移分
量向各杆投影，得
A
l1 y sin x cos
F
l2 x
y
l3 y sin x cos
A x 几何相容关系为 l3 l1 2l2 cos
y
代入物理关系 2FN3l 2FN1l 3FN 2l
3EA3 3EA1 EA2
A
解：设AC杆杆长为l，则AB、AD杆长为