线性回归模型论文回归模型论文
- 格式:doc
- 大小:74.00 KB
- 文档页数:11
沼气生成问题(一)问题提出:沼气的主要成分是甲烷,它是由含纤维素的有机物质在隔绝空气的情况下受到细菌分解作用所产生的一种有毒易燃气体。
在我国农村广泛的利用沼气池生成沼气,作为一种卫生快捷的燃料,一般使用植物秸秆残体在保持一定湿度和温度的条件下,并与空气隔绝一段时间后经自然分解而成。
经验证明,如果适当的加入一些有机肥料作为发酵剂,则可以加快沼气的形成。
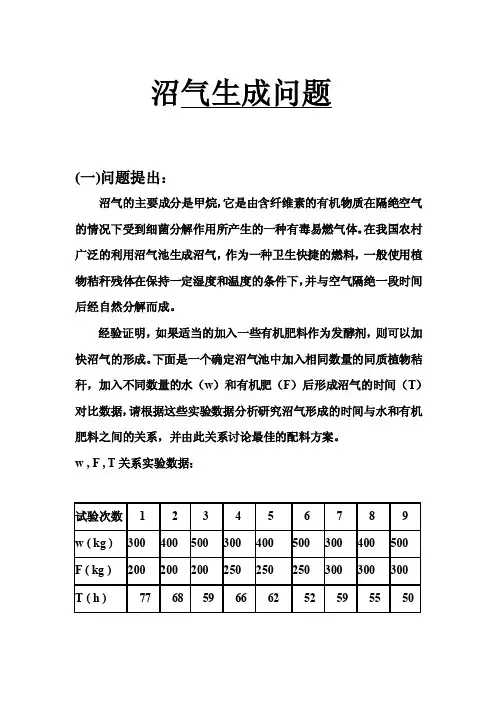
下面是一个确定沼气池中加入相同数量的同质植物秸秆,加入不同数量的水(w)和有机肥(F)后形成沼气的时间(T)对比数据,请根据这些实验数据分析研究沼气形成的时间与水和有机肥料之间的关系,并由此关系讨论最佳的配料方案。
w , F , T关系实验数据:(二)模型的假设与分析一、模型假设(1)设试验数据实在相同的试验条件下进行试验所取得的,即沼气池的大小形状相同,秸秆和有机肥料相同,其自身的含水量也相同。
(2)在此不考虑环境温度的影响,虽然在相同的条件下高温可以促使沼气的形成,但实际中的环境温度一般是不可控的,于是我们认为总是在一定的适宜温度范围内,温度因素对形成沼气的时间影响不大。
(3)每次试验是独立进行的,且w , F , T 的试验值是准确的。
二、模型分析根据沼气的自然形成原理和相关知识,我们知道在同等条件下,水分和肥料各自都对沼气的形成起到一定的促进作用,而且二者之间也存在着一定的交互效应,即二者用量多少的不同,其效果是不同的。
表现为沼气形成的时间不仅与水和肥料的用量有关,而且还与二者的交互作用有关。
因此,一般认为沼气形成时间T 的长短应该是加水量W 和肥料用量F 的二次多项式函数,为此,我们可以采用线性回归的方法来研究他们之间的关系。
(三)模型建立与求解为了便于问题的描述,我们并不直接将沼气形成的时间T 表示成w , F 的函数,根据试验数据的分布情况,在这里我们引入二个新的变量:为此,我们可以将时间 T 表示为 u1 , u2 的二次多项式函数。

实验二__多元线性回归模型和多重共线性范文多元线性回归是一种常用的统计分析方法,用于研究多个自变量与一个因变量之间的关系。
在进行多元线性回归分析时,一个重要的问题是多重共线性。
多重共线性是指多个自变量之间存在高度相关性,这会导致回归模型的不稳定性,参数估计的不准确性,以及对自变量的解释能力下降等问题。
在进行多元线性回归分析之前,首先需要对自变量之间的相关性进行检验。
常用的方法有相关系数、方差膨胀因子(VIF)等。
相关系数用于衡量两个变量之间的线性关系,其值介于-1和1之间,接近于1表示高度正相关,接近于-1表示高度负相关。
VIF用于衡量一个自变量与其他自变量之间的相关性,其值大于1且越接近于1,表示相关性越强。
如果发现多个自变量之间存在高度相关性,即相关系数接近于1或VIF接近于1,就需采取措施来解决多重共线性问题。
一种常用的方法是通过增加样本量来消除多重共线性。
增加样本量可以提高模型的稳定性,减小参数估计的方差。
但是,增加样本量并不能彻底解决多重共线性问题,只能部分缓解。
另一种常用的方法是通过变量选择来解决多重共线性问题。
变量选择可以将高度相关的自变量从模型中剔除,保留与因变量高度相关的自变量。
常用的变量选择方法包括前向选择、逐步回归和岭回归等。
这些方法都是根据一定的准则逐步筛选变量,直到得到最佳模型为止。
在变量选择中,需要注意在变量剔除的过程中,要确保剩余变量之间的相关性尽可能小,以提高模型的稳定性和准确性。
此外,还可以通过变换变量来解决多重共线性问题。
变换变量可以通过对自变量进行平方项、交互项等操作,以减小相关性。
变换变量的方法需要根据实际情况来选择,具体操作可以参考相关的统计学方法教材。
总之,多元线性回归模型在实际应用中经常遇到多重共线性问题。
通过检验自变量之间的相关性,选择合适的变量和适当的变量变换方法,可以有效解决多重共线性问题,提高模型的稳定性和准确性。
在具体的研究中,应根据实际情况选择适合的方法来解决多重共线性问题,以确保回归分析结果的可靠性和有效性。

《多元线性回归分析的实例研究》篇一一、引言多元线性回归分析是一种统计学方法,用于探究一个因变量与多个自变量之间的关系。
这种方法在各个领域的研究中广泛应用,如经济学、社会学、心理学等。
本文将通过一个具体的实例,展示多元线性回归分析的应用过程及其实证结果。
二、研究背景与目的本研究以某地区房价为研究对象,探讨房价与地理位置、房屋面积、房屋装修等因素之间的关系。
目的是通过多元线性回归分析,找出影响房价的主要因素,为房地产投资者和购房者提供参考依据。
三、数据收集与处理本研究采用某地区房地产交易数据,包括房价、地理位置、房屋面积、房屋装修等变量。
在数据收集过程中,我们确保数据的准确性和完整性,并对数据进行清洗和处理,以消除异常值和缺失值的影响。
四、多元线性回归分析(一)模型构建根据研究目的和收集的数据,构建多元线性回归模型。
假设房价为因变量Y,地理位置、房屋面积、房屋装修等因素为自变量X1、X2、X3。
则模型可以表示为:Y = β0 + β1X1 + β2X2 +β3X3 + ε。
其中,β0为常数项,β1、β2、β3为回归系数,ε为随机误差项。
(二)参数估计与假设检验利用统计软件对模型进行参数估计,得到各回归系数的估计值及其显著性水平。
通过假设检验,检验自变量与因变量之间的线性关系是否显著。
若显著性水平低于预设的阈值(如0.05),则认为自变量与因变量之间存在显著的线性关系。
(三)模型检验与优化对模型进行检验和优化,包括检查模型的拟合优度、自相关性和异方差性等。
若存在显著问题,则采取相应的方法进行修正和优化。
五、实证结果与分析(一)回归系数解释根据参数估计结果,得出各回归系数的估计值。
解释各系数在模型中的意义和作用,如地理位置对房价的影响程度、房屋面积对房价的影响程度等。
(二)实证结果分析根据实证结果,分析自变量与因变量之间的关系及影响程度。
通过对比各回归系数的估计值和显著性水平,找出影响房价的主要因素。
同时,结合实际情况,对实证结果进行深入分析和解释。

线性回归模型的研究毕业论文1 引言回归分析最早是由19世纪末期高尔顿(Sir Francis Galton)发展的。
1855年,他发表了一篇文章名为“遗传的身高向平均数方向的回归”,分析父母与其孩子之间身高的关系,发现父母的身高越高或的其孩子也越高,反之则越矮。
他把儿子跟父母身高这种现象拟合成一种线性关系。
但是他还发现了个有趣的现象,高个子的人生出来的儿子往往比他父亲矮一点更趋向于平均身高,矮个子的人生出来的儿子通常比他父亲高一点也趋向于平均身高。
高尔顿选用“回归”一词,把这一现象叫做“向平均数方向的回归”。
于是“线形回归”的术语被沿用下来了。
回归分析中,当研究的因果关系只涉及因变量和一个自变量时,叫做一元回归分析;当研究的因果关系涉及因变量和两个或两个以上自变量时,叫做多元回归分析。
此外,回归分析中,又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的,分为线性回归分析和非线性回归分析。
按照参数估计方法可以分为主成分回归、偏最小二乘回归、和岭回归。
一般采用线性回归分析,由自变量和规定因变量来确定变量之间的因果关系,从而建立线性回归模型。
模型的各个参数可以根据实测数据解。
接着评价回归模型能否够很好的拟合实际数据;如果不能够很好的拟合,则重新拟合;如果能很好的拟合,就可以根据自变量进行下一步推测。
回归分析是重要的统计推断方法。
在实际应用中,医学、农业、生物、林业、金融、管理、经济、社会等诸多方面随着科学的发展都需要运用到这个方法。
从而推动了回归分析的快速发展。
2 回归分析的概述2.1 回归分析的定义回归分析是应用极其广泛的数据分析方法之一。
回归分析(regression analysis)是确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法。
2.2 回归分析的主要容(1)从一组数据出发,确定某些变量之间的定量关系式,即建立数学模型并估计其中的未知参数。
估计参数的常用方法是最小二乘法。


《多元线性回归分析的实例研究》篇一一、引言多元线性回归分析是一种统计方法,用于研究多个变量之间的关系。
在社会科学、经济分析、医学等多个领域,这种分析方法的应用都十分重要。
本实例研究以一个具体的商业案例为例,展示了如何应用多元线性回归分析方法进行研究,以便深入理解和探索各个变量之间的潜在关系。
二、背景介绍以某电子商务公司的销售额预测为例。
电子商务公司销售量的影响因素很多,包括市场宣传、商品价格、消费者喜好等。
因此,本文通过收集多个因素的数据,使用多元线性回归分析,以期达到更准确的销售预测和因素分析。
三、数据收集与处理为了进行多元线性回归分析,我们首先需要收集相关数据。
在本例中,我们收集了以下几个关键变量的数据:销售额(因变量)、广告投入、商品价格、消费者年龄分布、消费者性别比例等。
这些数据来自电子商务公司的历史销售记录和调查问卷。
在收集到数据后,我们需要对数据进行清洗和处理。
这包括去除无效数据、处理缺失值、标准化处理等步骤。
经过处理后,我们可以得到一个干净且结构化的数据集,为后续的多元线性回归分析提供基础。
四、多元线性回归分析1. 模型建立根据所收集的数据和实际情况,我们建立了如下的多元线性回归模型:销售额= β0 + β1广告投入+ β2商品价格+ β3消费者年龄分布+ β4消费者性别比例+ ε其中,β0为常数项,β1、β2、β3和β4为回归系数,ε为误差项。
2. 模型参数估计通过使用统计软件进行多元线性回归分析,我们可以得到每个变量的回归系数和显著性水平等参数。
这些参数反映了各个变量对销售额的影响程度和方向。
3. 模型检验与优化为了检验模型的可靠性和准确性,我们需要对模型进行假设检验、R方检验和残差分析等步骤。
同时,我们还可以通过引入交互项、调整自变量等方式优化模型,提高预测精度。
五、结果分析与讨论1. 结果解读根据多元线性回归分析的结果,我们可以得到以下结论:广告投入、商品价格、消费者年龄分布和消费者性别比例均对销售额有显著影响。

《多元线性回归分析的实例研究》篇一一、引言多元线性回归分析是一种统计方法,用于研究多个变量之间的线性关系。
在实际生活和科研工作中,这种分析方法广泛应用于经济、医学、生态学等领域。
本文以一个具体实例为例,深入探讨多元线性回归分析的步骤和应用。
该实例关注于房屋价格的影响因素分析。
二、研究背景及目的随着房地产市场的发展,房屋价格受到多种因素的影响。
为了探究这些因素如何共同影响房屋价格,本文选取了一组具有代表性的房屋数据,并运用多元线性回归分析方法进行实证研究。
研究目的在于揭示影响房屋价格的主要因素,为购房者和房地产投资者提供参考依据。
三、数据与方法(一)数据来源本研究的数据来源于某城市房屋交易数据库,涵盖了多个区域的房屋信息,包括房屋价格、房屋面积、房屋年龄、周边环境、学区等因素。
(二)研究方法本研究采用多元线性回归分析方法,通过建立模型来研究各因素与房屋价格之间的线性关系。
具体步骤包括:数据清洗、变量选择、模型建立、模型检验和结果解释等。
四、多元线性回归分析步骤及结果(一)变量选择与数据清洗根据研究目的和前人研究成果,本研究选择了以下变量:房屋价格(因变量)、房屋面积、房屋年龄、周边环境(包括交通、商业、绿化等)、学区等(自变量)。
在数据清洗阶段,剔除了异常值和缺失值,确保数据的准确性和可靠性。
(二)模型建立根据选定的变量,建立多元线性回归模型。
模型形式如下:P = β0 + β1 × Area + β2 × Age + β3 × Environment + β4 × Schoo l + ε其中,P表示房屋价格,Area表示房屋面积,Age表示房屋年龄,Environment表示周边环境因素,School表示学区因素,βi 为各变量的回归系数,ε为随机误差项。
(三)模型检验通过SPSS软件进行模型检验。
首先进行多重共线性检验,发现各变量之间不存在明显的共线性问题。

应用回归分析课程设计报告课程:应用回归分析题目:人均可支配收入的分析年级:11金统专业:金融统计学号:姓名:指导教师:基于多元线性回归模型对我国城镇居民家庭人均可支配收入的分析摘要:收入分配和消费结构都是国民经济的重要课题居民消费的主要来源是居民收入而消费又是拉动经济增长的重要因素。
本文将通过多远统计分析方法对我国各地区城镇居民收入的现状进行分析。
通过分析找出我国城镇居民收入特点及其中存在的不足。
城镇居民可支配收入是检验我国社会主义现代化进程的一个标准。
本文根据我国城镇居民家庭人均可支配收入为研究对象,选取可能影响我国城镇居民家庭人均可支配收入的城乡居民储蓄存款年底余额、城乡居民储蓄存款年增加额、国民总收入、职工基本就业情况、城镇居民家庭恩格尔系数(%)5个因素,运用多元线性回归分析建立模型,先运用普通最小二乘估计求回归系数再对方程进行异方差、自相关、和多重共线性诊断,用迭代法消除了自变量之间的自相关。
对于多重共线性问题,先是用逐步回归和剔除变量的方法,最终转变为用方差扩大因子法城乡居民储蓄存款年增加额剔除城镇居民家庭恩格尔系数(%)解决多重共线性,建立最终回归方程432108.0039.0012.0470.5305x x x y +++-=∧标准化回归方程**3*24108.0863.0031.0x x x y ++=∧以其探究最后进入回归方程的几个变量在影响城镇居民收入孰轻孰重,达到学习与生活结合的效果。
分析出影响城镇居民收入的主要原因,并对模型联系实际进行分析,以供国家进行决策做参考。
关键词:多元线性回归 异方差 自相关 多重共线性 逐步回归 方差扩大因子(一)引言:改革开放以来我国的国民经济增长迅速居民的收入水平也大幅提高但居民收入分配差距也在不断扩大。
2008年的金融危机为我国带来的后遗症还在继续影响着居民正常生活物价上涨和通货膨胀的压力仍然困扰着老百姓收入和消费支出体系的健康发展至关重要。

摘要许多经济现象往往不是简单的与某一因素有关而是要受多个因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归。
当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元性回归。
本文在2007年全国各省市主要工业产品的产量与工业总产值的具体数据下,选用塑料、水泥、钢筋、平板玻璃、粗钢、盘条以及原煤等工业产品的产量作为研究对象,建立多元线性回归模型,并对模型做出参数估计.在此基础上对模型做出一定的解释,对于预测工业总产值具有一定的理论指导和现实意义。
关键词:多元线性回归模型;显著性检验;SPSS;预测The Application of Linear Regression Model in The Forecast of GrossIndustrial ProductionAbstractMany economic phenomena are often not simply associated with a number of factors. At this point we need to use two or more factors as independent variables to explain changes in the dependent variable. This is also known as multiple regression. When more than one independent variable and the dependent variable are linear relationship, the regression analysis is carried out by diversity regression.This article use the specific data of the output of major industrial products and industrial output in nationwide provinces in 2007, and select the output of plastics, cement, steel, plate glass, crude steel, wire rod and raw coal as study object to establish multiple linear regression model, and then make the model parameter estimation. Based on this,we make some explanations to the model. All of these are of momentous current significance and far-reaching historical significance to the forecast of industrial production.Key Words:Multiple Linear Regression Model;Significant Test;SPSS目录摘要...................................................................................................................................... Abstract (I)目录 (II)引言 01 中国经济现状 (1)1.1 中国经济现状 (1)工业生产总值的概述 (1)2 多元统计分析基础 (3)多元线性回归模型 (3)2.1.1 模型的建立及矩阵表示 (3)2.1.2 模型的假设 (3)2.2 多元线性回归参数估计 (4)2.2.1 最小二乘估计和正规方程组 (4)2.2.2 最小二乘估计的矩阵形式 (5)2.2.3 最小二乘估计量的性质 (6)2.3 回归拟合度评价和决定系数 (6)2.3.1 离差分解和决定系数 (6)2.3.2 决定系数的性质及修正可决系数 (7)2.4 统计检验 (8)回归参数的显著性检验(t检验) (8)回归方程的显著性检验(F检验) (9)2.4.3 多重共线性检验 (9)2.4.4 异方差检验 (10)3 工业生产总值的多因素模型分析 (12)建立多因素分析模型 (12)数据收集 (12)3.2.1 数据说明 (12)3.2.2 数据的搜集情况说明 (13)3.3 SPSS软件的使用 (14)3.3.1 SPSS简介 (14)3.3.2 SPSS多元线性回归分析 (14)3.4 统计检验 (16)3.5 计量经济学检验及模型修正 (18)3.5.1 异方差检验 (18)3.5.2 自相关检验 (21)结论 (26)参考文献 (27)致谢 (28)引言工业生产总值从数值上反应一个地区的工业生产规模,是衡量一个地区的经济繁荣程度的重要指标。

线性回归模型论文回归模型论文一种基于线性回归模型的运动矢量重估算法摘要:针对H.264/AVC空间分辨率缩减的视频转码,提出一种基于线性回归模型的运动矢量重估计算法。
它利用原始视频流的运动矢量与下采样视频流的运动矢量之间的相关性,运用线性回归模型建模,得到下采样视频的运动矢量。
仿真实验结果表明:在保持率失真性能的同时,计算复杂度明显降低。
关键词:视频转码;H.264;线形回归模型;运动矢量重估计A Motion Vector Re-estimation Algorithm based on Linear Regression ModelYANG Gao-bo1, XIA Zhong-chao1, ZHANG Zhao-yang2, WANG Hui-qian1(1.College of Computer and Communication, Hunan Univ, Changsha, Hunan410082, China;2.Key Lab of Advanced Display and System Applications, Ministry of Education, Shanghai Univ, Shanghai 200072, China) Abstract: For the spatial resolution reduction ofH.264/AVC stream, a motion re-estimation algorithm based on linear regression model is proposed in this paper. It exploits the correlation between the motion vectors of original video stream and those of down-sampled video, which is modelled bylinear regression model to obtain the estimated motion vectors. Experimental results demonstrate that the proposed approach can significantly reduce the computational complexity of the transcoder with only slight sacrifice of visual quality.Key words: video transcoding;H.264/AVC;linear regression model;motion vector re-estimation随着网络和多媒体通信的发展,不同网络上各种视频信息的交流需求在不断增加。

数据建模与分析线性回归小论文线性回归是一种常见的数据建模和分析方法,在多个领域中都有广泛的应用。
本文将通过探讨线性回归的基本概念、模型建立、评价指标和应用案例等方面,分析线性回归在数据建模与分析中的重要性和价值。
首先,线性回归是一种用于建立因变量和自变量之间线性关系的统计模型。
其基本假设是,在给定自变量的情况下,因变量是自变量的线性函数加上随机误差项的组合。
线性回归的目标是寻找最佳拟合直线,以最小化实际观测值与预测值之间的差异。
在进行线性回归建模时,首先需要选择合适的自变量,这可以通过领域知识、相关性分析和特征选择等方法来进行。
然后,根据选定的自变量,建立线性回归模型,这可以通过最小二乘法估计回归系数。
为了评价线性回归模型的性能,可以使用多个指标。
其中,最常见的指标是均方误差(Mean Squared Error, MSE)和决定系数(R-squared)。
均方误差反映了模型的预测误差大小,而决定系数则表示模型解释数据方差的能力。
此外,还可以使用假设检验和置信区间等方法来评价回归系数的显著性和可靠性。
线性回归在数据建模与分析中具有广泛的应用。
例如,在市场营销中,可以使用线性回归分析来预测产品销量与广告投入的关系,从而确定最佳的广告策略。
在经济学中,线性回归可以用于分析GDP与劳动力市场、物价等经济变量之间的关系。
在医学研究中,线性回归可以用于探索生物标志物与疾病之间的相关性。
总之,线性回归是一种常见且有价值的数据建模与分析方法。
通过选择合适的自变量、建立合理的模型和评价模型的性能,线性回归可以帮助我们探索变量之间的关系,预测未来趋势,并为决策提供依据。
然而,需要注意的是,线性回归的使用必须满足一些假设条件,如线性关系、正态分布等,对于非线性关系或异常数据,需要采用其他方法进行建模和分析。
《多元线性回归分析的实例研究》篇一一、引言多元线性回归分析是一种统计方法,用于研究多个变量之间的关系。
在社会科学、经济学、管理学等多个领域中,它被广泛用于预测和解释一个变量如何受到多个独立变量的影响。
本文将通过一个实际案例,详细介绍多元线性回归分析的应用过程。
二、案例背景假设我们正在研究一个城市的新房销售价格问题。
我们关注的是新房的销售价格(因变量),并假设它受到以下几个自变量的影响:房屋面积、地理位置、房屋年龄和装修情况。
我们的目标是建立一个多元线性回归模型,以解释这些因素如何共同影响新房销售价格。
三、数据收集与处理我们收集了该城市内一定时间内的新房销售数据,包括房屋面积、地理位置(我们将其转化为几个虚拟变量以表示不同区域)、房屋年龄和装修情况等数据。
同时,我们也收集了相应的销售价格数据。
在数据处理阶段,我们对数据进行清洗、整理和格式化,以确保数据的质量和准确性。
四、多元线性回归分析1. 模型设定根据我们的研究目的和所收集的数据,我们设定了一个多元线性回归模型。
模型的形式为:销售价格= β0 + β1 房屋面积+ β2 地理位置+ β3 房屋年龄+ β4 装修情况+ ε,其中β0为常数项,β1、β2、β3、β4为回归系数,ε为随机误差项。
2. 参数估计我们使用最小二乘法对模型参数进行估计。
通过计算,我们得到了各个回归系数的估计值以及对应的t值、p值等统计量。
3. 模型检验我们对模型进行了一系列检验,包括变量的共线性检验、模型的拟合优度检验、回归系数的显著性检验等。
通过检验,我们发现模型的整体拟合效果较好,各变量之间没有明显的共线性问题,且回归系数的显著性水平均较低。
五、结果分析1. 回归系数解释根据回归系数的估计值,我们可以得出以下结论:房屋面积、地理位置、房屋年龄和装修情况对新房销售价格均有显著影响。
其中,房屋面积的回归系数最大,说明房屋面积对销售价格的影响最大。
其次是地理位置和装修情况,而房屋年龄的回归系数相对较小。
多元线性回归模型及其应用摘要本文介绍了多元线性回归模型,其过程分为模型构建、模型参数估计、模型检验和模型预测等几个方面。
通过对与我国物价指数CPI相关的几个因素建立初始多元线性回归模型,分析CPI的影响因素,之后对该模型进行各种统计检验,在模型检验中发现初始模型中有部分变量的系数不能通过检验,可能存在多重共线性的问题,最后采用逐步回归分析法来进行去除显著性不高的变量,并且建立新的模型,最终找出了影响CPI的关键要素是农业生产资料价格和人均GDP,通过最终确定的CPI与其影响因素之间的线性回归方程可以清晰地得到各个指标对CPI的影响大小,进而为我国控制CPI提供方向性的建议指导。
关键词多元线性回归 CPI影响因素逐步回归Multiple linear regression model and its applicationAbstract This article introduces the multiple linear regression model, and its process is divided into several aspects: model construction, model parameter estimation, model testing and model prediction. By establishing an initial multiple linear regression model on several factors related to China's price index CPI, analyzing the influencing factors of CPI, and then carrying out various statistical tests on the model, it is found in the model test that the coefficients of some variables in the initial model cannot pass Test, there may be a problem of multicollinearity, and finally use a stepwise regression analysis method to remove less significant variables, and establish a new model, and finally find out that the key factors affecting CPI are agricultural production materials prices and GDP per capita, Through the final linear regression equation between the CPI and its influencing factors, we can clearly get the impact of various indicators on the CPI, and then provide directional recommendations for the control of CPI in China.Key words Multiple linear regression CPI influencing factors stepwise regression目录引言 (1)1. 多元线性回归分析基本理论 (2)1.1 多元线性回归模型的一般形式 (2)1.2 多元线性回归模型的基本假设 (2)1.3 参数估计 (2)1.3.1 回归系数的估计 (2)1.3.2 样本方差的估计 (3)1.4 模型检验 (3)1.4.1 回归方程的显著性检验 (4)1.4.2 回归系数的显著性检验 (4)1.4.3 回归方程的拟合优度检验 (4)1.5 模型预测 (5)1.6 自变量的筛选方法 (5)2. 多元线性回归在CPI影响因素中的应用 (6)2.1 数据筛选 (6)2.1.1 指标选取 (6)2.1.2 数据收集 (6)2.2实证分析 (7)2.1.3 建立模型 (7)2.1.4 参数估计 (8)2.1.5 模型检验 (8)2.1.6 模型优化 (9)2.1.7 残差检验 (11)结论与建议 (13)参考文献 (14)致谢................................................................ 错误!未定义书签。
楚雄师范学院毕业论文(设计)目录摘要 (Ⅰ)关键词 (Ⅰ)Abstract (Ⅱ)Keywords (Ⅱ)前言 (1)1.绪论 (1)1.1 研究意义 (1)1.2 研究背景 (2)2.Logistic回归模型简介 (2)2.1二分类Logistic回归模型 (3)2.2多分类Logistic回归模型 (4)2.3 Logisti c回归模型的参数估计方法 (5)3.用Logistic回归模型预测糖尿病人病情程度 (7)3.1问题分析 (7)3.2相关性分析 (8)3.3模型建立及检验 (10)3.4结论 (12)参考文献 (13)附表1 (14)附表2 (15)附表3 (17)附表4 (20)致谢 (22)用Logistic回归模型预测糖尿病人病情程度摘要:本文首先总结近年来有关Logistic回归模型的研究概况。
然后在Logistic回归模型的基础上,重点介绍了二分类和多分类变量Logistic回归模型。
并使用最大似然估计法对模型中的参数进行估计,然后根据拟合优度检验法对模型进行检验。
最后利用SPSS统计软件对糖尿病人的病情程度建立模型,进行系统的分析并将预测结果与实际结果进行比对。
关键词:Logistic回归模型;拟合优度;最大似然估计;回归系数Logistic regression model was used to predict the severity of diabeticpatientsAbstract:This topic summarizes some surveys researched in recent years about Logistic Regression Model. Then on the basis of Logistic Regression Model, introduce two categories and multiple categories variable of Logistic Regression Model, .Firstly, use maximum likelihood to estimste parameters of the model, and secondly, use the goodness of fit test for the model, thirdly, use SPSS statistical software to build model for the severity of patients with diabetes mellitus, carry out the system analysis and contrast the forecast and real result.Keywords:Logistic regression model; goodness of fit;maximum likelihood estimate; regression coefficients.前言Logistic回归模型作为重要的统计模型,对种群生态学的研究具有核心理论价值。
楚雄师范学院数学系09级01班韩金伟学号:*********** 2011—2012学年第二学期《数据分析》期末论文题目影响成品钢材需求量的回归分析姓名韩金伟学号***********系(院)数学系专业数学与应用数学2012年 6 月 19 日题目:影响成品钢材需求量的回归分析摘要:随着社会经济的不断发展,科学技术的不断进步,统计方法越来越成为人们必不可收的工具盒手段。
应用回归分析是其中的一个重要分支,本着国家经济水平的不断提高,我们采用回归分析的方法对我国成品钢材的需求量进行分析应用。
为了使分析的模型具有社会实际意义,我们引用了1980——1998年的成品钢材、原油、生铁、原煤、发电量、铁路货运量、固定资产投资额、居民消费、政府消费9个不同的量来进行回归分析。
通过建立回归模型充分说明成品钢材需求量与其他8个变量的关系,以及我国社会经济的实际发展情况和意义。
关键字:线性回归回归分析社会经济回归模型成品钢材多元回归国家经济社会发展目录第1章题目叙述 (1)第2章问题假设 (1)第3章问题分析 (2)第4章数据的预处理 (3)4.1 曲线统计图 (3)4.2 散点统计图 (4)4.3 样本的相关系数 (4)第5章回归模型的建立 (5)第6章回归模型的检验 (6)6.1 F检验 (6)6.2 T检验 (6)6.3 T检验分析 (6)6.4 Chow断点检验 (8)6.5 Chow预测检验 (8)第7章违背模型基本假设的情况 (9)7.1 异方差性的检验 (9)7.1.1残差图示检验 (9)7.1.2 怀特(White)检验 (9)7.2 自相关性的检验 (10)7.2.1 LM检验 (10)7.2.2 DW检验 (10)第8章自变量选择与逐步回归 (10)8.1 前进逐步回归法 (10)8.1.1 前进逐步回归 (10)8.1.2 前进逐步回归模型预测 (11)8.2 后退逐步回归法 (12)8.2.1 后退逐步回归 (12)8.2.2 后退逐步回归模型预测 (13)第9章多重共线性的诊断及消除 (14)9.1 多重共线性的诊断 (14)9.2 消除多重共线性 (15)第10章回归模型总结 (17)参考文献 (18)附录: (19)楚雄师范学院 数学系 09级01班 韩金伟 学号:20091021135影响成品钢材需求量的回归分析第1章 题目叙述理论上认为影响成品钢材的需求量的因素主要有经济发展水平、收入水平、产业发展、人民生活水平提高、能源转换技术等因素。
一元线性回归分析论文专业:姓名:学号:摘要回归分析是数理统计中处理变量之间一种较为成熟、实用和有效的办法。
它可以简便有效地利用调查的统计资料,对经济现象进行事先预计和推断,为此引出一元线性回归分析数学模型和解决问题的方法。
本文回顾了描述变量相关关系和回归分析方面的基本知识,系统阐述了一元线性回归模型的基本原理,并将所学的知识与实际生产生活相结合,解决实际问题。
目录第一章回归分析概述 (1)1.1相关关系基本知识: (1)1.2回归分析基本知识回顾: (2)1.2.1回归分析的定义 (2)1.2.2.回归模型的分类 (2)1.2.3.回归分析的步骤 (3)1.2.4.回归分析的任务 (3)第二章一元线性回归的基本理论 (4)2.1一元线性关系的判断 (4)2.2一元线性回归模型的建立 (4)2.3模型回归效果的显著性检验 (5)2.3.1线性假设的显著性检验(T检验) (5)2.3.2线性回归的方差分析(F检验) (6)2.4利用回归方程进行预测 (9)2.4.一元线性回归模型的使用条件和特点 (11)2.4.1一元线性回归模型的使用条件 (11)2.4.2.一元线性回归模型的特点 (12)第三章一元线性回归分析方法的实际应用 (13)3.1.典型实际问题 (13)3.2应用MATLAB与EXCEL软件对验数据进行分析 (14)3.2.1应用MATLAB分析 (14)3.2.2应用Excel软件分析 (18)第四章总结 (25)第一章回归分析概述随着科技的迅速发展,数学的应用不仅在它的传统领域——经济建设、工程技术等方面发挥着越来越重要的作用,而且不断向一些新的领域渗透,形成了许多交叉科学,如计量经济学、人口控制论、生物数学等。
数学模型成为人们认识和研究这些学科的一种重要的工具,如何利用所学知识,建立与实际生活背景更贴切的数学模型来解决我们经济生活中存在的问题是摆在人们面前的重要课题!本文回顾了描述变量相关关系和回归分析方面的基本知识,系统阐述了一元线性回归模型的基本原理,并将其应用于实际生活中。
多元线性回归统计预测模型摘要:本文以多元统计分析为理论基础,在对数据进行统计分析的基础上建立多元线性回归模型并对未知量作出预测,为相关决策提供依据和参考。
重点介绍了模型中参数的估计和自变量的优化选择及简单应用举例。
关键词:统计学;线性回归;预测模型一.引言多元线性回归统计预测模型是以统计学为理论基础建立数学模型,研究一个随机变量Y 与两个或两个以上一般变量X“X?,…,Xp之间相依关系,利用现有数据,统计并分析,研究问题的变化规律,建立多元线性回归的统计预测模型,来预测未来的变化情况。
它不仅能解决一些随机的数学问题,而且还可以通过建立适当的随机模型进而解决一些确定的数学问题,为相关决策提供依据和参考。
目前统计学与其他学科的相互渗透为统计学的应用开辟新的领域。
并被广泛的应用在各门学科上,从物理和社会科学到人文科学,甚至被用来工业、农业、商业及政府部门。
而多元线性回归是多元统计分析中的一个重要方法,被应用于众多自然科学领域的研究中。
多元线性回归分析作为一种较为科学的方法,可以在获得影响因素的前提下,将定性问题定量化,确定各因素对主体问题的具体影响程度。
二.多元线性回归的基本理论多元线性回归是多元统计分析中的一个重要方法,被广泛应用于众多自然科学领域的研究中。
多元线性回归分析的基本任务包括:根据因变量与多个自变量的实际观测值建立因变量对多个自变量的多元线性回归方程;检验、分析各个自变量对因自变量的综合线性影响的显著性;检验、分析各个自变量对因变量的单纯线性影响的显著性,选择仅对因变量有显著线性影响的自变量,建立最优多元线性回归方程;评定各个自变量对因变量影响的相对重要性以及测定最优多元线性回归方程的偏离度等。
由于多数的多元非线性回归问题都可以化为多元线性回归问题,所以这里仅讨论多元线性回归。
许多非线性回归和多项式回归都可以化为多元线性回归来解决,因而多元线性回归分析有着广泛的应用。
2.1多元线性回归模型的一般形式设随机变量y与一般变量内,修,…,勺线性回归模型为v, + /32X2+...+p p x p + s(2. 1)y = + /?r模型中Y为被解释变量(因变量),而内,修,…,”是P个可以精确测量并可控制的一般变量,称为解释变量(自变量)。
线性回归模型论文回归模型论文一种基于线性回归模型的运动矢量重估算法摘要:针对H.264/AVC空间分辨率缩减的视频转码,提出一种基于线性回归模型的运动矢量重估计算法。
它利用原始视频流的运动矢量与下采样视频流的运动矢量之间的相关性,运用线性回归模型建模,得到下采样视频的运动矢量。
仿真实验结果表明:在保持率失真性能的同时,计算复杂度明显降低。
关键词:视频转码;H.264;线形回归模型;运动矢量重估计A Motion Vector Re-estimation Algorithm based on Linear Regression ModelYANG Gao-bo1, XIA Zhong-chao1, ZHANG Zhao-yang2, WANG Hui-qian1(1.College of Computer and Communication, Hunan Univ, Changsha, Hunan410082, China;2.Key Lab of Advanced Display and System Applications, Ministry of Education, Shanghai Univ, Shanghai 200072, China) Abstract: For the spatial resolution reduction ofH.264/AVC stream, a motion re-estimation algorithm based on linear regression model is proposed in this paper. It exploits the correlation between the motion vectors of original video stream and those of down-sampled video, which is modelled bylinear regression model to obtain the estimated motion vectors. Experimental results demonstrate that the proposed approach can significantly reduce the computational complexity of the transcoder with only slight sacrifice of visual quality.Key words: video transcoding;H.264/AVC;linear regression model;motion vector re-estimation随着网络和多媒体通信的发展,不同网络上各种视频信息的交流需求在不断增加。
由于网络和终端设备的多样性,编码得到的视频流不一定是最优的。
当在具有不同的信道特征的网络上,向具有不同的计算和显示能力的用户终端传输视频流时,必须根据用户环境动态地调整视频流。
视频转码通过改变视频的码率和空间分辨率等格式,使经过处理后的视频流满足传输信道和解码器的特殊要求[1-2]。
目前,空间分辨率缩减的转码技术研究已经较多,但大多数是针对MPEG-x视频流。
H.264/AVC是最新的视频编码标准,它采用了可变分块大小运动估计,多种帧内预测模式以及多参考帧等新特征,具有编码效率高和网络适应性强等优点,正在得到广泛地应用。
因此,研究适合于H.264/AVC视频流的空间分辨率缩减转码技术具有重要的意义。
Zhang 等[3]提出一种下采样后快速模式匹配的算法,能节省转码的时间,但没有处理8×4,4×8,4×4帧间模式,转码质量不高。
Shen等[4] 提出了一种新的R-D模式优化选择算法,能加快转码的速度,却不能保证视频的质量。
Cock[5]等提出一种基于开环转码结构的低复杂度漂移误差补偿技术,但是计算复杂度高。
运动矢量重估计是H.264/AVC视频空间分辨率缩减转码的关键因素之一。
文献已有少量同类的研究,但并不成熟。
Shen等[6]提出通过对原始视频流的运动矢量进行加权,但没有对运动矢量的误差进行补偿,将可能产生块效应的积累,严重影响视频的质量。
Shanableh 等[7]提出直接利用原始视频流运动矢量的中值或平均值,代替下采样视频流的运动矢量。
它具有计算量小的优点,但是当某个块的运动矢量明显不同于周围的块时,将产生较大的误差。
视频转换编码的关键在于充分利用部分解码输入码流过程中易于得到的运动矢量等信息,以降低转码过程的计算量[2]。
考虑到原始视频流的运动矢量与空间分辨率缩减后视频流的运动矢量具有较强的相关性,本文提出了一种基于线性回归模型的运动矢量重估计算法,根据原始视频流的运动矢量得到下采样视频的运动矢量,适合于H.264空间分辨率缩减的视频转码。
1. 转码器的体系结构转码器的结构可以分为两类:级联像素域转码结构(CPDT)和DCT 域转码结构(DDT)。
相对DDT结构,CPDT具有结构灵活,漂移误差小等特点[8]。
本文采用CPDT实现H.264视频流的空间分辨率转码,原理框图如图1所示。
转码器由一个解码器和一个编码器级联而成,即先对编码码流进行解码,然后对重建视频帧进行下采样,再重新编码。
其中,基于线性回归模型的运动矢量重估计是本文的核心。
对于H.264编码器,运动估计占用了整个编码过程约70%的运算量。
因此,加快重编码过程的运动估计成为提高转码速度的关键。
原始视频流的运动矢量与下采样视频流的运动矢量之间具有很强的相关性,为利用原始视频流的运动矢量加快重编码过程的运动估计提供了可能。
此外,大量研究表明:解码得到的宏块编码模式与率失真优化(RDO)算法得到的宏块编码模式的相关性不强,通过原始数据流运动信息确定宏块编码模式计算速度提高较小,而视频质量影响较大[9]。
本文主要针对运动矢量重估计展开研究,宏块编码模式的确定则使用标准的RDO方法。
图1 空间分辨率转码结构Fig.1 Framework of spatial resolution transcoding视频下采样后的每个块都对应原始视频的一块区域。
图2反应了下采样前后视频流的运动矢量之间的映射关系。
其中,B表示下采样图像的某个分块,R表示该块在原始视频图像对应的区域,该区域由多个具有独立运动矢量的分块组成。
H.264支持7种帧间预测模式,每种预测模式i都对应从块Bi到区域Ri的映射。
假设原始视频数据流得到区域Ri的所有块的运动矢量为vi=(x1,x2,…,xM),其中M代表Ri中块的个数。
假设通过RD优化算法得到块Bi的运动矢量为yi,则待研究的转码就是要解决如何根据区域Ri的运动矢量vi得到块Bi运动矢量yi的问题。
图2 下采样图像和原始图像运动适量对应关系Fig.2 Map of motion vectors between down sampling and original images3. 运动矢量的合成和修正基于H.264转码的运动矢量研究算法一般包含两个步骤:第一,解码原始的压缩数据流,计算出运动矢量的估计值。
第二,在一个较小的范围内进行运动矢量的搜索和修正。
运动矢量的估计值越准确,有助于减小搜索范围,提高运动矢量修正的效率。
前文提到,原始视频流的运动矢量与下采样视频流的运动矢量有很大的相关性。
因此,需要通过一种模型表示这种相关性。
文献[10]将线性回归模型运用在MPEG-4编码端的运动估计过程中,文献[11]将线性回归模型应用在速率控制方面,都取得了较好的效果。
本文提出利用线性回归模型,进行视频转码过程的运动矢量重估计。
H.264有7种帧间预测模式,需要对每种预测模式分别建立线性回归模型,该模型定义如下:(1)其中, , ,…, 为未知参数,可以从当前视频序列采集数据对该模型进行训练,得到相应的未知参数,从而支持该视频序列的特征。
方法如下:1) 解码原始的压缩数据流,对其进行下采样。
2) 开始阶段用标准的H.264编码方式和R-D优化算法对其进行重编码,保存得到的所有块的运动矢量,按照宏块预测模式对其进行分类。
i表示宏块预测模式,Ni表示该预测模式的块的个数,它们的运动矢量表示为:{yn, n = 1, 2,…, Ni}。
3) 找到2)中的所有块在原始视频图像中的对应区域,用{xmn, m=1,2,…M, n=1, 2,…, Ni}表示它们对应的运动矢量。
4) 从上述方法获取的数据Si={( xmn, yn), m=1,2,…M ,n = 1, 2, …, Ni }中选取N组数据S = {( xmn, yn), m=1,2,…M ,n = 1, 2, …, M}对预测模式为i的线性回归模型进行训练。
5)将N组数据对应的的平均值确定为该预测模式下未知参数的值。
视频的特征会影响N的取值,而N值的大小,又会影响运动估计的速度和准确性。
通过实验发现:当N取8时,能得到较好的实验结果。
将数据S = {( xmn, yn), m=1,2,…M ,n = 1, 2, …, M },应用在线性回归模型(1)中可得:(2)根据式(2)可推导出:(3)(4)(5)每个线性回归模型的运动矢量都对应两个相互独立的方向,例如: Y = (y1, y2), X = {(x1m, x2m), m=1,2,…,M},= {( ,),m=1,2,…,M },该模型对应2个线性方程,如下所示:(6)因此,对7种不同的预测模式及两个相互独立的方向需要分别建立线形回归模型。
将求得的参数保存在转码器的缓冲区中,利用线性回归模型,后续帧在B块的运动矢量可以通过以下步骤获取:1)确定该块的预测模式i。
2)在原始视频图象中找到该块对应的区域R,记录该区域各块的运动矢量。
3)将得到的运动矢量运用到预测模式为i的线性回归模型中,求得B块的运动矢量。
4)通过1/4像素精度,快速搜索算法来获取最佳运动矢量。
4 实验结果和分析为了测试本文算法的性能,在以下实验平台进行了仿真实验:Pentium(R) 4 CPU 3.00GHz 2.99GHz,504MB内存的PC机,程序运行环境:VC++ 6.0。
输入视频流采用开源的H.264/AVC校验模型JM8.6得到,编码端的主要参数设置如表1所示。
视频测试序列选取Mother & Daughter, Foreman和Tempete (CIF 格式),它们具有不同的运动复杂度。
图3列出了这3种视频测试序列中的具有代表性的帧。
(a)Mother & Daughter(b) Foreman(c) Tempete图 3 视频测试序列Fig.3Testing Sequences将本文的方法(LRM)和下面3种方法进行比较:(1) BestRD:指重编码过程中,按照H.264编码标准直接进行CPDT,并使用R-D优化算法;(2) Benchmark:指重编码过程中,仍然按照H.264编码标准进行CPDT,但不使用R-D优化算法;(3)文献[7]( AMV):利用原始视频流运动矢量的平均值来替代下采样视频流的运动矢量。