2122公式法

2122公式法12122公式法12122公式法的原理基于对数字2和1的性质的利用。

根据2122公式法，如果将数字2和数字1进行乘法和加法运算，可以得到一系列的结果。

具体地说，将1与2相乘得到2，再将1与2相加得到3，然后将3与2相乘得到6，将3与2相加得到5，然后将5与2相乘得到10，将5与2相加得到7，以此类推。

首先是乘法问题。

假设有一个较大的数字需要与2相乘，可以使用2122公式法来快速计算。

具体操作是先将该数字与2相加，然后将得到的结果再与2相乘，如此反复进行下去，直到得到满意的结果。

例如，要计算789和2的乘积，可以按照以下步骤进行计算：将789与2相加得到791，然后将791与2相乘得到1582，再将1582与2相加得到1584，最后将1584与2相乘得到3168、因此，789和2的乘积为3168最后是平方问题。

2122公式法也可以用于快速计算一个数字的平方。

要进行快速的平方运算，可以使用2122公式法进行迭代计算。

具体步骤是先将数字与2相乘，然后将得到的结果与该数字相加，再将得到的结果与2相乘，如此反复进行下去，直到得到满意的结果。

例如，要计算25的平方，可以按照以下步骤进行计算：将25与2相乘得到50，然后将50与25相加得到75，再将75与2相乘得到150，最后得到25的平方为150。

总结来说，2122公式法是一种使用数字2和1进行乘法和加法运算的方法。

通过将数字与2相乘和相加，可以快速解决各种类型的数学问题，如乘法、加法和平方等。

该方法在进行大量计算时非常实用，可以提高计算的效率和准确性。

21.2.2 公式法教学目标1.理解一元二次方程求根公式的推导过程.2.掌握公式结构，知道用公式前先将方程化为一般形式，会用判别式判断根的情况.3.会利用求根公式解简单数字系数的一元二次方程.重点难点1.会用根的判别式判断方程根的情况.2. 能用求根公式解一元二次方程.教学过程一、回顾：1.配方法解一元二次方程的步骤♦ 移项:把常数项移到方程的右边;♦ 化 1：把二次项系数化为1；♦ 配方:方程两边都加上一次项系数一半的平方;♦ 开方:根据平方根意义,方程两边开平方;♦ 求解:解一元一次方程;♦ 定解:写出原方程的解.2.用配方法解一元二次方程：3x ²+6x-4=0二、复习引入任何一元二次方程都可以写成一般形式ax ²+bx+c=0（a ≠0） 例：x ²+2x=5；5x ²-3x=2；4x ²=5x-3我们学习了用配方法解数字系数的一元二次方程，能否用配方法解一般形式的一元二次方程ax²+bx+c=0（a≠0）？三、新课讲解配方法解一元二次方程的一般形式：ax²+bx+c=0（a≠0）1.移项，得ax²+bx=-c2.二次项系数化为1，得x²+ x=3.配方x²+ x+（ ）²= +（ ）² 即 （x+ ）²= a b a c -a b a b 2a c -a b 2ab 2因为，a≠0，所以4a²＞0，式子b²-4ac 的值有三种情况（1）b²-4ac ＞0则 ＞0，那么由（x+ ）²=,可得 x+ =±所以，方程有两个不等的实数根x1= ，x2=（2）b²-4ac=0则 =0 ，那么由（x+ ）²= 可得 （x+ ）²=0 即x1=x2=-所以，方程有两个相等的实数根（3）b²-4ac ＜0则 ＜0 ，那么由（x+ ）²=可得 （x+ ）²＜0因为任何数的平方都是非负数，所以无论x 取何值都不可能使方程成立 即，方程没有实数根注意:一元二次方程的根不可能多于两个，可能出现两个实数根，一个实数根，或者没有实数根一般的，式子b²-4ac 叫做方程ax²+bx+c=0（a≠0）的根的判别式，用希腊字母“Δ”表示,即Δ=b²-4ac 。

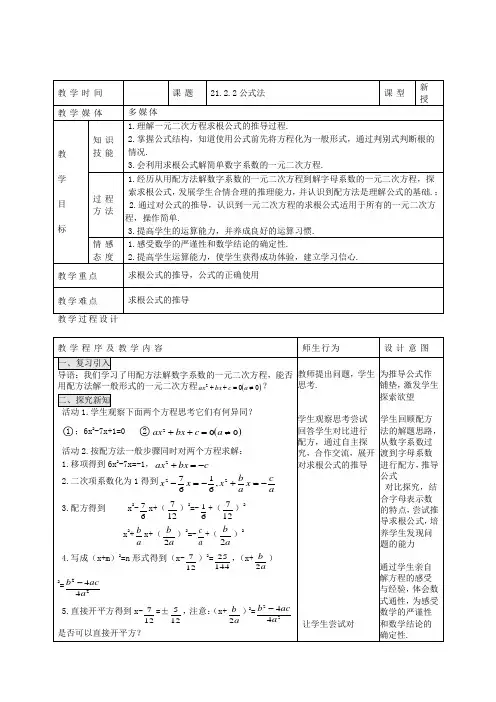
教学时间 课题21.2.2公式法课型新授教学媒体多媒体教 学 目 标知识 技能 1.理解一元二次方程求根公式的推导过程.2.掌握公式结构，知道使用公式前先将方程化为一般形式，通过判别式判断根的情况.3.会利用求根公式解简单数字系数的一元二次方程. 过程方法1.经历从用配方法解数字系数的一元二次方程到解字母系数的一元二次方程，探索求根公式，发展学生合情合理的推理能力，并认识到配方法是理解公式的基础.；2.通过对公式的推导，认识到一元二次方程的求根公式适用于所有的一元二次方程，操作简单.3.提高学生的运算能力，并养成良好的运算习惯. 情感 态度 1.感受数学的严谨性和数学结论的确定性.2.提高学生运算能力，使学生获得成功体验，建立学习信心.教学重点 求根公式的推导，公式的正确使用 教学难点 求根公式的推导教学过程设计教学程序及教学内容 师生行为 设计意图 一、复习引入导语：我们学习了用配方法解数字系数的一元二次方程，能否用配方法解一般形式的一元二次方程()002≠=++a c bx ax ？二、探究新知活动1.学生观察下面两个方程思考它们有何异同？○1；6x 2-7x+1=0 ○2()002≠=++a c bx ax 活动2.按配方法一般步骤同时对两个方程求解： 1.移项得到6x 2-7x=-1，c bx ax -=+22.二次项系数化为1得到ac x a b x x x -=+-=-22,61673.配方得到 x 2-76x+（712）2=-16+（712）2 x 2+b a x+（2b a ）2=-c a +（2b a ）24.写成（x+m ）2=n 形式得到（x-712）2=25144，（x+2b a ）2=2244b aca -5.直接开平方得到x-712=±512，注意：（x+2b a ）2=2244b ac a -是否可以直接开平方？教师提出问题，学生思考. 学生观察思考尝试回答学生对比进行配方，通过自主探究，合作交流，展开对求根公式的推导让学生尝试对为推导公式作铺垫，激发学生探索欲望学生回顾配方法的解题思路，从数字系数过渡到字母系数进行配方，推导公式对比探究，结合字母表示数的特点，尝试推导求根公式，培养学生发现问题的能力通过学生亲自解方程的感受与经验，体会数式通性，为感受数学的严谨性和数学结论的确定性.活动3.对（x+2b a ）2=2244b ac a -观察，分析，在0≠a 时对2244b ac a -的值与0的关系进行讨论活动4.归纳出一元二次方程的根的判别式和求根公式，公式法.活动5.初步使用公式解方程6x 2-7x+1=0.活动6.总结使用公式法的一般步骤：○1把方程整理成一般形式，确定a,b,c 的值，注意符号 ○2求出ac b 42-的值，方程()002≠=++a c bx ax ，当Δ＞0时，有两个不等实根；Δ=0时有两个相等实根；Δ<0时无实根.○3在ac b 42-≥0的前提下把a ，b ，c 的值带入公式x=242b b aca-±-进行计算，最后写出方程的根.三、课堂训练1.利用一元二次方程的根的判别式判断下列方程的根的情况（1）2x 2-4x-1=0 （2）5x+2=3x2（3）（x-2）（3x-5）=0 （4）4x 2-3x+1=02.课本例2 四、小结归纳 本节课应掌握：1.用根的判别式判断一个一元二次方程是否有实数根2.用求根公式求一元二次方程的根3. 一元二次方程求根公式适用于任意一个一元二次方程. 五、作业设计 必做：P17：4、5 选做：P12：1、2补充作业：某电厂规定：该厂家属区的每户居民一个月用电量不超过A 千瓦时，•那么这户居民这个月只交10元电费，如果超过A 千瓦时，那么这个月除了交10•元用电费外超过部分还要按每千瓦时100A 元收费．（1）若某户2月份用电90千瓦时，超过规定A 千瓦时，则超过部分电费为多少元？（•用A 表示）（2）下表是这户居民3月、4月的用电情况和交费情况月份 用电量（千瓦时） 交电费总金额（元） 3 80 25 44510根据上表数据，求电厂规定的A 值为多少？2244b ac a -的值进行分析 学生尝试归纳，师生总结学生初步使用公式，教师规范板书。

2122公式法32122公式法3考虑方程x^3+x^2-7x-6=0。

按照2122公式法的步骤，我们先找出方程中的系数a,b,c,d的值。

在这个例子中，a=1,b=1,c=-7,d=-6、然后，我们根据以下公式计算出四个根的值：x1 = (sqrt(3 * a * a - 2 * b) - 3 * a) / (3 * c)x2 = (-sqrt(3 * a * a - 2 * b) - 3 * a) / (3 * c)x3 = (sqrt(3 * a * a - 2 * b) + 3 * a) / (3 * c)x4 = (-sqrt(3 * a * a - 2 * b) + 3 * a) / (3 * c)在这个例子中，计算出的根分别为：x1=-1,x2=-2,x3=3和x4=-3现在，我们来解释一下2122公式法3的推导过程。

首先，我们考虑一个一般性的高次方程ax^n + bx^(n-1) + cx^(n-2) + ... + k = 0。

其中，a, b, c, ..., k是已知的实数，n是一个正整数，且n > 21.首先，我们将方程进行标准化，即将方程中的第一项系数变为1、这可以通过除以a来实现。

那么方程变为x^n+(b/a)x^(n-1)+(c/a)x^(n-2)+...+(k/a)=0。

2. 接下来，我们将方程进行变形。

我们引入一个新的未知数y，令前n-2项的和为yn。

也就是说，我们将方程变为：x^n + (b/a)x^(n-1) + yx^(n-2) + (k/a) - yn = 0。

3.然后，我们对方程进行合并。

我们可以将x^(n-2)分解为x^(n-2)*(x^2)。

那么方程可以进一步变为：x^2(x^(n-2) + (b/a)x^(n-3) + yx^(n-4) + ... + yn/(x^2)) + (k/a) - yn = 0。

4.我们令u=x^(n-2)，即u是一个新的未知数。