机械原理典型例题力分析
- 格式:ppt
- 大小:805.00 KB
- 文档页数:17


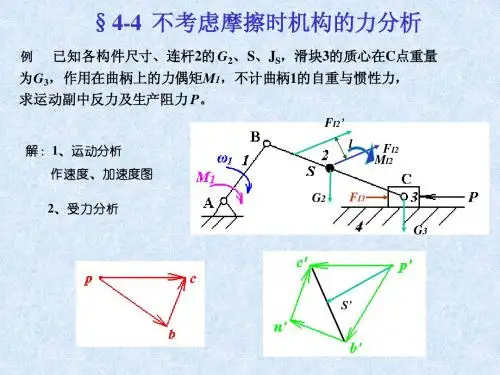
3 平面机构力分析(包括摩擦和自锁)1.对 机 构 进 行 力 分 析 的 目 的 是:(1) ;(2) 。
2.所 谓 静 力 分 析 是 指 的一种力分析方 法 , 它 一 般 适 用 于 情 况。
3.所 谓 动 态 静 力 分 析 是 指 的 一 种 力 分 析 方 法, 它 一 般 适 用 于 情 况。
4.绕 通 过 质 心 并 垂 直 于 运 动 平 面 的 轴 线 作 等 速 转 动 的 平 面 运 动 构 件, 其 惯 性 力P I= , 在 运 动 平 面 中 的惯 性 力 偶 矩MI=。
5.在滑动摩擦系数相同条件下,槽面摩擦比平面摩擦大,其原因是 。
6.机械中三角带传动比平型带传动用得更为广泛,从摩擦角度来看,其主要原因是 。
7.设机 器 中 的 实 际 驱 动 力 为rP , 在同 样 的 工 作 阻 力 和 不 考 虑 摩 擦 时 的 理 想 驱 动 力 为rP 0, 则 机 器 效 率 的 计 算 式 是η = 。
8.设 机 器 中 的 实 际 生 产 阻 力 为 rQ ,在 同 样 的 驱 动 力 作 用 下 不 考 虑 摩 擦 时 能 克 服 的 理 想 生 产 阻 力 为 rQ 0 , 则 机 器 效 率 的 计 算 式 是η=。
9.在 认 为 摩 擦 力 达 极 限 值 条 件 下 计 算 出 机 构 效 率η 后, 则 从 这 种 效率 观 点 考 虑, 机 器 发 生 自 锁 的 条 件 是 。
10.设 螺 纹 的 升 角为λ, 接 触 面 的 当 量 摩 擦 系 数 为f v ,则 螺 旋 副 自 锁的 条 件 是 。
11.在机械中阻力与 其作用点速度方向 。
A).相 同 ; B).一定相反 ; C).成锐角 ; D).相反或成钝角 。
12.在 机 械 中 驱 动 力 与 其 作 用 点 的 速 度 方 向 。
A 〕 一 定 同 向; B 〕 可 成 任 意 角 度; C 〕 相 同 或 成 锐 角; D 〕 成 钝 角。

平衡力(平衡力矩)是与作用在机械上的已知外力相平衡的未知外力(矩)重力惯性力机构力分析的任务、目的和方法f4-1f4-0驱动力(原动力)阻抗力(生产阻力和非生产阻力)运动副中的反力摩擦力和介质阻力作用在机械上的力:可能为驱动力或阻力在一个运动循环中所作的功为零运动副中摩擦力的确定移动副中摩擦力确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副例斜面机构例螺旋机构转动副平面高副f4-5f4-5f4-5运动副中摩擦力的确定移动副中摩擦力确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副例斜面机构例螺旋机构转动副平面高副f4-5f4-5f4-5螺纹的牙型有:矩形螺纹三角形螺纹梯形螺纹锯齿形螺纹15º30º3º30º运动副中摩擦力的确定移动副中摩擦力确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副例斜面机构例螺旋机构转动副平面高副f4-5f4-5f4-5螺纹的用途:传递动力或联接螺纹的旋向:右旋左旋运动副中摩擦力的确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副轴颈摩擦力确定转动副轴端摩擦力确定运动副中摩擦力的确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副转动副平面高副高副中摩擦力确定不考虑摩擦时机构的力分析f4-3例六杆机构力分析机构力分析的任务是确定F R ij (运动副中的反力)和需加于机构上的平衡力(矩)。
但F R ij 对整个机构来说是内力,必须将机构分解为若干个构件组后进行分析。
如何分?例铰链四杆机构例曲柄滑块机构1 各运动副的反力(设各构件的重力及惯性力不计)2 需施加于凸轮1上的驱动力矩在图示机构中,已知各构件的尺寸及机构的位置,各转动副中的摩擦圆如图中虚线圆所示,移动副及凸轮高副处的摩擦角为,作用在构件4上的工作阻力为Q 。
试求该图示位置:ϕϕR23R43ω34ω321 各运动副的反力(设各构件的重力及惯性力不计)2 需施加于凸轮1上的驱动力矩LR 2343ω25R 54R 52R 12R 51V B2B1R 12R 52523212=++R R R R 54R 34QV 45R 21R 32构件2: 1 各运动副的反力(设各构件的重力及惯性力不计)2 需施加于凸轮1上的驱动力矩ω34ω32ϕLR 2343ω25R 54R 52R 12R 51V B2B1R 12R 52523212=++R R R R 54R 34QV 45R 21R 32构件2:)( L 21211Nm R L R M l F l μμμ==ω34ω32ϕ。
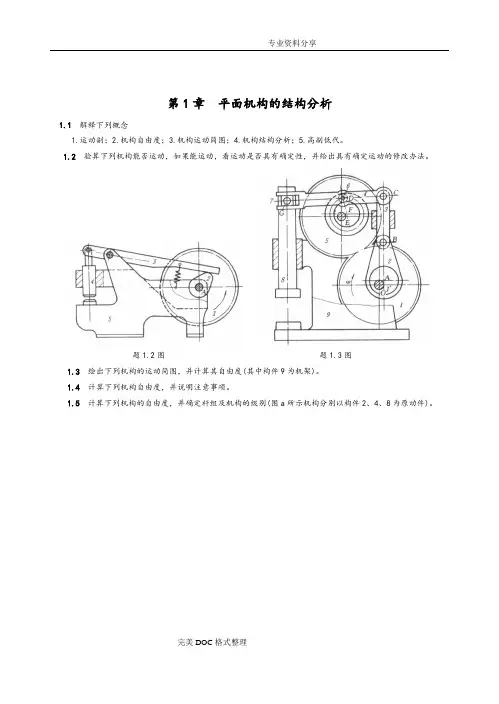
第1章平面机构的结构分析1.1解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
1.2验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题1.2图题1.3图1.3 绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度,并说明注意事项。
1.5计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE=120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题2.2图题2.3图2.4 在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。

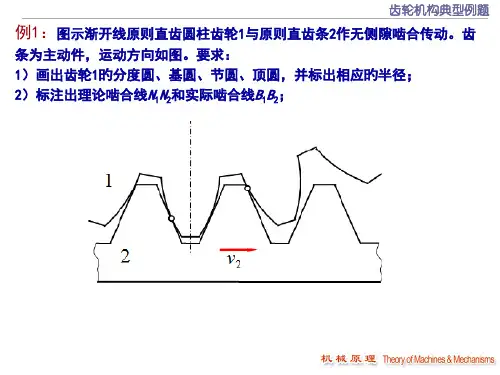


第六章 例题精选及答题技巧例5-1 某传动装置如例5-1图所示,已知:1z =60,2z =48,'2z =80,3z =120,'3z =60,4z =40,蜗杆'4z =2(右旋),涡轮5z =80,齿轮'5z =65,模数m=5 mm 。
主动轮1的转速为1n =240 r/min ,转向如图所示。
试求齿条6的移动速度6v 的大小和方向。
例5-1图解题要点:这是一个由圆柱齿轮、圆锥齿轮、蜗轮蜗杆、齿轮齿条所组成的定轴轮系。
解:为了求齿条6的移动速度6v 的大小,需要首先求出齿轮5'的转动角速度'5ω。
因此首先计算传动比15i 的大小: 322608060804012048432154325115=⨯⨯⨯⨯⨯⨯==='''z z z z z z z z n n i ===='3224015155i n n n 7.5 r/min 605.7260255⨯==''ππωn =0.785 rad/s 齿条6的移动速度等于齿轮5'的分度圆线速度,即:785.0655212155556⨯⨯⨯===''''ωωmz r v =127.6 mm/s 齿条6的运动方向采用画箭头的方法确定如例5-1图所示。
例5-2 如例5-2图所示,已知各轮齿数为1z 、2z 、3z 、4z 、5z 、6z ,1z 为主动件,转向如图箭头所示,试求:1. 传动比?/11==H H i ωω(列出表达式);2. 若已知各轮齿数1z =2z =4z =5z =20,3z =40,6z =60,求H i 1的大小及转向。
图 5-2解题要点:如例5-2图所示,从结构上看,此轮系由两部分组成,齿轮1、齿轮2、齿轮3组成定轴轮系,齿轮4、5、6及系杆H 组成行星轮系,二者之间属串联关系。
齿轮3和齿轮4属同一构件。
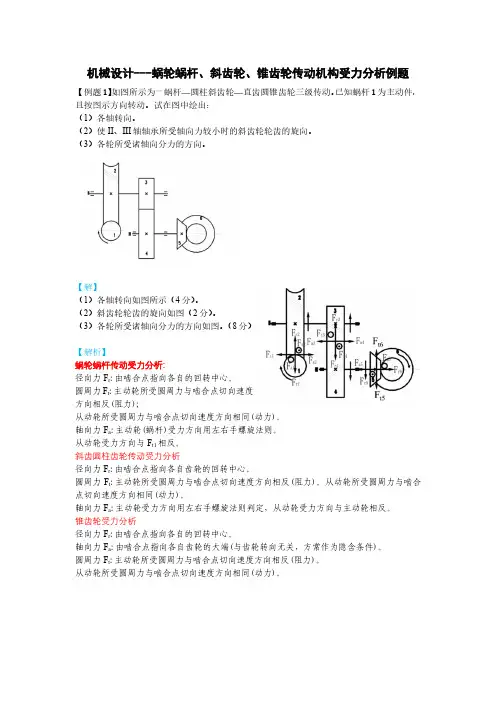
机械设计---蜗轮蜗杆、斜齿轮、锥齿轮传动机构受力分析例题【例题1】如图所示为一蜗杆—圆柱斜齿轮—直齿圆锥齿轮三级传动。
已知蜗杆1为主动件,且按图示方向转动。
试在图中绘出:
(1)各轴转向。
(2)使II、III轴轴承所受轴向力较小时的斜齿轮轮齿的旋向。
(3)各轮所受诸轴向分力的方向。
【解】
(1)各轴转向如图所示(4分)。
(2)斜齿轮轮齿的旋向如图(2分)。
(3)各轮所受诸轴向分力的方向如图。
(8分)
【解析】
蜗轮蜗杆传动受力分析:
径向力F r:由啮合点指向各自的回转中心。
圆周力F t:主动轮所受圆周力与啮合点切向速度
方向相反(阻力);
从动轮所受圆周力与啮合点切向速度方向相同(动力)。
轴向力F a:主动轮(蜗杆)受力方向用左右手螺旋法则。
从动轮受力方向与F t1相反。
斜齿圆柱齿轮传动受力分析
径向力F r:由啮合点指向各自齿轮的回转中心。
圆周力F t:主动轮所受圆周力与啮合点切向速度方向相反(阻力)。
从动轮所受圆周力与啮合点切向速度方向相同(动力)。
轴向力F a:主动轮受力方向用左右手螺旋法则判定,从动轮受力方向与主动轮相反。
锥齿轮受力分析
径向力F r:由啮合点指向各自的回转中心。
轴向力F a:由啮合点指向各自齿轮的大端(与齿轮转向无关,方常作为隐含条件)。
圆周力F t:主动轮所受圆周力与啮合点切向速度方向相反(阻力)。
从动轮所受圆周力与啮合点切向速度方向相同(动力)。
2—1l图示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构,将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图,分析其是否能实现设计意图,井提出修改方案。
2—12图示为一小型压力机。
图中齿轮1与偏心轮1’为同一构件,绕固定轴心O连续转动。
在齿轮5上开有凸轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C轴上下摆动;同时,又通过偏心轮1’、连杆2、滑杆3使C轴上下移动;最后,通过在摆杆4的又槽中的滑块7和铰链G使冲头8实现冲压运动。
试绘制其机构运动简图,并计算其自由度。
2—16试计算图示各机构的自由度。
图a、d为齿轮—连杆组合机构;图b为凸轮—连杆组合机构(图中D处为铰接在一起的两个滑块);图c为一精压机构。
并问在图d所示机构中,齿轮3、5和齿条7与齿轮5的啮合高副所提供的约束数目是否相同,为什么?3—4在图示的齿轮—连杆组合机构中,试用瞬心法求齿轮1与3的传动比。
4—13图示为一曲柄滑块机构的三个位置,F为作用在活塞上的力,转动副A及月上所画的虚线小圆为摩擦圆。
试决定在此三个位置时作用在连杆AB上的作用力的真实方向(构件重量及惯性力略去不计)。
5-8图a所示为一焊接用的楔形夹具。
利用这个夹具把两块要焊接的工件1及1’预先夹妥,以便焊接。
图中2为夹具体,3为楔块。
试确定其自锁条件(即当夹紧后,楔块3不会自动松脱出来的条件)。
图b为一颚式破碎机,在破碎矿石时要求矿石不致被向上挤出,试问角应满足什么条件?经分析可得出什么结论?6-7在图示的转子中,已知各偏心质量m1=10kg,m2=15kg,m3=20kg,m4=10kg,它们的回转半径大小分别为r l=40 cm,r2=r4=30 cm,r3=20 cm,方位如图所示。
若置于平衡基面Ⅰ及Ⅱ中的平衡质量m bⅠ及m bⅡ的回转半径均为50cm,试求m bⅠ及m bⅡ的大小和方位(l12=l23=l34)。
工程师中的机械原理题解析工程师在日常工作中经常面临各种机械原理题,这些题目旨在考察工程师对机械原理的理解和应用能力。
在本文中,我们将解析几个典型的机械原理题,帮助工程师更好地理解和掌握机械原理。
一、问题一这是一个关于杠杆的问题。
题目如下:一个杠杆的长度为3米,杠杆的支点到重物的距离为1米,重物的重量为500牛顿。
求杠杆支点处受力的大小。
分析:根据杠杆原理,杠杆支点处的受力与重物的重量和支点到重物的距离成反比。
即F1/F2 = d2/d1,其中F1为支点处受力的大小,F2为重物的重量,d1为重物到支点的距离,d2为支点处受力点到支点的距离。
解答:根据题目信息,可得出F1/500 = 1/3,解得F1=166.67牛顿。
所以,杠杆支点处受力的大小为166.67牛顿。
二、问题二这是一个关于摩擦力的问题。
题目如下:一个重量为200牛顿的物体放在水平地面上,施加一个力使其开始运动,已知物体运动时所需的最小施加力为40牛顿。
求摩擦系数。
分析:根据运动开始时所需的最小施加力与摩擦力之间的关系,可以利用下面的公式来计算摩擦系数:Ff = μN其中Ff为摩擦力,μ为摩擦系数,N为物体受力。
解答:根据题目信息,已知物体所需的最小施加力为40牛顿,物体的重力为200牛顿,可得Ff = 40牛顿,N = 200牛顿。
代入公式可得40 = μ * 200,解得μ = 0.2。
所以,摩擦系数为0.2。
三、问题三这是一个关于简单机械原理的问题。
题目如下:一个滑轮组由两个滑轮组成,滑轮组的直径比为3:1,质量比为2:1。
若施加在较小滑轮上的力为200牛顿,求施加在较大滑轮上的力。
分析:根据简单机械原理,滑轮组的受力关系为F1/F2 = d2/d1,其中F1为施加在较小滑轮上的力,F2为施加在较大滑轮上的力,d1为较小滑轮的直径,d2为较大滑轮的直径。
解答:根据题目信息,已知施加在较小滑轮上的力为200牛顿,较小滑轮的直径为d1,较大滑轮的直径为3d1,可得F1/F2 = 1/(3*1),即200/F2 = 1/3,解得F2 = 600牛顿。
机械原理大作业——正弦机构力分析姓名:郑豪学号:887班级:072125专业:机械设计制造及其自动化联系方式:指导老师:王玉丹完成时间:在图示的正弦机构中,已知mmAB l 100=,mm h 1201=,mm h 802=,s rad 101=ω(为常数),滑块2和构件3的重量分别为N G 402=和N G 1003=,质心2S 和3S 的位置如图所示,加于构件3上的生产阻力N F r400=,构件1的重力和惯性力略去不计。
试用解析法求机构在原动件的一个回转周期内各运动副反力和需加于构件1上的平衡力偶矩b M 。
(图像表示)解:(1)分别对三个构件进行受力分析如下图:(2)运动分析:滑块2: 12W L V AB s =212W L a AB s =构件3: 1sin φAB L S =113cos φW L V AB = 113sin 2φW L a AB -=(3)确定惯性力:2122212)(W L g G a m F AB s == 1133313sin )(2φW L g G a m F AB ==(4)各构件的平衡方程: 构件3:1323,0F F F Fr R y-==∑○1∑=,0xF4'4R R F F =○2212343/cos ,0h L F F MA R r s φ==∑○3构件2:∑==1122!cos ,0φF x F FR x○4∑-==1123212sin ,0φF F y F F R R y○5构件1:∑==x F x F F R R x1241,0○6 ∑==yF y F FR R y2!41,0○7∑==132cos ,0φAB R b AL F M M○8(5)根据式 ~~○8可以进行编程,以10°为步幅可以算得各个约束处的反力。
结果如表一所示。
表一各约束处反力表Φ1F r23/F r32F r43_1F r43_2F r12_x F r12_y F r41_x F r41_y Mb rad N N N N N N N N*m0 0.1795 0.3590 0.5386 0.71810.89761.0771 1.2566 1.4362 1.6157 1.79521.97472.1542 2.3338 2.5133 2.69282.87233.0518 3.2314 3.4109 3.5904 3.76993.94944.1290 4.3085 4.4880 4.66754.84705.0265 5.2061 5.3856 5.5651 5.74465.92416.1037 6.2832 400.0000382.1443364.8625348.7101334.2061321.8169311.9404304.8943300.9050300.1007302.5072308.0472316.5427327.7205341.2215356.6116373.3963391.0361408.9639426.6037443.3884458.7785472.2795483.4573491.9528497.4928499.8993499.0950495.1057488.0596478.1831465.7939451.2899435.1375417.8557400.0000500.0000470.0039426.9963374.1872314.6014250.8119184.7735117.771950.4893-16.8300-84.1427-151.3378-217.9780-283.0943-345.0675-401.6200-449.9252-486.8273-509.1470-514.0376-499.3489-463.9495-407.9684-332.9190-241.6872-138.3782-28.034983.7439191.2451289.0952372.6779438.4701484.2616509.2386513.9257500.0000500.0000470.0039426.9963374.1872314.6014250.8119184.7735117.771950.4893-16.8300-84.1427-151.3378-217.9780-283.0943-345.0675-401.6200-449.9252-486.8273-509.1470-514.0376-499.3489-463.9495-407.9684-332.9190-241.6872-138.3782-28.034983.7439191.2451289.0952372.6779438.4701484.2616509.2386513.9257500.000040.000039.357237.449434.338030.122924.939618.954712.36075.3693-1.7946-8.9008-15.7210-22.0359-27.6425-32.3607-36.0388-38.5585-39.8390-39.8390-38.5585-36.0388-32.3607-27.6425-22.0359-15.7210-8.9008-1.79465.369312.360718.954724.939630.122934.338037.449439.357240.0000400.0000375.0020350.8075328.1941307.8886290.5436276.7166266.8521261.2670260.1410263.5101271.2661283.1597298.8087317.7101339.2563362.7548387.4505412.5495437.2452460.7437482.2899501.1913516.8403528.7339536.4899539.8590538.7330533.1479523.2834509.4564492.1114471.8059449.1925424.9980400.000040.000039.357237.449434.338030.122924.939618.954712.36075.3693-1.7946-8.9008-15.7210-22.0359-27.6425-32.3607-36.0388-38.5585-39.8390-39.8390-38.5585-36.0388-32.3607-27.6425-22.0359-15.7210-8.9008-1.79465.369312.360718.954724.939630.122934.338037.449439.357240.0000400.0000375.0020350.8075328.1941307.8886290.5436276.7166266.8521261.2670260.1410263.5101271.2661283.1597298.8087317.7101339.2563362.7548387.4505412.5495437.2452460.7437482.2899501.1913516.8403528.7339536.4899539.8590538.7330533.1479523.2834509.4564492.1114471.8059449.1925424.9980400.000040.000037.600334.159729.935025.168120.065014.78199.42184.0391-1.3464-6.7314-12.1070-17.4382-22.6475-27.6054-32.1296-35.9940-38.9462-40.7318-41.1230-39.9479-37.1160-32.6375-26.6335-19.3350-11.0703-2.24286.699515.299623.127629.814235.077638.740940.739141.114140.0000(6)源程序代码如下:Lab=0.1;H1=0.12;H2=0.08;w=10; %曲柄角速度g=9.8; %重力加速度G2=40;m2=G2/g;G3=100;m3=G3/g;Fr=400; %构件3上的生产阻力fai=0:pi/36:2*pi;a2=Lab*w*w; %滑块2加速度a3=-Lab*w*w*sin(fai); %推杆3加速度F2=m2*a2; %滑块2惯性力F3=m3*a3; %滑块3惯性力Fr23=Fr-F3; %滑块2与推杆3之间的反力%Fr43_1=Fr43_2; %支座4对推杆3的反力Fr43_1=Lab*Fr23.*cos(fai)/H2;%支座4对推杆3的反力Fr12_x=F2*cos(fai); %铰支座2的水平分力Fr12_y=Fr23-F2*sin(fai);%铰支座2的竖直分力Fr41_x=Fr12_x; %铰支座1的水平分力Fr41_y=Fr12_y; %铰支座1的竖直分力Mb=Lab*Fr23.*cos(fai); %附加于曲柄1的平衡力偶figure(1);plot(fai,Fr23,'w');title('构件2、3之间反力图');xlabel('角度fai/rad');ylabel('反力Fr23(Fr32)/N');figure(2);plot(fai,Fr43_1,'w');title('构件3、4之间反力图');xlabel('角度fai/rad');ylabel('反力Fr43(Fr34)/N');figure(3);plot(fai,Fr12_x,'--w');hold on;plot(fai,Fr12_y,'w');legend('Fr12-x','Fr12-y');title('构件1、2之间反力图');xlabel('角度fai/rad');ylabel('反力Fr12(Fr21)/N');figure(4);plot(fai,Fr41_x,'--w');hold on;plot(fai,Fr41_y,'w');legend('Fr14-x','Fr14-y');title('构件1、4之间反力图');xlabel('角度fai/rad');ylabel('反力Fr14(Fr41)/N');figure(5);plot(fai,Mb,'w');title('构件1上的平衡力偶');xlabel('角度fai/rad');ylabel('Mb/Nm');(7)运行结果分别如图1~~5所示。