高中数学 平行四边形的存在性问题

平行四边形的存在性问题2019如果已知三个定点，探寻平行四边形的第四个顶点，符合条件的有3个点：以已知三个定点为三角形的顶点，过每个点画对边的平行线，三条直线两两相交，产生3个交点．如果已知两个定点，一般是把确定的一条线段按照边或对角线分为两种情况．根据平行四边形的对边平行且相等，灵活运用坐标平移，可以使得计算过程简便．根据平行四边形的中心对称的性质，灵活运用坐标对称，可以使得解题简便．引例12－2x＋3与x轴交于A如图，在平面直角坐标系中，已知抛物线y＝－x、B两点（A在,B的左侧），与y轴交于点C，顶点为P，如果以点P、A、C、D为顶点的四边形是平行四边形，求点D的坐标．2引例2－x3与+2x＋x＝,如图，在平面直角坐标系中，已知抛物线y为顶点的四边形是平、BM、A在这条抛物线上，点P在y轴上，如果以点P、轴交于A、B两点，点M M的坐标．行四边形，求点1Ax轴的一个交点为x平移后得到的抛物线，其对称轴为x=1，与,（2017?泰安）如图，是将抛物线y=﹣2．，与y轴的交点为C1（﹣，0），另一个交点为B 的坐标；NC，求点N2）求抛物线的函数表达式；（）若点N为抛物线上一点，且BC⊥（1为平行四边形，OAPQQ是抛物线上一点，点是一次函数y=x+的图象上一点，若四边形（3）点P 的坐标；若不存在，说明理由．Q是否存在？若存在，分别求出点P、Q这样的点P、1平行四边形的存在性问题．2.（2017?菏泽）如图，在平面直角坐标系中，抛物线y=ax+bx+1交y轴于点A，交x轴正半轴于点B（4，2）求抛物线的表达式；（1轴，垂足为C．，过点D作DC⊥x30），与过A点的直线相交于另一点D（，），连N于M，交抛物线于点作PN⊥x轴，交直线AD2（）点P在线段OC上（不与点O、C重合），过P 面积的最大值；CM，求△PCM 接为顶点的四边形ND、，使以点M、C、P3）若是x轴正半轴上的一动点，设OP的长为t，是否存在t（的值；若不存在，请说明理由．是平行四边形？若存在，求出t．3cbx++﹣抛物线CByx2x+与轴、轴分别交于点已知直线（2018?徐汇区二模）如图，y=﹣、，y= 轴交于另一个点A．xB 过点、C，且与）求该抛物线的表达式；（1是平行四边形OMNCNylMBCM2（）点是线段上一点，过点作直线∥轴交该抛物线于点，当四边形时，求它的面积；的坐标．，求点CAO∠是该抛物线上的一点，且满足∠D，设点）联结3（ACDBA=D2平行四边形的存在性问题．．4轴yB，与与x轴交于点A、+（2018?杨浦区二模）如图，在平面直角坐标系中，抛物线y=﹣xbx+c2 AC上方的一个动点．C，点P为抛物线上位于直线，直线交于点Cy=x+4经过点A、1）求抛物线的表达式；（的正切值；时，求∠PACCP1），当∥AO）如图（（2 P的坐标．AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时，求出此时点3（）∠当以3平行四边形的存在性问题．5．（2018?河南）如图，抛物线y=ax+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．2（1）求抛物线的解析式；（2）过点A的直线交直线BC于点M．①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．4平行四边形的存在性问题．6．（2018?浦东新区二模）已知平而直角坐标系xOy（如图），二次函数y=ax+bx+4的图象经过A（﹣2，20）、B（4，0）两点，与y轴交于点C点．（1）求这个二次函数的解析式；（2）如果点E在线段OC上，且∠CBE=∠ACO，求点E的坐标；（3）点M在y轴上，且位于点C上方，点N在直线BC上，点P为上述二次函数图象的对称轴上的点，如果以C、M、N、P为顶点的四边形是菱形，求点M的坐标．5平行四边形的存在性问题．2+bx+c与x轴相交于A，C2017?成都）如图1，在平面直角坐标系xOy中，抛物线：y=ax7.（C轴的正半轴上一点，将抛物线）是x（m，0（D0，4），AB=4，设点FB两点，顶点为C′．F 旋转180°，得到新的抛物线绕点轴的右侧有两个不同的公在y C′与抛物线C2）求抛物线C的函数表达式；（）若抛物线（1上一点，它到两坐标轴的C，2P是第一象限内抛物线共点，求m 的取值范围．（3）如图上的动点，试探究C′上的动点，N是P′，设M是C C′距离相等，点P 在抛物线上的对应点的值；若不能，请说明理由．能否成为正方形？若能，求出m四边形PMP′N6平行四边形的存在性问题．答案12平移后得到的抛物线，其对称轴为xy=﹣,（2017?泰安）如图，是将抛物线x=1，与x轴的一个交点为A（﹣1，0），另一个交点为B，与y轴的交点为C．（1）求抛物线的函数表达式；（2）若点N为抛物线上一点，且BC⊥NC，求点N的的图象上一点，若x+是抛物线上一点，点Q是一次函数y=坐标；（3）点P、P、Q是否存在？若存在，分别求出点为平行四边形，四边形OAPQ这样的点P 的坐标；若不存在，说明理由．Q优网版权所有）已知抛物线的对称轴，因而可以设出顶点式，利用待定系数法求1【分析】（函数解析式；⊥作NH的坐标，易证△）首先求得B和COBC是等腰直角三角形，过点N（22即可列方程求，根据aCH=NH+2a+3）y轴，垂足是H，设点N纵坐标是（a，﹣，﹣tPQ∥OA，设P（，且解；（3）四边形OAPQ是平行四边形，则PQ=OA=12，即可求解．y=x+t，代入+2t+3）2+k）【解答】解：（1）设抛物线的解析式是y=﹣（x﹣1．2 k=4）0=﹣（﹣1﹣1，+k，解得，把（﹣10）代入得22 y=﹣x；+2x+3则抛物线的解析式是y=﹣（x﹣1）+4，即2 OC=3．3），，﹣x中令+2x+3x=0，则y=3，即C的坐标是（0y=（2）在是等腰直角三角形．∴∠OC=OB，则△OBC，∴B∵的坐标是（3，0），∴OB=3 OCB=45°，H．过点N作NH⊥y轴，垂足是+CH=3+CH=3+NH，，∴，∴∠∵∠NCB=90°NCH=45°，∴NH=CHHO=OC22 a=1a=0，解得（舍去）或，32a﹣+．∴32a，﹣坐标是（设点Naa++）a3=a++ 1N∴的坐标是（，；）47平行四边形的存在性问题．（3）∵四边形OAPQ是平行四边形，则PQ=OA=1，且PQ∥OA，22，）+1+2t+3=（t+设P（t，﹣t3+2t+），代入y=x+，则﹣t22．+2t+3的值为3整理，得2t或﹣t=0，解得t=0或．∴﹣t．，，3）（1，3）或（，）、（，）P∴、Q的坐标是（0，，3）或（，0，3）（1P）、（，）．综上所述，、Q的坐标是（本题考查了待定系数法求二次函数解析式，以及等腰三角形、平行四【点评】OBC是等腰直角三角形是解题的关键．边形的性质，注意到△22，A+1交y轴于点.（2017?菏泽）如图，在平面直角坐标系中，抛物线y=ax+bx，过点3，）0交x轴正半轴于点B（4，），与过A点的直线相交于另一点D（上（不）点轴，垂足为D作DC⊥xC．（1）求抛物线的表达式；（2P在线段OC，连接、NAD于M，交抛物线于点轴，交直线C重合），过P作PN⊥x与点O ，求△CMPCM面积的最大值；、，使以点的长为轴正半轴上的一动点，设OPt，是否存在tM是（3）若Px的值；若不存在，请D、Nt为顶点的四边形是平行四边形？若存在，求出、C 说明理由．菁优网版权所有：二次函数综合题．【考点】HF2即可得出抛物线的1）代入3，点D（，y=ax+bx+），（）把（【分析】1B40 解析式；PCM坐标，再根据三角形的面积公式求出△、的代数式表示）先用含（2tPM 面积的最大值；PCM的函数关系式，然后运用配方法可求出△的面积与t的二元一为平行四边形，则有）若四边形3（DCMNt，故可得出关于MN=DC8平行四边形的存在性问题．次方程，解方程即可得到结论．2 1中得，y=ax，+bx+0），点D（3，），代入把点【解答】解：（1）B（4，2+；x+解得：，∴抛物线的表达式为y=﹣x1 ，y=kx+b（2）设直线AD的解析式为，），D（3，），∴，∴A∵（0，1，+1∴直线AD的解析式为y=xt+1，PM=，0）∴M（t，t+1），∴设P（t，PC=3﹣，t∵CD⊥x轴，∴∴S=PC?PM=（3﹣t）（t），+1PCM△22+（t﹣）S，∴=﹣tt++=﹣PCM△PCM面积的最大值是；∴△OP=t（3）∵，∴点M，N的横坐标为，t2 1），，﹣，t，+1）N（ttt++M设（t22∴|MN|CD=，﹣11t+﹣t﹣|=|tt+|，﹣=|t+，如果以点如图1M、CN为顶点的四边形是平行四边形，、D、22，﹣9t+10=0t=，即﹣∴MN=CDt+，整理得：3t2 tt=∴方程﹣，39 t+无实数根，∴不存在，﹣∵△= NDCM2如图，如果以点、、、为顶点的四边形是平行四边形，2t=∴，（负值舍去），，﹣tMN=CD∴，即t=DC、M t=∴当时，以点、为顶点的四边形是平行四边形．N、9平行四边形的存在性问题．本题考查的是二次函数的性质、待定系数法求函数解析式、平行四边【点评】形的判定，正确求出二次函数的解析式、利用配方法把一般式化为顶点式、求出函数的最值是解题的关键，注意菱形的判定定理的灵活运用．3、Bx轴、y轴分别交于点2.（2018?徐汇区二模）如图，已知直线y=﹣x+与．Ax轴交于另一个点，且与C，抛物线y=﹣+bx+c过点B、C）求该抛物线的表达式；1（，当四轴交该抛物线于点N上一点，过点是线段BC M作直线l∥y（2）点M是平行四边形时，求它的面积；边形OMNC的DD是该抛物线上的一点，且满足∠DBA=∠CAO，求点AC（3）联结，设点坐标．的坐标，然后利用待定系数法求二次1C）根据直线解析式求出点B、【分析】（函数解析式列式求解即可；（﹣MN=2，﹣+），则（2m2（）设M（，﹣m+），则Nm2的横坐标，+2）列方程可得MN=OC=2M，根据=﹣m+2mm2+）﹣（﹣根据平行四边形的面积公式可得结论；）分两种情况：3（的解析式AC xD①当在轴的下方：根据∥相等可设直线BD k，直线解析式BD 01 平行四边形的存在性问题．为：y=2x+b，把B（4，0）代入得直线BD的解析式为：y=2x﹣8，联立方程可得D的坐标；②当D在x轴的上方，根据对称可得M的坐标，利用待定系数法求直线BM的解析式，与二次函数的交点，联立方程可得D的坐标．【解答】解：（1）当x=0时，y=2，∴C（0，2），，），0x=4，∴B（4当y=0时，﹣x+2=0，，中得：+bx+cB（4，0）代入抛物线y=﹣（把C0，2）和；，∴该抛物线的表达式：解得：，，∴OC=2（）如图1，∵C0，2）（2，N（m，﹣+2）2设M（m，﹣m+），则2，2m+2+）﹣（﹣m+2）=﹣m MN=∴（﹣，是平行四边形时，MN=OC∥∵MNy轴，当四边形OMNC2；=m+2m=2，解得：m=2，∴S=OC×2=2×即﹣m2=4?OCMN12）分两种情况：（3，0），∴A（﹣1，1x当y=0时，﹣x+2=0，解得：=4，x=﹣21，2易得直线AC 的解析式为：y=2x+，by=2x+的解析式为：2①当D在x轴的下方时，如图，AC∥BD，∴设直线BD ，的解析式为：+0）代入得：0=2×4b，b=﹣8，∴直线BDy=2x﹣8（把B4，；5D（﹣，﹣18）（舍），=+﹣则2x8=﹣x2，解得：x﹣5x=4，∴21（图BE于3在②当Dx轴的上方时，如图，作抛物线的对称轴交直线BDM，将，2中的点）于ND，=x=对称轴是：﹣，与∴DABABE=CAO=∵∠∠∠，MN8﹣y=2xBE直线轴对称，关于x的解析式：11 平行四边形的存在性问题．，），M（，5时，y=﹣5，∴N（，﹣5）当x=，8y=﹣2x+直线BM的解析式为：，2），∴x=4（舍）D（3，x2x﹣+8=﹣x+2，解得：=3，21．））或（5，﹣183，2综上所述，点D的坐标为：（﹣本题是对二次函数的综合考查，主要有直线与坐标轴的交点的求解，【点评】待定系数法求二次函数和一次函数解析式，两直线平行的关系，对称性等知）题有难度，采用分类讨论的思想解决问题．识，（342与2018?杨浦区二模）如图，在平面直角坐标系中，抛物线y=bx+c﹣x+（．为抛物P、经过点4AC，点+，直线轴交于点，与、轴交于点xAByC y=x上方的一个动点．线上位于直线AC）求抛物线的表达式；（1的正切值；，当12（）如图（）CP时，求∠AO∥PAC为邻边的平行四边形第四个顶点恰好也在抛物线上时，求AO AP3（）∠当以、的坐标．P出此时点21 平行四边形的存在性问题．，然后根据待定），044），A（﹣【分析】（1）利用一次函数解析式确定C（0，系数法求抛物线解析式；，作），41，再利用对称性得到P（﹣2（2）先确定抛物线的对称轴为直线x=﹣，为等腰直角三角形得到AC=4，证明△OAC和△PCHPH⊥AC于H，如图1，然后根据正切的定义求解；AH=3PH=CH=，则，利用平行四为邻边的平行四边形第四个顶点为点Q，如图2（3）以AP、AO2，﹣4+4），则Q（tt边形的性质得PQ∥OA，PQ=OA=4，设P（t，﹣+﹣t222﹣4）+4﹣x+得﹣（t+4）4=﹣（t点坐标代入t﹣t+4），然后Qy=﹣x+2点坐标．t 的方程即可得到tP﹣t+4，再解关于，4）1（）当x=0时，y=x+4=4，则C（0，【解答】解：，）4=0，解得x=﹣4，则A（﹣4，0当y=0时，x+2，bx+c得）代入0把A（﹣4，），C（0，4y=﹣x，解得+2；﹣4xy=﹣x+∴抛物线解析式为，﹣=﹣1x=（2）抛物线的对称轴为直线，，PC=2）（﹣1对称，∴P2，4﹣与点∥而PCOA，∴点PC关于直线x=，1PH⊥AC于H，如图作，，AC=4OAC=45°OA=OC=4∵，∴△OAC为等腰直角三角形，∴∠为等腰直角三角形，∵PCHOAC=45°PCA=OA，∴∠∠，∴△PC∥，=3﹣CH=4AH=AC2=PH=CH=∴×，∴﹣；=PAH=∠中，PAH△=在Rttan，即∠的正切值为PAC31 平行四边形的存在性问题．（3）以AP、AO为邻边的平行四边形第四个顶点为点Q，如图2，∵四边形APQO为平行四边形，∴PQ∥OA，PQ=OA=4，22，+44，﹣t）﹣tt﹣t+4），则Q（t+t设P（，﹣2222t）﹣﹣（t+4）+4=+t+4，﹣t﹣t+4）代入y=﹣x﹣x+4得﹣（t4把（．﹣3，∴此时P点坐标为（﹣3，）+﹣t4，解得t=本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特【点评】征、二次函数的性质、等腰直角三角形的性质和平行四边形的性质；会利用待定系数法求函数解析式；理解坐标与图形性质．52直C．交c+6x+交x轴于A，B两点，y轴于点河南）．（2018?如图，抛物线y=ax．C ﹣线y=x5经过点B，）求抛物线的解析式；（1．（2）过点AM BC于点的直线交直线的平重合）C，作直线AM（不与点⊥①当AM BC时，过抛物线上一动点PB，为顶点的四边形是平行四边形，M，行线交直线BC于点Q若以点A，，P，Q的横坐标；求点P倍时，请直接写出点的的夹角等于∠与直线，当直线②连接ACAM BC ACB2的坐标．M41 平行四边形的存在性问题．，然后利用待定0）B（5，）1）利用一次函数解析式确定C（0，﹣5，【分析】（系数法求抛物线解析式；2为等腰直角三角形，再判断△OCB1，0）+6x﹣5=0得A（（2）①先解方程﹣x，接着AM=2，则△AMB为等腰直角三角形，所以∠得到∠OBC=OCB=45°BC⊥x轴交直线，PQ⊥BC，作PD根据平行四边形的性质得到PQ=AM=22，m）+6m﹣5，﹣PQ=4，设P于D，如图1，利用∠PDQ=45°得到PD=（m2m ﹣（+6m﹣55m﹣），讨论：当P点在直线BC上方时，PD=﹣m则D（m，2，然后分别6m﹣5）P点在直线BC下方时，PD=m﹣5﹣（﹣m+﹣5）=4；当点的横坐标；解方程即可得到P，于EAC作AC的垂直平分线交BC于M，交，②作AN⊥BC于NNH⊥x轴于H，1，再∠ACB如图2，利用等腰三角形的性质和三角形外角性质得到∠AMB=21，）3确定N（，﹣2，利用两直线垂直的问题可设）E点坐标为（，﹣y=5xAC的解析式为﹣5，EM得到直线）代入求出bb，把E（，﹣+的解析式为直线EMy=﹣x11点的坐标；作直线M，则解方程组y=的解析式为﹣x﹣得1∠BC上作点MAMC=，利用对称性得到∠MN关于点的对称点，如图2221，然后求（，设∠B=2AMACBM3=，根据中点坐标公式得到5﹣xx，）21 51 平行四边形的存在性问题．出x即可得到M的坐标，从而得到满足条件的点M的坐标．2【解答】解：（1）当x=0时，y=x﹣5=﹣5，则C（0，﹣5），当y=0时，x﹣5=0，解得x=5，则B（5，0），2，c得）代入y=ax，解得+6x+B（5，0），C（0，﹣5把2；+6x﹣5∴抛物线解析式为y=﹣x2，（1），0﹣5=0得x=1，x=5，则A（2）①解方程﹣x+6x21，OCB=45°为等腰直角三角形，∴∠OBC=∠），C（0，﹣5），∴△OCB∵B（5，0，AMB AM⊥BC，∴△为等腰直角三角形，∴AM=AB=×4=2∵，PQ AM∥∵以点A，M，P，Q为顶点的四边形是平行四边形，，⊥BC∴PQ=AM=2，PQPD=，∴1D，如图，则∠PDQ=45°PQ=×2=4，作PD⊥x轴交直线BC于2，m﹣5）P（m，﹣m）+6m﹣5，则D（m，设上方时，当P点在直线BC22，m﹣﹣5）=m=4+5m=4，解得m=1，PD=﹣m﹣+6m5﹣（m21下方时，BC P当点在直线22，=，m﹣5m=4，解得m﹣（﹣PD=m﹣5m=m+6m﹣5）=21；或4或综上所述，P点的横坐标为，EM轴于于N，NH⊥xH，作AC的垂直平分线交BC于，交AC于⊥②作ANBC1，如图2，M A=M B=2AM∠ACB，∴∠C，∴∠ACM=∠CAM∵11111，）3，∴N（，﹣2AH=BH=NH=2∵△ANB为等腰直角三角形，∴，），的解析式为易得AC y=5x﹣5E点坐标为（，﹣，﹣y=x+b EM设直线的解析式为1，b=）代入得﹣（把E，﹣+﹣﹣，解得b=∴直线EM的解析式为y=，﹣x﹣1 61 平行四边形的存在性问题．；）得，则M（，﹣解方程组1∠AM C=∠AM B=2M作直线BC上作点关于N点的对称点M，如图2，则∠1221，ACB，，﹣），∴，∴x=M（，∵（设Mx，x﹣5）3=22．的坐标为（综上所述，点M））或（，﹣，﹣本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特【点评】征、二次函数的性质、等腰直角的判定与性质和平行四边形的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想解决数学问题．624y=ax如图），二次函数++bx（2018?．（浦东新区二模）已知平而直角坐标系xOy点．轴交于点Cy4）（﹣的图象经过A2，0、B（，0）两点，与）求这个二次函数的解析式；1（的坐标；（2）如果点E∠ACO，求点CBE=OC E在线段上，且∠为上述二次函上，点P BC NCyM3（）点在轴上，且位于点上方，点在直线为顶点的四边形是菱形，求点数图象的对称轴上的点，如果以C、、、MNP的坐标．M71 平行四边形的存在性问题．）利用待定系数法即可得出结论；（1【分析】和再，得出，进而求出BC2（）先确定出OA=2，OC=4．即可得出结论；，进而建立方程，．进而得出（3）①当MC为菱形MCNP的边时，先求出即可得出结论；的边时，不存在，MC②当为菱形MCPN互相垂直平分，进而得CM、NP③当MC为菱形MNCP的对角线时，先判断出，即可得出结论．，MQ=CQ=1．出NQ=QP=1MQ=QC，即可得出QN=CQ=12，4），02（1）∵抛物线y=axbx++4与x轴交于点A（﹣，0），B（【解答】解：，∴，解得，∴抛物线的解析式为．BC于点H⊥（2）如图1，过点E作EH，OA=2）△在RtACO中，∵A（﹣2，0，∴，，∴OC=4．，∴OC=OB=4COBRt△中，∵∠COB=90°，在，中，．∴在⊥∵EHBC，∴CH=EHRt△ACO．中，EBHRtACO∵∠CBE=∠，在△．BH=2k）＞（设EH=kk0，则，，CH=k，∴．∴，∴，∴，∴81 平行四边形的存在性问题．（3）∵A（1，0），B（5，0），∴抛物线的对称轴为直线x=1，①当MC为菱形MCNP的边时，∴CM∥PN，∴∠PNC=∠NCO=45°．∵点P在二次函数的对称轴上，∴点P的横坐标为1，点N的横坐标为1．．∴是菱形，∴MCNP，∴，∴，∵四边形的边时，不存在，MCPN②当MC为菱形的对角线时，MNCP③如图2，当MC为菱形，NP互相垂直平分，∴NQ=QP=1．MQ=QC CM设NP交CM于点Q，∴、．BC上，∠NCM=∠OCB=45°∵点N在直线，，∴MQ=CQ=1，∴CM=2Rt△CQN中，∴∠NCQ=∠CNQ=45°，∴QN=CQ=1在，），6+CM=4+2=6，∴M（0∴OM=OC．）或M（0，6∴综上所述此题是二次函数综合题，主要考查了待定系数法，锐角三角函数，线【点评】段垂直平分线的判定和性质，特殊直角三角形的性质，用分类讨论的思想是解本题的关键．2，A：抛物线Cy=axx+bx+c与轴相交于xOy如图7.（2017?成都）1，在平面直角坐标系中，C轴的正半轴上一点，将抛物线，0）是x（，0B两点，顶点为D（，4）AB=4，设点Fm 的函数表达式；1，得到新的抛物线绕点F旋转180°C′．（）求抛物线C 的取值范围．yC与抛物线在轴的右侧有两个不同的公共点，求mC′2（）若抛物线在抛物线P23（）如图，是第一象限内抛物线上一点，它到两坐标轴的距离相等，点CP 91 平行四边形的存在性问题．C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．：二次函数综合题．菁优网版权所有【考点】HF2，y=ax4+，A（﹣2，0）设抛物线的解析式为（【分析】（1）由题意抛物线的顶点D0，4），把A（2﹣，由此即可解决问题；，0）代入可得a=2）的解析式为y=（x﹣2m）由题意抛物线（2C′的顶点坐标为（2m，﹣4），设抛物线C′22与抛物线C′，由题意，抛物线﹣﹣4，由，消去y得到x8=0﹣2mx+2m，解不等式组即可解在y轴的右侧有两个不同的公共点，则有C 决问题；．由题意易知轴于H 能成为正方形．作PMP′NPE⊥x轴于E，MH⊥x（3）情形1，四边形，PFM=90°PFM是等腰直角三角形时，四边形PMP′N是正方形，推出PF=FM，∠，P（22），当△，理由待定系+22），m﹣﹣易证△PFE≌△FMH，可得PE=FH=2，EF=HM=2m，可得M（m，）2﹣m（2数法即可解决问题；情形，如图，四边形PMP′N是正方形，同法可得Mm﹣2，利用待定系数法即可解决问题．，设抛物线的解析式为A0，4），（﹣2）0，）由题意抛物线的顶点【解答】解：（1D（2+y=ax4，2）由题意（4的函数表达式为Cy=﹣x+．2，∴抛物线a=02A把（﹣，）代入可得﹣2的解析式为，设抛物线42mC′抛物线的顶点坐标为（，﹣）C′y=，4）2m﹣（x﹣02 平行四边形的存在性问题．22，﹣x8=0﹣2mx+2m由，消去y得到轴的右侧有两个不同的公共点，C在y由题意，抛物线C′与抛物线，2＜m＜2，解得则有＜m＜2．∴满足条件的m的取值范围为2 3）结论：四边形PMP′N能成为正方形．（．轴于H轴于PE⊥xE，MH⊥x理由：1情形1，如图，作是正方形，22，），当△PFM是等腰直角三角形时，四边形PMP′N由题意易知P（，∴PF=FM，∠PFM=90°PE=FH=2，EF=HM=2﹣m，≌△易证△PFEFMH，可得，﹣2），∴M（m+2m2 4M∵点在y=﹣x上，+2（舍弃）3m=m﹣m2=﹣（+2）+4，解得﹣或﹣﹣3，∴PMP′N是正方形．3﹣m=∴时，四边形2mMPMP′N2情形，如图，四边形是正方形，同法可得（﹣，），m﹣2 12 平行四边形的存在性问题．22或0（舍弃），解得）（2中，﹣m=﹣m﹣2+4，m=64﹣代入m22mM把（﹣，﹣）y=x+ PMP′N是正方形．m=6∴时，四边形．或﹣m=PMP′N综上，四边形能成为正方形，3622 平行四边形的存在性问题．。

第6讲 平行四边形存在性问题专题探究【知识点睛】❖ 知识储备：①平行四边形是中心对称图形②中心对称图形的性质：对称中心平分中心对称图形内通过该点的任意线段，且使中心对称图形的面积被平分③中点公式： ❖ 方法策略： （1）有3个定点，找第4个点形成平行四边形时：①设第4个点的坐标②以3个定点组成的3条线段为对角线分类讨论③以中心对称图形的性质为等量关系列式求解例，如图所示，平面直角坐标系内有A 、B 、C 三点，在平面内找第4个点，构成平行四边形；（2）有2个定点，且另外两个动点均在特殊的位置上时，方法策略同上。

类型一 几何背景下的平行四边形存在性问题1．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，BD ＝12cm ，AC ＝6cm ，点E 在线段BO 上从点B 以1cm /s 的速度运动，点F 在线段OD 上从点O 以2cm /s 的速度运动．若点E ，F 同时运动，设运动时间为t 秒，当t ＝ 时，四边形AECF 是平行四)2,2),(),,(21212211y y x x P y x B y x A ++坐标为（，则其中点若如，当A 、B 已知，点C 在直线y=x 上，点D 在另一直线上，则设C （a,a ）；分类还分别分①以AB 为对角线，②以AC 为对角线，③以BC 为对角线；依其性质分别表示出D 点坐标；将点D 坐标再分别带入另一直线解析式，即可求出a 的值，C 、D 坐标就都能求出来了。

边形．2．如图，四边形ABCD中，AB∥DC，DC＝6cm，AB＝9cm．点P以1cm/s的速度由A点向B点运动，同时点Q以2cm/s的速度由C点向D点运动，其中一点到达终点时，另一点也停止运动，当线段PQ将四边形ABCD截出一个平行四边形时，此时的运动时间为s．3．如图，在▱ABCD中，AB＝10cm，F是AB的中点，E为边CD上一点，DE＝4cm．点M 从D点出发，沿D→C以1cm/s的速度匀速运动到点C；同时点N从点B出发，沿B→A 以2cm/s的速度匀速运动到点A．一个点停止运动后，另一个点也随之停止运动．当点M 运动时间是秒时，以点M，E，N，F为顶点的四边形是平行四边形．4．如图，在▱ABCD中，AC与BD交于点M，点F在AD上，AF＝6cm，BF＝12cm，∠FBM ＝∠CBM，点E是BC的中点，若点P以1cm/秒的速度从点A出发，沿AD向点F运动；点Q同时以2cm/秒的速度从点C出发，沿CB向点B运动，点P运动到F点时停止运动，点O也同时停止运动，当点P运动（）秒时，以点P、Q、E、F为顶点的四边形是平行四边形．A．3B．3或5C．5D．4或55．如图所示，在平行四边形ABCD中，AB＝5cm，AD＝9cm．点P在AD边上以1cm/s的速度从点A向点D运动，点Q在BC边上以4cm/s的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时，P、Q同时停止运动，设运动时间为t（s）且t＞0，当以P，D，Q，B为顶点的四边形是平行四边形时，则t的所有可能值为．6．如图，在平面直角坐标系中，已知点A的坐标为（9，0），点C的坐标为（3，3），四边形OABC是平行四边形，点D、E份别在边OA、BC上，且OD＝OA，CE＝4．动点P、Q在平行四边形OABC的一组邻边上，以点D、E、P、Q为顶点的四边形是平行四边形时，其面积为．7．如图，在四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，动点P、Q分别从A、C 同时出发，点P以1cm/s的速度由A向D运动，点Q以3cm/s的速度由C向B运动，其中一动点到达终点时，另一动点随之停止运动，设运动时间为t秒．（1）AP＝，BQ＝，（分别用含有t的式子表示）；（2）当四边形PQCD的面积是四边形ABQP面积的2倍时，求出t的值．（3）当点P、Q与四边形ABCD的任意两个顶点所形成的四边形是平行四边形时，直接写出t的值．类型二“三定一动”求平行四边形的顶点坐标1．在平面直角坐标系xOy中，已知A（1，﹣1），B（4，2），C（0，3），下列坐标不能与A、B、C构成平行四边形的是（）A．（﹣3，0）B．（5，﹣2）C．（3，6）D．（﹣3，﹣2）2．在平面直角坐标系中，点A、B、C的坐标分别是A（﹣2，5），B（﹣3，﹣1），C（1，﹣1），在x轴上方找到点D，使以A，B，C，D为顶点的四边形是平行四边形，那么点D的坐标是．3．在平面直角坐标系中，已知点A（4，0），点B（﹣3，2），点C（0，2），点P从点B出发，以2个单位每秒的速度沿射线BC运动，点Q从点A出发，开始以1个单位每秒的速度向原点O运动，到达原点后立刻以原来3倍的速度沿射线OA运动，若P，Q两点同时出发，设运动时间为t秒，则当t＝时，以点A，Q，C，P为顶点的四边形为平行四边形．4．如图，在平面直角坐标系的第一象限找一点A，第二象限找一点B，使OA＝，OB＝2，AB＝5，且A，B都是格点，连接OA，OB，AB．（画出一个△OAB即可）．（1）判断△OAB的形状，并说明理由；（2）是否存在点C，使得O，A，B，C四点构成的四边形为平行四边形？如果存在，请直接写出点C的坐标；如果不存在，请说明理由．5．如图，在平面直角坐标系中，矩形OABC的三个顶点A，O，C在坐标轴上，矩形的面积为12，对角线AC所在直线的解析式为y＝kx﹣4k（k≠0）．（1）求A，C的坐标；（2）若D为AC中点，过D的直线交y轴负半轴于E，交BC于F，且OE＝1，求直线EF的解析式；（3）在（2）的条件下，在坐标平面内是否存在一点G，使以C，D，F，G为顶点的四边形为平行四边形？若存在，请直接写出点G的坐标；若不存在，请说明理由．类型三“两定两动”求平行四边形的顶点坐标1．在平面直角坐标系中，已知A（﹣4，2），B（2，5），在x轴、y轴上分别有两动点C、D，若以点A，B，C，D为顶点的四边形是平行四边形，则点C的坐标为．2．在平面直角坐标系中，A（﹣1，1），B（3，2），C（2m，3m+1），点D在直线y＝﹣1上，若以A，B，C，D四点为顶点的四边形是平行四边形，则点D的坐标为．3．如图，在平面直角坐标系xOy，直线y＝x+1与y＝﹣2x+4交于点A，两直线与x轴分别交于点B和点C，D是直线AC上的一个动点，直线AB上是否存在点E，使得以E，D，O，A为顶点的四边形是平行四边形？若存在，求出点E的坐标；若不存在，请说明理由．4．如图，在平面直角坐标系中，直线y＝﹣x+3与x轴、y轴相交于A、B两点，点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到线段CD，此时点D恰好落在直线AB 上，过点D作DE⊥x轴于点E．（1）求证：△BOC≌△CED；（2）请直接写出点D的坐标，并求出直线BC的函数关系式；（3）若点P是x轴上的一个动点，点Q是线段CB上的点（不与点B、C重合），是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的P 点坐标．若不存在，请说明理由．5．如图，Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点A 在x轴上，点C在y轴上，OA＝6，∠CAO＝30°，将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE．（1）求点D的坐标；（2）在线段AC上有一动点P，连接EP和OP，求当△OPE周长最小时，点P的坐标，若M，N是x轴上两动点（M在点N左侧）且MN＝1，求当四边形CMNP周长最小时，M点的坐标；（3）设点M为直线CE上的一点，过点M作AC的平行线，交y轴于点N，是否存在这样的点M，使得以M、N、D、C为顶点的四边形是平行四边形？若存在，请求出符合条件的点M的坐标；若不存在，请说明理由．。

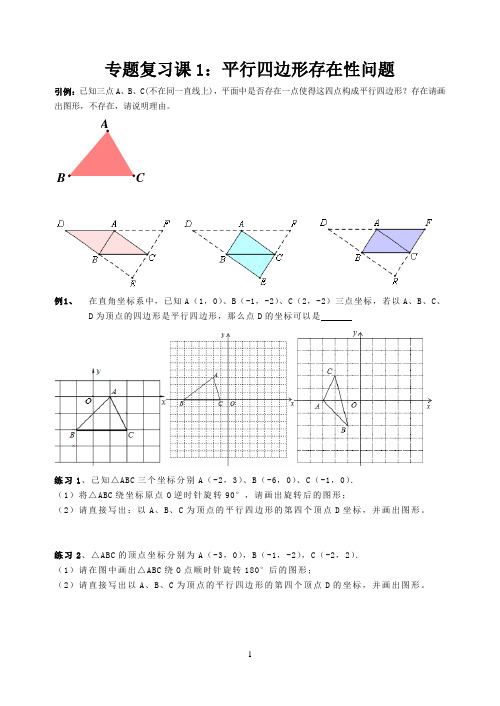
专题复习课1：平行四边形存在性问题引例：已知三点A、B、C(不在同一直线上)，平面中是否存在一点使得这四点构成平行四边形？存在请画出图形，不存在，请说明理由。

B例1、在直角坐标系中，已知A（1，0）、B（-1，-2）、C（2，-2）三点坐标，若以A、B、C、练习1、己知△ABC三个坐标分别A（-2，3）、B（-6，0）、C（-1，0）．（1）将△ABC绕坐标原点O逆时针旋转90°，请画出旋转后的图形；（2）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D坐标，并画出图形。

练习2、△ABC的顶点坐标分别为A（-3，0），B（-1，-2），C（-2，2）．（1）请在图中画出△ABC绕O点顺时针旋转180°后的图形；（2）请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标，并画出图形。

例2、如图，在平面直角坐标系中，点A（1，0）、B（4，0），点C在y轴的正半轴上，且OB = 2 OC．（1）求直线BC的解析式；（2）在直角坐标平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形，请写出点M的坐标．课后练习：1. 如图，一次函数 y = 13 x + 43 图像经过两个点，其中A （─ 1，m ），B （n ，n ）.（1）求点A 、B 的坐标；（2）坐标平面内是否存在点C ，使以A 、O 、B 、C 为顶点的四边形是平行四边形，若存在，请求出点C 的坐标；若不存在，请说明理由.2. 如图，点A （1，m ）和点B （─ 3，23 ）在反比例函数y = kx （k ≠ 0）的图像上，直线y = 2 x + b经过点A 且与x 轴交予点C.（1）求反比例函数的解析式及点A 、点C 的坐标；（2）在坐标平面内是否存在点D ，使O 、A 、C 、D 为顶点的四边形是平行四边形.①这样的点D 有几个，请直接写出点D 的坐标；②写出一条直线DC 的解析式.3. 如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数xky的图象上． （1）求m ，k 的值； （2）如果M 为x 轴上一点，N 为y 轴上一点，以点A ，B ，M ，N 为顶点的四边形是平行四边形，试求直线MN 的函数表达式． （第1题）（第2题）。

平行四边形的存在性问题的处理一、问题说明关于此类问题，其实已经不是考试的主流了，但是作业及期末考试偶有出现，同学们又不会进行处理，所以简单将解题思路讲解一下，同学们可以自己看看。

二、解题方法总结平行四边形的存在性问题中，已知两点，求双动点的存在性问题是比较经典的。

以这个问题为切入点，讲讲解决这类问题需要克服的两个难点：（1）分类的处理（如何找到所有存在的可能性）（2）计算技巧的处理（平移法）三、问题的演绎例1，（已知三点求一点）如图在坐标平面内再找一点D，使得点A,点B，点C,点D组成平行四边形。

（一）分类处理任意连接两个已知点，例如选择连接AC，对线段AC进行分类讨论（1）若AC是平行四边形的边，则BD一定会和AC平行，且长度等于AC，所以点D在点B的右上方或左下方（如下图）(3,0)(1,1)C1C2(3,0)C（2）若AC是平行四边形的对角线，则BD和AC相互平分，则点D位置如图综上所述存在3个点D满足要求（二）计算技巧的处理平行四边形的计算方法很多，从平移的角度去处理是非常简单的以D1为例：如红色箭头标注方向为例：∵点C(0,-1)往右平移1个单位往上平移2个单位得点A(1,1)∴点D1的坐标是点B以同样的方式平移得到，点D坐标为（4，2）同样类似的方法得到点D2的坐标为（2，-2）D3的坐标为（-2，0）D 3(3,0)2D 31例2，已知二次函数322--=x x y 上两点A（-1，0），C（2，-3），点M在X轴上运动，点N在抛物线上运动，求出所有的点M的坐标。

使得点A ，C,M,N组成平行四边形。

、解题分析：已知点A,点C，所以只需要对AC进行分类讨论，点M在X轴上运动，所以设成（a，0），点N通过点M平移得到，然后代入二次函数解析式求解即可。

设点M的坐标为（a,0）（1）若AC是边，则点N在M的左上方或者右下方当点N在左上方时，点N的坐标（a-3,3）将点N（a-3,3）代入322--=x x y 中解得724±=a 当点N在右上方时，点N的坐标（a+3,-3）将点N（a+3,-3）代入322--=x x y 中解得3-=a 或1-=a （舍）(2)若AC是对角线时，则点N的坐标为（1-a,-3）将点N（1-a,-3）代入322--=x x y 中解得1=a 或1-=a （舍）四、问题的拓展双动点的载体，可以是坐标轴，二次函数。

平行四边形，矩形，菱形的存在性问题一、平行四边形存在性问题1．在平面直角坐标系中，点A，B，C的坐标分别是A（﹣1，3），B（﹣5，﹣3），C（1，﹣3），在平面内找一点D，使四边形ABCD是平行四边形，则点D的坐标是．2．已知平行四边形ABCD的两条对角线相交于平面直角坐标系中的原点O，点A（﹣1，3），B（1，2），则点C，D的坐标分别为．3．在直角坐标系中，点A、B的坐标分别为（﹣2，4）、（﹣5，2），点M在x轴上，点N 在y轴上．如果以点A、B、M、N为顶点的四边形是平行四边形，那么符合条件的点M 有个．4．如图，在平面直角坐标系中，AD∥BC，AD＝5，B（﹣3，0），C（9，0），E是BC的中点，P是线段BC上一动点，当PB＝时，以点P、A、D、E为顶点的四边形是平行四边形．第4题第5题第6题5．如图，在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（4，0），点C在y 的正半轴上，且OB＝2OC，在直角坐标平面内确定点D，使得以点D、A、B、C为顶点的四边形是平行四边形，请写出点D的坐标为．6．如图，已知A（1，0）、C（0，1）、B（m，0）且m＞1，在平面内求一点P，使得以A、B、C、P为顶点的四边形是平行四边形，则点P的坐标为．7．已知点A（4，0），B（0，﹣2），C（a，a）及点D是一个平行四边形的四个顶点，则线段CD长的最小值为．8．（1）在图1，2，3中，给出平行四边形ABCD的顶点A，B，D的坐标（如图），图1，2，3中的顶点C的坐标分别是，，；（2）在图4中，若平行四边形ABCD的顶点A，B，D的坐标分别为（4，1）、（3，4）、（6，4），则顶点C的坐标为；（3）在图4中，平行四边形ABCD顶点坐标分别为A（a，b）、B（c，d）、C（m，n）、D（e，f），则其横坐标a，c，m，e之间的等量关系为；纵坐标b，d，n，f之间的等量关系为．9．如图，矩形OABC中，点A在x轴上，点C在y轴上，点B的坐标是（6，8），将矩形OABC沿直线BD折叠，使得点C恰好落在对角线OB上的点E处，折痕所在直线与y 轴、x轴分别交于点D、F．（1）请直接写出线段BO的长；（2）求折痕所在直线BD的解析式；（3）若点M在直线y＝﹣x上，则在直线BD上是否存在点P，使以C、D、M、P为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点P的坐标；否则，请说明理由．二、矩形存在性问题10．在平面直角坐标系中，已知点A（0，0），B（2，﹣2），C（4，0），D（2，2），则以这四个点为顶点的四边形ABCD是（）A．矩形B．菱形C．梯形D．正方形11．如图1，在四边形ABCD中，AB∥CD，∥BCD＝90°，AB＝AD＝10cm，BC＝8cm．点P 从点A出发，以每秒3cm的速度沿线段AB方向向B运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动．已知动点P、Q同时出发，当点P运动到点B 时，P、Q同时运动停止，设运动时间为t秒．（1）求CD的长；（2）当t为何值时，四边形PBQD为平行四边形？（3）在运动过程中，是否存在四边形BCQP是矩形？若存在，请求出t的值；若不存在，请说明理由．12．平行四边形AOBC在平面直角坐标系中的位置如图（1）．（1）写出点C的坐标；（2）在图（1）中，连接AB，OC得到图（2），求AB与OC的交点M点的坐标；（3）将图（2）中的线段BC向两方延长得到图（3），若点D，E为直线BC上不与B，C重合的动点，是否存在这样的D，E点，使得四边形OADE为矩形？若存在，请在图中画出矩形，并求出矩形OADE的面积和点D，E的坐标，若不存在，请说明理由．三、菱形存在性问题13．在直角坐标系中，A，B，C，D四个点的坐标依次为（﹣1，0），（x，y），（﹣1，5），（﹣5，z），若这四个点构成的四边形是菱形，则满足条件的z的值有（）A．1个B．3个C．4个D．5个14．如图1，直线l1：y＝﹣x+3与坐标轴分别交于点A，B，与直线l2：y＝x交于点C．（1）求A，B两点的坐标；（2）求∥BOC的面积；（3）如图2，若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO 方向作匀速滑动，分别交直线l1，l2及x轴于点M，N和Q．设运动时间为t（s），连接CQ．∥当OA＝3MN时，求t的值；∥试探究在坐标平面内是否存在点P，使得以O、Q、C、P为顶点的四边形构成菱形？若存在，请直接写出t的值；若不存在，请说明理由．参考答案1.根据题意得：D点的纵坐标一定是3；又由C点相对于B点横坐标移动了1﹣（﹣5）＝6，故可得点D横坐标为﹣1+6＝5，即顶点D的坐标为（5，3）．2．由题意知：点A与点C、点B与点D关于原点对称，∥点A，B的坐标分别为（﹣1，3），（1，2），∥点C，D的坐标分别是（1，﹣3），（﹣1，﹣2），3．有3个点．4．解：∥B（﹣3，0），C（9，0），∥OB＝3，OC＝9，∥BC＝OB+OC＝12，∥E是BC的中点，∥BE＝CE＝BC＝6，分为两种情况：∥当P在E的左边时，∥AD＝PE＝5，CE＝6，∥BP＝12﹣6﹣5＝1；∥当P在E的右边时，∥AD＝EP＝5，∥BP＝BE+EP＝6+5＝11；即当BP为1或11时，以点P、A、D、E为顶点的四边形为平行四边形；故答案为：1或11．5．如图，∥当BC为对角线时，易求M1（3，2）；∥当AC为对角线时，CM∥AB，且CM＝AB．所以M2（﹣3，2）；∥当AB为对角线时，AC∥BM，且AC＝BM．则|M y|＝OC＝2，|M x|＝OB+OA＝5，所以M3（5，﹣2）．综上所述，符合条件的点D的坐标是M1（3，2），M2（﹣3，2），M3（5，﹣2）．6．根据题意得：OA＝OC＝1，OB＝m，∥AB＝m﹣1，分三种情况：如图所示，∥以BC为对角线时，点P的坐标为（m﹣1，1）；∥以AC为对角线时，点P的坐标为（1﹣m，1）；∥以AB为对角线时，点P的坐标为（m+1，1）；综上所述：点P的坐标为（m﹣1，1）或（1﹣m，1）或（m+1，﹣1）；故答案为：（m﹣1，1）或（1﹣m，1）或（m+1，﹣1）．7．如图，由题意得：点C在直线y＝x上，∥如果AB、CD为对角线，AB与CD交于点F，当FC∥直线y＝x时，CD最小，易知直线AB为y＝x﹣2，∥AF＝FB，∥点F坐标为（2，﹣1），∥CF∥直线y＝x，设直线CF为y＝﹣x+b′，F（2，﹣1）代入得b′＝1，∥直线CF为y＝﹣x+1，由，解得：，∥点C坐标（，）．∥CD＝2CF＝2×＝3．∥如果CD是平行四边形的边，则CD＝AB＝＝2＞3，∥CD的最小值为3．故答案为：3．8.（1）利用平行四边形的性质：对边平行且相等，得出图1，2，3中顶点C的坐标分别是：（5，2）、（e+c，d），（c+e﹣a，d）．故答案为：（5，2）（e+c，d），（c+e﹣a，d）．（2）若平行四边形ABCD的顶点A，B，D的坐标分别为（4，1）、（3，4）、（6，4），则顶点C的坐标为（5，7）；故答案为：（5，7）；（3）如图4中，分别过点A，B，C，D作x轴的垂线，垂足分别为A1，B1，C1，D1，分别过A，D作AE∥BB1于E，DF∥CC1于点F．在平行四边形ABCD中，CD＝BA，又∥BB1∥CC1，∥∥EBA+∥ABC+∥BCF＝∥ABC+∥BCF+∥FCD＝180°．∥∥EBA＝∥FCD．在∥BEA∥∥CFD中，，∥∥BEA∥∥CFD（AAS），∥AE＝DF＝a﹣c，BE＝CF＝d﹣b．设C（x，y）．由e﹣x＝a﹣c，得x＝e+c﹣a．由y﹣f＝d﹣b，得y＝f+d﹣b．∥C（e+c﹣a，f+d﹣b），∥m＝e+c﹣a，n＝f+d﹣b，∥m+a＝e+c，n+b＝d+f．故答案为：m+a＝e+c，n+b＝d+f．9.解：（1）∥矩形OABC中，点A在x轴上，点C在y轴上，点B的坐标是（6，8），∥OA＝6，AB＝8，∥OAB＝90°，∥OB＝＝10，即线段BO的长是10；（2）设点D的坐标为（0，d），则OD＝d，CD＝8﹣d，∥BC＝6，CD＝DE，OB＝10，，∥，得d＝5，即点D的坐标为（0，5），设折痕所在直线BD的解析式为y＝kx+b，∥点D（0，5），点B（6，8）在直线BD上，∥，得，即折痕所在直线BD的解析式是y＝0.5x+5；（3）在直线BD上存在点P，使以C、D、M、P为顶点的四边形是平行四边形，点P的坐标为（﹣2，4）或（﹣8，1）；理由：∥点C（0，8），点D（0，5），∥OC＝8，OD＝5，∥CD＝3，∥以C、D、M、P为顶点的四边形是平行四边形，点M在直线y＝﹣x上，点P在直线BD上，∥CD＝MP，CD∥MP，或CD为平行四边形的对角线，当CD＝MP，CD∥MP时，设点M的坐标为（m，﹣0.5m），则P的坐标为（m，0.5m+5），则|（0.5m+5）﹣（﹣0.5m）|＝3，解得，m1＝﹣2，m2＝﹣8，当m＝﹣2时，点P的坐标为（﹣2，4），当m＝﹣8时，点P的坐标为（﹣8，1），当CD为平行四边形的对角线时，则点C和点D中点的坐标为（0，6.5），设点M的坐标为（m，﹣0.5m），则点P的坐标为（﹣m，13+0.5m），∥点P在直线BD上，直线BD的解析式是y＝0.5x+5，∥13+0.5m＝﹣0.5m+5，得m＝﹣8，∥点P的坐标为（8，9），由上可得，点P的坐标为（﹣2，4）、（﹣8，1）或（8，9）．10．D11．解：（1）过点A作AM∥CD于M，根据勾股定理，AD＝10，AM＝BC＝8，∥DM＝＝6，∥CD＝16；（2）当四边形PBQD为平行四边形时，点P在AB上，点Q在DC上，如图1，由题知：BP＝10﹣3t，DQ＝2t ∥10﹣3t＝2t，解得t＝2；（3）在运动过程中，不存在四边形BCQP是矩形，理由如下：∥AB∥CD，∥BCD＝90°，∥∥C＝90°，若要四边形BCQP是矩形，则当PB＝CQ时即10﹣3t＝16﹣2t，解得：t＝﹣6＜0，∥不存在．12.解：（1）∥四边形OACB是平行四边形，∥AC＝OB，∥A（1，3）、B（4，0），∥C（5，3）；（2）如图（2），设AB所在的直线的解析式为y＝kx+b，∥直线AB经过点A（1，3）、B（4，0），∥，∥AB所在直线的解析式为y＝﹣4x+4，由于OC所在直线的表达式为y＝x，联立方程解得：即M的坐标是（2.5，1.5）；（3）存在这样的D、E，使得四边形AOED是矩形．分别过点A、O作AD∥BC于点D，OE∥BC于点E，过E、D分别作x轴的垂线，垂足分别为F、G，∥四边形AOBC是平行四边形，∥AO∥BC，∥AD∥AO，∥四边形AOED是矩形，且与平行四边形AOBC面积相等，∥平行四边形AOBC的面积为12，∥矩形AOED的面积为12，由勾股定理知AO＝，∥OE＝，EB＝，∥EF＝＝＝1.2，OF＝＝＝3.6，∥点E的坐标为（3.6，﹣1.2），∥点D的坐标为（4.6，1.8）．13．如图，∥A（﹣1，0），C（﹣1，5），∥AC∥x轴，且AC＝5﹣0＝5，过点D（﹣5，z）作作x轴的垂线，则z的数值就在直线x＝﹣5上，；∥A、B、C、D四个点构成的四边形是菱形，∥当DC＝DA，z有1个值，当DC＝AC，则42+（5﹣z）2＝52，z有两个值，当AD＝AC，则42+z2＝52，则z有两个值，综上所知，符合条件的z的值有5个．故选：D．14.解：（1）对于直线y＝﹣x+3，令x＝0得到y＝3，令y＝0，得到x＝6，A（6，0）B（0，3）．（2）由，解得，∥C（2，2），∥S∥OBC＝×3×2＝3（3）∥∥M（6﹣t，﹣（6﹣t）+3），N（6﹣t，6﹣t），∥MN＝|﹣（6﹣t）+3﹣（6﹣t）|＝|t﹣6|，∥OA＝3MN，∥6＝3|t﹣6|，解得t＝或∥如图3中，由题意OC＝2，当OC为菱形的边时，可得Q1（﹣2，0），Q2（2，0），Q4（4，0）；当OC为菱形的对角线时，Q3（2，0），∥t＝（6+2）s或（6﹣2）s或2s或4s时，以O、Q、C、P为顶点的四边形构成菱形．。

专题08二次函数中特殊四边形存在性问题的四种考法类型一、平行四边形存在性问题(1)求抛物线的表达式；(2)如图1，连接BC ，PB ，PC ，设PBC 的面积为①求S 关于t 的函数表达式；②求P 点到直线BC 的距离的最大值，并求出此时点(3)如图2，设抛物线的对称轴为l ，l 与x 轴的交点为边形CDPM 是平行四边形？若存在，直接写出点【答案】(1)22y x=-(2)①23922S t t =-+；②点P 到直线BC 的距离的最大值为(3)存在，()1,6M 【分析】（1）待定系数法求解析式即可求解；（2）①在图1中，过点P 作PF y ∥轴，交BC 于点P 的坐标为()2,23t t t -++，则点F 的坐标为(t 2139222S PF OB t t =⋅=-+；②根据二次函数的性质得出当32t =时，S 取最大值，最大值为面积法求得点P 到直线BC 的距离，进而得出P （3）如图2，连接PC ，交抛物线对称轴l 于点设直线BC 的解析式为将()3,0B 、()0,3C 代入30,3m n n +=⎧⎨=⎩，解得：∴直线BC 的解析式为∵点P 的坐标为(,t t -∴点F 的坐标为(,t -∴(223PF t t =-++-∴1322S PF OB =⋅=-②12S PF OB =⋅=-∵302-<，∴当32t =时，S 取最大值，最大值为抛物线2y x bx =-++∴抛物线的对称轴为直线 1D C x x -=，∴1P M x x -=，∴2P x =，()2,3P ∴，在223y x x =-++中，当()0,3C ∴，∴3C D y y -=，∴3M P y y -=，∴6M y =，∴点M 的坐标为()1,6；当2P x ¹时，不存在，理由如下，若四边形CDPM 是平行四边形，则 点C 的横坐标为0，点∴点P 的横坐标12t =⨯又 2P x ¹，(1)求点C 的坐标；(2)点P 为直线AC 下方抛物线上一点，过点此时点P 的坐标；(3)抛物线顶点为M ，在平面内是否存在点若存在请求出N 点坐标并在备用图中画出图形；若不存在，请说明理由．【答案】(1)()4,5C (2)315,24P ⎛⎫- ⎪⎝⎭(3)存在，点N 的坐标为：()154N -，，【详解】（1）解：在2=23y x x --中，令解得：11x =-，23x =，()()1,0,3,0A B ∴-，直线y x m =+经过点()1,0A -，∴01m =-+，解得：1m =，∴直线AC 的解析式为1y x =+，联立方程组，得2123y x y x x =+⎧⎨=--⎩，解得：1110x y =-⎧⎨=⎩，2245x y =⎧⎨=⎩()4,5C ∴；（2）如图1，设点2(,23)P n n n --，则点∴2212334()PE n n n n n =+---=-++ 10-<，∴当32n =时，PE 取得最大值254，此时，（3） 2223(1)4y x x x =--=--，∴抛物线顶点为()14M -，，如图2，点,,,A B M N 为顶点的四边形是平行四边形时，设①BM 为对角线时，AN 的中点与BM ∴(1)3122m +-+=，04022n +-+=，解得：∴()154N -，，②AM 为对角线时，BN 的中点与AM ∴31122m +-+=，04022n +-+=，解得：(1)求此拋物线的解析式；(2)在抛物线的对称轴上有一点P ，使得PA PC +值最小，求最小值；(3)点M 为x 轴上一动点，在拋物线上是否存在一点N ，使以边形为平行四边形？若存在，直接写出点N 的坐标；若不存在，请说明理由．【答案】(1)215222y x x =--(2)552(3)54,2⎛⎫- ⎪⎝⎭，5214,2⎛⎫+ ⎪⎝⎭，5214,2⎛⎫- ⎪⎝⎭【分析】（1）把()1,0A -，()5,0B 两点代入求出a 、b 的值即可；（2）因为点A 关于对称轴对称的点B 的坐标为()5,0，连接BC 点坐标即可；（3）分点N 在x 轴下方或上方两种情况进行讨论．拋物线的解析式为212y x =-∴其对称轴为直线2b x a =-=-当0x =时，52y =-，50,2C ⎛⎫∴- ⎪⎝⎭，又()5,0B ，∴设BC 的解析式为(y kx b =+5052k b b +=⎧⎪∴⎨=-⎪⎩，解得：12k =，52b =-，∴BC 的解析式为1522y x =-，当2x =时，1532222y =⨯-=-，①当点N 在x 轴下方时，抛物线的对称轴为2x =，0,C ⎛- ⎝154,2N ⎛⎫∴- ⎪⎝⎭，②当点N 在x 轴上方时，如图，过点在2AN D △和2M CO △中，22N AD AN N DA ∠⎧⎪⎨⎪∠⎩252N D OC ∴==，即2N 点的纵坐标为21552222x x ∴--=，解得：2x =+25214,2N ⎛⎫∴+ ⎪⎝⎭，35214,2N ⎛⎫- ⎪⎝⎭综上所述符合条件的N 的坐标有⎛ ⎝【点睛】本题考查的是二次函数综合题，式、平行四边的判定与性质、全等三角形等知识，两点间距离的求解，在解答（意进行分类讨论．(1)求抛物线的解析式：(2)在抛物线的对称轴上是否存在点P ，使PCD 是以CD 为腰的等腰三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；(3)点E 在x 轴上运动，点F 在抛物线上运动，当以点B ，C ，E ，F 为顶点的四边形是平行四边形，直接写出点E 的坐标．【答案】(1)213222y x x =-++(2)存在，3,42⎛⎫ ⎪⎝⎭或35,22⎛⎫ ⎪⎝⎭或35,22⎛⎫- ⎪⎝⎭(3)541,02⎛⎫-+ ⎪ ⎪⎝⎭或541,02⎛⎫-- ⎪ ⎪⎝⎭或(7,0)或(1,0)【分析】（1）用待定系数法即可求解；（2）分两种情况：以C 为顶点，即CP CD =；以D 为顶点，即CD =等腰三角形的定义建立方程即可完成；（3）分三种情况：当BC 是对角线时；当BE 是对角线时；当BF 是对角线时；分别设点与F 的坐标，利用中点坐标公式即可求解．【详解】（1）解：∵点B 的坐标是(40)，，点C 的坐标是(02)，，∴16602a c c ++=⎧⎨=⎩，解得：122a c ⎧=-⎪⎨⎪=⎩，∴所求抛物线解析式为213222y x x =-++；（2）解：存在(1)求抛物线的表达式；(2)若点E 在第一象限内对称右侧的抛物线上，四边形ODEB 的面积为(3)在（2）的条件下，若点F 是对称轴上一点，点H 是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G ，使以E ，F ，G ，H 为顶点的四边形是菱形，且存在，请直接写出点G 的坐标；如果不存在，请说明理由．【答案】(1)232333y x x =-++(2)()2,33E 2039⎫⎪⎭或532,339⎛⎫⎪⎝⎭）根据待定系数法求解即可；∵232333y x x =-++()23143x =--+，∴()1,43D ．令232333y x x =-++中0y =，则解得=1x -或3x =，抛物线的对称轴与x轴交于点M，过点∵四边形EFGH 是菱形，EFG ∠∴EF FG GH EG ===，∵60EFG ∠=︒，∴EFG 是等边三角形．∴60FEG EF FG ∠=︒=，，∵()2,33E ，()0,33C ，(1,4D ∴2CE CD ==，()24333-+同理可证： EFG 是等边三角形，∵CF FE =，=GE FE ，∴DG ∴CDG CEG ∆∆≌．∴DCG ∠=∴直线CG 的表达式为：33y =与抛物线表达式联立得33y y ⎧=⎪⎨⎪=-(1)求抛物线的表达式；(2)若点D 是直线AC 上方拋物线上一动点，连接BC ，AD ADM △的面积为1S ，BCM 的面积为2S ，当121S S -=时，求点(3)如图2，若点P 是抛物线上一动点，过点P 作PQ x ⊥轴交直线上是否存在点E ，使以P ，Q ，E ，C 为顶点的四边形是菱形，若存在，请直接写出点坐标；若不存在，请说明理由【答案】(1)223y x x =-++(2)271,22⎛⎫+ ⎪ ⎪⎝⎭或271,22⎛⎫- ⎪ ⎪⎝⎭．(3)符合条件的点E 有三个，坐标为：()0,1E ，(10,132E -【分析】（1）把点()30A ，和()10B -，代入解析式求解即可；（2）由121S S -=得121S S =+从而121ABM ABM S S S S +=++ 程求解即可；（3）分类当CQ 为对角线和菱形边时，利用直线AC 与x 轴成标的方程，进而求出点的坐标．【详解】（1）把点()3,0A 和()1,0B -代入得：93330a b a b ++=⎧⎨-+=⎩解得：12a b =-⎧⎨=⎩，∴抛物线的解析式为223y x x =-++；（2）设(),D x y ，对于抛物线223y x x =-++，令0x =，则()0,3C ∴．121S S -= ，121S S ∴=+．∵()30A ，，()0,3C ，∴3OA OB ==，45OCA ∴∠=︒，此时四边形CEQP 是正方形．PQ EQ ∴=．设()2,23P m m m -++，则23PQ m m =-+，23m m m ∴-+=，解得m =此时32OE OC m =-=-=②当CQ 为菱形的边时，如图设()2,23P m m m -++，则∴HQ m =，2PQ m =-+作QH OC ⊥于点H ，45OCA ∠︒= ，∴22CQ HQ m ==．∴23CE PQ m m ==-+=解得：132m =-，23m =()323213OE =+-=+()10,132E ∴-，(20,1E +综上所述，符合条件的点【点睛】本题考查待定系数法求函数的解析式，二次函数的性质，二次函数与几何综合，数形结合是解题的关键．【变式训练2】如图1，在平面直角坐标系中，点（点A 在点B 左侧），与(1)求ABC 的面积；（3）解：∵抛物线212y x x =--∴()211942212y x x x =--+=-2＋＋∵将抛物线2142y x x =--+沿着水平方向向右平移∴新抛物线为：()112y x =--2＋∴原抛物线与新抛物线的交点，∴()()1111992222x x -=--22＋＋＋，∴解得：0x =，【点睛】本题考查了二次函数的图象及性质，二次函数与特殊图形，二次函数的平移规律，掌握二次函数与特殊图形的位置关系是解题的关键．类型三、矩形存在性问题(1)求抛物线的解析式；(2)如图，点P 是抛物线上位于直线直线AC 于点D ，交x 轴于点E ，(3)在抛物线上是否存在点M ，对于平面内任意点一条边的四边形为矩形，若存在，请直接写出【答案】(1)2142y x x =--(2)335,28P ⎛⎫- ⎪⎝⎭；254(3)()4,8M -、()8,4N -【分析】（1）把点()4,0A 和点B a 、b 的值；（2）先用待定系数法求出直线2211,422D t t t t ⎛⎫--- ⎪⎝⎭，然后求出最大值时t 的值，即可求出点P （3）假设抛物线上是存在点M ，一条边的四边形为矩形，过点O 点A 且与OH 平行的直线解析式，经计算验证可得过点立方程可求得M 的坐标，通过平移即可求得点【详解】（1）解：把点()4,0A 和点∵()4,0A ，()0,4C -，∴OAC 为等腰直角三角形，∴点H 为AC 的中点，即(H 则OH 所在的直线方程为y =∵四边形AMNC 为矩形，∴过A 与直线AC 相垂直的直线函数解析式中的∴设AM 所在的直线解析式为∵点A 在直线AM 上，(1)求点A 、B 、C 的坐标；(2)将抛物线L 向右平移1个单位，得到新抛物线对称轴l 上是否存在点D ，使得以点D 的坐标；若不存在，请说明理由．【答案】(1)()1,0A -，()3,0B (2)存在，点D 的坐标为()2,1或【分析】（1）分别令0y =和x （2）先求得平移后的抛物线L 角线时，根据矩形的性质求解即可．【详解】（1）解：令0y =，则解得11x =-，23x =，当AD 为对角线时，连接AC ，过点 ()1,0A -，()0,1C -，∴1OA OC ==，∴45OCA ∠=︒∴45OCG ∠=︒∴1OG OC ==，∴()1,0G ．设CG 所在直线解析式为y kx =+将()0,1C -，()1,0G 代入得，⎧⎨⎩解得11k b =⎧⎨=-⎩，∴CG 所在直线解析式为1y x =-当2x =时，1211y x =-=-=．∴()2,1D ．当AD 为边时，同理过点A 作AC 易得AH 所在直线解析式为y =当AC 为对角线时，DE 也为对角线，∴此种情况不存在．(1)求抛物线的表达式；(2)若点P 为第一象限内抛物线上的一点，设PBC 的面积为S ，求S 坐标；(3)已知M 是抛物线对称轴上一点，在平面内是否存在点N ，使以B 的四边形是矩形？若存在，直接写出N 点坐标；若不存在，请说明理由．【答案】(1)22+3y x x =-+(2)S 最大值为278，315(,)24P (3)存在，点1(2,(317))2N +或1(2,(317))2-或(2,1)-或(4,1)．【分析】（1）运用抛物线交点式解析式求解，设抛物线(1)(y a x x =+解；（2）如图，过点P 作PD AC ⊥，垂足为点D ，交BC 于点E ，设(,P m 的解析式3y x =-+，于是23PE m m =-+，从而13(22S PE OC m ==- 时，S 最大值为278，进而求得315(,)24P ；设2(,23)P m m m -++设直线BC 的解析式为y kx =033k hh =+⎧⎨=⎩，解得13k h =-⎧⎨=⎩∴3y x =-+则点(,3)E m m -+，2PE m =-∴2113(22S PE OC m ==´-+ ∴当32m =时，S 最大值为2782915233344m m -++=-++=∴315(,)24P ；（3）存在．设(1,)M p ，如图，223BC =222(13)(0)CM p p =-+-=如图，当BM 为对角线时，∠222BM CM BC =+，即26p p -+01330n p q +=+⎧⎨+=+⎩解得21n q =-⎧⎨=⎩∴点(2,1)N -如图，当CM 为对角线时，MBC ∠222BM BC CM +=，即26p p -+(1)求抛物线的对称轴方程；(2)若点P 满足PAB PBA ∠=∠，求点P 的坐标；(3)设M 是抛物线的对称轴上一点，N 是坐标平面内一点，正方形的面积．【答案】(1)32x =-(2)()51,51P --+(3)正方形AMPN 的面积为172或372【分析】（1）由4y x =+可知()4,0A -，()0,4B ，进而求得抛物线解析式为即可得抛物线的对称轴方程；（2）由题意可知PAB PBA ∠=∠，可知PA PB =，进而值OP 其与AB 交于点Q ，可得()2,2Q -，可求得OP 的解析式为则90PDM ACM ∠=∠=︒∴DPM PMD PMD ∠+∠=∠∴(AAS PDM MCA △≌△∴PD MC =，MD AC =，∵()4,0A -，3,02C ⎛⎫- ⎪⎝⎭，∴35422MD AC ==-=，则90PEM ACM ∠=∠=︒∴EPM PME PME ∠+∠=∠∴(AAS PEM MCA △≌△∴PE MC =，ME AC =，∵()4,0A -，3,02C ⎛⎫- ⎪⎝⎭，∴35422ME AC ==-=，则P y CE MC ME ==+=即：32P x m =-，P y m =-(1)求A ，B ，C 三点的坐标，并直接写出直线(2)在点P 的运动过程中，求使四边形(3)点N 为平面内任意一点，在（2N 为顶点的四边形是正方形？若存在，请直接写出点【答案】(1)()1,0A -，()3,0B ，C (2)32m =-(3)()1221,2Q +，2252,2Q ⎛+ ⎝【分析】（1）分别令0y =，0x =，可求出点∵()3,0B ，()0,3C ，∴3OB OC ==，∴BOC 是等腰直角三角形，∴点()221,2Q +，∴()22132322EQ =+--=-∴PE EQ =，此时点()221,2Q +使得以P ，E 如图，过点E 作EQ PM ⊥于点Q ，过点由（2）得：45BED ∠=︒，∵PM BC ∥，∴45BED DPQ ∠=∠=︒，∴PEQ ，PSQ 是等腰直角三角形，∴此时点Q 使得以P ，E ，Q ，N 为顶点的四边形是正方形；∴132222PS SE PE -===，∴点5232,12S ⎛⎫-- ⎪ ⎪⎝⎭，对于321y x =-++，当5212y =-时，222x =+，(1)求抛物线的解析式；(2)点E 在第一象限内，过点E 作EF y ∥轴，交BC 于点F ，作EH 点H 在点E 的左侧，以线段,EF EH 为邻边作矩形EFGH ，当矩形求线段EH 的长；(3)点M 在直线AC 上，点N 在平面内，当四边形OENM 是正方形时，请直接写出点标．【答案】(1)抛物线的解析式为2142y x x =-++；(2)4EH =；(3)点N 的坐标为()44，或7322⎛⎫- ⎪⎝⎭，．【分析】（1）利用待定系数法即可求解；（2）先求得直线BC 的解析式为4y x =-+，设2142x E x x ⎛ ⎝-++，对称性质求得21422H x x x ⎛⎫- ⎪+⎝-+⎭，，推出2122GH EF x -=-+矩形周长公式列一元二次方程计算即可求解；（3）先求得直线AC 的解析式为24y x =+，分别过点M 、E 作90OPE MQO ∠=∠=︒，90OEP ∠=︒∴OEP MOQ ≌△△，∴PE OQ =，PO MQ =，设2142m E m m ⎛⎫ ⎪⎝-++⎭，，∴PE OQ m ==-，12P m O M Q ==-∵点M 在直线AC 上，∴244212m m m -⎛⎫=+ ⎪⎝⎭-，解得m =当4m =时，()04M ，，()40E ，，即点M 与点C 重合，点E 与点B 重合时，四边形当1m =-时，512M ⎛⎫-- ⎪⎝⎭，，512E ⎛- ⎝，点O 向左平移52个单位，再向下平移则点E 向左平移52个单位，再向下平移∴551122N ⎛⎫--- ⎪⎝⎭，，即7322N ⎛⎫- ⎪⎝⎭，．课后训练(1)求抛物线的解析式；(2)如图2，点P 、Q 为直线BC 下方抛物线上的两点，点Q 的横坐标比点过点P 作PM y ∥轴交BC 于点M ，过点Q 作QN y ∥轴交BC 于点N ，求值及此时点Q 的坐标；(3)如图3，将抛物线()230y ax bx a =+-≠先向右平移1个单位长度，再向下平移长度得到新的抛物线y '，在y '的对称轴上有一点D ，坐标平面内有一点E D 、E 为顶点的四边形是矩形，请直接写出所有满足条件的点E 的坐标．【答案】(1)抛物线的解析式为2=23y x x --(2)当1a =时，max ()4PM QN +=，()2,3Q -(3)()1,2E --或()5,2-或3171,2⎛⎫-- ⎪ ⎪⎝⎭或3171,2⎛⎫-+ ⎪ ⎪⎝⎭【分析】（1）直接运用待定系数法即可解答；（2）设()2,23P a a a --，则()21,4Q a a +-，进而得到(),3M a a -，(N 出222422(1)4PM QN a a a +=-++=--+，最后根据二次函数的性质即可解答；（3）分以BC 为矩形一边和对角线两种情况，分别根据等腰直角三角形的性质、平移和矩形的判定定理解答即可．【详解】（1）解：把()1,0A -和()3,0B 代入()230y ax bx a =+-≠，得309330a b a b --=⎧⎨+-=⎩，解得1a =，2b =-∴222422(1)4PM QN a a a +=-++=--+∴当1a =时，max ()4PM QN +=∴()2,3Q -．（3）解：由题意可得：()()()222=1213152x y x x x x --'---=---=-，∴y '的对称轴为2x =∵抛物线()230y ax bx a =+-≠与y 轴交于点C ．∴()0,3C -,∵()3,0B ,∴3OC OB ==,45BCO CBO ∠=∠=︒；如图：当BC 为矩形一边时，且点D 在x 轴的下方，过D 作DF y ⊥轴，∵D 在y '的对称轴为2x =，∴2FD =，∴2CF FD ==,325OF =+=,即点()2,5D -，∴点C 向右平移2个单位、向下平移3个单位可得到点D ，则点B 向右平移2个单位、向下平移3个单位可得到()5,3E -；如图：当BC 为矩形一边时，且点D 在x 轴的上方，y '的对称轴为2x =与x 轴交于F ，∵D 在y '的对称轴为2x =，∴2FO =，∴321BF =-=，∵45CBO ∠=︒，即45DBO ∠=︒，∴321BF FD ==-=,即点()2,1D ，∴点B 向左平移1个单位、向上平移1个单位可得到点D ，则点C 向左平移1个单位、向上平移1个单位可得到点()1,2E --；如图：当BC 为矩形对角线时，设∴BC 的中点F 的坐标为32⎛ ⎝∴2322322m d n +⎧=⎪⎪⎨+⎪=⎪⎩，解得：m d =⎧⎨+⎩又∵DE BC =,∴()()22222133d n -+-=+联立173d n d n ⎧-=±⎪⎨+=⎪⎩，解得：∴点E 的坐标为3171,2⎛-- ⎝综上，存在()1,2E --或(5,的四边形是矩形．【点睛】本题主要考查了运用待定系数法求解析式、与几何的综合等知识点，掌握二次函数的性质和矩形的判定定理是解答本题的关键．2．如图，在平面直角坐标系中，抛物线与y 轴交于点C ，点P 为抛物线上的动点．(1)求该抛物线的函数表达式；(2)点D 为直线y x =上的动点，当点P 在第四象限时，求四边形PBDC 面积的最大值及此时点P 的坐标；(3)已知点E 为x 轴上一动点，点Q 为平面内任意一点，是否存在以点P ，C ，E ，Q 为顶点的四边形是以PC 为对角线的正方形，若存在，请直接写出点Q 的坐标，若不存在，请说明理由．【答案】(1)2=23y x x --(2)278，315,24P ⎛⎫- ⎪⎝⎭(3)3333,2⎛⎫+- ⎪ ⎪⎝⎭；3333,2⎛⎫-- ⎪ ⎪⎝⎭；(3,3)-；(3,2)【分析】（1）用待定系数法求函数的解析式即可；（2）作直线BC ，过P 作PH x ⊥轴于点G ，交BC 于点H ．设()2,23P m m m --，则(,3)H m m -，23PH m m =-+，则2139()228BPC S t ∆=--+，当32t =时，BPC △的面积最大值为从而求出此时四边形PBDC 面积的最大值，P 点坐标；（3）设()2,23P m m m --，(,0)E n ，分四种情况画出图形，利用正方形性质求解即可．【详解】（1）解：将(1,0)A -，(3,0)B 代入23y ax bx =+-中，得309330a b a b --=⎧⎨+--⎩，解得12a b =⎧⎨=-⎩．∴该抛物线的函数表达式为2=23y x x --．（2）解：作直线BC ，过P 作PH x ⊥轴于点G ，交BC 于点H ．设直线BC 的表达式为：y kx =+得303k n n +=⎧⎨=-⎩，解得13k n =⎧⎨=-⎩，3y x ∴=-．设()2,23P m m m --，则(,H m m ∵BPC CPH BPHS S S =+△△△∴1122BPC S PH OG PH BG =⋅+⋅△∴(21322BPC S PH OB m =⨯=-+△∴28323272BPC S m ⎛⎫=-+ ⎪⎝-⎭△，∴当32m =时，BPC △面积的最大值为BC 与直线y x =平行，1122DBC OBC S S OB OC ∴==⋅=△△∴四边形PBDC 面积的最大值为当32m =时，2332322y ⎛⎫-⨯- ⎪⎝⎭=315,24P ⎛⎫∴- ⎪⎝⎭（3）解：设()2,23P m m m --，I.如图，当点E 在原点时，即点∵四边形PECQ 为正方形，∴点3(3,)Q -，II.如解图3-2，当四边形PECQ 作PI x ⊥轴，垂足为I ，作QH ⊥又∵90CEO OCE ∠+∠=︒，∴OCE PEO ∠=∠，∴(ASA)OCE PEI ≅ △∴3CO IE ==，22EO IP m ==-同理可得：3QH CO IE ===，∴3OE OI IE m =+=+，HO IO=∴2323m m m +=--，解得：m ∴3332HO IO +==，∴点)33(3,32Q +-，同理可得：PI OE CH ==，IE QH =∴3OE IE IO m =-=+，∴2233m m m =---，解得：m =∴3332HO IO -+==，∴点3,(Q -IV.如解图3-4，当四边形PECQ 为正方形时，同理可得：PI OE CH ==，EI HQ =∴2323m m m -=--，解得：m =∴2HO IO ==，∴点(3,2)Q ，综上所述：点Q 坐标为3333,2⎛+- ⎝【点睛】此题重点考查二次函数的图象与性质、数解析式、正方形性质、全等三角形的判定与性质、一元二次方程的解法、数形结合与分类讨论数学思想的运用等知识与方法，此题综合性强，难度较大，属于考试压轴题．3．如图，抛物线212y x bx c =++与物线交于A 、D 两点，与y 轴交于点综上所述，341,22N ⎛⎫+ ⎪ ⎪⎝⎭或341,22N ⎛- ⎝【点睛】本题考查了待定系数法求解析式，面积问题，平行四边形的性质，熟练掌握是二次函数的性质解题的关键．4．在平面直角坐标系中，抛物线2y ax =(1)求抛物线的表达式；(2)若直线x m =与x 轴交于点求出抛物线上点M 的坐标；(3)若点P 为抛物线y ax =位长度后，Q 为平移后抛物线上一动点，在（构成平行四边形？若能构成，求出【答案】(1)223y x x =-++(2)315,24⎛⎫ ⎪⎝⎭(3)1(2-，15)4或3(2-，7)4或【分析】（1）利用待定系数法，即可求出抛物线的表达式；（2）由“直线x m =与x 轴交于点的坐标，进而可得出AN 再利用二次函数的性质，即可求出（3）利用平移的性质，可得出平移后抛物线的表达式为点的坐标特征，可求出点点P 的坐标为(1,)m ，点Q 线三种情况考虑，由平行四边形的对角线互相平分，可得出关于得出n 值，再将其代入点【详解】（1）解：将(1,0)-09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得：∴抛物线的表达式为y =-（2） 直线x m =与x 轴交于点∴点M 的坐标为2(,m m -。

二次函数专题复习—平行四边形存在性问题
《平行四边形存在性问题》教学设计
课题平行四边形存在性问题
解读理念面向全体学生，着眼于学生的中考，使学生会解决动点产生的平行四边形问题。

学情分析
学生对于平行四边形会按三种情况讨论，但这类问题涉及知识面多，很多学生求不出最后结果，这就需要教师进行必要的引导，帮助分析，寻找解决问题的策略。

教材分析内容标准
一、按情况分类
二、根据分类列方程组
三、根据点的坐标画图
教学目标
情感态度价值
观目标
培养学生观察、思考、归纳的良好思维习惯能力目标经历动点产生的平行四边形作图过程，
明确“动中求静”的解题策略。

知识目标理解和掌握动点产生的平行四边形问题
中所涉及的平行四边形的性质，二次函数性
质，方程等数学知识。

教学资源 1.北师大版九年级中考专题
2.课件
教学重点根据分类情况列方程
教学难点根据二次函数、中点坐标公式用所学知识求解。

方法解读教学方法启发式、探究式、参与式教学
教学准备1.把握教材，了解学生的知识基础和思维层次.
2.教师搜集相关资料，制作多媒体课件.。