离散数学05任务

第二篇集合论第四章集合及其运算4.1 集合的基本概念容提要4.1.1集合及其元素集合是一些确定的、作为整体识别的、互相区别的对象的总体。

组成集合的对象称为集合的成员或元素（member）。

通常用一对“{ }”把集合的元素括起来，表示一个集合。

元素对于集合的隶属关系是集合论的另一基本概念。

即当对象a是集合A的元素时，称元素a属于集合A，记为a∈A当对象a不是集合A的元素时，称a不属于A，记为⌝(a∈A)或a∉A对任何对象a和任何集合A，或者a∈A或者a∉A,两者恰居其一。

这正是集合对其元素的“确定性”要求。

定义4．1空集和只含有有限多个元素的集合称为有限集（finite sets），否则称为无限集（infinite sets）。

有限集合中元素的个数称为基数（cardina lit y）（无穷集合的基数概念将在以后重新严格定义）。

集合A的基数表示为|A|。

4.1.2 外延公理、概括公理和正规公理集合论依赖于三大基本原理：外延公理（extensionality axiom）、概括公理（comprehension axiom）和正规公理（regularity axiom）。

它们从根本上规定了集合概念的意义。

外延公理：两个集合A和B相等当且仅当它们具有相同的元素。

即对任意集合A，B,A=B ↔∀x(x∈A↔x∈B)外延公理事实上刻划了集合的下列特性：集合元素的“相异性”、“无序性”，及集合表示形式的不唯一性。

概括公理: 对任意个体域，任一谓词公式都确定一个以该域中的对象为元素的集合。

即对给定个体域U，对任意谓词公式P(x)，存在集合S，使得S＝{x ⎢x∈U∧P(x)}概括公理规定了集合元素的确定性,以及集合的描述法表示的理论依据，它还规定了空集的存在性。

正规公理：不存在集合A1，A2, A3，…，使得…∈A3 ∈ A2 ∈A1正规公理的一个自然推论是：对任何集合A，{A}≠A（否则有…∈A∈A∈A）。

从而规定了集合{A}与A的不同层次性,因而正规公理也就规定了集合不能是自己的元素。

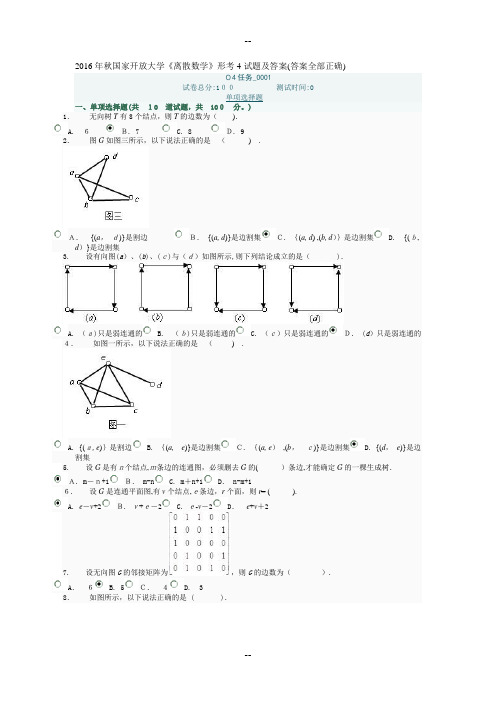
2016年秋国家开放大学《离散数学》形考4试题及答案(答案全部正确)０4任务_0001试卷总分:1００测试时间:0单项选择题一、单项选择题(共１0 道试题，共10０分。

)1．无向树T有8个结点，则T的边数为（)．A. ６Ｂ. 7 C. 8 Ｄ. 92．图G如图三所示，以下说法正确的是（).Ａ．{(a，ｄ)}是割边Ｂ．{(a, d)}是边割集Ｃ. ｛(a, d) ,(b, d）｝是边割集 D. {(ｂ, d）}是边割集3. 设有向图(a）、(b)、(ｃ)与（ｄ）如图所示,则下列结论成立的是（ )．A. （ａ)只是弱连通的B. （ｂ)只是弱连通的C. （ｃ）只是弱连通的Ｄ． (d）只是弱连通的４．如图一所示，以下说法正确的是（).A. {(ａ, e)｝是割边B. ｛(a,e)}是边割集Ｃ. ｛(a, e）,(b，ｃ)}是边割集 D. {(d，e)}是边割集5. 设G是有ｎ个结点,ｍ条边的连通图，必须删去G的(）条边,才能确定G的一棵生成树．Ａ. m－ｎ+1Ｂ． m-n C. m＋n+1D． n-m+1６. 设G是连通平面图,有v个结点,ｅ条边，r个面，则r= ().A. e－v+2Ｂ. ｖ+ｅ－2 C. ｅ-v－2D．e+v＋27. 设无向图G的邻接矩阵为，则G的边数为（）.A．６ B. 5Ｃ．４ D. 38．如图所示，以下说法正确的是 ( )．A. ｅ是割点B. {a，ｅ}是点割集C．｛ｂ, e}是点割集D．｛d}是点割集9. 无向简单图Ｇ是棵树，当且仅当（).A. Ｇ连通且边数比结点数少１B. G连通且结点数比边数少1C. G的边数比结点数少１D. Ｇ中没有回路．10．以下结论正确的是( ).Ａ. 无向完全图都是欧拉图 B. 有n个结点n-1条边的无向图都是树C. 无向完全图都是平面图D. 树的每条边都是割边0４任务＿０002试卷总分:１00 测试时间：0单项选择题一、单项选择题（共10 道试题，共1０0 分。

20春国家开放⼤学离散数学形考任务5资料参考答案离散数学形考任务5单项选择题
题⽬1
下列公式( A )为重⾔式．
选择⼀项：
A.
B.
C.
D.
题⽬2
下列等价公式成⽴的为( A )．
选择⼀项：
A. ┐P∧P┐Q∧Q
B. ┐P∨P Q
C. P∧Q P∨Q
D. ┐Q→P P→Q
题⽬3
下列等价公式成⽴的为( D )．
选择⼀项：
A. Q→(P∨Q)┐Q∧(P∨Q)
B. ┐P∧┐Q P∨Q
C. ┐P∨(P∧Q)Q
D. P→(┐Q→P)┐P→(P→Q)
题⽬4
下列公式中( C )为永真式．
选择⼀项：
A.
B.
C.
D.
题⽬5
前提条件的有效结论是( C )．
选择⼀项：
A. ┐P
B. P
C. ┐Q
D. Q
题⽬6
设命题公式G：，则使公式G取真值为1的P，Q，R赋值分别是( B )．选择⼀项：
A. 0, 0, 0
B. 1, 0, 0
C. 0, 1, 0
D. 0, 0, 1
题⽬7
设个体域D是整数集合，则命题的真值是（ C ）．选择⼀项：
A. F
B. 不确定
C. T
D. 以上说法都不是
题⽬8
设个体域为整数集，则公式的解释可为( A )．选择⼀项：
A. 对任⼀整数x存在整数y满⾜x+y=0
B. 存在⼀整数x对任意整数y满⾜x+y=0
C. 存在⼀整数x有整数y满⾜x+y=0
D. 任⼀整数x对任意整数y满⾜x+y=0
题⽬9。

习题5.11.设A=⎨a,b,c⎬，B=⎨1,2,3⎬，试说明下列A到B二元关系，哪些能构成A到B的函数？⑴f1=⎨<a,1>,<a,2>,<b,1>,<c,3>⎬⑵f2=⎨<a,1>,<b,1>,<c,1>⎬⑶f3=⎨<a,2>,<c,3>⎬⑷f4=⎨<a,3>,<b,2>,<c,3>,<b,3>⎬⑸f5=⎨<a,2>,<b,1>,<b,2>⎬解：⑴不能构成函数。

因为<a,1>∈f1且<a,2>∈f1⑵能构成函数⑶不能构成函数。

因为dom f3≠A⑷不能构成函数。

因为<b,2>∈f4且<b,3>∈f4⑸能构成函数。

2.试说明下列A上的二元关系，哪些能构成A到A的函数？⑴A=N(N为自然数集合)，f1=⎨<a,b>| a∈A∧b∈A∧a＋b＜10⎬⑵A=R(R为实数集合)，f2=⎨<a,b>| a∈A∧b∈A∧b=a2⎬⑶A=R(R为实数集合)，f3=⎨<a,b>| a∈A∧b∈A∧b2=a⎬⑷A=N(N为自然数集合)，f4=⎨<a,b>| a∈A∧b∈A∧b为小于a的素数的个数⎬⑸A=Z(Z为整数集合)，f5=⎨<a,b>| a∈A∧b∈A∧b=|2a|＋1⎬解：⑴不能构成函数。

由于1+1＜10且1+2＜10，所以<1,1>∈f1且<1,2>∈f1。

⑵能构成函数。

⑶不能构成函数。

由于12=1且(-1)2=1，所以<1,1>∈f3且<1,-1>∈f3。

⑷能构成函数。

⑸能构成函数。

3. 回答下列问题。

⑴设A=⎨a,b⎬，B=⎨1,2,3⎬。

求B A，验证|B A|= |B||A|。

第十四章部分课后习题参考答案5、设无向图G有10条边，3度与4度顶点各2个，其余顶点的度数均小于3,问G至少有多少个顶点？在最少顶点的情况下，写出度数列、厶(G)、.(G)。

解：由握手定理图G的度数之和为：2 10=203度与4度顶点各2个，这4个顶点的度数之和为14度。

其余顶点的度数共有6度。

其余顶点的度数均小于3,欲使G的顶点最少，其余顶点的度数应都取2,所以，G至少有7个顶点,出度数列为3,3,4,4,2,22 .1(G) = 4「(G) = 2 .7、设有向图D的度数列为2, 3, 2, 3,出度列为1, 2，1，1，求D的入度列，并求厶(D),、：(D)，：(D)「.(D),.厂(D),解：D的度数列为2, 3, 2, 3,出度列为1, 2, 1, 1, D的入度列为1,1,1,2..：(D) =3,、(D) =2, ：(D) =2,、• (D) = 1,.厂(D) = 2,、_(D) = 18设无向图中有6条边，3度与5度顶点各1个，其余顶点都是2度点，问该图有多少个顶点？解：由握手定理图G的度数之和为：2 6=12设2度点x个，则3 1 5 1 2x =12 , x=2，该图有4个顶点.14、下面给出的两个正整数数列中哪个是可图化的？对可图化的数列，试给出3种非同构的无向图，其中至少有两个时简单图。

(1) 2,2,3,3,4,4,5 (2) 2,2,2,2,3,3,4,4解：(1) 2+2+3+3+4+4+5=23 是奇数，不可图化；⑵2 + 2+2+2+3+3+4+4=16,是偶数，可图化；18、设有3个4阶4条边的无向简单图G1、G2、G3,证明它们至少有两个是同构的。

证明：4阶4条边的无向简单图的顶点的最大度数为3,度数之和为8,因而度数列为2, 2, 2, 2;3, 2, 2, 1; 3, 3, 1, 1。

但3, 3, 1, 1对应的图不是简单图。

所以从同构的观点看，4阶4条边的无向简单图只有两个：所以，G i 、G 2、G 3至少有两个是同构的。

离散数学（第五版）清华大学出版社第5章习题解答5.1 A:③; B:⑥; C:⑧; D:⑩; E:⑨分析S 为n 元集,那么S×S有n2个元素.S 上的一个二元运算就是函数n2n2f:S×S→S.这样的函数有n 个.因此{a,b}上的二元运算有n =16个.下面说明通过运算表判别二元运算性质及求特导元素的方法.1 °交换律若运算表中元素关于主对角线成对称分布,则该运算满足交换律.2 °幂等律设运算表表头元素的排列顺序为x1,x2,Lxn,如果主对角线元素的排列也为x1,x2,Lxn,则该运算满足幂等律.其他性质,如结合律或者涉及到两个运算表的分配律和吸收律,在运算表中没有明显的特征,只能针对所有可能的元素x,y,z等来验证相关的算律是否成立.3 °幺元e设运算表表头元素的排列顺序为x1.,x2,Lxn,如果元素xi所在的行和列的元素排列顺序也是x1,x2,Lxn,则xi为幺元.4 °零元θ.如果元素xi所在的行和列的元素都是xi,则xi是零元.5 °幂等元.设运算表表头元素的排列顺序为x1,x2,Lxn,如果主对角线上第i个元素恰为xii∈{1,2,L,n}那么xi是幂等元.易见幺元和零元都是幂等元.6 °可逆元素及其逆元.设xi为任意元素,如果xi所在的行和列都有幺元,并且这两个幺元关于主对角线成对称分布,比如说第i行第j列和第j行第i列的两个位置,那么xj与xi互为逆元.如果xi所在的行和列具有共同的幺元,则幺元一定在主对角线上,那么xi的逆元就是xi自己.如果xi所在的和地或者所在的列没有幺元,那么x 不是可逆元素.不难看出幺元e一定是可逆元素,且e−1=e;而i零元θ不是可逆元素.以本题为例,f1,f2,f3的运算表是对称分布的,因此,这三个运算是可交换的,62而f4不是可交换的.再看幂等律.四个运算表表头元素排列都是a,b,其中主对角线元素排列为a,b的只有f4,所以, f4遵从幂等律.下面考虑幺元.如果某元素所在的行和列元素的排列都是a,b,该元素就是幺元.不难看出只有f2中的a满足这一要求,因此,a 是f2的幺元,其他三个运算都不存在幺元.最后考虑零元.如果a所在的行和列元素都是a,那么a就是零元;同样的,若b所在的行和列元素都是b,那么b 就是零元.检查这四个运算表,f1中的a满足要求,是零元,其他运算都没有零元.在f4的运算表中,尽管a和b的列都满足要求,但行不满足要求.因而f4中也没有零元.5.2 A:①; B:③; C:⑤; D:⑦; E:⑩分析对于用解析表达式定义的二元运算°和*,差别它们是否满足交换律,结合律,幂等律,分配律和吸收律的方法总结如下:任取x,y,根据°运算的解析表达式验证等式xoy=yox是否成立.如果成立°运算就满足交换律.2 ° °运算的地合律任取x,y,z根据°运算的解析表达式验证等式(xoy)oz=xo(yoz)是否成立. 如果成立, °运算就是可结合的.3 ° °运算的幂等律任取x,根据°运算的解析表达式验证等式xox=x是否成立.如果成立,°运算满足幂等律.4 ° °运算对*运算的分配律任取x,y,z , 根据°和* 运算的解析表达式验证等式xo(y*z)=(xoy)*(xoz)和(y*z)ox=(yox)*(zox)是否成立。

国家开放大学电大本科《离散数学》网络课形考网考作业及答案100%通过考试说明：2020年秋期电大把该网络课纳入到“国开平台”进行考核，该课程共有5个形考任务，针对该门课程，本人汇总了该科所有的题，形成一个完整的标准题库，并且以后会不断更新，对考生的复习、作业和考试起着非常重要的作用，会给您节省大量的时间。

做考题时，利用本文档中的查找工具，把考题中的关键字输到查找工具的查找内容框内，就可迅速查找到该题答案。

本文库还有其他网核及教学考一体化答案，敬请查看。

课程总成绩 = 形成性考核×30% + 终结性考试×70%形考任务1单项选择题题目1若集合A＝{ a，{a}，{1，2}}，则下列表述正确的是（）．选择一项：题目2若集合A＝{2，a，{ a }，4}，则下列表述正确的是( )．选择一项：题目3设集合A={1 , 2 , 3 , 4}上的二元关系R={<1, 1>，<2, 2>，<2, 3>，<4, 4>}，S={<1, 1>，<2, 2>，<2, 3>，<3, 2>，<4, 4>}，则S是R的（）闭包．选择一项：A. 传递B. 对称C. 自反和传递D. 自反题目4设集合A={1, 2, 3}，B={3, 4, 5}，C={5, 6, 7}，则A∪B–C =( )．选择一项：A. {1, 2, 3, 5}B. {4, 5, 6, 7}C. {2, 3, 4, 5}D. {1, 2, 3, 4}题目5如果R1和R2是A上的自反关系，则R1∪R2，R1∩R2，R1-R2中自反关系有（）个．选择一项：A. 1B. 3C. 2D. 0题目6集合A={1, 2, 3, 4}上的关系R={<x，y>|x=y且x, y∈A}，则R的性质为（）．选择一项：A. 不是对称的B. 反自反C. 不是自反的D. 传递的题目7若集合A={1，2}，B={1，2，{1，2}}，则下列表述正确的是( )．选择一项：题目8设A={a，b，c}，B={1，2}，作f：A→B，则不同的函数个数为（）．选择一项：A. 3B. 2C. 8D. 6题目9设A={1, 2, 3, 4, 5, 6, 7, 8}，R是A上的整除关系，B={2, 4, 6}，则集合B的最大元、最小元、上界、下界依次。