数学：4.6 探索三角形相似的条件⑷ 同步练习集(北师大版八年级下)

2022-2023学年北师大版九年级数学上册《4.4探索三角形相似的条件》同步达标测试题（附答案）一．选择题（共12小题，满分48分）1．图形中，每个小网格均为正方形网格，带阴影部分的三角形中与如图△A1B1C1相似的是（）A．B．C．D．2．如图，在△ABC中，D，E两点分别在BC，AC上，且AD平分∠BAC，若∠ABE＝∠C，BE与AD相交于点F，则图中与△ABD相似的是（）A．△ABC B．△ABF C．△BFD D．△AEF3．如图，在△ABC中，点D、E分别在AB、AC边上，DE与BC不平行，那么下列条件中，不能判断△ADE∽△ACB的是（）A．∠ADE＝∠C B．∠AED＝∠B C．＝D．＝4．已知△ABC三边长是，，2，与△ABC相似的三角形三边长可能是（）A．1，，B．1，，C．1，，D．1，，5．如图，D是△ABC边AB上一点，添加一个条件后，仍然不能使△ACD∽△ABC的是（）A．∠ACB＝∠ADC B．∠ACD＝∠ABC C．D．6．已知Rt△ABC中，∠C＝90°，∠A≠∠B，点P是边AC上一点（不与A、C重合），过P点的一条直线与△ABC的边相交，所构成的三角形与原三角形相似，这样的直线有（）条．A．1B．2C．3D．47．如图，△ABC中，点D、E分别在AB、AC边上，则下列条件中，不一定能使△AED∽△ABC的是（）A．∠2＝∠B B．∠1＝∠C C．D．8．如图：点D在△ABC的边AB上，连接CD，下列条件：①∠ACD＝∠B；②∠ADC＝∠ACB；③AC2＝AD•AB；④AB•CD＝AC•BC．其中能判定△ACD∽△ABC的共有（）A．1个B．2个C．3个D．4个9．如图，在△ABC中，点D、E分别在边AB、AC上，则在下列四个条件中：①∠AED＝∠B；②DE∥BC；③；④AD•BC＝DE•AC，能满足△ADE∽△ACB的条件有（）A．1个B．2个C．3个D．4个10．如图，在△ABC中，AB＝AC＝8，BC＝6，点P从点B出发以1个单位/s的速度向点A运动，同时点Q从点C出发以2个单位/s的速度向点B运动．当以B，P，Q为顶点的三角形与△ABC相似时，运动时间为（）A．s B．s C．s或s D．以上均不对11．如图，在△ABC中，点D、E分别在边AB、AC上，则在下列五个条件中：①∠AED＝∠B；②DE∥BC；③＝；④AD•BC＝DE•AC；⑤∠ADE＝∠C，能满足△ADE∽△ACB的条件有（）A．1个B．2个C．3个D．4个12．如图，正方形ABCD中，F为AB上一点，E是BC延长线上一点，且AF＝EC，连接EF，DE，DF，M是FE中点，连接MC，设FE与DC相交于点N．则4个结论：①DN ＝DG；②△BFG∽△EDG∽△BDE；③CM垂直BD；④若MC＝，则BF＝2；正确的结论有（）个A．4B．3C．2D．1二．填空题（共4小题，满分20分）13．如图，∠B＝∠D，请你添加一个条件，使得△ABC∽△ADE，这个条件可以是．14．如图，在边长为4的正方形ABCD中，点E、F分别是BC、CD的中点，DE、AF交于点G，AF的中点为H，连接BG、DH．给出下列结论：①AF⊥DE；②DG＝；③HD∥BG；④△ABG∽△DHF．其中正确的结论有．（请填上所有正确结论的序号）15．如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC＝3AD，AB＝3AE，点F为BC边上一点，添加一个条件：，可以使得△FDB与△ADE 相似．（只需写出一个）16．如图，在△ABC中，P为AB上一点，在下列四个条件中：①∠ACP＝∠B；②∠APC ＝∠ACB；③AC2＝AP•AB；④AB•CP＝AP•CB，能满足△APC与△ACB相似的条件是（只填序号）．三．解答题（共8小题，满分52分）17．已知：如图，点C，D在线段AB上，△PCD是等边三角形，且AC＝1，CD＝2，DB ＝4．求证：△ACP∽△PDB．18．如图，已知∠1＝∠2，∠AED＝∠C，求证：△ABC∽△ADE．19．如图，AB•AE＝AD•AC，且∠1＝∠2，求证：△ABC∽△ADE．20．如图，点E是四边形ABCD的对角线BD上一点，且∠BAC＝∠BDC＝∠DAE．求证：△ABE∽△ACD．21．如图，在△ABC中，BD平分∠ABC，交AC于点D，点E是AB上一点，连接DE，BD2＝BC•BE．证明：△BCD∽△BDE．22．如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以4cm/s的速度移动．如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？23．如图，已知AD•AC＝AB•AE．求证：△ADE∽△ABC．24．如图，在△ABC中，AB＝AC＝1，BC＝，在AC边上截取AD＝BC，连接BD．（1）通过计算，判断AD2与AC•CD的大小关系；（2）求∠ABD的度数．参考答案一．选择题（共12小题，满分48分）1．解：因为△A1B1C1中有一个角是135°，选项中，有135°角的三角形只有B，且满足两边成比例夹角相等，故选：B．2．解：在△ABE与△ACB中，∠ABE＝∠C，∠BAE＝∠CAB，∴△ABE∽△ACB，∴∠AEB＝∠ABC，∵AD平分∠BAC，∴∠BAD＝∠EAF，∴△ABD∽△AEF．故选：D．3．解：∵∠DAE＝∠CAB，∴当∠ADE＝∠C时，△ADE∽△ACB；当∠AED＝∠B时，△ADE∽△ACB；当＝时，△ADE∽△ACB．故选：C．4．解：∵△ABC三边长是，，2，∴△ABC三边长的比为：2：＝1：：，∴△ABC相似的三角形三边长可能是1，，，故选：A．5．解：A、当∠ACB＝∠ADC时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；B、当∠ACD＝∠ABC时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；C、当＝时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；D、当＝时，无法得出△ACD∽△ABC，故此选项符合题意；故选：D．6．解：如图，过点P作AB的平行线，或作BC的平行线，或作AB的垂线，或作∠CPD＝∠B，共4条直线，故选：D．7．解：∠A＝∠A，A、若添加∠2＝∠B，可利用两角法判定△AED∽△ABC，故本选项错误；B、若添加∠1＝∠C，可利用两角法判定△AED∽△ABC，故本选项错误；C、若添加＝，可利用两边及其夹角法判定△AED∽△ABC，故本选项错误；D、若添加＝，不能判定△AED∽△ABC，故本选项正确；故选：D．8．解：①∠A＝∠A，∠ACD＝∠B，∴△ACD∽△ABC，②∵∠A＝∠A，∠ADC＝∠ACB，∴△ACD∽△ABC，③∵AC2＝AD•AB，∴，∵∠A＝∠A，∴△ACD∽△ABC，④条件不符合，不能判定△ACD∽△ABC，故选：C．9．解：①∠B＝∠AED，∠A＝∠A，则可判断△ADE∽△ACB，故①符合题意；②DE∥BC，则△ADE∽△ABC，故②不符合题意，③，且夹角∠A＝∠A，能确定△ADE∽△ACB，故③符合题意；④由AD•BC＝DE•AC可得＝，此时不确定∠ADE＝∠ACB，故不能确定△ADE∽△ACB，故④不符合题意，故选：B．10．解：设运动时间为t秒．BP＝t，CQ＝2t，BQ＝BC﹣CQ＝6﹣2t，当△BAC∽△BPQ，＝，即＝，解得t＝；当△BCA∽△BPQ，＝，即＝，解得t＝，综上所述，当以B，P，Q为顶点的三角形与△ABC相似时，运动时间为s或s，故选：C．11．解：①∠B＝∠AED，∠A＝∠A，则可判断△ADE∽△ACB，故①符合题意；②DE∥BC，则△ADE∽△ABC，故②不符合题意，③，且夹角∠A＝∠A，能确定△ADE∽△ACB，故③符合题意；④由AD•BC＝DE•AC可得，此时不确定∠ADE＝∠ACB，故不能确定△ADE∽△ACB；故④不符合题意，⑤∠ADE＝∠C，∠A＝∠A，则可判断△ADE∽△ACB，故⑤符合题意；故选：C．12．解：正方形ABCD中，AD＝CD，在△ADF和△CDE中，，∴△ADF≌△CDE（SAS），∴∠ADF＝∠CDE，DE＝DF，∴∠EDF＝∠FDC+∠CDE＝∠FDC+∠ADF＝∠ADC＝90°，∴∠DEF＝45°，∵∠DGN＝45°+∠FDG，∠DNG＝45°+∠CDE，∠FDG≠∠CDE，而∠FDG与∠CDE不一定相等，∴∠DGN与∠DNG不一定相等，故判断出①错误；∵△DEF是等腰直角三角形，∵∠ABD＝∠DEF＝45°，∠BGF＝∠EGD（对顶角相等），∴△BFG∽△EDG，∵∠DBE＝∠DEF＝45°，∠BDE＝∠EDG，∴△EDG∽△BDE，∴△BFG∽△EDG∽△BDE，故②正确；连接BM、DM．∵△AFD≌△CED，∴∠FDA＝∠EDC，DF＝DE，∴∠FDE＝∠ADC＝90°，∵M是EF的中点，∴MD＝EF，∵BM＝EF，∴MD＝MB，在△DCM与△BCM中，，∴△DCM≌△BCM（SSS），∴∠BCM＝∠DCM，∴CM在正方形ABCD的角平分线AC上，∴MC垂直平分BD；故③正确；过点M作MH⊥BC于H，则∠MCH＝45°，∵MC＝，∴MH＝＝1，∵M是EF的中点，BF⊥BC，MH⊥BC，∴MH是△BEF的中位线，∴BF＝2MH＝2，故④正确；综上所述，正确的结论有②③④．故选：B．二．填空题（共4小题，满分20分）13．解：∵∠B＝∠D，∴添加∠C＝∠E或∠BAC＝∠DAE或∠BAD＝∠CAE或＝，可证△ABC∽△ADE．故答案为：∠C＝∠E或∠BAC＝∠DAE或∠BAD＝∠CAE或＝．14．解：∵四边形ABCD为正方形，∴∠ADC＝∠BCD＝90°，AD＝CD，∵E和F分别为BC和CD中点，∴DF＝EC＝2，∴△ADF≌△DCE（SAS），∴∠AFD＝∠DEC，∠F AD＝∠EDC，∵∠EDC+∠DEC＝90°，∴∠EDC+∠AFD＝90°，∴∠DGF＝90°，即DE⊥AF，故①正确；∵AD＝4，DF＝CD＝2，∴AF＝，∴DG＝AD×DF÷AF＝，故②错误；∵H为AF中点，∴HD＝HF＝AF＝，∴∠HDF＝∠HFD，∵AB∥DC，∴∠HDF＝∠HFD＝∠BAG，∵AG＝＝，AB＝4，∴，∴△ABG∽△DHF，故④正确；∴∠ABG＝∠DHF，而AB≠AG，则∠ABG和∠AGB不相等，故∠AGB≠∠DHF，故HD与BG不平行，故③错误；故答案为：①④．15．解：DF∥AC，或∠BFD＝∠A．理由：∵∠A＝∠A，＝＝，∴△ADE∽△ACB，∴①当DF∥AC时，△BDF∽△BAC，∴△BDF∽△EAD．②当∠BFD＝∠A时，∵∠B＝∠AED，∴△FBD∽△AED．故答案为DF∥AC，或∠BFD＝∠A．16．解：前三项正确，因为他们分别符合有两组角对应相等的两个三角形相似；两组对应边的比相等且相应的夹角相等的两个三角形相似．故相似的条件是①，②，③．三．解答题（共8小题，满分52分）17．证明：∵△PCD是等边三角形，∴∠PCD＝∠PDC＝60°，PC＝CD＝PD＝2，∴∠PCA＝∠PDB＝120°，∵AC＝1，BD＝4，∴，＝，∴＝，∴△ACP∽△PDB．18．证明：∵∠1＝∠2，∴∠1+∠BAE＝∠2+∠BAE，即∠DAE＝∠BAC，∵∠AED＝∠C，∴△ABC∽△ADE．19．证明：如图，∵AB•AE＝AD•AC，∴＝．又∵∠1＝∠2，∴∠2+∠BAE＝∠1+∠BAE，即∠BAC＝∠DAE，∴△ABC∽△ADE．20．解：∵∠BAC＝∠BDC，∠AOB＝∠DOC，∴∠ABE＝∠ACD又∵∠BAC＝∠DAE∴∠BAC+∠EAC＝∠DAE+∠EAC∴∠DAC＝∠EAB∴△ABE∽△ACD．21．证明：∵BD平分∠ABC，∴∠DBE＝∠CBD．∵BD2＝BC•BE，∴，∴△BCD∽△BDE．22．解：设在开始运动后第x秒，△BPQ与△BAC相似，由题意得：AP＝2xcm，PB＝（8﹣2x）cm，BQ＝4x，分两种情况考虑：当∠BPQ＝∠C，∠B＝∠B时，△PBQ∽△CBA，∴，即解得：x＝0.8，当x＝0.8秒时，△BPQ与△BAC相似；当∠BPQ＝∠A，∠B＝∠B时，△BPQ∽△BAC，∴，即，解得：x＝2，当x＝2秒时，△BPQ与△BAC相似．综上，当x＝0.8秒或2秒时，△BPQ与△BAC相似．23．证明：∵AD•AC＝AE•AB，∴＝在△ABC与△ADE中∵＝，∠A＝∠A，∴△ABC∽△ADE．24．解：（1）∵AD＝BC，BC＝，∴AD＝，DC＝1﹣＝．∴AD2＝＝，AC•CD＝1×＝．∴AD2＝AC•CD．（2）∵AD＝BC，AD2＝AC•CD，∴BC2＝AC•CD，即．又∵∠C＝∠C，∴△BCD∽△ACB．∴，∠DBC＝∠A．∴DB＝CB＝AD．∴∠A＝∠ABD，∠C＝∠BDC．设∠A＝x，则∠ABD＝x，∠DBC＝x，∠C＝2x．∵∠A+∠ABC+∠C＝180°，∴x+2x+2x＝180°．解得：x＝36°．∴∠ABD＝36°．。

课题：§4.6探索三角形相似的条件（2）【学习目标】掌握三角形相似的判定方法2、3.并能准确运用。

【学习重点】掌握判定方法2、3并能灵活运用.【学前准备】1、什么叫相似三角形?_______________________________________________________。

2、三角形相似的判定方法1___________的两个三角形相似.3、如图，AF ∥CD ,∠1=∠2,∠B =∠D ,你能找出图中几对相似三角形？【师生探究、合作交流】1、 做一做（1）如果△ABC 与△A ′B ′C ′三边对应成比例，那么它们一定相似吗？已知△A ′B ′C ′画△ABC ，使B A AB ''、C B BC ''和A C CA ''都等于定值2①设法比较∠A 与∠A ′的大小、∠B 与∠B ′的大小、∠C 与∠C ′的大小。

②△ABC 与△A ′B ′C ′相似吗？说说你的理由。

③如果B A AB ''、C B BC ''和A C CA ''都等于定值21，△ABC 与△A ′B ′C ′相似吗？ 两个三角形相似。

（2）如果△ABC 与△A ′B ′C ′有一个角对应相等，且有两边对应成比例，那么它们一定相似吗？①如果这个角是这两条边的夹角，那么它们一定相似吗？如图，在△ABC 与△A ′B ′C ′中∠A=∠A ′，````AB AC A B A C =2，比较∠B 与∠B ′的大小（或∠C 与∠C ′的大小），判断△ABC 与△A ′B ′C ′是否相似？②如果两边对应成比例，其中一边的对角对应相等，这两个三角形相似吗？的两个三角形相似。

【小试牛刀】1、下图中△AEB 和△FEC 相似吗？30365445F ECBA2、随堂练习 1、习题4.8 3（做在书上）【小结】1.相似三角形的判定有几种方法？的两个三角形相似。

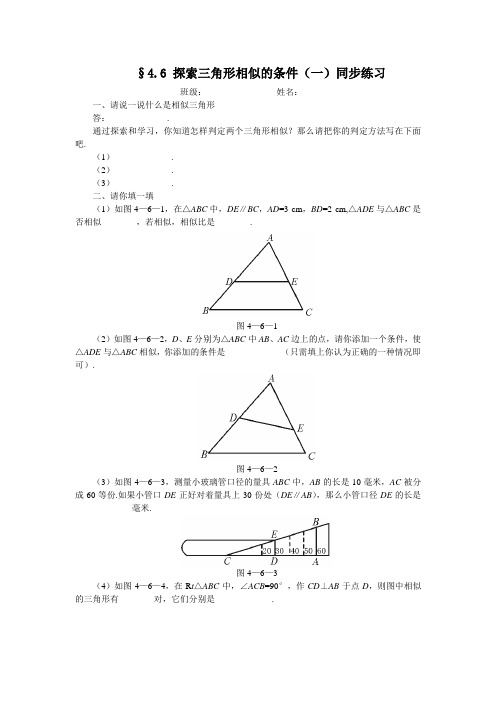
§4.6 探索三角形相似的条件（一）同步练习班级：_______ 姓名：_______一、请说一说什么是相似三角形答：_____________.通过探索和学习，你知道怎样判定两个三角形相似？那么请把你的判定方法写在下面吧.（1）_____________.（2）_____________.（3）_____________.二、请你填一填（1）如图4—6—1，在△ABC中，DE∥BC，AD=3 cm，BD=2 cm,△ADE与△ABC是否相似________，若相似，相似比是________.图4—6—1（2）如图4—6—2，D、E分别为△ABC中AB、AC边上的点，请你添加一个条件，使△ADE与△ABC相似，你添加的条件是_____________（只需填上你认为正确的一种情况即可）.图4—6—2（3）如图4—6—3，测量小玻璃管口径的量具ABC中，AB的长是10毫米，AC被分成60等份.如果小管口DE正好对着量具上30份处（DE∥AB），那么小管口径DE的长是_____________毫米.图4—6—3（4）如图4—6—4，在R t△ABC中，∠ACB=90°，作CD⊥AB于点D，则图中相似的三角形有________对，它们分别是_____________.图4—6—4三、认真选一选（1）下列各组图形中有可能不相似的是（ ） A.各有一个角是45°的两个等腰三角形 B.各有一个角是60°的两个等腰三角形 C.各有一个角是105°的两个等腰三角形 D.两个等腰直角三角形（2）△ABC 和△A ′B ′C ′符合下列条件，其中使△ABC 和△A ′B ′C ′不相似的是（ ）A.∠A =∠A ′=45° ∠B =26° ∠B ′=109°B.AB =1 AC =1.5 BC =2 A ′B ′=4 A ′C ′=2 B ′C ′=3C.∠A =∠B ′ AB =2 AC =2.4 A ′B ′=3.6 B ′C ′=3D.AB =3 AC =5 BC =7 A ′B ′=3 A ′C ′=5 B ′C ′=7（3）如图4—6—5，AB ∥CD ，AD 与BC 相交于点O ，那么在下列比例式中，正确的是（ ）A.AD OACD AB = B.BC OBOD OA = C.OCOBCD AB =D.ODOBAD BC =图4—6—5 图4—6—6（4）如图4—6—6，D 为△ABC 的边AB 上一点，且∠ABC =∠ACD ，AD =3 cm, AB =4 cm ，则AC 的长为（ ）A.2 cmB.3 cmC.12 cmD.23 cm四、用数学眼光看世界图4—6—7如图4—6—7，长梯AB 斜靠在墙壁上，梯脚B 距墙80 cm ，梯上点D 距墙70 cm ，量得BD 长55 cm ，求梯子的长.参考答案§4.6 探索三角形相似的条件（一）一、答：对应角相等、对应边成比例的两个三角形是相似三角形 判定两个三角形相似的方法详见课本，略. 二、（1）相似 3∶5 （2）∠C =∠ADE （或∠B =∠AED 等）（3）5 （4）三 △ACD ∽△ABC △BCD ∽△BAC △ACD ∽△CBD 三、（1）A （2）D （3）C （4）D 四、解：设梯子的长AB 为x cm （如图）由Rt △ADE ∽Rt △ABC 得：ABADBC DE = ∴xx 558070-= 解得：x =440答：梯子的长是440 cm.情感语录1.爱情合适就好，不要委屈将就，只要随意，彼此之间不要太大压力2.时间会把最正确的人带到你身边，在此之前，你要做的，是好好的照顾自己3.女人的眼泪是最无用的液体，但你让女人流泪说明你很无用4.总有一天，你会遇上那个人，陪你看日出，直到你的人生落幕5.最美的感动是我以为人去楼空的时候你依然在6.我莫名其妙的地笑了，原来只因为想到了你7.会离开的都是废品，能抢走的都是垃圾8.其实你不知道，如果可以，我愿意把整颗心都刻满你的名字9.女人谁不愿意青春永驻，但我愿意用来换一个疼我的你10.我们和好吧，我想和你拌嘴吵架，想闹小脾气，想为了你哭鼻子，我想你了11.如此情深，却难以启齿。

数学：4.6 探索三角形相似的条件同步练习集（北师大版八年级下4．6 探索三角形相似的条件⑸一、目标导航巩固三角形相似的方法及综合运用二、基础过关1．已知x1x?y?，则y2x?y的值为（）A．11 B．? C． 3 D． -3332．在比例尺为1∶20的图纸上画出的某个零件的长是32mm，则零件的实际长是（） A． 64m B． 64dm C． 64cm D． 64mm 3．已知C是线段AB 的黄金分割点(AC＞BC），则AC∶BC = ( )A． (5－1)∶2 B．（5 +1）∶2 C．（3－5）∶2 D．（3+5）∶24．如图，E是平行四边形ABCD的边BC的延长线上的一点，连结AE交CD于F，则图中共有相似三角形（）A． 1对 B． 2对 C． 3对 D． 4对(第4题图) (第5题图) (第6题图) (第 7题图) 5．ΔABC中，DE∥BC，且AD∶DB=2∶1，那么DE∶BC等于（） A．2∶1 B．1∶2 C．2∶3 D．3∶26．如图，P是RtΔABC的斜边BC上异于B、C的一点，过点P做直线截ΔABC，使截得的三角形与ΔABC相似，满足这样条件的直线共有（） A． 1条 B． 2条C． 3条 D． 4条7．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．ADAE?ABACCEEA? B．CFFB第1页（共5页）EFCFDEAD??C． D． ABCBBCBD8．如图，ΔABC中，P为AB上一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP?AB；④AB?CP=AP?CB，能满足ΔAPC与ΔA CB相似的条件是（） A．①②③ B．①③④ C．②③④ D．①②④9．如图，ΔADE绕正方形ABCD的顶点A顺时针旋转90°，得ΔABF，连结EF交AB于H，则下列结论错误的是（）A．AE⊥AF B．EF∶AF=2∶1 C． AF2=FH?FE D．FB∶FC=HB∶EC(第8题图) (第9题图) (第10题图)10．如图，在正方形网格上有6个斜三角形：①ΔABC，②ΔBCD，③ΔBDE，④ΔBFG，⑤ΔFGH，⑥ΔEFK．其中②～⑥中，与三角形①相似的是（）A．②③④ B．③④⑤ C．④⑤⑥ D．②③⑥三、能力提升11．已知两数4和8，试写出第三个数，使这三个数中，其中一个数是其余两数的比例中项，第三个数是 (只需写出一个即可)．12．已知D、E分别是ΔABC的边AB、AC上的点，请你添加一个条件，使ΔABC与ΔAED相似．你添加的条件是 (只需添加一个你认为适当的条件即可)．13．如图，锐角三角形ABC的边AB、AC上的高线CE和BF相交于点D，请写出图中的两对相似三角形：(用相似符号连接)．14．下列说法：①所有的等腰三角形都相似；②所有的等边三角形都相似；③所有等腰直角三角形都相似；④所有的直角三角形都相似．其中正确的是 (把你认为正确的说法的序号都填上)．15．如图，已知∠1=∠2，若再增加一个条件就能使结论“AB?ED=AD?BC”成立，则这个条件可以是．第2页（共5页）(第13题图) (第15题图) (第16题图) (第17题图) 三、计算或证明题16．在方格纸中，每个小格的顶点叫做格点．以格点连线为边的三角形叫做格点三角形．如图，请你在4×4的方格纸中，画一个格点三角形A1B1C1，使ΔA1B1C1与格点三角形ABC相似(相似比不为1)．17．请设计一种分法，将如图所示的直角三角形分割成四个小三角形，使得每个小三角形与原三角形都相似(要求画出分割线段，标出能够说明分法的必要记号，不要求写出画法，不要求说明理由)． 18．将两块完全相同的等腰直角三角板摆放成如图所示的样子，假设图中的所有点、线都在同一平面内，回答下列问题： (1)图中共有个三角形．(2)图中有相似(不包括全等)三角形吗？如果有，就把它们一一写出来．19．已知零件的外径为25cm，要求它的厚度x ，需先求出它的内孔直径AB，现用一个交叉卡钳(AC和BD的长相等)去量(如图)，若OA∶OC=OB∶OD=3，CD=7cm．求此零件的厚度x．20．如图，在梯形ABCD中，AD//BC，∠BAD=90°，对角线BD⊥DC．第3页（共5页）(1)ΔABD与ΔDCB相似吗？请说明理由． (2)如果AD=4，BC=9，求BD的长．21．已知：如图所示，D是AC上一点，BE∥AC，AE分别交BD，BC于点F，G，∠1=∠2．则BF是FG、EF的比例中项吗？请说明理由．22．如图，CD是RtΔABC的斜边AB上的高，∠BAC的平分线分别交BC、CD于点E、F． AC?AE=AF?AB吗？说明理由．23． E、F分别是矩形ABCD的边AD、BC的中点，若矩形ABCD∽矩形EABF，AB=1，求矩形ABCD的面积．第4页（共5页）四、聚沙成塔如图，在矩形ABCD中，AB=12�M，BC=6�M，点P沿AB边从点A开始向点B以2�M/s的速度移动；点Q沿DA边从点D开始向点A以1�M/s的速度移动．如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤6），那么⑴当t为何值时，△QAP为等腰直角三角形；⑵求四边形QAPC的面积，提出一个与计算结果有关的结论；⑶当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似?4．6探索三角形相似的条件⑸1．B；2．C；3．B；4．C；5．C；6．C；7．C；8．A；9．C；10．B；11．2等(答案不唯一)；12．DE//BC(答案不唯一)；13．△ABF∽△ACE，△BDE∽△CDF等；14．②③；15．∠B=∠D(答案不唯一)；16．略；17．略(只要符合条件即可)；18．⑴七．⑵△ABE∽△DCA∽△DAE；19．利用相似可求得答案: x= 2cm．20．⑴相似，证略．⑵BD=6．21．BF是FG，EF的比例中项．证△BFG∽△EFB即可． 22．证△ACF∽△AEB．23． 2．24．⑴AQ=AP，6－t=2t解得t=2．⑵S=12×6－Q的位置无关．⑶分两种情况:①t=3．②t=PBQ D C11×12t－×6(12－2t)=36．所以四边形的面积与点P，226． 5第5页（共5页）感谢您的阅读，祝您生活愉快。

4.4 探索三角形相似的条件课时4 黄金分割题型1 黄金分割的定义1、已知P为线段AB的黄金分割点，且AP<PB，则（）A.AP2=AB∙PBB.AP2=AB∙PBC.PB2=AP∙ABD.AP2+ BP2=AB22、如果C是线段AB的黄金分割点，并且AC>CB，AB=1，那么AC的长度为（）A.23 B.12C.√5−12D.3−√523、已知点C是线段AB的黄金分割点，且AB=6cm，则BC的长为（ ）A.(3√5−3)cmB.(9−3√5)cmC.(3√5−3)cm或(9−3√5)cmD. (9−3√5)cm或(6√5−6)cm4、宽与长的比是√5−12（约0.618）的矩形叫黄金矩形，矩形的长与宽分别为a和b，下列数据能构成黄金矩形的是（ ）A.a=4，b=√5+2B.a=4，b=√5−2C.a=2，b=√5+1D.a=2，b=√5−15、定义：如图1,点C在线段AB上,若满足AC2=BC⋅AB,则称点C为线段AB的黄金分割点。

如图2,在△ABC中,AB=AC=1,∠A=36°，BD平分∠ABC交AC于点D.(1)求证：点D是线段AC的黄金分割点；(2)求出线段AD的长。

题型2 黄金分割的应用6、主持人主持节目时,站在舞台的黄金分割点处最自然得体。

如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她要到达最理想的位置至少走（ ）A.(18−6√5)米B.(6√5−6)米C. (6√5+6)米D. (18−6√5)米或(6√5−6)米7、某种乐器的弦AB长为120cm,点A、B固定在乐器面板上,弦AB之间有一个支撑点C,且点C是AB的黄金分割点(AC>BC),则AC的长为( )A.(120−30√5)cmB.(160−60√5)cmC.(60√5−120)cmD.(60√5−60)cm8、宽与长的比是√5−1（约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调2和匀称的美感。

6 利用相似三角形测高基础过关全练知识点 1 利用阳光下的影子测量高度1.如图，小明同学利用相似三角形测量旗杆的高度，若测得标杆AB 长2m，它的影长BC为1m，同一时刻下，测得旗杆DE 的影长EF 为6m,则旗杆 DE 的高度为 ( )A.9 mB.10mC.11 mD.12m2.古希腊数学家泰勒斯曾利用立杆测影的方法，在金字塔影子的顶部直立一根木杆，借助太阳光测金字塔的高度.如图，木杆EF 长2米，它的影长 FD 是4米,同一时刻测得 OA 是268米,则金字塔的高度 BO 是米.知识点 2 利用标杆测量高度3.小明利用中国古代“计里画方”(比例缩放和直角坐标网格体系)的方法测量涂岭镇下炉村的“玉笏朝天”的高度.如图所示，“玉笏朝天”的高度记为AB，“玉笏朝天”在照板“内芯”上的高度记为EF，小明的眼睛P 点与BF 在同一水平线上.则选项中结论正确的是 ( )A.EFAB =PFBFB.EFAB=PFBPC.PEAP =PFBFD.PEAE=PFBP4.某数学小组开展测量本校旗杆高度的实践活动.他们制订了测量方案，并利用课余时间完成了实地测量，测量报告如下：课题测量旗杆的高度说明：在水平地面上直立一根标杆EF，观测者沿着直线BF 后退到点D，使眼睛C、标杆的顶端E、旗杆的顶端A 在同一直线上知识点 3 利用镜子的反射测量高度5.如图，小明为了测量一凉亭的高度AB，在凉亭的旁边放置一个与凉亭台阶BC等高的台阶D E，DE=BC=1m，A，B，C三点共线)，把一面镜子水平放置在平台上的点G处，测得CG=10m，然后沿直线CG后退到点E处，这时恰好在镜子里看到凉亭的顶端A,测得EG=2m,观测者身高EF=1.7 m,则凉亭的高度为 ( )A.8.5mB.9mC.9.5mD.10m6.【学科融合】如图1，在反射现象中，反射光线，入射光线和法线都在同一个平面内；反射光线和入射光线分别位于法线两侧；反射角r等于入射角 i.【问题解决】如图2，小亮在 P 处放置一面平面镜(平面镜的大小忽略不计)，他站在 C 处通过平面镜恰好能看到塔的顶端A，此时测得小亮到平面镜的距离CP为4米.已知平面镜到塔底部中心的距离PB 为247.5米，小亮眼睛到地面的距离DC为1.6米，C，P，B在同一水平直线上，且DC，AB 均垂直于 CB.请你计算塔的高度AB.能力提升全练7.如图，小明同学用自制的直角三角形纸板DEF 测量树的高度AB，他调整自己的位置，设法使斜边 DF 保持水平，并且边 DE 与点 B 在同一直线上，已知纸板的两条直角边 DE=40 cm, EF=20cm,测得边 DF离地面的高度AC=1.5m,CD=9m,则树高 AB 为 ( )A.4mB.4.5mC.5mD.6m8.四分仪是一种十分古老的测量仪器.图1是古代测量员用四分仪测量一方井的深度的示意图，将四分仪置于方井上的边沿上，通过窥衡杆测望井底点F，窥衡杆与四分仪的一边BC 交于点 H.图2 中，四分仪为正方形 ABCD，方井为矩形BEFG.若测量员从四分仪中读得AB 为1，BH 为0.5,实地测得 BE 为2.5,则井深 BG 为( )A.4B.5C.6D.79.下面是小明进行数学学科项目学习时，填写活动报告的部分内容.项目主题：测量河流的宽度.项目探究：河流宽度不能直接测量，需要借助一些工具，比如：镜子，标杆，皮尺，自制的直角三角形模板，……各组确定方案后，选择测量工具，画出测量示意图，并进行实地测量，得到具体数据，从而计算出河流的宽度.项目成果：下表是小明进行交流展示时的部分测量方案及测量数据：请你参与这个项目学习，并完成下列任务：(1)任务一：请你借助小明的测量数据，计算河流的宽度 AB.(2)任务二：请你写出这个方案中求河流宽度时用到的数学知识： (写出一条即可).(3)任务三：请你设计一个与小明不同的测量方案，并画图简要说明.素养探究全练10.小军想用镜子测量一棵古松树的高度，但因树旁有一条小河，故不能测量镜子与树之间的距离，于是他利用镜子进行两次测量，如图，第一次他把镜子放在点C处，他在点 F 处正好在镜中看到树顶 A 的像；第二次他把镜子放在点C'处，他在点 F'处正好在镜中看到树顶 A 的像.已知AB⊥BF',EF⊥BF',E'F'⊥BF',小军的眼睛距地面1.7m(即.EF=E′F′=1.7m),量得CC′=12m,CF=1.8m,C′F′=4.2m.求这棵古松树的高度AB.(镜子大小忽略不计)11.如图，广场上有两盏高度相同的路灯A、C，相距20m，晚上身高为1.8m的张明站在两个路灯之间的E 处，此时 ED 为张明在路灯A 照射下的影子，GE 为张明在路灯C照射下的影子，已知 DG=5m，求路灯的高度.。

§4.6探索三角形相似的条件(一)同步练习一、请说一说什么是相似三角形答：______________ .通过探索和学习，你知道怎样判定两个三角形相似？那么请把你的判定方法写在下面(1)____ . ______ .(2)__________ .(3.) _____________ .二、请你填一填(1)______ 如图4—6—1,在AABC 中，DE//BC, AD=3 cm, B£)=2 cm,/XADE与△ABC 是否相似________ ，•若相似，相似.比是_______ .(2)如图4—6—2, D、E分别为△ABC中AB、AC边上的点，请你添加一个条件，使△ADE与/\ABC相似，你添加的条件是_______________ (只需填上你认为正确的一种情况即可).图4—6—2(3)______ 如图4—6—3,测量小玻璃管口径的量具ABC中，的长是10毫米，AC被分成60等份.如果小管口DE正好对着量.具上30份处(DE〃AB),那么小管口径DE的长是毫米C D A图4—6—3(4)如图4—6—4,在RfAABC中，ZACB=90° ,作CD LAB于点D,则图中相似的三角形有_______ 对，它们分别是. _____________ .A. 2 cm C.12c m 图4—6—4三、认真选一选(1)下列各组图形中有可能不相似的是( )A.各有一个角是45°的两个等腰三角形B.各有一个角是60°的两个等腰三角形C.各有一个角是105°的两个等腰三角形D.两个等腰直角三角形(2)AABC和' B' C'符合下"列条件，其中使△ ABC和厶4，B' C，不相似的是( )A.ZA=ZA' =45°ZB=26°ZB' =109°B.AB=1 AC=1.5 BC=2 B' =4 A ' C ' =2 B z C z .=3C.ZA=ZB ' AB=2 AC=2A h，B' =3.6 B ' C ' =3D.AB=3 AC=5 BC=1 A，B，=爲 A，C，=后 B，C，=打(3)如图4—6—5, AB//CD, AD与BC相交于点O,那么在下列比例式中，正确的是( )A .ABOA B.竺OBCD-~~AD OD~~BCC .ABOBOBC~OC AD~~(4)如图4—6—6,D 为 H ABC的边AB 上一点，且ZABC^ZACD, AD=3 cm,AB=4 cm, 则AC的长为(一)B. cmD.2 y/3 cm四、用数学眼光看世界如图4 —6—7,长梯AB斜靠在墙壁上，梯脚B距墙80 cm,梯上点D距墙70 cm,量得BD 长55 cm,求梯子的长.参考答案§4.6 探索三角形相似的条件(一)一、答：对应角相等、对应边成比例的两个三角形是相似三角形判定两个三角形相似的方法详见课本，略.二 (1)相似 3 : 5 (2) ZC=ZADE (或ZB=/AED等)(3) 5 (4)三△AC£>S2W C AB CD ABAC AACD^ACBD三(1) A (2) D (3) C (4) D四、解：设梯子的长AB为xcm (如图)由RtAADE^RtAABC得:DE AD~BC~ AB.70 x-55"80 _ x解得：x=440答：梯子的长是440 cm.§4.6探索三角形相似的条件(二)同步练习一、请你填一填(1) __________________________________________________________________ 如图4—6—8,在AABC中，AC是BC、DC的比例中项，则△ABCs________________________ , 理由是_______ .D图4—6—8(2) _____________________________________________________________ 如图4—6—9, D、E、F分别是A ABC各边的中点，贝__________________________________ ，理由是(3 )如图4—6—10,若BC=3 cm, DE=cm.(4)如图4—6—11,正方形ABCD的边长为2, AE=EB, MN=\,线段MN的两端分二、认真选一选'(1)如图4—6—12,下列条件不能判定AABC与厶ADE相似的是(图4—6—A各竺AD ABc AE DELx.------- = -------AC BC开动脑筋图4—6—12B.ZB=ZADED.ZC=ZAED(2)在DABCD中，E 在BC 边上，AE 交 BD 于 F,若BE : EC=4 : 5,则BF : FD等于( )A.4 : 5B.5 : 4C.5 : 9D.4 : 9(3)如图4—6—13,在RtAABC 中，ZACB=90° , CD丄AB 于点、D, CD=2, BD=1,则AD的长是( )图4—6—13A.lB. ^2C.2D.4如图4—6—14,在四边形ABCD中，AC.相交于点O, ZABD=ZACD,试找出图中的相似三角形，并加以证明.图4—6—14用数学眼光看世如图4-6-15,为了估算河的宽度，我们可以在河对岸选定一点A,再在河的这一边选定点B 和点C,使得丄BC,然后选定点E,使EC丄BC,确定BC与AE的交点D,若测得劝=180米，DC=60米，EC=50米，你能知道小河的宽是多少吗？参考答案§4.6 探索三角形相似的条件(-二)-(1)△D4C 这两个三角形的两边对应成比例且夹角相等，这两个三角形相似(2.) AABC 这两个三角形的三边对应成比例，这两个三角形相似(3) 1.5 (4) 还或百5 5二(1) C (2) D (3) DH (1) AAOB^ADOC (2) LAODs\BOC 证明：(I) V ZABD^ZACD, ZAOB=ZDOC (对顶角相等)AAOB^ADOC(2)由(1)知厶AOB^ADOC.OA OB…OD _ OC '.OA OD•・ =OB OC又T ZAOD=ZBOC:.△AOD S A BOC四、解：•.•由已知得ZABD^ZDCE=9 0° , Z ADB= Z CDE :. /XABD A ECD AB BD ~EC~~DC 将EC=50, BD=180, DC=60代入上式得：—,/.AB=15050 60即：小河的宽是15 0米.。

4题DCBAM N4．6探索三角形相似的条件⑶一、目标导航三边对应成比例的两个三角形相似及应用． 二、基础过关1．两个三角形相似，则各自由三条中位线构成的两个三角形也相似． 2．腰与底成比例的两个等腰三角形相似． 三、能力提升3．△ABC 的三边长分别为1，，， △DEF 的三边长分别为，，2，则△ABC 与△DEF 是否相似．4．如图，四边形ABCD 为矩形，BNDMAN AM AB AD ==，则∠MAN 的度数为 度． 5． △ABC 中，AB:AC:BC=4:3:2， △ABC 中，AB:AC:BC=3:2:4，则△ABC 与△ABC 相似或不相似．6．在平面直角坐标系中，A2，0，B1，2，A 0，－4，B 4， －2，则△AOB 与△AOB 的关系是 相似或不相似．7．下列各组中的两个图形一定相似的是A ．两个直角三角形B ．两个等腰三角形C ．两个面积相等的三角形D ．两个等边三角形8．△ABC 和△DEF 满足下列条件，其中能使△ABC 与△DEF 相似的是 A ．AB=c ，AC=b ，BC=，DE=，EF=，DF= B ．AB=1，AC=1．5，BC=2，DE=12，EF=8，DF=1 C ．AB=3，AC=4，BC=6，DE=12，EF=8，DF=6 D ．AB=，AC=，BC=，DE=，EF=3，DF=39．要做甲，乙两个形状相同的三角形框架，已知三角形框架甲的三边为50cm ，60cm ，80cm ，三角形框架乙的一边长为20cm ，那么符合条件的三角形框架乙共有 A ．1种 B ．2 C ．3 D ．410．如图，已知AEACDE BC AD AB ==．求证:∠BAD=∠CAE．11．如图，D ，E ，F 分别是△ABC 的三边BC ，CA ，AB 的中点．求证: △DEF∽△ABC．EDC BAF EDCBA12．如图，O 是△ABC 内一点，D ，E ，F 分别OA ，OB ，OC ，上的点，DE//AB ，EF//BC ，DF//AC ．求证:△DEF∽△ABC．13．如图，四边形ABCD ，DCFE ，EFGH 是三个正方形．求∠1∠2∠3的度数．四、聚沙成塔如图，小正方形的边长均为1，则下列图中的三角形阴影部分与△ABC 相似的是OFED CBA 321F E DC BAHGCBA4．6探索三角形相似的条件⑶1．√；2．√；3．相似；4．90；5．相似；6．相似；7．D ；8．C ；9．C ；10．略；11．略；12．易得BCEFOC OF AC DF OA OD AB DE ====． 13．证:22===AG AF CG AC AC CF 得△ACF∽△ACG，所以∠1=∠CAF，即∠1∠2∠3=90． 14．A ．15． ⑴略． ⑵AQ 平分∠DAP 或△ADQ∽△AQP 等．。