高二数学 选修2-1《3.2立体几何中的向量方法(2)》导学案

3.2立体几何中的向量方法（二）教学目标：掌握利用向量法解决空间中的垂直关系教学重点：证明空间中垂直关系的方法教学难点：空间中的垂直关系如何转化为向量的运算问题教学过程：一.复习引入直线的方向向量和平面的法向量二.思考分析直线的方向向量和平面的法向量可以确定直线和平面的位置．因此，可用向量方法解决线面垂直关系的判断及证明．问题1：直线的方向向量与一平面的法向量平行，则该直线与平面有什么关系？提示：垂直．问题2：若两平面的法向量垂直，则两平面垂直吗？提示：垂直．三.抽象概括证明垂直关系的向量方法用向量法证明线线、线面、面面之间的垂直关系，主要是找出直线的方向向量、平面的法向量之间的关系，因此求直线的方向向量及平面的法向量是解题关键．四.例题分析及练习[例1]在棱长为a的正方体OABC－O1A1B1C1中，E，F分别是AB，BC上的动点，且AE＝BF，求证：A1F⊥C1E.[思路点拨]分析题意→建立空间直角坐标系→表示出A1，F，C1，E的坐标→A1F⊥C1E[精解详析]以O为坐标原点建立如图所示的空间直角坐标系，则A1(a,0，a)，C1(0，a，a)．设AE ＝BF ＝x ，则E (a ，x,0)，F (a －x ，a,0)．∴1A F u u u r＝(－x ，a ，－a )， 1C E u u u r＝(a ，x －a ，－a )． ∵1A F u u u r ·1C E u u u r ＝(－x ，a ，－a )·(a ，x －a ，－a )＝－ax ＋ax －a 2＋a 2＝0， ∴1A F u u u r ⊥1C E u u u r，即A 1F ⊥C 1E .[感悟体会] 利用向量法证明线线垂直往往转化为证明直线的方向向量垂直，即证明它们的方向向量的数量积为0.证明的关键是建立恰当的空间直角坐标系，正确地表示出点的坐标进而求直线的方向向量． 训练题组11．设直线l 1的方向向量为a ＝(2,1，－2)，直线l 2的方向向量为b ＝(2,2，m )，若l 1⊥l 2，则m ＝( )A ．1B ．－2C ．－3D ．3解析：l 1⊥l 2⇔a ⊥b ，∴2×2＋1×2＋(－2)×m ＝0，∴m ＝3. 答案：D2．正方体ABCD －A 1B 1C 1D 1中，E 为AC 的中点．证明：(1)BD 1⊥AC ；(2)BD 1⊥EB 1.证明：以D 为原点，DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴建立如图所示 的空间直角坐标系Dxyz .设正方体的棱长为1，则B (1,1,0)，D 1(0,0,1)，A (1，0,0)，C (0,1,0)， E (12，12，0)，B 1(1,1,1)．(1) 1BD u u u r＝(－1，－1,1)，AC uuu r ＝(－1，1,0)，∴1BD u u u r ·AC uuu r ＝(－1)×(－1)＋(－1)×1＋1×0＝0，∴1BD u u u r ⊥AC uuur ，∴BD 1⊥AC .(2) 1BD u u u r ＝(－1，－1,1)，1EB u u u r ＝(12，12，1)，∴1BD u u u r ·1EB u u u r ＝(－1)×12＋(－1)×12＋1×1＝0，∴1BD u u u r ⊥1EB u u u r，∴BD 1⊥EB 1.[例2] 如图所示，在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是BB 1，D 1B 1的中点． 求证：EF ⊥平面B 1AC .[思路点拨] 思路一：EF ⊥AB 1→EF ⊥B 1C →EF ⊥平面B 1AC思路二：求平面B 1AC 的法向量n EF ⊥平面B 1AC[精解详析] 法一：设AB uu u r ＝a ，AD uuu r＝c ，1AA u u u r ＝b ，则EF uuu r ＝1EB u u u r ＋1B F u u u r ＝12(1BB u u u r ＋11B D u u u u r )＝12(1AA u u u r ＋BD uuu r )＝12(1AA u u u r ＋AD uuu r －AB uu u r)＝12(－a ＋b ＋c )． ∵1AB u u u r ＝AB uu u r ＋1AA u u ur ＝a ＋b ，∴EF uuu r ·1AB u u u r ＝12(－a ＋b ＋c )·(a ＋b )＝12(b 2－a 2＋c ·a ＋c ·b )＝12(|b |2－|a |2＋0＋0)＝0.∴EF uuu r ⊥1AB u u ur ，即EF ⊥AB 1.同理，EF ⊥B 1C .又AB 1∩B 1C ＝B 1，∴EF ⊥平面B 1AC .法二：设正方体的棱长为2，以D 为原点，以DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，则A (2,0,0)，C (0,2,0)，B 1(2,2,2)，E (2,2,1)，F (1,1,2)．∴EF uuu r＝(1,1,2)－(2,2,1)＝(－1，－1,1)，1AB u u u r＝(2,2,2)－(2,0,0)＝(0,2,2)， AC uuu r＝(0,2,0)－(2,0,0)＝(－2,2,0)．∴EF uuu r ·1AB u u ur ＝(－1，－1,1)·(0,2,2)＝(－1)×0＋(－1)×2＋1×2＝0，EF uuu r ·AC uuur ＝(－1，－1,1)·(－2,2,0)＝2－2＋0＝0，∴EF uuu r ⊥1AB u u u r ，EF uuu r ⊥AC uuur ，∴EF ⊥AB 1，EF ⊥AC .又AB 1∩AC ＝A ，∴EF ⊥平面B 1AC .法三：同法二得1AB u u u r ＝(0,2,2)，AC uuu r ＝(－2,2,0)，EF uuu r＝(－1，－1,1)．设平面B 1AC 的法向量n ＝(x ，y ，z )，则1AB u u u r·n ＝0，AC uuu r ·n ＝0，即⎩⎪⎨⎪⎧2y ＋2z ＝0，－2x ＋2y ＝0.取x ＝1，则y ＝1，z ＝－1，∴n ＝(1,1，－1)， ∴EF uuu r ＝－n ，∴EF uuu r∥n ，∴EF ⊥平面B 1AC .[感悟体会] 法一选基底，将相关向量用基底表示出来，然后利用向量的计算来证明．法二、法三建立空间直角坐标系，利用坐标将向量的运算转化为实数(坐标)的运算，以达到证明的目的． 训练题组23．已知直线l 与平面α垂直，直线的一个方向向量为u ＝(1,3，z )，向量v ＝(3，－2,1)与平面α平行，则z ＝________.解析：∵l ⊥α，v ∥α，∴u ⊥v .∴(1,3，z )·(3，－2,1)＝0，即3－6＋z ＝0，z ＝3. 答案：34.如图所示，在正方体ABCD －A 1B 1C 1D 1中，O 为AC 与BD 的交点，G 为CC 1的中点，求证：A 1O ⊥平面GBD .证明：法一：设11A B u u u u r ＝a ，11AD u u u u r ＝b ，1A A u u u r ＝c ，则a ·b ＝0，b ·c ＝0，a ·c ＝0. 而1AO u u u r ＝1A A u u u r ＋AO uuu r ＝1A A u u u r ＋12(AB uu u r ＋AD uuu r )＝c ＋12(a ＋b )， BD uuu r ＝AD uuu r －AB uu u r＝b －a ， OG uuu r ＝OC uuu r ＋OG uuu r ＝12(AB uu u r ＋AD uuu r )＋121CC u u u r ＝12(a ＋b )－12c ，∴1AO u u u r ·BD uuu r ＝(c ＋12a ＋12b )·(b －a )＝c ·(b －a )＋12(a ＋b )·(b －a )＝c ·b －c ·a ＋12(b 2－a 2) ＝12(|b |2－|a |2)＝0. ∴1AO u u u r ⊥BD uuu r ，∴A 1O ⊥BD .同理可证，A 1O ⊥OG .又∵OG ∩BD ＝O ，∴A 1O ⊥平面GBD .法二：如图，取D 为坐标原点，DA ，DC ，DD 1所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系．设正方体棱长为2，则O (1,1,0)，A 1(2,0,2)，G (0,2,1)，B (2,2,0)，D (0,0,0)，∴1OA u u u r ＝(1，－1,2)，OB uuu r ＝(1,1,0)，BG uuu r ＝(－2,0,1)．而1OA u u u r ·OB uuur ＝1－1＋0＝0， 1OA u u u r ·BG uuu r ＝－2＋0＋2＝0，∴1OA u u u r ⊥OB uuu r ，1OA u u u r ⊥BG uuur ，即OA 1⊥OB ，OA 1⊥BG .而OB ∩BG ＝B ，∴OA 1⊥平面GBD .[例3] 三棱锥被平行于底面ABC 的平面所截得的几何体如右图所示，截面为A 1B 1C 1，∠BAC ＝90°，A 1A ⊥平面ABC ，A 1A ＝3，AB ＝AC ＝2A 1C 1＝2，D 为BC 的中点．证明：平面A 1AD ⊥平面BCC 1B 1.[思路点拨] 思路一：证明BC ⊥AD →证明BC ⊥AA 1→BC ⊥平面A 1AD →平面A 1AD ⊥平面BCC 1B 1思路二：求平面A 1AD 的法向量n 1→求平面BCC 1B 1的法向量n 2→证明n 1·n 2＝0→ 平面A 1AD ⊥平面BCC 1B 1[精解详析] 法一：如下图，建立空间直角坐标系，则A (0,0,0)，B (2,0,0)，C (0,2,0)，A 1(0,0，3)，C 1(0,1，3)．∵D 为BC 的中点，∴D 点坐标为(1,1,0)．∴AD uuu r＝(1,1,0)，1AA u u u r ＝(0,0，3)，BC uuu r ＝(－2,2,0)．∴AD uuu r ·BC uuur ＝1×(－2)＋1×2＋0×0＝0，1AA u u u r ·BC uuu r ＝0×(－2)＋0×2＋3×0＝0. ∴AD uuu r ⊥BC uuur ，1AA u u u r ⊥BC uuu r .∴BC ⊥AD ，BC ⊥AA 1.又A 1A ∩AD ＝A ，∴BC ⊥平面A 1AD .又BC ⊂平面BCC 1B 1，∴平面A 1AD ⊥平面BCC 1B 1.法二：同证法一建系后，得1AA u u u r ＝(0,0，3)，AD uuu r＝(1,1,0)，BC uuu r ＝(－2,2,0)，1CC u u u r ＝(0，－1，3)．设平面A 1AD 的法向量为n 1＝(x 1，y 1，z 1)，平面BCC 1B 1的法向量为n 2＝(x 2，y 2，z 2)．由⎩⎪⎨⎪⎧n 1·1AA u u u r ＝0，n 1·AD uuu r＝0，得⎩⎨⎧3z 1＝0，x 1＋y 1＝0.令y 1＝－1，则x 1＝1，z 1＝0，∴n 1＝(1，－1,0)． 由⎩⎪⎨⎪⎧n 2·BC uuu r ＝0，n 2·1CC u u u r ＝0，得⎩⎨⎧－2x 2＋2y 2＝0，－y 2＋3z 2＝0.令y 2＝1，则x 2＝1，z 2＝33，∴n 2＝(1,1，33)．∵n 1·n 2＝1－1＋0＝0，∴n 1⊥n 2.∴平面A 1AD ⊥平面BCC 1B 1.[感悟体会] 证明面面垂直通常有两种方法，一是利用面面垂直的判定定理转化为线面垂直、线线垂直去证明；二是证明两个平面的法向量互相垂直． 训练题组35．在正棱锥P －ABC 中，三条侧棱两两互相垂直，G 是△P AB 的重心，E ，F 分别为BC ，PB 上的点，且BE ∶EC ＝PF ∶FB ＝1∶2.求证：平面GEF ⊥平面PBC .证明：法一：如图，以三棱锥的顶点P 为原点，以P A ，PB ，PC 所在直线分别作为x 轴，y 轴，z 轴建立空间直角坐标系．令P A ＝PB ＝PC ＝3，则A (3,0,0)，B (0,3,0)，C (0,0,3)，E (0,2,1)，F (0,1,0)，G (1,1,0)，P (0,0,0)，于是PA u u r ＝(3,0,0)，FG uuu r ＝(1,0,0)，故PA u u r＝3FG uuu r ，∴P A ∥FG .而P A ⊥平面PBC ，∴FG ⊥平面PBC .又FG ⊂平面EFG ，∴平面EFG ⊥平面PBC . 法二：同证法一，建立空间直角坐标系，则E (0,2,1)，F (0,1,0)，G (1,1,0)．∴EF uuu r＝(0，－1，－1)，EG uuu r ＝(1，－1，－1)．设平面EFG 的法向量是n ＝(x ，y ，z )，则有n ⊥EF uuu r，n ⊥EG uuu r .∴⎩⎪⎨⎪⎧y ＋z ＝0，x －y －z ＝0.令y ＝1，得z ＝－1，x ＝0，即n ＝(0,1，－1)． 显然PA u u r＝(3,0,0)是平面PBC 的一个法向量．又n ·PA u u r ＝0，∴n ⊥PA u u r ，即平面PBC 的法向量与平面EFG 的法向量互相垂直，∴平面EFG ⊥平面PBC .6．正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是BB 1，CD 的中点，求证：平面AED ⊥平面A 1FD 1. 证明：如图，建立空间直角坐标系Dxyz .设正方体棱长为1，则E (1,1，12)，D 1(0,0,1)，F (0，12，0)，A (1,0,0)．∴DA uuu r ＝(1,0,0)＝11D A u u u u r ，DE uuu r ＝(1,1，12)， 1D F u u u u r ＝(0，12，－1)．设m ＝(x 1，y 1，z 1)，n ＝(x 2，y 2，z 2)分别是平面AED 和A 1FD 1的一个法向量．由⎩⎨⎧m ·DA uuu r ＝0，m ·DE uuu r ＝0⇒⎩⎪⎨⎪⎧ x 1＝0，x 1＋y 1＋12z 1＝0.令y 1＝1，得m ＝(0,1，－2)． 又由⎩⎪⎨⎪⎧n ·11D A u u u u r＝0，n ·1D F u u u u r＝0⇒⎩⎪⎨⎪⎧x 2＝0，12y 2－z 2＝0.令z 2＝1，得n ＝(0,2,1)． ∵m ·n ＝(0,1，－2)·(0,2,1)＝0，∴m ⊥n ，故平面AED ⊥平面A 1FD 1. 五.课堂小结与归纳1．用向量法证明线面垂直的方法与步骤(1)基向量法⎩⎪⎨⎪⎧①设出基向量，用基向量表示直线的方向向量②找出平面内两条不共线向量并分别用基向量表示③分别证明直线的方向向量与平面内两不共线向量垂直(2)坐标法⎩⎪⎪⎨⎪⎪⎧方法一⎩⎪⎨⎪⎧①建立空间直角坐标系②将直线的方向向量用坐标表示③将平面内任意两条相交直线的方向向量用坐标表示④分别证明直线的方向向量与平面内两向量垂直方法二⎩⎪⎨⎪⎧①建立空间坐标系②将直线的方向向量、平面的法向量分别用坐标表示④证明平面的法向量与直线的方向向量平行2．利用空间向量证明面面垂直，通常可以有两个途径，一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直，进而转化为线线垂直；二是直接求解两个平面的法向量，证明两个法向量垂直，从而得到两个平面垂直． 六.当堂训练1．若两个不同平面α，β的法向量分别为u ＝(1,2，－1)，v ＝(2,3,8)，则( ) A ．α∥β B ．α⊥βC ．α，β相交但不垂直 D ．以上均不正确 解析：u ·v ＝(1,2，－1)·(2,3,8)＝1×2＋2×3－1×8＝0，∴u ⊥v .∴α⊥β.答案：B2．若直线l ∥α，且l 的方向向量为(2，m,1)，平面α的法向量为(1，12，2)，则m 为( )A ．－4B ．－6C ．－8D ．8解析：∵l ∥α，平面α的法向量为(1，12，2)，∴(2，m,1)·(1，12，2)＝0.∴2＋12m ＋2＝0.∴m ＝－8.答案：C3．已知AB uu u r ＝(1,5，－2)，BC uuu r ＝(3,1，z )，若AB uu u r ⊥BC uuu r ，BP u u u r ＝(x －1，y ，－3)，且BPu u u r⊥平面ABC ，则BP u u u r等于( )A ．(337，－157，4)B ．(337，－157，－3)C ．(407，－157，4)D ．(407，157，－3)解析：由AB uu u r ·BC uuu r ＝0得3＋5－2z ＝0，∴z ＝4.又BP u u u r⊥平面ABC ， ∴⎩⎨⎧BP u u u r ·AB uu u r ＝0， BP u u u r ·BC uuur ＝0，即⎩⎪⎨⎪⎧x －1＋5y ＋6＝0，3x －3＋y －12＝0，解得⎩⎨⎧x ＝407，y ＝－157.答案：B4．在正方体ABCD －A 1B 1C 1D 1中，若E 为A 1C 1的中点，则直线CE 垂直于( ) A ．AC B ．BD C ．A 1DD ．AA 1解析：建立如图所示的坐标系．设正方体棱长为1，则A (1,0,0)，B (1,1,0)， C (0,1,0)，D (0,0,0)，A 1(1,0,1)，E (12，12，1)．∴CE ―→＝(12，12，1)－(0,1,0)＝(12，－12，1)，AC uuu r ＝(－1,1,0)，BD uuu r＝(－1，－1,0)，1A D u u u r ＝(－1,0，－1)，1A A u u u r ＝(0,0，－1)．∵CE u u u r ·BD uuu r ＝(12，－12，1)·(－1，－1,0)＝－12＋12＋0＝0， ∴CE u u u r ⊥BD uuu r，∴CE ⊥BD .答案：B5．在直角坐标系Oxyz 中，已知点P (2cos x ＋1,2cos 2x ＋2,0)和点Q (cos x ，－1,3)，其中x ∈[0，π]．若直线OP 与直线OQ 垂直，则x 的值为________．解析：由题意得OP uuu r ⊥OQ uuu r.∴cos x ·(2cos x ＋1)－(2cos 2x ＋2)＝0.∴2cos 2x －cos x ＝0.∴cos x ＝0或cos x ＝12.又x ∈[0，π]，∴x ＝π2或x ＝π3.答案：π2或π36．已知点P 是平行四边形ABCD 所在的平面外一点，且有AB uu u r ＝(2，－1，－4)，ADuuu r＝(4,2,0)，AP uu u r ＝(－1,2，－1)．给出结论：①AP ⊥AB ；②AP ⊥AD ；③AP uu u r是平面ABCD的法向量；④AP uu u r ∥BD uuu r.其中正确的是________．解析：由AP uu u r ·AB uu u r＝－2－2＋4＝0知AP ⊥AB ，故①正确； 由AP uu u r ·AD uuu r＝－4＋4＋0＝0，知AP ⊥AD ，故②正确；由①②知AP uu u r是平面ABCD 的法向量，故③正确，④不正确．答案：①②③7.如图，在四棱锥P －ABCD 中，底面ABCD 是矩形，P A ⊥平面ABCD ，AP ＝AB ＝2，BC ＝22，E ，F 分别是AD ，PC 的中点．求证：PC ⊥平面BEF .解：如图，以A 为坐标原点，AB ，AD ，AP 所在直线分别为x ，y ，z 轴建立空间直角坐标系．∵AP ＝AB ＝2，BC ＝AD ＝22，四边形ABCD 是矩形，∴A ，B ，C ，D ，P 的坐标为A (0，0,0)，B (2,0,0)，C (2,22，0)，D (0,22，0)，P (0,0,2)． 又E ，F 分别是AD ，PC 的中点，∴E (0，2，0)，F (1，2，1)．∴PC uuu r (2,22，－2)，BF uuu r ＝(－1，2，1)，EF uuu r＝(1,0,1)， ∴PC uuu r ·BF uuu r ＝－2＋4－2＝0，PC uuu r ·EF uuu r ＝2＋0－2＝0，∴PC uuu r ⊥BF uuu r ，PC uuu r ⊥EF uuu r ，∴PC ⊥BF ，PC ⊥EF .又BF ∩EF ＝F ，∴PC ⊥平面BEF . 8.已知正方体ABCD －A 1B 1C 1D 1中，E 为棱CC 1上的动点．(1)求证：A 1E ⊥BD ；(2)若平面A 1BD ⊥平面EBD ，试确定E 点的位置．解：以D 为坐标原点，以DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系．设正方体棱长为a ，则A (a,0,0)，B (a ，a,0)，C (0，a,0)，A 1(a,0，a )，C 1(0，a ，a )．设E (0，a ，e )(0≤e ≤a )．(1) 1A E u u u r ＝(－a ，a ，e －a )，BD uuu r ＝(－a ，－a,0)，1A E u u u r ·BD uuu r ＝a 2－a 2＋(e －a )·0＝0， ∴1A E u u u r ⊥BD uuu r，即A 1E ⊥BD .(2)设平面A 1BD ，平面EBD 的法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)．∵DB uuu r ＝(a ，a,0)，1DA u u u r ＝(a,0，a )，DE uuu r ＝(0，a ，e )，∴⎩⎪⎨⎪⎧ax 1＋ay 1＝0，ax 1＋az 1＝0.⎩⎪⎨⎪⎧ax 2＋ay 2＝0，ay 2＋ez 2＝0. 取x 1＝x 2＝1，得n 1＝(1，－1，－1)，n 2＝(1，－1，ae )．由平面A 1BD ⊥平面EBD 得n 1⊥n 2.∴2－a e ＝0，即e ＝a 2.∴当E 为CC 1的中点时，平面A 1BD ⊥平面EBD .。

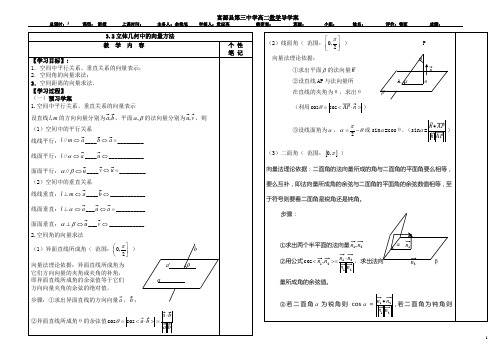
cos α=-2121n n n n •预习检测1．(1)设b a ,分别是不重合的直线21,l l 的方向向量. 根据下列条件判断21,l l 的位置关系： ①)2,6,4(-=a ，)1,3,2(--=b ②)2,0,5(=a ，)0,1,0(=b ③)1,1,2(---=a ，)8,2,4(--=b（2）设u ，v 分别是不同的平面βα,的法向量，根据下列条件判断βα,的位置关系：①)2,1,1(--=u ，)21,2,3(-=v②)0,0,3(=u ，)0,0,2(-=v ③)3,2,4(-=u ，)2,4,1(-=v（3）设u 是平面α的法向量，a 是直线l 的方向向量，根据下列条件判断α与l 的位置关系：①)1,2,2(-=u ，)4,8,6(-=a ②)0,3,2(-=u ，)0,12,8(-=a ③)5,4,1(=u ，)0,4,2(-=a 2.在正方体1111D C B A ABCD -中， （1）求面ABCD 的一个法向量 （2）求面11BC A 的一个法向量（3）若M 为CD 的中点，求面1AMD 的一个法向量.3.已知正方体1111D C B A ABCD -的棱长为2，E 、F 分别是11DD BB 、的中点，求证：（1）ADE FC 平面//1 （2）F C B ADE 11//平面平面4.在正方体1111D C B A ABCD -中，E 是棱BC 的中点，试在棱1CC 上求一点P ，使得平面DE C P B A 111平面⊥课堂学案1.如图所示，已知在四面体ABCD 中，O 是BD 的中点，CA=CB=CD=BD=2，AB=AD=2.（1）求证BCD AO 平面⊥ （2）求异面直线AB 与CD 所成的角的余弦值2.已知三棱锥ABC P -中，ABC PA 平面⊥，AC AB ⊥,AB AC PA 21==,N 为AB 上一点，AB=4AN ，M ，S 分别为PB ，BC 的中点.（1）证明：SN CM ⊥；（2）求SN 与平面CMN 所成角的大小.3.如图，在五面体ABCDEF 中，ABCD FA 平面⊥FE BC AD ////,AD AB ⊥,M为EC 的中点，AD FE BC AB AF 21====（1）求异面直线BF 与DE 所成的角的大小； （2）求二面角E CD A --的余弦值.4.已知正方体1111D C B A ABCD -的棱长为2，E ，F ，G 分别是AB A D C C ，，111的中点，求点A 到平面EFG 的距离.（三）达标检测1.正方体1111D C B A ABCD -中，1BB 与平面1ACD 所成角的余弦值为（ ）A.32B.33C.32 D.362.有以下结论：①若直线21,l l 的方向向量分别为)2,2,1(-=a ，)2,3,2(-=b ，则21l l ⊥ ②若平面βα,的法向量分别为)2,2,1(-=u ，)2,3,2(-=v ，则βα⊥ ③若直线l 的方向向量为)2,2,1(-=a ，平面α的法向量为)2,3,2(-=v ，则α⊥l .④已知平面βα,的法向量分别为)2,2,1(-=u ，),,2(z y v -=，若βα//，则16-=⋅z y .以上结论正确的序号为______________3.在正方体1111D C B A ABCD -中，求证：111//D CB BD A 平面平面4.如图，在直三棱柱111C B A ABC -中，BC AC ⊥,1CC BC AC ==,M 、N 分别是B A 1、11C B 的中点.（1）求证：BC A MN 1平面⊥；（2）求直线1BC 和平面BC A 1所成角的大小.5.如图所示，在直三棱柱111C B A ABC -中，A B =1，31==AA AC ,︒=∠60ABC . （1）证明：C A AB 1⊥.(2)求二面角B C A A --1的余弦值.。

第一课时： §3.2立体几何中的向量方法（一）教学要求：向量运算在几何证明与计算中的应用．掌握利用向量运算解几何题的方法，并能解简单的立体几何问题．教学重点：向量运算在几何证明与计算中的应用．教学难点：向量运算在几何证明与计算中的应用．教学过程：一、复习引入1. 用向量解决立体几何中的一些典型问题的基本思考方法是：⑴如何把已知的几何条件（如线段、角度等）转化为向量表示； ⑵考虑一些未知的向量能否用基向量或其他已知向量表式； ⑶如何对已经表示出来的向量进行运算，才能获得需要的结论？2. 通法分析：利用两个向量的数量积的定义及其性质可以解决哪些问题呢？ ⑴利用定义a ·b ＝|a ||b |cos ＜a ,b ＞或cos ＜a ,b ＞＝a b a b ⋅⋅r r r r ，可求两个向量的数量积或夹角问题；⑵利用性质a ⊥b ⇔a ·b ＝０可以解决线段或直线的垂直问题；⑶利用性质a ·a ＝｜a ｜2，可以解决线段的长或两点间的距离问题．二、例题讲解1. 出示例1：已知空间四边形OABC 中，OA BC ⊥，OB AC ⊥．求证：OC AB ⊥． 证明：·OC AB u u u u r u u u r ＝·()OC OB OA -u u u u r u u u r u u u r ＝·OC OB u u u u r u u u r －·OC OA u u u u r u u u r ． ∵OA BC ⊥，OB AC ⊥， ∴·0OA BC =u u u r u u u r ，·0OB AC =u u u r u u u u r ， ·()0OA OC OB -=u u u r u u u u r u u u r ，·()0OB OC OA -=u u u r u u u u r u u u r ． ∴··OA OC OA OB =u u u r u u u u r u u u r u u u r ，··OB OC OB OA =u u u r u u u u r u u u r u u u r ． ∴·OC OB u u u u r u u u r ＝·OC OA u u u u r u u u r ，·OC AB u u u u r u u u r ＝0． ∴OC AB ⊥ 2. 出示例2：如图，已知线段AB 在平面α内，线段AC α⊥，线段BD ⊥AB ，线段'DD α⊥，'30DBD ∠=o ，如果AB ＝a ，AC ＝BD ＝b ，求C 、D 间的距离．解：由AC α⊥，可知AC AB ⊥． 由'30DBD ∠=o 可知，＜,CA BD u u u r u u u u r ＞＝120o ， ∴2||CD u u u u r ＝2()CA AB BD ++u u u r u u u r u u u u r ＝2||CA u u u r ＋2||AB u u u r ＋2||BD u u u u r ＋2(·CA AB u u u r u u u r ＋·CA BD u u u r u u u u r ＋·AB BD u u u r u u u u r ) ＝22222cos120b a b b +++o ＝22a b +．∴22CD a b =+．3. 出示例3：如图，M 、N 分别是棱长为1的正方体''''ABCD A B C D -的棱'BB 、''B C 的中点．求异面直线MN 与'CD 所成的角．解：∵MN u u u u r ＝1(')2CC BC +u u u u r u u u r ，'CD u u u u r ＝'CC CD +u u u u r u u u u r ， ∴·'MN CD u u u u r u u u u r ＝1(')2CC BC +u u u u r u u u r ·(')CC CD +u u u u r u u u u r ＝12(2|'|CC u u u u r ＋'CC CD u u u u r u u u u r g ＋·'BC CC u u u r u u u u r ＋·BC CD u u u r u u u u r )． ∵'CC CD ⊥，'CC BC ⊥，BC CD ⊥，∴'0CC CD =u u u u r u u u u r g，·'0BC CC =u u u r u u u u r ，·0BC CD =u u u r u u u u r ， ∴·'MN CD u u u u r u u u u r ＝122|'|CC u u u u r ＝12． …求得 cos ＜,'MN CD u u u u r u u u u r ＞12=，∴＜,'MN CD u u u u r u u u u r ＞＝60o . 4. 小结：利用向量解几何题的一般方法：把线段或角度转化为向量表示式，并用已知向量表示未知向量，然后通过向量的运算去计算或证明．三、巩固练习 作业：课本P 116 练习 1、2题.第二课时： §3.2立体几何中的向量方法（二）教学要求：向量运算在几何证明与计算中的应用．掌握利用向量运算解几何题的方法，并能解简单的立体几何问题．教学重点：向量运算在几何证明与计算中的应用．教学难点：向量运算在几何证明与计算中的应用．教学过程：一、复习引入讨论：将立体几何问题转化为向量问题的途径？（1）通过一组基向量研究的向量法，它利用向量的概念及其运算解决问题；（2）通过空间直角坐标系研究的坐标法，它通过坐标把向量转化为数及其运算来解决问题.二、例题讲解1. 出示例1： 如图，在正方体1111ABCD A B C D -中，E 、F 分别是1BB 、CD 的中点，求证：1D F ⊥平面ADE ． 证明：不妨设已知正方体的棱长为１个单位长度，且设DA uuu r ＝i ，DC u u u u r ＝j ，1DD u u u u r ＝k ．以i 、j 、k 为坐标向量建立空间直角坐标系D －xyz ，则∵AD uuu u r ＝(-1,0,0)，1D F u u u u r ＝(0,12,-1)，∴AD uuu u r ·1D F u u u u r ＝(-1,0,0)·(0,12,-1)＝0，∴1D F ⊥AD ． 又 AE uuu r ＝(0,1,12)，∴AE uuu r ·1D F u u u u r ＝(0,1,12)·(0,12,-1)＝0， ∴1D F ⊥ AE ． 又 AD AE A =I ， ∴1D F ⊥平面ADE ．说明：⑴“不妨设”是我们在解题中常用的小技巧，通常可用于设定某些与题目要求无关的一些数据，以使问题的解决简单化．如在立体几何中求角的大小、判定直线与直线或直线与平面的位置关系时，可以约定一些基本的长度．⑵空间直角坐标些建立，可以选取任意一点和一个单位正交基底，但具体设置时仍应注意几何体中的点、线、面的特征，把它们放在恰当的位置，才能方便计算和证明．2. 出示例2：课本P 116 例3分析：如何转化为向量问题？进行怎样的向量运算？3. 出示例3：课本P 118 例4分析：如何转化为向量问题？进行怎样的向量运算？4. 出示例4：证：如果两条直线同垂直于一个平面，则这两条直线平行．改写为：已知：直线OA ⊥平面α，直线BD ⊥平面α，O 、B 为垂足．求证：OA //BD ． 证明：以点O 为原点，以射线OA 为非负z 轴，建立空间直角坐标系O -xyz ，i ,j ,k 为沿x 轴，y 轴，z 轴的坐标向量，且设BD uuu u r ＝(,,)x y z ． ∵BD ⊥α， ∴BD uuu u r ⊥i ，BD uuu u r ⊥j ， ∴BD uuu u r ·i ＝(,,)x y z ·(1,0,0)＝x ＝0，BD uuu u r ·j ＝(,,)x y z ·(0,1,0)＝y ＝0, ∴BD uuu u r ＝(0,0,z )．∴BD uuu u r ＝z k ．即BD uuu u r //k ．由已知O 、B 为两个不同的点，∴OA //BD ．5. 法向量定义：如果表示向量a 的有向线段所在直线垂直于平面α，则称这个向量垂直于平面α，记作a ⊥α．如果a ⊥α，那么向量a 叫做平面α的法向量．6. 小结：向量法解题“三步曲”：（1）化为向量问题 →（2）进行向量运算 →（3）回到图形问题.三、巩固练习 作业：课本P 120、 习题A 组 1、2题.第三课时： §3.2立体几何中的向量方法（三）教学要求：向量运算在几何证明与计算中的应用．掌握利用向量运算解几何题的方法，并能解简单的立体几何问题．教学重点：向量运算在几何证明与计算中的应用．教学难点：向量运算在几何证明与计算中的应用．教学过程：一、复习引入 1. 法向量定义：如果直线l α⊥平面, 取直线l 的方向向量为a r ，则向量a r 叫作平面α的法向量（normal vectors ）. 利用法向量，可以巧妙的解决空间角度和距离.2. 讨论：如何利用法向量求线面角？ → 面面角？ 直线AB 与平面α所成的角θ，可看成是向量AB u u u r 所在直线与平面α的法向量n 所在直线夹角的余角，从而求线面角转化为求直线所在的向量与平面的法向量的所成的线线角，根据两个向量所成角的余弦公式cos ,a b a b a b=r r r r g r r g ，我们可以得到如下向量法的公式： sin cos ,AB n AB n AB nθ==u u u r r g u u u r r u u u r r g .3. 讨论：如何利用向量求空间距离？两异面直线的距离，转化为与两异面直线都相交的线段在公垂向量上的投影长.点到平面的距离，转化为过这点的平面的斜线在平面的法向量上的投影长.二、例题讲解：1. 出示例1：长方体1111ABCD A B C D -中，AD =1AA =2，AB =4，E 、F 分别是11A D 、AB 的中点，O 是11BC B C 与的交点. 求直线OF 与平面DEF 所成角的正弦.解：以点D 为空间直角坐标系的原点，DA 、DC 、1DD 为坐标轴，建立如图所示的空间直角坐标系. 则(2,2,0),(1,0,2),(2,2,0),(1,4,1),(0,4,0)D E F O C . 设平面DEF 的法向量为 (,,)n x y z =r ， 则n DE n DF ⎧⊥⎪⎨⊥⎪⎩r u u u r r u u u r ， 而(1,0,2)DE =u u u r ， (2,2,0)DF =u u u r . ∴ 00n DE n DF ⎧=⎪⎨=⎪⎩r u u u r g r u u u r g ，即20220x z x y +=⎧⎨+=⎩, 解得::2:2:1x y z =-， ∴ (2,2,1)n =-r . ∵ ||||cos n OF n OF α•=r u u u r r u u u r ， 而(1,2,1)OF =--u u u r . ∴ cos α=2222276||||(2)211(2)(1)n OF n OF •==-•-+++-+-r u u u r r u u u r g 所以，直线OF 与平面DEF 所成角的正弦为76. 2. 变式： 用向量法求：二面角1A DE O --余弦；OF 与DE 的距离；O 点到平面DEF 的距离. 三、巩固练习作业：课本P 121、 习题A 组 5、6题.。

第三章 空间向量与立体几何3．2 立体几何中的向量方法（2）一、学习目标1.了1．理解直线与平面所成角的概念，能够利用向量方法解决线线、线面、面面的夹角问题，体会用空间向量解决立体几何问题的三步曲．2.理解点到平面的距离的概念，能灵活运用向量方法求各种空间距离，体会向量法在求空间距离中的作用.【重点、难点】重点：向量法求解线线、线面、面面的夹角、两点间的距离、点到平面的距离；难点：线线、线面、面面的夹角与向量的应用，两异面直线间的距离，线面距、面面距向点面距的转化.二、学习过程【探究新知】1．直线与平面的夹角：平面外一条直线与它在该平面内的投影的夹角；特别当直线与平面平行或在平面内时，直线与平面的夹角为0，当直线与平面垂直时，直线与平面的夹角为π2. 23(1)平移法：通过平移其中一条(也可两条同时平移)，使它们转化为两条相交直线，然后通过解三角形获解．(2)向量法：设直线l 1，l 2的方向向量分别为a ，b ，a与b的夹角为φ，则l 1与l 2所成角θ满足cos θ＝|cos φ|＝|a·b||a||b|. 4．直线与平面所成角的求法(1)几何法：找出斜线在平面上的射影，则斜线与射影所成角就是线面角，可通过解由斜线段、垂线段和射影线段构成的直角三角形获解．(2)向量法：设直线l 的方向向量为a ，平面α的一个法向量为n ，直线l 与平面α所成角为θ，a 与n的夹角为φ，则有cos θ＝sin φ，或sin θ＝|cos φ|＝|a·n||a||n|. 5．二面角的求法(1)几何法：作出二面角的平面角，然后通过解三角形获解．(2)向量法：设二面角α ­l ­β的两个半平面的法向量分别为n 1，n 2.①当平面α、β的法向量与α、β的关系如图1所示时，二面角α ­ l ­ β的平面角即为两法向量n 1，n 2的夹角〈n 1，n 2〉．图1 图2②当平面α、β的法向量与α、β的关系如图2所示时，二面角α ­ l ­ β的平面角与两法向量n 1，n 2的夹角〈n 1，n 2〉互补．6.空间中的距离7．点到平面距离的求法如图，BO ⊥平面α，垂足为O ，则点B 到平面α的距离就是线段BO 的长度．若AB 是平面α的任一条斜线段，则在Rt△BOA 中，|BO →|＝|BA →|·cos∠ABO ＝|BA →|·|BO →|·cos∠ABO |BO →|.如果令平面α的法向量为n ，考虑到法向量的方向，可以得到B 点到平面α的距离为|BO →|＝|AB →·n ||n |. 因此用向量法求一个点到平面的距离，可以分以下几步完成：(1)求出该平面的一个法向量；(2)找出从该点出发的平面的任一条斜线段对应的向量；(3)求出法向量与斜线段向量的数量积的绝对值再除以法向量的模，即可求出点到平面的距离．由于n |n|＝n 0可以视为平面的单位法向量，所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值，即d ＝|AB →·n 0|.【典型例题】例1．四棱锥PABCD 的底面是正方形，PA ⊥底面ABCD ，PA ＝AD ＝2，点M ，N 分别在棱PD ，PC 上，且PC ⊥平面AMN .(1)求AM 与PD 所成的角；(2)求二面角P ­ AM ­ N 的余弦值；(3)求直线CD 与平面AMN 所成角的余弦值．例2. (1) 如图1，正方形ABCD 和ABEF 的边长都是1，且它们所在平面互相垂直，点M 在AC 上，点N 在BF上．若CM ＝BN ＝22，求MN 的长． (2) 正方体ABCDA 1B 1C 1D 1的棱长为1，利用向量法求点C 1到A 1C 的距离．(3) 如图2，△BCD 与△MCD 都是边长为2的正三角形，平面MCD ⊥平面BCD ，AB ⊥平面BCD ，AB ＝2 3.求点A 到平面MBC 的距离．图2图1【变式拓展】1.如图，已知在长方体ABCD ­A 1B 1C 1D 1中，AB ＝2，AA 1＝1，直线BD 与平面AA 1B 1B 所成的角为30°，AE 垂直BD 于点E ，F 为A 1B 1的中点．(1)求异面直线AE 与BF 所成角的余弦值；(2)求平面BDF 与平面AA 1B 所成二面角的余弦值．三、总结反思用向量法求点面距的方法与步骤：(1)建坐标系：结合图形的特点建立恰当的空间直角坐标系；(2)求向量：在坐标系中求出点到平面内任一点对应的向量AB →；(3)求法向量：设出平面的法向量，利用向量垂直的条件转化为求解方程组，求出法向量n ；(4)得答案：代入公式d ＝|AB →·n ||n |求得答案． 四、随堂检测1．四棱锥PABCD 中，PD ⊥平面ABCD ，PA 与平面ABCD 所成的角为60°，在四边形ABCD 中，∠ADC ＝∠DAB＝90°，AB ＝4，CD ＝1，AD ＝2.(1)建立适当的坐标系，并写出点B 、P 的坐标；(2)求异面直线PA 与BC 所成的角的余弦值．2.已知正三棱柱ABCA1B1C1的底面边长为a，侧棱长为2a，M为A1B1的中点，求BC1与平面AMC1所成角的正弦值．3.若PA⊥平面ABC，AC⊥BC，PA＝AC＝1，BC＝2，求二面角A­PB­C的余弦值．4.如图所示，在120°的二面角α­AB­β中，AC⊂α，BD⊂β且AC⊥AB，BD⊥AB，垂足分别为A、B，已知AC＝AB＝BD＝6，试求线段CD的长．5. 如图，P为矩形ABCD所在平面外一点，PA⊥平面ABCD，若已知AB＝3，AD＝4，PA＝1，求点P到BD的距离．6. 正方体ABCDA1B1C1D1的棱长为2，E、F、G分别是C1C，D1A1，AB的中点，求点A到平面EFG的距离．。

立体几何中的向量方法课时分配:第一课立体几何中的向量方法1个课时第二课立体几何专1个课时第三课立体几何中的向量方法——求点坐标1个课时3. 2.1 立体几何中的向量方法【教学目标】1）知识与技能：进一步体会空间向量在解决立体几何问题中的广泛作用，再次熟悉立体几何中的向量方法“三步曲”；继续讨论如何利用已知条件适当建立空间直角坐标系，展示向量方法与坐标方法相结合的优越性；对立体几何中的三种方法（综合法、向量法、坐标法）的联系进行分析与小结．（2）过程与方法：在解决问题中，通过数形结合与问题转化的思想方法，加深对相关内容的理解。

（3）情感态度与价值观：体会把立方体几何几何转化为向量问题优势，培养探索精神。

【教学重点】坐标法与向量法结合【教学难点】适当地建立空间直角坐标系及添加辅助线．【学前准备】：多媒体，预习例题PB ⊥)1,,(-z y x )1,1,-021=所以=EDB 平面333(，，,21,0(213161=60的大小为D -2,=BA CD异面直线AB与CD所成角的余弦值为BD 1C 1B 1CDBA A 1EF 3，如下图，已知空间四边形OABC ，其对角线为OB 、AC ，M 、N 分别是对边OA 、BC 的中点，点G 在线段MN 上，且分MN 所成的定比为2，现用基向量、、表示向量，设=x+y+z，则x 、y 、z 的值分别为A.x =,y =,z =B.x =,y =,z =C.x =,y =,z =D.x =,y =,z =（中等题）5，如图,在长方体ABCD —A 1B 1C 1D 1中,已知AB= 4, AD =3, AA 1= 2. E 、F 分别是线段AB 、BC 上的点，且EB=FB=1，.求直线EC 1与FD 1所成的余弦值.解：以1,,DA DC DD 分别为,,x y z 轴建立坐标系，则E （3，3，0）、C 1（0，4，2）、D 1（0，0，2）、F （2，4，0）.从而1EC ＝（－3，1，2）、1FD ＝（－2，－4，2）所以直线EC 1与FD 1所成的余弦值为 11,cos FD EC ＝||||1111FD EC FD EC ∙∙＝1421立体几何专题【教学目标】内容:考查(1)空间几何体:结构特征、三视图、表面积和体积的计算. 常给出几何体的三视图，通过识图、想图、作图、用图，考查学生的空间想象能力及运算求解能力.(2)空间直线与平面的位置关系:线、面平行与垂直关系的判断和证明，其中垂直关系出现频率更高.空间角的计算，其中二面角的计算是理科生的重点，文科生则不做要求；三是空间距离的计算，重点考查点到平面的距离.如在文科高考解答题中，第（2）问往往要计算几何体的体积，其关键是求出点到平面的距离. (3）空间向量与立体几何:考查利用空间向量研究空间直线与平面的位置关系；利用空间向量求角和距离.一般地，论证平行与垂直关系，传统方法较方便，而在求空间角和空间距离上，则可显示出向量法的优越性.方法:解答题的命制,课标卷都采用了“一题多法”的命制办法，并体现向量坐标法优先的特征. 即同一试题可以用综合法（传统的方法）和空间向量两种方法来解决（向量法优先）强调数学通性通法的考查,淡化特殊技巧,无偏怪之题.立体几何专题的考查，理科和文科试卷，都强调对基础知识和基本能力的考查.文科相对强调几何的直观感知和简单的推理论证；而理科对空间想象、推理论证、运算求解有更高的要求.【学前准备】：多媒体，预习例题的面积为. 如图,在棱长为2的正方体到直线CC 1的距离的最小值为62的体积V）时，可，试判断V与V的大立体几何中的向量方法——求点坐标【教学目标】知识与技能：1、能够根据具体的立体图形寻找适当的位置建立空间直角坐标系；2、能够运用投影的知识解决相关点的坐标；3、能够利用中点坐标公式或者线段的比例关系解决相关点的坐标；4、能够掌握向量的相等、基本运算和共线等知识并应用于求点的坐标。

3.2 立体几何中的向量方法（2）【学习目标】1.掌握利用向量运算解几何题的方法，并能解简单的立体几何问题；2. 掌握向量运算在几何中求两点间距离和求空间图形中的角度的计算方法.【要点难点】利用向量运算解几何题【学习过程】一、自主预习（预习教材P105~ P107，找出迷惑之处.复习 1：已知a b 1 ， a 1, b 2 ，且 m 2a b ，求 m .复习 2：什么叫二面角？二面角的大小怎样胸怀？二面角的范围是什么？二、合作研究概括展现研究任务一：用向量求空间线段的长度问题：怎样用向量方法求空间线段的长度？三、议论沟通点拨提高2新知：用空间向量表示空间线段，而后利用公式aa 求出线段长度 .试一试：在长方体ABCD A' B'C ' D ' 中，已知AB 1,BC 2,CC'1,求 AC '的长 .反省：用向量方法求线段的长度，要点在于把未知量用已知条件中的向量表示.四、学能展现讲堂闯关例 1 如图，一个结晶体的形状为平行六面体，此中，以极点 A 为端点的三条棱长都相等，且它们相互的夹角都是60°，那么以这个极点为端点的晶体的对角线的长与棱长有什么关系？变式 1：上题中平行六面体的对角线BD1的长与棱长有什么关系？变式 2：假如一个平行六面体的各条棱长都相等，而且以某一极点为端点的各棱间的夹角都等于, 那么由这个平行六面体的对角线的长能够确立棱长吗?研究任务二：用向量求空间图形中的角度例 2 如图，甲站在水库底面上的点A处，乙站在水坝斜面上的点B处.从A，B到直线l（库底与水坝的交线）的距离 AC,BD 分别为 a, b ，CD的长为c， AB 的长为d .求库底与水坝所成二面角的余弦值 .变式 ：如图，60 的二面角的棱上有A, B两点，直线AC,BD 分别在这个二面角的两个半平面内，且都垂直于AB, 已知AB4, AC6,BD8,求 CD 的长 .※ 着手试一试练 1. 如图，已知线段AB 在平面α 内，线段DBD ' 30 ，假如 AB ＝ a ，AC ＝ BD ＝b ，求 ACC 、D ，线段间的距离 .BD ⊥ AB ，线段DD '，练 2. 如图， M 、N 分别是棱长为异面直线 MN 与 CD ' 所成的角 .1 的正方体ABCDA'B 'C 'D ' 的棱BB'、B' C ' 的中点．求五、学后反省※ 学习小结21. 求出空间线段的长度：用空间向量表示空间线段，而后利用公式aa ；2. 空间的二面角或异面直线的夹角，都能够转变为 利用公式 cos a ,ba b求解 .a b※ 知识拓展解空间图形问题时 ,能够分为 三步达成 :（ 1）成立立体图形与空间向量的联系，用空间向量表示问题中波及的点、直线、平面，把立体几何问题转变为向量问题 (还常成立坐标系来协助 )；（2）经过向量运算，研究点、直线、平面之间的地点关系以及它们之间距离和夹角等问题；（3）把向量的运算结果“翻译”成相应的几何意义 .【课后作业】：1. 如图，正方体ABCD A 'B 'C ' D ' 的棱长为1，M ,N 分别是BB', B'C'的中点，求：⑴MN ,CD '所成角的大小；⑵ MN , AD 所成角的大小；⑶ AN的。

3.2 立体几何中的向量方法-人教A版选修2-1教案一、教学目标1.了解向量的概念和性质；2.掌握立体几何中向量的加、减、数量积、向量积的计算方法；3.能够应用向量方法解决立体几何相关问题。

二、教学重点1.理解概念，掌握向量的加、减、数量积、向量积的计算方法；2.能够应用向量方法解决立体几何相关问题。

三、教学难点能够运用向量方法解决立体几何中的复杂问题。

四、教学内容及教学方法（一）教学内容本节课主要内容为立体几何中的向量方法，包括以下几个部分：1. 向量的概念和性质1.向量的定义；2.向量的模和方向；3.零向量和单位向量；4.向量的共线和平行；5.向量的反向和相等。

2. 向量的加减法1.向量的加法和减法定义；2.向量加减法的运算法则；3.向量相加减的几何意义。

3. 向量的数量积1.向量数量积的定义；2.向量数量积的运算法则；3.向量数量积的几何意义；4.向量数量积的性质。

4. 向量的向量积1.向量向量积的定义；2.向量向量积的运算法则；3.向量向量积的几何意义；4.向量向量积的性质。

（二）教学方法课堂教学应采用讲授与练习相结合的方法，通过引入具体的数学问题，逐步引入概念和定义，然后逐步将概念和定义转化为解决数学问题的方法。

在讲授的过程中，注意抓住学生对问题的兴趣点，让学生积极思考，在实际问题中理解各个概念和公式的含义。

五、教学过程安排（一）引入通过引入相关的实际问题，引发学生的兴趣和思考，达到引入立体几何中的向量方法的目的。

（二）概念和性质1.向量的定义和性质引入向量的定义和性质，引导学生理解向量的概念和性质，并能够熟练应用各种性质。

2.向量的共线和平行讲解向量的共线和平行的概念，巩固向量的基础概念。

3.向量的反向和相等讲解向量的反向和相等的概念，引导学生加深对向量的认识。

（三）向量的加减法通过具体例子引导学生理解向量加减的运算法则，并能够运用向量加减法解决实际问题。

1.向量加减法的定义和性质引导学生理解向量加减法的概念和性质，并掌握加减法的运算法则。

立体几何中的向量方法第一课时空间向量与平行、垂直关系预习课本P102～108，思考并完成以下问题1．平面的法向量的定义是什么？2．设直线l的方向向量u＝(a1，b1，c1)，平面α的法向量v＝(a2，b2，c2)，则l∥α，l ⊥α的充要条件分别是什么？[新知初探]1．平面的法向量(1)直线的方向向量直线的方向向量是指和这条直线平行或共线的向量．(2)平面的法向量直线l⊥α，取直线l的方向向量a，则a叫做平面α的法向量．2．空间平行关系的向量表示(1)线线平行设直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2，c2)，则l∥m⇔a∥b⇔a ＝λb⇔a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．(2)线面平行设直线l的方向向量为a＝(a1，b1，c1)，平面α的法向量为u＝(a2，b2，c2)，则l∥α⇔a⊥u⇔a·u＝0⇔a1a2＋b1b2＋c1c2＝0.(3)面面平行设平面α，β的法向量分别为u＝(a1，b1，c1)，v＝(a2，b2，c2)，则α∥β⇔u∥v⇔u＝λv ⇔a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．3．空间垂直关系的向量表示(1)线线垂直设直线l 的方向向量为a ＝(a 1，a 2，a 3)，直线m 的方向向量为b ＝(b 1，b 2，b 3)，则l ⊥m ⇔a ·b ＝0⇔a 1b 1＋a 2b 2＋a 3b 3＝0.(2)线面垂直设直线l 的方向向量是a ＝(a 1，b 1，c 1)，平面α的法向量是u ＝(a 2，b 2，c 2)，则l ⊥α⇔a ∥u ⇔a ＝λu ⇔a 1＝λa 2，b 1＝λb 2，c 1＝λc 2(λ∈R)．(3)面面垂直若平面α的法向量u ＝(a 1，b 1，c 1)，平面β的法向量v ＝(a 2，b 2，c 2)，则α⊥β ⇔u ⊥v ⇔u ·v ＝0⇔a 1a 2＋b 1b 2＋c 1c 2＝0.[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”) (1)直线l 的方向向量是惟一的( )(2)若点A ，B 是平面α上的任意两点，n 是平面α的法向量，则AB ·n ＝0( ) (3)若向量n 1，n 2为平面α的法向量，则以这两个向量为方向向量的两条不重合直线一定平行( )答案：(1)× (2)√ (3)√2．若A (1,0，－1)，B (2,1,2)在直线l 上，则直线l 的一个方向向量是( ) A ．(2,2,6) B ．(－1,1,3) C ．(3,1,1) D ．(－3,0,1)答案：A3．设直线l 1，l 2的方向向量分别为a ＝(－2,2,1)，b ＝(3，－2，m )，若l 1⊥l 2，则m 等于( )A ．－2B ．2C ．6D ．10 答案：D求平面的法向量[典例] α的一个法向量．[解] 因为A (1,2,3)，B (2,0，－1)，C (3，－2,0)，所以AB ＝(1，－2，－4)，AC ＝(2，－4，－3)．设平面α的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧n ·AB ＝0，n ·AC ＝0，即⎩⎪⎨⎪⎧x －2y －4z ＝0，2x －4y －3z ＝0.得z ＝0，x ＝2y ，令y ＝1，则x ＝2，所以平面α的一个法向量为n ＝(2,1,0)．利用待定系数法求法向量的解题步骤[活学活用]四边形ABCD 是直角梯形，∠ABC ＝90°，SA ⊥平面ABCD ，SA ＝AB ＝BC ＝2，AD ＝1.在如图所示的坐标系Axyz 中，分别求平面SCD 和平面SAB 的一个法向量．解：A (0,0,0)，D (1,0,0)，C (2,2,0)，S (0,0,2)．∵AD ⊥平面SAB ，∴AD ＝(1,0,0)是平面SAB 的一个法向量． 设平面SCD 的法向量为n ＝(1，y ，z )， 则n ·DC ＝(1，y ，z )·(1,2,0)＝1＋2y ＝0， ∴y ＝－12.又n ·DS ＝(1，y ，z )·(－1,0,2)＝－1＋2z ＝0， ∴z ＝12.∴n ＝⎝⎛⎭⎫1，－12，12即为平面SCD 的一个法向量. 用空间向量证明平行问题[典例] 11111DD 1的中点，求证：(1)FC 1∥平面ADE ； (2)平面ADE ∥平面B 1C 1F .[证明] 如图所示建立空间直角坐标系D -xyz ，则有D (0,0,0)，A (2,0,0)，C 1(0,2,2)，E (2,2,1)，F (0,0,1)，B 1(2，2,2)， 所以FC 1＝(0,2,1)，DA ＝(2,0,0)，AE ＝(0,2,1)．(1)设n 1＝(x 1，y 1，z 1)是平面ADE 的法向量， 则n 1⊥DA ，n 1⊥AE ，即⎩⎪⎨⎪⎧n 1·DA ＝2x 1＝0，n 1·AE ＝2y 1＋z 1＝0，得⎩⎪⎨⎪⎧x 1＝0，z 1＝－2y 1，令z 1＝2，则y 1＝－1， 所以n 1＝(0，－1,2)．因为FC 1·n 1＝－2＋2＝0，所以FC 1⊥n 1. 又因为FC 1⊄平面ADE ，所以FC 1∥平面ADE . (2)因为C B 11＝(2,0,0)，设n 2＝(x 2，y 2，z 2)是平面B 1C 1F 的一个法向量． 由n 2⊥FC 1，n 2⊥C B 11，得⎩⎪⎨⎪⎧n 2·FC 1＝2y 2＋z 2＝0，n 2·C B 11＝2x 2＝0，得⎩⎪⎨⎪⎧x 2＝0，z 2＝－2y 2.令z 2＝2，得y 2＝－1，所以n 2＝(0，－1,2)， 因为n 1＝n 2，所以平面ADE ∥平面B 1C 1F .利用向量法证明平行问题的两种途径(1)利用三角形法则和平面向量基本定理实现向量间的相互转化，得到向量的共线关系； (2)通过建立空间直角坐标系，借助直线的方向向量和平面的法向量进行平行关系的证明．[活学活用]在长方体ABCD -A 1B 1C 1D 1中，AB ＝4，AD ＝3，AA 1＝2，P ，Q ，R ，S 分别是AA 1，D 1C 1，AB ，CC 1的中点．求证：PQ ∥RS .证明：法一：以D 为原点，DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系D -xyz .则P (3,0,1)，Q (0,2,2)，R (3,2,0)，S (0,4,1)，PQ ＝(－3,2,1)，RS ＝(－3,2,1)，∴PQ ＝RS ，∴PQ ∥RS ，即PQ ∥RS .法二：RS ＝RC ＋CS ＝12DC －DA ＋12DD 1，PQ ＝PA 1＋A Q 1＝12DD 1＋12DC －DA ， ∴RS ＝PQ ，∴RS ∥PQ ， 即RS ∥PQ .利用空间向量证明垂直问题[典例] 如图，在四棱锥E -ABCD 中，AB ⊥平面BCE ，CD ⊥平面BCE ，AB ＝BC ＝CE ＝2CD ＝2，∠BCE ＝120°.求证：平面ADE ⊥平面ABE .[证明] 取BE 的中点O ，连接OC ，则OC ⊥EB ， 又AB ⊥平面BCE ，∴以O 为原点建立空间直角坐标系O -xyz .如图所示．则由已知条件有C (1,0,0)，E (0，－3，0)，D (1,0,1)，A (0，3，2)．设平面ADE 的法向量为n ＝(a ，b ，c )，则n ·EA ＝(a ，b ，c )·(0,23，2)＝23b ＋2c ＝0， n ·DA ＝(a ，b ，c )·(－1，3，1)＝－a ＋3b ＋c ＝0.令b＝1，则a＝0，c＝－3，∴n＝(0,1，－3)，又AB⊥平面BCE，∴AB⊥OC，∴OC⊥平面ABE，∴平面ABE的法向量可取为m＝(1,0,0)．∵n·m＝(0,1，－3)·(1,0,0)＝0，∴n⊥m，∴平面ADE⊥平面ABE.(1)用向量法判定线面垂直，只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直．(2)用向量法判定两个平面垂直，只需求出这两个平面的法向量，再看它们的数量积是否为0.在正方体ABCD-A1B1C1D1中，E，F分别为BB1，D1B1的中点，求证：EF⊥平面B1AC.证明：设正方体的棱长为2，建立如图所示的空间直角坐标系D-xyz，则A(2,0,0)，C(0,2,0)，B1(2,2,2)，E(2，2,1)，F(1,1,2)．法一：EF＝(－1，－1,1)，AB1＝(0,2,2)，AC＝(－2,2,0)，∴EF·AB1＝(－1，－1,1)·(0,2,2)＝0，EF ·AC＝(－1，－1,1)·(－2,2,0)＝0，∴EF⊥AB 1，EF⊥AC，又AB1∩AC＝A，∴EF⊥平面B 1AC.法二：设平面B1AC的法向量为n＝(x，y，z)．又AB1＝(0,2,2)，AC＝(－2,2,0)，则⎩⎪⎨⎪⎧ n ⊥AB 1，n ⊥AC ⇒⎩⎪⎨⎪⎧n ·AB 1＝2y ＋2z ＝0，n ·AC ＝－2x ＋2y ＝0，令x ＝1，可得平面B 1AC 的一个法向量为n ＝(1,1，－1)． 又EF ＝－n ，∴EF ∥n ，∴EF ⊥平面B 1AC .1．若n ＝(2，－3,1)是平面α的一个法向量，则下列向量中能作为平面α的法向量的是( )A ．(0，－3,1)B ．(2,0,1)C ．(－2，－3,1)D ．(－2,3，－1)解析：选D 问题即求与n 共线的一个向量．即n ＝(2，－3，1)＝－(－2,3，－1)． 2．已知直线l 与平面α垂直，直线l 的一个方向向量为u ＝(1，－3，z )，向量v ＝(3，－2,1)与平面α平行，则z 等于( )A ．3B ．6C ．－9D ．9解析：选C ∵l ⊥α，v 与平面α平行， ∴u ⊥v ，即u ·v ＝0， ∴1×3＋3×2＋z ×1＝0， ∴z ＝－9.3．已知A (1,0,0)，B (0,1,0)，C (0,0,1)，则平面ABC 的一个法向量是( ) A ．(1,1，－1) B ．(1，－1,1) C ．(－1,1,1) D ．(－1，－1，－1)解析：选DAB ＝(－1,1,0)，AC ＝(－1,0,1)．设平面ABC 的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧－x ＋y ＝0，－x ＋z ＝0，取x ＝－1，则y ＝－1，z ＝－1.故平面ABC 的一个法向量是(－1，－1，－1)．4．在正方体ABCD -A 1B 1C 1D 1中，若E 为A 1C 1的中点，则直线CE 垂直于( ) A ．AC B ．BD C ．A 1D D ．A 1A解析：选B 建立如图所示的空间直角坐标系．设正方体的棱长为1.则A (1,0,0)，B (1,1,0)，C (0,1,0)，D (0,0,0)，A 1(1,0,1)，C 1(0,1,1)，E ⎝⎛⎭⎫12，12，1， ∴CE ＝⎝⎛⎭⎫12，－12，1， AC ＝(－1,1,0)，BD ＝(－1，－1,0)，A D 1＝(－1,0，－1)，A A 1＝(0,0，－1)．∵CE ·BD ＝(－1)×12＋(－1)×⎝⎛⎭⎫－12＋0×1＝0，∴CE ⊥BD . 5.如图，在平行六面体ABCD -A 1B 1C 1D 1中，点M ，P ，Q 分别为棱AB ，CD ，BC 的中点，平行六面体的各棱长均相等．给出下列结论：①A 1M ∥D 1P ； ②A 1M ∥B 1Q ； ③A 1M ∥平面DCC 1D 1； ④A 1M ∥平面D 1PQB 1.这四个结论中正确的个数为( ) A ．1 B ．2 C ．3D ．4解析：选C ∵A M 1＝A A 1＋AM ＝A A 1＋12AB ，D P 1＝D D 1＋DP ＝A A 1＋12AB ，∴A M 1∥D P 1，从而A 1M ∥D 1P ，可得①③④正确． 又B 1Q 与D 1P 不平行，故②不正确．6. 已知点P 是平行四边形ABCD 所在的平面外一点，如果AB ＝(2，－1，－4)，AD ＝(4,2,0)，AP ＝(－1,2，－1)．对于结论：①AP ⊥AB ；②AP ⊥AD ；③AP 是平面ABCD 的法向量；④AP ∥BD .其中正确的是_______(填序号)．解析：由于AP ·AB ＝－1×2＋(－1)×2＋(－4)×(－1)＝0，AP ·AD ＝4×(－1)＋2×2＋0×(－1)＝0，所以①②③正确． 答案：①②③7．在直角坐标系O -xyz 中，已知点P (2cos x ＋1,2cos 2x ＋2,0)和点Q (cos x ，－1,3)，其中x ∈[0，π]，若直线OP 与直线OQ 垂直，则x 的值为________．解析：由OP ⊥OQ ，得OP ·OQ ＝0. 即(2cos x ＋1)·cos x ＋(2cos 2x ＋2)·(－1)＝0. ∴cos x ＝0或cos x ＝12.∵x ∈[0，π]，∴x ＝π2或x ＝π3.答案：π2或π38.如图所示，在直三棱柱ABC -A 1B 1C 1中，底面是以∠ABC 为直角的等腰三角形，AC ＝2a ，BB 1＝3a ，D 是A 1C 1的中点，点E 在棱AA 1上，要使CE ⊥面B 1DE ，则AE ＝________.解析：建立如图所示的空间直角坐标系， 则B 1(0,0,3a )，C (0，2a,0)， D2a 2，2a 2，3a . 设E (2a,0，z )(0≤z ≤3a )， 则CE ＝()2a ，－2a ，z ，B E 1＝(2a,0，z －3a )，B D 1＝⎝⎛⎭⎫2a 2，2a2，0.又CE ·B D 1＝a 2－a 2＋0＝0，故由题意得2a 2＋z 2－3az ＝0，解得z ＝a 或2a . 故AE ＝a 或2a . 答案：a 或2a9.如图，在四棱锥P -ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD ＝DC ，E 为PC 的中点，EF ⊥BP 于点F .求证：(1)PA ∥平面EDB ； (2)PB ⊥平面EFD .证明：以D 为坐标原点，DA ，DC ，DP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系D -xyz ，如图，设DC ＝PD ＝1，则P (0,0,1)，A (1,0,0)，D (0,0,0)，B (1,1,0)，E ⎝⎛⎭⎫0，12，12. ∴PB ＝(1,1，－1)，DE ＝⎝⎛⎭⎫0，12，12，EB ＝⎝⎛⎭⎫1，12，－12，设F (x ，y ，z )，则PF ＝(x ，y ，z －1)，EF ＝⎝⎛⎭⎫x ，y －12，z －12. ∵EF ⊥PB ，∴x ＋⎝⎛⎭⎫y －12－⎝⎛⎭⎫z －12＝0，即x ＋y －z ＝0.① 又∵PF ∥PB ，可设PF ＝λPB ， ∴x ＝λ，y ＝λ，z －1＝－λ.② 由①②可知，x ＝13，y ＝13，z ＝23，∴EF ＝⎝⎛⎭⎫13，－16，16. (1)设n 1＝(x 1，y 1，z 1)为平面EDB 的一个法向量，则有⎩⎪⎨⎪⎧n 1·DE ＝0，n 1·EB ＝0，即⎩⎨⎧12y 1＋12z 1＝0，x 1＋12y 1－12z 1＝0，∴⎩⎪⎨⎪⎧x 1＝z 1，y 1＝－z 1. 取z 1＝－1，则n 1＝(－1,1，－1)． ∵PA ＝(1,0，－1)，∴PA ·n 1＝0. 又∵PA ⊄平面EDB ，∴PA ∥平面EDB .(2)设n 2＝(x 2，y 2，z 2)为平面EFD 的一个法向量，则有⎩⎪⎨⎪⎧n 2·EF ＝0，n 2·DE ＝0，即⎩⎨⎧13x 2－16y 2＋16z 2＝0，12y 2＋12z 2＝0，∴⎩⎪⎨⎪⎧x 2＝－z 2，y 2＝－z 2.取z 2＝1，则n 2＝(－1，－1,1)．∴PB ∥n 2，∴PB ⊥平面EFD .10．已知在长方体ABCD -A 1B 1C 1D 1中，E ，M 分别是BC ，AE 的中点，AD ＝AA 1＝a ，AB ＝2a .试问在线段CD 1上是否存在一点N 使MN ∥平面ADD 1A 1，若存在确定N 的位置，若不存在说明理由．解：以D 为原点，建立如图所示的空间直角坐标系， 则A (a ，0,0)，B (a,2a,0)， C (0，2a,0)，D 1(0,0，a )， E ⎝⎛⎭⎫12a ，2a ，0，M ⎝⎛⎭⎫34a ，a ，0， DC ＝(0,2a,0)，CD 1＝(0，－2a ，a )，假设CD 1上存在点N 使MN ∥平面ADD 1A 1并设CN ＝λCD 1＝(0，－2aλ，aλ)(0<λ<1)．则DN ＝DC ＋CN ＝(0,2a,0)＋(0，－2aλ，aλ) ＝(0,2a (1－λ)，aλ)，MN ＝DN －DM ＝⎝⎛⎭⎫－34a ，a －2aλ，aλ. 又DC 是平面ADD 1A 1的一个法向量． ∴MN ⊥DC ，则2a (a －2aλ)＝0，λ＝12.又MN ⊄平面ADD 1A 1.故存在N 为CD 1的中点使MN ∥平面ADD 1A 1.层级二 应试能力达标1．已知a ＝⎝⎛⎭⎫1，2，52，b ＝⎝⎛⎭⎫32，x ，y 分别是直线l 1，l 2的一个方向向量．若l 1∥l 2，则( )A ．x ＝3，y ＝152B ．x ＝32，y ＝154C ．x ＝3，y ＝15D ．x ＝3，y ＝154解析：选D ∵l 1∥l 2，∴321＝x 2＝y 52，∴x ＝3，y ＝154，故选D.2.在如图所示的空间直角坐标系中，ABCD -A 1B 1C 1D 1是棱长为1的正方体，给出下列结论：①平面ABB 1A 1的一个法向量为(0,1,0)； ②平面B 1CD 的一个法向量为(1,1,1)； ③平面B 1CD 1的一个法向量为(1,1,1)； ④平面ABC 1D 1的一个法向量为(0,1,1)． 其中正确结论的个数为( ) A ．1 B ．2 C ．3D ．4解析：选B ∵AD ＝(0,1,0)，AB ⊥AD ，AA 1⊥AD ，又AB ∩AA 1＝A ，∴AD ⊥平面ABB 1A 1，∴①正确；∵CD ＝(－1,0,0)，而(1,1,1)·CD ＝－1≠0，∴(1,1,1)不是平面B 1CD 的法向量，∴②不正确；∵B C 1＝(0,1，－1)，CD 1＝(－1,0,1)，(1,1,1)·B C 1＝0，(1,1,1)·CD 1＝0，B 1C ∩CD 1＝C ，∴(1,1,1)是平面B 1CD 1的一个法向量，∴③正确；∵BC 1＝(0,1,1)，而BC 1·(0,1,1)＝2≠0，∴(0,1,1)不是平面ABC 1D 1的法向量，即④不正确．因此正确结论的个数为2，选B.3．已知平面α内有一个点A (2，－1,2)，α的一个法向量为n ＝(3,1,2)，则下列点P 中，在平面α内的是( )A ．(1，－1,1) B.⎝⎛⎭⎫1，3，32 C.⎝⎛⎭⎫1，－3，32D.⎝⎛⎭⎫－1，3，－32 解析：选B 要判断点P 是否在平面α内，只需判断向量与平面α的法向量n 是否垂直，即·n 是否为0，因此，要对各个选项进行检验．对于选项A ，＝(1,0,1)，则·n ＝(1,0,1)·(3,1,2)＝5≠0，故排除A ；对于选项B ，＝⎝⎛⎭⎫1，－4，12，则·n ＝⎝⎛⎭⎫1，－4，12·(3,1,2)＝0，故B 正确；同理可排除C 、D.故选B.4.在正方体ABCD -A 1B 1C 1D 1中，棱长为a ，M ，N 分别为A 1B ，AC 的中点，则MN 与平面BB 1C 1C 的位置关系是( )A ．相交B ．平行C ．垂直D ．不能确定解析：选B 建系如图，设正方体的棱长为2，则A (2,2,2)，A 1(2,2,0)，C (0,0,2)，B (2,0,2)，∴M (2,1,1)，N (1,1,2)， ∴MN ＝(－1,0,1)．又平面BB 1C 1C 的一个法向量为n ＝(0,1,0)， ∵－1×0＋0×1＋1×0＝0， ∴MN ⊥n ，∴MN ∥平面BB 1C 1C .故选B.5．若直线l 的一个方向向量为a ＝(1,0,2)，平面α的一个法向量为u ＝(－2,0，－4)，则直线l 与平面α的位置关系为________．解析：∵u ＝－2a ，∴a ∥u ，∴l ⊥α. 答案：l ⊥α6．已知AB ＝(1,5，－2)，BC ＝(3,1，z )，若AB ⊥BC ，BP ＝(x －1，y ，－3)，且BP ⊥平面ABC ，则BP ＝________.解析：∵AB ⊥BC ，∴AB ·BC ＝0，∴3＋5－2z ＝0， ∴z ＝4.∵BP ＝(x －1，y ，－3)，且BP ⊥平面ABC ，∴⎩⎪⎨⎪⎧BP ·AB ＝0， BP ·BC ＝0，即⎩⎪⎨⎪⎧x －1＋5y ＋6＝0，3x －3＋y －12＝0，解得⎩⎨⎧x ＝407，y ＝－157，故BP ＝⎝⎛⎭⎫337，－157，－3. 答案：⎝⎛⎭⎫337，－157，－3 7.如图，在正四棱柱ABCD -A 1B 1C 1D 1中，底面边长为22，侧棱长为4，E ，F 分别是棱AB ，BC 的中点．求证：平面B 1EF ⊥平面BDD 1B 1.证明：以D 为坐标原点，DA ，DC ，DD 1所在的直线分别为x 轴、y 轴、z轴建立空间直角坐标系如图，由题意，知D (0,0,0)，A (22，0,0)，C (0,22，0)，B 1(22，22，4)， E (22，2，0)，F (2，22，0)， 则B E 1＝(0，－2，－4)，EF ＝(－2，2，0)．设平面B 1EF 的法向量为n ＝(x ，y ，z )．则n ·B E 1＝－2y －4z ＝0，n ·EF ＝－2x ＋2y ＝0， 得x ＝y ，z ＝－24y ，令y ＝1，得n ＝⎝⎛⎭⎫1，1，－24.又平面BDD 1B 1的一个法向量为AC ＝(－22，22，0)， 而n ·AC ＝1×(－22)＋1×22＋⎝⎛⎭⎫－24×0＝0， 即n ⊥AC ，∴平面B 1EF ⊥平面BDD 1B 1.8.如图，在三棱锥P -ABC 中，三条侧棱PA ，PB ，PC 两两垂直，且PA ＝PB ＝PC ＝3，G 是△PAB 的重心，E ，F 分别为BC ，PB 上的点，且BE ∶EC ＝PF ∶FB ＝1∶2.(1)求证：平面GEF ⊥平面PBC ； (2)求证：EG 与直线PG 和BC 都垂直．证明：(1)如图，以三棱锥的顶点P 为原点，以PA ，PB ，PC 所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系P -xyz .则A (3,0,0)，B (0,3,0)，C (0,0,3)，E (0,2,1)，F (0,1,0)，G (1,1,0)，P (0，0,0)． 于是EF ＝(0，－1，－1)，EG ＝(1，－1，－1)． 设平面GEF 的法向量是n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ⊥EF ，n ⊥EG ，即⎩⎪⎨⎪⎧y ＋z ＝0，x －y －z ＝0，可取n ＝(0,1，－1)．显然PA ＝(3,0,0)是平面PBC 的一个法向量． 又n ·PA ＝0， ∴n ⊥PA ，即平面PBC 的法向量与平面GEF 的法向量垂直， ∴平面GEF ⊥平面PBC .(2)由(1)，知EG ＝(1，－1，－1)，PG ＝(1,1,0)，BC ＝(0，－3,3)，∴EG ·PG ＝0，EG ·BC ＝0， ∴EG ⊥PG ，EG ⊥BC ，∴EG 与直线PG 和BC 都垂直．第二课时 空间向量与空间角、距离预习课本P109～110，思考并完成以下问题1．如何利用空间向量求两异面直线所成的角，直线与平面所成的角及二面角？2．如何利用空间向量求点到平面的距离？[新知初探]1．空间角及向量求法 角的分类 向量求法范围 异面直线所成的角设两异面直线所成的角为θ，它们的方向向量为a ，b ，则cos θ＝|cos 〈a ，b 〉|＝|a ·b ||a ||b |0，π2直线与平面所成的角设直线l与平面α所成的角为θ，l的方向向量为a，平面α的法向量为n，则sin θ＝|cos〈a，n〉|＝|a·n||a||n|0，π2二面角设二面角α-l-β的平面角为θ，平面α，β的法向量为n1，n2，则|cos θ|＝|cos〈n1，n2〉|＝|n1·n2||n1||n2|[0，π] 2．空间距离的向量求法分类向量求法两点距设A，B为空间中任意两点，则d＝|AB|点面距设平面α的法向量为n，B∉α，A∈α，则B点到平面α的距离d＝|BA·n||n|[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)(1)两异面直线所成的角与两直线的方向向量所成的角相等()(2)直线l与平面α的法向量的夹角的余角就是直线l与平面α所成的角()(3)二面角α-l-β的大小为θ，平面α，β的法向量分别为n1，n2，则θ＝n1，n2()答案：(1)×(2)×(3)×2．已知向量m，n分别是直线l和平面α的方向向量、法向量，若cos m，n＝－12，则直线l与平面α所成的角为()A．30°B．60°C．120°D．150°答案：A3．已知两平面的法向量分别为m＝(0,1,0)，n＝(0,1,1)，则两平面所成的二面角的大小为()A．45°B．135°C．45°或135°D．90°答案：C求两异面直线所成的角[典例]顶点A，B，V分别在x，y，z轴上，D是线段AB的中点，且AC＝BC＝2，∠VDC ＝π3，求异面直线AC 与VD 所成角的余弦值．[解] AC ＝BC ＝2，D 是AB 的中点，所以 C (0,0,0)，A (2,0,0)，B (0,2,0)，D (1,1,0)．在Rt △VCD 中，CD ＝2，∠VDC ＝π3，故V (0,0，6)．所以AC ＝(－2,0,0)，VD ＝(1,1，－6)．所以cos 〈AC ，VD 〉＝AC ·VD |AC ||VD |＝－22·22＝－24.所以异面直线AC 与VD 所成角的余弦值为24.利用空间向量求两条异面直线所成的角，可以避免复杂的几何作图和论证过程，只需通过相应的向量运算即可，但应注意：用向量法求两条异面直线所成的角是通过两条直线的方向向量的夹角来求解的，而两条异面直线所成角θ的取值范围是0，π2，两向量的夹角α的取值范围是[0，π]，所以cos θ＝|cos α|.[活学活用]如图所示，在平行六面体ABCD －A 1B 1C 1D 1中，面ABCD 与面D 1C 1CD 垂直，且∠D 1DC ＝π3，DC ＝DD 1＝2，DA ＝3，∠ADC ＝π2，求异面直线A 1C 与AD 1所成角的余弦值．解：建立如图所示的空间直角坐标系，则A (3，0,0)，D 1(0,1，3)，C (0,2,0)，D (0,0,0)．由AA 1＝DD 1得A 1(3，1，3)． ∴A C 1＝(－3，1，－3)．D A 1＝(3，－1，－3)．∴cos 〈A C 1，D A 1〉＝A C 1·D A1| A C 1|·|D A 1|＝(－3，1，－3)·(3，－1，－3)7·7＝－17.∴异面直线A 1C 与AD 1所成角的余弦值为17.求直线与平面所成的角[典例] 如图，在四棱锥P -ABCD 中，底面为直角梯形，AD ∥BC ，∠BAD ＝90°，PA ⊥底面ABCD ，且PA ＝AD ＝AB ＝2BC ，M ，N 分别为PC ，PB 的中点．(1)求证：PB ⊥DM ；(2)求BD 与平面 ADMN 所成的角．[解] 如图，以点A 为坐标原点建立空间直角坐标系，设BC ＝1，则A (0,0,0)，P (0,0,2)，B (2,0,0)，D (0,2,0)，C (2,1,0)，M ⎝⎛⎭⎫1，12，1. (1)证明：PB ·DM ＝(2,0，－2)·⎝⎛⎭⎫1，－32，1＝0， ∴PB ⊥DM ，即PB ⊥DM .(2)∵PB ·AD ＝(2,0，－2)·(0,2,0)＝0， ∴PB ⊥AD .又∵PB ⊥DM ，∴PB ⊥平面ADMN . 即PB 为平面ADMN 的一个法向量．因此〈PB ，DB 〉的余角即是BD 与平面ADMN 所成的角．∵cos 〈PB ，DB 〉＝PB ·DB | PB |·|DB |＝422×22＝12，∴〈PB ，DB 〉＝π3，∴BD 与平面ADMN 所成的角为π6.求直线与平面的夹角的方法与步骤思路一：找直线在平面内的射影，充分利用面与面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值)．思路二：用向量法求直线与平面的夹角可利用向量夹角公式或法向量．利用法向量求直线与平面的夹角的基本步骤：(1)建立空间直角坐标系； (2)求直线的方向向量AB ； (3)求平面的法向量n ；(4)计算：设线面角为θ，则sin θ＝|n ·AB ||n |·|AB |.[活学活用]如图所示，在正方体ABCD -A 1B 1C 1D 1 中，E 是棱DD 1的中点． 求直线BE 和平面ABB 1A 1所成的角的正弦值．解：设正方体的棱长为 1.如图所示，以AB ，AD ，AA 1为单位正交基底建立空间直角坐标系O -xyz .依题意，得B (1,0,0)，E 0,1，12，A (0,0,0)，D (0,1,0)，所以BE ＝⎝⎛⎭⎫－1，1，12，AD ＝(0,1,0)．在正方体ABCD -A 1B 1C 1D 1中，因为AD ⊥平面ABB 1A 1，所以AD 是平面ABB 1A 1的一个法向量．设直线BE 和平面ABB 1A 1所成的角为θ，则sin θ＝|BE ·AD ||BE |·|AD |＝132×1＝23.故直线BE 和平面ABB 1A 1所成的角的正弦值为23.求二面角[典例] 如图，四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等，AC ∩BD ＝O ，A 1C 1∩B 1D 1＝O 1，四边形ACC 1A 1和四边形BDD 1B 1均为矩形．(1)证明：O 1O ⊥底面ABCD .(2)若∠CBA ＝60°，求二面角C 1-OB 1-D 的余弦值．[解] (1)证明：因为四边形ACC 1A 1和四边形BDD 1B 1均为矩形，所以CC 1⊥AC ，DD 1⊥BD ，又CC 1∥DD 1∥OO 1，所以OO 1⊥AC ，OO 1⊥BD ， 因为AC ∩BD ＝O ，所以O 1O ⊥底面ABCD .(2)因为四棱柱的所有棱长都相等，所以四边形ABCD 为菱形，AC ⊥BD .又O 1O ⊥底面ABCD ，所以OB ，OC ，OO 1两两垂直．如图，以O 为原点，OB ，OC ，OO 1所在直线分别为x ，y ，z 轴，建立空间直角坐标系．设棱长为2，因为∠CBA ＝60°，所以OB ＝3，OC ＝1， 所以O (0,0,0)，B 1(3，0,2)，C 1(0,1,2)， 平面BDD 1B 1的一个法向量为n ＝(0,1,0)， 设平面OC 1B 1的法向量为m ＝(x ，y ，z )，则由m ⊥OB 1，m ⊥OC 1，所以⎩⎪⎨⎪⎧3x ＋2z ＝0，y ＋2z ＝0取z ＝－3，则x ＝2，y ＝23， 所以m ＝(2,23，－3)， 所以cos m ，n ＝m·n |m ||n |＝2319＝25719. 由图形可知二面角C 1-OB 1-D 的大小为锐角， 所以二面角C 1-OB 1-D 的余弦值为25719.[一题多变]1．[变设问]本例条件不变，求二面角B -A 1C -D 的余弦值． 解：建立如图所示的空间直角坐标系．设棱长为2，则A 1(0，－1,2)，B (3，0,0)，C (0,1,0)，D ()－3，0，0.所以BC ＝()－3，1，0，A C 1＝(0,2，－2)，CD ＝(－3，－1,0)． 设平面A 1BC 的法向量为n 1＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧n 1·A C 1＝0，n 1·BC ＝0，即⎩⎪⎨⎪⎧2y 1－2z 1＝0，－3x 1＋y 1＝0，取x 1＝3，则y 1＝z 1＝3， 故n 1＝(3，3,3)．设平面A 1CD 的法向量为n 2＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧n 2·A C 1＝0，n 2·A C 1＝0，即⎩⎪⎨⎪⎧2y 2－2z 2＝0，－3x 2－y 2＝0，取x 2＝3，则y 2＝z 2＝－3， 故n 2＝(3，－3，－3)． 所以cos n 1，n 2＝n 1·n 2|n 1||n 2|＝－1521＝－57. 由图形可知二面角B -A 1C -D 的大小为钝角， 所以二面角B -A 1C -D 的余弦值为－57.2．[变条件、变设问]本例四棱柱中，∠CBA ＝60°改为∠CBA ＝90°，设E ，F 分别是棱BC ，CD 的中点，求平面AB 1E 与平面AD 1F 所成锐二面角的余弦值．解：以A 为坐标原点建立空间直角坐标系，如图所示，设此棱柱的棱长为1，则A (0,0,0)，B 1(1,0,1)，E ⎝⎛⎭⎫1，12，0，D 1(0,1,1)， F ⎝⎛⎭⎫12，1，0，AE ＝⎝⎛⎭⎫1，12，0，AB 1＝(1,0,1)，AF ＝⎝⎛⎭⎫12，1，0，AD 1＝(0,1,1)． 设平面AB 1E 的法向量为n 1＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧n 1·AB 1＝0，n 1·AE ＝0，即⎩⎪⎨⎪⎧x 1＋z 1＝0，x 1＋12y 1＝0，令y 1＝2，则x 1＝－1，z 1＝1，所以n 1＝(－1,2,1)．设平面AD 1F 的法向量为n 2＝(x 2，y 2，z 2)．则⎩⎪⎨⎪⎧n 2·AD 1＝0，n 2·AF ＝0，即⎩⎪⎨⎪⎧y 2＋z 2＝0，12x 2＋y 2＝0.令x 2＝2，则y 2＝－1，z 2＝1. 所以n 2＝(2，－1,1)．所以平面AB 1E 与平面AD 1F 所成锐二面角的余弦值为|n 1·n 2||n 1||n 2|＝36×6＝12.向量法求二面角(或其某个三角函数值)的四个步骤(1)建立适当的坐标系，写出相应点的坐标； (2)求出两个半平面的法向量n 1，n 2；(3)设二面角的平面角为θ，则|cos θ|＝|cos n 1，n 2|；(4)根据图形判断θ为钝角还是锐角，从而求出θ(或其三角函数值)．用空间向量求距离[典例] 四棱锥P -ABCD 中，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ＝DA ＝2，F ，E 分别为AD ，PC 的中点．(1)求证：DE ∥平面PFB ； (2)求点E 到平面PFB 的距离．[解] (1)证明：以D 为原点， 建立如图所示的空间直角坐标系， 则P (0,0,2)，F (1,0,0)，B (2,2,0)，E (0,1,1)．FP ＝(－1,0,2)，FB ＝(1,2,0)，DE ＝(0,1,1)，∴DE ＝12FP ＋12FB ，∴DE ∥平面PFB . 又∵DE ⊄平面PFB ，∴DE ∥平面PFB . (2)∵DE ∥平面PFB ，∴点E 到平面PFB 的距离等于点D 到平面PFB 的距离． 设平面PFB 的一个法向量n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·FB ＝0，n ·FP ＝0⇒⎩⎪⎨⎪⎧x ＋2y ＝0，－x ＋2z ＝0，令x ＝2，得y ＝－1，z ＝1.∴n ＝(2，－1,1)，又∵FD ＝(－1,0,0)， ∴点D 到平面PFB 的距离 d ＝|FD ·n ||n |＝26＝63. ∴点E 到平面PFB 的距离为63.求点到平面的距离的四步骤[活学活用]在棱长为1的正方体ABCD -A 1B 1C 1D 1中，E ，F 分别是A 1B 1，CD 的中点，求点B 到平面AEC 1F 的距离．解：以D 为原点，建立如图所示的空间直角坐标系，则A (1,0,0)，F ⎝⎛⎭⎫0，12，0，E ⎝⎛⎭⎫1，12，1，B (1,1,0)．∴AE ＝⎝⎛⎭⎫0，12，1，AF ＝－1，12，0. 设平面AEC 1F 的法向量为n ＝(1，λ，μ)，则n ·AE ＝0，n ·AF ＝0.∴⎩⎨⎧12λ＋μ＝0，－1＋12λ＝0，∴⎩⎪⎨⎪⎧λ＝2，μ＝－1， ∴n ＝(1,2，－1)． 又∵AB ＝(0,1,0)，∴点B 到平面AEC 1F 的距离d ＝|AB ·n |＝26＝63.1．已知平面α的一个法向量为n ＝(－2，－2,1)，点A (－1,3,0)在平面α内，则点P (－2,1,4)到平面α的距离为( )A ．10B ．3 C.83D.103解析：选D 点P 到平面α的距离d ＝|PA ·n |＝|－2－4－4|4＋4＋1＝103.2．已知正四棱柱ABCD -A 1B 1C 1D 1中，AA 1＝2AB ，则CD 与平面BDC 1所成角的正弦值等于( )A.23 B.33C.23D.13解析：选A 建立如图所示的空间直角坐标系，设AA 1＝2AB ＝2，则B (1,1,0)，C (0,1,0)，D (0,0,0)，C 1(0,1,2)，故DB ＝(1,1,0)，DC 1＝(0,1,2)，DC＝(0,1,0)．设平面BDC 1的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·DB ＝0，n ·DC 1＝0，即⎩⎪⎨⎪⎧x ＋y ＝0，y ＋2z ＝0，令z ＝1，则y ＝－2，x ＝2，所以平面BDC 1的一个法向量为n ＝(2，－2,1)．设直线CD 与平面BDC 1所成的角为θ，则sin θ＝|cos 〈n ，DC 〉|＝|n ·DC ||n |·|DC |＝23，故选A.3．在60°的二面角α-l -β的棱l 上有两点A ，B ，直线AC ，BD 分别在这个二面角的两个半平面内，AC ⊥l ，BD ⊥l ，若AB ＝4，AC ＝6，BD ＝8，则CD 的长为( )A ．229B ．217C ．2 5D ．241解析：选B 由已知，可得AC ⊥AB ，BD ⊥AB ，∵二面角的大小为60°，则〈，〉＝60°.∴〈，〉＝120°，∴||2＝(＋＋)2＝||2＋||2＋||2＋2·＋2·＋2·36＋16＋64＋2×6×8×cos 120°＝68.∴CD ＝68＝217.4．在长方体ABCD -A 1B 1C 1D 1中，AB ＝2，BC ＝2，DD 1＝3，则AC 与BD 1所成角的余弦值为( )A ．0 B.37070 C ．－37070 D.7070解析：选A 建立如图坐标系，则D 1(0,0,3)，B (2,2,0)，A (2,0,0)，C (0,2,0)，∴BD 1＝(－2，－2,3)，AC ＝(－2,2,0)．∴cos 〈BD 1，AC 〉＝BD 1·AC|BD 1||AC |＝0.∴〈BD 1，AC 〉＝90°，其余弦值为0.5．正方形ABCD 所在平面外有一点P ，PA ⊥平面ABCD .若PA ＝AB ，则平面PAB 与平面PCD 所成的二面角的大小为( )A ．30°B ．45°C ．60°D ．90° 解析：选B 建系如图，设AB ＝1， 则A (0,0,0)，B (0,1,0)， P (0,0,1)，D (1,0,0)，C (1,1,0)． 平面PAB 的法向量为n 1＝(1,0,0)． 设平面PCD 的法向量n 2＝(x ，y ，z )，则⎩⎪⎨⎪⎧n 2·PD ＝0，n 2·CD ＝0，得⎩⎪⎨⎪⎧x －z ＝0，y ＝0.令x ＝1，则z ＝1.∴n 2＝(1,0,1)， cos 〈n 1，n 2〉＝12＝22. ∴平面PAB 与平面PCD 所成的二面角的余弦值为22. ∴此角的大小为45°.6．直线l 的方向向量a ＝(－2,3,2)，平面α的一个法向量n ＝(4,0,1)，则直线l 与平面α所成角的正弦值为___________________________________________________________．解析：设直线l 与平面α所成的角是θ，a ，n 所成的角为β，sin θ＝|cos β|＝|(－2，3，2)·(4，0，1)|17×17＝617. 答案：6177．在正方体ABCD -A 1B 1C 1D 1中，M ，N 分别是棱AA 1和BB 1的中点，则sin 〈CM ，D N 1〉＝________.解析：建立如图所示空间直角坐标系，设正方体棱长为2. 则C (0,2,0)，M (2,0,1)，D 1(0,0,2)，N (2,2,1)． ∴CM ＝(2，－2,1)，D N 1＝(2,2，－1)．cos 〈CM ，D N 1〉＝4－4－13×3＝－19.∴sin 〈CM ，D N 1〉＝459.答案：4598.如图正方体ABCD -A 1B 1C 1D 1的棱长为1，O 是平面A 1B 1C 1D 1的中心，则BO 与平面ABC 1D 1所成角的正弦值为________．解析：建立空间直角坐标系如图，则B (1,1,0)，O ⎝⎛⎭⎫12，12，1，DA 1＝(1,0,1)是平面ABC 1D 1的一个法向量．又OB ＝⎝⎛⎭⎫12，12，－1，∴BO 与平面ABC 1D 1所成角的正弦值为 |OB ·DA 1||OB |·|DA 1|＝1262×2＝36. 答案：369.如图，在四棱锥PABCD 中，AB ⊥PA ，AB ∥CD ，且PB ＝BC ＝BD ＝6，CD ＝2AB ＝22，∠PAD ＝120°.(1)求证：平面PAD ⊥平面PCD ；(2)求直线PD 与平面PBC 所成的角的正弦值． 解：(1)证明：取CD 的中点E ，连接BE . ∵BC ＝BD ，E 为CD 中点，∴BE ⊥CD ， 又∵AB ∥CD ，AB ＝12CD ＝DE ，∴四边形ABED 是矩形，∴AB ⊥AD ，又AB ⊥PA ，PA ⊂平面PAD ，AD ⊂平面PAD ，PA ∩AD ＝A ，∴AB ⊥平面PAD . ∵AB ∥CD ，∴CD ⊥平面PAD ， 又CD ⊂平面PCD ， ∴平面PAD ⊥平面PCD .(2)以A 为原点，AB 为x 轴，AD 为y 轴，以平面ABCD 过点A 的垂线为z 轴建立空间直角坐标系Axyz ，如图所示：∵PB ＝BD ＝6，AB ＝2，AB ⊥PA ，AB ⊥AD ， ∴PA ＝AD ＝2.∴P (0，－1，3)，D (0,2,0)，B (2，0,0)，C (22，2,0)， ∴＝(0,3，－3)，＝(－2，－1，3)，＝(2，2,0)．设平面PBC 的法向量n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·＝0，n ·＝0.∴⎩⎪⎨⎪⎧2x ＋2y ＝0，－2x －y ＋3z ＝0， 取x ＝2，得n ＝⎝⎛⎭⎫2，－1，33，∴cos 〈n ，〉＝n ·|n |||＝－4103·23＝－105. ∴直线PD 与平面PBC 所成的角的正弦值为105. 10.如图，四棱锥P -ABCD 中，PA ⊥底面ABCD ，AB ∥CD ，AD ＝CD ＝1，∠BAD ＝120°，∠ACB ＝90°.(1)求证：BC ⊥平面PAC ； (2)若二面角D -PC -A 的余弦值为55，求点A 到平面PBC 的距离． 解：(1)证明：∵PA ⊥底面ABCD ，BC ⊂平面ABCD ， ∴PA ⊥BC ，∵∠ACB ＝90°，∴BC ⊥AC ，又PA ∩AC ＝A ， ∴BC ⊥平面PAC .(2)设AP ＝h ，取CD 的中点E ，则AE ⊥CD ，∴AE ⊥AB .又PA ⊥底面ABCD ，∴PA ⊥AE ，PA ⊥AB ，故建立如图所示的空间直角坐标系，则A (0,0,0)，P (0,0，h )，C32，12，0， D32，－12，0，B (0,2,0)， PC ＝⎝⎛⎭⎫32，12，－h ，DC ＝(0,1,0)，设平面PDC 的法向量n 1＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧n 1·PC ＝0，n 1·DC ＝0，即⎩⎪⎨⎪⎧32x 1＋12y 1－hz 1＝0，y 1＝0，取x 1＝h ，∴n 1＝⎝⎛⎭⎫h ，0，32. 由(1)知平面PAC 的一个法向量为BC ＝32，－32，0， ∴|cos n 1，BC|＝32h h 2＋34×3＝55， 解得h ＝3，同理可求得平面PBC 的一个法向量n 2＝(3，3，2)， 所以，点A 到平面PBC 的距离为 d ＝|AP ·n 2||n 2|＝234＝32. 层级二 应试能力达标1.如图所示，已知四棱锥P -ABCD 中，底面ABCD 是菱形，且PA ⊥平面ABCD ，PA ＝AD ＝AC ，点F 为PC 的中点，则二面角C -BF -D 的正切值为( )A.36 B.34C.33D.233解析：选D 如图所示，设AC 与BD 交于O ，连接OF .以O 为坐标原点，OB ，OC ，OF 所在直线分别为x ，y ，z 轴建立空间直角坐标系O -xyz .设PA ＝AD ＝AC ＝1，则BD ＝3， 所以O (0,0,0)，B⎝⎛⎭⎫32，0，0，F ⎝⎛⎭⎫0，0，12，C ⎝⎛⎭⎫0，12，0，OC ＝⎝⎛⎭⎫0，12，0，易知OC为平面BDF 的一个法向量，由BC ＝⎝⎛⎭⎫－32，12，0，FB ＝⎝⎛⎭⎫32，0，－12，可得平面BCF 的一个法向量为n ＝(1，3，3)．所以cos n ，OC ＝217，sin n ，OC ＝277，所以tan n ，OC＝233.2．在长方体ABCD -A 1B 1C 1D 1中，B 1C 和C 1D 与底面所成角分别为60°和45°，则异面直线B 1C 和C 1D 所成角的余弦值为( )A.64 B.104 C.32 D.34解析：选A 建立如图的空间直角坐标系，可知∠CB 1C 1＝60°，∠DC 1D 1＝45°，设B 1C 1＝1，CC 1＝3＝DD 1.∴C 1D 1＝3，则有B 1(3，0,0)，C (3，1，3)，C 1(3，1,0)，D (0,1，3)．∴B C 1＝(0,1，3)，C D 1＝(－3，0，3)． ∴cos 〈B C 1，C D 1〉＝B C 1·C D1|B C 1||C D 1|＝326＝64.3．在三棱锥P -ABC 中，AB ⊥BC ，AB ＝BC ＝12PA ，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ，则直线OD 与平面PBC 所成角的正弦值为( )A.216 B.833 C.21060 D.21030解析：选D 不妨设AB ＝BC ＝12PA ＝2，∵OP ⊥底面ABC ，∴PO ＝14.根据题意，以B 为原点，BA ，BC 所在直线分别为x ，y 轴建立空间直角坐标系B -xyz ，如图所示．则A (2,0,0)，B (0,0,0)，C (0,2,0)，P (1,1，14)． ∵点O ，D 分别是AC ，PC 的中点， ∴OD ＝12AP ＝⎝⎛⎭⎫－12，12，142. 又BC ＝(0,2,0)，BP ＝(1,1，14)， 设平面PBC 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·BC ＝0，n ·BP ＝0，即⎩⎪⎨⎪⎧y ＝0，x ＋y ＋14z ＝0，取n ＝(－14，0,1)，高中数学打印版∴cos n，ODn·OD＝＝|n|| OD |32010，∴sin θ＝32010(θ 为 OD 与平面 PBC 所成的角)，故选 D.4．正方体 ABCD -A1B1C1D1 中，BB1 与平面 ACD1 所成角的余弦值为( )2 A. 33 B. 3C.23D.6 3解析：选 D 不妨设正方体的棱长为 1，如图建立空间直角坐标系，则D(0,0,0)，B(1,1,0)，B1(1,1,1)．平面 ACD1 的法向量为 DB1 ＝(1,1,1)，又 BB1 ＝(0,0,1)，∴cosDB1 ， BB1DB1 ·BB113＝＝| DB1 || BB1 |3×1＝ 3 .∴BB1 与平面 ACD1 所成角的余弦值为1－332＝6 3.5.如图，已知正三棱柱 ABC-A1B1C1 的各条棱长都相等，M 是侧棱 CC1 的中点，则异面直线 AB1 和 BM 所成角的大小是________．解析：建立如图所示的空间直角坐标系，O 为 BC 中点，设三棱柱的棱长为 2a，则点 A( 3a,0,0)，B(0，a,0)，B1(0，a,2a)，M(0，－a，a)，AB1 ＝(－ 3a，a,2a)， BM ＝(0，－2a，a)， 所以 AB1 ·BM ＝0，因此异面直线 AB1 与 BM 所成的角为 90°. 答案：90°校对完成版本高中数学打印版6.正三角形 ABC 与正三角形 BCD 所在的平面互相垂直，则直线 CD 与平 面 ABD 所成角的正弦值为________．解析：取 BC 的中点 O，连接 AO，DO，建立如图所示的空间直角坐标系 O -xyz.设 BC＝1，则 A0，0， 23，B0，－21，0，C0，12，0，D 23，0,0，所以 BA ＝0，12， 23， BD ＝ 23，21，0， CD ＝ 23，－12，0.设平面 ABD 的法向量为 n＝(x，y，z)，n·BA ＝0， 则n·BD ＝0，12y＋ 23z＝0， 所以 23x＋12y＝0，取 x＝1，则 y＝－ 3，z＝1，所以 n＝(1，－ 3，1)，所以 cosn，CD＝23＋3 25×1 ＝515，因此直线 CD 与平面 ABD 所成角的正弦值为15 5.答案：15 57.如图，四边形 ABCD 中，△BCD 为正三角形，AD＝AB＝2，BD＝2 3， AC 与 BD 交于 O 点，将△ACD 沿边 AC 折起，使 D 点至 P 点，已知 PO 与 平面 ABCD 所成的角为 θ，且 P 点在平面 ABCD 内的射影落在△ACD 内．(1)求证：AC⊥平面 PBD；(2)若已知二面角 APBD 的余弦值为 721，求 θ 的大小．解：(1)证明：由题意，O 为 BD 的中点，则 AC⊥BD，校对完成版本高中数学打印版又 AC⊥PO，BD∩PO＝O， 所以 AC⊥平面 PBD. (2)以 OB 为 x 轴，OC 为 y 轴，过 O 垂直于平面 ABC 向上的直线 为 z 轴建立如图所示空间直角坐标系， 则 A(0，－1,0)，B( 3，0,0)，P(－ 3cos θ，0， 3sin θ)，则 ＝( 3，1,0)， ＝(－ 3cos θ，1， 3sin θ)， 平面 PBD 的法向量为 j＝(0,1,0)， 设平面 ABP 的法向量为 n＝(x，y，z)，n⊥ 则由n⊥， 3x＋y＝0， 得， － 3xcos θ＋y＋ 3zsin θ＝0.令 x＝1，得 n＝1，－ 3，cossinθ＋θ 1.∴cos〈n，j〉＝||nn|·|jj||＝3＝cos θ＋12721，4＋ sin2θcos θ＋12 ∴ sin2θ ＝3，化简得cosθ＝12，又 θ∈0，π2，∴θ＝π3.8.如图所示，四边形 ABCD 为直角梯形，AB∥CD，AB⊥BC，△ABE 为等边三角形，且平面 ABCD⊥平面 ABE，AB＝2CD＝2BC＝2，P 为 CE 的中点．(1)求证：AB⊥DE； (2)求平面 ADE 与平面 BCE 所成锐二面角的余弦值； (3)在△ABE 内是否存在一点 Q，使 PQ⊥平面 CDE？如果存在，求出 PQ 的长；如果 不存在，请说明理由． 解：(1)证明：如图，取 AB 的中点 O，连接 OD，OE.因为△ABE 是等边三角形，所以 AB⊥OE.校对完成版本高中数学打印版因为四边形 ABCD 是直角梯形，CD＝12AB，AB∥CD， 所以四边形 OBCD 是平行四边形，OD∥BC.又 AB⊥BC，所以 AB⊥OD.又 OE∩OD＝O，所以 AB⊥平面 ODE.又 DE⊂平面 ODE，所以 AB⊥DE.(2)因为平面 ABCD⊥平面 ABE，AB⊥OE，所以 OE⊥平面 ABCD. 又 OD⊂平面 ABCD，所以 OE⊥OD.如图所示，以 O 为坐标原点建立空间直角坐标系．则 A(1,0,0)，B(－1,0,0)，D(0,0,1)，C(－1,0,1)，E(0， 3，0)，所以AD ＝(－1,0,1)， DE ＝(0, 3，－1)，设平面 ADE 的法向量为 n1＝(x1，y1，z1)，n1·DE ＝0， 3y1－z1＝0，则即n1·AD ＝0， －x1＋z1＝0，令 z1＝1，则 x1＝1，y1＝ 33，所以 n1＝1， 33，1.同理求得平面 BCE 的法向量为 n2＝(－ 3，1,0)．设平面 ADE 与平面 BCE 所成的锐二面角为 θ，则 cos θ＝||nn11|·|nn22||＝ 77.所以平面ADE与平面BCE所成锐二面角的余弦值为7 7.(3)假设在△ABE 内存在满足题意的点 Q，设 Q(x2，y2,0)．因为 P－12， 23，12，校对完成版本高中数学打印版所以 PQ ＝x2＋12，y2－ 23，－12.又 CD ＝(1,0,0)， DE ＝(0， 3，－1)， PQ ·CD ＝0 依题意 PQ ·DE ＝0x2＋12＝0， ，即 3×y2－ 23＋12＝0，解得 x2＝－12，y2＝ 33，则点 Q 在△ABE 内．所以存在点Q－12，33，0，使PQ⊥平面CDE，此时PQ＝3 3.(时间 120 分钟 满分 150 分)一、选择题(本大题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．设空间向量 a＝(1,2,1)，b＝(2,2,3)，则 a·b＝( )A．(2,4,3)B．(3,4,4)C．9D．－5解析：选 C ∵a＝(1,2,1)，b＝(2,2,3)，∴a·b＝1×2＋2×2＋1×3＝9.2．设 l1 的方向向量为 a＝(1,2，－2)，l2 的方向向量为 b＝(－2,3，m)，若 l1⊥l2，则 m 等于( )A．1B．21 C.2D．3解析：选 B 若 l1⊥l2，则 a⊥b，∴a·b＝0，∴1×(－2)＋2×3＋(－2m)＝0，解得 m＝2.3．已知向量 i，j，k 是一组单位正交向量，m＝8j＋3k，n＝－i＋5j－4k，则 m·n＝( )A．7B．－20C．28D．11解析：选 C 因为 m＝(0,8,3)，n＝(－1,5，－4)，所以 m·n＝0＋40－12＝28.校对完成版本高中数学打印版4．已知二面角 αlβ 的大小为π3，m，n 为异面直线，且 m⊥α，n⊥β，则 m，n 所成的 角为( )A.π6B.π3C.π2D.23π解析：选 B 设 m，n 的方向向量分别为 m，n.由 m⊥α，n⊥β 知 m，n 分别是平面 α，β 的法向量．∵|cos〈m，n〉|＝cos π3＝12，∴〈m，n〉＝π3或23π.但由于两异面直线所成的角的范围为0，π2，故异面直线 m，n 所成的角为π3.5．已知空间三点 O(0,0,0)，A(－1,1,0)，B(0,1,1)在直线 OA 上有一点 H 满足 BH⊥OA，则点 H 的坐标为( )A．(－2,2,0)B．(2，－2,0)C.－12，12，0D.12，－12，0解析：选 C 由 ＝(－1,1,0)，且点 H 在直线 OA 上，可设 H(－λ，λ，0)，则 BH―→＝(－λ，λ－1，－1)．又 BH⊥OA，∴ ·OA―→＝0，即(－λ，λ－1，－1)·(－1,1,0)＝0，即 λ＋λ－1＝0，解得 λ＝12，∴H－12，12，0.6．如图，三棱锥 SABC 中，棱 SA，SB，SC 两两垂直，且 SA＝SB ＝SC，则二面角 ABCS 大小的正切值为( )A．1 C. 2B.2 2D．2解析：选 C ∵三棱锥 SABC 中，棱 SA，SB，SC 两两垂直，且 SA＝SB校对完成版本高中数学打印版＝SC，∴SA⊥平面 SBC，且 AB＝AC＝ SA2＋SB2，取 BC 的中点 D，连接 SD，AD，则 SD⊥BC，AD⊥BC，则∠ADS 是二面角 ABCS 的平面角，设 SA＝SB＝SC＝1，则 SD＝ 22，则tan∠ADS＝SSDA＝1＝ 22，故选 C.27．在空间直角坐标系 Oxyz 中，i，j，k 分别是 x 轴、y 轴、z 轴的方向向量，设 a 为非零向量，且〈a，i〉＝45°，〈a，j〉＝60°，则〈a，k〉＝( )A．30°B．45°C．60°D．90°解析：选 C 如图所示，设|a|＝m(m>0)，a＝ ，PA⊥平面 xOy，则在 Rt△PBO 中，|PB|＝| |· sin〈a，i〉＝ 22m， 在 Rt△PCO 中， |OC|＝| |·cos〈a，j〉＝m2 ， ∴|AB|＝m2 ， 在 Rt△PAB 中，|PA|＝ |PB|2－|AB|2＝24m2－m42＝m2 ，∴|OD|＝m2 ，在 Rt△PDO 中，cos〈a，k〉＝||OODP||＝12，又 0°≤〈a，k〉≤180°，∴〈a，k〉＝60°.8.如图，在正四棱柱 ABCD A1B1C1D1 中，AA1＝2，AB＝BC＝1，动点 P， Q 分别在线段 C1D，AC 上，则线段 PQ 长度的最小值是( )2 A. 33 B. 3校对完成版本。

第三章第二节立体几何中的向量方法第二课时学习目标1.能用向量方法证明有关线线，线面，面面的垂直和平行问题;2.会利用坐标计算法向量.________________________________________________________________________________ 自学探究问题1. 自行梳理平行与垂直的关系，它们的相关判定与性质是怎样的？问题2. 用向量研究空间线面关系，设空间两条直线21,l l 的方向向量分别为21,e e ，两个平面21,αα的法向量分别为21,n n ，则有哪些结论?请填下表.【技能提炼】1. 如图，已知矩形ABCD 和矩形ADEF 所在平面互相垂直，点N M ,分别在对角线AEBD ,上，且AE AN BD BM 31,31==,求证：//MN 平面CDEA 1 D 1B 1ADBCC 1EF2.在正方体1111D C B A ABCD -中,E,F 分别是BB 1,,CD 中点， 求证：D 1F ⊥平面ADE教师问题创生学生问题发现变式反馈1.平面α的一个法向量为(1,2,0)，平面β的一个法向量为(2，－1,0)，则平面α与平面β的位置关系是( )A ．平行B ．相交但不垂直C ．垂直D ．不能确定2．已知a ＝(2,4,5)，b ＝(3，x ，y)分别是直线l 1、l 2的方向向量，若l 1∥l 2，则( )A ．x ＝6，y ＝15B ．x ＝3，y ＝152C ．x ＝3，y ＝15D ．x ＝6，y ＝152*3. 如图，已知P 是正方形ABCD 平面外一点，M 、N 分别是P A 、BD 上的点，且PM MA ＝BN ND ＝58.求证：直线MN ∥平面PBC .4.在正方体ABCD —A 1B 1C 1D 1中，E ，F 分别是棱AB ，BC 的中点，试在棱BB 1上找一点M ，使得D 1M⊥平面EFB 1.。