材料力学(II)第二章-材料力学-孙训方

材料力学孙训方
材料力学是研究材料中力学行为和性能的一门学科。

它研究物体在外力作用下的受力、变形和破坏规律，对于材料的设计、制备和应用具有重要意义。

材料力学的研究对象主要包括金属、塑料、陶瓷、复合材料等各种材料。

通过对材料的载荷作用、应变和应力的关系研究，可以分析和预测材料在不同工况下的力学行为，从而为材料的设计和应用提供理论基础和指导。

材料力学的研究内容主要包括弹性力学、塑性力学、疲劳力学和断裂力学等。

弹性力学研究材料在小应力作用下的弹性变形规律，通过弹性模量、泊松比和剪切模量等参数来描述材料的弹性性能。

塑性力学研究材料在大应力作用下的塑性变形规律，探讨材料的变形硬化、屈服和流变行为。

疲劳力学研究材料在交变应力作用下的疲劳寿命，分析材料的疲劳断裂机制和寿命预测方法。

断裂力学研究材料在应力超过其强度极限时的断裂行为，研究材料的断裂韧性和断裂机制。

材料力学的应用领域广泛，包括工程结构设计、材料加工、材料选型等。

在工程结构设计方面，材料力学可以用于预测和优化结构在不同载荷下的应力和变形，提高结构的安全性和可靠性。

在材料加工方面，材料力学可以指导材料的成形和加工过程，控制材料的变形和应力分布，提高材料的加工性能和工艺效率。

在材料选型方面，材料力学可以评估材料的力学性能和耐久性能，为不同工程应用提供合适的材料选择依据。

总之，材料力学是研究材料力学行为和性能的重要学科，在工程设计和材料加工中具有重要的应用价值。

通过材料力学的研究，可以深入了解材料的力学特性，为材料的设计和应用提供科学的理论支持。

[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F kF l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(lxr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=， 2211222)(u d x l d d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+- du d d l dx 122-=，)()(22)(221212udud d l du u d d lx A dx -⋅-=⋅-=ππ因此，)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。

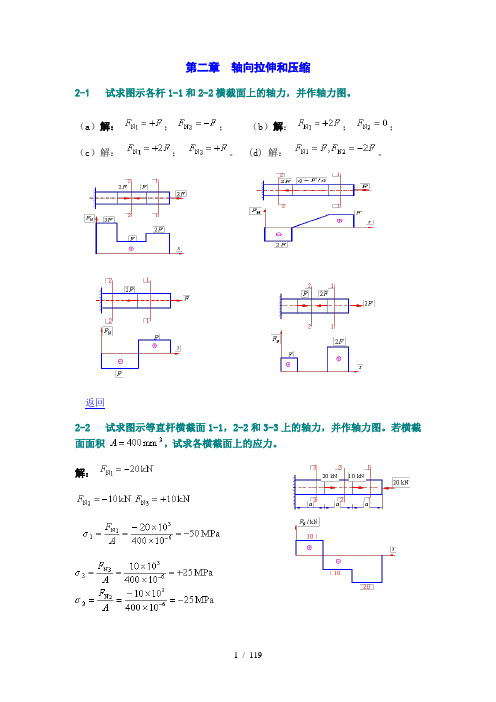
第二章轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d) 解：。

返回2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

试求C点的水平位移和铅垂位移。

解：（1）受力图（a）（2）变形协调图（b）因，故=（向下）（向下）为保证，点A移至，由图中几何关系知；第三章扭转3-1 一传动轴作匀速转动，转速，轴上装有五个轮子，主动轮Ⅱ输入的功率为60kW，从动轮，Ⅰ，Ⅲ，Ⅳ，Ⅴ依次输出18kW，12kW,22kW和8kW。

[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(lxr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=， 2211222)(u d x l d d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+- du d d l dx 122-=，)()(22)(221212udud d l du u d d lx A dx -⋅-=⋅-=ππ因此，)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。

材料力学课后习题答案（孙训方版）1. 弹簧的力学性质1.1 弹簧的刚度计算弹簧的刚度（k）是描述弹簧力学性质的重要指标，它代表了单位位移产生的恢复力大小。

弹簧的刚度可以通过以下公式计算：k = (F - F₀) / Δx其中，k为弹簧的刚度，F为施加在弹簧上的力，F₀为弹簧未受力时的长度恢复力，Δx为弹簧的位移。

1.2 弹簧势能的计算当弹簧发生位移时，由于其具有弹性而储存了一定的势能。

弹簧势能可以通过以下公式计算：Ep = (1/2) * k * Δx²其中，Ep为弹簧的势能，k为弹簧的刚度，Δx为弹簧的位移。

2. 常见材料的力学性质2.1 钢材的力学性质钢材是一种常见的工程材料，具有优良的力学性质。

以下是一些钢材的力学性质参数：钢材种类弹性模量（E）屈服强度（σy）抗拉强度（σu）延伸率（ε）铁石炭钢200 GPa250 MPa400 MPa20%不锈钢190 GPa210 MPa400 MPa15%高速钢235 GPa250 MPa500 MPa10%钢材的弹性模量决定了其在受力时的变形程度，屈服强度代表着材料开始发生可见整体变形的临界点，抗拉强度则反映了材料能够承受的最大应力。

延伸率则描述了材料可以在破坏之前发生高强度塑性变形的能力。

2.2 铝材的力学性质铝材是一种轻质金属材料，在航空航天、交通运输等领域有着广泛的应用。

以下是一些铝材的力学性质参数：铝材种类弹性模量（E）屈服强度（σy）抗拉强度（σu）延伸率（ε）6061-T669 GPa240 MPa260 MPa12%7075-T671 GPa470 MPa510 MPa9%2024-T673 GPa450 MPa500 MPa10%铝材相较于钢材，具有更轻的密度和较好的耐腐蚀性能。

弹性模量较低导致了铝材的刚度较小，而抗拉强度较高则提供了较好的耐久性能。

3. 弯曲应变的计算当受力物体发生弯曲时，会导致内部产生应变。

弯曲应变的计算可以使用公式：ε = (M * h) / (E * I)其中，ε为弯曲应变，M为弯矩，h为截面到受力轴的距离，E为弹性模量，I为截面的惯性矩。