材料力学第二章计算题

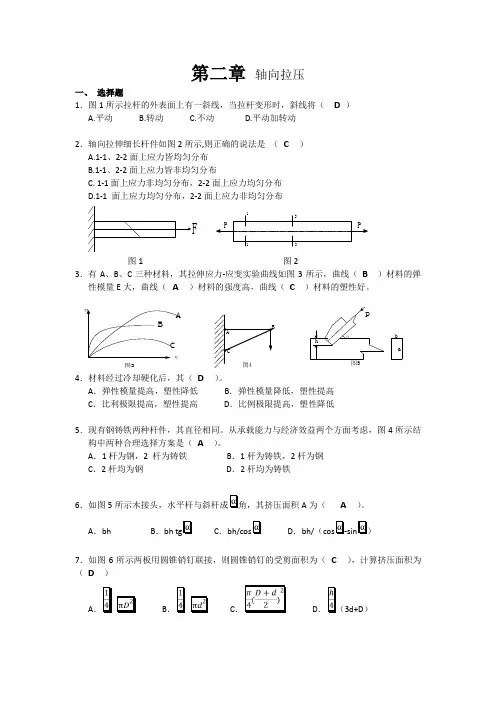
第二章轴向拉压一、选择题1．图1所示拉杆的外表面上有一斜线，当拉杆变形时，斜线将( D)A．平动B．转动C．不动D．平动加转动2．轴向拉伸细长杆件如图2所示，其中1-1面靠近集中力作用的左端面，则正确的说法应是( C)A．1-1、2-2面上应力皆均匀分布B．1-1、2-2面上应力皆非均匀分布C．1-1面上应力非均匀分布，2-2面上应力均匀分布D．1-1面上应力均匀分布，2-2面上应力非均匀分布（图1）（图2）3．有A、B、C三种材料，其拉伸应力—应变实验曲线如图3所示，曲线( B)材料的弹性模量E大，曲线( A )材料的强度高，曲线( C)材料的塑性好。

4．材料经过冷作硬化后，其( D)。

A．弹性模量提高，塑性降低B．弹性模量降低，塑性提高C．比例极限提高，塑性提高D．比例极限提高，塑性降低5．现有钢、铸铁两种杆材，其直径相同。

从承载能力与经济效益两个方面考虑，图4所示结构中两种合理选择方案是( A)。

A．1杆为钢，2杆为铸铁B．1杆为铸铁，2杆为钢C．2杆均为钢D．2杆均为铸铁（图3）（图4）（图5）6．在低碳钢的拉伸试验中，材料的应力变化不大而变形显著增加的是（B）。

A. 弹性阶段；B.屈服阶段；C.强化阶段；D.局部变形阶段。

7．铸铁试件压缩破坏（B）。

A. 断口与轴线垂直；B. 断口为与轴线大致呈450~550倾角的斜面；C. 断口呈螺旋面；D. 以上皆有可能。

8．为使材料有一定的强度储备，安全系数取值应（ A ）。

A .大于1； B. 等于1； C.小于1； D. 都有可能。

9. 等截面直杆在两个外力的作用下发生轴向压缩变形时，这对外力所具备的特点一定是等值、( C )。

A 反向、共线B 反向，过截面形心C 方向相对，作用线与杆轴线重合D 方向相对，沿同一直线作用10. 图6所示一阶梯形杆件受拉力Ｐ的作用，其截面1-1，2-2，3-3上的内力分别为N 1，N 2和N 3，三者的关系为( B )。

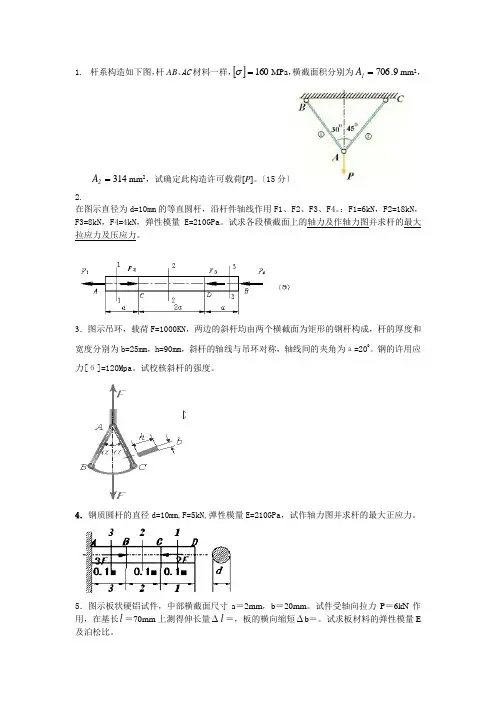
1. 杆系构造如下图，杆AB 、AC 材料一样，[]160=σMPa ，横截面积分别为9.706=1A mm 2，314=2A mm 2，试确定此构造许可载荷[P ]。

〔15分〕2.在图示直径为d=10mm 的等直圆杆，沿杆件轴线作用F1、F2、F3、F4。

：F1=6kN ，F2=18kN ，F3=8kN ，F4=4kN ，弹性模量E=210GPa 。

试求各段横截面上的轴力及作轴力图并求杆的最大拉应力及压应力。

3．图示吊环，载荷F=1000KN ，两边的斜杆均由两个横截面为矩形的钢杆构成，杆的厚度和宽度分别为b=25mm ，h=90mm ，斜杆的轴线与吊环对称，轴线间的夹角为а=200。

钢的许用应力[б]=120Mpa 。

试校核斜杆的强度。

4．钢质圆杆的直径d=10mm,F=5kN,弹性模量E=210GPa ，试作轴力图并求杆的最大正应力。

5．图示板状硬铝试件，中部横截面尺寸a ＝2mm ，b ＝20mm 。

试件受轴向拉力P ＝6kN 作用，在基长l ＝70mm 上测得伸长量∆l ＝，板的横向缩短∆b ＝。

试求板材料的弹性模量E 及泊松比。

6．钢制直杆，各段长度及载荷情况如图。

各段横截面面积分别为A 1＝A 3＝300mm 2，A 2＝200mm 2。

材料弹性模量E ＝200GPa 。

材料许用应力［σ］＝210MPa 。

试作杆的轴力图并校核杆的强度。

7．图示钢杆的横截面面积为2200mm A =，钢的弹性模量GPa E 200=，求各端杆的应变、伸长及全杆的总伸长。

8．等截面实心圆截面杆件的直径d=40mm ，材料的弹性模量E=200GPa 。

AB ＝BC ＝CD ＝1m ，在B 、C 、D 截面分别作用有P 、2P 、2P 大小的力，方向和作用线如下图，P=10KN 。

①做此杆件的轴力图；②求此杆件内的最大正应力；③求杆件C 截面的铅垂位移。

9．图示为一轴心受力杆，横截面面积A AB ＝A CD ＝400mm 2，A BC ＝200mm 2。

第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a ）解：（1）求指定截面上的轴力 FN =-11FF F N -=+-=-222（2）作轴力图轴力图如图所示。

（b ）解：（1）求指定截面上的轴力 FN 211=-2222=+-=-F F N （2）作轴力图FF F F N =+-=-2233 轴力图如图所示。

（c ）解：（1）求指定截面上的轴力 FN 211=-FF F N =+-=-222（2）作轴力图FF F F N 32233=+-=- 轴力图如图所示。

（d ）解：（1）求指定截面上的轴力 FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-（2）作轴力图 中间段的轴力方程为： x aFF x N ⋅-=)(]0,(a x ∈轴力图如图所示。

[习题2-2] 试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

2400mm A =解：（1）求指定截面上的轴力kNN 2011-=- )(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力MPa mm N A N 504001*********-=⨯-==--σMPa mm N A N 254001010232222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

21200mm A =22300mm A =23400mm A =解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。

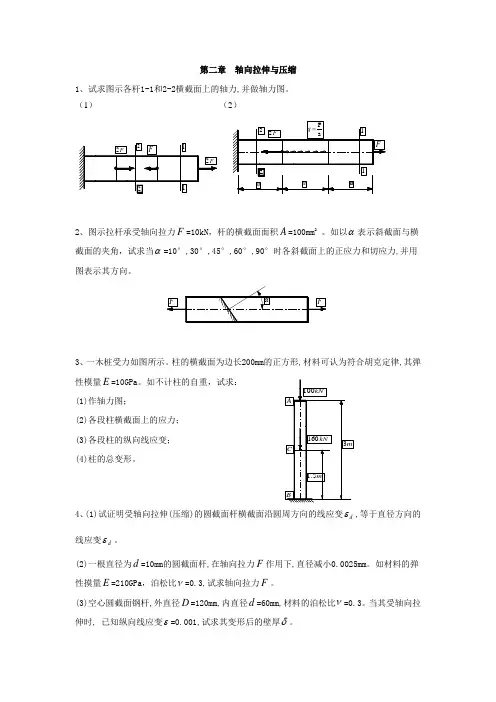
第二章 轴向拉伸与压缩1、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。

（1） （2）2、图示拉杆承受轴向拉力F =10kN ，杆的横截面面积A =100mm 2。

如以α表示斜截面与横截面的夹角，试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。

3、一木桩受力如图所示。

柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。

如不计柱的自重，试求：(1)作轴力图；(2)各段柱横截面上的应力； (3)各段柱的纵向线应变；(4)柱的总变形。

4、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。

(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。

如材料的弹性摸量E =210GPa ，泊松比ν=0.3,试求轴向拉力F 。

(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。

当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。

5、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。

已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa，钢丝的自重不计。

试求：(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律)；(2) 钢丝在C点下降的距离∆；(3) 荷载F的值。

6、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。

试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。

已知材料的许用应力[σ=170MPa，试选择杆AB,AD的角钢型号。

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。

[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EC横截面上的应力。

解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。

由平衡条件可知：②以C节点为研究对象，其受力图如图所示。

由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。

荷载，材料的密度，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。

解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。

第2章 材料力学2-1 什么是内力？什么是截面法？如何用截面法求内力？解：内力是系统内的相互作用力。

抵抗受外力作用而变形的能力。

求解内力的普遍方法是截面法，即假想截开、任意留取、平衡求力。

为了显示杆件轴向拉压时的内力，以截面m-m 将一杆件切为左、右两段，如图2-3（a ）所示。

在分离的截面上，有使杆件产生轴向变形的内力分量，即轴力N F 。

以杆件左段为研究对象，列平衡方程∑=0x F ，即得轴力F =N F 。

轴力N F 的作用线与杆件的轴线重合，方向如图2-3（b ）和图2-3（c ）所示。

由于截面m-m 左右两侧的轴力互为作用力和反作用力，因而它们大小相等、方向相反。

为使截面m-m 左右两侧的轴力具有相同的正负号，必须规定轴力的正负。

轴力的正负由杆件的变形确定。

当轴力的方向与截面的外法线方向一致时，杆件受拉伸长，其轴力为正；反之，当轴力的方向与截面的外法线方向相反时，杆件受压缩短，其轴力为负。

通常未知轴力按正向假设，由计算结果确定实际指向，如图2-4所示。

图2-3 轴力分析 图2-4 轴力的方向 由此可知，杆件轴力的确定方法完全与静力分析的方法相同，而且在建立平衡方程时无需考虑杆件变形的形式。

2-2 写出拉压胡克定律的表达式，解释每个代号的含义，并说明其适用范围。

解： EAL F L N =∆ 此式称为胡克定律。

比例常数E 称为材料的弹性模量，是材料固有的力学性质，与泊松比μ同为表征材料的弹性常数。

对同一种材料，E 为常数。

弹性模量具有应力的单位，常用GPa 表示；分母EA 称为杆件的抗拉压刚度，是衡量材料抵抗弹性变形能力的一个指标。

将式（2-3）、式（2-5）代入式（2-1），得胡克定律的另一表达式为εσE = 由此，胡克定律又可简述为若应力未超过某一极限值，则应力与应变呈正比。

当应力值超过比例极限P R 后，低碳钢ε-σ曲线已不是直线，胡克定律不再适用。

此时，若将外力卸去，试件的变形也随之全部消失，这种变形即为弹性变形，e R 称为弹性极限2-3 塑性材料和脆性材料的力学性能有哪些主要区别？解：构件在实际工作中所能承受的应力都是有限度的，因此，把构件材料失效时的应力称为极限应力，用u σ表示。