材料力学第二章习题【含答案】
- 格式：doc
- 大小：229.50 KB
- 文档页数：4
下载文档原格式
合集下载
材料力学习题册答案-第2章-拉压
第二章 轴向拉压
一、 选择题
1．图 1 所示拉杆的外表面上有一斜线，当拉杆变形时，斜线将（
A.平动
B.转动
C.不动
D.平动加转动
D）
2．轴向拉伸细长杆件如图 2 所示,则正确的说法是 （ C ）
A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C. 1-1 面上应力非均匀分布，2-2 面上应力均匀分布 D.1-1 面上应力均匀分布，2-2 面上应力非均匀分布
30KN 1
300mm
l1 解：(1) 轴力图如下
2
400mm
l2
10KN
-
40KN
50KN 3
400mm
l3
10KN
+
10KN
（2）
(3)右端面的位移
=
= 即右端面向左移动 0.204mm。
8.一杆系结构如图所示，试作图表示节点 C 的垂直位移，设 EA 为常数。
A
30
C
30 ΔL2 60 ΔL1
CD 段：σ3＝ ＝
Pa＝25MPa
2.图为变截面圆钢杆 ABCD，已知 =20KN， = =35KN， = =300mm， =400mm,
D
3
C
P3
2
，绘出轴力图并求杆的最大最小应力。
B
1 P2
A
P1
l3 解：
-
50KN
l2 15KN
l1
20KN
+
AB 段：σ1＝
＝
＝176.9MPa
BC 段：σ2＝
反力均匀分布，圆柱承受轴向压力 P，则基座剪切面的剪力
。ห้องสมุดไป่ตู้
一、 选择题
1．图 1 所示拉杆的外表面上有一斜线，当拉杆变形时，斜线将（
A.平动
B.转动
C.不动
D.平动加转动
D）
2．轴向拉伸细长杆件如图 2 所示,则正确的说法是 （ C ）
A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C. 1-1 面上应力非均匀分布，2-2 面上应力均匀分布 D.1-1 面上应力均匀分布，2-2 面上应力非均匀分布
30KN 1
300mm
l1 解：(1) 轴力图如下
2
400mm
l2
10KN
-
40KN
50KN 3
400mm
l3
10KN
+
10KN
（2）
(3)右端面的位移
=
= 即右端面向左移动 0.204mm。
8.一杆系结构如图所示，试作图表示节点 C 的垂直位移，设 EA 为常数。
A
30
C
30 ΔL2 60 ΔL1
CD 段：σ3＝ ＝
Pa＝25MPa
2.图为变截面圆钢杆 ABCD，已知 =20KN， = =35KN， = =300mm， =400mm,
D
3
C
P3
2
，绘出轴力图并求杆的最大最小应力。
B
1 P2
A
P1
l3 解：
-
50KN
l2 15KN
l1
20KN
+
AB 段：σ1＝
＝
＝176.9MPa
BC 段：σ2＝
反力均匀分布，圆柱承受轴向压力 P，则基座剪切面的剪力
。ห้องสมุดไป่ตู้
材料力学第二章 轴 向拉压习题及答案
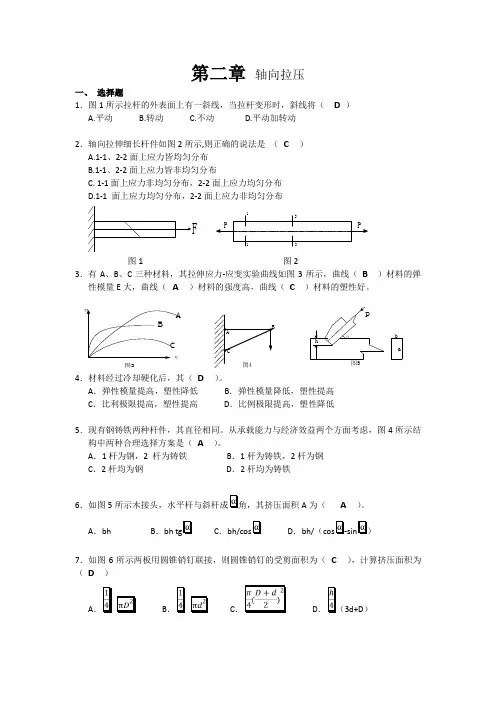
第二章轴向拉压一、选择题1．图1所示拉杆的外表面上有一斜线，当拉杆变形时，斜线将( D)A．平动B．转动C．不动D．平动加转动2．轴向拉伸细长杆件如图2所示，其中1-1面靠近集中力作用的左端面，则正确的说法应是( C)A．1-1、2-2面上应力皆均匀分布B．1-1、2-2面上应力皆非均匀分布C．1-1面上应力非均匀分布，2-2面上应力均匀分布D．1-1面上应力均匀分布，2-2面上应力非均匀分布（图1）（图2）3．有A、B、C三种材料，其拉伸应力—应变实验曲线如图3所示，曲线( B)材料的弹性模量E大，曲线( A )材料的强度高，曲线( C)材料的塑性好。
4．材料经过冷作硬化后，其( D)。
A．弹性模量提高，塑性降低B．弹性模量降低，塑性提高C．比例极限提高，塑性提高D．比例极限提高，塑性降低5．现有钢、铸铁两种杆材，其直径相同。
从承载能力与经济效益两个方面考虑，图4所示结构中两种合理选择方案是( A)。
A．1杆为钢，2杆为铸铁B．1杆为铸铁，2杆为钢C．2杆均为钢D．2杆均为铸铁（图3）（图4）（图5）6．在低碳钢的拉伸试验中，材料的应力变化不大而变形显著增加的是（B）。
A. 弹性阶段；B.屈服阶段；C.强化阶段；D.局部变形阶段。
7．铸铁试件压缩破坏（B）。
A. 断口与轴线垂直；B. 断口为与轴线大致呈450~550倾角的斜面；C. 断口呈螺旋面；D. 以上皆有可能。
8．为使材料有一定的强度储备，安全系数取值应（ A ）。
A .大于1； B. 等于1； C.小于1； D. 都有可能。
9. 等截面直杆在两个外力的作用下发生轴向压缩变形时，这对外力所具备的特点一定是等值、( C )。
A 反向、共线B 反向，过截面形心C 方向相对，作用线与杆轴线重合D 方向相对，沿同一直线作用10. 图6所示一阶梯形杆件受拉力Ｐ的作用，其截面1-1，2-2，3-3上的内力分别为N 1，N 2和N 3，三者的关系为( B )。
材料力学第二章习题选及其解答
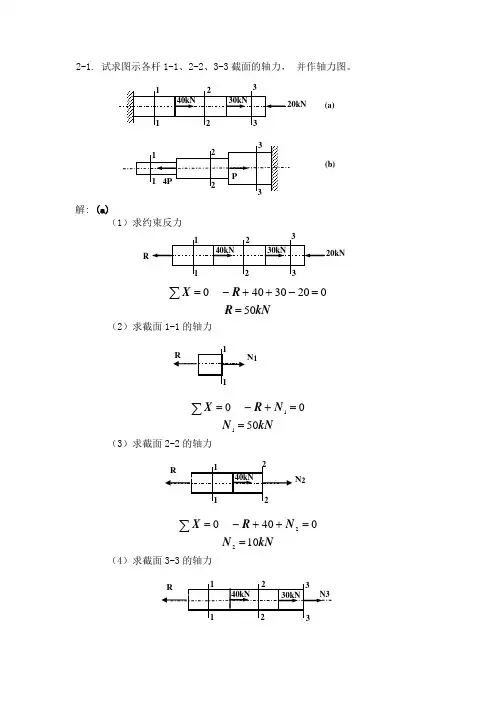
2-1. 试求图示各杆1-1、2-2、3-3截面的轴力， 并作轴力图。
解: (a)（1）求约束反力kNR R X 500203040 0==-++-=∑（2）求截面1-1的轴力kNN NR X 500011==+-=∑（3）求截面2-2的轴力kNN NR X 10040 022==++-=∑（4）求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑（5）画轴力图(b)（1）求截面1-1的轴力01=N（2）求截面2-2的轴力 PN4022==（3）求截面3-3的轴力PN P P NX 304 033==-+=∑（4）画轴力图2-2. 作用图示零件上的拉力P=38kN ，试问零件内最大拉应力发生于哪个横截面上？并求其值。
解：（1）1-1截面MPa A P 86.6720)2250(3103811=⨯-⨯==σ（2）2-2截面MPa A P 33.63152021038322=⨯⨯⨯==σ（3）3-3截面MPa A P 24.45215)2250(1038333=⨯⨯-⨯==σ（4）最大拉应力MPa 86.671max ==σσ2-3. 在图示结构中，若钢拉杆BC 的横截面直径为10mm ，试求拉杆内的应力。
设由BC 联接的两部分均为刚体。
3 3解：（1）以刚体CAE 为研究对象∑=⨯-⨯+⨯=035.15.4 0'P N N mC E A （2）以刚体BDE 为研究对象075.05.1 0=⨯-⨯=∑B E DN N m（3）联立求解kNN N N N N C EE C B 6 '=∴==（4）拉杆内的应力MPa A N B 4.7610410623=⨯⨯⨯==πσ 2-4. 图示结构中，1、2两杆的横截面直径分别为10mm 和20mm ，试求两杆内的应力。
设两根横梁皆为刚体。
解：（1）以整体为研究对象，易见A 处的水平约束反力为零； （2）以AB 为研究对象由平衡方程知0===A B B R Y X（3）以杆BD由平衡方程求得KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑（4）杆内的应力为1MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-7. 某拉伸试验机的示意图如图所示。
2章习题参考答案材料力学课后习题题解
杆①和杆②都满足强度要求。
2.24 图示结构，BC杆为5号槽钢，其许用应力[σ]1=160MPa； AB杆为100×50mm2的矩形截面木杆，许用应力[σ]2=8MPa。试 求：（1）当F=50kN时，校核该结构的强度；（2）许用荷 载[F]。 解：受力分析如图
F F
C
A
y
0: (1)
F
FBC sin 60o FBA sin 30o 0
Fx = 0: FAB = F
因此
LAB
FABl Fl EA EA
（b）受力分析如图， 由C点平衡可知：
F C A D F
(b)
F C F AC B A FAC FAB FAD F AD D F FBD FAB FCB FCB FBD
Fx 0 : F
FBC FAC
B
F
x
0:
FAB 45o 30o C A F 1m 45o 30o FAC A F
FAB cos 45o FAC cos 30o 0 2 FAB 3FAC FAB 3 FAC 2
LAB cos 45o LAC cos 30o LAB LAC cos 30 o cos 45
max 10MPa
2.6 钢杆受轴向外力如图所示，横截面面积为500mm2，试求 ab斜截面上的应力。 解： FN=20kN
a
30
o
20kN
FN FN pα = = cos30o A A0 α
FN α pα cos 30 cos 2 30o A0
o
b a b a b
FN
sα
τ α
B
FAy
1m 1m
F
FDC 4 10 F 40 F 10 [ ] 160 2 2 6 ADC 3 d 3 20 10
2.24 图示结构，BC杆为5号槽钢，其许用应力[σ]1=160MPa； AB杆为100×50mm2的矩形截面木杆，许用应力[σ]2=8MPa。试 求：（1）当F=50kN时，校核该结构的强度；（2）许用荷 载[F]。 解：受力分析如图
F F
C
A
y
0: (1)
F
FBC sin 60o FBA sin 30o 0
Fx = 0: FAB = F
因此
LAB
FABl Fl EA EA
（b）受力分析如图， 由C点平衡可知：
F C A D F
(b)
F C F AC B A FAC FAB FAD F AD D F FBD FAB FCB FCB FBD
Fx 0 : F
FBC FAC
B
F
x
0:
FAB 45o 30o C A F 1m 45o 30o FAC A F
FAB cos 45o FAC cos 30o 0 2 FAB 3FAC FAB 3 FAC 2
LAB cos 45o LAC cos 30o LAB LAC cos 30 o cos 45
max 10MPa
2.6 钢杆受轴向外力如图所示，横截面面积为500mm2，试求 ab斜截面上的应力。 解： FN=20kN
a
30
o
20kN
FN FN pα = = cos30o A A0 α
FN α pα cos 30 cos 2 30o A0
o
b a b a b
FN
sα
τ α
B
FAy
1m 1m
F
FDC 4 10 F 40 F 10 [ ] 160 2 2 6 ADC 3 d 3 20 10
材料力学第2章答案
问：（1）用这一试验机作拉断试验时，试样直径最大可达多大？
（2）若设计时取试验机的安全因数 n = 2 ，则杆 CD 的横截面面积为多少？
8
（3）若试样直径 d = 10 mm ，今欲测弹性模量 E ，则所加载荷最大不能超过多少？
解（1） σ
2-5 何谓失效？极限应力、安全因数和许用应力间有何关系？何谓强度条件？利用强度 条件可以解决哪些形式的强度问题？
答 失效（包括强度失效、刚度失效和稳定性失效）是指构件不能正常工作。 许用应力=极限应力/安全因数。 利用强度条件可以解决强度校核、截面设计和确定许用载荷等。
2-6 试指出下列概念的区别：比例极限与弹性极限；弹性变形与塑性变形；延伸率与正 应变；强度极限与极限应力；工作应力与许用应力。
α = 90° τ 90° = 0
2-5 图 示 拉 杆 沿 斜 截 面 m − m 由 两 部 分 胶 合 而 成 ， 设 在 胶 合 面 上 许 用 拉 应 力 [σ ] = 100 MPa ，许用切应力[τ ] = 50 MPa 。并设胶合面的强度控制杆件的拉力。问：
（1）为使杆件承受最大拉力 F ，角α 的值应为多少？ （2）若杆件横截面面积为 4 cm2，并规定α ≤ 60° ，确定许用载荷[F ] 。
∑ Fx = 0 ， FCx = 0
图（c）
∑ M D = 0 ， FC'y = 0
图（b）
∑ M B = 0 ， FN1 = 10 kN （拉）
∑ Fy = 0 ， FN2 = 20 kN （拉）
6
σ1
=
FN1 A1
=
4FN1 πd12
=
4 ×10 ×103 π ×102 ×10−6
= 127 MPa
（2）若设计时取试验机的安全因数 n = 2 ，则杆 CD 的横截面面积为多少？
8
（3）若试样直径 d = 10 mm ，今欲测弹性模量 E ，则所加载荷最大不能超过多少？
解（1） σ
2-5 何谓失效？极限应力、安全因数和许用应力间有何关系？何谓强度条件？利用强度 条件可以解决哪些形式的强度问题？
答 失效（包括强度失效、刚度失效和稳定性失效）是指构件不能正常工作。 许用应力=极限应力/安全因数。 利用强度条件可以解决强度校核、截面设计和确定许用载荷等。
2-6 试指出下列概念的区别：比例极限与弹性极限；弹性变形与塑性变形；延伸率与正 应变；强度极限与极限应力；工作应力与许用应力。
α = 90° τ 90° = 0
2-5 图 示 拉 杆 沿 斜 截 面 m − m 由 两 部 分 胶 合 而 成 ， 设 在 胶 合 面 上 许 用 拉 应 力 [σ ] = 100 MPa ，许用切应力[τ ] = 50 MPa 。并设胶合面的强度控制杆件的拉力。问：
（1）为使杆件承受最大拉力 F ，角α 的值应为多少？ （2）若杆件横截面面积为 4 cm2，并规定α ≤ 60° ，确定许用载荷[F ] 。
∑ Fx = 0 ， FCx = 0
图（c）
∑ M D = 0 ， FC'y = 0
图（b）
∑ M B = 0 ， FN1 = 10 kN （拉）
∑ Fy = 0 ， FN2 = 20 kN （拉）
6
σ1
=
FN1 A1
=
4FN1 πd12
=
4 ×10 ×103 π ×102 ×10−6
= 127 MPa
《材料力学》课后习题答案(详细)
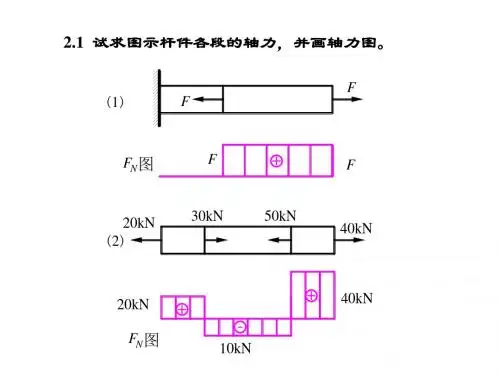
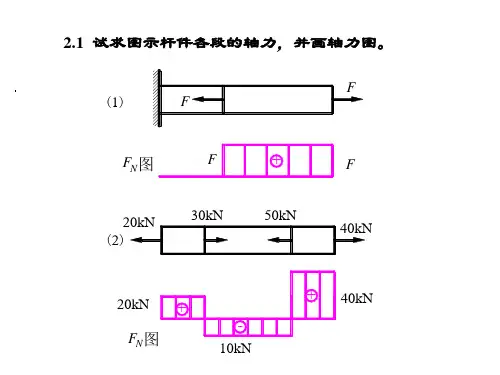
第二章轴向拉(压)变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：（1）求指定截面上的轴力FN =-11FF F N -=+-=-222（2）作轴力图轴力图如图所示。
（b）解：（1）求指定截面上的轴力FN 211=-02222=+-=-F F N （2）作轴力图FF F F N =+-=-2233轴力图如图所示。
（c）解：（1）求指定截面上的轴力FN 211=-FF F N =+-=-222（2）作轴力图FF F F N 32233=+-=-轴力图如图所示。
（d）解：（1）求指定截面上的轴力FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-（2）作轴力图中间段的轴力方程为：x aF F x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积2400mm A =，试求各横截面上的应力。
解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力MPa mm N A N 504001020231111-=⨯-==--σMPamm N A N 254001010232222-=⨯-==--σMPa mmN A N 254001010233333=⨯==--σ[习题2-3]试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积21200mm A =，22300mm A =，23400mm A =，并求各横截面上的应力。
解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力MPa mm N A N 10020010202311111-=⨯-==--σMPa mmN A N 3.3330010102322222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-4]图示一混合屋架结构的计算简图。
第2章材料力学练习题及答案xt
第2章 材料力学2-1 什么是内力？什么是截面法？如何用截面法求内力？解：内力是系统内的相互作用力。
抵抗受外力作用而变形的能力。
求解内力的普遍方法是截面法，即假想截开、任意留取、平衡求力。
为了显示杆件轴向拉压时的内力，以截面m-m 将一杆件切为左、右两段，如图2-3（a ）所示。
在分离的截面上，有使杆件产生轴向变形的内力分量，即轴力N F 。
以杆件左段为研究对象，列平衡方程∑=0x F ，即得轴力F =N F 。
轴力N F 的作用线与杆件的轴线重合，方向如图2-3（b ）和图2-3（c ）所示。
由于截面m-m 左右两侧的轴力互为作用力和反作用力，因而它们大小相等、方向相反。
为使截面m-m 左右两侧的轴力具有相同的正负号，必须规定轴力的正负。
轴力的正负由杆件的变形确定。
当轴力的方向与截面的外法线方向一致时，杆件受拉伸长，其轴力为正；反之，当轴力的方向与截面的外法线方向相反时，杆件受压缩短，其轴力为负。
通常未知轴力按正向假设，由计算结果确定实际指向，如图2-4所示。
图2-3 轴力分析 图2-4 轴力的方向 由此可知，杆件轴力的确定方法完全与静力分析的方法相同，而且在建立平衡方程时无需考虑杆件变形的形式。
2-2 写出拉压胡克定律的表达式，解释每个代号的含义，并说明其适用范围。
解： EAL F L N =∆ 此式称为胡克定律。
比例常数E 称为材料的弹性模量，是材料固有的力学性质，与泊松比μ同为表征材料的弹性常数。
对同一种材料，E 为常数。
弹性模量具有应力的单位，常用GPa 表示；分母EA 称为杆件的抗拉压刚度，是衡量材料抵抗弹性变形能力的一个指标。
将式（2-3）、式（2-5）代入式（2-1），得胡克定律的另一表达式为εσE = 由此，胡克定律又可简述为若应力未超过某一极限值，则应力与应变呈正比。
当应力值超过比例极限P R 后，低碳钢ε-σ曲线已不是直线，胡克定律不再适用。
此时，若将外力卸去，试件的变形也随之全部消失，这种变形即为弹性变形，e R 称为弹性极限2-3 塑性材料和脆性材料的力学性能有哪些主要区别？解：构件在实际工作中所能承受的应力都是有限度的，因此，把构件材料失效时的应力称为极限应力，用u σ表示。
《材料力学》第二章课后习题及参考答案
简答题2答案
在材料力学中，应力和应变是描述材料受力状态的基本物理量。应力表示单位面积上的 力，而应变则表示材料的变形程度。
简答题3答案
弹性力学和塑性力学是材料力学的重要分支。弹性力学主要研究材料在弹性范围内的应 力、应变和位移，而塑性力学则研究材料在塑性变形阶段的力学行为。
选择题答案
80%
选择题1答案
选择题3解析
这道题考察了学生对材料力学中 弯曲应力的理解，学生需要理解 弯曲应力的概念和计算方法，并 能够根据实际情况进行选择和应 用。
计算题解析
01
计算题1解析
这道题主要考察了学生对材料力学中拉压杆的计算能力，学生需要掌握
拉压杆的应力、应变计算方法，并能够根据实际情况进行选择和应用。
02
计算题2解析
计算题2答案
根据题意，先求出梁的剪力和弯矩，然后根据剪力和弯矩的关系 求出梁的位移分布，最后根据位移和应力的关系求出应力分布。
03
习题解析Biblioteka 简答题解析简答题1解析这道题考查了学生对材料力学 基本概念的理解，需要明确应 力和应变的概念及关系，并能 够解释在材料力学中如何应用 。
简答题2解析
这道题主要考察了学生对材料 力学中弹性模量的理解，以及 如何利用弹性模量进行相关计 算。学生需要理解弹性模量的 物理意义，掌握其计算方法。
C. 材料力学的任务之一是研究材 料的各种力学性能，包括强度、 刚度和稳定性等。
100%
选择题2答案
D. 在材料力学中，应力和应变是 描述材料受力状态的基本物理量 。
80%
选择题3答案
B. 材料力学主要研究材料的力学 性能和内部结构的关系，包括弹 性、塑性和韧性等。
计算题答案
在材料力学中，应力和应变是描述材料受力状态的基本物理量。应力表示单位面积上的 力，而应变则表示材料的变形程度。
简答题3答案
弹性力学和塑性力学是材料力学的重要分支。弹性力学主要研究材料在弹性范围内的应 力、应变和位移，而塑性力学则研究材料在塑性变形阶段的力学行为。
选择题答案
80%
选择题1答案
选择题3解析
这道题考察了学生对材料力学中 弯曲应力的理解，学生需要理解 弯曲应力的概念和计算方法，并 能够根据实际情况进行选择和应 用。
计算题解析
01
计算题1解析
这道题主要考察了学生对材料力学中拉压杆的计算能力，学生需要掌握
拉压杆的应力、应变计算方法，并能够根据实际情况进行选择和应用。
02
计算题2解析
计算题2答案
根据题意，先求出梁的剪力和弯矩，然后根据剪力和弯矩的关系 求出梁的位移分布，最后根据位移和应力的关系求出应力分布。
03
习题解析Biblioteka 简答题解析简答题1解析这道题考查了学生对材料力学 基本概念的理解，需要明确应 力和应变的概念及关系，并能 够解释在材料力学中如何应用 。
简答题2解析
这道题主要考察了学生对材料 力学中弹性模量的理解，以及 如何利用弹性模量进行相关计 算。学生需要理解弹性模量的 物理意义，掌握其计算方法。
C. 材料力学的任务之一是研究材 料的各种力学性能，包括强度、 刚度和稳定性等。
100%
选择题2答案
D. 在材料力学中，应力和应变是 描述材料受力状态的基本物理量 。
80%
选择题3答案
B. 材料力学主要研究材料的力学 性能和内部结构的关系，包括弹 性、塑性和韧性等。
计算题答案
材料力学第二章轴向拉伸与压缩习题答案
3-10图示凸缘联轴节传递的力偶矩为 ，凸缘之间用四个对称分布在 圆周上的螺栓联接，螺栓的内径 ，螺栓材料的许用切应力 。试校核螺栓的剪切强度。
解：
设每个螺栓承受的剪力为 ，则由
可得
螺栓的切应力
MPa MPa
∴螺栓满足剪切强度条件。
3-11图示矩形截面木拉杆的接头。已知轴向拉力 ，截面的宽度 ，木材顺纹的许用挤压应力 ，顺纹的许用切应力 。试求接头处所需的尺寸l和a。
解：
1．求支反力，作剪力图和弯矩图。
，
2．按正应力强度条件选择工字钢型号
由 ≤ ，得到
≥
查表选 14工字钢，其
， ，
3．切应力强度校核
满足切应力强度条件。
∴选择 14工字钢。
5-17图示木梁受移动载荷 作用。已知木材的许用正应力 ，许用切应力 ， ，木梁的横截面为矩形截面，其高宽比 。试选择此梁的横截面尺寸。
≤
可得 ≤ ①
D点受力如图(b)所示，由平衡条件可得：
CD杆受压，压力为 ，由压杆的强度条件
≤
可得 ≤ ②
由①②可得结构的许用载荷为 。
3-8图示横担结构，小车可在梁AC上移动。已知小车上作用的载荷 ，斜杆AB为圆截面钢杆，钢的许用应力 。若载荷F通过小车对梁AC的作用可简化为一集中力，试确定斜杆AB的直径d。
截面上的剪力和弯矩为： ，
2．求1-1横截面上a、b两点的应力
5-10为了改善载荷分布，在主梁AB上安置辅助梁CD。若主梁和辅助梁的抗弯截面系数分别为 和 ，材料相同，试求a的合理长度。
解：
1．作主梁AB和辅助梁CD的弯矩图
2．求主梁和辅助梁中的最大正应力
主梁：
辅助梁：
3．求 的合理长度
解：
设每个螺栓承受的剪力为 ，则由
可得
螺栓的切应力
MPa MPa
∴螺栓满足剪切强度条件。
3-11图示矩形截面木拉杆的接头。已知轴向拉力 ，截面的宽度 ，木材顺纹的许用挤压应力 ，顺纹的许用切应力 。试求接头处所需的尺寸l和a。
解：
1．求支反力，作剪力图和弯矩图。
，
2．按正应力强度条件选择工字钢型号
由 ≤ ，得到
≥
查表选 14工字钢，其
， ，
3．切应力强度校核
满足切应力强度条件。
∴选择 14工字钢。
5-17图示木梁受移动载荷 作用。已知木材的许用正应力 ，许用切应力 ， ，木梁的横截面为矩形截面，其高宽比 。试选择此梁的横截面尺寸。
≤
可得 ≤ ①
D点受力如图(b)所示，由平衡条件可得：
CD杆受压，压力为 ，由压杆的强度条件
≤
可得 ≤ ②
由①②可得结构的许用载荷为 。
3-8图示横担结构，小车可在梁AC上移动。已知小车上作用的载荷 ，斜杆AB为圆截面钢杆，钢的许用应力 。若载荷F通过小车对梁AC的作用可简化为一集中力，试确定斜杆AB的直径d。
截面上的剪力和弯矩为： ，
2．求1-1横截面上a、b两点的应力
5-10为了改善载荷分布，在主梁AB上安置辅助梁CD。若主梁和辅助梁的抗弯截面系数分别为 和 ，材料相同，试求a的合理长度。
解：
1．作主梁AB和辅助梁CD的弯矩图
2．求主梁和辅助梁中的最大正应力
主梁：
辅助梁：
3．求 的合理长度
材料力学答案第二章
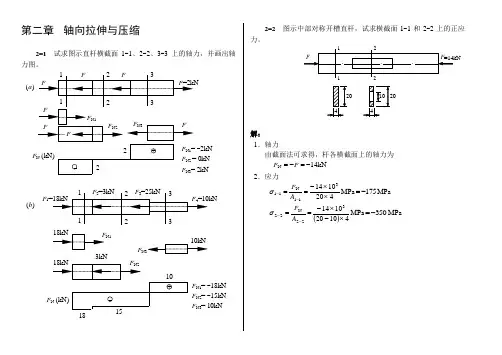
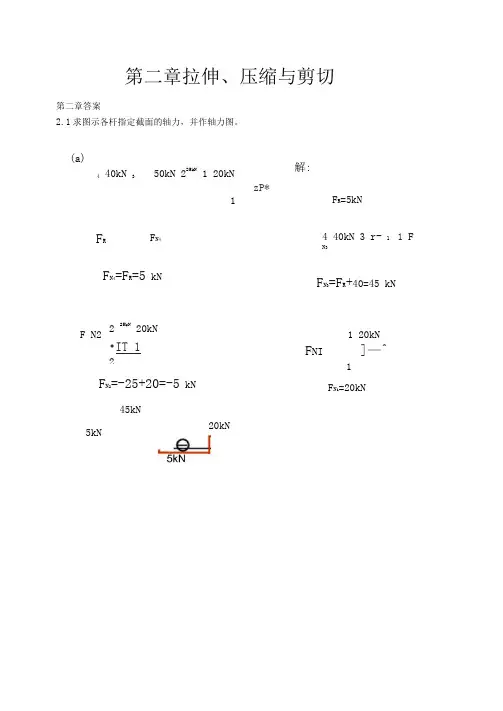
第二章拉伸、压缩与剪切第二章答案2.1求图示各杆指定截面的轴力，并作轴力图。
(a)4 40kN 350kN 225kN 1 20kNzP*1解:F R=5kNF R F N4 4 40kN 3 r - 1 1 FN3F N4=F R=5 kN FN3=F R+40=45 kNF N22 25kN 20kN•IT 121 20kNF NI]—^1F N2=-25+20=-5 kN FN i=20kN 45kN5kN20kN6kN10kN1 10kN2 6kN6kN1 — 1截面:F N 1=10 kN2—2截面:F N 2=10-10=010kN10kNF N 23—3截面:F N 33—I_|_6kN3F N 3=6 kN10kN1F N 1I © I2.2图示一面积为100mm 200mm的矩形截面杆，受拉力 F = 20kN的作用，试求：（1）m-m 上的应力；（2）最大正应力max 和最大剪应力 max 的大小及其作用1MPa2.3图示一正方形截面的阶梯形混凝土柱。
设重力加速度2.04 103kg/m 3，F = 100kN ，许用应力和b 。
解: pF 20 10330°0.1 0.21MPacos 230.75 MPa4严旦 0.433M Pa2 2max0.5 MPa-的斜截面 6面的方位角。
maxg = 9.8m/s 2,混凝土的密度为2MPa 。
试根据强度条件选择截面宽度a解:2.04 1039.8 22. 4N i4a2, 1 F NJ10 4 N/m 2 P4a2―3P100F N2在图示杆系中,BC试求夹角的值。
4a2103[],AC和100 103106 4 2 1040.228m4b2104 4 0.228 104 4 b2304.16V2 106 4 2 1040.398m 398mmBC两杆的材料相同，且抗拉和抗压许用应力相等，同为杆保持水平，长度为I ,AC杆的长度可随角的大小而变。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
浙江科技学院2015-2016学年第一学期考试试卷 A 卷
考试科目材料力学考试方式闭完成时限 2 小时拟题人陈梦涛审核人批准人2015 年9 月17 日建工学院2014年级土木工程专业
一、单项选择题（每小题3分，计30分）
1. 对于塑性材料来说，胡克定律(Hooke's law)使用的范围是。
A.p
σσ
<； B.
p
σσ
>； C.
s
σσ
<； D.
s
σσ
>
2．实心圆截面杆直径为D，受拉伸时的绝对变形为mm
l1
=
∆。
仅当直径变为2D时，绝对变形l∆为。
、
A．1mm B．1/2 mm C．1/4 mm D．2mm
3. 下列有关受压柱截面核心的说法中，正确的是。
A．当压力P作用在截面核心内时，柱中只有拉应力。
B．当压力P作用在截面核心内时，柱中只有压应力。
C．当压力P作用在截面核心外时，柱中只有压应力。
D．当压力P作用在截面核心外时，柱中只有拉应力。
4. 构件的强度、刚度和稳定性。
A.只与材料的力学性质有关；
B.只与构件的形状尺寸关；
C.与二者都有关；
D.与二者都无关。
5. 如右图所示，设虚线表示为单元体变形后的形状，则该单元体的剪
应变为。
A. α;
B.π/2-α;
C.π/2-2α; α
6. 图示一杆件的拉压刚度为EA，在图示外力作用下其
应变能U的下列表达式是。
7.应力－应变曲线的纵、横坐标分别为σ＝FN /A，ε＝△L / L，其中。
和L 均为初始值；和L 均为瞬时值；
为初始值，L 为瞬时值；为瞬时值，L 均为初始值。
8. 设一阶梯形杆的轴力沿杆轴是变化的，则发生破坏的截面上。
A.外力一定最大，且面积一定最小；
B.轴力一定最大，且面积一定最小；
#
C.轴力不一定最大，但面积一定最小;
D.轴力与面积之比一定最大。
9. 图示拉杆的外表面上画有一斜线，当拉杆受力变形时，斜线将
发生。
题5图
题6图
题9图
A.平动；
B.转动
C.平动加转动；
D.不动
10.图10所示钢杆，放置在两刚性平面之间，杆内无初始应力。
当温度均匀升
高m℃后，杆上任一点A处的应力ζ与纵向应变ε之值的可能发生的情形
是。
A、ζ≠0,ε=0 ；
B、ζ=0,ε=0；
C、ζ≠0,ε≠0 ；
D、ζ=0,ε≠0
二、画出各构件的内力图(第1，2小题各3分，第3小题4分，共10分)
题10图（1）（2）
}
（3）
}
三，是非题（每小题3分，共12分）
（）1．低碳钢一类的塑性材料，各种复杂应力状态下都会发生屈服，所以一般采用形状改变能密度理论；
；
（）2．衡量脆性材料拉伸强度的唯一指标是材料的拉伸强度
b
（）3．对于拉伸曲线上没有屈服平台的合金塑性材料，工程上规定σ作为名义屈服极限，此时相对应的应变量为ε=%
（）4．若梁某截面的上表面正应力为-120MPa，则该截面的下表面正应力为＋120Mpa；四．计算题（共48分）
1．（13分）现有如图所示一实心圆钢杆AB和AC在A点以铰链相
互连接，在A点处有一铅垂向下的力F=35kN。
已知杆AB和AC的直
径分别为12mm和15mm，圆钢杆的弹性模量E=210GPa。
求：①AB、
AC杆的应力及线应变②A点在铅垂方向的位移;
"
（题1图）
2．（10分）简易起重设备的计算简图如图所示，若已知斜杆AB是用两根63mm*40mm*4mm的不等边角钢组成，该角钢的许用应力
[σ]=170MPa。
试问在提起重量为P=24kN的物体时，该起重
机能否顺利完成工作
…
》
3. （7分）图示结构中BD为刚性梁，杆1，2用同一种材料制成，横截面面积相等，
P kN，求1，2杆的轴力。
50
!
4．（8分）已知混凝土的密度为×103kg/m3，许用压应力[σ]=2MPa。
试按强度条件确定所示混凝土柱所需的横截面积A1和A2。
若混凝土的弹性模量E=20GPa，
试求柱顶A的位移。
…
;
5.（12分）结构受力如图a所示。
BD杆可视为刚体，AB和CD两杆的横截面面积分别为150mm2,400mm2,其材料的应力-应变曲线分别表示于图b中。
求
(1)当F到达何值时，BD杆件开始明显倾斜(以AB杆获BC杆中的
应力到达屈服极限时作为杆件产生明显变形的标志)；(2)若设计
要求安全系数N=2，试求结构能承受的许用荷载[F]。