塑料齿轮强度校核方法1

齿轮校核强度验算
齿轮校核强度验算
２０１２年０３月２９日
目录
１．选择齿轮材料 (7)
２．初步确定主要参数 (9)
２．１接触强度确定中心距 (9)
２．２初步确定模数、齿数、螺旋角、齿宽、变位系数等几何参数 (10)
３．齿面接触强度核算 (11)
３．１分度圆上名义切向力t F (11)
３．２使用系数A K (11)
３．３动载系数v K (11)
３．４螺旋线载荷分布系数βH K (13)
３．５齿间载荷分布系数αH K (13)
３．６节点区域系数H Z (13)
３．７弹性系数E Z (13)
３．８重合度系数εZ (15)
３．１０小齿轮大齿轮的单对齿啮系数B Z、
Z (15)
D
３．１１计算接触应力Hσ (16)
３．１２寿命系数NT Z (16)
３．１３润滑油膜影响系数R V L Z Z Z (16)
３．１４齿面工作硬化系数W Z (18)
３．１５尺寸系数X Z (18)
３．１６安全系数H S (18)
４齿轮弯曲强度核算 (19)
４．１螺旋线载荷分布系数βF K (19)
４．２螺旋线载荷分布系数αF K (19)
４．３齿轮系数αF Y (19)
４．４应力修正系数αS Y (20)
４．５重合度系数εY (20)
４．７计算齿根应力Fσ (22)
４．８试验齿轮的应力修正系数ST Y (22)
４．９寿命系数NT Y (22)
４．１０相对齿根角敏感系数T re Y1δ (24)
４．１１相对齿根表面敏感系数T Rre Y1 (30)
４．１２尺寸系数x Y (30)
４．１３弯曲强度的安全系数F S (30)。

齿轮传动机构设计及强度校核一、概述1.优点：传动效率高；工作可靠、寿命长；传动比准确；结构紧凑；功率和速度适用范围很广。

2.缺点：制造成本高；精度低时振动和噪声较大；不宜用于轴间距离较大的传动。

3.设计齿轮——设计确定齿轮的主要参数以及结构形式主要参数有：模数m、齿数z、螺旋角β以及齿宽b、中心距a、直径（分度圆、齿顶圆、齿根圆）、变位系数、力的大小。

齿轮类型：—外形及轴线：—根据装置形式：开式齿轮：齿轮完全外露，润滑条件差，易磨损，用于低速简易设备的传动中闭式齿轮：齿轮完全封闭，润滑条件好半开式齿轮有简单的防护罩—根据齿面硬度(hardness)：硬度：金属抵抗其它更硬物体压入其表面的能力；硬度越高，耐磨性越好硬度检测方法：布氏硬度法（HBS）洛氏硬度法（HRC）软齿面齿面硬度≤350HBS 或≤38HRC硬齿面齿面硬度＞350HBS或＞38HRC二．齿轮传动的失效形式和设计准则齿轮传动的失效形式1）轮齿折断(Tooth breakage)疲劳折断齿根受弯曲应力-初始疲劳裂纹-裂纹不断扩展-轮齿折断2）过载折断短时过载或严重冲击，静强度不够全齿折断—齿宽较小的齿轮局部折断—斜齿轮或齿宽较大的直齿轮措施：增大模数（主要方法）、增大齿根过渡圆角半径、增加刚度（使载荷分布均匀）、采用合适的热处理（增加芯部的韧性）、提高齿面精度、正变位等。

备注：疲劳折断是闭式硬齿面的主要失效形式！疲劳折断产生机理：齿面受交变的接触应力-齿面受交变的接触应力-润滑油进入裂纹并产生挤压-表层金属剥落-麻点状凹坑注意：凹坑先出现在节线附近的齿根表面上，再向其它部位扩展；其形成与润滑油的存在密切相关；常发生于闭式软齿面(HBS≤350)传动中；开式传动中一般不会出现点蚀现象（磨损较快）；措施：提高齿面硬度和质量、增大直径（主要方法）等。

3、齿面胶合产生机理：高速重载-摩擦热使油膜破裂-齿面金属直接接触并粘接-齿面相对滑动-较软齿面金属沿滑动方向被撕落。

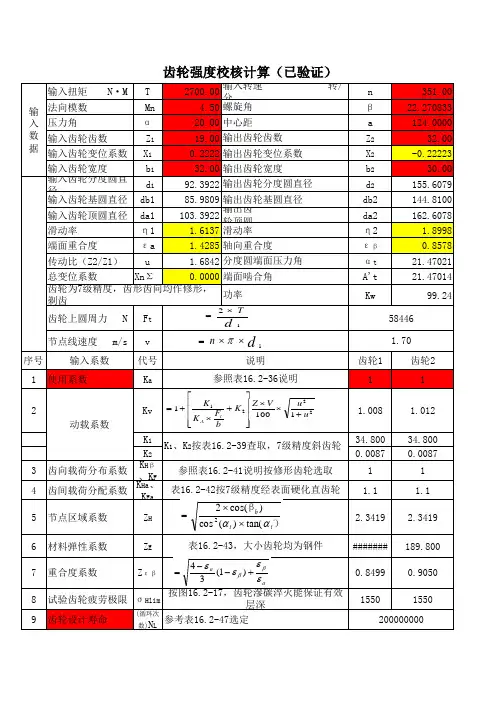
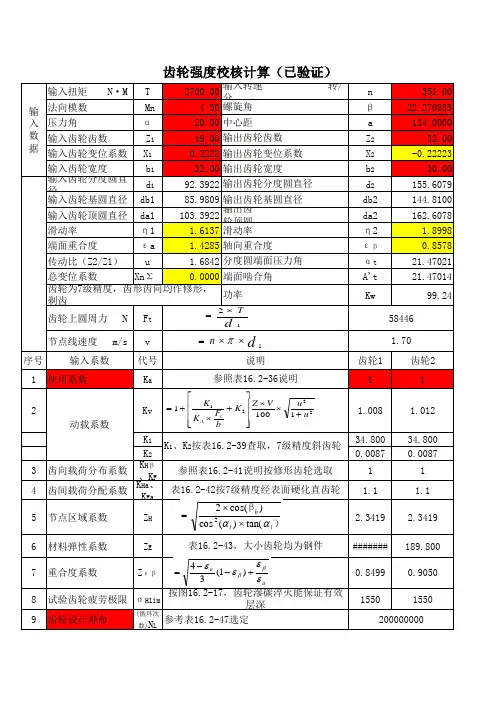
2齿轮的设计及校核齿轮是一种常见的动力传递装置，广泛应用于机械传动中。

齿轮的设计和校核是确保齿轮传动系统正常工作的重要环节。

本文将从齿轮的设计和校核两个方面进行分析，详细介绍其原理和方法。

齿轮的设计是根据传动的要求和工作条件，确定齿轮的尺寸、型号、齿数等参数的过程。

首先需要确定传动的速比、转矩要求等。

然后根据这些参数，计算出齿轮的模数、齿轮的宽度、齿轮的材料等。

根据实际情况，可以选择使用标准齿轮或定制齿轮。

齿轮的校核是验证设计参数的合理性和齿轮传动系统的可靠性的过程。

主要包括以下几个方面：1.齿轮强度校核。

根据所选用的齿轮材料，计算其强度参数，并与设计需求进行比较。

常用的齿轮强度计算方法有弗赖德、路中曼等。

2.齿面接触强度校核。

通过计算齿轮齿面接触应力和接触应力分布，判断齿面接触是否能满足传动要求。

根据计算结果，可以调整齿轮的齿形和齿数等参数。

3.齿轮轴承能力校核。

根据齿轮传动的工作转矩，计算齿轮轴承的最大受力，并与轴承的额定负载进行比较。

如果超过了轴承的额定负载，需要重新选择适合的轴承。

4.齿轮的热强度校核。

计算齿轮的热强度参数，判断齿轮在长时间高速工作时的热强度能否满足要求。

如果不能满足，可能需要进行降速设计或采取散热措施。

5.齿轮的动态特性校核。

根据齿轮的质量、转动惯量等参数，计算齿轮系统的固有频率和谐振现象，并进行分析和校核。

如果存在谐振问题，需要采取减振措施。

在齿轮的设计和校核过程中，需要使用一些专业软件和标准规范进行计算和判断。

一般常用的计算软件有Ansys、AutoCAD等，相关的标准规范有GB/T 3456.2-2024等。

总之，齿轮的设计和校核是确保齿轮传动系统正常运行的关键步骤。

只有在设计和校核过程中充分考虑到齿轮的强度、接触、轴承、热强度和动态特性等方面的要求，才能保证齿轮传动系统的可靠性和稳定性。

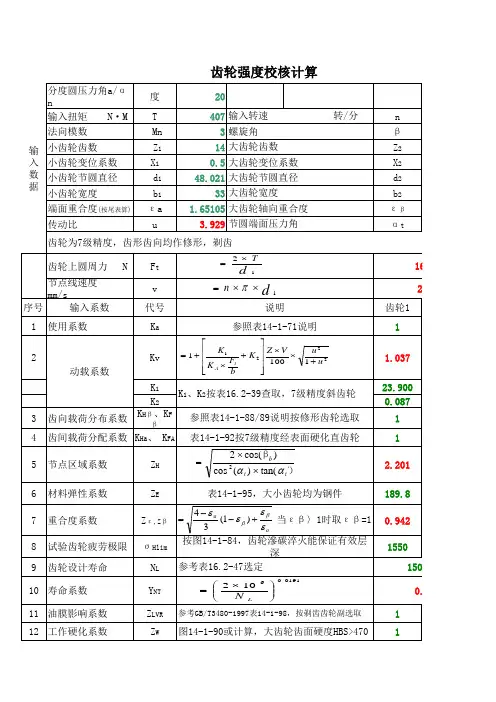
齿轮强度校核的新方法齿轮是机械传动中常用的零件，其强度校核关系到传动的安全可靠性。

传统的齿轮强度校核方法包括按照ISO、AGMA等标准计算齿面弯曲应力和齿面接触疲劳强度，并结合材料强度等因素评估齿轮的可靠性。

然而，传统方法存在一些缺陷，如对于非标准齿轮的强度校核方法不够完备，对于齿轮生命的评估基于经验公式容易出现误差等。

因此，近年来学者们在齿轮强度校核方法上进行了不少探索，提出了一些新的方法，下面介绍其中的一些代表性工作。

一、基于有限元方法的优化设计有限元法是近年来齿轮强度校核的一种新方法，通过构建齿轮三维有限元模型，在有限元软件的支持下，对齿轮进行数值模拟，计算齿轮的应力、位移和应变等变量。

这种方法具有精度高、计算量大等优点，适用于非标准齿轮的设计和强度校核。

例如，杨岩等人提出一种基于有限元法的齿轮强度优化设计方法。

该方法在传统齿轮强度校核的基础上，考虑了齿轮拉伸应力和绕组应力的影响，利用有限元软件建立了齿轮三维模型，进行了应力分析和齿向刚度分析，分别优化了齿轮齿形和齿向刚度，从而提高了齿轮的强度和可靠性。

二、基于机器学习的预测模型机器学习作为新兴的数据挖掘技术，目前在齿轮强度校核领域也得到了应用。

机器学习模型可以通过学习样本数据，建立起齿轮强度与各因素之间的关系模型，从而预测齿轮的强度和寿命等参数。

比如，赵少军等人提出了一种基于深度学习的齿轮寿命预测方法。

该方法采用了卷积神经网络(CNN)作为预测模型，在大量实验数据的支持下，通过训练CNN模型，学习了各因素之间的关联规律，成功地实现了齿轮寿命的预测。

这种方法具有自适应性强、精度高等优点。

三、基于反演方法的强度分析反演方法是一种基于逆问题和反演理论的分析方法，通过测量一些间接的或非直接的数据，推断原始问题的解。

在齿轮强度校核领域，反演方法可以通过测量齿轮的应力数据，反推得到齿轮的强度和材料性质等参数。

比如，王磊等人提出了一种基于反演方法的齿轮强度分析方法。

塑料齿轮强度校核方法马瑞伍，余毅，张光彦（深圳市创晶辉精密塑胶模具有限公司，广东省深圳市518000）【摘要】随着动力传递型塑料齿轮应用领域的不断拓展，如何评估或校核塑料齿轮的强度成为设计者不得不考虑的难题。

由于塑料材料种类繁多，且不同种类的塑料性能指标差异很大，所以迄今为止有关塑料齿轮的强度算法还未形成统一的标准。

目前，具有代表性的塑料齿轮强度算法主要四种：①尼曼&温特尔法；②VDI2545标准法；③KISSsoft软件基于VDI2545标准修正法；④宝理“Duracon”法。

由于第②种算法已经废止，第③种算法主要以软件形式发布，因此本文将主大于，直径已超过①节中做了②未考虑温度对塑料强度的影响。

③KISSsoft软件基于VDI2545标准修正法：该算法是KISSsoft公司基于VDI2545标准而提出的塑料齿轮强度的一种修正算法。

该方法主要是修正VDI2545标准中强度受温度变化的影响关系。

同时，该公司与各大主流塑料材料供应商合作，提供了POM、PA12、PA66、PEEK四种主要塑齿材料的性能数据，并采用软件形式发布，为塑料齿轮设计者评估塑料齿轮的强度提供了软件工具。

④宝理“Duracon”法：该算法是日本宝理公司发布的一种针对共聚聚甲醛（POM）材料的塑料齿轮强度评估算法。

鉴于第②种算法已经废止，第③种算法主要以软件形式发布，因此本文将主要介绍第①、④两种算法。

尼曼&温特尔法尼曼&温特尔在其名着《机械零件》一书中指出：塑料齿轮可能出现和钢齿轮相同的破坏形式：点蚀、磨损、轮齿折断。

当塑料齿轮与钢齿轮配对时，只须验算塑料齿轮的承载能力。

在热塑性塑料中还须注意其它的一些限制：① 齿形可能因软化而破坏。

② 轮齿温度是一个重要的影响参数。

③ 因弹性模量E 比较低，必须检验变形。

④ 在静载时有发生蠕变的危险。

用系数K 和U 可对应力作出初步的暂时性估计：式中，① F ——圆周力，单位：N 。

塑料齿轮强度校核方法马瑞伍，余毅，张光彦（深圳市创晶辉精密塑胶模具有限公司，广东省深圳市518000）【摘要】随着动力传递型塑料齿轮应用领域的不断拓展，如何评估或校核塑料齿轮的强度成为设计者不得不考虑的难题。

由于塑料材料种类繁多，且不同种类的塑料性能指标差异很大，所以迄今为止有关塑料齿轮的强度算法还未形成统一的标准。

目前，具有代表性的塑料齿轮强度算法主要四种：①尼曼&温特尔法；②VDI 2545标准法；③KISSsoft软件基于VDI 2545标准修正法；④宝理“Duracon”法。

由于第②种算法已经废止，第③种算法主要以软件形式发布，因此本文将主要介绍第①和第④种算法，以期能为塑料齿轮的设计起到一定的借鉴意义。

【关键词】塑料齿轮强度设计1引言在国内，塑料齿轮起步于20世纪70年代。

在发展初期，塑料齿轮主要应用集中在水电气三表的计数器、定时器、石英闹钟、电动玩具等小型产品中。

这时期的塑料齿轮的多为直径一般不大于25mm，传递功率一般不超过0.2KW的直齿轮。

换言之，早期的塑料齿轮主要用于小空间内的运动传递，属于运动传递型齿轮。

随着注塑模具技术与注塑装备及注塑工艺水平的不断提高，模塑成型尺寸更大、强度更高的塑料齿轮成为可能。

现在，塑料齿轮传递动力可达 1.5KW，直径已超过150mm。

动力型塑料齿轮已经成为众多产品动力传递系统的重要组成部分。

虽然动力型塑料齿轮的应用越来越广泛，但相应的塑料齿轮强度计算理论或标准却比较匮乏。

目前，塑料齿轮的强度计算多以金属齿轮的强度计算方法为参考，通过修正或修改某些系数来计算或评估塑料齿轮的强度是否满足使用要求，然后再通过实验方法验证强度是否满足使用要求。

下面，本文将介绍具有代表性的塑料齿轮强度的计算方法或观点，以期能够为塑料齿轮的强度设计提供借鉴。

2塑料齿轮强度计算方法从查阅到的相关文献资料看，塑料齿轮的强度计算方法基本上沿用了金属齿轮的强度校核理论及计算公式。

1. 选择齿轮材料及精度等级见表7-4，小齿轮选用45钢调质，硬度为220HBW ；大齿轮选用45钢正火，硬度为170HBW 。

初步估计齿轮线速度v ＜10m/s ，见表7-7，选择8级精度 2. 确定齿轮许用应力通过查机械设计手册，查得σlim H 和σlim Fσ1lim H =570MPa, σ2lim H =530MP σ1lim F =200MPa, σ2lim F =190MPa 见表7-10，查得S H 和S F S H =1，S F =1.3根据设计要求，齿轮工作年限为20年，每年52周，每周工作日为5天，单班制，每天工作8小时，所以 应力循环数：L h =20×52×5×8h=416000hN 1=60n 1jL h =60×500×1×416000=1.248×1010 N 2= N 1/i=1.248×1010/3=4.16×109 通过查机械设计手册，查得Z N 和Y N Z 1N =1，Z 2N =1.07 Y 1N = Y 2N =1由式（7-23）、式（7-26），求得许用应力 [σ1H ]=H H N S Z 1lim 1σ=15701⨯MPa=570MPa （7-23）[σ2H ]=H H N S Z 2lim 2σ=153007.1⨯MPa=567MPa （7-23） [σ1F ]=F F N S Y 1lim 1σ=3.12001⨯MPa=154MPa （7-26） [σ2F ]=F F N S Y 2lim 2σ=3.11901⨯MPa=146MPa （7-26） 3. 按齿面接触疲劳强度设计 1)小齿轮所传递的转矩 T 1=9.55×1061n P =9.55×106×500.4N ·mm=76400N ·mm 2)载荷因数K见表7-8，选取K=1.1 3）齿数z 1和齿宽因数Ψd选择小齿轮的齿数z 1=25，则大齿轮的齿数z 2=25×3=75，因是一级锥齿减速器，故为不对称布置，见表7-12，选取Ψd =1 4）齿数比μμ= z 2/ z 1=75/25=3 5）材料弹性系数因为两齿轮材料均为钢，见表7-9，查得Z E =189.8MPa 6）计算小齿轮直径d 1及模数m因为是软齿面，由齿面接触强度公式（7-22）计算 d 1》[]3d 12H E1)＋(KT Z 53.3μψμσ）（=3231)1＋3(764001.1)5678.18953.3(⨯⨯⨯⨯mm=53.9mm m=11z d =259.53=2.16mm见表7-1，取标准模数m=2.5mm 4. 计算大、小齿轮的几何尺寸 d 1=mz 1=2.5×25mm=62.5mmd 1a =m(z 1＋2h *a )=2.5×(25＋2×1)mm=67.5mmd 1f =m(z 1－2h *a －2c *)=2.5×(25－2×1－2×0.25)mm=56,25mmd 2=mz 2=2.5×75mm=187.5mmd 2a = m(z 2＋2h *a )=2.5×(75＋2×1)mm=192.5mmd 2f =m(z 2－2h *a －2c *)=2.5×(75－2×1－2×0.25)mm=181.5mm h 1=h 2=m(2h *a ＋c *)=2.5×（2×1＋0.25）mm=5.625mma=2)＋(m 21z z =2)75＋25(5.2⨯mm=125mm b=Ψd d 1=1×62.5mm=62.5mm 取b 1=70mm,b 2=65mm 5. 校核齿根弯曲疲劳强度 见表7-11，查得 Y F1=2.65,Y 1F =2.215 Y 1S =1.59,Y 2S =1.785 σ1F =11121z bm KT 2S F Y Y =MPa 59.165.2255.25.62746001.122⨯⨯⨯⨯⨯⨯=72.5MPa σ2F =11221S F S F F Y Y Y Y σ=MPa 59.165.2785.1215.25.72⨯⨯⨯=68.03MPa 6. 验算齿轮圆周速度 V=100060n d 11⨯π=1000605005.6214.3⨯⨯⨯m/s=1.64m/sV=1.64m/s﹤10m/s, 故合适。

塑料齿轮强度校核方法马瑞伍，余毅，张光彦（深圳市创晶辉精密塑胶模具有限公司，广东省深圳市518000）【摘要】随着动力传递型塑料齿轮应用领域的不断拓展，如何评估或校核塑料齿轮的强度成为设计者不得不考虑的难题。

由于塑料材料种类繁多，且不同种类的塑料性能指标差异很大，所以迄今为止有关塑料齿轮的强度算法还未形成统一的标准。

目前，具有代表性的塑料齿轮强度算法主要四种：①尼曼&温特尔法；②VDI 2545标准法；③KISSsoft软件基于VDI 2545标准修正法；④宝理“Duracon”法。

由于第②种算法已经废止，第③种算法主要以软件形式发布，因此本文将主要介绍第①和第④种算法，以期能为塑料齿轮的设计起到一定的借鉴意义。

【关键词】塑料齿轮强度设计1引言在国内，塑料齿轮起步于20世纪70年代。

在发展初期，塑料齿轮主要应用集中在水电气三表的计数器、定时器、石英闹钟、电动玩具等小型产品中。

这时期的塑料齿轮的多为直径一般不大于25mm，传递功率一般不超过0.2KW的直齿轮。

换言之，早期的塑料齿轮主要用于小空间内的运动传递，属于运动传递型齿轮。

随着注塑模具技术与注塑装备及注塑工艺水平的不断提高，模塑成型尺寸更大、强度更高的塑料齿轮成为可能。

现在，塑料齿轮传递动力可达 1.5KW，直径已超过150mm。

动力型塑料齿轮已经成为众多产品动力传递系统的重要组成部分。

虽然动力型塑料齿轮的应用越来越广泛，但相应的塑料齿轮强度计算理论或标准却比较匮乏。

目前，塑料齿轮的强度计算多以金属齿轮的强度计算方法为参考，通过修正或修改某些系数来计算或评估塑料齿轮的强度是否满足使用要求，然后再通过实验方法验证强度是否满足使用要求。

下面，本文将介绍具有代表性的塑料齿轮强度的计算方法或观点，以期能够为塑料齿轮的强度设计提供借鉴。

2塑料齿轮强度计算方法从查阅到的相关文献资料看，塑料齿轮的强度计算方法基本上沿用了金属齿轮的强度校核理论及计算公式。

齿轮传动机构设计及强度校核一、概述1.优点：传动效率高；工作可靠、寿命长；传动比准确；结构紧凑；功率和速度适用范围很广。

2.缺点：制造成本高；精度低时振动和噪声较大；不宜用于轴间距离较大的传动。

3.设计齿轮——设计确定齿轮的主要参数以及结构形式主要参数有：模数m、齿数z、螺旋角β以及齿宽b、中心距a、直径（分度圆、齿顶圆、齿根圆）、变位系数、力的大小。

齿轮类型：—外形及轴线：—根据装置形式：开式齿轮：齿轮完全外露，润滑条件差，易磨损，用于低速简易设备的传动中闭式齿轮：齿轮完全封闭，润滑条件好半开式齿轮有简单的防护罩—根据齿面硬度(hardness)：硬度：金属抵抗其它更硬物体压入其表面的能力；硬度越高，耐磨性越好硬度检测方法：布氏硬度法（HBS）洛氏硬度法（HRC）软齿面齿面硬度≤350HBS 或≤38HRC硬齿面齿面硬度＞350HBS或＞38HRC二．齿轮传动的失效形式和设计准则齿轮传动的失效形式1）轮齿折断(Tooth breakage)疲劳折断齿根受弯曲应力-初始疲劳裂纹-裂纹不断扩展-轮齿折断2）过载折断短时过载或严重冲击，静强度不够全齿折断—齿宽较小的齿轮局部折断—斜齿轮或齿宽较大的直齿轮措施：增大模数（主要方法）、增大齿根过渡圆角半径、增加刚度（使载荷分布均匀）、采用合适的热处理（增加芯部的韧性）、提高齿面精度、正变位等。

备注：疲劳折断是闭式硬齿面的主要失效形式！疲劳折断产生机理：齿面受交变的接触应力-齿面受交变的接触应力-润滑油进入裂纹并产生挤压-表层金属剥落-麻点状凹坑注意：凹坑先出现在节线附近的齿根表面上，再向其它部位扩展；其形成与润滑油的存在密切相关；常发生于闭式软齿面(HBS≤350)传动中；开式传动中一般不会出现点蚀现象（磨损较快）；措施：提高齿面硬度和质量、增大直径（主要方法）等。

3、齿面胶合产生机理：高速重载-摩擦热使油膜破裂-齿面金属直接接触并粘接-齿面相对滑动-较软齿面金属沿滑动方向被撕落。

齿轮强度校核的新方法随着工业生产技术的发展，传动机构在机械设备中扮演着越来越重要的角色。

其中，齿轮传动因其结构简单、转速高、传动比稳定等特点而广泛应用于各个领域。

齿轮传动系统中，齿轮的强度是影响其工作性能和寿命的重要因素。

因此，在设计齿轮传动时，必须进行齿轮强度校核。

传统的齿轮强度校核方法主要采用等效应力法和正反弯曲应力法。

虽然这些方法已经被广泛应用，但是在某些情况下，这些方法存在一些局限性。

如等效应力法只适用于齿轮荷载偏轻的情况，而且无法考虑齿形、啮合顺序和啮合频率等因素的影响。

而正反弯曲应力法则无法考虑弯矩的影响。

基于以上问题，近年来，学者们开始探索新的齿轮强度校核方法。

其中，基于有限元分析的齿轮强度校核方法备受关注。

有限元分析法有限元分析法是一种基于数值模拟的分析方法，其可以模拟实际齿轮的工作状态，准确地计算齿轮的应力分布、变形和应变分布等参数。

在有限元分析中，齿轮传动系统可以分解成许多小的单元，然后对每个小单元进行建模计算，最后将结果汇总得到整个传动系统的结果。

这种方法可以考虑到齿轮工作时的复杂状态，准确地计算齿轮的应力和变形。

但是，这种方法也存在一些问题。

首先，有限元分析需要大量的计算量和高级的计算技术，所以需要高性能计算机和专门的软件支持。

其次，齿轮强度校核中常常涉及到多个变量，如材料、齿形、模数等，因此在建模时需要选择合适的参数和模型。

此外，在建模时还需要对一些细节进行精细化处理，以确保计算结果的准确性。

基于有限元分析的齿轮强度校核一体化软件为了解决齿轮强度校核中的这些问题，最近一个新的解决方案出现了——基于有限元分析的齿轮强度校核一体化软件。

这种软件可以帮助使用者通过简单的界面实现对齿轮传动系统进行建模和计算。

用户只需输入有关参数和模型，软件就可以自动进行建模和计算，并输出齿轮的应力、变形和应变等结果。

这种软件的优点在于减少了计算量，降低了计算成本，最大程度地提高了计算的准确性。

塑料齿轮强度校核计算公式塑料齿轮强度校核计算公式是确定齿轮可靠性、性能以及使用寿命的一个重要指标。

塑料齿轮具有重量轻、耐磨、密封性好、低噪音等特点，被广泛应用于各种工业领域。

塑料齿轮强度计算公式的关键是齿轮的模数和齿轮宽度。

齿轮模数M的选择需要满足齿面强度、齿根强度和齿轮弹性变形等多重需求。

在选择齿轮模数时，应考虑齿轮的负载、使用环境和传动预期寿命等因素，合理选择模数可有效提高齿轮的强度和使用寿命。

齿轮宽度b的选择需要考虑到载荷和转速的影响。

在确定齿轮宽度时，应保证齿轮齿面与齿根处的应力在允许范围内，并能有效防止齿轮断裂和损坏。

针对塑料齿轮强度校核计算公式，以下是一个详细的计算步骤：第一步：确定齿轮模数和齿轮宽度根据实际应用需求选择合适的齿轮模数和齿轮宽度，需确保齿轮荷载和转速在安全范围内。

第二步：计算材料弹性模量和抗拉强度根据塑料材料相关数据，计算出材料的弹性模量和抗拉强度。

第三步：计算齿顶和齿根处的齿面应力使用公式计算齿顶和齿根处的齿面应力，考虑到载荷和转速等相关因素，确保齿面应力不超过允许范围。

第四步：计算齿根处的齿根应力使用公式计算齿根处的齿根应力，考虑到载荷和转速等相关因素，确保齿根应力不超过允许范围。

第五步：计算齿宽处的弯曲应力使用公式计算齿宽处的弯曲应力，考虑到载荷和转速等相关因素，确保弯曲应力不超过允许范围。

第六步：计算齿轮使用寿命根据齿轮的应力与材料强度、疲劳寿命关系等因素，计算出齿轮的使用寿命。

可根据需求选择不同的寿命要求，来评估齿轮的可靠性和性能。

在进行塑料齿轮强度校核计算时，应注意各项参数的正确性和精度，确保计算的可靠性和准确性。

在实际应用中，还需对齿轮材料、工艺等方面做好相关控制和检测，来从根本上保证齿轮的强度和使用寿命。

总之，塑料齿轮强度校核计算是一个重要的工作，正确的计算公式和步骤对于确保齿轮的可靠性和性能至关重要。

希望以上介绍能为广大读者提供一定的指导和帮助。