最优化与最优控制

最优化与最优控制课程的教学改革建议作者：任华玲来源：《教育教学论坛》 2017年第16期摘要：本文总结了研究生课程教学中存在的问题，尤其是最优化与最优控制这门研究生专业基础课目前教学中存在的问题。

在此基础上，给出了几点切实可行的教学改革建议，为后期专业课的学习打下坚实的理论基础，并为培养研究生从事科学研究的能力作好准备。

关键词：专业基础课；最优化与最优控制；教学改革中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2017）16-0141-02一、最优化与最优控制课程的性质和教学目标最优化与最优控制课程是硕士研究生系统分析与集成、系统理论等专业的专业基础课，该课程以最优化与最优控制的基本概念、建模方法、基本理论、求解方法等为主要内容，为相关专业硕士研究生在以后的科研中遇到优化问题而提供引导思路，起到“抛砖引玉”的作用。

其主要教学目标包括：掌握最优化和最优控制方法的基本思路、特点和适用条件；掌握相关理论和算法；能够应用这些方法对实际问题进行建模；了解现代优化方法发展的前沿和最新的优化工具软件。

二、最优化与最优控制教学中存在的问题1.研究生课程教学中普遍存在的问题。

首先谈谈研究生课程教学中普遍存在的问题。

研究生课程的学习对提高研究生培养质量具有非常重要的作用，但研究生与本科生不同，他们已经具备了较扎实的基础知识，然而目前仍有许多研究生课程还是主要采用传统的灌输式教学方式。

这种让学生被动接受知识的方法无法调动学生学习的积极性和主动性，也没有考虑学生学业及个人需求的差异性，教学效果不佳。

另外，大部分研究生课程没有统一教材，任课教师忙于科研工作难以及时更新教学内容，导致一些公共基础的教学内容陈旧或不够全面[1]。

然而，专业基础课是进一步学习后期相关专业课程的基础，其学习质量的优劣将直接关系到专业课教学的学习效果，关系到学生能否在理论深度上更好地理解和掌握专业课的学习，关系到在专业课中能否发挥出一定的自主和创新能力[2]。

最优控制与最优化问题中的动态规划方法动态规划方法是一种在最优控制和最优化问题中常用的方法。

它通过将问题分解为子问题，并利用子问题的最优解来求解整体问题的最优解。

本文将介绍动态规划方法的基本原理和应用，以及其在最优控制和最优化问题中的具体应用案例。

一、动态规划方法的基本原理动态规划方法的基本原理是将原问题分解为若干个子问题，并通过求解子问题的最优解来求解整体问题的最优解。

具体来说，动态规划方法有以下几个基本步骤：1. 定义状态：将问题的解表示为一个或多个状态变量。

2. 确定状态转移方程：根据问题的特点和约束条件，确定状态之间的转移关系。

3. 确定边界条件：确定问题的边界条件，即最简单的情况下的解。

4. 递推求解：利用状态转移方程和边界条件，递推求解问题的最优解。

二、动态规划方法在最优控制中的应用动态规划方法在最优控制中有广泛的应用。

最优控制问题的目标是找到一种控制策略，使得系统在给定的约束条件下达到最优性能。

动态规划方法可以用来求解最优控制问题的控制策略。

以倒立摆控制为例，倒立摆是一种常见的控制系统，其目标是使摆杆保持竖直位置。

动态规划方法可以将倒立摆控制问题分解为一系列子问题，每个子问题都是在给定状态下选择最优的控制动作。

通过递推求解子问题的最优解，最终可以得到整个控制过程的最优策略。

三、动态规划方法在最优化问题中的应用动态规划方法在最优化问题中也有广泛的应用。

最优化问题的目标是找到一组变量的最优取值，使得目标函数达到最小或最大值。

动态规划方法可以用来求解最优化问题的最优解。

以旅行商问题为例，旅行商问题是一个经典的最优化问题，其目标是找到一条路径，使得旅行商能够经过所有城市并且总路程最短。

动态规划方法可以将旅行商问题分解为一系列子问题，每个子问题都是在给定状态下选择最优的下一个城市。

通过递推求解子问题的最优解，最终可以得到整个旅行路径的最优解。

四、动态规划方法的优缺点动态规划方法有以下几个优点：1. 可以求解复杂的最优控制和最优化问题，具有较高的求解效率。

最优化及最优控制计算研究精确罚函数途径摘要最优化及最优控制是现代控制领域中研究的重点之一。

随着科技发展和信息技术的广泛应用，人们对最优化与最优控制的需求越来越强烈。

而在最优化与最优控制中，精确罚函数方法是一种重要的技术手段，它已被广泛应用于各种实际问题的求解中。

本文主要介绍精确罚函数方法的研究现状和应用，包括其基本概念、基本原理及其数值求解方法，并对精确罚函数方法进行了深入的剖析和思考。

关键词：最优化、最优控制、精确罚函数、数值求解AbstractOptimization and optimal control are one of the research focuses in the field of modern control. With the development of science and technology and the widespread application of information technology, people's demand for optimization and optimal control is becoming more and more urgent. In optimization and optimal control, the accurate penalty function method is an important technical means, which has been widely used in the solution of various practical problems. This paper mainly introduces the research status and application of the accurate penalty function method, including its basic concepts, basic principles, and numerical solution methods, and deeply analyzes and thinks about the accurate penalty function method.Keywords: optimization, optimal control, accurate penalty function, numerical solution1.引言目前，最优化与最优控制已经成为现代控制领域中研究的重点之一，其在各个领域中得到了广泛的应用，特别是对于涉及到大量数据和多变量的问题求解中，最优化与最优控制更是不可或缺的重要手段。

控制系统中的最优控制与最优化技术随着科技的不断进步和应用范围的扩大，控制系统在各行各业中的重要性也日益凸显。

最优控制与最优化技术作为控制系统中的重要概念和方法，在提高系统性能和效率方面发挥着关键作用。

本文将就控制系统中的最优控制与最优化技术进行深入探讨。

一、最优控制的定义与概念最优控制是指在满足给定约束条件的前提下，通过使某种性能准则达到最大或最小值来确定控制器参数或控制策略的问题。

最优控制的实现可以使系统在最短时间内达到期望状态或在给定资源条件下获得最佳性能。

最优化技术是实现最优控制的关键方法之一，它利用数学和计算方法来寻找系统中使性能准则达到最大或最小值的最优解。

最优化技术广泛应用于各种领域，例如经济学、工程学、管理学等，其中最为常见的应用是在控制系统中。

二、最优控制的分类最优控制可以分为离散最优控制和连续最优控制两大类。

离散最优控制是指在离散时间点上确定控制器参数或控制策略的问题。

典型的离散最优控制方法包括动态规划、贝尔曼方程等。

连续最优控制是指在连续时间范围内确定控制器参数或控制策略的问题。

常见的连续最优控制方法有经典最优控制、最速控制、最小能耗控制等。

三、最优化技术在控制系统中的应用最优化技术在控制系统中有着广泛的应用。

以下是一些常见的应用领域。

1. 机器人控制机器人控制是利用最优化技术来实现机器人移动、定位和路径规划等问题。

通过对机器人运动过程中的能耗、时间等指标进行优化，可以实现机器人的高效控制和优化运动。

2. 制造业控制在制造业中，最优化技术可以用来优化物料和生产设备的调度、工艺参数的优化以及生产线的平衡等问题。

通过合理地设计和优化控制策略，可以提高制造业的生产效率和产品质量。

3. 能源系统控制能源系统控制是指在能源产生、传输和消费过程中，通过最优化技术实现能源的高效利用。

例如在电力系统中，可以通过最优化技术对电网的输电线路和发电机组进行优化调度，以最大限度地提高电网的稳定性和电能的利用率。

《最优化与最优控制》教学大纲课程编号：4050141开课院系：自动化学院控制科学与工程系课程类别：专业选修适用专业：自动化课内总学时：32学分：2实验学时：0设计学时：0上机学时：0先修课程：数学分析、线性代数、常微分方程、自动控制原理执笔：邵立珍审阅：董洁一、课程教学目的最优化与最优控制在工程技术，经济，管理等领域有广泛的应用。

通过本课程的学习，使学生学会最优化的基本理论和算法，学会最优控制基本概念和理论。

二、课程教学基本要求1．课程重点：要求学生掌握典型的最优化算法，了解最优化的基本理论，掌握最优控制基本概念，掌握极大值原理，动态规划法了解典型最优控制问题。

2．课程难点：极大值原理，动态规划法。

3．能力培养要求：能够解决一些典型的最优控制问题，首先能够将实际问题，描述为最优控制问题，然后根据问题的条件，选择合适的求解工具并得到正确的答案。

三、课程教学内容与学时课堂教学（32学时）1．最优化概论(2学时)最优化问题的数学模型最优化方法及其结构线性搜索2．无约束最优化方法(4学时)局部极小的条件牛顿法拟牛顿法共轭梯度法方向集法3．约束优化的理论与方法(8学时) 约束问题和Lagrange乘子法一阶最优条件二阶最优条件罚函数与障碍函数乘子法4．二次规划(6学时)等式约束法Lagrange方法有效集法5．最优控制概论(2学时)经典控制与现代控制理论简介最优控制问题的产生最优控制问题的一般提法最优控制问题分类6．变分法与最优控制(4学时)变分法用变分法解最优控制7．极大值原理(4学时)末端自由的极大值原理末端受约束的极大值原理时变系统,复合型性能指标问题8．动态规划法(2学时)多步决策与动态规划离散系统动态规划法连续系统动态规划法实验（上机、设计）教学（0学时）四、教材与参考书教材1. 王晓陵，陆军编，《最优化方法与最优控制》，哈尔滨工程大学出版社，2008年，第1版参考书1. 吴受章编，《最优控制理论与应用》，机械工业出版社，2008年，第1版2.李国勇编，《最优控制理论与应用》，国防工业出版社，2008年，第1版3. 赫孝良等编，《最优化与最优控制》，西安交通大学出版社，1992年，第1版4．解学书编，《最优控制理论与应用》，清华大学出版社出版社，1986年，第1版五、作业选择教材和参考书中的部分习题。

第七章 最优控制（Optimal Control ）最优化（Optimization ）：生产过程的控制，企业的生产调度，对资金、材料、设备的分配，经济政策的制定等都与最优化有关。

最优控制：通常是针对控制系统本身而言的，目的是使一个机组、一台设备、或一个生产过程实现局部最优。

7-1概述1．最优分配问题：仓库（水泥） 运费（元/包） 工地（需要水泥）问应怎样发送这些水泥，才能使运费最省？设：从甲仓库运往A 、B 、C 工地的水泥数分别为1x 、2x 、3x ；从乙仓库运往A 、B 、C 工地的水泥数分别为4x 、5x 、6x 目标函数()x f （总运费）：()65432195442x x x x x x x f +++++= 最优化的任务：确定[]Tx x x x x x x 654321=的值，使()x f 为最小。

约束条件：⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+≤++≤++1200600900180********241654321x x x x x x x x x x x x该问题称为具有不等式约束条件的线性最优化问题，属于静态最优化问题，变量x 与时间无关2．动态最优化问题动态最优化问题：在最优控制系统中，受控对象是一个动态系统，所有变量都是时间的函数。

目标函数：是时间函数的函数，称为泛函数（简称泛函） 例：目标泛函 ()()[]⎰=ft t dt t t u t x L J 0,,基本约束条件（受控对象的状态方程）：()()()[]t t u t x f t x ,,= J----标量L----标量函数()t x ----n 维状态矢量 ()t u ----r 维控制矢量f ----n 维矢量函数最优控制问题：在满足约束条件下，寻求最优控制函数()t u ，使目标泛函J 取极值（最小或最大），即()max min =J 。

3．求解动态最优化问题的方法古典变分法、极小（大）值原理、动态规划法7-2研究最优控制的前提条件1．给出受控系统的动态描述，即状态方程()()()[]t t u t x f t x,,= 2．明确控制作用域控制集：()(){}0,≤=u x j t u U ϕ()()r m m j u x j ≤=≤;,,2,10, ϕ----()t u 满足的约束条件容许控制：()U t u ∈ 3．明确始端条件 固定始端：()0t x 给定 自由始端：()0t x 任意可变始端：()00Ω∈t x 始端集：()()[]{}0000==Ωt x j t x ρ()[]()n m m j t x j ≤==;,2,100 ρ----()0t x 必须满足的约束条件 4． 明确终端条件固定终端：f t 、()f t x 给定 自由终端：f t 给定、()f t x 任意可变终端：()f f t x Ω∈ 目标集：()()[]{}0==Ωf j t x ff t x ϕ()[]()n m m j t x f j ≤==;,2,10 ϕ----()f t x 必须满足的约束条件5． 给出目标泛函（即性能指标） 对于连续时间系统，一般表示为：()[]()()[]⎰+Φ=ft t f dt t t u t x L t x J 0,, （综合型或鲍尔扎型）()[]f t x Φ----终端指标函数，反映对终端性能的要求；()()[]⎰ft t dt t t u t x L 0,,----动态指标函数，L 为状态控制过程中对动态品质及能量或燃料消耗的要求等。

144 第七章 动态规划系统的数学模型、目标函数和求解方法是最优化问题的三个要素。

对于一个已知状态空间描述的控制系统来说，在确定了控制目标(性能指标)后，就需要寻求一个控制函数，使性能指标取最小(或最大)值。

在控制界普遍认为，庞特里亚金(Понтрягин)的最小值原理和贝尔曼(Bellman)的动态规划是求解最优控制问题的两种有效方法。

在第五章和第六章中，应用最小值原理给出了性能指标达到极值的必要条件，特别地，对于具有线性二次型性能指标的最优控制系统，能够得到最优控制的解析表达式，便于实现状态反馈控制。

本章介绍动态规划的主要内容—最优性原理，它在处理多级决策过程是非常有效的。

动态规划处理问题的思路是，把要处理的最优化问题转化为许多有序、相关的子问题，即多级决策过程，如果每一个子问题的解对全局都是最优的，那么，总的决策就是最优的。

本章先阐述多级决策过程的基本概念，其次介绍最优性原理，然后讨论用动态规划求解离散系统和连续系统的线性调节问题。

7-1 多级决策过程所谓多级决策过程如图7-1所示。

多级过程是由在时间或空间上(图7-2)顺序相关的若干级子过程组成的一个完整过程。

在每一级都需要有相应的决策，对整个过程性能指标而言，该决策应当是最优的。

显然某一级的决策确定后，必然会影响后一级过程的决策，从而影响到自当前一级过程到终端级过程的决策和整体性能指标。

由于在某一级时，子过程的初始状态是由前面多级过程及其决策的结果，初始状态往往不是唯一的，即可供选择的决策往往不止一个。

多级决策问题，就是要在允许选择的决策中选择一个最优的策略，使整体性能指标最优。

图7-1中的虚线框表示一级子过程，它可以代表任何类型的子过程。

图7-1将线性离散系统展示成一个时间上的多级决策过程，每一级子过程的状态方程是))u(B())x(A()1x(k k k k k +=+，1,,1,0-=N k 。

(7-1)系统从状态)0(x 经)1(x 、)2(x 、…转移到状态)(x N 的过程称为N 级过程。

第一章 最优化方法的一般概念人们在处理日常生活、生产过程、经营管理、社会发展等实际问题时，都希望获得最佳的处理结果。

在有多种方案及各种具体措施可供选择时，处理结果与所选取方案和具体措施密切相关。

获取最佳处理结果的问题称为最优化问题。

针对最优化问题，如何选取满足要求的方案和具体措施，使所得结果最佳的方法称为最优化方法。

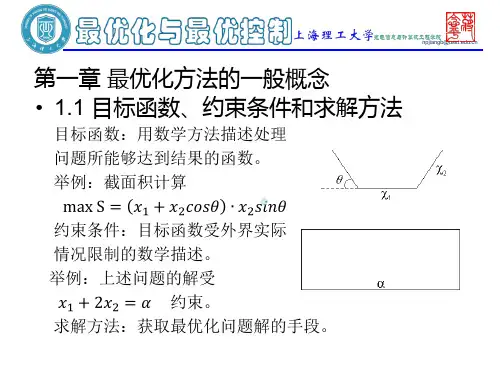
1-1 目标函数、约束条件和求解方法目标函数就是用数学方法描述处理问题所能够达到结果的函数，该函数的自变量是表示可供选择的方案及具体措施的一些参数或函数，最佳结果表现为目标函数取极值。

在处理实际问题时，通常会受到经济效率、物理条件、政策界限等许多方面的限制，这些限制的数学描述称为最优化问题的约束条件。

求解方法是获得最佳结果的必要手段，该方法使目标函数取极值，所得结果称为最优解。

针对各种类型的最优化问题，找出可靠、快捷的处理方法是最优化方法(理论)的研究范畴。

目标函数、约束条件和求解方法是最优化问题的三个基本要素。

无约束条件的最优化问题称为理想最优化问题，所得结果称为理想最优解。

下面用三个简单的例子，说明最优化问题的目标函数和约束条件。

例1-1 有一块薄的塑料板，宽为a ，对称地把两边折起，做成槽(如图1-1)。

欲使槽的横截面积S 最大，1x 、2x 和θ的最优值是多少？该问题要找出最优参数1x 、2x 和θ，使槽的横截面积S 最大，所以，目标函数为θθsin )cos (max 221x x x S ⋅+=； (1-1)由于底边与两个斜边的总长度应等于塑料板宽度a ，即约束条件为a x x =+212。

(1-2)有许多最优化问题可以方便地将等式约束条件代入目标函数中，使原问题转换为无约束条件的最优化问题，便于求解。

例1-1为无约束条件的最优化问题时，目标函数如下θθsin )cos 2(max 222x x x a S ⋅+-=。

(1-3)例1-2 仓库里存有20米长的钢管，现场施工需要100根6米长和80根8米长的钢管，问最少需要领取多少根20米长的钢管？用一根20米长的钢管，截出8米管或6米长管的方法只有三种，设：1x —1根长管截 成2根8米管的根数；2x —1根长管截成1根8米管和2根6米管的根数；3x —1根长管 截成3根6米管的根数。

最优化方法与最优控制课程设计一、设计背景随着现代科技的迅猛发展和社会竞争的加剧，各领域都需要越来越高效、精确、优化的设计方法和控制策略。

其中，最优化方法和最优控制技术是目前工程和科学领域中广泛应用的重要工具。

为了培养具有创新、实际和实践能力的工科人才，本次课程设计旨在通过对最优化方法和最优控制的讲解和实践，让学生更好地掌握和应用相关知识和技能。

二、设计目标通过本次课程设计，学生将会达到以下目标：1.掌握最优化方法和最优控制技术的基本理论和基本方法。

2.学会使用常见的数学建模软件，如Matlab等进行系统建模和仿真分析。

3.能够独立和团队完成一个小型的最优化或最优控制项目，提高实践能力和工程实践能力。

三、设计内容本次课程设计包含以下主要内容：1. 最优化方法最优化问题是在已知约束和目标函数的情况下，寻找能够使目标函数达到最大值或最小值的决策变量。

本部分主要包括以下内容：1.1. 常见最优化方法：线性规划、非线性规划、整数规划等。

1.2. 最优化算法：梯度下降法、共轭梯度法、拟牛顿法、遗传算法等。

1.3. 最优化软件：Matlab、Gurobi、CPLEX等。

2. 最优控制方法最优控制是指将控制问题描述为寻求使性能指标最优的动态过程。

本部分主要包括以下内容：2.1. 常见最优控制方法：最优控制基本原理、极小值原理与动态规划、Pontryagin最小值原理、最优控制的数值方法等。

2.2. 最优控制软件：Matlab、Simulink、LabVIEW等。

3. 课程设计环节选做题目：利用所学知识设计一个最优化或最优控制的小型项目，完成以下步骤：3.1. 对所选项目进行问题陈述和问题定义，明确项目的目标和指标。

3.2. 采用合适的数学建模方法，将该项目建立为数学模型。

3.3. 选择相应的最优化或最优控制方法，探究寻找最优解的过程。

3.4. 采用合适的软件工具，在计算机上进行仿真分析和可视化呈现。

3.5. 编写实验报告，总结和分析实验结果，分享并展示项目成果。

自动控制系统的优化与最优控制自动控制系统在现代工业中起着至关重要的作用，它能够实现生产过程的自动化、提高生产效率，同时减少人工操作的干预。

为了更好地发挥自动控制系统的作用，优化和最优控制成为了控制系统设计与应用中的重要内容。

本文将对自动控制系统的优化与最优控制进行探讨。

一、自动控制系统的优化自动控制系统的优化是指通过对系统结构、参数以及控制算法进行调整和改进，使系统的性能指标达到最优，如稳定性、响应速度、鲁棒性等。

优化的过程一般包括以下几个步骤：1. 需求分析：明确系统的性能指标和优化目标，如响应时间的要求、稳定性要求等。

2. 建模与仿真：通过数学建模和仿真分析，获得系统的数学模型，并根据模型进行性能分析，以便确定系统的优化方向。

3. 参数调整与优化：根据系统的模型和性能分析结果，对系统的结构、参数以及控制算法进行调整和优化，以实现优化目标。

4. 仿真与验证：将优化后的系统模型进行仿真与验证，评估系统的性能指标是否达到了预期的要求。

二、最优控制理论与方法最优控制是指在满足系统约束条件的前提下，通过选择最优的控制策略，使得系统满足某个性能指标的最佳化问题。

最优控制方法一般包括动态规划、变分法、最优化方法等。

下面介绍两种常见的最优控制方法。

1. 动态规划：动态规划是一种通过将原始问题拆分为子问题，并存储子问题的最优值来求解整体最优解的方法。

在最优控制中，可以将系统的控制问题拆分为不同的阶段，并通过动态规划的方法来求解每个阶段的最优控制策略，从而得到整体的最优控制策略。

2. 变分法：变分法是一种通过构建能量函数或者性能指标的泛函形式，利用变分法求解泛函极值问题的方法。

在最优控制中，可以将系统的性能指标表示为一个泛函，并通过变分法的求解方法来求取使得泛函极小化的最优控制策略。

常见的变分法包括最小时间、最小能耗、最小误差等。

三、优化与最优控制在工业中的应用自动控制系统的优化与最优控制方法在工业中有广泛的应用。

解2°：按二次函数计算。

取0x 0=；⎥⎦⎤⎢⎣⎡+++=Λ24222)x (2121x x x x ；⎥⎦⎤⎢⎣⎡=H =4222)x (A ； ⎥⎦⎤⎢⎣⎡=Λ20)x (0；⎥⎦⎤⎢⎣⎡-=Λ-=20)x (p 00； 25.0)p p /()x (p 0T 00T00=Λ-=A s ；⎥⎦⎤⎢⎣⎡-=5.00x 1；⎥⎦⎤⎢⎣⎡-=Λ01)x (1； ⎥⎦⎤⎢⎣⎡-=Λ+Λ-=5.01p )}p p /(p )x ({)x (p 00T001T 11A A ； 1)p p /()x (p 1T 11T 11=Λ-=A s ；T 2]11[x -=；收敛性检查：[]T 200)x (=Λ；得到[]T 11x -=*，4)x (=*f 。

2-2-6 变尺度法在梯度法中，是以)x (f 在k x 处的最速下降方向)x (p k k Λ-=作为搜索方向。

这种搜 索是局部性的，搜索会产生拉锯现象，使收敛放慢。

若要快速收敛，搜索方向应取k x 处的 牛顿方向，即)x ()x (p 1k k k ΛH -=-，式中 )x (k H 是 k x x =处的海森矩阵。

显然，要得到牛顿方向，需要计算二阶导数及海森 矩阵的逆矩阵，相当麻烦。

如果I =H )x (，则梯度方向和牛顿方向一致。

为了克服梯度法 和牛顿法的缺点，可按k k k k k H H g )x (p -=Λ-= (2-32)方向进行搜索。

为保证向下降方向搜索，且计算方便，要求矩阵k H 具有以下性质：1. k H 是正定的；2. 保证110p ,,p ,p -n 关于矩阵A 是共轭的；3. 1+k H 与k H 具有递推关系，即k k k H H H ∆+=+1， (2-33)式中 k H ∆称为校正矩阵。

为使110p ,,p ,p -n 关于矩阵A 共轭，并注意到式(2-32)则有0p p 1T =+k i A ，0g p 11T =++k k i AH ，k i ,,1,0 =。