当前位置：文档之家 › 电阻电路的等效变换分析

电阻电路的等效变换分析

  • 格式：ppt
  • 大小：2.48 MB
  • 文档页数：106

下载文档原格式

  / 106

合集下载

电阻电路等效变换

电阻电路等效变换
第三页
特例：两电阻并联
Req
R1R2 R1 R2
i1
R2 R1 R2
i
i2
R1 R1 R2
i
二、电阻的混联 —串、并联的组合
采用逐次等效的办法
第四页
例2－1 求Rab=?
6 15
5
①
5
③
① Re'q R3 R4 10 ②
③
Req
R1
R '' eq
6 6
12
② R'' eq
电阻电路等效变换
第一页
§2-1电阻的串联和并联
一、串联 电阻首尾相联，流过同一电流的连接方式，称为串联(图2－2a)
VAR:
u u1 u2 un R1i R2i Rni (R1 R2 Rn )i
VAR: u Reqi
即若干电阻串联等效于一个电阻，Req=R1+R2+···+Rn
①等效变换法 Rin,Req的计算方法： ②根据Rin的定义
i u
图2－18a
i u
图2－18b
第十八页
例2－8 求图2-19电路的输入电阻 Rin=?
i
u
l2
l1
i1
i2
图2－19
解: 标明电压、电流及参考方向, 则:
u Rin i
选择回路 l1, 列写KVL: 3i2 4i2 2i1 0 i2 2i1
R3 R1
例2－5 求图2-9a电路中电流 I1, I2, I3 , I4。
I I2 I1
解: 思路 Δ→Y
Req I
I1
I2
I3
I4
48
Rb 4 4 8 2, 同理,求得 : Rc 2, Rd 1, Req (1 Rb ) //(5 Rd ) Rc 4

电阻的等效变换技巧

电阻的等效变换技巧

电阻的等效变换技巧电阻的等效变换技巧是电路分析中常用的一种方法，通过将电路中的电阻按照等效电路的要求进行变换，可以简化复杂的电路分析问题，提高分析的效率。

下面将介绍电阻的串、并联、三角形转星型等效变换技巧。

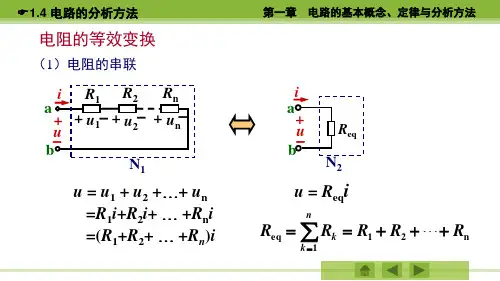
1. 串联电阻的等效变换当若干个电阻串联时，可以通过求和的方式得到等效电阻。

假设要将电阻R1、R2、R3串联，则它们的等效电阻为Req = R1 + R2 + R3。

这是因为电流在串联电路中是恒定的，所以电阻的总和就是电流通过的路径上的总阻抗。

2. 并联电阻的等效变换当若干个电阻并联时，可以通过求倒数和再求倒数的方式得到等效电阻。

假设要将电阻R1、R2、R3并联，则它们的等效电阻为Req = (1/R1 + 1/R2 + 1/R3)^-1。

这是因为电压在并联电路中是恒定的，所以电阻的倒数之和的倒数就是电流通过的总阻抗。

3. 三角形转星型等效变换在某些情况下，三角形电阻网络需要转换为星型电阻网络以便于分析。

假设有三个电阻Ra、Rb、Rc构成的三角形网络，可以通过以下公式得到等效电阻值：Rab = (Ra * Rb + Rb * Rc + Rc * Ra) / (Rc)Rac = (Ra * Rb + Rb * Rc + Rc * Ra) / (Rb)Rb= (Ra * Rb + Rb * Rc + Rc * Ra) / (Ra)这是因为在三角形电阻网络中，可以将其中任意两个电阻并联得到一个新的等效电阻，再将得到的等效电阻与剩余的电阻串联，最后得到总的等效电阻。

以上是电阻的等效变换技巧的基本介绍，这些方法可以帮助我们简化复杂的电路分析问题，提高分析的效率。

在实际应用中，可以根据具体情况选择不同的等效变换方法，以便更好地解决问题。

同时，还可以通过使用等效变换技巧，将复杂电路转换为简单的等效电路，以便更好地理解和分析电路的工作原理。

电阻电路的等效变换

电阻电路的等效变换

a
c
f
R1
R4
R3
R2
R5
b
Y形连接：各个电阻都有一端接在一个公共结点上，另一端则分别接到三个端子上。
形连接：各个电阻分别接在3个端子的每两个之间。
请学生分析电桥电路中电阻的连接特点：Y形连接和形连接。
1
i
1
1
i
s
R
u
_
பைடு நூலகம்
+ i
+
Ri
s
_
u
R
_
Gu
u
i
s
-
=
R
在具体解题当中应该注意三点： 1）电源等效变换时的参考方向,电流源的流向与电压源内部电流方向一致。 2）受控电压源和受控电流源之间的等效变换同独立电源，注意：受控源的控制支路在等效变换中应该保留
已知：电路如图所示，求：图中的开路电压 。
R
0
i
+
+
u
s
R
1
i
a
R
1
u
oc
-
_
3.应用
4.例题：
含受控源一端口网络
+
-
us
i
i
u
R
S
in
=
含受控源一端口网络
+
-
u
is
u
i
S
=
R
in
根据定义：
说明：因为求解的是端口的输入电阻，要注意在端口上的电压和电流的关系的参考方向标法，此处为关联参考方向的表达式。若非关联求解公式要加负号。
3．例题
例1. 求图示一端口的的输入电阻.

电阻的等效变换

电阻的等效变换

R1 R1 R2
u
u2
R2 R1 R2
u
1.4 电路的分析方法
（2）电阻的并联
i
a + u
b
i1 R1
i2 R2
…
in Rn
N1
i = i1+ i2++ in
= G1u+G2u++ Gnu
=（G1+ G2+… +Gn）u
第一章 电路的基本概念、定律与分析方法
i
a +
u b
Req
N2
i = Gequ
1.4 电路的分析方法
电阻的等效变换
（1）电阻的串联
i R1 R2 Rn
aБайду номын сангаас+
bu
+ u1 + u2 + un
N1
u = u1 + u2 ++ un =R1i+R2i+ +Rni =(R1+R2+ +Rn)i
第一章 电路的基本概念、定律与分析方法
i
a
+
bu
Req
N2
u = Reqi
n
Req Rk R1 R2 Rn k 1
…
in Rn
N1
Req
R1 R2 R1 R2
两个电阻并联时
i1
R2 R1 R2
i
i2
R1 R1 R2
i
1.4 电路的分析方法
第一章 电路的基本概念、定律与分析方法
例1 求解端口ab的等效电阻 。
a
解：1.找到并联电阻进行等效。

电阻电路的等效变换(电路分析基础课件)

电阻电路的等效变换(电路分析基础课件)
03
02
01
等效变换的目的
等效变换的基本原则
电压和电流保持不变
在等效变换过程中，电路中的电压和电流值应保持不变。
元件参数相同
等效变换后的元件参数应与原电路中的元件参数相同。
功率平衡
等效变换后的电路应满足功率平衡条件，即电源提供的功率等于负载消耗的功率。
02
电阻的串并联等效变换
总结词
当多个电阻以串联方式连接时，总电阻值等于各电阻值之和。
详细描述
在并联电阻的等效变换中，总电阻倒数1/R_eq等于各个并联电阻倒数1/R1、1/R2、...、1/Rn之和。这种等效变换在电路分析中非常有用，因为它可以帮助我们简化电路模型。
01
02
03
04
电阻并联的等效变换
串并联电阻的等效变换
总结词：串并联电阻的等效变换是电路分析中的重要概念，它涉及到将复杂的串并联电路简化为易于分析的形式。
等效变换方法：对于非线性电阻电路，可以采用分段线性化方法，将非线性电阻的伏安特性曲线分段近似为直线，然后进行等效变换。
05
等效变换在电路分析中的应用
在计算电流和电压中的应用
总结词：简化计算
详细描述：通过等效变换，可以将复杂的电阻电路简化为简单的电路，从而更容易计算电流和电压。
总结词：提高精度
总结词：扩展应用范围
电阻串联的等效变换
总结词
当多个电阻以并联方式连接时，总电阻值倒数等于各电阻值倒数之和。
详细描述
在电路中，如果多个电阻以并联方式连接，则总电阻的倒数等于各电阻倒数之和。这是因为多个电阻并联时，它们共享相同的电压，因此总电流等于各支路电流之和。
总结词
并联电阻的等效变换可以通过公式1/R_eq = 1/R1 + 1/R2 + ... + 1/Rn表示。

电阻电路的等效变换

电阻电路的等效变换

B
A
C
A
①电明路确等效变换的条件：
两电路具有相同的VCR； ②电路等效变换的对象：
③电路等效变换的目的： 化简电路，方便计算。
2.2 电阻的等效变换
目的与要求
会对串、并联电路进行分析、计算
重点与 难点
重点： 1.串联分压原理 2.并联分流原理 3.串、并联电路的分析、计算
难点： 网络等效
2.2 电阻的等效变换

u31Y R2 u23Y R1 R1R2 R2R3 R3R1
i3 =u31 /R31 – u23 /R23
根据等效条件，比较式(3)与式(1)，得 Y的变换条件：
R 12

R1
R2

R1R 2 R3
R 23

R2

R3

R2R3 R1
R 31

R3

R1

R3R1 R2
ik
inu R1 R2源自RkRn_
(a)各电阻两端为同一电压（KVL)； (b)总电流等于流过各并联电阻的电流之和(KCL)。
i = i1+ i2+ …+ ik+ …+in
②等效电阻
i
i
+
i1 i2
ik
in
+
u R1 R2
Rk
Rn 等效 u
Req
_
_
由KCL:
i = i1+ i2+ …+ ik+ …+in
=R1i2+R2i2+ +Rni2
表明 =p1+ p2++ pn

验证电阻的等效变换实验报告

验证电阻的等效变换实验报告

验证电阻的等效变换实验报告引言：电阻是电路中常见的元件，它的作用是限制电流的流动。

在电路设计和分析中，经常需要对电阻进行等效变换，以简化电路的计算和分析。

本实验旨在验证电阻的等效变换原理，并通过实验数据来验证等效电阻的准确性。

实验目的：通过实验验证电阻的等效变换原理，并验证等效电阻的准确性。

实验器材：1. 电阻箱2. 电压表3. 电流表4. 电源实验步骤：1. 将电阻箱连接到电路中，接入电源。

2. 使用电压表和电流表测量电路中的电压和电流。

3. 记录测量结果，并计算电阻的等效值。

4. 将测量结果与理论计算结果进行比较，验证等效电阻的准确性。

实验结果与讨论：通过实验测量得到的电压和电流数据，我们可以计算出电阻的等效值。

实验中我们选择了不同的电阻值进行测量，并比较了实验结果与理论计算结果。

实验结果表明，实际测量得到的电阻值与理论计算结果非常接近，验证了电阻的等效变换原理的准确性。

在实验中，我们还发现了一些误差存在，可能是由于仪器的精度限制或者电路中其他因素的影响。

结论：通过本次实验，我们验证了电阻的等效变换原理，并验证了等效电阻的准确性。

实验结果表明，电阻的等效变换可以简化电路的计算和分析，提高工程设计的效率。

进一步的工作：在今后的研究中，可以进一步探究不同类型电阻的等效变换原理，并研究其在实际电路中的应用。

此外，可以对实验中的误差进行进一步分析和探讨，以提高实验结果的准确性。

致谢：感谢实验中使用的仪器设备和实验室的支持。

感谢老师对实验的指导和帮助。

参考文献：[1] 《电路分析基础》[2] 《电工技术手册》附录：实验数据表格实验数据表格电阻值（Ω）电压（V）电流（A）等效电阻（Ω）--------------------------------------------100 5 0.05 100200 10 0.05 200300 15 0.05 300以上为电阻的等效变换实验报告，通过实验验证了电阻的等效变换原理，并验证了等效电阻的准确性。

电阻电路的等效变换

电阻电路的等效变换

电阻电路的等效变换电阻电路的等效变换是指将一个电阻电路转化为另一个等效的电阻电路，使得两个电路在电学性质上完全相同。

等效变换在电路分析和设计中起着重要的作用，能够简化电路分析过程，提高计算效率。

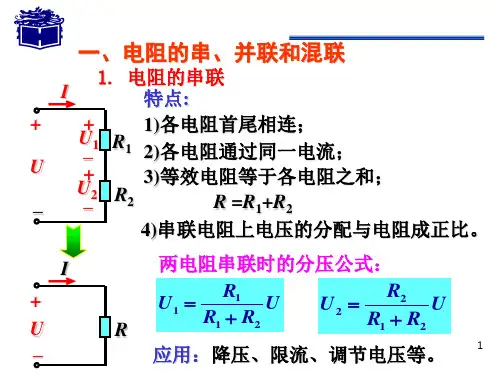
一、串联电阻的等效变换串联电阻是指多个电阻按顺序连接在一起，电流依次通过每个电阻。

当电路中有多个串联电阻时，可以通过等效变换将其转化为一个等效电阻。

假设有两个串联电阻R1和R2，其等效电阻为Req。

根据欧姆定律可知，串联电阻中的电流相同。

根据电阻的定义可知，电阻与电流和电压之间存在线性关系，即R = U / I。

因此，R1和R2的电阻值可以表示为R1 = U / I1，R2 = U / I2。

在串联电路中，电流I1通过R1，电流I2通过R2，由于串联电路中电流只有一个路径，所以I1 = I2。

将上述两个等式相等，可得到R1 / I1 = R2 / I2，即R1 / R2 = I1 / I2。

由此可推导出串联电阻的等效电阻为Req = R1 + R2。

二、并联电阻的等效变换并联电阻是指多个电阻同时连接在一起，电流分别通过每个电阻。

当电路中有多个并联电阻时，可以通过等效变换将其转化为一个等效电阻。

假设有两个并联电阻R1和R2，其等效电阻为Req。

根据欧姆定律可知，电压在并联电路中相同。

根据电阻的定义可知，电阻与电流和电压之间存在线性关系，即R = U / I。

因此，R1和R2的电阻值可以表示为R1 = U1 / I，R2 = U2 / I。

在并联电路中，电压U1作用在R1上，电压U2作用在R2上，由于并联电路中电压相同，所以U1 = U2。

将上述两个等式相等，可得到R1 / U1 = R2 / U2，即R1 / R2 = U1 / U2。

由此可推导出并联电阻的等效电阻为1 / Req = 1 / R1 + 1 / R2。

三、星型-三角形转换星型电阻网络和三角形电阻网络是常见的电阻网络拓扑结构。

在电路分析中，有时需要将星型电阻网络转换为三角形电阻网络，或将三角形电阻网络转换为星型电阻网络，以便于进行电路分析。

电阻串、并联电路的等效变换

电阻串、并联电路的等效变换
6
解: (4) 根据欧姆定律
U 125 I A 10A R 12.5
(5) 根据分流公式
R34 5 I1 I 10A 5A R2 R34 55
R2 5 I2 I 10A 5A R2 R34 55
7
应用：降压、限流、调节电压等。
1
I + I1 U – I + U – I2
2.电阻的并联 特点: (1)各电阻的首、尾分别相连； (2)各电阻两端的电压相同； (3)等效电阻的倒数等于各电阻倒数之和； 1 1 1 R2
I + I1 U – I + U – R I2 R1 R2
(4)并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式：
U R2 R1 1 I1 I R1 R1 R2 R1 R2 I R1 R2
R1 I2 I R1 R2
应用：分流、调节电流等。
3
3.电阻的混联 既有串联又有并联的连接方式。 如下图所示：
4
【例1】有一混联电路，R1＝10Ω ,R2＝5Ω ,R3＝ 2Ω ,R4＝3Ω,电源电压U＝125V，求：电流I、 I1 R I 1、 I 2 。 2 I R1 AR R B 3 4 + U I2 – 解: (1) R3和R4可等效成一个电阻R34 R34 ＝ R3+R4 ＝（2+3）Ω＝5Ω I1 R
2
I R1
+ U –
A R B 34 I2
5
解: (2) R2和R34可等效成一个电阻RAB I R1 A RAB B
+ U –
R2 R34 5 5 RAB 2.5 R2 R34 5 5
(3) R1和RAB可等效成一个电阻R I R + U – R ＝ R1+RAB ＝(10+2.5）Ω＝12.5Ω

电阻网络中的三角形星形等效变换解析

电阻网络中的三角形星形等效变换解析

电阻网络中的三角形星形等效变换解析引言:电阻网络是电路分析中常见的一种形式，使用电阻、电源和连接线将电路元件组装在一起。

在电路分析中，对于复杂的电阻网络，我们经常需要简化电路结构以便更方便地进行计算和分析。

其中一种常见的简化方法就是进行等效变换。

一、三角形到星形等效变换1. 三角形等效变换的原理在电阻网络中，当使用三个电阻相互连接而成三角形时，我们可以通过将三角形转换为星形来简化电路结构。

这种等效变换的原理是基于KCL（电流守恒定律）。

根据KCL，三角形中的每个节点的电流总和为零。

因此，我们可以通过连接三角形中的节点中间电路的电阻，将三角形转换为星形。

2. 三角形到星形等效变换的公式在进行三角形到星形等效变换时，我们需要计算三角形电阻与星形电阻的关系。

假设三角形电阻分别为R1、R2和R3，星形电阻分别为Rab、Rbc和Rca，则它们之间的关系为：1/Rab = 1/R1 + 1/R2 + 1/R31/Rbc = 1/R1 + 1/R2 + 1/R31/Rca = 1/R1 + 1/R2 + 1/R33. 三角形到星形等效变换的实例以一个简单的三角形电阻网络为例，假设三角形中的三个电阻分别为10Ω、20Ω和30Ω。

我们来计算它们的星形等效电阻。

根据上述公式，我们可以得到：1/Rab = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/601/Rbc = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/601/Rca = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/60通过求倒数，并计算总电阻，我们可以得到星形电阻的数值为：Rab = 60/7 ΩRbc = 60/7 ΩRca = 60/7 Ω二、星形到三角形等效变换1. 星形等效变换的原理与三角形到星形等效变换相反，我们可以通过将星形转换为三角形来简化电路结构。

第2章电阻电路的等效变换

第2章电阻电路的等效变换

总电流
U S 18 I= = A = 6A R 3
由分流公式得
6 I1 = I = × 6A = 4A 4× 4 9 6 + (1 + ) 4+4
再分流得
6
1 I x = I 1 = 2A 2
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.4 Y形电路和Δ形电路之间 的等效变换
返回
电路分析基础
如何等效化简电桥测温电路? 如何等效化简电桥测温电路?
返回
电路分析基础
第2章 电阻电路的等效变换
2.1 等效变换
电阻电路
线性电阻电路
非线性电阻电路
简化线性电阻电路的主要依据是等效变换
返回
电路分析基础
第2章 电阻电路的等效变换
2.1.1 一端口网络的定义
二端网络
一端口网络
流入一个端子的电流必定等于流出另一端子的电流
Ig =
Rp Rg + R p
× 10 × 10 −3 = 1 × 10 −3 mA
解之得应并联的电阻为
0.1RG 2 × 10 3 Rp = = Ω ≈ 222.22Ω 0.9 9
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.3 电阻的混联
判别电路的串并联关系根据以下原则： 判别电路的串并联关系根据以下原则： （1）看电路的结构特点。 看电路的结构特点。 （2）看电压、电流关系。 看电压、电流关系。 （3）对电路作变形等效。 对电路作变形等效。 （4）找出等电位点。 找出等电位点。
R4 R5 R2(R3 + ) R4+R5 R = R1 + R4 R5 R2 + (R3 + ) R4 + R5

电路分析课件-电阻电路的等效变换

电路分析课件-电阻电路的等效变换

º
例 兩個並聯電阻的分流：
i º
R1
i1 R2
i2
i1
1
1 R1 R1 1
R2
i
R2 R1 R2
i
º
i2
1
1 R2 R1 1
R2
i
R1
R1 R2
i
（4） 功率
p1=G1u2， p2=G2u2，， pn=Gnu2 p1: p2 : : pn= G1 : G2 : :Gn =1/R1 : 1/R2 : … : 1/Rn
u12Y=R1i1Y–R2i2Y u23Y=R2i2Y – R3i3Y (2) u31Y=R3i3Y – R1i1Y i1Y+i2Y+i3Y = 0
由式(2)解得：
i1Y
u12YR3 u31YR2 R1R2 R2 R3 R3R1
i2Y
u23Y R1u12Y R3 R1R2 R2 R3 R3R1
R1
Rin (R1 R2 ) // R3
無源電 阻網路
例
6 + US
_ i1
6i1
－
+
3
6i1
6
－+
3
i1
i+
U _
i
i1
3i1 6
1.5i1
U 6i1 3i1 9i1
外加電壓源
Rin
U i
9i1 1.5i1
6
例
外加電流源
5 + i
i2 i1 u 0.1u1 +
u_1
15
－
u1 15i1
1k 10V
1k
I
0.5I
º
+

电阻电路的等效变换法

电阻电路的等效变换法

i
R1
+
u
R2
-
VAR:
i + u VAR：
R=R1+R2
注意：当电路中的某一部分用其等效电路替代后，未被替代部分的电压电流均 应保持不变，即“对外等效”。
§2-1 引言
三、等效法
1、等效法：将复杂电路进行等效化简，从而求出各i. u, p的一种分析方法
2、本章内容
电阻的等效变换 电源的等效变换
第二章 电阻电路的等效变换法
R4
Rg
R2
R3
若R1 R3=R2 R4
R1
R4
则电桥平衡
或者
R2
R3
R1
R4
x
R2
R3
第二章 电阻电路的等效变换法
§2-3 Y—△等效变换
一、电阻的Y、△联接 1、为什么需Y—△变换 2、Y形联接
Байду номын сангаас
§2-3 Y—△等效变换
3、△形联接 a
4、举例： 上图：R1.R2.R3 R3.R4.R5——△ R1.R3.R4 R2.R3.R5——Y
+
i
+
US -
U
R0 -
i
+
US R0
R0
U
-
§2-5 两种实际电源的等效变换
2、实际电流源——实际电压源
iS R0
+
i
iSR0 -
R0
3、说明： 注意极性 等效对外电路等效，内部不等效 举例说明其应用 受控源也可以同样等效（但不能将受控变掉）
§2-5 两种实际电源的等效变换
+
U1
-
R0

电路基本分析第二章电阻电路的等效变换法

电路基本分析第二章电阻电路的等效变换法

Chapter 2
方法二：将Y→△（如下图），自己练习。
1
2Ω
R12
2
1Ω 2Ω
1
2Ω
1Ω
2
1Ω
3
1
1
R12
R13 2 Ω
2
1Ω
2 1Ω
R23
3
1
R12
2
说明:使用△-Y 等效变换公式前，应先标出三个端头标 号，再套用公式计算。
Chapter 2
小结: 1 .一个内部不含独立电源的单口网络对外可以等效为一
电路对外可等效为一个理想电压源us和一个内阻Rs串 联的电压源模型。
Chapter 2
2. n个实际电流源并联：
isn
Gsn
i s2
is1
is3 Gs3
Gs2
i +a Gs1 u
-
b
i＇
a
+
is
Gs
u＇
-
b
由KCL得端口电压电流关系：
i i s 1 i s 2 i s 3 i s n G s 1 G s 2 G s 3 G s n u
解得：
i1

R1R2
R3u12 R2R3
R3R1

R1R2
R2u31 R2R3
R3R1
i2

R1R2
R1u23 R2R3
R3R1

R1R2
R3u12 R2R3
R3R1
i3

R1R2
R2u31 R2R3
R3R1

R1R2
R1u23 R2R3
R3R1

第二章 电阻电路的等效变换

第二章 电阻电路的等效变换
将三个串联的电阻等效为一个电阻，其电阻为
R R2 R1 R3 4 2 6 12
由图(b)电路可求得电阻RL的电流和电压分别为：
i uS 15V 1A R RL 12 3
u RLi 3 1A 3V
例2－3电路如图2－7(a)所示。已知iS1=10A, iS2=5A, iS3=1A, G1=1S, G2=2S和G3=3S，求电流i1和i3。
u2

R3i1

(R2

R3
)i2

对电阻三角形联接的三端网络，外加两个电流源i1 和i2，将电流源与电阻的并联单口等效变换为一个
电压源与电阻的串联单口，得到图(b)电路，由此得
到
i12

R31i1 R23i2 R12 R23 R31
uu12

R31i1 R31i12 R31 (i1 i12 ) R23i12 R23i2 R23 (i2 i12 )
例2－2 图(a)所示电路。已知uS1=10V, uS2=20V, uS3=5V, R1=2, R2=4, R3=6和RL=3。求电阻RL的电流和电压。
解:为求电阻RL的电压和电流，可将三个串联的电压 源等效为一个电压源，其电压为
uS uS2 uS1 uS3 20V 10V 5V 15V
R3

R12
R23 R31 R23
R31
(2 13)
由此 解得
R2

R12
R12 R23 R23

R31

(2 14)
R2

R3

R23 (R12

R31 )

电阻电路的等效变换

电阻电路的等效变换

R23
R31
R12 R3 R31 R2 R1 R2 R3
R12 R31 R1
R1
R12
R12 R31 R23
R31
已知电阻，求Y形电阻
R1
R12
R12 R31 R23
R31
R2
R12
R23 R12 R23
R31
R3
R12
R31 R23 R23
R31
请用文字概括以上三个公式
R31 i3/ 3
已知电阻，求Y形电阻
R1
R 12
R12R 31 R 23 R 31
R2
R 12
R 23R12 R 23 R 31
R3
R 12
R 31R 23 R 23 R 31
R1
R2
R3
RY
1 3
R
用电导表示时 已知Y电阻，求形电阻
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
Y形电阻两两乘积之和 Y形不相邻电阻
Y连接的三个电阻相等R1=R2=R3=RY时 已知Y电阻，求形电阻
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3 R1
R31
R1 R2
R2 R3 R2
R3 R1
R R12 R23 R31 3 RY
连接的三个电阻相等R12=R23=R31=R 时
并联 16 64 12.8
10
16 64
串联12.8 7.2 20
并联 20 30 12 20 30
例： 电路如图，求等效电阻 Rab 和 Rcd。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

电路为二端网络(或一端口网络)。
无
源
i
无
一
i
源
端 口
2. 两端电路等效的概念
两个两端电路，端口具有相同的电压、电流关系,则称 它们是等效的电路。
+
等效
i
B
u
-
+
i
C
u
-
对A电路中的电流、电压和功率而言，满足
B
A
C
A
（1）电路等效变换的条件
明 确 （2）电路等效变换的对象
（3）电路等效变换的目的
两电路具有相同的VCR
i
+
u
_
Ⅰ、KVL u= u1+ u2 +…+uk+…+un
由欧姆定律 uk = Rk i ( k=1, 2, …, n )
u= (R1+ R2 +…+Rk+…+ Rn) i
+
u
_
Ⅱ、设端口间只通过一个电阻连接，则
u= Reqi Ⅲ、 由等价条件得
Req=( R1+ R2 +…+Rn) = Rk
结论： 串联电路的总电阻等于各分电阻之和。
例1. º
Req º
4 2
3 6
Req = 4∥(2+3∥6) = 2
例2.
40 º
Req
30
º
30
40 º
40
Req
30 30
º
Req = (40∥40)+(30∥30∥30) = 30
2.2 电阻的星形连接与三角形连接的等效变换
（ Y 形连接与形连接）
下图是电阻的两种连接方式：
+i1 u12
即 电流分配与电导成正比
对于两电阻并联
i
º i1
i2
R1
R2
º
i1
1/
1/ R1 R1 1/
R2
i
R2 R1 R2
i
i2
1/
1 / R2 R1 1 /
R2
i
R1 R1 R2
i
4. 功率关系 p1=G1u2， p2=G2u2，， pn=Gnu2 p1: p2 : : pn= G1 : G2 : :Gn
3. 串联电阻上电压的分配
显然 uk Rk i Rk Rk u Reqi Req Rk
即 电压与电阻成正比
故有
uk
Rk Rj
u
ºi +
+ u_1
R1
u+ _ u_n Rn º
例：两个电阻分压, 如下图
i º ++
u-1 R1
u1
R1 R1 R2
u
uu2 R2
_+
u2
R2 R1 R2
u
第二章 电阻电路的等效变换分析
2. 1 电阻的串、并联等效变换
电阻电路 分析方法
仅由电源和线性电阻构成的电路
（1）欧姆定律和基尔霍夫定律是分 析电阻电路的依据；
（2）等效变换的方法,也称化简的方法
1. 两端电路（网络）
任何一个复杂的电路, 向外引出两个端钮，且从一
个端子流入的电流等于从另一端子流出的电流，则称这一
º
( 注意方向 !)
4. 功率关系
p1=R1i2， p2=R2i2，， pn=Rni2
p1: p2 : : pn= R1 : R2 : :Rn
总功率
p=ui=Reqi i=Reqi2 =(R1+ R2+ …+Rn ) i2 =R1i2+R2i2+ +Rni2 =p1+ p2++ pn
故可以直接用等效电阻计算串联电路“内部”的总功率。 （对照前面：“对外等效”，对内不一定等效。）
2.1.2 电阻并联 (Parallel Connection)
i
+
i1 i2
ik
in
u R1 R2
Rk
Rn
_
1. 电路特点:
(a) 各电阻两端分别接在一起，两端为同一电压 (KVL)； (b) 总电流等于流过各并联电阻的电流之和 (KCL)。
2. 等效i 电阻Req
i
+
i1 i2
ik
in 等效 +
R12
– 1
u31 R31
– i2
i3 +
2 +
R23 u23
3 –
三角形连接
形
+ i1Y 1 –
u12Y
– i2Y R2 2
+
R1
u31Y
u23Y
R3 i3Y +
3–
星形连接 Y形
+i1 u12
R12
– 1
u31 R31
– i2
2 +
R23 u23
连接
i3 + 3
–
+ i1Y 1 –
u12Y
– i2Y R2 2
+
R1
u31Y
u23Y
R3 i3Y +
3–
Y连接
显然、Y连接方式，既非串联也非并联。特点： 都通过3个端子，与外部相连。
下面要证明：这两个电路，当它们的电阻满足一定的关系时， 是能够相互等效的。
等效的条件: i1 =i1Y , i2 =i2Y , i3 =i3Y ,
且 u12 =u12Y , u23 =u23Y , u31 =u31Y
u R1 R2
Rk
Rn
u
Req
_
_
Ⅰ、 由KCL: i = i1+ i2+ …+ ik+ in 故有 i = u/R1 +u/R2 + …+u/Rn=u(1/R1+1/R2+…+1/Rn)
Ⅱ、 设端口间只通过一个电阻连接，则
i = u / Req
Ⅲ、由等价条件得
1/Req= 1/R1+1/R2+…+1/Rn
令 G =1 / R, 称为电导
Geq=G1+G2+…+Gk+…+Gn= Gk= 1/Rk
º Req=? 1.3 6.5 13
º
3. 并联电阻的电流分配
由
ik u / Rk Gk i u / Req Geq
故 ik Gk i Gk
Req=1.3∥6.5∥13 由 G =1/1.3+1/6.5+1/13 = 1 故 Req=1/G=1
2.1.1 电阻串联 (Resistors Series)
1. 电路特点:
R1
Rk
Rn
i
+ u1 _ + uk _ + un _
+
u
_
(a) 各电阻顺序连接，流过同一电流 (KCL)； (b) 总电压等于各串联电阻的电压之和 (KVL)。
2. 等效电阻Req
R1
RkRnReqi+ u1 _ + uk _ + un _ 等效
未变化的外电路A中的电 压、电流和功率
化简电路，方便计算
+ +
i
r
US _
1
R1
i1 i5
i3
R3
u
_ R2
i2
R4
i4
2
+ +
i
r
US _
1
u
Req
_
2
可以用Req替代的条件：端子1-2以右部分有相同的 伏安特性。 Req称为等效电阻。
用等效电阻替代电路的某部分以后，未被替代部 分的电压、电流应保持不变。即“对外等效”，对内不 一定等效。例如，要求解实际电路1-2右端的i1等，须用 原电路求。
+ i1 u12 R12
– 1
u31 R31
– i2
i3 +
2 +
总功率
p=ui=uuGeq=Gequ2 = (G1+ G2+ …+Gn ) u2 =G1u2+G2u2+ +Gnu2 =p1+ p2++ pn
故可以直接用等效电阻计算并联电路“内部”的总功率。
（对照前面：“对外等效”，对内不一定等效。）
2.1.3 电阻的串并联 要求：弄清楚串、并联的概念。
计算举例：