下载文档原格式
MOEA-D算法的改进及其在多目标测试用例排序中的应用摘要多目标测试用例排序（MOTS）作为软件测试中的重要问题之一，旨在将测试用例按照覆盖率、故障检测能力等多维度指标进行排序，以达到自动化选择测试用例的目的。
MOEA/D（Multi-objective Evolutionary Algorithm based on Decomposition）算法是一种较为有效的解决MOTS问题的算法，然而，MOEA/D算法中存在一些问题，如权重分配策略、解集过度重叠等，需要进行改进。
本文通过研究MOEA/D算法中的问题，提出改进算法，即MOEA/D-IT，该算法采用非均匀分配策略以解决权重分配问题，并结合均匀分配策略进行解集划分，从而解决解集过度重叠的问题。
最后，将MOEA/D-IT算法应用于实际问题中的MOTS问题，结果表明改进算法在解决MOTS问题方面具有明显优势。
关键词：多目标测试用例排序；MOEA/D算法；权重分配策略；解集过度重叠；MOEA/D-IT算法1. 引言随着软件规模和复杂度的不断提高，软件测试变得越来越重要。
测试用例是评估软件质量和性能的关键因素，测试用例的质量和数量对软件测试的效率和效果有很大的影响。
因此，如何自动化生成高质量的测试用例并选择测试用例来实现全面测试是软件测试研究的重点之一。
多目标测试用例排序（MOTS）作为软件测试中的重要问题之一，旨在将测试用例按照指定的多维度指标进行排序，以达到自动化选择测试用例的目的。
目前，MOTS问题通常被认为是一个多目标优化问题，需要使用多目标优化算法来解决。
MOEA/D（Multi-objective Evolutionary Algorithm based on Decomposition）算法是一种基于分解思想的多目标优化算法，该算法将多目标问题转化为多个单目标子问题，并使用进化算法求解。
MOEA/D算法具有许多优点，如快速收敛，较好的解集质量等。
p算法,k算法,破圈法,穷举法,ew算法,d算法,bf算法,fw算法的基本原理和应用场合-回复这是一篇关于几种常见算法的基本原理和应用场合的文章，我们将一一回答你提出的问题。
首先，让我们来了解一下最常见的算法之一——穷举法。
穷举法的基本原理是通过遍历所有可能的解空间，从中找到满足条件的解。
它的应用场合包括但不限于密码破解、密码学中的攻击问题、组合问题、排列问题等。
接下来，我们来介绍下破圈法。
破圈法是一种用于解决循环链表中环的问题的算法。
它的基本原理是使用快慢指针来检测链表中是否存在环，如果存在环，则通过慢指针每次向前移动一步，快指针每次向前移动两步的方式，最终两个指针会相遇于环的起点。
因此，破圈法的应用场合主要是解决链表中环的问题，例如判断链表是否有环、找到环的起点等。
下一种算法是ew算法。
ew算法的全称是Exponent Weighted algorithm，是一种加权指数算法。
这个算法的基本原理是通过对历史数据进行加权取值，使得最新数据的权重更高，从而反映最新数据的变化情况。
它的应用场合主要是用于计算带有时间概念的数据的指数平滑移动平均值，例如股票价格的预测、网络流量的预测等。
接下来，让我们来介绍一下d算法。
d算法是一种图搜索算法，用于解决有向图的单源最短路径问题。
它的基本原理是通过迭代更新节点的距离值，直到找到从源节点到目标节点的最短路径为止。
d算法的应用场合包括路由选择、网络优化、数据挖掘等。
接下来，我们来介绍bf算法。
bf算法的全称是Bellman-Ford算法，它是一种用于解决带有负权边的图的单源最短路径问题的算法。
bf算法的基本原理是通过反复松弛边的操作来逐步更新节点的距离值，直到找到从源节点到目标节点的最短路径为止。
bf算法的应用场合主要是解决带有负权边的网络中的路由选择问题，例如计算机网络中的数据包路由等。
最后，让我们来介绍一下fw算法。
fw算法的全称是Floyd-Warshall算法，它是一种用于解决带有负权边的有向图的多源最短路径问题的算法。
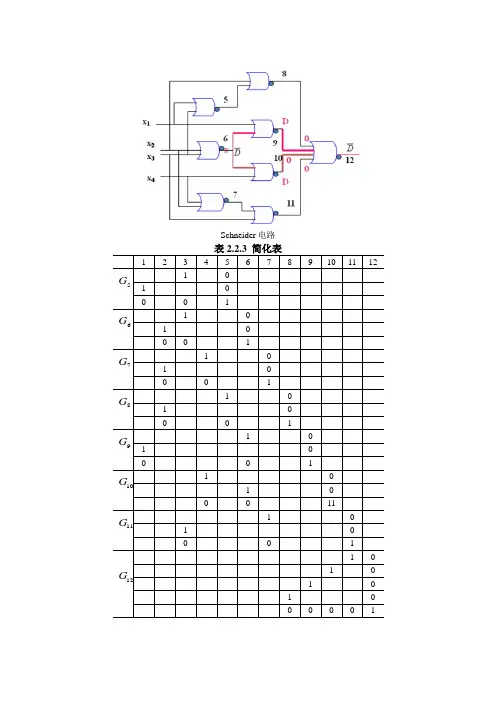
Schneider 电路表2.2.3 简化表1 2 3 4 5 6 7 8 9 10 11 12 5G× 1 0 1 × 0 0 0 1 6G× 1 0 1 × 0 0 0 1 7G× 1 0 1 × 0 0 0 1 8G× 1 0 1 × 0 0 0 1 9G× 1 0 1 × 0 0 0 1 10G1 × 0 × 1 0 0 0 11 11G× 1 0 1 × 0 0 0 1 12G× × × 1 0 × × 1 × 0 × 1 × × 0 1 × × × 01表2.2.4 传递d 矢量1 2 34 56 7 8 9 10 11 12 5G 0dd dd6Gdd dd7G 0dd dd8G 0dd dd9Gdd dd10G 0dd dd11Gdd d0 d12G0 0 0dd 0 0d0 d 0d0 0 ddd表2.2.5 d 驱赶的第一阶段t活动矢量 d 扇出 注释12 3 4 5 6 7 8 9 10 11 12pdcfdt{6}{9,10}6G s-a-0的初始d 矢量表2.2.6 d 驱赶的第二阶段d 交的结果 t活动矢量 d 扇出 注释12 3 4 5 6 7 8 9 10 11 12tddt{6}{9,10}故障的初始矢量 0{9}t d0 0 0 dd0,1t{6,9} {10,12}通过的9G 单通路 0{10}t d0 0 0 dd0,2t{6,10} {9，12}通过的10G 单通路表2.2.7 d 驱赶的第三阶段d 交的结果 t活动矢量 d 扇出 注释12 3 4 5 6 7 8 910 11 120,1t0 0 0 d d{10,12} 取自表2.2.6 0,1{10}t d0 0 0 0 d d d 0,1,1t{9,10} {12} 通过9G 和10G 的双通路0,1{12}t d0 0 0 d 0 d 00 d 0,1,2t{12} 00,2t0 0 0 dd{9,10,12} 取自表2.2.6 0,2{9}t d0 0 0 0 d d d0,2,1t {9,10} {12} 与0,1,1t相同0,2{12}t ddd 0d0,2,2t{12}表2.2.8 d 驱赶的最后阶段d 交的结果 t活动矢量 d 扇出 注释12 3 4 5 6 7 8 91011 120,1,1t0 0 0 0 d dd0,1,1,1t{12} {12}取自表2.2.6 0,1,1{12}t ddddd表2.2.9 t 0,1,2的相容性d 交的结果注释 1 2 3 4 5 6 7 8 910 11 12 0,1,2t 0 0 0 d 0 d0 d 取11G =011G (a) × 1 0 11G (b)1 ×0 取11G (b)顶点3矛盾0,1,2td 11G (a)0 0 0 d 1 0 d0 0 d 取10G =010G (a) 1 × 0 10G (b)×1取10G (b)顶点6矛盾 0,1,2t d 11G (a) d10G (a)0 0 0 1 d 1 0d0 0 d取8G =08G (a) 1 × 0 8G (a)顶点2矛盾 8G (b)×10,1,2t d 11G (a) d10G (a)d 7G (b)0 0 0 1 1 d 1 0 d 0 d取7G =17G (a)0 0 17G (c)顶点4矛盾表2.2.9 t 0,1,1,1的相容性d 交的结果注释 12 3 4 5 6 7 8 91011 12 检测0,1,1,1t0 0 0 0 d 0 d d0 d 取11G =011G (a) × 1 011G (b)1 ×0 取11G (b)顶点3矛盾0,1,1,1td 11G (a)0 0 0 0 d 1 0 d d0 d 取8G =18G (a)1 × 0 8G (a)顶点2矛盾 8G (b)×10,1,1,1td 11G (a) d 8G (b)0 0 0 0 1 d 1 0d d0 d取5G =17G (c)0 0 10,1,1,1td 11G (a) d 8G (b)d 7G (c)0 0 0 0 1 d 1 0d d0 d取5G =15G (c)0 0 1有效的测试1d1d dd X=(0，0，0，0)。
d值法的原理
d值法是一种常用于计算无向图中节点重要性的算法。
它基于节点的度数和连接到该节点的节点的d值来计算节点的重要性。
这种算法的原理很简单，但是它在实际应用中具有广泛的用途。
我们需要了解一个概念：节点的度数。
节点的度数是指连接到该节点的边的数量。
在无向图中，节点的度数等于该节点的邻居节点数。
在有向图中，节点的度数分为入度和出度。
d值法的核心在于计算节点的d值。
一个节点的d值等于其邻居节点的度数之和。
这个值越大，意味着越多的节点与它相连，这也就代表着这个节点的重要性越大。
在实际应用中，d值法可以用于计算网站中页面的重要性。
在这种情况下，页面可以看作是节点，连接两个页面的链接可以看作是边。
页面的重要性可以用其d值来计算。
在搜索引擎优化中，这种算法可以用来确定哪些页面应该排在搜索结果的前面。
除了计算页面的重要性外，d值法还可以用于社交网络分析、推荐系统、信用评级等领域。
在社交网络分析中，节点可以表示人或组织，边可以表示朋友关系或合作关系。
通过计算节点的d值，我们可以确定哪些人或组织在网络中具有重要的地位。
在推荐系统中，d 值可以用来确定哪些物品应该被推荐给用户。
在信用评级中，d值可以用来确定哪些人或组织具有更高的信用度。
d值法是一种实用的算法，可以用于计算无向图中节点的重要性。
它的原理简单，但是具有广泛的应用价值。
在实际应用中，我们可以根据具体情况来调整算法的参数，以得出最有价值的结果。
d分位值算法
D分位值（D-quantile）算法是一种统计方法，用于处理具有不确定性和风险的数据，以避免极端事件的影响。
该算法通过计算分位数来对数据进行分段，并将每个分段视为独立的概率分布。
D分位值算法的基本步骤如下：
1. 将数据按照从小到大的顺序进行排序。
2. 计算数据的分位数，即数据集中第p%的数据点。
3. 根据分位数的值，将数据分成若干个分段，每个分段内的数据具有相似的概率分布。
4. 对于每个分段，计算其概率密度函数（PDF）和累积分布函数（CDF）。
5. 对于每个分段，根据其PDF和CDF的值，计算该分段的D分位值。
D 分位值是指在该分段内，有D%的数据点小于或等于该值。
6. 将所有分段的D分位值进行合并，得到最终的D分位值结果。
D分位值算法可以应用于金融、保险、医疗等领域，用于处理具有不确定性和风险的数据，以做出更加合理和准确的决策。
d加密原理d加密技术是一种把用户的数据进行加密处理的技术，其它处理结果也就是加密后的数据，它是一种可以将用户的数据保护起来的有效的方式，也是目前数据加密技术领域中最为重要的一种技术。
d加密技术是根据一定的算法原理，从而将用户的数据保护起来，让用户的数据不能被他人破解读取，从而达到数据安全目的。
d加密技术的基本原理是：任何给定的一段数据，都可以通过一定的加密算法，把这段数据加密成一个新的数据，新的数据中只有加密算法的持有者才能将其解密还原成原来的数据，让他人无法解读。
d加密技术也就是通过这种方式，把用户的数据保护起来，让他人无法读取。
d加密技术是一种把用户的信息进行加密，使他人无法破解的有效数据加密技术。
它的实现原理是，根据一定的加密算法，把一段原始数据变换成一段新的数据，这段新数据只有加密算法持有者才能解密还原成原始的数据，其他的任何人都无法破解读取。
d加密技术有几种，其中最常用的包括d加密、对称加密、Hash 加密和非对称加密。
d加密是一种几乎每个系统都用的加密技术，它的原理是将用户的数据，通过特定的算法处理，将其加密，以达到保护数据安全的目的；对称加密原理是用一个密钥来加密和解密用户的数据，两个方面都需要使用这个密钥，只有拥有这个密钥的人才能解密这段数据；Hash加密是用一个哈希算法，对文件，文本或者密码进行加密；非对称加密则是两个人使用不同的密钥，来进行加解密操作，只有拥有特定的密钥才能解密这段数据。
d加密技术能够有效的保护用户的数据，让加密的信息无法被他人破解读取，以此来达到保护用户隐私的目的。
但是，d加密技术也有其对应的弊端：一是加密的数据如果被丢失，很可能就不可能被解密；二是加密所花费的计算资源较大，需要耗费很多系统资源进行处理。
总之，d加密技术是当今保护用户数据安全的重要技术之一，可以有效的保护用户的数据不被他人破解，但也会有弊端，因此，使用者需要根据实际情况来决定是否使用d加密技术。
最短路径
--------------------------------------------------------------------------------
从某源点到其余顶点之间的最短路径
设有向网G=（V，E），以某指定顶点为源点v0，求从v0出发到图中所有其余各项点的最短路径。
以图5-5-1所示的有向网络为例，
若指定v0为源点，通过分析可以得到从v0出发到其余各项点的最短路径和路径长度为：
v0 → v1 ：无路径
v0 → v2 ：10
v0 → v3 ：50 （经v4）
v0 → v4 ：30
v0 → v5 ：60 （经v4、v3）
图5-5-1 带权有向图
如何在计算机中求得从v0到其余各项点的最短路径呢？迪杰斯特拉(Dijkstra)于1959年提出了一个按路径长度递增的次序产生最短路径的算法。
其基本思想是：把图中所有顶点分成两组，第一组包括已确定最短路径的顶点(初始只包括顶点v0)，第二组包括尚未确定最短路径的顶点，然后按最短路径长度递增的次序逐个把第二组的顶点加到第一组中去，直至从v0出发可以到达的所有顶点都包括到第一组中。
在这过程中，总保持从v0到第一组各顶点的最短路程长度都不大于从v0到第二组的任何顶点的最短路径长度。
另外，每一个顶点对应一个距离值，第一组的顶点对应的距离值就是从v0到此顶点的只包括第一组的顶点为中间顶点的最短路径长度。
设有向图G有n个顶点（v0为源点），其存储结构用邻接矩阵表示。
算法实现时需要设置三个数组s[n]、dist[n]和path[n]。
s用以标记那些已经找到最短路径的顶点，若s[i]=1，则表示已经找到源点到顶点vi的最短路径，若s[i]＝0，则表示从源点到顶点vi的最短路径尚未求得，数组的初态只包括顶点v0，即s[0]=1。
数组dist记录源点到其他各顶点当前的最短距离，其初值为：
dist[i]=G.arcs[0][i] i=1，2，…，n-1
path是最短路径的路径数组，其中path[i]表示从源点v0到顶点vi之间的最短路径上该顶
点的前驱顶点，若从源点到顶点vi无路径，
则path[i]=-1。
算法执行时从s以外的顶点集合V-S中选出一个顶点vw，使dist[w]的值最小。
然后将vw加入集合s中，即s[w]=1；同时调整集合V-S中的各个顶点的距离值：从原来的dist[j]和dist[w]+cost[w][j]中选择较小的值作为新的dist[j]。
以图5-5-1为例，当集合s中只有v0时，dist[3]= ∞，当加入顶点v4后，使dist[4]+cost[4][3]<dist[3],因此将dist[3]更新为50。
重复上述过程，直到s中包含图中所有顶点，或再也没有可加入到s中的顶点为止。
采用迪杰斯特拉算法求最短路径的算法描述如下：
算法5.8
void Dijkstra(Mgraph Gn, int v0,int path[],int dist[]){
/* 求有向网Gn的v0顶点到其余顶点v的最短路径，path[v]是v0到v的最短路径
上的前驱顶点，dist[v]是路径长度*/
int s[VEX_NUM];
for(v=0; v<VEX_NUM; v++){ /*初始化s、dist和path*/
s[v]=0; dist[v]=Gn.arcs[v0][v];
if(dist[v]<MAXINT) path[v]=v0;
else path[v]=-1;
}
dist[vo]=0;s[v0]=1; /*初始时源点v0∈S集*/
/* 循环求v0到某个顶点v的最短路径，并将v加入S集*/
for(i=1;i<VEX_NUM -1;i++){
min=MAXINT;
for(w=0;w<VEX_NUM;w++)
if(!s[w] && dist[w]<min)
{ /*顶点w不属于S集且离v0更近*/
v=w;min=dist[w];
}
s[v]=1; /*顶点v并入S*/
for(j=0;j<VEX_NUM;j++) /*更新当前最短路径及距离*/
if(!s[j] && (min+Gn.arcs[v][j]<dist[j]))
{
dist[j]=min+Gn.arcs[k][j];
path[j]=v;
}/*if*/
}/*for*/
}/*Dijkstra*/
void Putpath(int v0,int p[],int d[]){
/*输出源点v0到其余顶点的最短路径和路径长度*/
for(i=0;i<VEX_UNM;i++)
if(d[i]<MAXINT && i!=v0){
printf("v%d<--",i);
next=p[i];
while(next!=v0){
printf("v%d<--",next);
next=p[next];
}
printf("v%d:%d\n",v0,d[i]);
else
if(i!=v0) printf("v%d<--v%d:no path\n",i,v0); }/*Putpath*/
(满屏显示)。
