重庆大学画法几何习题集及题解完整版

格式：ppt
大小：766.50 KB
文档页数：99

下载文档原格式

重庆大学画法几何习题集及题解完整_2022年学习资料

4-13以AB为边长作正三角形，使其与V面成30°角。本题-有几解？-本题有4解-39-d''-a-16页
2005习题集第17页一相对位置1-4一15已知直线AB∥△CDE,求ab。-d'-⊙-e-l
2005习题集第17页一相对位置1-4-17以下二题过点A作平面△ABC平行于平面P。-a-D -⊙-p
2005习题集第16页一平面3-4-10求平面对投影面的倾角：-a求对H面的倾角o-b求对V面倾角B-d
2005习题集第16页一平面3-4-11已知AB为平面P对V面的最大斜度线，求作该平面的投影和 -H面的倾角。-b-a
2005习题集第16页一平面3-4-12已知△ABC对H面的倾角=60°，试完成其V面投影。-a
3-14求作一水平线与三直线AB、CD、EF均相交。-'-d'-Q-e'f-b'-X-L-12
3-15过点C作正平线CD与直线AB相交-a'-b'l-X-12页
3-16过点C作直线CD与直线AB相交，交点距V-面20mm,且D点属于V面。-b'-X-a2页
3-17已知对角线AC和点B的V面投影，试完成菱-形ABCD的两投影。-X-a-c-13页
2005习题集第19页一相对位置3-4-23求直线MN与△ABC的交点，并判别可见性。-b-n -a'-m'
2005习题集第19页一相对位置3-4-24过L点作直线LK同时与AB、CD相交。-&-a'-71
4-25求二平面的交线，并判别可见性。-19页
19页重庆大学画法几何习题集及题解完整
4-26过K点作KL∥△ABC,且与EP相交。-'-k-b-e-19页

画法几何习题集及题解

a′
a′
a
p′
p′
c′ c′
cp
p
整理ppt
b
49
15页
2005习题集第15页—平面2
4-6 取一点K属于平面P，且距V面20mm，距H面15mm。
k′ p′
p′
15
k p
p
整理ppt
20
50
15页
(a)
(b)
(c)
2005习题集第15页—平面2
4-7 判别已知点和直线是否属于平面。
k′ p′
p′ k′
p〞
k
整理ppt
P ⊥W
45
14页
2005习题集第14页—平面1
4-2 已知下列各平面及其所属的点K的一个投影,
a、补画出平面及其所属的K点所缺的投影, b、标明平面(P)和投影面的相对位置; c、标明投影面垂直面对投影面的倾角。
p′ k′
p′
k〞
k′
k〞
p′ k′
p〞 k〞
k p
P ∥V
c′ X b′
b c
a
整理ppt
19
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
N，n′
(1)
b
k′
a
X
m′
n O
a
M，m
b k
B0
整理ppt
20
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
13页
3–19 三角形ABC为一直角三角形,其中∠B＝90°，边BC＝25mm，且其β＝ 30°，试完成该三角形的两面投影。

画法几何习题集答案

b’ p’ o’ n1’’
a’
c’
4’
m’
a c
po
4 m
n1 b
• 做法：
2’ • 延长 ac .34交
于m,求出 m’,
延长2‘1’交点
3’ 为o’,p,’ 在ab
求出p,bc利用
3 定比性求出o, 连接po交21
于n,求出n’,连
2
接mn,m’n’.
42 已知直线AB平行于平面CDE求直线的正面投影
b’ 55mm
高度差
a’
水平投影
a
水平投影
b
12判别下列各直线的空间位置，并注明反映实际长度的投影
g’
d’
f’
a’
b’
e’
c’
h’
c
a
b
e
f
d
g (h)
直线 AB CD
空间位水平线侧平线
置
实长投 ab
影
c’’d’’
EF GH
正平线铅垂线
e’f’ g’h’
13 判别CDE 三点是否在直线AB上
• 1、在正立面上分别连接m’c’交点 p’,n’a’交点q’,,n’b’ 交点r’.如图所示
• 2、做出三个点的水平投影p,q,r
• 3、连接mp,nq,nr
• 4、做a’ ,b’,c’对应的水平投影a,b,c，并连接。
26 在∆ ABC内任作一条正平线和一条水平线
b’
n’ a’
m’ c’
20mm b1 X2
67用换面法确定两交错直线间的距离返回做出投影
c’ n’
b’
a’ m’
X
X1
a

画法几何及机械制图习题集-贺光谊-重庆大学出版社

画法几何及机械制图习题集贺光谊唐之清主编重庆大学出版社画法几何及机械制图习题集贺光谊唐之清主编责任编辑:曾令维版式设计:曾令维责任校对:廖应碧责任印制:张立全*重庆大学出版社出版发行出版人:张鸽盛社址:重庆市沙坪坝正街174号重庆大学(A区)内邮编:400044电话:(023)6510237865105781传真:(023)6510368665105565网址:ht tp://w 邮箱:fxk@(市场营销部)全国新华书店经销重庆大学建大印刷厂印刷*开本:787×10921/8印张:20.5字数:256千1994年4月第1版2003年5月第7次印刷印数:28501—31500ISBN7-5624-0846-7/T H・41定价:18.00元本书如有印刷、装订等质量问题,本社负责调换版权所有翻印必究序近年来我国高等专科教育发展很快,各校招收专科生的人数呈逐年上升趋势,但是专科教材颇为匮乏,专科教材建设工作进展迟缓,在一定程度上制约了专科教育的发展。

在重庆大学出版社的倡议下,中国西部地区14所院校(云南工学院、贵州工学院、宁夏工学院、新疆工学院、陕西工学院、广西大学、广西工学院、兰州工业高等专科学校、昆明工学院、攀枝花大学、四川工业学院、四川轻化工学院、渝州大学、重庆大学)联合起来,编写、出版机类和电类专科教材,开创了一条出版系列教材的新路。

这是一项有远见的战略决策,得到国家教委的肯定和支持。

质量是这套教材的生命。

围绕提高系列教材质量,采取了一系列重要举措:第一,组织数十名教学专家反复研究机类、电类三年制专科的培养目标和教学计划,根据高等工程专科教育的培养目标———培养技术应用型人才,确定了专科学生应该具备的知识和能力结构,据此制订了教学计划,提出了50门课程的编写书目。

第二,通过主编会议审定了50门课程的编写大纲,不过分强调每门课程自身的系统性和完整性,从系列教材的整体优化原则出发,理顺了各门课程之间的关系,既保证了各门课程的基本内容,又避免了重复和交叉。

画法几何习题集答案

• 1、在正立面上分别连接m’c’交点 p’,n’a’交点q’,,n’b’ 交点r’.如图所示
• 2、做出三个点的水平投影p,q,r
• 3、连接mp,nq,nr
• 4、做a’ ,b’,c’对应的水平投影a,b,c，并连接。
26 在∆ ABC内任作一条正平线和一条水平线
b’
n’ a’
m’ c’
b’
k’ m’
n’
a’
c’
b
k m
a
n
c
做法：
1、连接c’m’ 交a’b’于k’ 2、做k’k垂
直于ox轴交ab 于k
3、连接kc 4、因为m在 kc上，所以M 在平面内，n 不在kc上，所以N不在平面
内
25 补出平面形内∆ABC的水平投影
n’
p’
c’
a’
m’
q’
b’ r’
n p
c
m
a
q
b r
• 做法：
b’ p’ o’ n1’’
a’
c’
4’
m’
a c
po
4 m
n1 b
• 做法：
2’ • 延长 ac .34交
于m,求出 m’,
延长2‘1’交点
3’ 为o’,p,’ 在ab
求出p,bc利用
3 定比性求出o, 连接po交21
于n,求出n’,连
2
接mn,m’n’.
42 已知直线AB平行于平面CDE求直线的正面投影
b’
a’
x
x1
a
a1’
c’ c b c1’
b1’
实长
c1
x2
a1(b1)
64、在平面ABCD内过A点做直线与AB成30o角

画法几何习题集及题解

2–5 试判别下列投影图中A、B、C、D、E 五点的相对位置(填入表中)。
a′( c′) b′
A点在B点的正左方
A点在C点的正前方
d′ c
B点在C点的右前方
e′
e
A点在D点的右后上方
B点在E点的左前上方
a
b
d
.
7
8页
2005习题集第8页—点
2-6 已知Ａ点的两面投影,求点Ｂ、C 、D的三面投影,使 B点在A点的正下方10,C点在A点的正前方10,D 点在A点的正左方15,并判断可见性。(单位mm)
3–8 下列各图中,用标记小圆圈代表线段的实长,其中正确的投影
图是( c) 。
a
b′
a′
b
a
b
a
a
a
b
b
b
(a)
(b).
(c)
24
11页
2005习题集第11页—直线3 3–9 下列各图中,反映两直线垂直相交的是( b ) 。
c′
b′
a′
a′
a′
b′ c′
c′
b′
b
a
c
(a)
b
a
c
(b)
.
b
c
a
(c)
N，n′
(1)
b
k′
a
X
m′
n O
a
M，m
–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
N，n′
n〞
(2)
b′
b〞
k′
a′ m′
n b
k
a
.

画法几何习题集答案

b
X
Z
A W
O
B H
Y
10 求直线AB的实长，及对两投影面的倾角
α ，β
实长
a’
β
高度差
• 做法提示：
• 求α 在水平投影上作，一直角边
b’
是水平投影，另
一直角边为高度
a
差。
宽度差
α
实长
b
•求β在正面投影上，一直角边是水正面投影，另一直角边为宽度差。
11已知直线AB的实际长度为55mm,求水平投影
a’
bc于m,作
m’
m’m ∥oz,交
n’
b’c’于m’,连接
b’
a’m’,作c’n’
⊥am交于n’,
b
作nn’ ⊥am交
a
于n,利用直角
mn
三角形求出
倾角β
c
31 判别直线AB是否平行于平面CDEF
• 作法：
c’
b’
f’ • 作e’f’ ∥a’b’,
a’
交c’d’于m’,
e’
m’
作mm’ ∥oz,
29 求∆ ABC对H面的倾角α
• 做法：
c’
• 作a’m’ ∥ox,
a’
n’ m’
交b’c’于m’,作 m’m ∥oz,交
bc于m,连接
b’
am,作bn
⊥am交于n,
b
作nn’ ⊥a’m’
a
α
m
n
交于n’,利用直角三角形求
出倾角α
c
30 求∆ ABC对V面的倾角β
• 做法：
c’
β
• 作am ∥ox,交
c’
∥ oz,连接ce,作

重庆大学画法几何习题集及题解完整版

(b) 。
k′ b′b′ a′ k′
a′ X
xk a
k
b
a (a)
k′ b′
k′
a′
c′
a′
OX
cc ′
ox
a
c
k
b
a (b)
b′
b′
b
a′ c′
OX
k′ c′
a′ O k
c c′
c
aox
ck
b
a
(c)
k
15页
2005习题集第15页—平面2
4-5 △ABC属于平面P，试求作其H面投影。
b′
b′
4-6 取一点K属于距H面15mm
N，n′
(1)
b
k′
a
X
m′
n O
b
k
a
B0
M，m
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
N，n′
n〞
(2)
b′
b〞
k′
a′ m′
n b
k
a
M，m
a〞
m〞
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。 N，n′
(2)
a′ k′
b′
m′ n a
b
M，m
10页
2005习题集第11页—直线3
3–7 下列各图中,表示点M属于直线AB的是(a b ) 。
m′ b′ a′
a
m′
b
a
m′
b

画法几何全主编习题集答案

db c ab’a’c’d’Xb1'd1'c1'a1'c1d1m1n1'b1（a1）m1'm’n’nmX1 X2n12-4 直线与平面、平面与平面的相对位置1.求直线AB与平面的交点，并判别直线的可见性。

4.求两平面的交线。

6.作一直线使与两交叉直线AB,CD相交，同时平行于直线KL。

作直线AE平行于直线KL；求CD与平面（AE和AB确定）的交点M；作MN平行于KL。

7.过点C作CD平行于AB，且点D于A,B等距。

说明：为使图形清晰，将AB的正面投影改变了一些方向。

过AB的中点E作AB的中垂面；求CD与中垂面的交点D。

其中MN为P H中垂面的交线。

8.求点K到直线AB的距离。

距离距离9.求点A到三角形BCD的距离。

说明：为使图形清晰，将A点的水平投影往上移动了一些。

11.已知线段AB,CD正交，作线段AB的正面投影。

13.过点K作直线与交叉两直线AB和CD相交。

14.作一直线使与交叉二直线DE,FG相交，并垂直于三角形ABC。

作直线BC垂直于平面；求三角形ABC的实形（略);90°减角ABC即为所求（略)。

15.求直线与平面之间的夹角。

作直线EM垂直于三角形ABC;求FG与平面（DE和EM确定）的交点K；过K作EM的平行线KN。

16.已知菱形ABCD的一边AD在直线AE上，另一边AB平行于三角形LMN，点B在直线FG上，求作菱形的两面投影。

16.过点A 作平行于三角形LMN 的平面；求FG 与平面的交点B;求AB 的实长，AE 的实长，在AE 上截取AD=AB,得D;再作AB,AD 的平行线即可。

2-5 投影变换1.用换面法求直线AB 的实长及其与H 面的倾角α。

2.已知AB 垂直于BC ，补全BC 的水平投影。

Y坐标差4.已知点A与三角形DEF的距离为10，求A的正面投影。

7.已知两平行直线AB及CD相距15mm,求CD的水平投影。

11.在直线AB上找一点K使它与三角形MNC及三角形MND等距。

画法几何及机械制图习题集完整答案第一、二、三章

△ZAD
ad
X b
a d′ a
a′ a
c
O 共有四解当BC的a=30°时只有两解当a﹥30°则无解。
a
3—22 直线AB 上一点C距点A为30mm，过点C作直线AB的垂线，且与直线EF相交，求作该直线的两面投影。
a′ e′
k′ c′
f′ b′
X
c a e
b k b1 ′ c1′
O
f
f1′ k1 ′
(2) b′
a′ c′
a′
△Z
c′
d′ d′
X
b 实长
O
X
b′ 实长
O d
d a c
△Z
a (b) c
3—19 水平线AK是等腰三角形△ABC底边BC的高，点B在V面前方10mm，点C在H面内，求作△ABC的两面投影。
b′
k′ X
a′
c′
b
a
10
O
k
c
3—20 已知正方形ABCD的一边BC在MN上，求作该正方形的两面投影。
Z
a′
a〞
30°30°
X
O
YW
a
该直线为侧平线
YH
3—12 过点A作直线段，使它的实长为30mm,α=30°，β=45°。问有几个答案？（思考题：当α+β﹥90°时，有无答案？）
b′ a′ b′
△Z △Z 30
△Z 30°
LH
b′ X
b
b′ O
b 30 △Y 45° LV
a
b b
有四个答案当α+β﹥90°时，无答案
e1′ a1′
30
3—23 已知等边三角形ABC的C点在V面内，求作此三角形的两面投影，问有几个答案？若ab按箭头方向平移，移至何处时，只有一个答案，再移动时，情况如何？ b1 a1 ab按箭头方向平 X1 b′

画法几何习题集答案

a’
bc于m,作
m’
m’m ∥oz,交
n’
b’c’于m’,连接
b’
a’m’,作c’n’
⊥am交于n’,
b
作nn’ ⊥am交
a
于n,利用直角
mn
三角形求出
倾角β
c
31 判别直线AB是否平行于平面CDEF
• 作法：
c’
b’
f’ • 作e’f’ ∥a’b’,
a’
交c’d’于m’,
e’
m’
作mm’ ∥oz,
33 过A点作平面平行∆ DEF
a’
d’ a
d
e’
n’ • 作法：
• 作a’m’
f’ ∥e’f’,作am
m’
∥ef, mm
∥oz.
e
• 作a’n’
∥d’f’,作an
n
∥df, nn’
∥oz.
f m
34 过直线AB作平面平行于直线CD
b’
m’ a’
c’
b
a
c
m
• 作法：
• 作am ∥cd,
d’
作a’m’
d’
• 做法：
c’
k’
b’ • 过k 点作kk’
a’
∥oz交a’b’于
e’ k’.b’k’为实线，
a
中段为虚线，
k
d
e 下段为实线。
c
b
37 作出直线AB与∆ CDE的交点并判别可见性
d’
a’ m’
k’
c’
n’
b’
e’
• 做法：连接 mm’,nn’ ∥oz, 连接mn交ab于 k,作kk’
∥oz,a’k’,bk为

画法几何习题集答案

a’
bc于m,作
m’
m’m ∥oz,交
n’
b’c’于m’,连接
b’
a’m’,作c’n’
⊥am交于n’,
b
作nn’ ⊥am交
a
于n,利用直角
mn
三角形求出
倾角β
c
31 判别直线AB是否平行于平面CDEF
• 作法：
c’
b’
f’ • 作e’f’ ∥a’b’,
a’
交c’d’于m’,
e’
m’
作mm’ ∥oz,
b’ p’ o’ n1’’
a’
c’
4’
m’
a c
po
4 m
n1 b
• 做法：
2’ • 延长 ac .34交
于m,求出 m’,
延长2‘1’交点
3’ 为o’,p,’ 在ab
求出p,bc利用
3 定比性求出o, 连接po交21
于n,求出n’,连
2
接mn,m’n’.
42 已知直线AB平行于平面CDE求直线的正面投影
33 过A点作平面平行∆ DEF
a’
d’ a
d
e’
n’ • 作法：
• 作a’m’
f’ ∥e’f’,作am
m’
∥ef, mm
∥oz.
e
• 作a’n’
∥d’f’,作an
n
∥df, nn’
∥oz.
f m
34 过直线AB作平面平行于直线CD
b’
m’ a’
c’
b
a
c
m
• 作法：
• 作am ∥cd,
d’
作a’m’
20mm b1 X2
67用换面法确定两交错直线间的距离返回做出投影

画法几何习题集答案

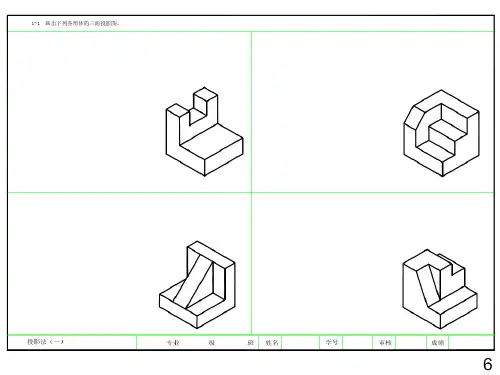
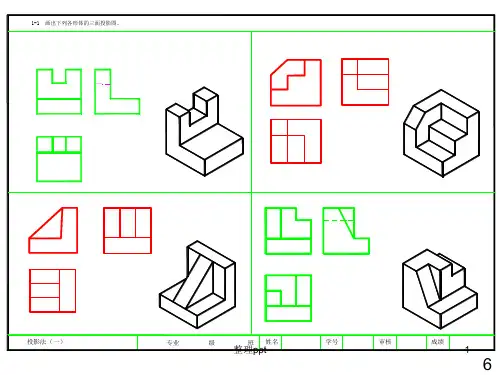
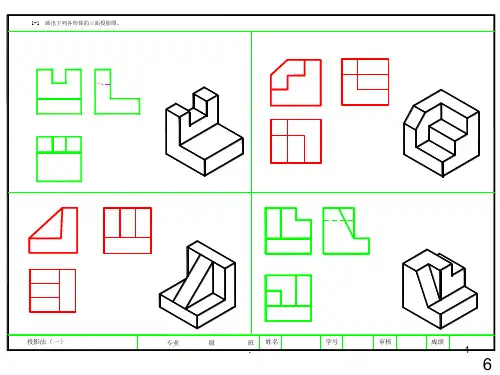
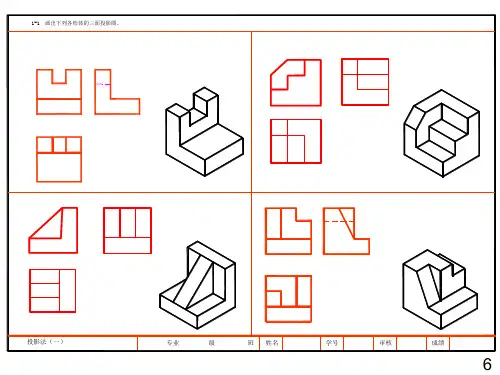
画法几何习题集答案问题一：如何确定一个平面图形在空间中的投影？答案：确定一个平面图形在空间中的投影，首先需要确定投影面和视图。

通常，我们使用正投影法，将图形投影到三个相互垂直的平面上，即前视图（正视图）、侧视图和俯视图。

通过这三个视图，可以完整地表达出空间图形的形状和尺寸。

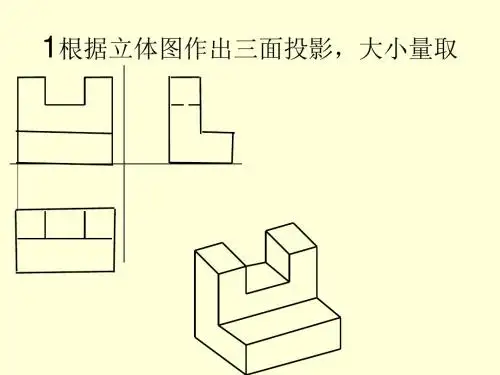
问题二：如何绘制一个长方体的三视图？答案：绘制长方体的三视图需要从三个不同的方向观察长方体。

首先，绘制前视图，显示长方体的正面和侧面；然后，绘制侧视图，显示长方体的侧面和背面；最后，绘制俯视图，显示长方体的顶面和底面。

每个视图都应该展示长方体的相应边长和高度。

问题三：如何通过已知的两个视图来恢复第三个视图？答案：通过已知的两个视图来恢复第三个视图，需要利用空间几何关系和已知的尺寸。

首先，分析已知视图中的尺寸和形状，确定缺失视图的轮廓。

然后，根据已知视图中的尺寸和比例，计算缺失视图中的线段长度和角度。

最后，将计算出的数据绘制成缺失的视图。

问题四：如何判断两个平面图形是否平行或垂直？答案：判断两个平面图形是否平行或垂直，可以通过观察它们的投影。

如果两个图形在所有视图中的投影都保持相同的相对位置，并且没有相交线，那么这两个图形是平行的。

如果两个图形在某个视图中的投影相交于一条直线，并且在其他视图中没有相交，那么这两个图形是垂直的。

问题五：如何计算空间中两点之间的距离？答案：计算空间中两点之间的距离，可以使用空间两点距离公式。

设两点的坐标分别为 \( P_1(x_1, y_1, z_1) \) 和 \( P_2(x_2, y_2, z_2) \)，则两点之间的距离 \( d \) 可以通过以下公式计算：\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]结束语：画法几何习题的解答需要对空间图形有深刻的理解，以及对几何原理和绘图技巧的熟练掌握。

通过不断的练习和思考，可以提高解决画法几何问题的能力。

画法几何习题及答案ppt课件.ppt

2-1 根据点的空间位置，画出点的投影图
（3）
b
a'
a
c'
X
O
b'
d'
d
c
2-3 根据点到投影面的距离，画出点的三面投影
a'
a"
点ABCD E
到H面为 30 20 15 0 0 z
b'
b'
到V面为 10 35 30 0 20 y 到W面为 25 10 0 20 35 x
c'
c"
ee'' d d'
d"
c'
a'
b'
d'
c" a"
d" b"
a d cb
A
D
C
(b)
5-2 画出五棱柱的侧面投影，并补全其表面上的点、线的投影
a'
e'
d'
c′
a" e" d"
c"
E A
D
C
ca de
5-3 画出该平面体的侧面投影，并补全其表面上的点、线的投影
c'
c"
d'
d"
a'
e'
ea""
c a de
C E
D
A
5-4 画出五棱柱的水平投影，并补全其表面上的点、线的投影
c'
d'
1'
e'
a'
2'
b'
c
d

画法几何习题集答案

a’
bc于m,作
m’
m’m ∥oz,交
n’
b’c’于m’,连接
b’
a’m’,作c’n’
⊥am交于n’,
b
作nn’ ⊥am交
a
于n,利用直角
mn
三角形求出
倾角β
c
31 判别直线AB是否平行于平面CDEF
• 作法：
c’
b’
f’ • 作e’f’ ∥a’b’,
a’
交c’d’于m’,
e’
m’
作mm’ ∥oz,
b1’ b’
y1b
y1c
a’d’,ad,延长
c1’
ad 作垂线X1，
X
b
• 作 cc1’⊥X1,
d
Zc
y1a
y1c X1
c a
• 作 bb1’⊥X1, 到X1的距离分别是Zc,Zb,连接b1’c1’作
b1b1’,a1a1’,c 1c1’ ⊥b1’c1’,
距离分别是
y1b,y1a,y1c. 连接 a1b1c1.
1根据立体图作出三面投影，大小量取
5,6根据A点的坐标，作出三面投影和立体图
Z a’
高 X
长宽
a
Y
a’’
Y
Z
V a’
W A
X
O a’’
a
H
Y
根据长对正，宽相等，高平齐
d’ a’
c’ b’
a b
c d
d’’ a’’
c’’
b’’
9 作出直线AB的侧面投影，画立体图
’
a’
a’’
b’
b’’
a V
d’
• 做法：
c’

重庆大学画法几何习题集及题解完整版

3-13 判别下列AB与CD两直线的相对位置。（3）
X
a′
1 4(3) d′
c′ 2
b′
c
3b 4
1(2)
a
d
AB 相叉于 CD
3-13 判别下列AB与CD两直线的相对位置。（4）
X
d′ a′
d″ a″
1(2)
3 b′
c′
d
2 b
1(3)
a
c
b″ c″
AB 相叉于 CD
3-14求作一水平线与三直线AB、CD、EF均相交。
参考布图二
几何作图
专业
级
班姓名
学号
审核
成绩
5
花格 1:5 楼梯踏步 1:20
立体交叉公路 1:1000 (单位:米)
(校名)
制图 (姓名) (日期) 校核 (姓名) (日期)
几何作图
(图号)
(比例) (班级)
1-1 画出下列各形体的三面投影图。
投影法（一）
专业
级
班姓名
学号
审核
成绩
6
1-2 画出该形体的侧面投影图。
1-3 画出该形体的正面投影图。
1-4 画出该形体的水平投影图。
1-5 画出该形体的水平投影图。
投影法（二）
专业
级
班姓名
学号
审核
成绩
7
2005习题集第8页—点
2–1 已知点的两个投影,求第三面投影。
Z
a′ b′
c′
a〞 b〞 c〞
X
O
ac
b
YH
YW
8页
2005习题集第8页—点
2–2 已知点的两个投影,求第三投影。并在表格中填上它们的

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1-1 画出下列各形体的三面投影图。
投影法（一）
专业
级
班姓名
学号
审核
成绩
6
1-2 画出该形体的侧面投影图。
1-3 画出该形体的正面投影图。
1-4 画出该形体的水平投影图。
1-5 画出该形体的水平投影图。
投影法（二）
专业
级
班姓名
学号
审核
成绩
7
2005习题集第8页—点
2–5 试判别下列投影图中A、B、C、D、E 五点的相对位置(填入表中)。
4-17 以下二题过点A作平面△ABC平行于平面P。
a′
a′
a′
p′
p′
a′
p′
p′
a p
a
a
p
p
p
17页
2005习题集第18页—相对位置2
4-20 (2)
d′
a′
c′ e′ b′ e
c
a (b)
d
18页
2005习题集第18页—相对位置2 a′
4-20 (4)
k′ p′
b′ a
p
b
18页
2005习题集第18页—相对位置2
q′
p
q
P
Q
q p
P
Q
20页
第21页 4-31求点K到直线AB的真实距离。
b′
l′ a′ a
l k
b
21页
第21页 4-32求点K到△ABC的真实距离。
4-13 以AB为边长作正三角形，使其与V面成30°角。本题有几解？
a′
本题有4解
30°
d′ b′
a
b
16页
2005习题集第17页—相对位置1
4－15 已知直线AB∥△CDE，求ab。
4－16 作图判别直
d′ d′
b′
b′ b′
c′
c′
c
c
d
e′
e′
a′
a′
ea
e a
a′
a
17页
2005习题集第17页—相对位置1
4-21 求两平面的交线，并判别可见性。
a′
a′
3′
3′
a′ 2′
1′ a
1
2′
2′
c′ b′
1′
c′
b′
1′
a
b′
1
3
3
b
c
2 cb
(1)2 18页
4-21
a′ 2′
b′
1′ b
2(1)
a
3′
4′ c′
3(4)
c
18页
2005习题集第19页—相对位置3
4–23 求直线MN与△ABC的交点,并判别可见性。
a′( c′) b′
A点在B点的
A点在C点的
d′ c
B点在C点的
e′
e
A点在D点的
B点在E点的
a
b
d
8页
2005习题集第10页—直线2
3–3 (1) 求线段AB的实长和a角 (2) 求线段AB与V、W的倾角g和b角。
b′ a′
a′
X
a
(1)
b
X
b′
b a
(2)
10页
3–4 (1) 已知线段AB的H面投影ab 及V面投影a′, AB＝45mm,完成AB 的V面投影。有几解？
c′
b
a
15页
2005习题集第16页—平面3
4-9 已知五边形ABCDE的V面投影及其一边AB的H面投影，并知AC为正平线，试完成其H面投影。
cc′′ bb′′
aa′ ′
bb aa
dd′′ ee′′
16页
2005习题集第16页—平面3
4–10 求平面对投影面的倾角﹕
(a) 求对H面的倾角a
(b) 求对V面的倾角b
b′
a′
o′
c′
X
b
a
d′ c
d
13页
3–19 三角形ABC为一直角三角形,其中∠B＝90°，边BC＝25mm，且其β＝ 30°，试完成该三角形的两面投影。
b′ a′
X
a
b
13页
3–20 已知点C到直线AB的距离为35mm，求c′。
a′
X
a
b
13页
3–21 已知AB垂直于BC，BC＝30mm，点C属于 V面，求b′c′、bc。
2′
b′
d′
1′
3′
a′
c′
2 c
a 1
b 3
d
16页
2005习题集第16页—平面3
4-11 已知AB为平面P对V面的最大斜度线,求作该平面的投影和对 H面的倾角a。
b′
a′ b
a
16页
2005习题集第16页—平面3
4-12 已知△ABC对H面的倾角a＝60°,试完成其V面投影。
a′
c′
b
a
c
16页
19页
19页
4-26 过K点作KL∥△ABC，且与EF相交。
a′
a′
a
a
e′
bb′ ′e′l′ Nhomakorabeac′
c′ k′
k′
ck
b
c
ke
l
f′
f′
f
19页
4-29含已知直线AB作平面△ABC垂直于已知平面P
p′
c′
a′
a′
c′
p′
b′
b′
a
c
c
p
p
b
b
a
20页
4-30判别两已知平面是否垂直。
p′
q′
p′
(2) 已知线段AB的V面投影 a′b′及H面投影a, b＝30°,完成AB的H面投影ab。有几解？
b′
a′
a′
X
b
X
a
有解
a
有解
10页
3–5 已知C点属于线段AB, 且AC︰CB＝3 ︰1, 求作C点的V、H投影。
(1)
a′
(2)
a′
b′
X
X b′
b a
b
a
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
(2) b′
a′
b
a
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
(2) a′
b′ a
b
10页
3-14求作一水平线与三直线AB、CD、EF均相交。
a′
c′
X
b′
b
c
a
d′ e′(f′)
f
d e
a′ m′
a m
b′n′
c′
c
n
b
m′ a′
a m
b′
n′ c′ bn
c
19页
2005习题集第19页—相对位置3
4–24 过L点作直线LK同时与AB、CD相交。
l′
b′
d′
a′
l
a
c′ d
b c
19页
4-25 求二平面的交线，并判别可见性。
2′ b′
1′ a′
1 a
c′ 3′ 3c
b
1′ a′
1 a
b′
a′ X
a
b
13页
3–22 已知等边三角形ABC一边BC属于EF，完成此三角形的V、H投影。
f′ e′ X e
f
13页
2005习题集第14页—平面1
4-1 已知相交二直线决定的平面P的投影,试求其迹线。
b′
a′
c′
a
b
c
14页
2005习题集第15页—平面2
4-5 △ABC属于平面P，试求作其H面投影。
b′
b′
4-6 取一点K属于距H面15mm
a′
a′
p′
p′
c′ c′
p
p
15页
2005习题集第15页—平面2
4-6 取一点K属于平面P，且距V面20mm，距H面15mm。
p′
p′
p
p
15页
2005习题集第15页—平面2
4-8 求作属于△ABC与投影面H、V等距离点的轨迹。
b′ b′
a′
a′
b
12页
3–15 过点C作正平线CD与直线AB相交
a′
c′ b′
X b
c
a
12页
3–16 过点C作直线CD与直线AB相交，交点距V 面20mm，且D点属于V面。
b′
a′ X
a
b
12页
3–17 已知对角线AC和点B的V面投影，试完成菱形ABCD的两投影。
a′
c′
X a
c
13页
3–18 矩形ABCD的对角线AC为水平线，试完成该矩形的V面投影。

重庆大学画法几何习题集及题解完整版

合集下载

重庆大学画法几何习题集及题解完整_2022年学习资料

画法几何习题集及题解

画法几何习题集答案

画法几何及机械制图习题集-贺光谊-重庆大学出版社

画法几何习题集答案

画法几何习题集及题解

画法几何习题集答案

重庆大学画法几何习题集及题解完整版

画法几何全主编习题集答案

画法几何及机械制图习题集完整答案第一、二、三章

画法几何习题集答案

画法几何习题集答案

画法几何习题集答案

画法几何习题及答案ppt课件.ppt

画法几何习题集答案

重庆大学画法几何习题集及题解完整版

文档推荐

最新文档