第十二章 达朗贝尔原理(动静法)
- 格式:ppt
- 大小:1.49 MB
- 文档页数:55


基础部分——动力学第12 章达朗贝尔原理惯性力Jean le Rond d’Alembert (1717-1783)达朗贝尔达朗贝尔原理达朗贝尔原理具体内容:a F F m −=−='惯性力定义:质点惯性力aF m −=I 一、惯性力的概念aF m −='2222d d d d z ty m t[注意]不是真实力直角坐标自然坐标aF m −=I−a m 质点的达朗贝尔原理二、质点的达朗贝尔原理合力:NF I FI N =++F F F 注意:◆◆优点:◆可以将动力学问题从形式上转化为静力学动静法◆给动力学问题提供了一种统一的解题格式。
如何测定车辆的加速度?虚加惯性力解:达朗贝尔原理[例12-1]IF 摆式加速计的原理⇒⇒构成形式上的平衡力系质点系的达朗贝尔原理内力外力表明:惯性力系外力平面任意力系实际应用时,同静力学问题一样,选取研究对象;刚体惯性力系的简化简化方法一、质点系惯性力系的主矢与主矩无关有关二、刚体惯性力系的简化◆质心C结论:1IF2IF3IF IRFCm aF−=IR⇒交点O简化tI iF nI iF αα特殊情形:●●αOz O J M −=I 作用在O 点C m a F −=IR t I iFn I iFn IRFt IRF OM I αt I iFn I iFα[思考]求:向交点O 简化的主矢?主矩?)(41t IR↑=L m F αOCαωL /4)(412n IR →=L m F ωα2I 487mL M O=(逆)①2IR ωme F =②αCz O J M −=I (与α反向)③0, 0I IR ==O M F (惯性力主矢、主矩均为零)IRF OM I α(作用于质心C )C m a F −=IR αCz C J M −=I 质心C IRF CM I α特殊情形:●●⇒[思考]εmr F =t IRrR r mF −=22n IRωε2I 21mr M C=求:惯性力系向质心C 简化的主矢?主矩?达朗贝尔原理上节课内容回顾(质点惯性力)或:质心C Cm a F −=IRαOz O J M −=I Cm a F −=IR 交点O t I iFn I iFn IRFt IRF OM I ααOz O J M −=I C m a F −=IR 交点O t I iFn I iFn IRFt IRF OM I αCm a F −=IR αCz C J M −=I质心C IRF CM I α质心C[思考]求:向交点O 简化的主矢?主矩?)(41t IR↑=L m F αOCαωL /4)(412n IR →=L m F ωα2I 487mL M O =问:若向质心C 简化,则主矢?e =−∑Cx xma F 平面运动微分方程0)( e=−∑αCz C J MF 0e =−∑Cy yma F IRF CM I α⇒⇒[例12-2]解:惯性力系αt RI Fn IRFn AFt A FAM I αtRI Fn IR F nA F t AF AM I α惯性力系)解题步骤及要点:注意:F IR = ma C M I O = J Oz αα思考:AC CθASO[例12-3]先解:惯性力系m gF IR M I C F sF NαR a C =CθASOm gF IRF OxF OyM I C再惯性力系M O[例12-4]解:惯性力系 1I F OM I 2I F α)(=∑F OMα11r a =2211 α22r a =1I F OM I 2I F α[思考题] A BCD E )(118↓=g a A mgF 113T =111≥f主动力系惯性力系RFIRF OMIRF IRF OM I tI iFn I iF∑∑==ii iyzi i i zx z y m J x z m J RF IRF OM I tI iFn I iFRF IRF OM Ill F M l F M y x y x /)]()[( 2I I 2R ⋅−+⋅−ll F M l F M x y x y /)]()[(2I I 2R ⋅++⋅+−ll F M l F M y x y x /)]()[(1I I 1R ⋅++⋅+−ll F M l F M x y x y /)]()[( 1I I 1R ⋅−+⋅−xF R −约束力静动主动力惯性力动约束力I x 02=ωJ 质心过)04222≠+=−ωααωωα惯性主轴z 轴为中心惯性主轴静平衡过质心⇒动平衡中心惯性主轴⇒[例12-5]静平衡动平衡爆破时烟囱怎样倒塌θOAωα解:m g)cos 1(3θ−lg F OxF OyMI On RI F t IRF 受力分析[例12-6])]([)(sin ⋅−−+−+⋅x x l l x x l mg ααθ1()(sin mgl −θB注意:求内力(矩)时惯性力的处理!xθxAB()ml x lα−m l lαBM BxF x mg lByF12-5-1 关于惯性力系的简化OA ωαMI OnR I FtIRFOAωαMI CnRIFtRIFC 思考思考12-5-2 刚体平面运动时有关动力学量的计算mv+C12-5-3 本章知识结构框图达朗贝尔原理惯性力系的简化质点系达朗贝尔原理定轴转动的约束力一般质点系刚体静、动约束力静、动平衡课后学习建议:◆。








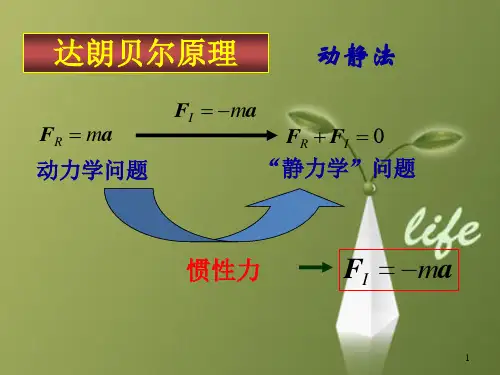
第12章 达朗贝尔原理12.1 主要内容12.1.1 质点的达朗贝尔原理设一质量为m 的质点M ,在主动力F 、约束力F N 的作用下运动,根据牛顿第二定律m a =F +F N移项后整理得F +F N +F I =0其中F I = –ma 称为惯性力,它可表述为:质点在作非惯性运动的任意瞬时,对于施力于它的物体会作用一个惯性力,这个力的方向与其加速度的方向相反,大小等于其质量与加速度的乘积。
此式表明:在质点运动的任意瞬时,如果在其质点上假想地加上一惯性力F I ,则此惯性力与主动力、约束力在形式上组成一平衡力系。
这就是质点的达朗贝尔原理。
12.1.2 质点系的达朗贝尔原理设某质点系由n 个质点组成。
如果在某质点i m 上假想地加上一惯性力F I i =–m i a i则对于整个质点系来说,在运动的任意瞬时,虚加于质点系上各质点的惯性力与作用于该质点系上的主动力、约束力将组成一平衡力系,即0I N =∑+∑+∑i i i F F F()()()0I N =∑+∑+∑i O i O i O F M F M F M这就是质点系的达朗贝尔原理。
12.1.3 刚体惯性力系的简化(1)、刚体平移平移刚体的惯性力系可简化为一合力F I = –m a c它的作用线通过刚体的质心,方向与平移加速度的方向相反,大小等于刚体质量与加速度的乘积。
(2)、定轴转动惯性力系简化的主矢为c M a F -=RI惯性力系对简化中心O 的主矩为:()()kj i k j i M z y x z xz yz yz xz o M M M I I I I I I I I 22I ++=-++-=εωωε 绕定轴转动刚体的惯性力系向转轴上任意点O 简化时,惯性力主矢、主矩由上式计算。
但应注意,惯性力系的简化结果,主矢和主矩必须作用在同一个简化中心上。
(3)、平面运动随同质心平移而虚加的惯性力系将合成为一合力F I ,合力作用线通过质心,方向与a c 的方向相反,大小等于刚体的质量与质心加速度的乘积,即F I =–M a c相对质心转动而虚加的惯性力系的主矢等于零(质心在转轴上),主矩为一惯性力偶,且作用于质心C 处,它的转向与角加速度ε的转向相反,大小等于角加速度与刚体对于质心的转动惯量的乘积,即M I = –I c ε12.1.4 定轴转动刚体的轴承动约束力设刚体上的惯性力系向O 点简化的主矢和主矩为ji ji y x c c c c F F x y M y x M F I I 22I )()(+=-++=εωεω ()()k j i kj i z y x z xz yz yz xz o M M M I I I I I M I I I 22I ++=-++-=εωεωε 根据达朗贝尔原理求解可知,轴承动约束力由两部分组成:一是由主动力引起的,与运动无关,为静约束力;二是由惯性力主矢、主矩引起的,为附加动约束力。