姿态动力学
- 格式:ppt
- 大小:3.51 MB
- 文档页数:65

反作用飞轮整星零动量轮控系统(七B)班级:飞行器设计与工程1班(0818201)组员:李迪(1081820108)李涧青(1081310118)孙启龙(1081820106)目录1 基本内容 (3)2 模型的建立 (3)2.1系统控制框图 (3)2.2姿态动力学模型 (4)2.3 控制器设计 (5)2.4 执行机构 (6)2.5 建模结果 (7)3 仿真实现 (8)3.1 无干扰力矩 (8)3.2 干扰力矩作用 (11)3.3 飞轮故障的问题解决 (14)1 基本内容(1)建立带有飞轮的三轴稳定对地定向航天器的姿态动力学和姿态运动学模型。
(2)设计PD或PID控制器的轮控系统。
(3)完成数学仿真和分析。
2 模型的建立典型航天器的姿态控制系统模型主要包括姿态动力学,姿态运动学,控制器,轨道动力学和空间环境五大基本模块。
根据题目要求,对于本列,主要从被控对象字体动力学模型,执行机构和控制器三方面入手进行模型的建立。
以欧拉角为姿态参数,姿态动力学采用基于陀螺体的多刚体姿态动力学方程,姿态运动学模型采用zyx顺序欧拉角的姿态运动学方程。
控制器采用PD控制率。
执行机构采用4斜装的反作用飞轮构型方案。
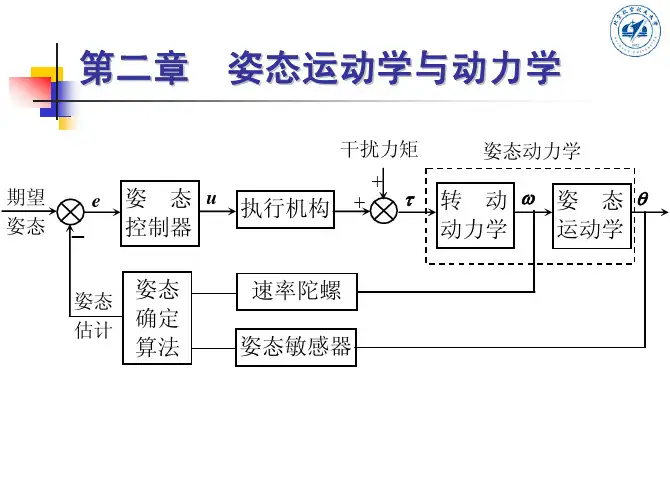
2.1系统控制框图如图1所示,其中姿态动力学模块和姿态运动学模块是描述系统模型的最基本模块,姿态动力学模块提供系统的动力学计算,姿态运动学模块提供不同姿态描述之间的转换关系,控制器模块是待设计的控制律模块,执行机构获得期望力矩信号,输出控制力矩。
图1 整星零动量轮控系统框图2.2姿态动力学模型考虑刚体固连坐标系下,转动角速度分量为[]T z y xωωωω=,转动惯量为I ,c T 为控制力矩,d T 为干扰力矩,U 为安装矩阵。
则建立的欧拉动力学方程为dw w T Uh h U I I =+++⨯⨯ωωωω 对上式进行变形得到表达式:()ww d Uh h U I T I ⨯⨯----=ωωωω 1 (1) 然后对ω积分得到转动角速度ω。



航天器姿态动力学部分复习分考题第一章1. 动量矩是怎样定义的?写出其在本体坐标系的分量的表达式(两种)。
2. 写出惯量张量的一般计算表达式。
对于主轴系惯量张量的表达式是怎样的?3. 刚体动能的定义式、一般计算式和主轴系中的计算式是怎样的?4. 绕原点转动运动的基本定理及其表达式是什么?欧拉动力学方程在本体系的一般表达式怎样?,在主轴系中的表达式又怎样?5. 欧拉角(进动角,章动角,自转角)是哪两个坐标点的夹角关系?是按怎样的顺序旋转得到的?表示的几何意义是什么?6. 写出关于按313顺序定义的欧拉角的欧拉运动学方程。
7. 常质量航天动力学方程是根据什么原理建立的?在哪个坐标系上列写标量方程?写出其具体方程。
用什么方法求解该动力方程组?*8. 什么是定向性?9. 什么是稳定性?10. 根据什么原理来说明定向性,写出该定向性的数学表达式。
11. 什么情况下有定向性?说明典型的定向性情况。
12. 对自旋卫星定向性和稳定性的关系是什么?13. 写出自旋卫星稳定性的分析过程。
14. 自旋稳定有什么优缺点?15. 内能耗散系统用什么模型?16. 说明内能耗散对系统稳定性的影响。
17. 双自旋稳定方式是怎样提出来的?其根据是什么?18. 写出双自旋卫星稳定性分析的过程。
19. 双自旋稳定系统的优缺点是什么?第二章20. 环境力矩有哪些?这些力矩有什么特点?有什么作用?21. 什么是引力梯度力矩?并通过实例来解释。
22. 刚体的引力梯度矩是怎样定义的?写出其计算表达式。
说明其性质。
23. 引力梯度力矩作用下,欧拉角如何定义?引力梯度力矩如何计算?欧拉运动学方程和动力学方程如何建立?24. 如何推导姿态动力学方程的线性化方程?从线性化方程可以看出姿态运动有什么特点?25. 怎样进行引力梯度稳定系统的稳定性分析?26. 详细解释ky-kr相平面的物理定义。
27. 如何在ky-kr相平面上表示引力梯度系统的稳定性条件(稳定域)?28. 引力梯度系统有什么特点?第三章29. 说明小推力器系统控制姿态的原理。

航天器姿态动力学运动学
在航天器设计中,姿态控制是一个至关重要的部分。
姿态控制是指控制航天器在三维空间中的方向和位置,使其完成所需任务。
姿态控制需要涉及到航天器的动力学和运动学。
航天器的动力学是指航天器在运动中所受到的力和力矩的关系。
这些力和力矩包括重力、大气阻力、推进器推力、太阳辐射压力等。
这些力和力矩的作用使得航天器不断地发生运动和旋转。
因此,动力学分析对于设计姿态控制系统非常重要。
在动力学分析中,需要确定航天器的质心、惯性张量和各种外力的大小和方向。
通过对这些因素的分析,可以确定航天器的运动方程和控制方程。
航天器的运动学是指航天器在运动中的位置、速度和加速度的关系。
运动学分析可以帮助设计姿态控制算法和控制器。
在运动学分析中,需要确定航天器的姿态、角速度和角加速度。
角速度和角加速度可以通过陀螺仪和加速度计等传感器获得。
通过对这些参数的分析,可以确定航天器的运动方程和控制方程。
姿态控制系统的设计需要综合考虑航天器的动力学和运动学。
姿态控制系统的主要任务是使航天器保持所需的方向和位置。
为实现这一目标,需要使用推进器或姿态控制轮等控制设备来产生力矩,控制航天器的姿态和角速度。
在设计姿态控制系统时,需要考虑到系统的控制精度、控制速度、重量和功耗等因素。
航天器姿态控制需要综合考虑航天器的动力学和运动学。
通过对航天器的动力学和运动学进行分析,可以确定航天器的运动方程和控制方程,为设计姿态控制系统提供基础。
姿态控制系统的设计需要综合考虑控制精度、控制速度、重量和功耗等因素,以实现航天器在三维空间中的精确控制。

姿态动力学姿态动力学是研究物体或系统在受到外力或扰动时,其姿态随时间变化的学科。
它在工程学、物理学和生物学等领域中具有重要的应用价值。
姿态动力学的研究主要涉及刚体运动学、刚体动力学和刚体控制三个方面。
刚体运动学是姿态动力学的基础。
它研究物体在空间中的位置、速度和加速度等几何性质与时间的关系。
刚体运动学可以通过对物体的几何形状、坐标系和运动规律的描述来实现。
通过刚体运动学的研究,我们可以了解物体的运动轨迹、速度变化和加速度变化等信息,从而为后续的刚体动力学分析提供基础。
刚体动力学是姿态动力学的核心内容。
它研究物体在受到外力或扰动作用下,其姿态随时间的变化规律。
刚体动力学可以通过牛顿运动定律、动量守恒定律和角动量守恒定律等基本原理来描述物体的运动行为。
通过刚体动力学的研究,我们可以分析物体受力的来源、力的大小和方向,进而了解物体的运动规律和能量变化等重要信息。
刚体控制是姿态动力学的关键环节。
它研究如何通过施加外力或扰动来控制物体的姿态变化。
刚体控制可以通过设计合适的控制策略和控制器来实现。
通过刚体控制的研究,我们可以控制物体的位置、速度和加速度等运动状态,实现对物体的精确控制和调节。
姿态动力学的研究在许多领域中都有广泛的应用。
在航天器设计中,姿态动力学可以用于分析航天器在重力场中的姿态变化,为航天任务的规划和控制提供重要依据。
在机器人技术中,姿态动力学可以用于分析机器人在复杂环境中的运动规律,为机器人的路径规划和运动控制提供支持。
在运动生物学中,姿态动力学可以用于研究动物和人类的运动机制,揭示运动过程中关节、肌肉和神经系统的协调性。
姿态动力学作为一门综合性学科,在工程学、物理学和生物学等领域中具有广泛的应用价值。
通过对刚体运动学、刚体动力学和刚体控制的研究,我们可以更深入地了解物体的运动规律和控制方法,为相关领域的科学研究和工程应用提供有力支持。
希望未来能有更多的科学家和工程师投身于姿态动力学的研究,为人类社会的发展和进步做出更大的贡献。




1.采用某组欧拉角描述飞行器的姿态,有时会出现奇异。
试给出一种避免奇异的方案,并对该方案进行详细论述。
此外,各种姿态参数之间是有联系并可相互转换的,请分析并介绍多种姿态参数之间的内在关系。
2.采用欧拉角的形式描述航天器的姿态机动任务,除了出现奇异问题外,还存在非路径最优的问题。
试给出一种路径最优的航天器姿态运动描述方案,并详细论述该方案的描述思路和公式。
3.除了课堂上所讲解的牛顿欧拉法(动量定理和角动量定理)推导航天器的姿态动力学方法外,还有哪些比较常用的推导方法?试着对其他推导方法进行详细讲解。
4.牛顿欧拉法推导航天器姿态动力学方程时,是没有考虑到航天器所携带的柔性部件,如果考虑了柔性部件,使用Kane方程推导系统动力学较为方便,试以一个建立带有柔性部件的航天器姿态动力学的例子,对该方法进行讲解。
5.对于航天器的执行机构,特别是飞轮和控制力矩陀螺,它们除了能够提供有效的力矩以进行姿态控制,但是他们也具有一定的振动特性,试通过飞轮和控制力矩陀螺的动力学模型(静动不平衡),去解释两者产生振动的原因。
6.飞轮作为航天器姿态控制执行机构的过程中,一直加速会造成飞轮的饱和,试给大家描述两种以上的飞轮的饱和卸载方式,并结合航天器姿态控制系统回路进行讲解,要绘制出整个系统的控制系统框图。
7.控制力矩陀螺分为常速控制力矩陀螺和变速控制力矩陀螺,试着对变速控制力矩陀螺的操纵律及其他相关知识进行讲解。
8.本课堂上没有讲到过多的航天器姿态确定模块,即没有讲到敏感器测量元件的工作原理以及在理论分析中进行的研究。
试在整个航天器姿态控制系统下,对姿态确定目前研究的重点和难点进行讲解,至少需要讲清楚一种滤波算法。
9.利用地球磁场,可以实现粗略的姿态确定。
以一颗CubeSat卫星为例,设计基于磁强计的姿态确定系统。
进一步,设计依靠磁强计加太阳敏感器的姿态确定系统。
给出系统模型和滤波算法。
(地磁场模型可为磁耦极子模型,或采用真实地磁模型)10.利用航天器自身的磁矩与地磁场的作用,可以实现小型卫星的姿态控制。
姿态动力学姿态动力学是研究物体运动中的姿态变化的科学,主要应用于航空航天、机器人、体育运动等领域。
姿态动力学的研究对于设计和控制运动系统具有重大的理论和实践意义。
姿态动力学主要研究物体在运动过程中的姿态变化规律,包括物体的位置、朝向、角速度、角加速度等参数的变化。
研究姿态动力学可以帮助我们了解物体的运动轨迹和运动方式,从而更好地设计运动系统的控制算法和控制器。
在航空航天领域,姿态动力学是设计和控制飞行器的重要基础。
通过研究姿态动力学,我们可以了解飞行器在不同飞行状态下的姿态变化规律,从而提高飞行器的操纵性和稳定性。
同时,姿态动力学还可以帮助我们优化飞行器的控制算法,提高其控制精度和灵敏度。
在机器人领域,姿态动力学是研究机器人运动和控制的重要理论。
通过研究姿态动力学,我们可以了解机器人在不同环境下的姿态变化规律,从而提高机器人的运动能力和适应性。
同时,姿态动力学还可以为机器人的轨迹规划、动作控制和障碍物避让等问题提供指导,使机器人具备更加智能和灵活的行动能力。
在体育运动领域,姿态动力学对于运动员的训练和竞技表现具有重要意义。
通过研究姿态动力学,我们可以了解运动员在不同动作和姿势下的姿态变化规律,从而帮助运动员改善动作技术和提高运动能力。
同时,姿态动力学还可以用于运动员的运动捕捉和数据分析,帮助教练员进行更加科学和精确的训练指导。
综上所述,姿态动力学是研究物体运动中姿态变化的科学,具有广泛的应用领域和重要的理论意义。
通过研究姿态动力学,我们可以深入理解物体的运动特性,从而为设计和控制运动系统提供指导。
姿态动力学的研究将有助于推动航空航天、机器人和体育运动等领域的发展,为人类的科技进步和生活改善做出贡献。
大气飞行器姿态动力学大气飞行器姿态动力学是研究飞行器在大气中的姿态变化和动力学特性的学科。
它涉及到飞行器在不同飞行阶段的姿态控制、姿态稳定以及姿态变化对飞行性能的影响等内容。
本文将从姿态动力学的基本概念、飞行器的姿态控制方法以及姿态变化对飞行性能的影响进行讨论。
一、姿态动力学的基本概念姿态动力学研究的对象是飞行器在大气中的姿态变化和动力学特性。
姿态是指飞行器在空间中的方向和位置,通常用欧拉角表示。
动力学是指飞行器在外界力和力矩的作用下的运动规律。
姿态动力学研究的目的是分析飞行器在不同姿态下的稳定性和控制性能,为飞行器的设计和飞行控制提供理论基础。
二、飞行器的姿态控制方法飞行器的姿态控制主要通过控制飞行器的姿态角来实现。
常用的姿态控制方法包括基于姿态角的PID控制、基于模型预测的控制和基于自适应控制等。
PID控制是一种经典的姿态控制方法,通过调节姿态角的偏差和变化率来控制飞行器的姿态。
模型预测控制是一种基于飞行器动力学模型的控制方法,通过预测飞行器未来的姿态变化来控制姿态。
自适应控制是一种根据飞行器动力学特性和环境变化自动调整控制参数的方法,可以提高飞行器的适应性和鲁棒性。
三、姿态变化对飞行性能的影响飞行器的姿态变化对其飞行性能有着重要影响。
首先,姿态变化会改变飞行器的气动特性,影响飞行器的升力和阻力,进而影响飞行器的飞行速度和操纵性能。
其次,姿态变化会改变飞行器的重心位置和质量分布,影响飞行器的稳定性和操纵性。
此外,姿态变化还会对飞行器的能量消耗和燃料消耗产生影响,进而影响飞行器的续航能力和航程。
大气飞行器姿态动力学是研究飞行器在大气中的姿态变化和动力学特性的学科。
姿态动力学的研究对于飞行器的设计和飞行控制具有重要意义。
通过合理的姿态控制方法和优化的姿态变化策略,可以提高飞行器的飞行性能和操纵性能,进一步推动航空航天技术的发展。
航天器姿态动力学一、航天器姿态动力学的概念航天器姿态动力学是研究航天器在空间中的运动规律及其控制方法的学科。
它主要涉及到航天器的姿态稳定、控制和调整等方面,是保证航天器飞行安全和有效完成任务的重要基础。
二、航天器姿态动力学的基本原理1.牛顿定律:物体在外力作用下,会产生加速度,其大小与作用力成正比,方向与作用力相同。
2.角动量守恒定律:在没有外力作用时,系统总角动量守恒。
3.能量守恒定律:在没有外力作用时,系统总能量守恒。
三、航天器姿态控制方法1.反推式控制:通过测量航天器状态参数来计算出所需推力,并通过发射喷气口实现对姿态的调整。
2.主动式控制:通过安装陀螺仪等传感器来测量姿态角速度,并通过发射喷气口或调整反应轮转速来实现对姿态的调整。
3.混合式控制:将反推式和主动式两种方法结合起来使用,以实现更加精确的姿态控制。
四、航天器姿态稳定方法1.惯性稳定:通过安装陀螺仪等传感器来测量姿态角速度,从而实现对航天器姿态的自动调整。
2.主动稳定:通过安装反应轮或推进器等设备,使得航天器能够主动地进行姿态调整,以保持其稳定状态。
3.混合稳定:将惯性稳定和主动稳定两种方法结合起来使用,以实现更加精确的姿态稳定。
五、航天器姿态动力学的应用1.卫星通信:卫星需要保持一定的轨道和姿态才能有效地进行通信。
2.地球观测:卫星需要保持一定的轨道和姿态才能进行地球观测,并获取准确的数据。
3.空间探索:太空飞行器需要进行精确的姿态控制,以实现对目标星球或行星的探测和研究。
六、总结航天器姿态动力学是一门重要的学科,在现代航天技术中发挥着重要作用。
通过对其基本原理、控制方法和应用领域的研究,可以更好地保障航天器的飞行安全和有效完成任务。