结
③由性质定理列条件,下结论。
求证:如果一条直线与一个平面平行,那么夹在这条直线和这个 平面间的平行线段相等。
已知:AB∥α, AC∥BD, AC∩α=C, BD∩α=D.
求证: AC = BD.
A
B
证明:∵AC∥BD
∴A,B,D,C四点在同一个平面内. 连接CD,
∵AB∥α,AB⊂面ABDC,
面ABDC∩α=CD
A.平行 B.相交且垂直 C.异面直线 D.相交成60°
C C
A
A
D
B(D)
B
解:选D.将上面的展开图还原成正方体,
点B与点D重合.容易知道AB=BC=CA,
从而△ABC是等边三角形.所以选D.
利用直线和平面平行的性质定理解题的步骤:
找
①找一个与已知平面相交且过该直线的平面;
定
②确定两平面的交线;
<m>
<m>
<m>
<m>
</m>
合作
应用
竞技
探究1. 如果一条直线与一个平面平行,那么这条直线与这个平面内的
直线有怎样的位置关系?
a
a
平行
异面
探究2. 如果一条直线a与平面α 平行,那么α 内的直线满足什么条件,才能
与直线a平行呢?
已知a∥α,a⊂β,α∩β = b. 求证:a∥b.
证明:∵ α∩β = b
∴ b⊂α
β
a
∵ a∥α
∴ a与b不相交
又a⊂β,b⊂β ∴ a与b不异面
b
α
∴ a∥b .
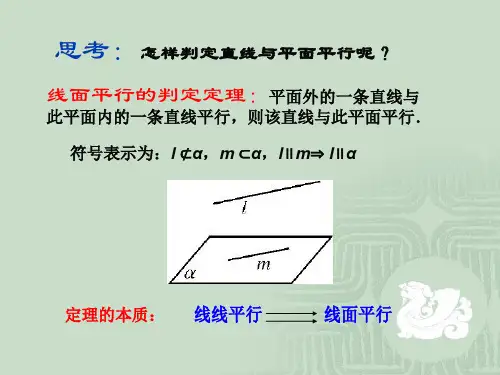
直线与平面平行的性质定理:
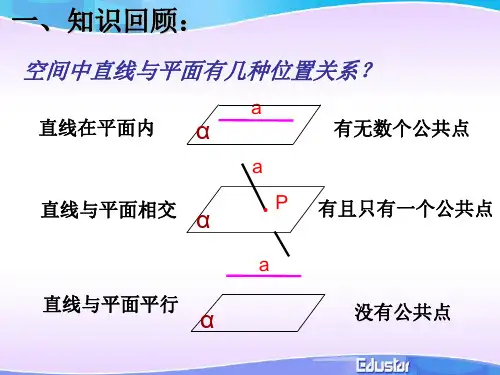
一条直线与一个平面平行,如果过该直线的平面与已知平面相交, 那么该直线与交线平行。