地震子波的再认识

子波干涉研究在地震解释中的应用
子波干涉技术在地震解释中有着广泛的应用。

以下是一些主要的应用领域：
1.振幅补偿：子波干涉可以用于振幅补偿，从而提高地震
记录的分辨率和清晰度。

2.噪声去除：子波干涉可以用于降低地震信号中的噪声水
平，从而提高地震数据的解释精度。

3.波形对比：子波干涉可以用于比较不同地震记录之间的
波形差异，从而确定地震事件的特征和性质。

4.层位解释：子波干涉可以用于解释地震层位，从而确定
地下地质结构。

5.反射特征分析：子波干涉可以用于分析地震信号的反射
特征，从而确定地下异常体，如断层、岩溶洞穴等。

总之，子波干涉技术在地震解释中有着广泛的应用，可以帮助解释人员更准确地识别地震事件，提高地震解释的精度和可靠性。

盲解卷积算法1. 原理：几个重要概念：1.1 褶积模型假设：假设1：地层是由具有常速的水平层组成；假设2：震源产生一个平面压缩波(P 波)，法向入射到层边界上，在这种情况下，不产生剪切波(S 波)；假设3：震源波形在地下传播过程中不变，即它是稳定的； 假设4：噪音成分是零；假设5：震源波形是已知的；假设6：反射系数序列是一个随机过程。

这意味着地震记录具有地； 震子波的特征，即它们的自相关和振幅谱是相似的；假设7：地震子波是最小相位的，因此，它有一个最小相位的逆。

1.2 反滤波如果定义滤波算子为f (t),则f (t) 与已知地震记录x(t)的褶积得到一个对地层脉冲响应e(t)的估计e(t) = f (t)∗ x(t)； （1） x(t) = w(t)* f (t)* x(t)； （2） δ(t) = w(t)* f (t)； （3）1()()*()f t t w t δ= （4） 用流程图表示为：1.3 震源反子波计算震源反子波在数学上是利用z 变换来实现的。

例如，假设基本子波为两点时间序列（1，－0.5)1()12w z z =-2111()1 (12412)F z z z z ==+++-； （5） 2111()1 (12412)F z z z z ==+++- （6） ()F z 的系数11(1,,,...)24代表逆滤波算子f(t)有关的时间序列。

可以看出它有无限多个系数，然而它们递减的很快。

如同任何滤波过程一样，实际应用的算子都是被截断的。

1.4 最小平方反滤波当输入子波良好，其z 变换的逆可以用一收敛序列表示，则上面所描述的反滤波将得到一个很好的近似于尖脉冲的输出.将下面问题列出方程式：给定输入子波(1－0.5)，寻找一个二项滤波器(a,b)，使实际输出与期望输出(1,0,0)之间的误差在最小二乘的意义上最小。

将滤波器(a,b)与输入子波(1,-0.5)褶积以计算实际输出。

误差的累积能量L 定义为实际的与期望的输出的系数之差的平方和：222(1)()()22a b L a b =-+-+- （7） 目的是寻找系数(a,b)使L 最小，这要求变量L 随系数(a,b)而变并使之为零对上式进行简化，取L 对a 和b 的偏导数，并使其为零，得到： 522502a b a b ⎧-=⎪⎪⎨⎪-+=⎪⎩（8） 有两个方程和两个未知数即滤波器系数(a,b)，可变成下列普通矩阵形式：5/21215/20a b -⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭（9） 求解滤波系数，我们得到(a,b)为(0.95,0.38)。

3、联合对比
图2-9 水平剖面
图2-10 偏移剖面
第三节 与复杂地质现象有关的异常波
一、绕射波 1．绕射波的产生
图2-11绕射波的产生
图2-12 绕射波的时距曲线
1、绕射波的主要特征
1）绕射波时距曲线是双曲线正常时差进行动校正时， 由于校正量不足，校正后的绕射波时距曲线其形状仍然是 曲线。
2）时距曲线的极小点在绕射点的正上方，射波时距 曲线的极小点总是在绕射点的正上方。绕射波时距曲线与 反射波时距曲线相切。
面深度平面图。
2-4 水平剖面上的断面波
图2-15偏移剖面上的断面波
图2-16 断层面的确定
三、 多次波
图2-17 几个重要的多次反射波类型示意图
图2-18 海底多次波引起的构造地层假象
一、地震地质解释在构造解释方面的应用
所谓地震地质解释就是依据时间剖面的波形特征 和地质规律赋予地震反射层明确的地质意义。
勘探早期地震资料解释主要以盆地构造、地层和沉 积体系解释为主，目的是确定盆地的基本形态、性质、 盆地演化历史、主要断裂、构造特征、地层展布、沉积 环境和相态分布。
勘探后期地震资料解释则以精细构造解释和储层预 测为主，目的有是确定各种隐蔽的低幅度圈闭、砂体横 向展部、油气检测和早期油气藏描述等方面的工作。
图1-14 地震子波的形成
图1-15几种子波能量分布、波形和相位的关系 最小相位子波，有时称为前载子波，能量集中在 前端；大多数脉冲地震震源产生的原始脉冲是接近最 小相位的，因此，地震子波一般是最小相位（最小延 迟）子波。 最大相位子波则能量主要集中在尾部。 零相位子波能量集中在中间，且波形对称。
第二章 地震解释基本方法
第一节 地震反射层位的地质解释

值。
纵横波速度比： V p / Vs
2
上式可以统一用泊松比来替代：
2(1 ) 1 1 2
• 纵波速度大于横波速度。对自然界中常见的岩石 来说，σ=0.25。=1.73, 横波速度最多达到纵波 速度的0.707倍。
• 0.05(坚硬岩石)≤ σ ≤0.45（松软介质）
• 液体中不产生切应变，即μ=0，VS =0 。液体中
• 透射角与入射角符合折射定律；透射线和入射 线、界面点的法线在一个平面内。
O
ρ1 v1
入射角
ρ2 v2
透射角
ρ3 v3
法线 S
α
β
反射波
反射角 界面1
透射 波
界面2
二、反射、透射波的一些基本概念
• 1、反射系数
• R=（Z2-Z1）/（Z2+Z1）=（ρ2ν2ρ1ν1）/ （ρ2ν2+ ρ1ν1）
• 实际的地层介质中，地震波的速度随埋 深增加而增加，因而能形成良好的折射 界面，但折射界面总是少于反射界面；
• 折射波存在有盲区，即得不到折射波的 地区，且界面越深，盲区越长；
• 深浅层折射波相互干涉，对反射波有一 定的影响。
六、多层介质中地震波的传播
在具有多界面的
介质中，各层介
O
S
质的速度不同，
二、地震波的形成
1、地震子波：当地震波传播一定距离后，其
形状逐渐稳定，具有2-3个相位，有一定的延 续时间的地震波，称为地震子波，它是地震记 录的基本元素。 • 地震子波在继续传播的过程中，严格来讲其幅 度和形状都会发生变化，近似可以认为地震子 波的形状基本不变，但其振幅有大有小、极性 有正有负，到达接收点的时间有先有后。
• 折射波：滑行波在滑行的过程中，下层 介质中的质点就会产生振动，形成新的 震源，并在上层介质中产生新的地震波。

实验分析
根据所学知识对实验结果进行分析；
地震子波由震源激发，在地层中传播，因为在沉积地层中，每层介质的物理性质不相同，从而使得地震波的传播速度也不相同。当地震波传播到两层介质的分界面时，会发生反射，由于每层介质的反射系数不同，所以反射波的能量也不相同，检波器接收到不同时刻的、不同能量的反射波，形成一个地震记录。
subplot(2,2,4),plot(f2,'k'),title('最小相位子波地震记录')
f1(i)=0;
f2(i)=0;
end
fori=1:n+m-1%地震记录长度
forj=1:m%地层深度
ifi-j>0&i-j<=200%满足雷克子波的时间序列长度
a1(j)=r(j)*w1(i-j);
a2(j)=r(j)*w2(i-j);
f1(i)=f1(i)+a1(j);
f2(i)=f2(i)+a2(j);
地震子波波形显示及一维地震合成记录
姓名：杨肖迪学号：050422009040专业：地球信息科学与技术2009级
实验目的
1.认识地震子波（以雷克子波为例），对子波的波形有直观的认识。
2.利用褶积公式合成一维地震记录。
实验步骤
1.雷克子波
（零相位子波）
（最小相位子波）
其中 代表子波的中心频率， 代表子波宽度,随着 的增大，子波能量后移，当 =7时，最小相位子波可视为混合相位子波，这里 = 25 Hz， =4;
end
end
end
subplot(2,2,1),plot(w1,'k'),axis([0,200,-1,1]),title('零相位子波')

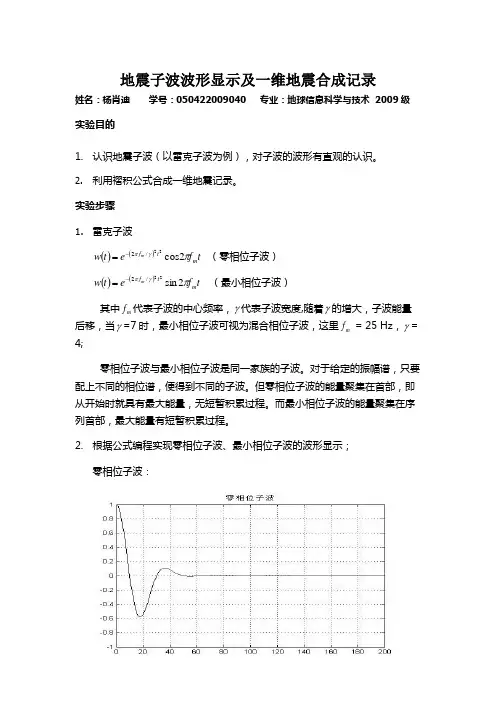
名词解释：6*5=30简答：5*9=45计算：1*10=10论述：1*15=15地震地质综合解释思考题参考答案1、名词解释：（★）1）地震子波：在震源附近，地震波以冲击波的形式传播，当传播到一定距离时，波形逐渐稳定，此时的地震波被称为地震子波。

2）反射系数：在垂直人射的情况下，纵波入射时将只考虑产生的反射纵波和透射纵波的情况。

这时界面的反射系数定义为：3）弹性参数：地震波是在岩层中传播的弹性波，在弹性力学中，引入了一些物理量来描述弹性体的弹性特征，在研究地震波动力学时经常用到的弹性参数如下：杨氏模量E、泊松比σ、切变模量μ、体变模量K、λ系数、λ、μ合称拉梅常数2）波阻抗：波在某介质中传播的速度与介质密度的乘积定义为该介质的波阻抗。

3）信噪比：所谓信噪比，通俗地讲就是有用的地震波与无用地震波的能量（振幅）之比。

4）振幅：质点振动离开平衡位置的最大位移（幅度）称为振幅。

5）频谱：组成一个复杂振动的各个谐振动分量的特性与其频率的关系的总和，就称为这个振动的频谱6）正花状构造：与压扭性走滑断裂相对水平运动相伴生的构造样式，在走滑断裂上部形成背形构造7）负花状构造：与张扭性走滑断裂相对水平运动相伴生的构造样式，在走滑断裂上部形成向形构造8）地震相：是一个可以在区域内固定的，由地震反射层组成的三维单元，其反射结构、振幅，连续性、频率和层速度等要素，与邻近相单元不同。

9）底超：是在一个沉积层序底界上的超覆尖灭现象，它又分为上超和下超两种基本类型。

（1）上超：是一套当初是水平的地层对着一个原始倾斜面超覆尖灭，或者是一套原始倾斜的地层对着一个原始倾角更大的斜面逆倾向的超覆尖灭。

（2）下超：是一套原始是倾斜的地层对着一个原始水平倾角或者倾斜面沿下倾方向前进超覆。

10）地层下其上覆地层之间（顶界）的接触关系有顶超和削蚀。

（1）顶超：是在一个沉积层序的上界面处地层的退覆侧向消失现象。

（2）削蚀作用：是某一地层因侵蚀作用而引起的侧向消失。

地震子波名词解释
地震子波是指在地震波中存在的一些特定类型的波形，它们是地震波通过不同的传播介质和路径所形成的。

地震子波包括纵波（P波）、横波（S波）、面波（Rayleigh波和Love波）等。

1. 纵波（P波）：纵波是一种沿着地震波传播方向上颤动的波动，它使岩石在传播路径上以压缩和扩张的方式振动。

2. 横波（S波）：横波是一种在垂直于地震波传播方向上颤动
的波动，它使岩石在传播路径上以横向振动的方式传播。

3. 面波：面波是一种沿着地表或地下界面传播的波动，它同时具有纵波和横波的特点。

面波主要包括Rayleigh波和Love波。

4. Rayleigh波：Rayleigh波是一种沿地球表面传播的面波，其
振动轨迹呈现出向前旋转的椭圆形。

它具有明显的滚动和向后运动的特点，是地震波中能量传播最远的一种波动。

5. Love波：Love波是一种沿地球表面传播的面波，其振动轨
迹呈现出向前旋转的椭圆形。

与Rayleigh波相比，Love波振
幅较小，以横向振动为主，传播速度较快。

地震子波频率浅析
云美厚;丁伟
【期刊名称】《石油物探》
【年(卷),期】2005(044)006
【摘要】地震子波频率概念的合理选择与准确应用对于地震采集设计、地震模拟研究、地震资料处理、地震属性分析以及质量评价等是非常重要的.针对目前地震子波频率由于定义方式出现的各种概念(视频率、主频、峰值频率、中心频率等)以及理解上出现的偏差等问题,首先从时间域定义和频率域定义2个方面进行了归纳和总结,并在此基础上对3种常用地震子波(Ricker子波,Zinc子波,正弦指数衰减子波)进行了分析和研究,得出视频率与主频概念一致,但不同地震子波的峰值频率、中心频率和视频率(或主频)之间并不完全一致的结论;而对于实际地震资料,将峰值频率近似看作地震子波的主频是可以的,但在地震子波已知的情形下这样做是不恰当的,甚至可能会得出错误的结论和认识.
【总页数】4页(P578-581)
【作者】云美厚;丁伟
【作者单位】中国石化胜利石油管理局地球物理勘探开发公司,山东,东营,257100;中国石化胜利石油管理局地球物理勘探开发公司,山东,东营,257100
【正文语种】中文
【中图分类】P631.4
【相关文献】
1.一种地震子波峰值频率的估计方法 [J], 杨森林;高静怀
2.浅析(对初始频率的)瞬态频率偏差 [J], 王丰玉;张洪战
3.电力系统频率问题浅析与频率特性研究综述 [J], 陈雪梅; 陆超; 韩英铎
4.浅析自交与自由交配中基因频率与基因型频率的变化规律 [J], 杨景国
5.电力系统频率问题浅析与频率特性研究综述 [J], 陈雪梅; 陆超; 韩英铎
因版权原因，仅展示原文概要，查看原文内容请购买。

第一节关于地震波极性判断问题地震反射波的极性是正还是负，它直接影响到反演波阻抗后，速度变高还是变低，因此是一个重要的问题。

但是这个很简单的问题，到目前为止，尚未完全争论清楚。

按理说，问题是再简单不过的，即：SEG格式规定，初至波起跳向下，记录数值是负的，此称“正常记录”。

那末，这种记录作波阻抗时，应该把极性反过来。

但在实际中，往往不反过来，反而能在解释中与地层对得更好。

奇哉！现在看来，这个问题很复杂。

仔细思考起来，本人有以下几点认识。

（1）地震子波是混合相位的，包括可控震源的子波，也因为大地的吸收作用，回到地面的子波已变成混合相位。

它的第一个向下跳的波谷很小，而跟着来的波峰及波谷很大。

请读者参看图72。

注意该图72的子波起跳是朝上的，不过这并不妨碍对问题的分析。

脉冲反褶积及预测反褶积都假设子波是最小相位，而当子波是混合相位时，反褶积后子波的波形向前压缩得不够好。

因而随着原始子波形态的不同以及所采用白噪系数的不同，反褶积后的子波有时波峰最大，有时波谷最大，见图72中我已用+-符号标出。

并且最大值并不在起跳的位置上，而有不同程度的延迟，见图72（注意该图子波的起跳朝上）。

以SEG规定的正常极性记录为例（起跳朝下），如果反褶积作得效果较好，那么第一个起跳波谷可能还是小于后面的第一波峰。

这时候，整个记录看起来似乎是“正极性”的。

如果反褶积用了较大的自噪系数，或者子波的相位谱离开零相位较远，那末，反褶积后可能以第二波谷为最强，剖面上看起来似乎是“负极性”的。

（2）如果叠后加作预测反褶积或谱白化，则频谱成分又起了变化，波形又明显变瘦，视周期变小。

加上最后还要采用时变滤波，滤波门的不同又会造成子波波形的进一步变化。

因此，不同的处理方法可以得到不同的子波波形，有时两个相位可变成三个相位。

剖面形态也可以各不相同，“视极性”也就各异。

这样一说，是否天下大乱了呢？是的！的确有些乱套。

有一个搞解释的人拿着两张不同流程的剖面给我看：一条剖面上T g波是两个相位，中间波谷最强。

地震子波的再认识一、地震子波观点：地震子波是地震记录褶积模型的一个重量，往常指由 2 至 3 个或多个相位构成的地震脉冲，切实地说，地震子波就是地震能量由震源经过复杂的地下路径流传到接收器所记录下来的质点运动速度〔陆上检波器〕或压力〔海上检波器〕的远场时间域响应。

一个子波能够由它的振幅谱和相位谱来定义，相位谱的种类能够是零相位、常数相位、最小相位、混淆相位等；对零相位和常数相位子波而言，可简单将其看作是一系列不一样振幅和频次的正弦波的会合，全部的正弦波都是零相位或常数相位的〔如 90°〕；在频次域中，子波提取问题由两局部构成：确立振幅谱和相位谱，确立相位谱更为困难，并且是反演中偏差的主要根源。

二、子波提取方法：子波提取方法分为三个主要种类： 1) 、纯确立法：即用地表检波器或其余仪器直接丈量子波； 2) 、纯统计法：即只依据地震数据测定子波，这类方法很难测定靠谱性的相位谱； 3) 、使用测井曲线法：即便用测井曲线与地震数据联合，理论上这类方法能够提取井点地点精准的相位信息，但问题是该方法要求测井和地震间一定要有优秀的对应关系，而将深度域样点变换为双程旅游时的深时变换可能产生不适合的对应关系，而这类不适合的对应关系势必影响子波提取的结果。

子波在各地震道之间是变化的，并且是旅游时间函数，即子波是时变和空变的，也就是说，对每个地震剖面而言，都应当能提取大批的子波，但在实质应用中提取可变子波可能会惹起更多的不确立性，比较适用的做法是对整个剖面或某个目的层只提取单调的均匀子波。

三、零相位子波和常数相位子波：零相位子波和常数相位子波 ( Zero Phase and Constant Phase Wavelets. ) 第一，让我们来考虑雷克子波 ( Ricker Wavelet ) ，雷克子波由一个波峰和两波谷，或叫两个旁瓣构成 , 雷克子波依靠它的主频，也就是说，它的振幅谱的峰值频次，或主周期在时间域的反函数〔主周期能够经过丈量波谷到波谷的时间来获取〕。

地震资料解释中必须弄懂的50个基本概念！地震资料解释中的基本概念.1. 地震资料解释是将地震信息转换成地质信息。

核心就是依据地震剖面的反射特征和地震信息，应用地震勘探原理和地质基础理论，赋予其明确的地质意义和概念模型2.地震解释的发展阶段: 地震构造解释阶段----在构造地质学和地震成像基本原理的基础上，确定地下主要反射界面的埋藏深度，落实和描述地下岩层的构造形态特征，为钻探提供有力的构造圈闭是其主要目的。

地震沉积解释阶段----以地震地层学和层序地层学理论（思想方法）为基础，以落实隐蔽油气藏、描述地下储层空间几何形态为主要目的.地震资料综合解释阶段----以地震资料为基础，综合一切可能获得的资料（包括地质、钻井、测井以及地球化学和其他地球物理资料），合理判断和分析各种地震信息的地质意义，以达到精确重现地下地质情况。

3.地震子波：震源激发时产生尖脉冲，在激发点附近的介质中以冲击波的形式传播，当传播到一定距离时，波形逐渐稳定，称该时刻的地震波为地震子波4.地震剖面的种类：时间剖面有两种：一是水平叠加时间剖面，简称水平剖面；二是叠加偏移时间剖面，简称偏移剖面。

时间剖面的显示：波形剖面，变面积剖面，变密度剖面，波形加变面积剖面，彩色显示剖面，5. 时间剖面的特点：时间剖面由图头和记录两部分组成。

图头部分：位于剖面的起始部分，用以说明剖面的工区、测线号、起止桩号、剖面性质、野外施工参数和处理方法与流程，其显示内容由处理人员提出。

记录部分：是时间剖面的主要部分。

横轴：代表共中心点叠加道的位置，一般用CDP点号和相应的测线桩号表示。

CDP点距为道距的一半，通常为25m。

桩号SP，单位为米或千米。

纵轴：双程反射时间T。

单位为秒。

速度谱：每km一组显示于剖面上方地形线: 显示于剖面上方或下方。

基准面：统一或浮动的，多选在低速带之下。

地震剖面上0秒所对应的海拔。

视周期：相邻波峰(谷)之间的时间长度视主频：视周期的倒数。

地震子波的定义
地震子波是指地震波在地下介质中传播时所形成的波形信号。

在地震勘探中，
地震子波是通过地震波在地下反射、折射、散射等作用形成的地震信号，可以提供地下地质结构和构造信息，是地震勘探中非常重要的数据。

地震子波的形成是由地震波的震源和地下介质的特性共同决定的。

地震子波的
形状可以反映地下地质介质的性质，如地震子波的振幅、频率、波形等特征可以揭示地下岩性、构造、孔隙度等信息。

地震子波的振幅可以反映地下不同地质体的反射系数差异，频率可以反映地下介质的孔隙度和地震波在介质中的衰减情况，波形可以揭示地下地质构造的复杂程度。

地震子波的特性对地震勘探的成像和解释具有重要意义。

通过地震子波的分析
可以确定地下地质体的位置、形状、性质等信息，从而为地震勘探提供可靠的地质模型。

地震子波的解释可以帮助地质学家理解地下地质结构的复杂性，为石油勘探、地质灾害监测、地质灾害预测等领域提供支持。

总的来说，地震子波是地震波在地下传播时的波形信号，可以提供地下地质结
构和构造信息，是地震勘探中的重要数据之一。

地震子波的分析和解释对地震勘探的成像和解释具有重要的意义，可以帮助地质学家更好地理解地下地质结构的复杂性，为地质勘探和地质灾害监测提供支持。

地震子波的研究将为地震地质学的发展和地质勘探技术的进步提供重要的理论基础。

没有子波时的子波处理：
各种各样的统计性反褶积方法
利用声波测井数据提取地震子波 工作流程
同一剖面段不同深度统计的子波特征不同，子波是时变的
井下不同 深度记录 的直达波 波形基本 保持不变
当这个子 波在地层 中传播时， 由于地层 吸收衰减， 子波发生 了变化， 据此我们 可以进行
地层滤 波模拟
子波频 率误差 对子波 处理效 果影响
零相位子波，线性相位谱
线性相位谱，零相位子波 负的斜率，时移向正的方向移动 斜率越大，时移越大
线性相位谱，零相位子波 正的斜率，时移向负的方向移动 斜率越大，时移越大
混合相位子波，常相位谱
零相位子波，常相位移动，常相位谱，混合相位子波 常相位移1800，子波反向 常相位移为 00 和 3600，子波一样
道反演要求道上的正值对应正的反射系数
反演时，正值反演结果是速度增加，对应正的反射系数，因 此反演之前要作极性检查，确定是否为正极性，否则要作极 性处理
二、相位和子波相位特性图解
零相位子波，零相位谱 零相位子波，线性相位谱 混合相位子波，常相位谱 混合相位子波，常相位谱 + 线性相位谱
零相位子波，零相位谱
数据处理目标是使子波成为冲激函数，但由于S/N和原 始记录带宽，实际只能得到频带有限的子波 处理常用两种子波：带通子波和 Ricker（雷克）子波
带通子波由通带范围内各个频率谐波合成，每个谐波长度
无限，在相当长时间段内不能相互抵消，是旁瓣形状复 杂的基本原因
脉冲反褶积后进行带通滤波，理论上子波就成为带通滤 波器的因子
层位标定制作合成记录，用理论雷克子波，其合成记录可视 为正极性状态，可邦助判断记录的极性状态 从井旁实际记录中提取子波，可改善合成记录与实际记录的 相似程度，有利于标定准确，但不能用于判断实际记录的极 性状态 用合成记录进行层位标定，不仅要注意子波特性的确定，而 且要注重反射系数序列的可靠性：

2008年12月第43卷 增刊2*河北省涿州市东方地球物理公司研究院,072751本文于2008年3月20日收到。

#处理技术#地震数据处理中关于地震子波相位特性的探讨苏贵仕*¹沈克非º 丁学垠º(¹东方地球物理公司研究院,河北涿州072751;º东方地球物理公司研究院海外业务部,河北涿州072751)苏贵仕,沈克非,丁学垠.地震数据处理中关于地震子波相位特性的探讨.石油地球物理勘探,2008,43(增刊2):121~124摘要 本文就实际地震数据处理中常用的地震子波最小相位化、预滤波、叠前反褶积和叠后地震子波零相位化等四个处理模块对地震子波相位特性的影响进行了探讨。

当地震记录是由可控震源激发得到时,其地震子波是可控震源扫描信号的自相关,呈零相位子波特性,此时需将零相位子波转化为最小相位子波,为后续的反褶积处理做准备;当地震记录是由炸药震源激发得到时,其地震子波一般被认为是最小相位子波,在对此地震数据进行叠前反褶积处理之前首先使用一个高通滤波器对其进行预滤波处理(这个滤波器必须是最小相位的,因为最小相位地震子波只有经过最小相位滤波器滤波后才是最小相位的),然后进行叠前反褶积处理(主要包括脉冲反褶积、地表一致性反褶积等,该处理过程要求输入地震数据的地震子波是最小相位的),经过这些反褶积处理后的地震数据的子波也认为是最小相位的;因零相位子波的地震剖面分辨率最高,所以最后还需再对叠后数据的最小相位子波进行零相位化处理。

以上认识已在巴基斯坦E 工区二维地震资料的处理中得到验证。

关键词 地震子波 最小相位 预滤波 叠前反褶积 零相位化1 引言地震数据处理的目的是将野外采集的地震记录用处理模块进行处理后得到成像好、分辨率高的地震剖面,地震记录可描述为地震子波与地层脉冲响应或地下反射系数系列的褶积。

就某种意义上说,地震数据处理实际上是一个对地震子波不断改造的过程。

地震_思考题及作业2思考题及作业1.什么叫地震波的振动图？什么叫地震波的波剖面？振动图：地震波传播过程中，某一质点的位移是随时间变化的，描述某一质点位移与时间关系的图形。

波剖面：一个质点的振动必然带来相邻质点的振动，同一时刻不同质点的振动形式称为波剖面。

2.视速度是如何定义的？视速度：就是沿测线方向观测到的传播速度。

视速度定理：V*=V/cosα, V*表示真速度，V表示真速度，α为地震波射线与其自身的地表投影的夹角。

3.在弹性分界面，P、SV、SH波分别以α角入射时，各能产生哪些波，哪些是同类波，哪些是转换波？请画图说明。

无论纵波（P）还是横波（SV，SH）倾斜入射到弹性分界面时，都将同时产生反射横波、反射纵波、透射横波、透射纵波。

与入射波型相同的波如称为同类波，波型改变的则称为转换波。

转换波的反射和透射遵循斯奈尔定律。

转换波的产生，是由于入射波作用在分界面上可分解为垂直界面的力和切向力两部分，结果产生体变和切变及其相应的纵波和横波。

因此，转换波的能量与入射角有关，垂直入射时不能形成转换波；只有入射角相当大时，才有足够能量的转换波可被记录下来。

故在地震勘探中主要利用同类波，在一些特殊问题中才用转换波。

4.简述产生折射波的机制及条件，并说明什么是临界角。

产生机制：地震波在传播中遇到下层的波速大于上层波速的弹性分界面，而且入射角达到临界角（使透射角为90°）时，透射波将沿分界面滑行，又引起界面上部地层质点振动并传回地面，这种波称为折射波。

条件：下层的波速大于上层波速的弹性分界面，透射角为90°。

透射角：即折射角为90度时的入射角叫做临界角。

5.简述瑞雷面波的传播特征①瑞雷面波只存在于自由界面附近②瑞雷面波比横波传播慢；③瑞雷面波使介质质点沿椭圆轨道运行，因此它是面的椭圆极化波；④瑞雷面波波长越长，随离开自由界面的深度衰减越慢（既面波在介质中穿透越深）；6.何为地震子波地震子波是地震记录褶积模型的一个分量，通常指由2至3个或多个相位组成的地震脉冲，确切地说，地震子波就是地震能量由震源通过复杂的地下路径传播到接收器所记录下来的质点运动速度（陆上检波器）或压力（海上检波器）的远场时间域响应。

地震子波比喻
地震子波如同大自然的奏鸣曲，在大地深处默默酝酿着力量。

当地壳突然崩裂，释放出巨大的能量，子波仿佛是一只骤雨中的蝇，猛然飞起，席卷着无尽的能量浩荡而来。

子波的到来宛如一阵狂风，带动了地球的颤动。

它们像音符一样，快速传播着，通过地壳中的岩石、土壤和岩层，以肆虐的力量向四面八方扩散。

这种扩散就像是一汪涟漪，从震源中心蔓延开来。

子波有着多样的特性，有的像炸雷一样震耳欲聋，有的则如孔雀开屏，令人目眩神迷。

它们以不同的频率、振幅和波速出现，有时一种子波过后，另一种就跟随而至，形成令人难以想象的景象。

这些子波的行进速度有快有慢，有的能迅速穿越地下，犹如箭矢射出；有的则在岩层之间蜿蜒前行，像是游鱼穿梭。

它们的传播路径也因地质条件的不同而有所差别，有时会顺着山脉蜿蜒，有时则会幽灵般扩散，造成错位的效果。

尽管如此，子波的到来总是给人带来巨大的震荡和破坏。

它们如同大自然的警钟，提醒着人类要谦卑地面对地球的伟力。

在地震的瞬间，子波的到来仿佛将时间凝固，人们被迫面对生死，亲手见证着大地的愤怒。

然而，地震子波的余波并不会永远持续，它们将逐渐减弱、消散，最终沉寂。

大地也会在震后重新平静下来，恢复它的宁静与和谐。

这一过程仿佛是宇宙的轮回，一切在变化中长存。

地震子波比喻
（原创实用版）
目录
1.地震子波的定义和特点
2.地震子波的类型和产生原因
3.地震子波的传播和影响
4.地震子波比喻的意义和应用
正文
地震子波是指地震发生时，地壳内部结构受到地震波的激发而产生的次级波。

地震子波是地震波的重要组成部分，具有较高的能量和破坏力。

地震子波在地震发生过程中，可以对建筑物和自然环境产生极大的影响。

地震子波的类型主要有纵波和横波两种。

纵波是指地震波在传播过程中，振动方向与波的传播方向一致的波。

纵波的传播速度快，破坏力较小，通常是地震子波中的主要组成部分。

横波是指地震波在传播过程中，振动方向与波的传播方向垂直的波。

横波的传播速度慢，破坏力较大，通常是地震子波中的次要组成部分。

地震子波的产生原因主要有地壳内部结构的复杂性、地震波的传播过程中的折射和反射等。

地震子波的产生和传播过程，可以导致地壳内部结构的振动和变形，从而对建筑物和自然环境产生影响。

地震子波的传播和影响是地震学研究的重要内容。

地震子波的传播速度和破坏力，可以对地震的预警和防范产生重要影响。

地震子波的传播和影响，可以通过地震波的传播和反射、地震波的衰减和叠加等过程进行研究和模拟。

地震子波比喻是一种地震学研究的重要方法。

地震子波比喻可以通过对地震子波的特征和行为进行类比，来揭示地震子波的内在机制和传播规
律。