椭圆练习题及答案

高三椭圆练习题及答案1. 技术背景在二维几何中，椭圆是一种重要的图形，具有许多应用。

高三学生需要掌握椭圆的基本概念、性质和相关的计算方法。

为了帮助高三学生巩固椭圆的知识，以下是一些椭圆练习题及答案。

2. 填空题(1) 如果椭圆E的长半轴和短半轴分别为a和b，则椭圆的离心率为________。

(2) 椭圆的焦点和直径的关系是________。

(3) 椭圆的离心率小于1，原点(0,0)在椭圆的________。

(4) 椭圆的离心率等于1，原点(0,0)在椭圆的________。

(5) 椭圆的离心率大于1，原点(0,0)在椭圆的________。

答案：(1) 椭圆的离心率为c/a；(2) 椭圆的焦点和直径的关系是焦点到椭圆周上任意一点的距离之和等于该点到椭圆的两个直径的距离之和；(3) 原点(0,0)在椭圆的右焦点所在的象限；(4) 原点(0,0)在椭圆的焦点所在的象限；(5) 原点(0,0)在椭圆的左焦点所在的象限。

3. 选择题(1) 下列各图中，哪个是椭圆？A. B. C. D. 答案：C. (2) 椭圆的离心率等于1，这个椭圆的形状是________。

A. 长圆B. 倍圆C. 圆D. 短圆答案：C. 圆4. 计算题已知椭圆的焦点为F1(-3, 0)和F2(3, 0)，离心率为2/3，求椭圆的方程。

答案：椭圆的焦距为2ae = 6，离心距为2c = 2/3 * 2a，解得a = 9，所以椭圆的方程为(x^2)/81 + (y^2)/36 = 1。

5. 应用题小明要设计一个椭圆形的游泳池，他希望池子的长半轴为8米，短半轴为6米。

假设池子的边界是一个完整的椭圆，求池子的周长和面积。

答案：椭圆的周长为2π * √((a^2 + b^2)/2) = 2π * √((8^2 + 6^2)/2) ≈ 39.97米。

高二数学椭圆练习题及答案一：选择题 1.已知方程表示焦点在x轴上的椭圆，则m的取值范围是2.已知椭圆，长轴在y轴上、若焦距为4，则m等于 4．已知点F1、F2分别是椭圆+=1的左、右焦点，弦AB过点F1，若△ABF26．方程=10，化简的结果是7．设θ是三角形的一个内角，且，则方程xsinθ﹣ycosθ=1表示的曲线221、22129.从椭圆上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP，则该椭10.若点O和点F分别为椭圆的中心和左焦点，点P 为椭圆上的任意一点，则的最大值为11.如图，点F为椭圆=1的一个焦点，若椭圆上存在一点P，满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点，则该椭圆的离心率为12．椭圆顶点A，B，若右焦点F到直线AB的距离等于，则椭圆的离心率e=高二数学周测一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是满足题目要求的。

1.平面内有两定点A、B及动点P，设命题甲是：“|PA|+|PB|是定值”，命题乙是：“点P的轨迹是以A．B 为焦点的椭圆”，那么 A.甲是乙成立的充分不必要条件B.甲是乙成立的必要不充分条件C.甲是乙成立的充要条件D.甲是乙成立的非充分非必要条件.若椭圆2kx?ky?1的一个焦点是，则k的是 A.2211B.C. D.3228D．3x2－y2＝363．双曲线与椭圆4x2＋y2＝64有公共的焦点，它们的离心率互为倒数，则双曲线方程为 A．y2－3x2＝36B．x2－3y2＝36C．3y2－x2＝364.已知F1、F2是椭圆的两个焦点，过F1且与椭圆长轴垂直的直线交椭圆于A、B两点，若△ABF2是正三角形，则这个椭圆的离心率是 A.23B.33C.22D.2x2y25.椭圆2?2?1的两个焦点F1,F2三等分它的两条准线间的距离，那么它的离心率abA.B. C． D.336x2y26.已知是直线l被椭圆??1所截得的线段的中点，则l 的方程为369A.x?2y?0B. x?2y?4?0C.x?3y?4?0D. x?2y?8?0x2y27．设F1，F2分别是椭圆2?2?1的左、右焦点，若在其右准线上存在P,ab使线段PF1的中垂线过点F2，则椭圆离心率的取值范围是?A.?0 ?2???B.?01?C.?1?D.? ??x2y28．在椭圆，F为椭圆右焦点，在椭圆上有一点M，使|MP|+2|MF|??1内有一点P43的值最小，则这一最小值是 A．D．457B． 2C．3二、填空题.双曲线3mx2－my2＝3的一个焦点是，则m的值是x2y210.已知方程??1表示椭圆，则k的取值范围是____________.3?k2?kx2y211.设F1、F2是椭圆C：+=1的焦点，在曲线C上满足PF1?PF2=0的点P的个数124为________x2y2?12. 已知椭圆+=1的两个焦点为F1、F2,P为椭圆上一点，满足∠F1PF2=，则△F1PF2433的面积为_________________.13.已知椭圆C的焦点F1和F2，长轴长6，设直线y?x?2交椭圆C于A、B两点，则线段AB的中点坐标 .14. 已知圆A：?x?2??y?16，圆B：?x?2??y?14．动圆C与圆A内切，且222与圆B外切．则动圆圆心的轨迹方程为.三、解答题 x2y215. 求以椭圆＋1的两个顶点为焦点，以椭圆的焦点为顶点的169双曲线方程，并求此双曲线的实轴长、虚轴长、离心率及渐近线方程．16. 从双曲线C:x?y?1上一点Q引直线l:x?y?2的垂线，垂足为N，求线段QN的中点P的轨迹方程.17. 已知动点P与平面上两定点A，对应的准线方程为y??且离心率e为和42时，求直线l的方程.92，4234的等比中项.平分？2求椭圆方程，是否存在直线l与椭圆交于不同的两点M、N，且线段MN恰为直线x??若存在，求出直线l的斜率的取值范围，若不存在，请说明理由.x219. 设F1、F2分别是椭圆?y2?1的左、右焦点.4若P是该椭圆上的一个动点，求PF1?PF2的最大值和最小值;设过定点M的直线l与椭圆交于不同的两点A、B，且∠AOB为锐角，求直线l的斜率k的取值范围.x2y220. 知椭圆2??1的左、右焦点分别为F1、F2，离心ab率e?x?2。

椭圆练习题带答案,知识点总结(基础版)椭圆是平面内与两个定点F1、F2的距离的和等于常数2a （其中2a>F1F2）的点的轨迹。

这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。

当椭圆焦点在x轴上时，标准方程为x^2/a^2+y^2/b^2=1（a>b>0）。

当椭圆焦点在y轴上时，标准方程为x^2/b^2+y^2/a^2=1（a>b>0）。

椭圆的范围为-a≤x≤a，-b≤y≤b。

椭圆有x轴和y轴两条对称轴，对称中心为坐标原点O(0,0)。

椭圆的长轴长为2a，短轴长为2b。

椭圆的顶点坐标为(±a,0)，(0,±b)。

椭圆的焦点坐标为(±c,0)，其中c^2=a^2-b^2.椭圆的离心率为e=c/a（其中0<e<1）。

a、b、c、e的几何意义：a叫做长半轴长；b叫做短半轴长；c叫做半焦距；a、b、c之间满足a^2=b^2+c^2.e叫做椭圆的离心率，e可以刻画椭圆的扁平程度，e越大，椭圆越扁，e 越小，椭圆越圆。

对于椭圆上任一点P和椭圆的一个焦点F，PF_max=a+c，PF_min=a-c。

当点P在短轴端点位置时，∠F1PF2取最大值（余弦定理）。

椭圆方程常用三角换元为x=acosθ，y=bsinθ。

弦长公式为：设直线y=kx+b交椭圆于P1(x1,y1)，P2(x2,y2)，则|P1P2|=√(1+k^2(x1-x2)^2)或|P1P2|=√(1+(y1-y2)^2/k^2)（k≠0）。

判断点P(x,y)是否在椭圆内，当且仅当x^2/a^2+y^2/b^21.若椭圆x^2/a^2+y^2/b^2=1（a>b>0）的离心率为c/a，短轴长为4√2，则它的长轴长为2a=6.1.在椭圆$x^2/a^2+y^2=1$的内部，点$A(a,1)$，则$a$的取值范围是$-2<a<2$。

2.已知椭圆方程$x^2/16+y^2/8=1$，焦点为$F_1,F_2$，点$P$在椭圆上且$\angle F_1PF_2=\pi/3$。

椭圆练习题一.选择题：１.已知椭圆上的一点P ，到椭圆一个焦点的距离为３，则P 到另一焦点距离为（ D ）A ．２B ．３C ．５D ．７２．中心在原点，焦点在横轴上，长轴长为4，短轴长为２，则椭圆方程是（ C ）A. B. C. D. ３.与椭圆9x 2+4y 2=36有相同焦点，且短轴长为4的椭圆方程是( B )A４．椭圆的一个焦点是，那么等于（ A ）A. B.C.D.５．若椭圆短轴上的两顶点与一焦点的连线互相垂直，则离心率等于( B ) A.B.C.D.６．椭圆两焦点为 ， ，P 在椭圆上，若 △的面积的最大值为12，则椭圆方程为（ B ）A.B .C .D . ７．椭圆的两个焦点是F 1(－1, 0), F 2(1, 0)，P 为椭圆上一点，且|F 1F 2|是|PF 1|与|PF 2|的等差中项，则该椭圆方程是（ C ）。

A ＋＝1B ＋＝1C ＋＝1D ＋＝1８.椭圆的两个焦点和中心，将两准线间的距离四等分，则它的焦点与短轴端点连线的夹角为( C )(A)450 (B)600 (C)900 (D)120９．椭圆上的点M 到焦点F 1的距离是2，N 是MF 1的中点，则|ON |为（ A ） A. 4 B . 2 C. 8 D .1162522=+y x 22143x y +=22134x y +=2214x y +=2214y x +=51858014520125201202522222222=+=+=+=+y x D y x C y x B y x 2255x ky -=(0,2)k 1-1512221(4,0)F -2(4,0)F 12PF F 221169x y +=221259x y +=2212516x y +=221254x y +=16x 29y 216x 212y 24x 23y 23x 24y 2221259x y +=2310．已知△ABC 的顶点B 、C 在椭圆x 23＋y 2＝1上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则△ABC 的周长是 ( C )（A ）2 3 （B ）6 （C ）4 3 （D ）12二、填空题：11．方程表示焦点在轴的椭圆时，实数的取值范围_____12．过点且与椭圆有共同的焦点的椭圆的标准方程为_13．设,,△的周长是，则的顶点的轨迹方程为14．如图：从椭圆上一点向轴作垂线，恰好通过椭圆的左焦点，且它的长轴端点及短轴的端点的连线∥，则该椭圆的离心率等于_____________三、解答题：15.已知椭圆的对称轴为坐标轴，离心率，短轴长为，求椭圆的方程。

五年级上册椭圆的面积练习试题及参考答案练题1. 计算下列椭圆的面积：- 长轴长度为6cm，短轴长度为4cm的椭圆。

- 长轴长度为15mm，短轴长度为12mm的椭圆。

- 长轴长度为10m，短轴长度为6m的椭圆。

2. 求下列椭圆面积的一半：- 长轴长度为14cm，短轴长度为10cm的椭圆。

- 长轴长度为8mm，短轴长度为6mm的椭圆。

- 长轴长度为24m，短轴长度为18m的椭圆。

3. 根据提供的信息，计算椭圆的面积：- 长轴长度为16cm，短轴长度为8cm的椭圆的周长为32cm。

- 长轴长度为20mm，周长为50mm的椭圆的短轴长度为10mm。

参考答案1. 椭圆的面积公式为$πab$，其中$a$和$b$分别为椭圆长轴的一半和短轴的一半。

因此，计算面积如下：- 面积为$π×3×2=18π(cm^2)$。

- 面积为$π×15÷2×12÷2=45π(mm^2)$。

- 面积为$π×5×3=15π(m^2)$。

2. 面积一半即为$π×14÷2×10÷2÷2=35π(cm^2)$。

- 面积一半即为$π×8÷2×6÷2÷2=12π(mm^2)$。

- 面积一半即为$π×12÷2×9÷2÷2=27π(m^2)$。

3. 根据椭圆周长公式$2π\sqrt{\dfrac{a^2+b^2}{2}}$，可以求出椭圆长轴的一半和短轴的一半，从而计算出椭圆的面积。

计算如下：- 长轴的一半为$4cm$，短轴的一半为$2cm$，面积为$π×4×2=8π(cm^2)$。

- 短轴的一半为$5mm$，长轴的一半为$15mm-\dfrac{50mm}{2π}=\dfrac{25mm}{π}$，面积为$π×5×\dfrac{25mm}{π}=125mm^2$。

高二椭圆基础练习题及答案练习题1：已知椭圆E的长轴长为6，短轴长为4。

若椭圆E的焦点F到点P 的距离等于点P到长轴的距离与点A到长轴的距离之和，且点A在椭圆E的右半部分上。

求椭圆E的方程。

解答：设椭圆E的焦点坐标为F(a,0)，其中a为焦点到原点的距离。

设点P(x,y)。

根据题意，有：PF = PA + PA'根据椭圆的定义，有：PF = √[(x-a)^2 + y^2]PA = √[(x-a)^2 + (y-4)^2]PA' = √[(x+a)^2 + (y+4)^2]将上述式子代入PF = PA + PA'，整理得：√[(x-a)^2 + y^2] = √[(x-a)^2 + (y-4)^2] + √[(x+a)^2 + (y+4)^2]对上式两边进行平方运算，得：(x-a)^2 + y^2 = [(x-a)^2 + (y-4)^2] + 2√[(x-a)^2 + (y-4)^2]√[(x+a)^2 + (y+4)^2] + (x+a)^2 + (y+4)^2对上式进行整理，得：0 = -8x^2 + 8a^2 - 32a - 64由于长轴长为6，短轴长为4，求平方可得：36 = 4a^2解得a = ±3/2将a = ±3/2 代入上式，得到两个椭圆E的方程：E1：-8x^2 + 18 - 48 = 0，即4x^2 = 15E2：-8x^2 + 18 + 48 = 0，即4x^2 = 33练习题2：已知椭圆E的焦点坐标为F(0,2)，G(0,-2)，长轴长为8。

设直线y = mx + 3与椭圆E相切于点P，求m的值。

解答：设点P(x,y)，则点P在直线y = mx + 3上，故有：y = mx + 3又由于点P位于椭圆E上，满足椭圆的方程，即有：x^2/16 + y^2/4 = 1将y = mx + 3代入上式，得到关于x的二次方程：x^2/16 + (mx + 3)^2/4 = 1化简得：(4+m^2)x^2 + 24mx + 144 - 64 = 0上述方程为判别式为0的二次方程，故有：(24m)^2 - 4(4+m^2)(144 - 64) = 0进行整理得到最终的方程：208m^2 - 256 = 0解得m = ±8/√13练习题3：已知椭圆O的焦点坐标为F1(-4,0)，F2(4,0)，离心率为2/3。

完整版)椭圆经典练习题两套(带答案)A组基础过关1.选择题1.已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于多少？A。

2B。

2/3C。

1/2D。

1/3解析：由题意得2a=2b，所以a=b，又a²=b²+c²，所以b=c，所以a=2c，e=c/a=1/2，答案为C。

2.中心在原点，焦点在x轴上，若长轴长为18，且两个焦点恰好将长轴三等分，则此椭圆的方程是什么？A。

(x²/81)+(y²/72)=1B。

(x²/81)+(y²/9)=1C。

(x²/81)+(y²/45)=1D。

(x²/81)+(y²/36)=1解析：依题意知2a=18，所以a=9，2c=3×2a，所以c=3，所以b=a-c=81-9=72，所以椭圆方程为(x²/81)+(y²/72)=1，答案为A。

3.椭圆x²+4y²=1的离心率是多少？A。

2/3B。

2C。

1/2D。

3解析：先将x²+4y²=1化为标准方程，得(x/1)²+(y/(1/2))²=1，所以a=1，b=1/2，所以c=√(a²-b²)=√(3)/2，所以e=c/a=√(3)/2，答案为A。

2.解答题1.设F₁、F₂分别是椭圆4x²+y²=1的左、右焦点，P是第一象限内该椭圆上的一点，且PF₁⊥PF₂，则点P的横坐标为多少？解析：由题意知，点P即为圆x²+y²=3与椭圆4x²+y²=1在第一象限的交点，解方程组x²+y²=3和4x²+y²=1，得点P的横坐标为√(2/3)，答案为√(2/3)。

2.已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为2，且椭圆G上一点到其两个焦点的距离之和为12，则椭圆G的方程是什么？解析：依题意设椭圆G的方程为a²x²+b²y²=1(a>b>0)，因为椭圆上一点到其两个焦点的距离之和为12，所以2a=12，所以a=6，又因为椭圆的离心率为2，所以c=a/2=3，所以b=√(a²-c²)=3√5，所以椭圆G的方程为36x²+45y²=1，答案为C。

椭圆及其标准方程练习题一、课前练习：1．判断下列各椭圆的焦点位置，并说出焦点坐标、焦距。

（1） （2） （3）2．求适合下列条件的椭圆标准方程：两个焦点的坐标分别为（- 4，0），（4，0），椭圆上一点P 到两焦点距离的和等于10。

3．方程表示焦点在轴的椭圆时，实数m 的取值范围是 。

二、典例：例1：已知椭圆两个焦点的坐标分别是（- 2，0），（2，0），并且经过点（25，- 23），求它的标准方程。

变式练习1：与椭圆x 2+4y 2=16有相同焦点，且过点（5，-6），的椭圆方程是 。

14322=+y x 1422=+y x 1422=+y x 221||12x y m +=-y例2：如图，在圆x 2+y 2=4上任取一点P ，过点P 作x 轴的垂线段PD ，D 为垂足．当点P 在圆上运动时，线段PD 的中点M 的轨迹是什么？例3：如图，设A 、B 的坐标分别为（- 5，0），（5，0），直线AM ，BM 相交于点M ，且它们的斜率之积为 -94，求点M 的轨迹方程。

变式练习2：已知定圆x 2+y 2-6x -55=0，动圆M 和已知圆内切且过点P （-3，0），求圆心M 的轨迹及其方程。

三、巩固练习：1．椭圆的焦距是 ，焦点坐标为 ；若CD 为过左焦点F 1的弦，则△F 2CD 的周长为 。

1．平面内有两定点A 、B 及动点P ，设命题甲是：“|PA|+|PB|是定值”，命题乙是：“点P 的轨迹是以A 、B 为焦点的椭圆”，那么-------------------------------------------------------------------------------------------------（ ）A ．甲是乙成立的充分不必要条件B ．甲是乙成立的必要不充分条件C ．甲是乙成立的充要条件D ．甲是乙成立的非充分非必要条件191622=+y x2．椭圆5x 2 - ky 2=5的一个焦点是（0，2），那么k 等于-------------------------------------------------------（ ）A ．- 1B ．1C ．5D ．- 54．若方程x 2+ky 2=2表示焦点在y 轴上的椭圆，则实数k 的取值范围为-----------------------------------（ ）A ．（0，+∞）B ．（0，2）C ．（1，+∞）D ．（0，1）5．设定点F 1（0，－3）、F 2（0，3），动点P 满足条件，则点P 的轨迹是（ ）A ．椭圆 B ．线段 C ．不存在 D ．椭圆或线段6．椭圆和具有-----------------------------------------------------------------（）A ．相同的离心率B ．相同的焦点C ．相同的顶点D ．相同的长、短轴7．已知：△ABC 的一边长BC =6，周长为16，求顶点A 的轨迹方程。

椭圆练习题一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中有只有一项是符合题目要求的．）1．椭圆的焦距是（）A．2 B ．C ．D ．2．F1、F2是定点，|F1F2|=6，动点M满足|MF1|+|MF2|=6，则点M的轨迹是（）A．椭圆B．直线C．线段D．圆3．若椭圆的两焦点为（－2，0）和（2，0），且椭圆过点，则椭圆方程是（）A ．B ．C ．D ．4．方程暗示焦点在y轴上的椭圆，则k的取值范围是（）A ．B．（0，2）C．（1，+∞）D．（0，1）5．过椭圆的一个焦点的直线与椭圆交于、两点，则、与椭圆的另一焦点构成，那么的周长是（）A ． B． 2 C ． D． 16．已知椭圆的对称轴是坐标轴，离心率为，长轴长为12，则椭圆方程为（）A ．或B ．C ．或????????????????????????????????D ．或??．??已知＜??，则曲线和有（）A．相同的短轴 B．相同的焦点 C．相同的离心率 D．相同的长轴8．椭圆的焦点、，P 为椭圆上的一点，已知，则△的面积为（）A．9 B．12 C．10 D．89．椭圆的焦点为和，点P 在椭圆上，若线段的中点在y 轴上，那么是的（）A．4倍 B．5倍 C．7倍 D．3倍10．椭圆内有一点P（3，2）过点P的弦恰好以P为中点，那么这弦所在直线的方程为（）A ．B ．C ．D．11．椭圆上的点到直线的最大距离是（）A．3 B ．C ．D ．12．过点M（－2，0）的直线M 与椭圆交于P1，P2，线段P1P2的中点为P，设直线M 的斜率为k1（），直线OP的斜率为k2，则k1k2的值为（）A．2 B．－2 C ．D ．－二、填空题：（本大题共4小题，每小题4分，共16分，把答案填在题中横线上．）13．椭圆的离心率为，则．14．设是椭圆上的一点，是椭圆的两个焦点，则的最大值为；最小值为．15．直线y=x －被椭圆x2+4y2=4截得的弦长为．16．已知圆为圆上一点，AQ的垂直平分线交CQ于M，则点M的轨迹方程为．三、解答题：（本大题共6小题，共74分，解答应写出文字说明．证明过程或演算步调．）17．已知三角形的两顶点为，它的周长为,求顶点轨迹方程．18．椭圆的一个顶点为A（2，0），其长轴长是短轴长的2倍，求椭圆的尺度方程．19．点P到定点F（2，0）的距离和它到定直线x=8的距离的比为1：2，求点P的轨迹方程，并指出轨迹是什么图形．20．中心在原点，一焦点为F1（0，5）的椭圆被直线y=3x－2截得的弦的中点横坐标是，求此椭圆的方程．21.已知椭圆的中心在坐标原点O，焦点在坐标轴上，直线y=x+1与椭圆交于P和Q，且OP⊥OQ，|PQ|=，求椭圆方程22．椭圆＞＞与直线交于、两点，且，其中为坐标原点． （1）求的值；（2）若椭圆的离心率满足≤≤，求椭圆长轴的取值范围． 椭圆练习题参考答案 题号1 2 3 4 5 6 7 8 9 10 11 12 答案 A C D D AB D13、3或 14、 4 ， 1 15、16、17、18、解：（1）当A(2,0)为长轴端点时，a=2 , b=1，椭圆的尺度方程为：；（2）当为短轴端点时，，，椭圆的尺度方程为：；19．解：设P （x ，y ），根据题意，|PF|=(x2)2y2 ,d=|x8|,因为|PF|d =12 ,所以 (x2)2y2 |x8| = 12 .化简，得3x2+4y2=48,整理，得x216 +y212=1,所以，点P 的轨迹是椭圆。

椭圆练习题答案1. 题目：已知椭圆的长轴长为2a，短轴长为2b，求椭圆的焦点距离。

答案：椭圆的焦点距离为 \(2c\)，其中 \(c = \sqrt{a^2 -b^2}\)。

2. 题目：若椭圆的方程为 \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)，且 \(a = 5\)，\(b = 3\)，求椭圆的方程。

答案：椭圆的方程为 \(\frac{x^2}{25} + \frac{y^2}{9} = 1\)。

3. 题目：椭圆上一点P(x,y)到焦点F的距离与到长轴端点的距离之比为常数e，求证P点的轨迹是椭圆。

答案：设椭圆的长轴端点为A和B，根据椭圆的定义，点P到焦点F的距离与到长轴端点的距离之比等于离心率e，即\(\frac{|PF|}{|PA|} = e\)。

根据椭圆的性质，可以证明P点的轨迹满足椭圆方程。

4. 题目：已知椭圆的离心率为 \(\frac{1}{2}\)，求椭圆的焦点距离与长轴长度的关系。

答案：已知离心率 \(e = \frac{c}{a} = \frac{1}{2}\)，则焦点距离 \(2c = a\)。

5. 题目：椭圆上一点P(x,y)与原点O(0,0)连线的斜率为\(\frac{y}{x}\)，求点P的轨迹方程。

答案：设点P的坐标为 \((x, y)\)，则 \(\frac{y}{x} = k\)，即 \(y = kx\)。

将 \(y = kx\) 代入椭圆方程 \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)，得到点P的轨迹方程。

6. 题目：椭圆的焦点在x轴上，求椭圆的中心坐标。

答案：椭圆的中心坐标为原点 \((0, 0)\)。

7. 题目：已知椭圆的方程为 \(\frac{x^2}{16} + \frac{y^2}{9} =1\)，求椭圆的面积。

答案：椭圆的面积为 \(A = \pi ab = \pi \times 4 \times 3 =12\pi\)。

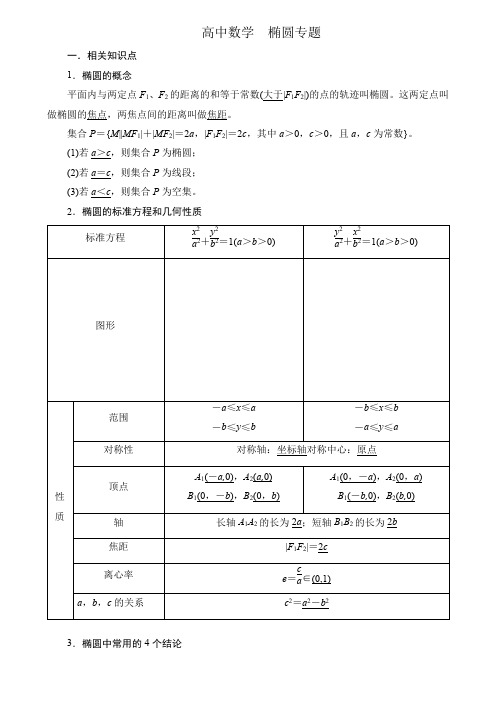
高中数学椭圆专题一．相关知识点1．椭圆的概念平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆。

这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。

集合P＝{M||MF1|＋|MF2|＝2a，|F1F2|＝2c，其中a＞0，c＞0，且a，c为常数}。

(1)若a＞c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a＜c，则集合P为空集。

2．椭圆的标准方程和几何性质3．椭圆中常用的4个结论(1)设椭圆x2a2＋y2b2＝1(a＞b＞0)上任意一点P(x，y)，则当x＝0时，|OP|有最小值b，这时P在短轴端点处；当x＝±a时，|OP|有最大值a，这时P在长轴端点处。

(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形，其中a是斜边长，a2＝b2＋c2。

(3)已知过焦点F1的弦AB，则△ABF2的周长为4a。

(4)若P为椭圆上任一点，F为其焦点，则a－c≤|PF|≤a＋c。

一、细品教材1．(选修1－1P34例1改编)若F1(3,0)，F2(－3,0)，点P到F1，F2距离之和为10，则P点的轨迹方程是()A.x225＋y216＝1 B.x2100＋y29＝1 C.y225＋x216＝1 D.x225＋y216＝1或y225＋x216＝12．(选修1－1P42A组T6改编)设椭圆的两个焦点分别为F1，F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF2为等腰直角三角形，则椭圆的离心率是()A.22 B.2－12C．2－ 2 D.2－1走进教材答案1．A; 2．D 二、双基查验1．设P是椭圆x24＋y29＝1上的点，若F1，F2是椭圆的两个焦点，则|PF1|＋|PF2|等于()A．4B．8 C．6 D．182．方程x25－m＋y2m＋3＝1表示椭圆，则m的范围是()A．(－3,5) B．(－5,3) C．(－3,1)∪(1,5) D．(－5,1)∪(1,3)3．椭圆x 29＋y 24＋k ＝1的离心率为45，则k 的值为( )A ．－21B ．21C ．－1925或21 D.1925或214．已知椭圆的一个焦点为F (1,0)，离心率为12，则椭圆的标准方程为________。

1 / 3 数学选修2-1椭圆练习题及详细答案（含准线练习题）1．若椭圆my 12m 3x 22-+=1的准线平行于y 轴，则m 的取值范围是 。

答案：－3<m <02．椭圆的长半轴是短半轴的3倍，过左焦点倾斜角为30°的弦长为2则此椭圆的标准方程是 。

答案：9x 2＋y 2=13. 椭圆的中心在原点，焦点在x 轴上，若椭圆的一个焦点将长轴分成的两段的比例中项等于椭圆的焦距，又已知直线2x －y －4=0被此椭圆所截得的弦长为354，求此椭圆的方程。

答案：4x 2＋5y 2=24提示：∵椭圆的一个焦点将长轴分成的两段的比例中项等于椭圆的焦距, ∴4c 2=(a ＋c )(a －c ),解得a 2=5c 2, ∴b 2=4c 2, 将4 x 2＋5y 2=m 与2x －y －4=0联立，代入消去y 得24x 2－80x ＋80－m =0, 由弦长公式l =2k 1+|x 1－x 2|得354=5×1840m 3-,解得m =24,∴椭圆的方程是4x 2＋5y 2=24 4．证明：椭圆上任意一点到中心的距离的平方与到两焦点距离的乘积之和为一定值。

|PF1|²=(x - c)² + y²=[a²(x - c)² + a²y²]/a²=[a²x² - 2a²cx + a²c² + a²y²]/a² /***--根据b²x² + a²y² = a²b² ***/=[a²x² - 2a²cx + a²c² + a²b² - b²x²]/a²=[(a²-b²)x² - 2a²cx + a²(b² + c²)]/a²=[c²x² -2a²cx + a^4]/a²=(a² - cx)²/a²∴PF1 = (a² - cx)/a = a - (c/a)x = a - ex同理可证：PF2 = a + ex5. 已知椭圆的对称轴是坐标轴，离心率e =32，长轴长为6，那么椭圆的方程是（ ）。

高三椭圆练习题含答案1. 设椭圆的焦距为f，离心率为e，则第一焦点坐标为(-f,0)，第二焦点坐标为(f,0)。

设椭圆的长轴为2a，短轴为2b，则有等式：f =√(a^2 - b^2) = a * e，其中e为离心率。

2. 设椭圆的焦距为f，离心率为e，离心率定义为e = c / a，其中c为焦点到椭圆中心的距离，a为椭圆的半长轴的长度。

根据定义，椭圆的离心率始终小于1。

3. 椭圆的标准方程为x^2/a^2 + y^2/b^2 = 1，其中a为椭圆的半长轴，b为椭圆的半短轴。

4. 已知椭圆的焦点坐标为(-5, 0)和(5, 0)，离心率为2/3。

求该椭圆的半长轴和半短轴长度。

解答：根据离心率的定义，可知椭圆的焦点到椭圆中心的距离为a * e = 5* 2/3 = 10/3。

由于焦点到椭圆中心距离为a * e，而椭圆的焦点坐标为(-5, 0)和(5, 0)，因此椭圆的中心坐标为(0,0)。

由此可知，半长轴的长度为a = 大于等于5 + 10/3 = 25/3，半短轴的长度为b = √(a^2 - c^2) = √((25/3)^2 - (10/3)^2) = √(625/9 - 100/9) =√(525/9) = √175/3 = √(25 * 7)/3 = 5√7/3。

所以，该椭圆的半长轴长度为25/3，半短轴长度为5√7/3。

5. 已知椭圆的离心率为1/2，焦点坐标为(-3, 0)和(3, 0)。

求该椭圆的长轴与短轴的长度之比。

解答：根据焦点的坐标和离心率的定义，可知椭圆的半长轴的长度为 a = 3 * 2 = 6, 离心率为e = c / a = 1/2，其中c为焦点到椭圆中心的距离。

由此可知，焦点到椭圆中心的距离为c = a * e = 6 * 1/2 = 3。

椭圆的中心即为原点，因此椭圆的标准方程为x^2/36 + y^2/b^2 = 1。

根据焦点到椭圆中心的距离c = 3，可知椭圆的焦点坐标为(-3, 0)和(3, 0)。

椭圆练习题1A 组 基础过关一、选择题(每小题5分，共25分)1．(2012·厦门模拟)已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于 ( )．A.12B.22C. 2D.32解析 由题意得2a ＝22b ⇒a ＝2b ，又a 2＝b 2＋c 2⇒b ＝c ⇒a ＝2c ⇒e ＝22. 答案 B2．(2012·长沙调研)中心在原点，焦点在x 轴上，若长轴长为18，且两个焦点恰好将长轴三等分，则此椭圆的方程是( )． A.x 281＋y 272＝1B.x 281＋y 29＝1C.x 281＋y 245＝1D.x 281＋y 236＝1解析 依题意知：2a ＝18，∴a ＝9,2c ＝13×2a ，∴c ＝3， ∴b 2＝a 2－c 2＝81－9＝72，∴椭圆方程为x 281＋y 272＝1.答案 A3．(2012·长春模拟)椭圆x 2＋4y 2＝1的离心率为( )． A.32 B.34 C.22 D.23解析 先将x 2＋4y 2＝1化为标准方程x 21＋y 214＝1，则a ＝1，b ＝12，c ＝a 2－b 2＝32.离心率e ＝c a ＝32. 答案 A4．(2012·佛山月考)设F 1、F 2分别是椭圆x 24＋y 2＝1的左、右焦点，P 是第一象限内该椭圆上的一点，且PF 1⊥PF 2，则点P 的横坐标为( )． A ．1 B.83 C ．2 2 D.263解析 由题意知，点P 即为圆x 2＋y 2＝3与椭圆x 24＋y 2＝1在第一象限的交点，解方程组⎩⎪⎨⎪⎧x 2＋y 2＝3，x 24＋y 2＝1，得点P 的横坐标为263.答案 D5．(2011·惠州模拟)已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且椭圆G 上一点到其两个焦点的距离之和为12，则椭圆G 的方程为( )． A.x 24＋y 29＝1 B.x 29＋y 24＝1 C.x 236＋y 29＝1 D.x 29＋y 236＝1解析 依题意设椭圆G 的方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，∵椭圆上一点到其两个焦点的距离之和为12， ∴2a ＝12，∴a ＝6， ∵椭圆的离心率为32. ∴a 2－b 2a ＝32， ∴36－b 26＝32.解得b 2＝9，∴椭圆G 的方程为：x 236＋y 29＝1. 答案 C二、填空题(每小题4分，共12分)6．若椭圆x 225＋y 216＝1上一点P 到焦点F 1的距离为6，则点P 到另一个焦点F 2的距离是________．解析 由椭圆的定义可知，|PF 1|＋|PF 2|＝2a ，所以点P 到其另一个焦点F 2的距离为|PF 2|＝2a －|PF 1|＝10－6＝4. 答案 47．(2011·皖南八校联考)已知F 1、F 2是椭圆C 的左、右焦点，点P 在椭圆上，且满足|PF 1|＝2|PF 2|，∠PF 1F 2＝30°，则椭圆的离心率为________． 解析 在三角形PF 1F 2中，由正弦定理得 sin ∠PF 2F 1＝1，即∠PF 2F 1＝π2，设|PF 2|＝1，则|PF 1|＝2，|F 2F 1|＝3， ∴离心率e ＝2c 2a ＝33. 答案 338．(2011·江西)若椭圆x 2a 2＋y 2b 2＝1的焦点在x 轴上，过点⎝ ⎛⎭⎪⎫1，12作圆x 2＋y 2＝1的切线，切点分别为A ，B ，直线AB 恰好经过椭圆的右焦点和上顶点，则椭圆方程是________．解析 由题可设斜率存在的切线的方程为y －12＝k (x －1)(k 为切线的斜率)， 即2k x －2y －2k ＋1＝0， 由|－2k ＋1|4k 2＋4＝1，解得k ＝－34， 所以圆x 2＋y 2＝1的一条切线方程为3x ＋4y －5＝0， 求得切点A ⎝ ⎛⎭⎪⎫35，45，易知另一切点B (1,0)，则直线AB 的方程为y ＝－2x ＋2. 令y ＝0得右焦点为(1,0)，令x ＝0得上顶点为(0,2)．∴a 2＝b 2＋c 2＝5， 故得所求椭圆方程为x 25＋y 24＝1. 答案 x 25＋y 24＝1 三、解答题(共23分)9．(11分)已知点P (3,4)是椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)上的一点，F 1，F 2是椭圆的两焦点，若PF 1⊥PF 2.试求：(1)椭圆的方程；(2)△PF 1F 2的面积． 解 (1)∵P 点在椭圆上， ∴9a 2＋16b 2＝1.① 又PF 1⊥PF 2，∴43＋c ·43－c ＝－1，得：c 2＝25，②又a 2＝b 2＋c 2，③由①②③得a 2＝45，b 2＝20. 椭圆方程为x 245＋y 220＝1.(2)S △PF 1F 2＝12|F 1F 2|×4＝5×4＝20.10．(12分)(2011·陕西)如图，设P 是圆x 2＋y 2＝25上的动点，点D 是P 在x 轴上的投影，M 为PD 上一点，且|MD |＝45|PD |.(1)当P 在圆上运动时，求点M 的轨迹C 的方程； (2)求过点(3,0)且斜率为45的直线被C 所截线段的长度． 解 (1)设M 的坐标为(x ，y )，P 的坐标为(x P ，y P )， 由已知得⎩⎪⎨⎪⎧x P＝x ，y P ＝54y ，∵P 在圆上，∴x 2＋⎝ ⎛⎭⎪⎫54y 2＝25，即C 的方程为x 225＋y 216＝1.(2)过点(3,0)且斜率为45的直线方程为y ＝45(x －3)， 设直线与C 的交点为A (x 1，y 1)，B (x 2，y 2)， 将直线方程y ＝45(x －3)代入C 的方程，得 x 225＋(x －3)225＝1，即x 2－3x －8＝0. ∴x 1＝3－412，x 2＝3＋412.∴线段AB 的长度为|AB |＝(x 1－x 2)2＋(y 1－y 2)2＝⎝ ⎛⎭⎪⎫1＋1625(x 1－x 2)2＝ 4125×41＝415.B 级 提高题一、选择题(每小题5分，共10分)1．(2012·丽水模拟)若P 是以F 1，F 2为焦点的椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)上的一点，且PF 1→·PF 2→＝0，tan ∠PF 1F 2＝12，则此椭圆的离心率为( )． A.53 B.23 C.13 D.12解析 在Rt △PF 1F 2中，设|PF 2|＝1，则|PF 2|＝2.|F 1F 2|＝5，∴e ＝2c 2a ＝53. 答案 A2．(2011·汕头一模)已知椭圆x 24＋y 22＝1上有一点P ，F 1，F 2是椭圆的左、右焦点，若△F 1PF 2为直角三角形，则这样的点P 有( )． A ．3个 B ．4个 C ．6个 D ．8个解析 当∠PF 1F 2为直角时，根据椭圆的对称性知，这样的点P 有2个；同理当∠PF 2F 1为直角时，这样的点P 有2个；当P 点为椭圆的短轴端点时，∠F 1PF 2最大，且为直角，此时这样的点P 有2个．故符合要求的点P 有6个． 答案 C二、填空题(每小题4分，共8分)3．(2011·镇江调研)已知F 1(－c,0)，F 2(c,0)为椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的两个焦点，P 为椭圆上一点且PF 1→·PF 2→＝c 2，则此椭圆离心率的取值范围是________． 解析 设P (x ，y )，则PF 1→·PF 2→＝(－c －x ，－y )· (c －x ，－y )＝x 2－c 2＋y 2＝c 2①将y 2＝b 2－b 2a 2x 2代入①式解得x 2＝(3c 2－a 2)a 2c 2，又x 2∈[0，a 2]，∴2c 2≤a 2≤3c 2，∴e ＝c a ∈⎣⎢⎡⎦⎥⎤33，22.答案 ⎣⎢⎡⎦⎥⎤33，224．(2011·浙江)设F 1，F 2分别为椭圆x 23＋y 2＝1的左，右焦点，点A ，B 在椭圆上，若F 1A →＝5F 2B →，则点A 的坐标是________．解析 根据题意设A 点坐标为(m ，n )，B 点坐标为(c ，d )．F 1、F 2分别为椭圆的左、右焦点，其坐标分别为(－2，0)、(2，0)，可得F 1A →＝(m ＋2，n )，F 2B →＝(c －2，d )，∵F 1A →＝5F 2B →，∴c ＝m ＋625，d ＝n 5.∵点A 、B 都在椭圆上，∴m 23＋n 2＝1，⎝ ⎛⎭⎪⎫m ＋62523＋⎝ ⎛⎭⎪⎫n 52＝1.解得m ＝0，n ＝±1，故点A 坐标为(0，±1)．答案 (0，±1) 三、解答题(共22分)5．(10分)(2011·大连模拟)设A ，B 分别为椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左，右顶点，⎝ ⎛⎭⎪⎫1，32为椭圆上一点，椭圆长半轴的长等于焦距． (1)求椭圆的方程；(2)设P (4，x )(x ≠0)，若直线AP ，BP 分别与椭圆相交异于A ，B 的点M ，N ，求证：∠MBN 为钝角．(1)解 (1)依题意，得a ＝2c ，b 2＝a 2－c 2＝3c 2，设椭圆方程为x 24c 2＋y 23c 2＝1，将⎝ ⎛⎭⎪⎫1，32代入，得c 2＝1，故椭圆方程为x 24＋y 23＝1.(2)证明 由(1)，知A (－2,0)，B (2,0)，设M (x 0，y 0)，则－2＜x 0＜2，y 20＝34(4－x 20)，由P ，A ，M 三点共线，得x ＝6y 0x 0＋2， BM →＝(x 0－2，y 0)，BP →＝⎝ ⎛⎭⎪⎫2，6y 0x 0＋2， BM →·BP →＝2x 0－4＋6y 20x 0＋2＝52(2－x 0)＞0，即∠MBP 为锐角，则∠MBN 为钝角．6．(★)(12分)(2011·西安五校一模)已知中心在原点，焦点在x 轴上的椭圆C 的离心率为12，且经过点M ⎝ ⎛⎭⎪⎫1，32.(1)求椭圆C 的方程；(2)是否存在过点P (2,1)的直线l 1与椭圆C 相交于不同的两点A ，B ，满足P A →·PB →＝PM →2若存在，求出直线l 1的方程；若不存在，请说明理由． 解 (1)设椭圆C 的方程为x 2a 2＋y2b 2＝1(a ＞b ＞0)，由题意得⎩⎪⎨⎪⎧1a 2＋94b 2＝1，c a ＝12，a 2＝b 2＋c 2，解得a 2＝4，b 2＝3.故椭圆C 的方程为x 24＋y 23＝1.(2)假设存在直线l 1且由题意得斜率存在，设满足条件的方程为y ＝k 1(x －2)＋1，代入椭圆C 的方程得，(3＋4k 21)x 2－8k 1(2k 1－1)x ＋16k 21－16k 1－8＝0.因为直线l 1与椭圆C 相交于不同的两点A ，B ，设A ，B 两点的坐标分别为(x 1，y 1)，(x 2，y 2)，所以Δ＝[－8k 1(2k 1－1)]2－4(3＋4k 21)(16k 21－16k 1－8)＝32(6k 1＋3)＞0，所以k 1＞－12.又x 1＋x 2＝8k 1(2k 1－1)3＋4k 21，x 1x 2＝16k 21－16k 1－83＋4k 21， 因为P A →·PB→＝PM →2，即(x 1－2)(x 2－2)＋(y 1－1)(y 2－1)＝54， 所以(x 1－2)·(x 2－2)(1＋k 21)＝|PM |2＝54. 即[x 1x 2－2(x 1＋x 2)＋4](1＋k 21)＝54.所以⎣⎢⎡⎦⎥⎤16k 21－16k 1－83＋4k 21－2·8k 1(2k 1－1)3＋4k 21＋4(1＋k 21)＝4＋4k 213＋4k 21＝54，解得k 1＝±12. 因为k 1＞－12，所以k 1＝12.于是存在直线l 1满足条件，其方程为y ＝12x .【点评】 解决解析几何中的探索性问题的一般步骤为：,第一步：假设结论成立.,第二步：以存在为条件，进行推理求解.,第三步：明确规范结论，若能推出合理结果，经验证成立即可肯定正确.若推出矛盾，即否定假设.,第四步：回顾检验本题若忽略Δ＞0这一隐含条件，结果会造成两解.椭圆练习题2一、填空题1．椭圆63222=+y x 的焦距为______________。

高二数学椭圆专项练习题及参考答案代入e=a/c=a/(a/2)=2，即椭圆的离心率为2。

5. 椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的焦点为$F_1$、$F_2$，$P$是椭圆上的任一点，$M$为$PF_1$的中点，若$PF_1$的长度为$s$，那么$OM$的长度等于$\sqrt{a^2-s^2}$。

1. 在椭圆上，焦点F和弦AB的垂直平分线交于M，AB交x轴于N。

求2. 已知椭圆的对称轴为坐标轴，离心率为2/3，长轴长为6。

求椭圆的方程。

3. 若x²/y² + 1 = 1表示焦点在y轴上的椭圆，则m的值是多少？4. 已知方程25-m/16+m = 1表示椭圆。

求m的值。

5. 椭圆的两焦点将准线间的距离分成三等分。

求该椭圆的离心率。

6. 椭圆x²/4 + y²/9 = 1上一点P到右焦点F₁的距离为b，则P点到左准线的距离是多少？7. 椭圆x²/4 + y²/9 = 1在t ∈ [0, 2π)时，x = sec t，y = ___。

求该椭圆的焦点坐标。

8. 曲线x + (m-1)y - 3my + 2m = 0表示椭圆。

求m的取值。

9. 椭圆432x² + 169y² = 上的一点A到左焦点的距离为多少？10. 椭圆x²/16 + y²/25 = 1上一点P到焦点F₂的距离为b。

求P点到左准线的距离。

11. 方程-3x² + y²sin²(2α + π/2) = 1表示椭圆。

求sin²α的取值。

12. 若λ-6x+5λy-5λλ-6 = 0表示焦点在x轴上的椭圆，则λ的值为多少？13. 椭圆259x² + 432y² = 上的一点到左焦点的距离是到右焦点的距离的4倍。

求该点的坐标。

14. 椭圆中心在原点，焦点在x轴上，两准线的距离为5。

高二数学椭圆练习题答案1. 小题已知椭圆的长轴长度为10，短轴长度为6，求其离心率：解析：椭圆的离心率定义为e=c/a，其中c为焦点到椭圆中心的距离，a为长轴的一半。

根据题意，长轴a=10/2=5，焦距c对应的是长轴的一半，即c=5/2。

代入公式，得到离心率e=(5/2)/5=1/2。

因此，椭圆的离心率为1/2。

2. 小题已知椭圆的离心率为1/4，长轴焦点的坐标为(0, 3)，求椭圆的方程。

解析：由于已知椭圆的离心率为1/4，离心率e=c/a=1/4，其中c为焦点到椭圆中心的距离，a为长轴的一半。

根据焦点的坐标(0, 3)，可知焦距c=3。

代入公式，得到1/4=3/a，解方程可得a=12。

椭圆的方程为x^2/144+y^2/36=1。

3. 小题已知椭圆与x轴的交点为(-6, 0)和(6, 0)，焦点到椭圆上一点的距离为10，求椭圆的方程。

解析：由已知椭圆与x轴的交点可得长轴的一半为6。

焦点到椭圆上一点的距离为10，由于椭圆是关于x轴对称的，焦点坐标可以设为(0, c)和(0, -c)，其中c为焦点到椭圆中心的距离。

根据题意可得c=10/2=5。

根据椭圆定义的离心率e=c/a，解方程可得c=ae，代入已知值可得5=6e，解方程可得e=5/6。

椭圆的方程为x^2/36+y^2/16=1。

4. 小题已知椭圆的焦千差为8，焦点到椭圆的某一点的距离为6，求椭圆的方程。

解析：由焦千差可得2ae=8，焦点到椭圆某一点的距离为6，由于椭圆是关于y轴对称的，焦点坐标可以设为(c, 0)和(-c, 0)，其中c为焦点到椭圆中心的距离。

根据题意可得2a=6/2=3。

代入第一个等式可以求得2e=8/3，即e=4/3。

椭圆的方程为x^2/9+y^2/16=1。

5. 小题已知椭圆长轴与x轴交于点A，焦点到点A和点A到点B的距离之和为6，求椭圆的方程。

解析：由已知条件可得椭圆长轴的一半为3（6/2=3）。

设焦点坐标为(c, 0)和(-c, 0)，点A的坐标为(a, 0)，点B的坐标为(a+2c, 0)。

椭圆练习及参考答案一、单选题(共 50 分)1.椭圆x 29+y28=1的左右焦点为F1，F2，P为椭圆上第一象限内任意一点，F1关于P的对称点为M，关于F2的对称点为N，则ΔMF1N的周长为（）A.8B.10C.16D.22【详解】因为F1关于P的对称点为M，关于F2的对称点为N,所以PF2为△F1MN的中位线,所以MF1+MN=2PF1+2PF2=2(PF1+PF2)=2×2a=12,F1N=2F1F2=4c=4√9−8=4,所以ΔMF1N的周长为12+4=16.【点睛】本题考查了点与点的对称性,椭圆的定义,属于基础题.2.已知定圆C1:(x+5)2+y2=1，C2:(x−5)2+y2=225，动圆C满足与C1外切且与C2内切，则动圆圆心C的轨迹方程为（）A.x 264+y239=1 B.x239+y264=1 C.x2256+y2241=1 D.x2241+y2256=1【详解】解：设动圆圆心C的坐标为(x,y)，半径为r，则|CC1|=r+1,|CC2|=15−r，∴|CC1|+|CC2|=r+1+15−r=16>|C1C2|=10，由椭圆的定义知，点C的轨迹是以C1,C2为焦点的椭圆，则2a=16,a=8,c=5，b2=82−52=39，椭圆的方程为：x264+y239=1【点睛】考查圆与圆的位置关系，考查椭圆的定义，考查学生分析解决问题的能力，中档题．3.设F1、F2是椭圆E：x 2a2+y2b2=1(a>b>0)的左、右焦点，P为直线x=3a2上一点，ΔF2PF1是底角为30∘的等腰三角形，则E的离心率为（）A.12B.23C.34D.45试题分析：如下图所示，ΔF2PF1是底角为30∘的等腰三角形，则有|F1F2|=|PF2|,∠PF1F2=∠F2PF1=30∘所以∠PF2A=60∘,∠F2PA=30∘，所以|PF2|=2|AF2|=2(32a−c)=3a−2c又因为|F1F2|=2c，所以，2c=3a−2c，所以e=ca =34所以答案选C.考点：椭圆的简单几何性质.4.椭圆x 29+y26=1的焦点为F1,F2，点P在椭圆上，若|PF1|=4，则ΔPF1F2的面积为（）A.2√3B.3√2C.√32D.√23【详解】解：∵椭圆x29+y26=1的焦点为F1、F2，点P在椭圆上，|PF1|＝4，∴F1（−√3，0），F2（√3，0），|PF2|＝6﹣4＝2，|F1F2|＝2√3，则△PF1F2是直角三角形，∴△PF1F2的面积为S=12×2×2√3=2√3．【点睛】本题考查椭圆的简单性质，三角形的面积的求法，是基础题，解题时要认真审题，注意椭圆性质的合理运用．5.已知椭圆x 24+y2=1的焦点分别是F1，F2，点M在该椭圆上，如果F1M⃑⃑⃑⃑⃑⃑⃑⃑ ⋅F2M⃑⃑⃑⃑⃑⃑⃑⃑ =0，那么点M到y轴的距离是()A.√2B.2√63C.3√22D.1【详解】设M（x，y），则椭圆x24+y2=1…①，∵椭圆x24+y2=1的焦点分别是F1，F2，∴F1（−√3，0），F2（√3，0）∵F 1M ⃑⃑⃑⃑⃑⃑⃑⃑ ＝(x −√3，y)，F 2M ⃑⃑⃑⃑⃑⃑⃑⃑ ＝(x +√3，y)， F 1M ⃑⃑⃑⃑⃑⃑⃑⃑ ⋅F 2M ⃑⃑⃑⃑⃑⃑⃑⃑ =0，∴x 2+y 2=3…②由①②得x 2=83，x =±2√63， ∴点M 到y 轴的距离为2√63，故选B ．【点睛】本题考查了椭圆的方程及向量运算，属于中档题． 7.已知直线l 与椭圆x 216+y 22=1交于A,B 两点，AB 中点是M (−2,1)，则直线l 的斜率为（ ）A.-4B.-14C.14D.4【详解】设交点坐标A (x 1,y 1),B (x 2,y 2)，则{x 1216+y 122=1x 2216+y 222=1，两式相减得，(x 1+x 2)(x 1−x 2)16+(y 1+y 2)(y 1−y 2)2=0 ，故y 1−y2x 1−x 2=−2(x 1+x 2)16(y 1+y 2)=−2×(−2×2)16×(1×2)=14 ，故选C【点睛】本题考查了直线与椭圆的相交弦问题，一般涉及弦的中点和直线斜率问题时，可采用“点差法”，建立中点坐标与斜率的关系求解.8.如图，在平面直角坐标系xOy 中，F 是椭圆x 2a 2+y 2b 2=1(a >b >0)的右焦点，直线y =b2与椭圆交于B,C 两点，且∠BFC =90°，则该椭圆的离心率为( )A.√63B.2√33C.12D.√22【详解】将y =b2代入椭圆方程得：B (−√32a,b2)，C (√32a,b2)又椭圆焦点F (c,0) ∴BF ⃑⃑⃑⃑⃑ =(c +√32a,−b 2)，CF ⃑⃑⃑⃑⃑ =(c −√32a,−b 2) ∵∠BFC =90∘∴BF ⃑⃑⃑⃑⃑ ⋅CF⃑⃑⃑⃑⃑ =c 2−34a 2+b 24=c 2−34a 2+a 2−c 24=34c 2−12a 2=0∴e 2=c 2a 2=23 ∴e =√63，故选A 【点睛】本题考查椭圆离心率的求解问题，关键是能够利用垂直关系构造出关于a,c 的齐次方程，从而根据e =ca 求得离心率.9.设F 1，F 2分别是椭圆x 225+y 216=1的左、右焦点，P 为椭圆上任一点，点M 的坐标为(6,4)，则|PM |+|PF 1|的最大值为（） A.13B.15C.16D.25【详解】如图所示，由椭圆x 225+y 216=1，可得a =5,b =4,c =√a 2−b 2=3，所以F 1(−3,0),F 2(3,0)，由椭圆的定义可得|PF 1|+|PF 2|=2a =10，所以|PM |+|PF 1|=|PM |+2a −|PF 2|=10+(|PM |−|PF 2|)≤10+|MF 2|=10+√32+42=15,则|PM |+|PF 1|的最大值15．故选B ． 【点睛】本题主要考查了椭圆的定义及标准方程的应用，以及三角形三边大小关系的应用，其中解答中熟练应用椭圆的定义转化是解答的关键，着重考查了推理与运算能力，属于基础题．10.椭圆C ：x 2a 2+y 2b 2=1（a ＞b ＞0）的长轴长、短轴长和焦距成等差数列，若点P 为椭圆C 上的任意一点，且P 在第一象限，O 为坐标原点，F （3，0）为椭圆C 的右焦点，则OP ⃑⃑⃑⃑⃑ •PF ⃑⃑⃑⃑⃑ 的取值范围为（ ） A.(−16,−10)B.(−10,−394)C.(−16,−394]D.(−∞,−394]【详解】因为椭圆C 的长轴长、短轴长和焦距成等差数列 所以2a +2c =4b ，即a +c =2b F(3,0)为椭圆C 的右焦点，所以c=3 在椭圆中，a 2=c 2+b 2所以{a 2=c 2+b 2a +c =2bc =3 ，解方程组得{a =5b =4c =3所以椭圆方程为x 225+y 216=1设P(m,n) (0<m <5)则m 225+n 216=1，则n 2=16−1625m 2 OP ⃑⃑⃑⃑⃑ ⋅PF ⃑⃑⃑⃑⃑ =(m,n )(3−m,−n ) =3m −m 2−n 2=3m −m 2−(16−1625m 2) =−925m 2+3m −16=−925(m −256)2−394因为0<m <5，所以当m =256时，OP ⃑⃑⃑⃑⃑ ⋅PF⃑⃑⃑⃑⃑ 取得最大值为−394当m 趋近于0时，OP ⃑⃑⃑⃑⃑ ⋅PF ⃑⃑⃑⃑⃑ 的值趋近于-16 ，所以OP ⃑⃑⃑⃑⃑ ⋅PF⃑⃑⃑⃑⃑ 的取值范围为(-16,-394] 【点睛】本题考查了椭圆性质的综合应用，向量在解析几何中的用法，属于中档题． 二、填空题(共 25 分) 11.已知椭圆x 24+y 23=1的左、右焦点为F 1，F 2，则椭圆的离心率为_____，过F 2且垂直于长轴的直线与椭圆交于点A ，则|F 1A |＝_____． 【详解】椭圆x 24+y 23=1，可得a ＝2，b =√3，则c ＝1，所以椭圆的离心率为：e =c a =12．过F 2且垂直于长轴的直线与椭圆交于点A ，所以|AF 2|=b 2a=32，由椭圆的定义可知：|F 1A |＝2a ﹣|AF 2|＝4−32=52．故答案为12；52．【点睛】本题考查椭圆的离心率和椭圆的定义，解题时由椭圆标准方程确定出a,b 再计算出c ，可求离心率，而求椭圆上的点到焦点的距离时，可以与椭圆定义联系起来．12.如果椭圆x 2144+y 236=1上一点P 到焦点F 1的距离等于10，那么点P 到另一个焦点F 2的距离是______． 【详解】由椭圆x 2144+y 236=1，可得a =12，由椭圆的定义可知：|PF 1|+|PF 2|=2a =24，因为椭圆x 2144+y 236=1上一点P 到焦点F 1的距离等于10，那么点P 到另一个焦点F 2的距离是：24-10=14．故答案为14．【点睛】本题考查椭圆的简单性质以及椭圆的定义的应用，考查计算能力．属于基础题. 13.已知椭圆中心在原点，一个焦点为F(−2√3,0)，且长轴长是短轴长的2倍.则该椭圆的长轴长为______；其标准方程是________． 【详解】解：已知{a =2b,c =2√3a 2−b 2=c 2∴{b 2=4a 2=162a =8则该椭圆的长轴长为8；其标准方程是x 216+y 24=1．故答案为椭圆的长轴长为8；其标准方程是x 216+y 24=1．【点睛】本题主要考查椭圆的标准方程．属基础题．14.已知P 是椭圆x 210+y 2=1上的一点，F 1,F 2是椭圆的两个焦点，当∠F 1PF 2=2π3时，则ΔPF 1F 2的面积为_____．【详解】设|PF 1|=m ，|PF 2|=n ，则m +n =2a =2√10在ΔPF 1F 2中，由余弦定理得：F 1F 22=m 2+n 2−2mncos∠F 1PF 2即：36=(m +n )2−2mn −2mncos2π3=40−mn ，解得：mn =4∴S ΔPF 1F 2=12mnsin 2π3=√3 【点睛】本题考查焦点三角形面积的求解，关键是能够利用余弦定理构造出关于焦半径之积的方程，属于常考题型.15.已知P 是椭圆E:x 2a 2+y 2b 2=1(a >b >0)上异于点A(−a,0)，B(a,0)的一点，E 的离心率为√32，则直线AP 与BP 的斜率之积为__________．【解析】设P (x 0,y 0)，有x 02a 2+y 02b 2=1，且c a =√32，得b a =12，k AP k BP =y 0x+a ⋅y 0x−a=y 02x 02−a 2=y 02(1−y 02b 2)a 2−a 2=−14．点睛：本题考查椭圆的几何性质．由离心率，得到a,b,c 的比例关系．本题中由题意可知，题目由点P 的位置决定，所以设P (x 0,y 0)，得到斜率关系k AP k BP =y 0x 0+a ⋅y 0x0−a=y 02x02−a 2=y 02(1−y 02b 2)a 2−a 2=−14，为定值．三、解答题(共 34 分)16.已知点A(0,−2)，椭圆E:x 2a2+y2b2=1(a>b>0)的离心率为√22,F是椭圆E的右焦点，直线AF的斜率为2，O为坐标原点．（1）求E的方程；（2）设过点P(0，√3)且斜率为k的直线l与椭圆E交于不同的两M、N，且|MN|=8√27，求k的值.【详解】解：（1）由离心率e=ca =√22，则a=√2c，直线AF的斜率k=0−(−2)c−0=2，则c＝1，a=√2，b2＝a2﹣c2＝1，∴椭圆E的方程为x 22+y2=1；（2）设直线l：y＝kx﹣√3，设M（x1，y1），N（x2，y2），则{y=kx−√3x22+y2=1，整理得：（1+2k2）x2﹣4√3kx+4＝0，△＝（﹣4√3k）2﹣4×4×（1+2k2）＞0，即k2＞1，∴x1+x2=4√3k1+2k2，x1x2=41+2k2，∴|MN|=√1+k2|x1−x2|=√1+k2√(x1+x2)2−4x1x2=4√(1+k2)(k2−1)1+2k2=8√27，即17k4−32k2−57=0,解得：k2=3或−1917（舍去）∴k＝±√3，【点睛】考查直线与椭圆的位置关系，椭圆的求法，弦长的计算，考查转化思想以及计算能力．17.设O为坐标原点，动点M在椭圆E:x 24+y22=1上，过点M作x轴的垂线，垂足为N，点P满足NP⃑⃑⃑⃑⃑⃑ =√2NM⃑⃑⃑⃑⃑⃑⃑ .(1)求点P的轨迹方程；(2)设A(1,0)，在x轴上是否存在一定点B，使|BP|=2|AP|总成立？若存在，求出B点坐标；若不存在，说明理由.【详解】（1）设P(x,y)，M(x1,y1)，则N(x1,0)∵M 在椭圆E 上 ∴x 124+y 122=1…①由NP ⃑⃑⃑⃑⃑⃑ =√2NM ⃑⃑⃑⃑⃑⃑⃑ 知：{x =x 1y =√2y 1 ，即：{x 1=x y 1=√22y ，代入①得：x 2+y 2=4即点P 的轨迹方程为：x 2+y 2=4…② （2）假设存在点B (m,0)满足条件，设P (x,y )由|BP |=2|AP |得：√(x −m )2+y 2=2√(x −1)2+y 2 即：3x 2+3y 2+(2m −8)x =m 2−4此方程与(1)中②表示同一方程，故：{2m −8=0m 2−4=12，解得：m =4∴存在点B (4,0)满足条件【点睛】本题考查椭圆的综合应用问题，涉及到动点轨迹的求解、定点问题的求解等知识；求解定点问题的关键是能够通过假设存在的方式，利用已知中的等量关系建立起关于变量的方程，通过求解方程确定变量的取值，从而得到定点是否存在.18.已知点M (2√33,√33)在椭圆C ：x 2a 2+y 2b 2=1(a >b >0)上，且点M 到C 的左、右焦点的距离之和为2√2.（1）求C 的方程；（2）设O 为坐标原点，若C 的弦AB 的中点在线段OM （不含端点O ，M ）上，求OA ⃑⃑⃑⃑⃑ ⋅OB ⃑⃑⃑⃑⃑ 的取值范围.【详解】（1）由条件知43a 2+13b 2=1，2a =2√2，所以a =√2，b =1， ∴椭圆C 的方程为x 22+y 2=1.（2）设点A 、B 的坐标为A (x 1,y 1)，B (x 2,y 2)，则AB 中点(x 1+x 22,y 1+y 22)在线段OM 上，且k OM =12，∴x 1+x 2=2(y 1+y 2)，又x 122+y 12=1，x 222+y 22=1，两式相减得(x 1−x 2)(x 1+x 2)2+(y 1−y 2)(y 1+y 2)=0，易知x 1−x 2≠0，y 1+y 2≠0，所以y 1−y 2x 1−x 2=−x 1+x22(y 1+y 2)=−1，即k AB =−1. 设AB 方程为y =−x +m ，代入x 22+y 2=1并整理得3x 2−4mx +2m 2−2=0.由Δ=8(3−m 2)>0解得m 2<3，又由x 1+x 22=2m 3∈√3)，∴0<m <√3.由韦达定理得x 1+x 2=4m 3，x 1x 2=2(m 2−1)3，故OA ⃑⃑⃑⃑⃑ ⋅OB ⃑⃑⃑⃑⃑ =x 1x 2+y 1y 2=x 1x 2+(−x 1+m )(−x 2+m ) =2x 1x 2−m (x 1+x 2)+m 2=4(m 2−1)3−4m 23+m 2 =m 2−43.而0<m <√3，所以OA ⃑⃑⃑⃑⃑ ⋅OB⃑⃑⃑⃑⃑ 的取值范围是(−43,53). 【点睛】本小题主要考查椭圆的定义和标准方程，考查直线和椭圆的位置关系，考查点差法，考查向量数量积的坐标运算，考查运算求解能力，属于中档题.19.已知Q 为圆x 2+y 2=1上一动点，Q 在x 轴，y 轴上的射影分别为点A ，B ，动点P 满足BA ⃑⃑⃑⃑⃑ =AP ⃑⃑⃑⃑⃑ ，记动点P 的轨迹为曲线C . （1）求曲线C 的方程；（2）过点(0,−35)的直线与曲线C 交于M ，N 两点，判断以MN 为直径的圆是否过定点？求出定点的坐标；若不是，请说明理由.【详解】（1）设Q(x 0,y 0)，P (x,y)，则x 02+y 02=1，由BA ⃑⃑⃑⃑⃑ =AP ⃑⃑⃑⃑⃑ ，可得{x 0=x2y 0=−y，代入x 02+y 02=1，得x 24+y 2=1，故曲线C 的方程为x 24+y 2=1； （2）假设存在满足条件的定点，由对称性可知该定点必在y 轴上，设定点为H(0,m)， 当直线l 的斜率存在时，设直线l 的方程为y =kx −35，联立{y =kx −35x 24+y 2=1得(1+4k 2)x 2−245kx −6425=0，设M(x 1,y 1)，N(x 2,y 2)，则x 1+x 2=24k5(1+4k 2)，x 1x 2=−6425(1+4k 2)，所以y 1+y 2=k(x 1+x 2)−65=−65(1+4k 2)，y 1y 2=(kx 1−35)(kx 2−35)=k 2x 1x 2−35k(x 1+x 2)+925=9−100k 225(1+4k 2)， 因为HM ⃑⃑⃑⃑⃑⃑⃑ =(x 1,y 1−m)，HN ⃑⃑⃑⃑⃑⃑ =(x 2,y 2−m)，所以HM ⃑⃑⃑⃑⃑⃑⃑ ⋅HN ⃑⃑⃑⃑⃑⃑ =x 1x 2+y 1y 2−m(y 1+y 2)+m 2=100(m 2−1)k 2+25m 2+30m−5525(1+4k 2)=0，对任意的k 恒成立，所以{100(m 2−1)=025m 2+30m −55=0 ，解得m =1，即定点为H(0,1)， 当直线l 的斜率不存在时，以MN 为直径的圆也过点(0,1)， 故以MN 为直径的圆过定点(0,1).【点睛】本题主要考查椭圆的标准方程的求解、及直线与圆锥曲线的位置关系的应用问题,解答此类题目，通常联立直线方程与椭圆（圆锥曲线）方程的方程组，应用一元二次方程根与系数的关系进行求解，此类问题易错点是复杂式子的变形能力不足，导致错解，能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等．20.已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的离心率为√22，直线bx −y +√2a =0经过椭圆C 的左焦点. （1）求椭圆C 的标准方程；（2）若直线bx −y +4=0与y 轴交于点P ，A 、B 是椭圆C 上的两个动点，且它们在y 轴的两侧，∠APB的平分线在y 轴上，|PA |≠|PB ||，则直线AB 是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由.【详解】（1）在直线方程bx −y +√2a =0中令y =0，则x =−√2ab ，故c =√2ab ，又c a=√22，故b =2，所以a =4，所以椭圆标准方程为：x 28+y 24=1.（2）因为A 、B 在在y 轴的两侧，故AB 的斜率必存在， 设AB 的方程为y =kx +b ，A (x 1,y 1)，B (x 2,y 2)， 因为P 在y 轴上且P 在直线2x −y +4=0，故P (0,4). 因为∠APB 的平分线在y 轴上，所以y 1−4x 1+y 2−4x 2=0，而y 1=kx 1+b,y 2=kx 2+b ，代入整理得到：2kx 1x 2+(b −4)(x 1+x 2)=0. 由{y =kx +b x 2+2y 2=8可得(1+2k 2)x 2+4kbx +2b 2−8=0，所以x1+x2=−4kb1+2k2,x1x2=2b2−81+2k2，所以2k×2b 2−81+2k2+(b−4)(−4kb1+2k2)=0，化简得到k(b−1)=0，所以对任意的k，总有b=1，故直线AB过定点(0,1).【点睛】求椭圆的标准方程，关键是基本量的确定，方法有待定系数法、定义法等. 直线与圆锥曲线的位置关系中的定点、定值、最值问题，一般可通过联立方程组并消元得到关于x或y的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系中含有x1x2,x1+x2或y1y2,y1+y2，最后利用韦达定理把关系式转化为若干变量的方程（或函数），从而可求定点、定值、最值问题.21.已知椭圆的离心率为√32，椭圆C的长轴长为4．（1）求椭圆C的方程；（2）已知直线与椭圆C交于A，B两点，是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O？若存在，求出k的值；若不存在，请说明理由试题解析：（1）设椭圆的焦半距为c，则由题设，得{a=2ca=√32，解得{a=2c=√3，………2分所以b2=a2−c2=4−3=1，故所求椭圆C的方程为．…………..4分（2）存在实数k使得以线段AB为直径的圆恰好经过坐标原点O．理由如下：设点A(x1,y1)，B(x2,y2)，将直线l的方程代入，并整理，得．（*）………………………………….6分则，．………………………………………8分因为以线段AB 为直径的圆恰好经过坐标原点O ，所以OA ⃑⃑⃑⃑⃑ ⋅OB ⃑⃑⃑⃑⃑ =0，即．又,于是，…………….10分解得k =±√112，………………………………..11分经检验知：此时（*）式的Δ＞0，符合题意．所以当k =±√112时，以线段AB 为直径的圆恰好经过坐标原点O ．………………12分考点：直线与圆锥曲线的综合问题；椭圆的标准方程22.设曲线E 是焦点在x 轴上的椭圆，两个焦点分别是是F 1，F 2，且|F 1F 2|=2，M 是曲线上的任意一点，且点M 到两个焦点距离之和为4.（1）求E 的标准方程；（2）设E 的左顶点为D ，若直线l ：y =kx +m 与曲线E 交于两点A ，B （A ，B 不是左右顶点），且满足|DA ⃑⃑⃑⃑⃑ +DB ⃑⃑⃑⃑⃑⃑ |=|DA ⃑⃑⃑⃑⃑ −DB⃑⃑⃑⃑⃑⃑ |，求证：直线l 恒过定点，并求出该定点的坐标. 【详解】（1）设椭圆方程为x 2a 2+y 2b 2=1(a >b >0)， 由题意{2a =42c =2 ，即{a =2c =1，∴b =√a 2−c 2=√3， ∴椭圆E 的方程是x 24+y 23=1.（2）由（1）可知D (−2,0)，设A (x 1,y 1)，B (x 2,y 2)，联立{y =kx +m x 24+y 23=1 ，得(3+4k 2)x 2+8mkx +4(m 2−3)=0，Δ=(8mk)2−4(3+4k 2)(4m 2−12)=16(12k 2−3m 2+9)>0，即3+4k 2−m 2>0，∴x 1+x 2=−8mk 3+4k 2，x 1x 2=4(m 2−3)3+4k 2，又y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+mk (x 1+x 2)+m 2 =3m 2−12k 23+4k 2，∵|DA ⃑⃑⃑⃑⃑ +DB ⃑⃑⃑⃑⃑⃑ |=|DA ⃑⃑⃑⃑⃑ −DB ⃑⃑⃑⃑⃑⃑ |，∴DA ⃑⃑⃑⃑⃑ ⊥DB ⃑⃑⃑⃑⃑⃑ ，即DA ⃑⃑⃑⃑⃑ ⋅DB⃑⃑⃑⃑⃑⃑ =0， 即(x 1+2,y 1)⋅(x 2+2,y 2)=x 1x 2+2(x 1+x 2)+4+y 1y 2=0， ∴4m 2−123+4k 2+2×−8mk 3+4k 2+4+3m 2−12k 23+4k 2=0，∴7m 2−16mk +4k 2=0， 解得m 1=2k ，m 2=27k ，且均满足即3+4k 2−m 2>0，当m 1=2k 时，l 的方程为y =kx +2k =k (x +2)，直线恒过(−2,0)，与已知矛盾；当m 2=27k ，l 的方程为y =kx +27k =k (x +27)，直线恒过(−27,0).【点睛】考查求椭圆的标准方程，直线与椭圆相交问题、椭圆中直线过定点问题．对直线与椭圆相交问题，一般设交点为A (x 1,y 1)，B (x 2,y 2)，由直线方程与椭圆方程联立消元用韦达定理得x 1+x 2,x 1x 2，再把这个结论代入题中另一条件可得参数k,m 的关系，求得定点．23.已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,M 为椭圆上一动点，当ΔMF 1F 2的面积最大时，其内切圆半径为b 3，设过点F 2的直线l 被椭圆C 截得线段RS ,当l ⊥x 轴时，|RS |=3.（1）求椭圆C 的标准方程；（2）若点A 为椭圆C 的左顶点，P,Q 是椭圆上异于左、右顶点的两点，设直线AP,AQ 的斜率分别为k 1,k 2，若k 1k 2=−14，试问直线PQ 是否过定点？若过定点，求该定点的坐标；若不过定点，请说明理由.【详解】解：（1）由题意及三角形内切圆的性质可得12⋅2c ⋅b =12(2a +2c)⋅b 3，得c a =12① 将x =c 代入x 2a 2+y 2b 2=1，结合a 2=b 2+c 2②，得y =±b 2a ，所以2b 2a =3③，由①②③得a =2,b =√3故椭圆C 的标准方程为x 24+y 23=1（2）设点P,Q 的坐标分别为（x 1,y 1），（x 2,y 2）.①当直线PQ 的斜率不存在时，由题意得P （1，32），Q （1，−32）或P （1，−32），Q （1，32）， 直线PQ 的方程为x =1②当直线PQ的斜率存在时，设直线PQ的方程为y=kx+m，联立得{x24+y23=1y=kx+m，消去y得（4k2+3）x2+8kmx+4m2−12=0，由Δ=64k2m2−4(4k2+3)(4m2−12)=48(4k2−m2+3)>0，得4k2+3>m2x1+x2=−8km4k2+3,x1x2=4m2−124k2+3.(1)）由k1k2=y1y2(x1+2)(x2+2)=−14,可得4y1y2+(x1+2)(x2+2)=0，得4(kx1+m)(kx2+m)+(x1+2)(x2+2)=0，整理得(4k2+1)x1x2+(4km+2)(x1+x2)+4m2+4=0,(2)由（1）和（2）得m2−km−2k2=0，解得m=2k或m=−k当m=2k时，直线PQ的方程为y=kx+2k，过定点(−2,0)，不合题意；当m=−k时，直线PQ的方程为y=kx−k，过定点(1,0)，综上直线PQ过定点，定点坐标为(1,0).【点睛】本题考查求椭圆的标准方程，直线与椭圆的综合问题以及直线过定点问题，属于综合题．。

高二数学椭圆专项练习题及参考答案训练指要熟练掌握椭圆的定义、标准方程、几何性质；会用待定系数法求椭圆方程. 一、选择题1.椭圆中心在坐标原点，对称轴为坐标轴，离心率为0.6，长、短轴之和为36，则椭圆方程为A.16410022=+y xB.11006422=+y x C.1100641641002222=+=+y x y x 或 D.110818102222=+=+y x y x 或 2.若方程x 2＋ky 2＝2，表示焦点在y 轴上的椭圆，那么实数k 的取值范围是 A.(0，＋∞) B.(0，2) C.(1，＋∞) D.(0，1)3.已知圆x 2＋y 2＝4，又Q (3，0)，P 为圆上任一点，则PQ 的中垂线与OP 之交点M 轨迹为(O 为原点) A.直线 B.圆 C.椭圆 D.双曲线二、填空题4.设椭圆1204522=+y x 的两个焦点为F 1、F 2，P 为椭圆上一点，且PF 1⊥PF 2，则||PF 1|－|PF 2||＝_________.5.(2002年全国高考题)椭圆5x 2+ky 2=5的一个焦点是(0，2)，那么k =_________. 三、解答题6.椭圆2222by a x +=1(a ＞b ＞0),B (0,b )、B ′(0,-b ),A (a ,0),F 为椭圆的右焦点，若直线AB ⊥B ′F ,求椭圆的离心率.7.在面积为1的△PMN 中，tan M =21,tan N =-2，建立适当的坐标系，求以M 、N 为焦点且过点P 的椭圆方程.8.如图，从椭圆2222by a x +＝1(a ＞b ＞0)上一点M 向x 轴作垂线，恰好通过椭圆的左焦点F 1，且它的长轴端点A 及短轴的端点B 的连线AB ∥OM .(1)求椭圆的离心率e ；(2)设Q 是椭圆上任意一点，F 2是右焦点，求∠F 1QF 2的取值范围；(3)设Q 是椭圆上一点，当QF 2⊥AB 时，延长QF 2与椭圆交于另一点P ，若△F 1PQ 的面积为203，求此时椭圆的方程.参考答案一、1.C 2.D 3.C 二、4.25,40||||100)2(||||562|||:|212222121=⋅⇒⎪⎭⎪⎬⎫==+==+PF PF c PF PF a PF PF 提示 ∴(|PF 1|－|PF 2|)2=100－2×40=20. ||PF 1|－|PF 2||=25. 5.1 三、6.215- 7.以MN 所在直线为x 轴，线段MN 的中垂线为y 轴建立坐标系，可得椭圆方程为.1315422=+y x 8.(1)22 (2)［0,2π］ (3)1255022=+y x 提示：(1)∵MF 1⊥x 轴，∴x M =－c ,代入椭圆方程求得y M =ab 2,∴k OM =－,,2ab k ac b AB -= ∵OM ∥AB ,∴－c b abac b =⇒-=2 从而e =22. (2)设|QF 1|=r 1,|QF 2|=r 2,∠F 1QF 2=θ,则r 1+r 2=2a ,|F 1F 2|=2c.由余弦定理,得cos θ=212222124r r c r r -+1242)(21221221221-=--+=r r a r r c r r r r≥,01)2(2212=-+r r a 当且仅当r 1=r 2时，上式取等号. ∴0≤cos θ≤1,θ∈［0,2π］. (3)椭圆方程可化为122222=+cy c x ,又PQ ⊥AB ，∴k PQ =－.21==bak ABPQ :y =2(x －c )代入椭圆方程，得5x 2－8cx +2c 2=0.求得|PQ |=,526c F 1到PQ 的距离为d =,362c ∴.25320||2121=⇒=⋅=∆c d PQ S PQ F ∴椭圆方程为.1255022=+y x椭圆训练题：1. 椭圆19822=++y m x 的离心率21=e ，则m=__________ 2. 椭圆4x 2+2y 2=1的准线方程是_______________3. 已知F 1、F 2为椭圆192522=+y x 的两个焦点，A 、B 为过F 1的直线与椭圆的两个交点，则△ABF 2的周长是____________4. 椭圆12222=+by a x ()0>>b a 上有一点P 到其右焦点的距离是长轴两端点到右焦点的距离的等差中项，则P 点的坐标是_______________5. 椭圆12222=+by a x 焦点为F 1、F 2，P 是椭圆上的任一点，M 为P F 1的中点，若P F 1的长为s ，那么OM 的长等于____________6. 过椭圆1273622=+y x 的一个焦点F 作与椭圆轴不垂直的弦AB ，AB 的垂直平分线交AB 于M ，交x 轴于N ，则FN ：AB =___________ 7. 已知椭圆的对称轴是坐标轴，离心率32=e ，长轴长是6，则椭圆的方程是____________ 8. 方程1162522=++-my m x 表示焦点在y 轴上的椭圆，则m 的值是______________ 9. 椭圆的两焦点把准线间的距离三等分，则这椭圆的离心率是______________10. 椭圆142222=+by b x 上一点P 到右焦点F 2的距离为b ，则P 点到左准线的距离是_______11. 椭圆⎪⎭⎫⎝⎛∈=+2,4,1csc sec 2222ππt t y t x ，这个椭圆的焦点坐标是__________ 12. 曲线()023122=+--+m my y m x 表示椭圆，那么m 的取值是______________13. 椭圆13422=+y x 上的一点()11,y x A ，A 点到左焦点的距离为25，则x 1=___________ 14. 椭圆()()19216122=-+-y x 的两个焦点坐标是______________15. 椭圆中心在原点，焦点在x 轴上，两准线的距离是5518，焦距为52，其方程为______ 16. 椭圆上一点P 与两个焦点F 1、F 2所成的PF 1F 2中，βα=∠=∠1221,F PF F PF ，则它的离心率e=__________17. 方程142sin 322=⎪⎭⎫ ⎝⎛+-παy x 表示椭圆，则的取值是______________18. 若()()065562222=--+-λλλλy x 表示焦点在x 轴上的椭圆，则的值是________19. 椭圆192522=+y x 上不同的三点()()2211,,59,4,,y x C B y x A ⎪⎭⎫⎝⎛与焦点()0,4F 的距离成等差数列，则=+21x x ____________20. P 是椭圆192522=+y x 上一点，它到左焦点的距离是它到右焦点的距离的4倍，则P 点的坐标是_______________21. 中心在原点，对称轴在坐标轴上，长轴为短轴的2倍，且过()6,2-的椭圆方程是______ 22. 在面积为1的△PMN 中，2tan ,21tan -==N M ，那么以M 、N 为焦点且过P 的椭圆方程是_____________23. 已知△ABC ，()()0,3,0,3-B A 且三边AC 、AB 、BC 的长成等差数列，则顶点C 的轨迹方程是_________24. 椭圆1422=+y m x 的焦距为2，则m 的值是__________ 25. 椭圆14922=+y x 的焦点到准线的距离是____________ 26. 椭圆()112222=-+m y m x 的准线平行于x 轴，则m 的值是__________ 27. 中心在原点，准线方程为4±=x ，离心率为21的椭圆方程是_______ 28. 椭圆的焦距等于长轴长与短轴长的比例中顶，则离心率等于___________29. 中心在原点，一焦点为()50,01F 的椭圆被直线23-=x y 截得的弦的中点横坐标为21，则此椭圆方程是_________ 30. 椭圆的中心为()0,0，对称轴是坐标轴，短轴的一个端点与两个焦点构成面积为12的三角形，两准线间的距离是225，则此椭圆方程是_____________ 31. 过点()2,3-且与椭圆369422=+y x 有相同焦点的椭圆方程是____________32. 将椭圆192522=+y x 绕其左焦点逆时针方向旋转90︒，所得椭圆方程是_______ 33. 椭圆192522=+y x 上一点M 到右准线的距离是7.5，那么M 点右焦半径是______ 34. AB 是椭圆14322=+y x 的长轴，F 1是一个焦点，过AB 的每一个十等分点作AB 的垂线，交椭圆同一侧于点P 1，P 2，P 3，，P 9，则11912111BF F P F P F P AF ++⋅⋅⋅+++的值是________35. 中心在原点，一焦点为F （0，1），长短轴长度比为t ，则此椭圆方程是__________ 36. 若方程222x ky +=表示焦点在y 轴的椭圆，则k 的取值是__________37. 椭圆221123x y +=的焦点为F 1、F 2，点P 为椭圆上一点，若线段PF 1的中点在y 轴上，那么1PF ：2PF =___________ 38. 经过()()123,2,23,1M M --两点的椭圆方程是_____________39. 以椭圆的右焦点F 2（F 1为左焦点）为圆心作一圆，使此圆过椭圆中心并交椭圆于M 、N ，若直线MF 1是圆F 2的切线，则椭圆的离心率是___________40. 椭圆的两个焦点F 1、F 2及中心O 将两准线间的距离四等分，则一焦点与短轴两个端点连线的夹角是__________41. 点A (),0a 到椭圆2212x y +=上的点之间的最短距离是___________ 42. 椭圆2214x y +=与圆()2221x y r -+=有公共点，则r 的取值是________ 43. 若k R ∈，直线1y kx =+与椭圆2215x y m+=总有公共点，则m 的值是___________ 44. 设P 是椭圆上一点，两个焦点F 1、F 2，如果00211275,15PF F PF F ∠=∠=，则离心率等于__________45. P 是椭圆22143x y +=上任一点，两个焦点F 1、F 2，那么12F PF ∠的最大值是_______ 46. 椭圆2244x y +=长轴上一个顶点为A ，以A 为直角顶点作一个内接于椭圆的等腰直角三角形，则此直角三角形的面积是__________47. 椭圆长轴长为6，焦距42，过焦点F 1作一倾角为的直线交椭圆于M 、N 两点，当MN 等于短轴长时，的值是_______48. 设椭圆22143x y +=的长轴两端点A 、B ，点P 在椭圆上，那么直线PA 与PB 的斜率之积是__________49. 倾斜角为4π的直线与椭圆2214x y +=交于A 、B 两点，则线段AB 的中点M 的轨迹方程是______________50. 已知点A （0，1）是椭圆上的一点，P 是椭圆上任一点，当弦长AP 取最大值时，点P的坐标是_____________1. 544-或 2. 1y =± 3. 20 4. ()()0,0,b b -或 5. 2sa - 6. 1:4 7. 2222119559x y x y +=+=或 8.9252m <<9.10.11. (0, 12. ()1,+∞ 13. 114. ()()1,115.22194x y+= 16. cos2cos2αβαβ+- 17.()37,,88k k k Z ππππ⎛⎫++∈⎪⎝⎭18.)19. 820. 1515,44⎛⎛ ⎝⎭⎝⎭或21.222211148371352x y x y +=+=或 22. 2241153x y += 23. 2213627x y += 24. 53或25. 26. 102m m <≠且 27. 22143x y +=28. 29.2212575x y += 30. 222211259925x y x y +=+=或 31.2211510x y += 32. ()()22441925x y +-+= 33. 634. 2035.222221111x y t t t +=-- 36. ()0,1 37. 7 38. 221155x y +=39.1 40.2π41. a a +42. 3⎤⎥⎣⎦ 43. m ≥1且m ≠544.3 45. 60︒ 46. 162547. 566ππ或 48. 34-49. 1,4y x x ⎛⎫⎛=-∈ ⎪⎝⎝⎭50. 133⎛⎫±- ⎪ ⎪⎝⎭一、选择题：本大题共12小题，每小题5分，共60分．请将唯一正确结论的代号填入题后的括号内．1．椭圆3m 2y mx 222++＝１的准线平行于x 轴，则实数m 的取值范围是 （ ）A ．－１＜m ＜３B ．－23＜m ＜3且m ≠0C ．－１＜m ＜３且m ≠0D ．m ＜－1且m ≠02． a 、b 、c 、p 分别表示椭圆的半长轴、半短轴、半焦距、焦点到相应准线的距离，则它们的关系是 （ ）A ．p=22a bB ．p=ba 2C ．p=ca 2D ．p=cb 23．短轴长为5，离心率为32的椭圆的两个焦点分别为F 1、F 2，过F 1作直线交椭圆于A 、B两点，则ΔABF 2的周长为 （ ）A ．24B ．12C ．6D ．34．下列命题是真命题的是（ ）A ．到两定点距离之和为常数的点的轨迹是椭圆B ．到定直线x=ca 2和定F(c ，0)的距离之比为ac 的点的轨迹是椭圆C ．到定点F(-c ，0)和定直线x=-ca 2的距离之比为ac(a>c>0)的点的轨迹 是左半个椭圆D ．到定直线x=ca 2和定点F(c ，0)的距离之比为ca (a>c>0)的点的轨迹是椭圆5．P 是椭圆4x 2+3y 2=1上任意一点，F 1、F 2是焦点，那么∠F 1PF 2的最大值是（ ）A ．600B ．300C ．1200D ．906．椭圆22b 4x +22b y =1上一点P 到右准线的距离是23b ，则该点到椭圆左焦点的距离是（ ）A ．bB ．23b C ．3b D ．2b 7．椭圆12x 2+3y 2=1的焦点为F 1和F 2，点P 在椭圆上，如果线段F 1P 的中点在y 轴上，那么|PF 1|是|PF 2|的 （ ）A ．7倍B ．5倍C ．4倍D ．3倍8．设椭圆22a x +22b y =1(a>b>0)的两个焦点是F 1和F 2，长轴是A 1A 2，P 是椭圆上异于A 1、A 2的点，考虑如下四个命题：①|PF 1|-|A 1F 1|=|A 1F 2|-|PF 2|； ②a-c<|PF 1|<a+c ； ③若b 越接近于a ，则离心率越接近于1； ④直线PA 1与PA 2的斜率之积等于-22a b ．其中正确的命题是 （ ）A ．①②④B ．①②③C ．②③④D ．①④9．过点Ｍ（－２，０）的直线l 与椭圆x 2＋2y 2＝2交于Ｐ１、Ｐ２两点，线段Ｐ１Ｐ２的中点为Ｐ，设直线l 的斜率为k 1（k 1≠0），直线ＯＰ的斜率为k 2，则k 1k 2的值为 （ ） A ．２B ．－２C ．21D ．－2110．已知椭圆22a x +22by =1(a>b>0)的两顶点A(a ，0)、B(0，b)，右焦点为F ，且F 到直线AB的距离等于F 到原点的距离，则椭圆的离心率e 满足 （ ）A ．0<e<22B ．22<e<1C ． 0<e<2-1D ．2-1<e<111．设Ｆ１、Ｆ２是椭圆2222b y ax +＝１（a ＞b ＞0）的两个焦点，以Ｆ１为圆心，且过椭圆中心的圆与椭圆的一个交点为Ｍ，若直线Ｆ２Ｍ与圆Ｆ１相切，则该椭圆的离心率是（ ）A ．２－3B ．3－１C ．23 D ．2212．在椭圆4x 2+3y 2=1内有一点P （1，-1），F 为椭圆右焦点，在椭圆上有一点M ，使|MP|+2|MF|的值最小，则这一最小值是` （ ）A ．25B ．27 C ．3D ．4二、填空题：本大题共4小题，每小题4分，共16分．请将最简结果填入题中的横线上． 13．椭圆3x 2+ky 2=1的离心率是2x 2-11x+5=0的根，则k= ．14．如图，∠ＯＦＢ＝6π，ＳΔＡＢＦ＝２－3，则以ＯＡ为长半轴，ＯＢ 为短半轴，Ｆ为一个焦点的椭圆的标准方程为 ．15．过椭圆3y 2x 22+＝１的下焦点，且与圆x 2＋y 2－3x ＋y ＋23＝0相切的直线的斜率是 ． 16．过椭圆9x 2+5y 2=1的左焦点作一条长为12的弦AB ，将椭圆绕其左准线旋转一周，则弦AB 扫过的面积为 ．三、解答题：本大题共6小题，共74分．解答题应写出必要的计算步骤或推理过程． 17．（本小题满分12分）已知A 、B 为椭圆22a x +22a 9y 25=1上两点，F 2为椭圆的右焦点，若|AF 2|+|BF 2|=58a ，AB 中点到椭圆左准线的距离为23，求该椭圆方程．18．（本小题满分12分）设中心在原点，焦点在x 轴上的椭圆的离心率为23，并且椭圆与圆x 2+y 2-4x-2y+25=0交于A 、B 两点，若线段AB 的长等于圆的直径． （1） 求直线AB 的方程； （2） 求椭圆的方程． 19．（本小题满分12分）已知9x 2+5y 2=1的焦点F 1、F 2，在直线l ：x+y-6=0上找一点M ，求以F 1、F 2为焦点，通过点M 且长轴最短的椭圆方程．20．（本小题满分12分）一条变动的直线l 与椭圆4x 2+2y 2=1交于P 、Q 两点，M 是l 上的动点，满足关系|MP|·|MQ|=2．若直线l 在变动过程中始终保持其斜率等于1．求动点M 的轨迹方程，并说明曲线的形状．21．（本小题满分12分）设椭圆22a x +22by =1的两焦点为F 1、F 2，长轴两端点为A 1、A 2．（1） P 是椭圆上一点，且∠F 1PF 2=600，求ΔF 1PF 2的面积；（2） 若椭圆上存在一点Q ，使∠A 1QA 2=1200，求椭圆离心率e 的取值范围．22．（本小题满分14分）已知椭圆的一个顶点为Ａ（０，－１），焦点在x 轴上，若右焦点到直线x －y ＋22＝0的距离为３． （1）求椭圆的方程；（2）设椭圆与直线y ＝kx ＋m （k ≠0）相交于不同的两点Ｍ、Ｎ，当｜ＡＭ｜＝｜ＡＮ｜时，求m 的取值范围．椭圆训练试卷参考答案一、B D C D A A A A ＤC B C 二、13．4或4914．12y 8x 22=+15．5623±16．18π三、17．解：设A(x 1，y 1)，B(x 2，y 2)，由焦点半径公式有a-ex 1+a-ex 2=58a ，∴x 1+x 2=21a(∵e=54)，即AB中点横坐标为41a ，又左准线方程为x=-45a ，∴41a+45a=23，即a=1，∴椭圆方程为x 2+925y 2=1．18．解：（1）直线AB 的方程为y=-21x+2； （2）所求椭圆的方程为12x 2+3y 2=1． 19．解：由9x2+5y 2=1，得F 1（2，0），F 2（-2，0），F 1关于直线l 的对称点F 1/（6，4），连F 1/F 2交l 于一点，即为所求的点M ，∴2a=|MF 1|+|MF 2|=|F 1/F 2|=45，∴a=25，又c=2，∴b 2=16，故所求椭圆方程为20x 2+16y 2=1．20．解：设动点M(x ，y)，动直线l ：y=x+m ，并设P(x 1，y 1)，Q(x 2，y 2)是方程组⎩⎨⎧=-++=04y 2x ,m x y 22的解，消去y ，得3x 2+4mx+2m 2-4=0，其Δ=16m 2-12(2m 2-4)>0，∴-6<m<6，x 1+x 2=-3m4， x 1x 2=34m 22-，故|MP|=2|x-x 1|，|MQ|=2|x-x 2|．由|MP||MQ|=2，得|x-x 1||x-x 2|=1，也即|x 2-(x 1+x 2)x+x 1x 2|=1，于是有|x 2+3mx 4+34m 22-|=1．∵m=y -x ，∴|x 2+2y 2-4|=3．由x 2+2y 2-4=3，得椭圆7x 2+7y 22=1夹在直线y=x ±6间两段弧，且不包含端点．由x 2+2y 2-4=-3，得椭圆x 2+2y 2=1．21．解：（1）设|PF 1|=r 1，|PF 2|=r 2，则S 21F PF ∆=21r 1r 2sin∠F 1PF 2，由r 1+r 2=2a ， 4c 2=r 12+r 22-2cos∠F 1PF 2，得r 1r 2=212PF F cos 1b 2∠+．代入面积公式，得 S 21F PF ∆=2121PF F cos 1PF F sin ∠+∠b 2=b 2tg∠2PF F 21=33b 2．（2）设∠A 1QB=α，∠A 2QB=β，点Q(x 0，y 0)(0<y 0<b)．tgθ=tg(α+β)=βα-β+αtg tg 1tg tg =22020000y x a 1y x a y x a --++-=220200a y x ay 2-+．∵220a x +220b y =1，∴x 02=a 2-22ba -y 02．∴tgθ=202220y b b a ay 2-- =022y c ab 2-=-3．∴2ab 2≤3c 2y 0≤3c 2b ，即3c 4+4a 2c 2-4a 4≥0，∴3e 4+4e 2-4≥0，解之得e 2≥32，∴36≤e<1为所求．22．解：（1）用待定系数法．椭圆方程为22y 3x +＝１．（2）设Ｐ为弦ＭＮ的中点．由⎪⎩⎪⎨⎧=++=,1y 3x ,m kx y 22得（3k 2＋1）x 2＋6kmx ＋3（m 2－1）＝0．由Δ＞０，得m 2＜3k2＋1 ①，∴x P ＝1k 3mk 32x x 2N M +-=+，从而，y P ＝kx p ＋m ＝1k 3m 2+．∴k AP ＝km 31k 3m 2++-．由ＭＮ⊥ＡＰ，得 km 31k 3m 2++-＝－k 1，即2m ＝3k 2＋1 ②．将②代入①，得2m ＞m 2，解得０＜m ＜2．由②得k 2＝31m 2-＞０．解得m ＞21．故所求m 的取值范围为（21，２）．。

解析几何——椭圆精炼专题一、 选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中有只有一项是符合题目要求的．） 1．椭圆63222=+y x 的焦距是（ ）A ．2B ．)23(2-C ．52D ．)23(2+2．F 1、F 2是定点，|F 1F 2|=6，动点M 满足|MF 1|+|MF 2|=6，则点M 的轨迹是（ ） A ．椭圆 B ．直线 C ．线段 D ．圆 3．若椭圆的两焦点为（－2，0）和（2，0），且椭圆过点)23,25(-，则椭圆方程是 （ ）A ．14822=+x y B ．161022=+x y C ．18422=+x y D ．161022=+y x4．方程222=+ky x 表示焦点在y 轴上的椭圆，则k 的取值范围是（ ）A ．),0(+∞B ．（0，2）C ．（1，+∞）D ．（0，1）5． 过椭圆12422=+y x 的一个焦点1F 的直线与椭圆交于A 、B 两点，则A 、B 与椭圆的另一焦点2F 构成2ABF ∆，那么2ABF ∆的周长是（ ） A ． 22 B ． 2 C ． 2 D ． 16．已知椭圆的对称轴是坐标轴，离心率为31，长轴长为12，则椭圆方程为（ ） A ．112814422=+y x 或114412822=+y x B ． 14622=+y x C ．1323622=+y x 或1363222=+y x D ． 16422=+y x 或14622=+y x 7． 已知k ＜4，则曲线14922=+y x 和14922=-+-k y k x 有（ ） A ． 相同的短轴 B ． 相同的焦点 C ． 相同的离心率 D ． 相同的长轴8．椭圆192522=+y x 的焦点1F 、2F ，P 为椭圆上的一点，已知21PF PF ⊥，则△21PF F 的面积为（ ）A ．9B ．12C ．10D ．89．椭圆131222=+y x 的焦点为1F 和2F ，点P 在椭圆上，若线段1PF 的中点在y 轴上，那么1PF 是2PF 的（ ）A ．4倍B ．5倍C ．7倍D ．3倍 10．椭圆1449422=+y x 内有一点P （3，2）过点P 的弦恰好以P 为中点，那么这弦所在直线的方程为（ ）A ．01223=-+y xB ．01232=-+y xC ．014494=-+y xD ． 014449=-+y x11．椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是（ ）A ．3B ．11C ．22D ．1012．过点M （－2，0）的直线M 与椭圆1222=+y x 交于P 1，P 2，线段P 1P 2的中点为P ，设直线M 的斜率为k 1（01≠k ），直线OP 的斜率为k 2，则k 1k 2的值为（ ）A ．2B ．－2C ．21 D ．－21二、 填空题：（本大题共4小题，每小题4分，共16分，把答案填在题中横线上．）13．椭圆2214x y m +=的离心率为12，则m = ． 14．设P 是椭圆2214x y +=上的一点，12,F F 是椭圆的两个焦点，则12PF PF 的最大值为 ；最小值为 ．15．直线y =x －21被椭圆x 2+4y 2=4截得的弦长为 ．16．已知圆Q A y x C ),0,1(25)1(:22及点=++为圆上一点，AQ 的垂直平分线交CQ 于M ，则点M 的轨迹方程为 ． 三、解答题：（本大题共6小题，共74分，解答应写出文字说明．证明过程或演算步骤．） 17．已知三角形ABC 的两顶点为(2,0),(2,0)B C -，它的周长为10,求顶点A 轨迹方程． 18．椭圆的一个顶点为A （2，0），其长轴长是短轴长的2倍，求椭圆的标准方程． 19．点P 到定点F （2，0）的距离和它到定直线x =8的距离的比为1：2，求点P 的轨迹方程，并指出轨迹是什么图形． 20．中心在原点，一焦点为F 1（0，52）的椭圆被直线y =3x －2截得的弦的中点横坐标是21，求此椭圆的方程．21.已知椭圆的中心在坐标原点O ，焦点在坐标轴上，直线y =x +1与椭圆交于P 和Q ，且OP ⊥OQ ，|PQ |=210，求椭圆方程 22．椭圆12222=+by a x (a ＞b ＞)0与直线1=+y x 交于P 、Q 两点，且OQ OP ⊥，其中O 为坐标原点． （1）求2211ba +的值； （2）若椭圆的离心率e 满足33≤e ≤22，求椭圆长轴的取值范围．椭圆练习题参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A CDDABD13、3或316 14、 4 ， 1 15、5382 16、121425422=+y x 17、3)(x 15922±≠=+y x 18、解：（1）当A (2,0)为长轴端点时，a =2 , b =1，椭圆的标准方程为： ；（2）当为短轴端点时，，，椭圆的标准方程为： ；19．解：设P （x ，y ），根据题意，|PF|=(x-2)2-y 2,d=|x-8|,因为|PF|d =12 ,所以 (x-2)2-y 2 |x-8| = 12.化简，得3x 2+4y 2=48,整理，得x 216 +y 212=1,所以，点P 的轨迹是椭圆。