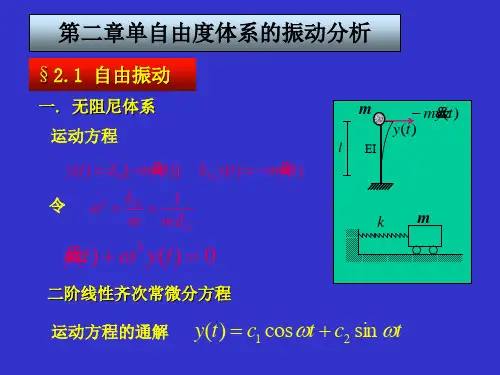
第2章 分析动力学基础2.1 基本概念 2.1.1 约束对质点系各质点的位移和速度提供的限制，约束在数学上通过约束方程来表达。
对于n 个质点组成的系统，约束方程的一般形式为：m k t r r r r r r fn n k ,1,0),,...,,,,...,,(2121== 或简写为：m k t rr f i i k ,1,0),,(== 式中，i r 、i r分别为质点i 的位置矢量和速度矢量，t 为时间，m 为约束方程的个数。
注：弹性支座不对位置和速度提供直接限制，不作为约束。
约束方程的分类： （1） 几何约束和运动约束几何约束：约束方程中不显含速度项，如：0),(=t r f i k运动约束：约束方程中显含速度项，如：0),,(=t rr f i i k 下图中，如果圆轮与地面之间无滑动，则其约束方程为：0=-ϕ a xc（2） 定常约束和非定常约束定常约束：约束方程中不显含时间t ，如：0),(=i i k r r f 非定常约束：约束方程中显含时间t ，如：0),,(=t rr f i i k222l y x =+ 222)(ut l y x -=+（3） 完整约束与非完整约束完整约束：几何约束以及可积分的运动约束 非完整约束：不可积分的运动约束方程0=-ϕ a xc 可积分为0=-ϕa x c ，因此是完整约束。
（4） 单面约束与双面约束单面约束：约束方程为不等式，如：0),,(≤t r r f i i k 双面约束：约束方程为等式，如：0),,(=t rr f i i k 下图中，如果考虑到绳子可以缩短，则其约束方程为：222l y x ≤+，表现为不等式形式，就是一个单面约束。
一般分析力学的研究对象为：完整的双面约束，方程为：0),(=t r f i k。
2.1.2 广义坐标与自由度广义坐标：描述系统位置状态的独立参数，称为系统的广义坐标。
广义坐标的个数：（1） 空间质点系：m n N -=3 （2） 平面质点系：m n N -=2对于如图双连刚杆的平面两质点系统，约束方程为：⎩⎨⎧=-+-=+22212212212121)()(l y y x x l y x 广义坐标个数为：2222=-⨯=N ，具体地可选择为：),(21x x ；),(21y y ；),(21y x ；),(21x y ；),(21ϕϕ等。
如果系统的位移状态),(t x u 可以通过一组基函数)(x f i 来线性组合，如：∑=ii i x f t q t x u )()(),(，由于各系数)(t q i 相互独立，因此系数)(t q i 也是一种广义坐标。
例：简支梁的挠度曲线可表示为∑=ii lxi t q t x y πsin)(),(，)(t q i 为与基函数lxi πsin对应的广义坐标。
根据广义坐标的概念，设系统的广义坐标个数为N ，当选定系统的广义坐标),1(N k q k =后，系统的位置状态可以由全部广义坐标来表示，也即有：),(),,...,,(21t q r t q q q r r k i N i i==，n i ,1=自由度：某瞬时，系统独立运动的个数。
自由度强调的是独立运动也即独立速度，广义坐标强调的是独立坐标（位移）。
对于完整系统，自由度与广义坐标的个数相同；对于非完整系统，由于存在非完整约束，对独立速度的限制多于对独立坐标的限制，因此自由度数比广义坐标个数少。
2.1.3 力的功对于力k t Z j t Y i t X t F)()()()(++=，设在微小时间间隔dt 内力作用点的位移为k dz j dy i dx r d++=，则该力做的功称为元功：dz t X dy t X dx t X dr t F r d t F W )()()(cos )()(++==⋅=θδ式中，θ为)(t F 与r d的夹角。
经过一段路径AB ，做的总功为：⎰⎰++=⋅=B ABAdz t Z dy t Y dx t X r d t F W )()()()(对于力偶)(t M ，设在微小时间间隔dt 内物体在力偶作用下的转角为ϕd ，则元功为：ϕδd t M W )(=转过一定角度121ϕϕϕ-=∆，做的总功为：⎰=21)(ϕϕϕδd t M W力、力偶在单位时间内做的功称为功率：r t F dt r d t F dt W dt dW p⋅=⋅===)()(δ ϕϕδ )()(t M dtd t M dt W dt dW p ==== 2.1.4 有势力与势能有势力：在作用点变化过程中，力做的功如果只与起止位置有关，而与中间路径无关，则这个力称为有势力，有势力所在的空间称为该有势力的势力场，如重力与重力场。
势能：在势力场中，物体从位置),,(z y x M 运动到任选的位置),,(0000z y x M ，有势力所作的功称为物体在位置M 相对于位置0M 的势能，以V 表示：⎰⎰++=⋅=0M MM MZdz Ydy Xdx r d F V位置0M 的势能等于零，称为零势能位置（点、状态）。
势能V 是位置),,(z y x M 的函数，记为),,(z y x V 。
有势力分量与势能具有如下关系：x V X ∂∂-=，y V Y ∂∂-=，zVZ ∂∂-=证明如下：当),,(z y x M 具有微小变化变为),,('dz z dy y dx x M +++时，势能的增量为：][''''0000Zdz Ydy Xdx rd F rd F r d F rd F r d F rd F r d F dV M MMM M M M M M M M M ++-=⋅-=⋅-=⋅=⋅+⋅=⋅-⋅=⎰⎰⎰⎰⎰⎰因此有：x V X ∂∂-=，y V Y ∂∂-=，zVZ ∂∂-=当弹性体变形后，恢复变形到原始状态的过程中，弹性力会做功，做的功等于变形状态改变释放的变形能，只与前后变形状态有关，因此具有势能的性质。
弹性体因变形而具有变性能为：⎰ΩΩ+++++=d V zx zx yz yz xy xy z z y y x x )(21γτγτγτεσεσεσ 2.1.5 虚位移虚位移：某瞬时，约束所容许的任意微小位移。
要点1：“某瞬时”意味着虚位移不考虑时间的变化，也即是虚位移无时间过程。
要点2：“约束所容许”表示不破坏约束，满足约束条件。
要点3：“微小位移”指位移小到只考虑一阶变化。
要点4：“任意”指无需考虑真实的力、速度和时间等真实运动因素，可以人为地设定。
要点5：对于一个系统，由于存在内部的约束联系，各位置点的虚位移不具有完全的任意性。
要点6：根据定义，独立虚位移的个数等于系统的自由度数。
概念辨析：可能位移：考虑时间，但不考虑运动的原因，约束所容许的位移称为可能位移。
真实位移：同时考虑时间和运动的原因，约束所容许的位移称为真实位移，真实位移是可能位移中的一种。
可能位移和真实位移不具有“微小”性，因此可能位移不一定是虚位移。
设系统的广义坐标为),1(N k q k =，系统的位置状态可以由全部广义坐标表示为：),(),,...,,(21t q r t q q q r r k i N i i==，n i ,1=根据微积分的概念，任一质点i 的位移增量有如下关系：dt t r dq q r dt t r dq q r dq q r dq q r r d i Nk k ki i N N i i ii ∂∂+∂∂=∂∂+∂∂++∂∂+∂∂=∑= 12211...略去上式中与时间有关的增量，将k dq 变为虚位移k q δ，则可得到质点i 的虚位移：∑=∂∂=N k k ki i q q r r 1δδ上式建立了任一点虚位移与广义坐标虚位移的关系。
由于各广义坐标是独立的，因此各广义坐标可以独立发生虚位移。
当只有一个广义坐标k q 有虚位移k q δ时，质点i 的虚位移为：k ki i q q r r δδ∂∂=另外，根据约束方程也可建立虚位移之间的关系，方法如下：对于约束方程0),(=t r f i k，有：0)(11=∂∂+∂∂+∂∂=∂∂∑∑==ni i i ki i k i i k ni i i k z z f y y f x x f r r f δδδδ 例如：222)(ut l y x -=+有：022=⋅+⋅y y x x δδ0=⋅+⋅y y x x δδ2.1.5 虚功与广义力虚功：力在虚位移上所做的功称为虚功。
力系i F中各力作用点的虚位移为：∑=∂∂=N k k ki i q q r r 1δδ则总虚功为：∑∑∑∑∑∑∑=======∂∂⋅=∂∂⋅=∂∂⋅=⋅=N k k n i k i i N k n i k k ii n i N k k k i i ni i i q q r F q q r F q q r F r F W 1111111])([)()()(δδδδδ记：∑=∂∂⋅=ni k i i k q rF Q 1)( 为与k q δ对应的广义力，则有：∑==Nk k k q Q W 1δδ广义力的计算方法：（1）记：k Z j Y i X F i i i i++=，得：∑∑==∂∂+∂∂+∂∂=∂∂⋅=n i k i i k i i k i i ni k ii k q z Z q y Y q x X q r F Q 11)()(（2）单独使一个广义坐标k q 发生虚位移k q δ，此时的虚功为：k k q Q W δδ=因此有：kk q W Q δδ=（3）如果所有力均为有势力，根据：i i x V X ∂∂-=，ii y V Y ∂∂-=，i i z VZ ∂∂-= 得：kni kii k i i k i i ni ki i k i i k i ini k i i k q V q z z V q y y V q x x V q z Z q y Y q x X q r F Q ∂∂-=∂∂∂∂+∂∂∂∂+∂∂∂∂-=∂∂+∂∂+∂∂=∂∂⋅=∑∑∑===111)()()(例题2-1：如图双摆，以1ϕ、2ϕ为广义坐标，对于重力g m P 11=、g m P 22=的广义力。
解： 方法1：111cos ϕl y =221121111sin δϕϕδl y -=2221112sin sin δϕϕδϕϕδl l y --=222211121222111211112211sin sin )()sin sin ()sin (δϕϕδϕϕδϕϕδϕϕδϕϕδδδl P l P P l l P l P y P y P W -+-=--+-=+= 因此有：11211sin )(ϕl P P Q +-= 2222sin ϕl P Q -=方法2：首先只让1ϕ产生一个虚位移1δϕ，两质点的虚位移为：1121δϕδδl r r ==虚功为：1112111121111122111sin )(sin sin sin sin δϕϕϕδϕϕδϕϕδϕδδl P P l P l P r P r P W +-=--=--= 因此广义力为：11211sin )(ϕl P P Q +-=再只让2ϕ产生一个虚位移2δϕ，两质点的虚位移为：1=r δ 222δϕδl r =虚功为：22222222222sin sin sin δϕϕϕδϕϕδδl P l P r P W -=-=-= 因此广义力为：2222sin ϕl P Q -=方法3：111cos ϕl y =22112以O 处为重力势能零点，系统的势能为：2221121*********211cos cos )()cos cos (cos ϕϕϕϕϕl P l P P l l P l P y P y P V -+-=+--=--= 广义力为：112111sin )(ϕϕl P P VQ +-=∂∂-= 22222sin ϕϕl P VQ -=∂∂-= 2.2 虚功（虚位移）原理 2.2.1 理想约束虚功的计算公式为：∑∑===⋅=N k k k n i i i q Q r F W 11)(δδδ一个系统可能有很多力，但是有些力在虚位移上不做功。
