《结构动力学》结构动力学大作业 研究生课程考核试卷

结构动力学试题及答案（本文按试题和答案格式进行编写）试题一：1. 请问什么是结构动力学？2. 简述结构动力学的研究对象和主要内容。

3. 结构动力学分析常用的方法有哪些？4. 结构动力学分析中常用的数学模型有哪些？5. 结构动力学的应用领域有哪些？答案一：1. 结构动力学是研究结构在外力作用下的动态响应及其稳定性的学科。

2. 结构动力学的研究对象是各种工程结构，主要内容包括结构的振动、冲击响应、瞬态响应和稳态响应等。

3. 结构动力学分析常用的方法有模态分析法、频率响应分析法、时程分析法等。

4. 结构动力学分析中常用的数学模型有单自由度体系、多自由度体系、连续体系等。

5. 结构动力学的应用领域广泛，包括建筑结构工程、桥梁工程、风力发电机组、地震工程等。

试题二：1. 结构动力学分析中，模态分析的基本原理是什么？2. 简述模态分析的步骤和计算方法。

3. 常用的模态分析软件有哪些？4. 请问什么是结构的固有频率和阻尼比？5. 结构的模态振型对结构动力响应有什么影响？答案二：1. 模态分析是基于结构的振动特性，通过求解结构的固有频率、模态振型和阻尼比等参数，来研究结构的动力响应。

2. 模态分析的步骤包括建立结构有限元模型、求解结构的固有频率和模态振型、计算结构的阻尼比等。

常用的计算方法有有限元法、拉普拉斯变换法等。

3. 常用的模态分析软件有ANSYS、ABAQUS、MSC.NASTRAN等。

4. 结构的固有频率是结构在无外力作用下自由振动的频率，阻尼比是结构振动过程中能量耗散的程度。

5. 结构的模态振型对结构动力响应有很大影响，不同的模态振型会导致不同的振动特性和反应。

试题三：1. 结构动力学分析中，频率响应分析的基本原理是什么？2. 简述频率响应分析的步骤和计算方法。

3. 频率响应分析和模态分析有什么区别？4. 结构的频率响应函数和传递函数有什么区别？5. 频率响应分析在结构设计中的应用有哪些？答案三：1. 频率响应分析是研究结构在单频激励下的响应特性，通过求解结构的频率响应函数，来获得结构的响应。

考生请注意：1．本试题共6 题，共2 页，考生请认真检查；2．答题时，直接将答题内容写在我校提供的答题纸上；答在试卷上一律无效；3．本试题不得拆开，拆开后遗失后果自负。

一、简述题（本题共20分，每小题5分）1．自由振动、强迫振动自由振动：系统受到初始激励作用后，仅靠其本身的弹性恢复力“自由地”振动，其振动特性仅取决于系统本身的物理特性（质量和刚度）。

强迫振动：系统受到外界持续的激励作用而“被动地”进行振动，其振动特性除取决于系统本身的特性外，还取决于激励的特性。

2．广义坐标、振型函数广义坐标：是一种坐标形式，它是有几组互相正交的模态组成，任何变量都可由这几组模态的唯一线性组合而成。

振型函数：是一种函数形式，描述振型在几维空间中的振幅值的表现。

3．稳态响应、瞬态响应稳态响应：当系统在外力作用下，经过一段时间后，系统振动趋于稳定时的响应。

瞬态响应：当系统在外力作用下，在系统振动趋于稳定之前的响应。

瞬态响应发生在稳态响应之前，他们组合构成完整的外力作用时的振动响应。

4．哈密顿原理具有完整约束的动力学系统，在满足协调性条件、约束条件或边界条件，同时满足起始t1时刻与结束t2时刻条件的可能的位移随时间变化的形式中，真实解对应的那种变化形式使Lagrange泛函L取最小值，即2 1(T V W)0t t dt式中：T为系统的动能，V为系统的势能，W为外力所作虚功。

二．质量均为m 的两个球，系于具有很大张力T 的弦上，如图所示，求系统的固有频率。

（本题10分）解：由于弦的张力T 很大，两个球只能在竖向发生微幅振动。

（1分）如下图所示，两个球在外力1()F t 和2()F t 作用下发生竖向微幅振动，位移分别为1x 和2x 。

对两个球，分别作受力分析：外荷载；惯性力； 张力分力。

（3分）运用达朗贝尔原理，分别列出 两个球的竖向运动方程：12111()x x x mx T T F t L L-+⋅-⋅=22122()x x xmx T T F t L L-+⋅+⋅= （5分）写成矩阵形式：1112222()002()TT x x F t m L L m x T T x F t L L ⎡⎤-⎢⎥⎧⎫⎧⎫⎧⎫⎡⎤+=⎢⎥⎨⎬⎨⎬⎨⎬⎢⎥⎣⎦⎩⎭⎩⎭⎩⎭⎢⎥-⎢⎥⎣⎦得频率方程：[][]222202T Tm LLK M T T m L Lωωω---==-- （7分） 解得： 1ω=2ω= （10分）ll l F 2(t)三．图示简支梁，梁长为4l ，在四等分处有3个质量m 1=m 2=m 3=m ，梁的抗弯刚度为EI ，忽略梁自身的质量，要求：（1）写出系统振动方程；（2）求系统的各阶固有频率； （3）画出相应的主振型。

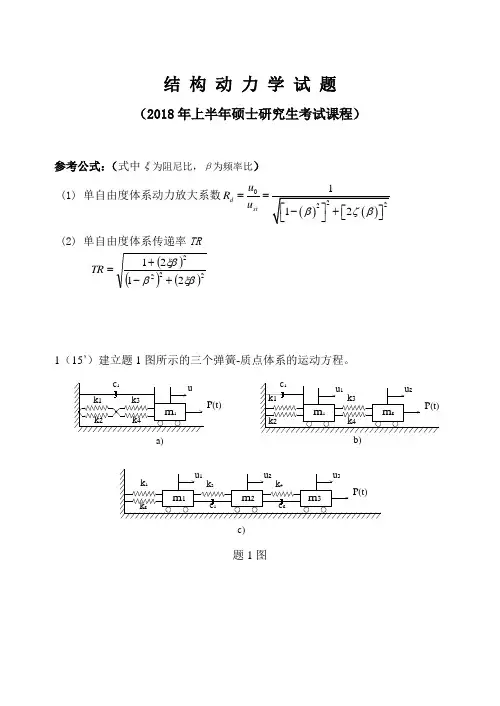
结 构 动 力 学 试 题（2018年上半年硕士研究生考试课程）参考公式：（式中ξ为阻尼比，β为频率比） (1) 单自由度体系动力放大系数0d stu R u ==(2) 单自由度体系传递率TR()()()22222121ξββξβ+-+=TR1（15’）建立题1图所示的三个弹簧-质点体系的运动方程。

❍☎♦✆◆❍♍♋✆♌✆♍✆♍♍❍☎♦✆◆❍◆☎♦✆◆❍◆题1图2（20’）汽车在多跨连续梁桥梁上行驶，桥梁跨度均为L=32m,桥面由于长时徐变效应而产生12cm 的挠度（如题2图所示）。

桥面可以用振幅为12.0cm 的正弦曲线来近似，汽车可以用一个单质点体系模拟，如果汽车重m=2.8tf ，等效弹簧刚度k=280E3 N/m ，等效阻尼比5.0=ξ，求:（1）汽车以72km/h ν=行驶时，汽车的竖向运动()t u t 的振幅t u 0；（2）发生共振时汽车的行驶速度（此处指使振幅最大时的速度）。

题2图3（15’）如题3图所示，一总质量为m 的刚性梁两端由弹簧支撑，梁的质量均匀分布、两弹簧的刚度分别为k 和2k 。

定义的两个自由度u 1和u 2示于图中，建立结构体系的运动方程，并求出的振型和自振频率。

题3图4（15’）题4图所示动力体系为：AB 、BC 杆件都为均布质量刚杆，单位均布质量分别为m 1 、m 2，M 为集中质量，C1及C2为阻尼系数，K1及K2为刚度系数，在C 点作用有压力N 。

以B 点竖向位移B u u =为广义坐标，试求： （1）列出体系的运动方程 （2）求出体系的自振频率 （3）求出临界压力N 。

题4图5（15’）工程场地竖向加速度为0.10g u g =，振动频率为10f Hz =，安放一个质量50m kg =的敏感仪器。

仪器固定在刚度14/k kN m =，阻尼比10%ξ=的橡胶隔振垫上，求： （1） 传递到仪器上的加速度是多少？（2） 如果仪器只能承受0.0038g 的加速度，给出解决方案。

某大学《结构动力学》课程考试试卷适用专业： 考试日期:考试时间:120分钟 考试形式:闭卷 试卷总分:100分1、求解单自由振动位移方程0y 2=+y ω，设初始时刻t =0质点有初始位移y 0和初始速度v 0？(10)2、如图所示为一等截面竖直悬臂杆，长度为l ，截面面积为A ，惯性矩为I ， 弹性模量为E ，杆顶有重物，其重量为W 。

设杆件本身质量可忽略不计，试分别求水平振动和竖向振动时的自振周期？（15分）3、如下为简谐荷载作用下单自由度体系的强迫振动位移公式，试分析进入平稳阶段后动力系数随ωθ变化特性？(15))sin (sin 11)(y t t y t stωωθθωθ--= 4、突加荷载作用下求t>0时位移如何计算？（15分）⎭⎬⎫⎩⎨⎧><=000)(0t F t t F p p ，当，当5、有阻尼振动的动力系数β随ωθ变化的公式如下，其中ξ为阻尼系数，求共振动力系数和最大动力系数？分析其之间的关系？（15分） /2122222241-⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫⎝⎛-=ωθξωθβ6、6、某结构自由振动经过10个周期后，振幅降为原来的10%。

试求结构的阻尼比ξ和在简谐荷载作用下共振时的动力系数？（15分）7、如图所示为两层钢架，其横梁为无限刚性，设质量集中在楼层上，一二层质量分别为m 1和m 2，层间侧移刚度等别为k 1和k 2，试求刚架水平振动时的自振频率和主振型？（15分）（其中m 1= m 2，k 1= k 2）某大学《结构动力学》课程考试试卷答案适用专业： 考试日期:考试时间:120分钟 考试形式:闭卷 试卷总分:100分1、求解单自由振动位移方程0y 2=+y ω，设初始时刻t =0质点有初始位移y 0和初始速度v 0？(10)答：02=+y y ωmk=ω t C t C t y ωωcos sin )(21+= 0)0(y y =，0)0(yν= C 1=ων0,C 2=y(0) t t y t y ωωνωsin cos )(00+=2、如图所示为一等截面竖直悬臂杆，长度为l ，截面面积为A ，惯性矩为I ， 弹性模量为E ，杆顶有重物，其重量为W 。

结构动力学试题及答案一、选择题1. 在结构动力学中，下列哪项不是描述结构动力响应的参数？A. 自然频率B. 阻尼比C. 静力平衡D. 模态阻尼2. 以下哪个不是结构动力学分析中的常用方法？A. 模态分析B. 时域分析C. 频域分析D. 静力分析二、简答题1. 简述结构动力学中模态分析的目的和重要性。

2. 描述阻尼对结构动力响应的影响。

三、计算题1. 假设一个单自由度系统，其质量为m，刚度为k，初始位移为x0，初始速度为v0。

若外力为F(t) = F0 * sin(ωt)，求该系统在任意时间t的位移响应。

答案一、选择题1. 正确答案：C. 静力平衡解析：静力平衡是静力学的概念，与结构动力学无关。

2. 正确答案：D. 静力分析解析：静力分析是分析结构在静载荷作用下的响应，而结构动力学分析动态载荷下的结构响应。

二、简答题1. 模态分析的目的在于识别结构的自然振动特性，包括自然频率、阻尼比和模态形状。

它的重要性在于：- 预测结构在动态载荷下的响应。

- 为控制结构的振动提供基础数据。

- 优化设计，提高结构的抗震性能。

2. 阻尼对结构动力响应的影响主要表现在：- 减少振动幅度，提高结构的稳定性。

- 改变系统的自然频率和模态形状。

- 影响系统的动态响应时间。

三、计算题1. 单自由度系统的位移响应可以通过以下步骤求解：- 写出系统的动力学方程：m * d²x/dt² + c * dx/dt + k * x = F(t)- 应用初始条件：x(0) = x0, v(0) = v0- 应用外力：F(t) = F0 * sin(ωt)- 通过傅里叶变换或拉普拉斯变换求解方程。

- 应用逆变换得到位移响应的解析解或数值解。

位移响应的一般形式为：x(t) = X * cos(ωt - φ) + Y *sin(ωt - φ)，其中X和Y是与系统参数和初始条件有关的常数，φ是相位角。

具体的数值需要根据系统参数和初始条件进行计算。

西南交通大学研究生试试卷课程代码A11101课程名称建筑结构高等动力学考试时间150分钟阅卷教师签字：一、是非题（将判断结果填入括弧：以O 表示正确，以X 表示错误）(本大题共5小题，总计10分)1.图a 示两端固定梁的自振频率大于图b 示简支梁的自振频率。

（ ）2.在图示结构中，若要使其自振周期T 增大，可以增大EI 。

（ ）3.简谐荷载作用于单自由度体系时，干扰力频率越接近自振频率，动力系数 (绝对值)越大。

( )4.增加约束使得体系的频率减小或保持不变。

( )5.设不考虑阻尼因素，承受简谐荷载(同频率、同相角)的多自由度体系，稳态时任意一点的内力与荷载同时达到幅值。

( )二、选择题（将选中答案的字母填入括弧内）(本大题共5小题，总计15分)1.设有图示桁架，若不考虑各杆重量时，其动力自由度为：A ．单自由度；B ．两个自由度；C ．三个自由度；D ．四个自由度。

（ ）22.图示体系受动力荷载作用，杆重不计，不考虑阻尼，当发生共振时，θ值应为：A ．()3/4ma EI ；B ．()33/4ma EI ； C ．()37/3ma EI ；D ．()3/3ma EI 。

3. 体系的跨度、约束、质点位置不变，下列哪种情况周期最短：A ．质量小 ，刚度小；B ．质量大 ，刚度大 ；C ．质量小 ，刚度大；D ．质量大 ，刚度小 。

( )4. 多自由度体系的自振频率和振型取决于：A ．干扰力的大小和方向；B ．初始位移；C ．结构的质量分布和刚度(或柔度)系数；D ．初始速度 。

( )5.从以下三式中选一合适的曲线方程，用能量法求图示体系的第一频率。

设EI =常数。

(式中A 、f 为常数 )A ．(1cos(/2))y A x l π=-；B ．2334(16/5)(2)y f l l x lx x =-+；C ．(/2)(1cos(2/))y f x l π=-；D ．()()2242(16/5)/4y f l x x l=-。

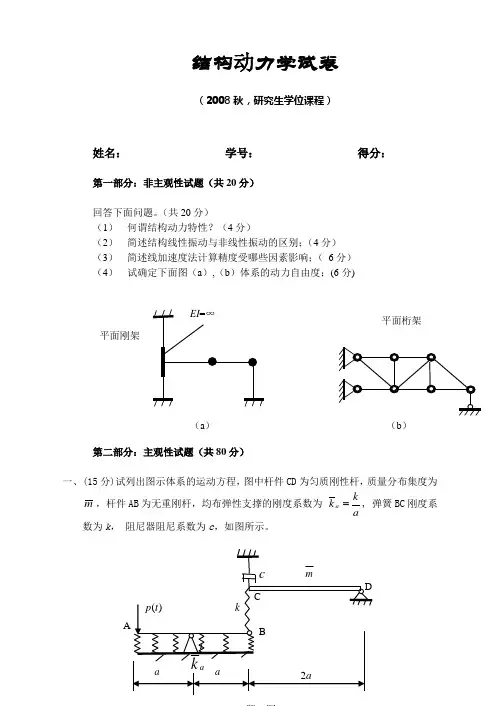
结构动力学试卷
（2008秋，研究生学位课程）
姓名： 学号： 得分：
第一部分：非主观性试题（共20分）
回答下面问题。

（共20分）
（1） 何谓结构动力特性？（4分）
（2） 简述结构线性振动与非线性振动的区别；（4分） （3） 简述线加速度法计算精度受哪些因素影响；（ 6分） （4） 试确定下面图（a ）,（b ）体系的动力自由度；(6分)
第二部分：主观性试题（共80分）
一、(15分)试列出图示体系的运动方程，图中杆件CD 为匀质刚性杆，质量分布集度为
m ，杆件AB 为无重刚杆，均布弹性支撑的刚度系数为 a k
k a
, 弹簧BC 刚度系数为k ， 阻尼器阻尼系数为c ，如图所示。

（a ） 平面刚架
平面桁架
题一图
二、(20分)试求题二图所示体系：（1）自振周期；（2）阻尼比；（3）稳态振幅。

质点质量为m , 阻尼系数为C ，各杆为无重杆，各杆尺寸与刚度如图所示,ω=2θ。

二、 (20分)试求题三图所示体系的稳态振幅。

0sin t
θ
()sin p t p t
θ=题三图 ()sin p t p t
θ=题三图
四、（15分）对题四图所示结构，试：（1）列出振型方程，并写出边界条件；（2）求稳态振幅。

不计杆BC 段质量。

五、（10分）试求题五图所示结构各构件的一致刚度矩阵与一致质量矩阵，并集成结
构的刚度与质量矩阵。

题五图
,
m
P P 0=(1,0,2)
,0,(1,0,3)(1,
0,4)(1,0,5)。

《结构动⼒学》试卷《结构动⼒学》试题B 卷⼀、填空题。

（11分）1、右图所⽰振动体系不计杆件的轴向变形，则动⼒⾃由度数⽬是。

（3分）2、单⾃由度体系只有当阻尼⽐ξ 1时才会产⽣振动现象。

（3、已知结构的⾃振周期s T 3.0=，阻尼⽐04.0=ξ，质量m 在0,300==v mm y 的初始条件下开始振动，则⾄少经过个周期后振幅可以衰减到mm 1.0以下。

（3分）4、多⾃由度框架结构顶部刚度和质量突然变时，⾃由振动中顶部位移很⼤的现象称。

（3分）⼆、判断以下说法是否正确，对错误的说法加以改正。

（6×3分=18分）1、凡是⼤⼩、⽅向、作⽤点位置随时间变化的荷载，在结构动⼒计算中都必须看作动⼒荷载。

（）2、超静定结构体系的动⼒⾃由度数⽬⼀定等于其超静定次数。

（）3、为了避免共振，要错开激励频率和结构固有频率，⼀般通过改变激励频率来实现。

（）4、求冲击荷载作⽤下结构的反应谱曲线时⼀般不计阻尼的影响。

（）5、求静定的多⾃由度体系的频率和振型，⼀般采⽤刚度法⽐采⽤柔度法⽅便。

（）6、⽤瑞利法时若取重量作⽤下的静变形曲线为试函数，求得的基频的精度不⾼。

（）三、选择题。

（6×3分=18分）1、对单⾃由度体系的⾃由振动，下列说法正确的是（）A C 、振幅和初相⾓仅与初始条件有关 2、图⽰（a ）、（b A 、b a ωω<B 、∞→EA 时b a ωω≈C 、0→EA 时b a ωω≈D 、b a ωω=3、（1）⽆阻尼的⾃由振动（2）不计阻尼，零初始条件下t P θsin 产⽣的过渡阶段的振动（3）有阻尼的⾃由振动（4）突加荷载引起的⽆阻尼强迫振动 A 、（1）（2）（3） B 、（1）（2）（4） C 、（2）（3） D 、（1）（4）⼀、填空题。

（11分）1、2 （3分）2、< （3分）3、14 （3分）4、⼩鞭梢效应（3分）⼆、判断以下说法是否正确，对错误的说法加以改正。

华北电力大学研究生课程考试试题（A/B卷）
20 ～20 学年第学期
课程编号：课程名称：结构动力学
年级：开课单位：命题教师：
考核方式：考试时间：分钟共页
姓名：学号：班级：
1、（15分）单自由度建筑物的重量为900 kN，在位移为3.1 cm时（t=0）突然释放，使建筑产生自由振动。

如果往复振动的最大位移为2.2cm（T n=0.64秒），试求：(a) 建筑物的刚度k；(b) 阻尼比ζ；(c) 阻尼系数c。

2、（15分）一质量为m1的块体用刚度为k的
弹簧悬挂处于平衡状态（如下图所示）。

另一质量为m2的块体由高度h自由落下到块体m1上并与之完全粘接，确定由此引起的运动u(t)，u(t)由m1—k体系的静平衡位置起算。

3、（15分）采用Duhamel积分法计算无阻尼单自由度结构在矩形脉冲作用下的位移时程，初始时刻结构处于静止状态，脉冲时程为：
4、（15分）如图所示的二层结构，柱截面抗弯刚度均为EI，采用集中质量法近似，将结构的质量集中于刚性梁的中部，分别为m1和m2，建立结构在外荷载p1(t)和p2(t)作用下的强迫运动方程。

5、（20分）对上题4给出的二层结构，设m1＝m2＝m，(a)确定结构的自振频率和振型(用m，EI和h表示)；(b)验证振型的正交性；(c)按正交标准化(归一化)方法将振型标准化；(d)比较未标准化和标准化的振型质量和振型刚度，并用两种振型质量和振型刚度计算结构的自振频率。

6、（20分）如果上题4中二层结构的初始速度为0而初始位移如下图所示，突然释放使结构自由振动，忽略结构的阻尼，确定结构的运动。

结构动力学试卷试卷号：PB060032一、( 本 大 题15分 )图 示 体 系 ，不 计 杆 质 量 ，试 求 其 自 振 频 率 。

/2二、( 本 大 题15分 )求 图 示 体 系 支 座 弯 矩 M A 的 最 大 值 。

荷 载P t P t (),.==004sin θθω 。

/2/2三、( 本 大 题20分 )求 图 示 体 系 的 自 振 频 率 和 主 振 型 ，并 作 出 振 型 图 。

已 知 ：m m m 12==， EI = 常 数 。

2m24m 4m四、( 本 大 题20分 )试 作 图 示 体 系 的 动 力 弯 矩 图。

柱 高 均 为 h ，柱 刚 度 EI =常 数 。

llθ=13257.EImh30.50.5P五、( 本 大 题30分 )求 图 示 体 系 的 自 振 频 率 ，不 计 梁 自 重 。

EI = 常 数 ，k 为 弹 簧 刚 度 。

ll试卷号：PB060033一、( 本 大 题15分 )试 求 图 示 体 系 在 初 位 移 等 于 l/1000，初 速 度 等 于 零 时 的 解 答 。

θωω=020.( 为 自 振 频 率 )，不 计 阻 尼 。

l二、( 本 大 题15分 )求 图 示 体 系 在 简 谐 荷 载 作 用 下 质 点 的 振 幅 。

θωθωω112113234==,, 为 自 振 频 率 。

1m1m1m三、( 本 大 题20分 )求 图 示 梁 的 自 振 频 率 及 主 振 型 ，并 画 主 振 型 图 形 。

杆 件 分 布 质 量 不 计 。

aaam四、( 本 大 题20分 )试 作 图 示 体 系 的 动 力 弯 矩 图 ，已 知 ：θ=0825673.EIml 。

0.5l0.5l2m五、( 本 大 题30分 )求 图 示 体 系 的 自 振 频 率 。

l /2l /2l m试卷号：PB060034一、( 本 大 题15分 )求 图 示 结 构 的 频 率 方 程 。

结 构 动 力 学 试 题 参 考 答 案 及 评 分 标 准（2006年上半年硕士研究生考试课程）1 解： a ）刚度即是使质点产生单位位移所需施加的力，设为k ，则：当质点产生位移Δ时，有：K Δ＝K 1Δ+K 2Δ；所以，等效刚度K ＝K 1+K 2()()12s I p W ku u k k u u W mu uW p t uδδδδδδδ-==+-==由虚功原理得：()()12k k u mu p t ++=3’b ）112212k k k ∆=∆=∆⎧⎨∆+∆=∆⎩联立解得： 1212k k k k k =+ 与a ）同理，得：()1212k k u mu p t k k +=+ 3’c ）()3312113k k k k k ∆=∆⎧⎪∆=+∆⎨⎪∆+∆=∆⎩联立解得：312123()k k k k k k k +=++与a ）同理，得：()312123()k k k u mu p t k k k ++=++ 4’2 解：()1212121221222222111224sin s D I p W k u u k u uW C u u C u u C u u C u uW m u u m u L u L m u u m u u m L u m Lu m L W m g L m g L δδδδδδδδδδθδθδδθδδθθδθδθδθθδθ-=+⎛⎫⎛⎫-=+⨯=+ ⎪ ⎪⎝⎭⎝⎭⎛⎫-=+++ ⎪⎝⎭=++++=-=-虚功原理：0s I D p W W W W δδδδ+++= 得：12212122222100040000m m m L k ku u u C C m L m L m g L θθθθ⎡⎤⎧⎫⎧⎫+++⎡⎤⎡⎤⎧⎫⎧⎫⎪⎪⎪⎪⎢⎥++=⎨⎬⎨⎬⎨⎬⎨⎬⎢⎥⎢⎥⎢⎥⎩⎭⎩⎭⎣⎦⎣⎦⎪⎪⎪⎪⎩⎭⎩⎭⎣⎦6’ 6’ 8’3 解：由题可知：0.66D T s = cm u 1.3)0(= () 2.4D u T cm = 所以：111 3.1ln ln 4.07%22 2.4i i u u ξππ+=== 5’9.528/n w rad s ====2323900109.528/9.8833710/8337/n K mw N m KN m ==⨯⨯=⨯= 5’阻尼系数：3220.0407900109.528/9.871227/71.23/n C mw N s m KN s m ξ==⨯⨯⨯⨯=∙=∙ 5’4 解：以k m -1体系静平衡位置作为原点则1m ,2m 共同作用的静平衡位置kgm u st 2=碰撞之前2m的速度2v m =’ 碰撞之后：动量守恒12()(0)m m u m +=即(0)u =动力方程：()()()120st st m m u u K u u ''+-+-=()122m m u Ku m g ⇒++=解得： ⎪⎪⎭⎫ ⎝⎛+=++=212sin cos m m K w K g m t w B t w A u n n n 将(0)0u =及(0)u =2,m g A B m k =-=于是：22cos n n n m g m g u w t m w t k Kw =-++⎛= ⎝式中5’ 5’ 5’5 解：一根钢梁的刚度为1348EIK l=所以体系的刚度：861339696 2.0610 4.561026523.3/2.4EI K K KN m l -⨯⨯⨯⨯==== 1’500.267 4.09106523.3st P u m K -===⨯ 1’100.6/n w rad s === 2’30021060w ππ⨯== /rad s 1’ 100.3123100.6n w w πβ=== 1’ 01.0=ξ0 1.108d stu R u ==== 2’ 550 4.0910 1.108 4.5310st d u u R m --==⨯⨯=⨯ 2’ 设 ()φ-=wt u u sin 0 则 ()φ--=''wt w u u sin 20 所以： 加速度振幅()2252200 4.531010 4.4710/a u w m s π--==⨯⨯=⨯ 5’6 解：利用虚功原理：11222s W ku u ku u δδδ-=+........2121221212212I mm l l u u u u u u u u l W δδδ⎛⎫⎛⎫++--⎛⎫⎛⎫ ⎪ ⎪-=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由W s δ＋W I δ＝0可得：0)632()63(2..1..221..2..11=+++++u u u u u u u u m m K m m K δδ；由u 1δ、u 2δ为任意数方程成立，故：⎪⎪⎩⎪⎪⎨⎧=++=++0632063..1..22..2..11u u u u u u m m K m m K 写成矩阵形式为：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡00200366321..2..1u u u u K K m m m m8’ 运动特征方程为：（[K]-ω2[M]）{φ}=0；可得：2[K]-[M]0ω=即：03266322=----ωωm k m m m k ⇒结构得自振频率为：.1=ω 1.5925m k ；.2=ω 3.0764mk。

结 构 动 力 学 试 题（2018年上半年硕士研究生考试课程）参考公式：（式中ξ为阻尼比，β为频率比） (1) 单自由度体系动力放大系数0d stu R u ==(2) 单自由度体系传递率TR()()()22222121ξββξβ+-+=TR1（15’）建立题1图所示的三个弹簧-质点体系的运动方程。

❍☎♦✆◆❍♍♋✆♌✆♍✆♍♍❍☎♦✆◆❍◆☎♦✆◆❍◆题1图2（20’）汽车在多跨连续梁桥梁上行驶，桥梁跨度均为L=32m,桥面由于长时徐变效应而产生12cm 的挠度（如题2图所示）。

桥面可以用振幅为12.0cm 的正弦曲线来近似，汽车可以用一个单质点体系模拟，如果汽车重m=2.8tf ，等效弹簧刚度k=280E3 N/m ，等效阻尼比5.0=ξ，求:（1）汽车以72km/h ν=行驶时，汽车的竖向运动()t u t 的振幅t u 0；（2）发生共振时汽车的行驶速度（此处指使振幅最大时的速度）。

题2图3（15’）如题3图所示，一总质量为m 的刚性梁两端由弹簧支撑，梁的质量均匀分布、两弹簧的刚度分别为k 和2k 。

定义的两个自由度u 1和u 2示于图中，建立结构体系的运动方程，并求出的振型和自振频率。

题3图4（15’）题4图所示动力体系为：AB 、BC 杆件都为均布质量刚杆，单位均布质量分别为m 1 、m 2，M 为集中质量，C1及C2为阻尼系数，K1及K2为刚度系数，在C 点作用有压力N 。

以B 点竖向位移B u u =为广义坐标，试求： （1）列出体系的运动方程 （2）求出体系的自振频率 （3）求出临界压力N 。

题4图5（15’）工程场地竖向加速度为0.10g u g =，振动频率为10f Hz =，安放一个质量50m kg =的敏感仪器。

仪器固定在刚度14/k kN m =，阻尼比10%ξ=的橡胶隔振垫上，求： （1） 传递到仪器上的加速度是多少？（2） 如果仪器只能承受0.0038g 的加速度，给出解决方案。

结构动力学试题及答案一、选择题（每题2分，共10分）1. 结构动力学中，动力响应分析通常不包括以下哪一项？A. 自振频率分析B. 模态分析C. 静力分析D. 动力放大系数分析答案：C2. 在结构动力学中，下列哪一项不是确定结构动力特性的基本参数？A. 质量B. 刚度C. 阻尼D. 材料强度答案：D3. 单自由度振动系统的动力平衡方程中，下列哪一项是正确的？A. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t)B. m\(\ddot{x}\) + c\(\dot{x}\) + kx = 0C. m\(\ddot{x}\) + c\(\dot{x}\) + kx = FD. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t) - F答案：A4. 对于多自由度振动系统，下列哪一项不是求解动力响应的方法？A. 模态叠加法B. 直接积分法C. 能量守恒法D. 振型分解法答案：C5. 在结构动力学中，阻尼比通常用来描述阻尼的相对大小，其定义为：A. 临界阻尼比B. 阻尼比C. 阻尼比的倒数D. 阻尼比的平方答案：B二、填空题（每题2分，共10分）1. 结构动力学中，当外力作用频率与结构的_________相等时，结构会发生共振。

答案：自振频率2. 多自由度振动系统的振型是指系统在自由振动时的_________。

答案：位移分布模式3. 动力响应分析中，_________是指在给定的外力作用下，结构的响应随时间变化的过程。

答案：动力响应4. 在结构动力学中，_________是指结构在动力作用下，其响应与外力作用的关系。

答案：动力特性5. 阻尼比越大，结构的_________越小，振动衰减越快。

答案：振幅三、简答题（每题5分，共20分）1. 简述结构动力学中模态分析的目的和意义。

答案：模态分析的目的是确定结构的自振频率和振型，意义在于了解结构的动力特性，为结构设计提供依据，以及评估结构在动力作用下的安全性和稳定性。

结 构 动 力 学 试 题（2006年上半年硕士研究生考试课程）参考公式：(1)对数衰减率1ln ii u u δ+==（ζ<5%时可假设1-ζ2=1） (2) 单自由度体系动力放大系数0d st u R u ==(3) 单自由度体系自由振动计算公式：(0)()(0)cos sin n n n u u t u t t ωωω=+(4) 跨度L 简支梁跨中集中荷载P 作用下跨中位移v ＝PL 3/(48EI)1 建立题1图所示的三个弹簧-质点体系的运动方程（10’）。

题1图2 如题2图所示一质量为m1的质量块可水平运动，其上部与一无重刚杆相连，无重刚杆与刚度为k2的弹簧及阻尼系数为c2的阻尼器相连，m1右端与刚度为k1的弹簧相连，左端与阻尼系数为c1的阻尼器相连。

摆锤m2以长为L的无重刚杆与滑块以铰相连，摆锤只能在图示铅垂面内摆动。

建立以广义坐标u和θ表示的体系运动方程（坐标原点取静平衡位置，假定系统作微幅振动，sinθ=tanθ=θ、cosθ=1、可忽略所有二次及以上项）。

计算结果要求以刚度矩阵，质量矩阵，阻尼矩阵的形式给出。

（20’）题2图3 单自由度建筑物的重量为900kN，在位移为3.1cm时（t＝0）突然释放，使建筑产生自由振动。

如果往复振动一周后的最大位移为2.4cm（t＝0.66s），试求：（1）建筑物的刚度k；（2）阻尼比ξ；（3）阻尼系数c。

（15’）4 一质量为m1的块体用刚度为k的弹簧悬挂处于平衡状态（如题4图所示）。

另一质量为m2的块体由高度h自由落下到块体m1上并与之完全粘接，确定由此引起的运动u(t)，u(t)由m1-k体系的静平衡位置起算。

（20’）题4图5 重645kg空调机固定于两平行简支钢梁的中部（见题5图）。

梁的跨度2.4m，每根梁截面的惯性矩为4.56×10-6m4，空调机转速300r/min，产生0.267kN的不平衡力，假设体系阻尼比为1％，并忽略钢梁的自重，求空调机的竖向位移振幅和加速度振幅。

研究生课程考核试卷
（适用于课程论文、提交报告）
科目：结构动力学大作业教师：刘纲
姓名：刘亚南学号：20131613144 专业：建筑与土木工程类别：专业
上课时间：2013 年11 月至2014 年1 月
考生成绩：
卷面成绩平时成绩课程综合成绩阅卷评语：
阅卷教师(签名)
重庆大学研究生院制
土木工程学院2013级硕士研究生考试试题
科目名称：结构动力学考试日期：2014年1月总分：20分
1、按规定设计一个2跨3层钢筋混凝土平面框架结构（部分要求如附件名单所示；未作规定部分自定）。

根据所设计的结构参数，求该结构的一致质量矩阵、一致刚度矩阵；
2、至少采用两种方法求该框架结构的频率和振型；
3、输入地震波（地震波要求如附件名单所示），采用时程分析法，利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。

要求给出：
（1）框架结构图，并给出一致质量矩阵和一致刚度矩阵；
（2）出两种方法名称及对应的频率和振型；
（3）输入地震波的波形图，计算所得各楼层位移反应时程图。

结构动力学-刘亚南（20131613144）
目录
题目一
1、框架设计 (2)
2、结构的一致质量矩阵 (3)
3、结构的一致刚度矩阵 (6)
题目二
1、建立框架结构的运动微分方程 (10)
2、用Rayleigh法求近似基频 (10)
3、用Stodola法求频率 (12)
题目三
1、框架资料 (15)
2、分析方法 (15)
3、具体操作步骤 (16)
4、地震波的波形图 (21)
5、时程反应图 (21)
第1页/共26页。

结构动力学结构动力学试卷（练习题库）1、结构动力计算与静力计算的主要区别是什么？2、什么是动力自由度，确定体系动力自由度的目的是什么？3、结构动力自由度与体系几何分析中的自由度有何区别？4、结构的动力特性一般指什么？5、什么是阻尼、阻尼力，产生阻尼的原因一般有哪些？什么是等效粘滞阻尼？6、采用集中质量法、广义位移法（坐标法）和有限元法都可使无限自由度体系简化为有限自由度体系，它们采用的手7、建立运动微分方程有哪几种基本方法？各种方法的适用条件是什么？8、直接动力平衡法中常用的有哪些具体方法？它们所建立的方程各代表什么条件？9、刚度法与柔度法所建立的体系运动方程间有何联系？各在什么情况下使用方便？10、计重力与不计重力所得到的运动方程是一样的吗？11、自由振动的振幅与哪些量有关？12、什么叫动力系数，动力系数大小与哪些因素有关？单自由度体系位移动力系数与内力动力系数是否一样？13、若要避开共振应采取何种措施？14、增加体系的刚度一定能减小受迫振动的振幅吗？15、突加荷载与矩形脉冲荷载有何差别。

16、平断面假定17、弯曲要素18、梁的边界条件19、叠加原理20、三弯矩方程21、平断面假定22、梁的边界条件23、叠加原理24、三弯矩方程25、虚位移原理26、虚力原理27、位能驻值原理28、板条梁29、开口和闭口薄壁杆件。

30、应力的重新分布。

31、几何不变体32、自由度33、多余约束34、超静定结构35、形常数和载常数36、试简述影响线与内力图的区别？37、力法和位移法的解题思路？38、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。

39、有多余约束的体系一定是几何不变体系。

40、计算自由度W小于等于零是体系几何不变的充要条件。

41、两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。

42、静定结构的全部内力及反力，只根据平衡条件求得，且解答是唯一的。