山东省青岛市一中2017年自主招生考试笔试数学试题

2017年山东省青岛十九中自主招生数学试卷一、选择题（本题满分36分，共有6道小题，每小题6分）1．（6分）计算＝（）A．5﹣B．4﹣C．﹣2﹣D．﹣1﹣2．（6分）满足不等式组的x的取值范围是（）A．﹣3＜x＜﹣1B．x＞3C．﹣1＜x＜3D．x＜﹣33．（6分）如图所示，在正方体ABCD﹣A1B1C1D1中，点E，F分别是AB，AD中点，则△EFB1在面DCC1D1上的投影是（）A．B．C．D．4．（6分）一组数据﹣3，a，5，3，b，其中a＞0，b＞0，平均数为3，极差为10，则这组数据的众数为（）A．7B．5C．3D．﹣35．（6分）已知两函数y1和y2，若函数y＝y1﹣y2的图象与x轴有两个不同的交点，则称y1和y2这两个函数是“关联函数”．着函数y＝ax2与函数y2＝x﹣1是“关联函数”，则a 的取值范围是（）A．a＜且a≠0B．a≥C．a≤D．a＜6．（6分）如图，在△ABC中，以AB为直径的圆O交AC于点D，过D作DE⊥BC于点E，且∠BDE＝∠A，若AB＝10，AC＝16，则sin A＝（）A．B．C．D．二、填空题（本题满分30分，共有5道小题，每小题6分）7．（6分）如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，当n ＝9时，y＝．8．（6分）青岛第十九中学台东校区教学楼的俯视图如图所示，其中四边形ABEF与四边形BCDE均为直角梯形，∠BAF＝∠BCD＝90°，AF＝CD＝18m，EF＝50m，AB＝56m，则∠ABC的度数为．9．（6分）函数y＝kx图象与函数y＝的图象交于A，B两点，若BC∥x轴，AC∥y轴，则△ABC的面积为．10．（6分）如图，AB是圆O的直径，AB＝8，点M在圆O上，∠MOB＝60°，N是的中点，P为AB上一动点，则PM+PN的最小值是．11．（6分）已知二次函数y＝ax2+bx+c（a≠0）的图象开口向下，并过点（1，0），且9a﹣3b+c＝0，则下列说法正确的序号是．①函数的对称轴是直线x＝﹣1；②若A（﹣2，y1），B（）是抛物线上的两点，则y1＜y2；③满足不等式bx+c＞0的x的范围是x＜；④若a＝﹣1，则二次函数的解析式为y＝﹣x2﹣2x+3．三、解答题（本题满分54分，共有4道小题）12．（12分）2017年3月，青岛十九中高一年级举行“诗词大会“比赛，根据参赛学生的成绩划分为A、B、C、D四个等级，并绘制了不完整的两种统计图，根据图中提供的信息，回答下列问题：（1）参加“诗词大会”的学生共有人，并把条形统计图补充完整；（2）扇形统计图中，m＝，n＝；（3）4月份全市将举行“诗词大会”比赛，要求每个学校选派两位同学参加比赛，我校获A等级的学生中恰有两名男生，利用树状图或列表的方法，求从我校获A等级的学生中选出一男一女两位同学参加比赛的概率．13．（13分）青岛十九中新校广场上拟建造一圆形喷水池，在水池中央垂直于水面处要安装一个柱子OA，水流由柱子顶端A处的喷头喷出，喷出的水流呈抛物线形，O点恰好在水面中心，OA为1.5m，水流最高点为B，AB与水平面成45°角，B点距离水面的垂直高度为3.5m．（1）按如图所示的平面直角坐标系，求抛物线的解析式；（2）喷水池的半径至少为多少米，才能使水流不至于落到水池外？14．（14分）已知△ABC中，∠ABC＝45°，BA＝BC，BE平分∠ABC，CD⊥AB于D，CD 交BE于F．（1）求证：AD＝DF；（2）设BC＝a，求的值．15．（15分）如图，抛物线的解析式为y＝x2﹣2x﹣3，图象与x轴交于A，B两点（A点在B 点左侧），与y轴交于C点，顶点为D．（1）设P是线段BC上一点，过P作PE垂直x轴于点E，若S△BPE＝S△AOC，试求出满足条件的点P的坐标．（2）设点Q在抛物线位于第四象限的部分上运动，过Q作QF垂直x轴于点F，若△BFQ ∽△DCB，试求出满足条件的点Q的坐标．。

青岛一中2017年自主招生考试笔试数学试题一、选择题(本题满分24分,共有6道小题,每小题4分)1.若(a+b)2+|2a-b-24|=0,则a 的算术平方根是()A.2B.4C.22D.222.如图,⊙O 是△ABC 的外接圆,若∠OCB=40°,则∠A 的度数等于()第2题第4题A.60° B.50° C.45°D.40°3.点A(x 1,y 1)、B(x 2,y 2)、C(x 3,y 3)都在反比例函数x 1-a -a 2y 2的图象上,且21x x ＜＜0＜3x ，则y 1、y 2、y 3的大小关系是()A.213y y y ＜＜B.321y y y ＜＜C.123y y y ＜＜D.312y y y ＜＜4.如图,三个区域A 、B 、C 栽种观赏植物,要求同一个区域中种同一种植物,相邻的两个区域种不同的植物,现有3种不同的植物可供选择,那么栽种方案有() A.27种B.18种C.12种D.6种5.在凸8边形的所有内角中,锐角的个数最多是() A.1B.2 C.3 D.46.如果有2017名学生排成一列,按1,2,3,4,3,2,1,2,3,4,3,2,,的规律报数,那么第2017名学生所报的数是() A.1B.2 C.3 D.4二、填空题(本题满分16分,共有4道小题,每小题4分)7.方程02x 6-x -x 2的解为_______.8.如图,AB ∥CD,E 、F 分别为AC 、BD 的中点,若AB=10,CD=6,则EF 的长是_________.第8题第10题9.规定符号“i ”满足i 2=-1,则20182016i i ___________.10.如图,矩形ABCD 的对角线AC=10,AB=6,则图中五个小矩形的周长之和等于_________. 三、解答题(本题满分80分,共有7道小题）11.(本小题满分10分）先化简1-x 4x 4-x 1-x 1-122再求值,已知x 是整数且满足-3＜x ＜312.(本小题满分10分)如图,在等边三角形ABC 中,D 是BC 边上的一点,延长AD 至E,使AE=AC,∠BAE 的平分线交△ABC 的高BF 于点O,求cos ∠AEO.。

学校姓名考场座位号2024年自主招生素质检测数学试题注意事项:1.本试卷满分为150分,考试时间为120分钟㊂2.全卷包括 试题卷 (4页)和 答题卡 (2页)两部分㊂3.答题一律要求用0.5m m 黑色签字笔在答题卡上规定的地方答卷,作图题使用2B 铅笔作答,考试不使用计算器㊂4.考试结束后,请将 试题卷 和 答题卡 一并交回㊂一㊁选择题:共10小题,每小题5分,共50分㊂在每小题给出的四个选项中,只有一项是符合题目要求的㊂1.由5个相同的小立方体搭成的几何体如图所示,现拿走一个小立方体,得到几何体的主视图与左视图均没有变化,则拿走的小立方体是A .①B .②C .③D .④2.黄山景色绝美,景观奇特. 五一 假期,黄山风景区进山游客近13万人,黄山景区门票旺季190元/人,以此计算, 五一 假期黄山景区进山门票总收入用科学计数法表示为A .0.247ˑ107B .2.47ˑ107C .2.47ˑ108D .247ˑ1053.下列因式分解正确的是A .2x 2+y 2+4x y =(2x +y )2B .x 3-2x y +x y 2=x (x -y )2C .x 2-(3y -1)2=(x -1+3y )(x +1-3y )D .a x 2-a y 2+1=a (x +y )(x -y )+14.已知点A (x 1,y 1),B (x 2,y 2)是抛物线y =a x 2-3x +3上两点,当a -x 1-x 2=2时,y 1=y 2,则该抛物线与坐标轴的交点个数为A .3个或0个B .3个或1个C .2个或0个D .2个5.若关于x 的不等式组x +2a <03x +a <15的解集中的任意x 的值,都能使不等式x -4<0成立,则实数a 的取值范围为A .a <-3B .a <-2C .a ȡ-2D .a ȡ36.如图,已知әA B C 中,A D 为øB A C 的平分线,A B =8,B C =6,A C =10,则D C 的值为A .10B .2C .5D .17.如图,B (-2,0),C (4,0),且B E 所在的直线与A C 垂直,øA C B -øB A O =45ʎ,连接O D ,若射线O D 上有一点M ,横坐标为6,则әB O M 的面积为A .3B .6C .23D .728.定义:用M a ,b ,c 表示这三个数的中位数,用M i n {a ,b ,c }表示这三个数的最小数.例如:M {-1,12,0}=0,M i n {-1,12,0}=-1.如果M {4,x 2,2x -1}=M i n {4,x 2,2x -1},则x 的值为A .2或-2B .1或12C .2或12D .1或529.如图,әA B C 中,A B =B C ,øB =120ʎ,E 为平面内一点,若A E =3,C E =2,则B E 的值可能为A .2.5B .3C .0.3D .0.510.如图,直线A B :y =13x +b 与反比例函数y =kx相交于点A (3,5),与y 轴交于点B ,将射线A B 绕点A 逆时针旋转45ʎ,交反比例函数图象于点C ,则点A ㊁B ㊁C 构成的三角形面积为A .12B .1110C .232D .554二㊁填空题:共4小题,每小题5分,共20分㊂11.某市为改善市容,绿化环境,计划经过两年时间,绿地面积增加44%,则这两年平均绿地面积的增长率为.12.若x 9+x 8+ +x 2+x +1=0,则x 的值为.13.定义:对于函数y =l g x (x >0),y 随x 的增大而增大,且l g 10=1,l g xy=l g x -l g y ,l g x y =l g x +l g y .若1a +5b =5,则l g a +l g b 的最大值为.14.已知二次函数y =2x 2+b x +c 图象的对称轴为直线x =34,且过点(3,10),若其与直线y =3交于A ㊁B 两点,与直线y =x +5交于P ㊁Q 两点,则P Q 2A B值为.三㊁解答题:共5题,共80分㊂解答应写出文字说明,证明过程和解题步骤㊂15.(12分)(1)若13a +25b =1,23a +35b =3,求a 2-b 2+8b -172025;(2)先化简再求值:m +2m -m -1m -2ːm -4m 2-4m +4,其中m =2s i n 30ʎ㊃t a n 45ʎ-32t a n 30ʎ.16.(12分)请按以下要求完成尺规作图.(1)如图1,菱形A B C D 中,点P 在对角线B D 上,请作出一对以B D 所在直线为对称轴的全等三角形,使交B A 于点M ,交B C 于点N ,әP B M ɸәP B N .你有几种解法?请在下图中完成;(保留必要作图痕迹,不写作法)(2)如图2,点P 是菱形A B C D 内部一点,请作出一条过点P 的直线,交射线B A ㊁射线B C 于点M ㊁N ,且B M =B N ,聪明的你肯定有多种不同作法?请在下图中完成两种作法,并选择其中一种证明:B M =B N .(保留必要作图痕迹,不写作法)17.(15分)如图,直角三角形A B C中,以直角边A B为直径作圆交A C于点D,过点D作D MʅA B于点M,E为D M的中点,连接A E并延长交B C于点F,B F=E F.(1)求证:C F=B F;(2)求t a nøD E F;(3)若D F=2,求圆的面积.18.(19分)已知四边形A B C D,A B=4,点P在射线B C上运动,连接A P.(1)若四边形A B C D为正方形,点M在A P上,且øA D M=øA P D.请判断A M㊁A P㊁A C之间数量关系,并说明理由;(2)若四边形A B C D为菱形呢?øB=60ʎ,其他条件与(1)同,则(1)中的结论还成立吗?并说明理由;(3)若四边形A B C D为正方形,将线段A P绕点P顺时针旋转90ʎ于P Q,此时D Q的最小值为多少?A Q+D Q的最小值呢?并说明理由.19.(22分)已知抛物线y=a x2+b x+c的顶点坐标为A(1,4),与x轴交点分别为点B㊁C(点B在点C 左侧),与y轴交点为D,一次函数y=k x+4(k>0)与x轴所形成的夹角的正切值为4,方程k x+4=a x2+b x+c有两个相等的实数根.(1)求该抛物线的解析式;(2)点M是该抛物线上一动点,则在抛物线对称轴上是否存在点N,使得以A㊁B㊁M㊁N为顶点的四边形为平行四边形?若存在,请求出所有满足条件的点N坐标及该平行四边形的面积;若不存在,请说明理由;(3)若将该抛物线向左平移1个单位,再向下平移4个单位得到抛物线y',点D关于x轴的对称点为D',若过点D'的直线与y'交于P㊁Q两点(点P在点Q左侧),点Q关于y轴的对称点为Q',若әP Q O与әP Q Q'面积相等,求直线P Q的解析式.2024年自主招生素质检测数学参考答案选择题:共10小题,每小题5分,满分50分㊂题号12345678910答案CBCBCABDAD填空题:共4小题,每小题5分,满分20分㊂11.20% 12.-1 13.1 14.2654.ʌ解析ɔ x 1+x 2=a -2,抛物线的对称轴x =--32a,ʑ32a =a -22⇒a 2-2a -3=0⇒(a +1)(a -3)=0⇒a 1=-1,a 2=3,ʑ①当a 1=-1时,y =-x 2-3x +3,Δ=9+12>0,与坐标轴的交点个数为3个;②当a 2=3时,y =3x 2-3x +3,Δ=9-4ˑ3ˑ3<0,与坐标轴的交点个数为1个.5.ʌ解析ɔ x <-2a ,x <15-a 3,①-2a >15-a 3,解得a <-3,ʑx <15-a 3,ȵx <4,ʑ15-a 3ɤ4,解得a ȡ3(舍去);②-2a ɤ15-a 3,解得a ȡ-3,ʑx <-2a ,ȵx <4,ʑ-2a ɤ4,解得a ȡ-2.6.ʌ解析ɔ 由角平分线定理S әA B D S әA C D =A B ㊃h A C ㊃h =45=B D D C ,ʑ45=6-D C D C ,解得D C =103.7.ʌ解析ɔ øB E O =øB A E +øA B E ,øA C B =øB A O +45ʎ,R t әB O E ʐR t әB D C ,ʑøB E O =øA C B ,ʑøA B D =45ʎ,则әA B D 为等腰直角三角形,A D =B D ,ʑR t әA E D ɸR t әB C D ,ʑA E =B C ,S әA E D =S әB C D ,ʑh 1=h 2,ʑ点D 在øA O C 的角平分线上,M (6,6),S әB O M =2ˑ62=6.8.ʌ解析ɔ 由图像知x 2=2x -1,解得x =1;或2x -1=4,解得x =52.9.ʌ解析ɔ 设B E =x ,将әA B E 绕B 点顺时针旋转120ʎ到әC B E ',C E '=A E =3,øE B E '=120ʎ,B E =B E '=x ,易得E E '=3x ,在әC E E '中,C E '-C E <E E '<C E '+C E ,即3-2<3x <2+3,解得33<x <533.10.ʌ解析ɔ 由题知,直线y =13x +b 与反比例函数y =k x相交于点A(3,5),则13ˑ3+b =5,解得b =4,k =15,法一:直线A C 与y 轴交于点M ,从M 点作直线A B 的垂线,垂足为N ,A M =(m -5)2+32,MN =(4-m )s i n θ=(4-m )310,A M =2MN ,ʑ(m -5)2+9=95(m -4)2⇒5(m -5)2+45=9(m -4)2,2m 2-11m -13=0⇒(2m -13)(m +1)=0,ʑm =132(舍)或m =-1,直线A C 的方程为y =2x -1.2x -1=15x ⇒2x 2-x -15=0⇒(2x +5)(x -3)=0,解得x 1=-52,x 2=3,ʑ点C (-52,-6),S әA B C =5ˑ(3+52)2=554.法二:易知l A B :y =13x +4,设l A C :y =k 2x +b ,由倒角公式得t a n 45ʎ=k 2-k 11+k 1k 2=k 2-131+13k 2=1,k 2-13=13k 2+1,两边平方得k 2=2或k 2=-12(舍),又l A C 过点A ,ʑl A C :y =2x -1(与y 轴交点为M ),与y =15x 联立得x C =-52,ʑS әA B C =12BM |x A -x C |=554.12.ʌ答案ɔ -1ʌ解析ɔ 若x =0,等式不成立,则x ʂ0,等式两边同乘x ,ʑx 10+x 9+x 8+ +x 2+x =0⇒x 10-1=0⇒x 10=1,解得x =ʃ1.当x =1时,等式不成立;当x =-1时,等式成立.13.ʌ解析ɔ l g a +l g b =l ga b ,即求a b 的最大值,12a +54b ȡ212a ㊃54b =258a b ,258a b ɤ5⇒a b ɤ10.14.ʌ解析ɔ 由题知,-b 4=34,解得b =-3,抛物线过点(3,10),代入数据解得c =1,抛物线y =2x 2-3x +1,当y =3时,2x 2-3x +1=3,解得x 1=-12,x 2=2,A B =52,当y =x +5时,2x 2-3x +1=x +5⇒x 2-2x -2=0⇒x 3+x 4=2,x 3x 4=-2,(x 3-x 4)2=(x 3+x 4)2-4x 3x 4=12,P Q =(1+k 2)(x 3-x 4)2=26,P Q 2A B =265.15.(12分)ʌ解析ɔ (1)13a +25b =1, ①23a +35b =3, ②①+②得a +b =4,(2分) a 2-b 2+8b -17=(a +b )(a -b )+8b -17=4a -4b +8b -17=4a +4b -17=-1,(4分)a 2-b 2+8b -17 2025=-1.(6分)(2)原式=m +2m -m -1m -2㊃(m -2)2m -4=m 2-4-(m 2-m )m (m -2)㊃(m -2)2m -4=m -4m (m -2)㊃(m -2)2m -4=m -2m,(8分)m =2ˑ12-32ˑ33=12,(10分) ʑ原式=12-212=-3.(12分) 16.(12分)ʌ解析ɔ (1)提示:作P M ㊁P N 分别垂直于A B ㊁A C ,如图1;(2分)过P 点作MN 垂直于B D ,如图2;(4分)P 作E F ʊB C A B 于点E C D 于点F E M =E P M P 交B C 于点N作法二:先作B M '=B N ',交A B 于点M ',交B C 于点N ',连接M 'N ',将直线M 'N '平移过点P ,交A B 于点M ,交B C 于点N ,即MN 为所求直线,如图4;(8分)选择作法一证明:ȵE M =E P ,ʑøE M P =øE P M ,ȵE F ʊB C ,ʑøE P M =øB NM ,ʑøE M P =øB NM ,ʑB M =B N .(12分)选择作法二证明:ȵB M '=B N ',ʑøB M 'N '=øB N 'M ',M 'N 'ʊMN ,ʑøB MN =øB M 'N ',øB NM =øB N 'M ',ʑøB MN =øB NM ,ʑB M =B N .(12分)(作法不限,合理即可)17.ʌ解析ɔ (1)ȵD M ʊB C ,ʑәA D E ʐәA C F ,әA E M ʐәA F B ,ʑA E A F =D E C F ,A E A F =E M B F,(2分) ȵD E =E M ,ʑC F =B F ;(4分)(2)取A B 的中点O ,即为圆心,连接O F ,设圆O 的半径为r ,延长A B 交D F 延长线于G ,由(1)知,F 为R t әB C D 中斜边B C 的中点,ʑD F =B F =E F ,ʑøF D E =øD E F =øA E M ,ȵøG +øG D M =øE A M +øA E M =90ʎ,则øG =øE A M ,ʑA F =F G ,在әA F G 中,F B ʅA G ,则A B =B G =2r ,A O =r ,O G =3r ,(6分)ȵO F ʊA C ,ʑO G A O =F G D F=3,即F G =3D F ,(8分) ȵD F =B F ,ʑF G =3B F ,ʑc o s øB F G =B F F G =13,ʑt a n øD E F =t a n øE D F =t a n øB F G =B G B F=22;(10分)(3)ȵD F =B F ,ʑB F =2,由(2)知,t a n øB F G =B G B F=22,ʑB G =42,(12分)ȵB G =2r ,ʑr =22.(13分)S 圆O =πr 2=8π.(15分)18.ʌ解析ɔ (1)A C 2=2A M ㊃A P .(2分)理由如下:如图1,ȵøA D M =øA P D ,øD A M =øP A D ,ʑәA D M ʐәA P D ,ʑA D A P =A M A D ,ʑA D 2=A M ㊃A P ,在正方形A B C D 中,A D =22A C,ʑ(22A C )2=A M ㊃A P ,ʑA C 2=2A M ㊃A P .(6分)(2)(1)中的结论不成立.(7分) 理由如下:如图2,ȵøA D M =øA P D ,øD A M =øP A D ,ʑәA D M ʐәA P D ,ʑA D A P =A M A D,ʑA D 2=A M ㊃A P ,ȵ在菱形A B C D 中,øB =60ʎ,则B C =A B =A C =A D ,ʑA C 2=A M ㊃A P .(11分)(3)如图3,过点Q 分别作Q E ʅB C 的延长线于点E ,Q F ʅC D 于点F ,ʑQ F =C E ,设B P =m ,A P =Q P ʑR t әA B P ɸR t әP E Q ,则B P =Q E =m ,A B =P E =4,ȵC E +P C =B P +P C =4,ʑC E =B P =m ,在R t әD F Q 中,Q F =C E =m ,D F =C D -C F =4-m ,(15分) D Q 2=D F 2+Q F 2=(4-m )2+m 2=2m 2-8m +16=2(m -2)2+8,当m =2时,D Q 取得最小值,D Q m i n =22,(17分) 分析易知Q 在C D '上运动,作D 关于C D '的对称点C ',连接Q C ',则(A Q +D Q )m i n =(A Q +Q C ')m i n =A C '=42+82=45.(19分) 19.ʌ解析ɔ (1)由题可知k =4,ʑy =4x +4(2分) 2的顶点坐标为A y =a x -12即4x +4=a (x -1)2+4⇒a x 2-(2a +4)x +a =0有两个相等的实数根,ʑΔ=(2a +4)2-4a 2=0,解得a =-1,ʑ抛物线的解析式为y =-(x -1)2+4=-x 2+2x +3;(5分)(2)设M 点坐标为(m ,-m 2+2m +3),N 点坐标为(1,n ),A (1,4),令-x 2+2x +3=0,解得x 1=-1,x 2=3,所以B (-1,0),C (3,0),(7分)若A B 为对角线,1-12=m +12,解得m =-1(舍去);若A M 为对角线,m +12=1-12,解得m =-1(舍去);若A N 为对角线,1+12=m -12,解得m =3;(9分) 4+n 2=0-m 2+2m +32,解得n =-4,此时M (3,0),N (1,-4),(10分)S ▱A B M N =4ˑ82=16;(12分) (3)由题可知,抛物线y '=-x 2,点D (0,3)关于x 轴的对称点D '(0,-3),直线P Q 过点D ',设直线P Q 的解析式为y P Q =k x -3,若k >0,如图1,S әP Q O =S әP Q Q ',则Q 'O ʊP Q ,则әQ 'H O ɸәQ H D ',所以O H =12O D '=32,H (0,-32),所以Q (62,-32),Q '(-62,-32),直线P Q 的解析式为y P Q =62x -3;(16分)若k <0,如图2,过点Q '作直线l ʊP Q ,取l 与y 轴交点M ,作O L ʅP Q 于点L ,MH ʅP Q 于点H ,所以O L ʊHM ,S әP Q O =S әP Q O ',所以O L =HM ,所以四边形O L MH 为平行四边形,则对角线互相平分,所以M (0,-6),同理,әD 'K Q ɸәM K Q ',所以D 'K =K M =12D 'M =32,所以K (0,-92),(20分) 因为点Q 的纵坐标为-92,所以Q (322,-92),直线P Q 的解析式为y P Q =-22x -3.(21分)综上,直线P Q 的解析式为y P Q =6x -3或y P Q =-2x -3.分)。

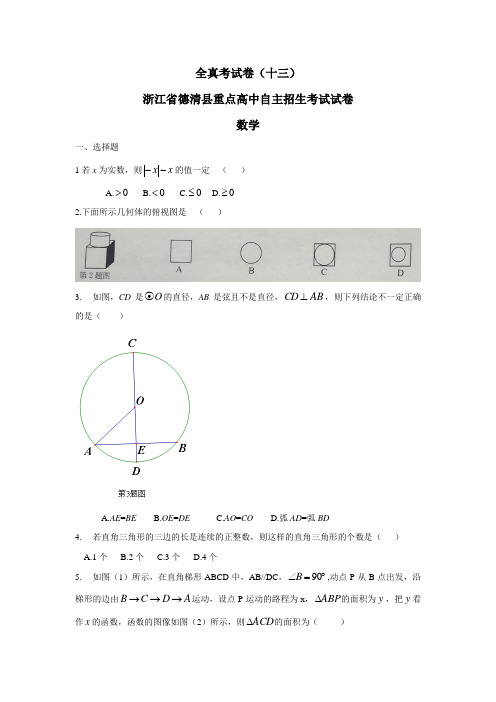
全真考试卷（十三）浙江省德清县重点高中自主招生考试试卷数学一、选择题1若x 为实数，则x x --的值一定 （ ）A.0>B.0<C.0≤D.0≥2.下面所示几何体的俯视图是 （ ）3. 如图，CD 是O ⊙的直径，AB 是弦且不是直径，AB CD ⊥，则下列结论不一定正确的是（ ）A. A E =BEB.OE =DEC.AO =COD.弧AD =弧BD4. 若直角三角形的三边的长是连续的正整数，则这样的直角三角形的个数是（ ）A.1个B.2个C.3个D.4个5. 如图（1）所示，在直角梯形ABCD 中，AB//DC ，︒=∠90B ,动点P 从B 点出发，沿梯形的边由A D C B →→→运动，设点P 运动的路程为x ，ABP ∆的面积为y ，把y 看作x 的函数，函数的图像如图（2）所示，则ACD ∆的面积为（ ）A.10B.16C.18D.326.用“▲”，“●”，“◆”分别表示三种物体的重量，若▲●◆▲◆●●▲+=-=，则“▲”，“●”，“◆”这三种物理的重量比为（ ）A.2:3:4B.2:4:3C.3:4:5D.3:5:47. 已知()b a b a <<0,为抛物线()()2----=d c x c x y 与x 轴交点的横坐标，则b c c a -+-的值是（ ）A.a b -B.b a -C.b a -或a b -D.08. 在平行四边形ABCD 中，点F 事BC 的中点，AF 与BD 交于点E ，则ABE ∆与四边形EFCD 的面积之比是 （ ）A.31B.32C.52D.53 9. 如图，在锐角ABC ∆中，︒=∠60A ,︒=∠45ACB ，以BC 为弦作O ⊙，交AC 于点D ，OD 与BC 交于点E ，AB 与O ⊙相切.给出下列结论：①弧︒=90BD ;②DO//AB ；③CD=AD ；④BDE ∆相似于BCD ∆；⑤2=DEBE .10. 若b a ,满足0320118,082011322=++=++b b a a ，且1≠ab ，则b a 的值为（ ） A.38 B.38- C.83 D.83- 二、填空题11.在平面直角坐标系xOy 中，已知二次函数的图像关于y 轴对称，其顶点在原点O ，且过点()4,2P ，则该二次函数的表达式是________.12.如图，用红、蓝、黄三色将图中区域,,,A B C D 染色，要求有公共边界的相邻区域不能染相同的颜色，则满足区域A 恰好染蓝色的概率为________.13.用半径为r 的圆形铁皮，做成n 个相同圆锥的侧面（不浪费材料，不计接缝处的材料损耗），则每个圆锥的底面半径为_______.14.不等式21ax x <+对任意的实数x 都能成立，则a 的条件为________.15.设,x y 为实数，代数式2254824x y xy x +-++的最小值为_______.16.如图，已知,90Rt ABC Rt DEF C F ∆≅∆∠=∠=︒,3,4AC DF BC EF ====, DEF ∆绕着斜边AB 的中点D 旋转，DE 、DF 分别交AC 、BC 所在的直线于点P 、Q.当BDQ ∆为等腰三角形时，AP 的长为________.三、解答题17.已知703392xy x y x y xy+++=⎧⎨+=+⎩，求22x y xy +的值. 18.如图，O ⊙的直径AB 为10cm ，ACB ∠的平分线交AB 于点E ，交O ⊙于点D ，求弦AD 的长.19.某礼品经销商在春节前购进了甲、乙两种规格的礼品盒200盒，共花费了17800元.已知甲、乙两种规格的礼品盒的进价和售价如下表：（1）该礼品经销商购进甲、乙两种规格的礼品盒各多少盒？（2）由于市场供不应求，该礼品经销商计划再购进两种礼品盒50盒，而此次投入不超过5000元，为使得获利最大，应如何进货.20.已知函数222,04,0x x xyx x x⎧+≤⎪=⎨->⎪⎩.（1）若1y=-，求对应x值.（2）若3y<，求对应x的取值范围.21.如图（1），直线l 上有两点A 、B ，AB =4cm ，过l 外一点作直线CD//l ，射线BC 与l 所成的锐角160∠=︒，线段BC=2cm ，动点P 、Q 分别从B 、C 同时出发，P 以1cm/s 的速度沿由B 向C 的方向在直线BC 上运动，Q 以2cm/s 的速度沿由C 向D 的方向运动，设P 、Q 运动的时间为t （s ），当2t >，PA 交CD 于点E.（1）当5t s =时，求CE 、QE 的长.（2）若运动时间为t ，用含t 的代数式表示CE 和QE 的长，并求出运动时间为几秒时QE=3CE.（3）若以直线l 为x 轴建立直角坐标系（图（2）），O 为坐标原点，OA=2cm ，直线CD 与y 轴交于点M ，点N 在y 轴上且OM=MN ，求经过三点N 、A 、B 的抛物线的解析式.（4）点P 、Q 运动过程中，当QE 恰好平分APQ ∆，求点P 的坐标，并判断点P 是否在（3）问的抛物线上？。

密封青岛一中 2016 年自主招生考试数学试题（考试时间：60 分钟；满分：120 分）友情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！本试题共有 24 道题。

其中 1—8 题为选择题，请将所选答案的标号填写在第一题下面给出表格的相应位置上；9—14 题为填空题，请将做出的答案填写在第二题下面给出表格的相应位置上；15—24 题请在试卷给出的本题位置上做答。

一、选择题（本题满分 24 分，共有 8 道小题，每小题 3 分）题号 12345678本题得分阅卷人答案1.下列计算正确的是()⎛ 1 ⎫-23 ⎪ (- 2)2(- 2)0- 5 - 3A 、⎝ ⎭ ＝9B 、 ＝－2C 、＝－1D 、＝22. 在平行四边形、等腰梯形、等腰三角形、矩形、菱形五个图形中，既是中心对称图形又是轴对称图形的有（ ）A ．1 个B ．2 个C ．3 个D ．4 个3. PM 2.5 是大气压中直径小于或等于 0.0000025m 的颗粒物，将 0.0000025 用科学记数法表示为（）A ．0.25×10－5B ．0.25×10－6C ．2.5×10－5D ．2.5×10－64. 如图是由几个相同的小立方块组成的三视图，小立方块的个数是（ ）A ．3 个B ．4 个C ．5 个D ．6 个 5.如图，在平行四边形 ABCD 中，点 E 在 AD 上，连接 CE 并延长与 BA 的延长线交于点 F ， 若 AE ＝2ED ，CD ＝3cm ，则 AF 的长为（）A ．5cmB ．6cmC ．7 cmD ． 8cm座号学校_________________姓名_________________考试号_________________线6.如图，▱ABCD 的顶点 A 、B 、D 在⊙O 上，顶点 C 在⊙O 的直径 BE 上，∠ADC=54°， 连接 AE ，则∠AEB 的度数为（ ）A ．36°B ．46°C ．27°D ．63°（ 第 5 题图）（ 第 6 题图）7. 某机械厂七月份生产零件 50 万个，第三季度生产零件 196 万个．设该厂八、九月份平均每月的增长率为 x ，那么 x 满足的方程是（ ）A ．50（1+x ）2=196B ．50+50（1+x ）2=196C ．50+50（1+x ）+50（1+x ）2=196D ．50+50（1+x ）+50（1+2x ）=1968. 在同一坐标系内，一次函数 y ＝ax ＋b 与二次函数 y ＝ax 2＋8x ＋b 的图象可能是（）A B C D二、填空题（本题满分 18 分，共有 6 道小题，每小题 3 分）题号 91011本题得分答案题号 121314阅卷人答案9. (- 3)0+ 7 ( 1) 2-1 ⨯ + ﹣2| = _。

2017年山东省青岛一中自主招生物理试卷（样题）一、单项选择题（本题满分24分，共8个小题，每小题3分）下列各小题的四个选项中只有一个是符合要求的1．（3分）有位意大利物理学家经历了“观察﹣疑问﹣猜想﹣证实”的历程，探究了摆动规律，他还通过实验分析得出“物体的运动并不需要力来维持”的结论，这位物理学家是（）A．牛顿B．伽利略C．法拉第D．奥斯特2．（3分）某种物质熔化过程中温度随时间变化的图线如图所示，据图可知，该物质（）A．是晶体，熔点是30℃B．是非晶体，熔点是0℃C．熔化前，升温比熔化后升温快D．熔化时，与外界不发生热传递3．（3分）在做凸透镜成像实验时，将点燃的蜡烛沿着光具座，从凸透镜二倍焦距以外的某位置向焦点移动。

在此过程中，像的大小及像距的变化情况是（）A．像和像距都逐渐变大B．像和像距都逐渐变小C．像逐渐变大，像距逐渐变小D．像逐渐变小，像距逐渐变大4．（3分）如图所示，在静止的小车上有一充满液体的密闭容器，容器内分别静止着气泡P、悬浮在液体中的物体Q、沉底的金属球M．当小车带着容器由静止开始向右运动时，三个小球的位置相对容器的运动情况是（）A．P球不动，Q球向左，M球向右B．P球向左，Q球不动，M球向右C．P球向右，Q球不动，M球向左D．P球向左，Q球向右，M球不动5．（3分）把6个相同电灯接成如图（甲）（乙）所示两电路，调节变阻器，两组电灯均能正常发光。

设两个变阻器接入电路的阻值分别为R1、R2，流过的电流分别为I1、I2，则（）A．I1＞3I2，R2＝3R1B．I1＝3I2，R2＜3R1C．I1＝3I2，R2＞3R1D．I1＜3I2，R2＝3R16．（3分）为了方便居民出入，高层建筑楼内一般都安装了电梯。

为了安全，电梯都规定了最大载客量，并设置了超载自动报警系统，其工作原理如图所示。

当电梯所载人数增多时，压敏电阻R2受到的压力增大，阻值减小。

由图可知，电铃响时，（）A．电磁铁的磁性最弱B．弹簧的弹性势能最小C．控制电路中的电流最小D．工作电路中不会工作7．（3分）下列关于光的反射的一些说法中，正确的是（）A．我能看到卷子上的字，是由于我的眼睛发出的光射到了字上B．我要想在墙上的大镜子前看到我的全身像，镜子的高度至少要与我的身高一样C．平面镜也可成缩小的像D．如果我在一块平面镜中看到了你的眼睛，那么你也一定会通过这面镜子看到我的眼睛8．（3分）将一个重为G的小球从空中某点静止释放，落在竖直放置的轻弹簧上，压缩到最低点后，再被弹起，若不计空气阻力，则小球运动到最低点时，（）A．小球的动能最大B．小球的重力势能最大C．小球受的合力不为零D．小球受的合力为零二、不定项选择题（本题满分24分，共4个小题）每小题中至少有一个或多个选项是正确的，每小题全选对得6分，漏选得3分，错选或不选得0分9．（6分）如图所示，木块a放在粗糙水平桌面上，木块b放在木块a上面，在水平拉力F 作用下一起向右做匀速直线运动，空气阻力不计，下列判断正确的是（）A．b在水平方向上不受力B．b在水平方向上受到向右的摩擦力C．拉力F和a受到的摩擦力大小相等D．拉力F大于a受到的摩擦力10．（6分）甲同学骑自行车去看望乙同学，得知消息后，乙同学步行迎接甲，接到后同车返回。

2017年山东省青岛一中自主招生物理试卷一、单项选择题：（本题满分24分，共8个小题，每小题3分）下列各小题的四个选项中只有一个是符合要求的．1．（3分）“最美人间四月天，蜜蜂蝴蝶舞蹁跹”。

人能听见的声音的频率范围一般在20赫兹至20000赫兹之间。

下面有关说法中正确的是（）A．蜜蜂在人身后飞，人可以听见。

蝴蝶在人身后飞，人听不见B．蜜蜂在人身后飞，人可以听见。

蝴蝶在人身后飞，人也能听见C．2赫兹至10赫兹的次声，只要振幅足够大，人耳就能听见D．声音不需要介质在真空中也能传播2．（3分）如图所示，A和B是能自由运动的正方体，C和D是容器自身凸起的一部分，现在往容器中注入一些水，则下列说法中错误的是（）A．A物体一定受到浮力作用B．B物体一定受到浮力作用C．C部分一定受到浮力作用D．D部分一定受到浮力作用3．（3分）粗糙的水平面有一个重50牛顿的物体，用10牛顿的水平推力使其在10秒内匀速前进了20米，则再此过程中（）A．推力做了1000焦耳的功B．推力的功率为20瓦C．重力做了1000焦耳的功D．摩擦阻力为50牛顿4．（3分）如图，仔细观察甲、乙、丙三杯水，判断下列说法中正确的是（）A．甲杯中水的内能最大B．乙杯中水的内能最大C．丙杯中水的内能最大D．乙、丙杯中水的内能一样大5．（3分）在如图所示的电路中，用滑动变阻器调节灯的亮度，若要求滑片P向右端滑动时灯逐渐变亮，应选择下列哪种接法（）A．M接A，N接B B．M接A，N接D C．M接C，N接B D．M接C，N接D 6．（3分）百米运动员起跑后，6s末的速度为9.3m/s，10s末到达终点时的速度为15.5m/s，他跑全程的平均速度为（）A．12.2m/s B．11.8m/s C．10m/s D．10.2m/s7．（3分）如图（甲）、（乙）滑轮组装置，所有摩擦不计，分别用F1、F2竖直匀速拉动重物G，已知每个滑轮重为，则力F1和F2之比为（）A．1：1B．3：2C．2：3D．3：48．（3分）如图所示的家庭电路中，闭合开关后灯泡不亮。

青岛一中2017年自主招生考试物理试题（满分100分，时间60分）一、单项选择题：（本题满分24分，共8个小题，每小题3分）下列各小题的四个选项中只有一个是符合要求的．1．“最美人间四月天，蜜蜂蝴蝶舞蹁跹”．人能听见的声音的频率范围一般在20赫兹至20000赫兹之间．下面有关说法中正确的是（）A．蜜蜂在人身后飞，人可以听见．蝴蝶在人身后飞，人听不见B．蜜蜂在人身后飞，人可以听见．蝴蝶在人身后飞，人也能听见C．2赫兹至10赫兹的次声，只要振幅足够大，人耳就能听见D．声音不需要介质在真空中也能传播2．如图所示，A和B是能自由运动的正方体，C和D是容器自身凸起的一部分，现在往容器中注入一些水，则下列说法中错误的是（）A．A物体一定受到浮力作用B．B物体一定受到浮力作用C．C部分一定受到浮力作用D．D部分一定受到浮力作用3．粗糙的水平面有一个重50牛顿的物体，用10牛顿的水平推力使其在10秒内匀速前进了20米，则再此过程中（）A．推力做了1000焦耳的功B．推力的功率为20瓦C．重力做了1000焦耳的功D．摩擦阻力为50牛顿4．仔细观察下图中甲，乙，丙三杯水，下列说法中正确的是（）A．甲杯中水的内能最大B．乙杯中水的内能最大C．丙杯中水的内能最大D．乙、丙两杯中水的内能一样大5．在如图所示的电路中，用滑动变阻器调节灯的亮度，若滑片P向右端滑动的时灯逐渐变亮，应选择下列哪种接法（）A．M接A，N接B B．M接C，N接DC ．M 接C ，N 接BD ．M 接A ，N 接D6．百米运动员起跑后，6s 末的速度为9.3m /s ，10s 末到达终点时的速度为15.5m /s ，他跑全程的平均速度为（ ） A ．12.2m /sB ．11.8m /sC ．10m /sD ．10.2m /s7．如图甲、乙滑轮组，所有摩擦不计，分别用1F 、2F 竖直匀速拉动重为G 的物体，已知每个滑轮重力为/2G ，则力1F 、2F 之比为（ ）A ．1:1B ．3:2C ．3:4D ．2:38．如图所示的家庭电路中，闭合开关后灯泡不亮．用试电笔检测插座的两孔，发现只有插入右孔时氖管才发光．用试电笔检测A 点氖管发光，检测B 点氖管不发光．发生这一现象的原因可能是（ ）A ．灯泡短路B ．灯丝断了C ．开关接触不良D ．插座短路二、不定向选择题：（本题满分24分，共4个小题）每小题中至少有一个或多个选项是正确的，（每小题全选对得6分，漏选得3分，错选或不选得0分）． 9．以下说法正确的是（ ）A ．利用光的反射可以成像，利用光的折射可以成像，利用光的直线传播也可以成像B ．有一个完全潜入水中的人，看见岸边站着的另一个人感觉象变高了C ．矫正近视眼的眼镜是一个凸透镜D ．“猴子捞月”的寓言故事中说，猴子看到井中有个月亮，以为月亮掉进水中了，站在物理的角度讲“水中的月亮到水面的距离等于天上的月亮到水面的距离” 10．以下说法正确的是（ ）A ．夏天，我们看到冰棒冒的“白气”，这些“白气”就是水蒸气B ．舞台烟雾是利用干冰升华吸热制冷，使空气中的水蒸气液化形成的C ．晶体在凝固过程中，液体固体共存，放出热量，温度降低D ．医院里常用的体温计，是利用液体热胀冷缩的性质制成的，其玻璃泡内的液体是水银 12．下面的例子中，说法中正确的是（ ）A ．“物体速度的大小改变了，速度的方向改变了，或者是速度的大小和方向都改变了”．就可以认为是“物体的运动状态的改变了”B ．物体受力越大，运动的越快，其惯性就越大C ．磁场是一种看不见的特殊物质，磁感线也是真实存在的D ．在研究凸透镜成像的实验中，物体的位置和像的位置分居在透镜两侧，相距100厘米．所成的像是一个等大的、倒立的实像，则此凸透镜的焦距是25厘米12．如图所示，一轻弹簧固定于O 点，另一端系一重物，将重物从与悬点O 在同一高度且弹簧保持原长的A 点由静止释放，让它自由摆下，不计空气阻力，在重物由A 点摆向最低点的过程中（ ）A ．重物的重力势能减少B ．重物的重力势能增加C ．重物的机械能减少D ．重物的机械能不变三、填空题（共10分）13．（6分）直升飞机在空中悬停，一人背着伞包从飞机上跳下，伞包并没有立即打开，把人和背上的伞包作为一个整体研究，它受到了向下重力和向上的空气阻力作用，且重力大于阻力，人下落的速度越来越快． 若此时突然打开降落伞，人受到的阻力会大于人重力，那么，在开伞瞬间，人会向__________（填“上”或“下”）运动．14．（4分）如图所示是定值电阻R 和小灯泡L 两端电压和通过电流的U I -关系图线．由图可知，定值电阻R 的阻值为__________Ω；小灯泡L 两端电压为2V 时阻值为__________Ω．四、实验题（10分）15．某同学设计了如图所示的实验来测量电阻1R 的阻值，另一定值电阻的阻值25R =欧姆．3R 是一个电阻箱（电阻箱也是一种变阻器，其电阻大小可调且阻值可知），操作步骤如下： （1）闭合1S ，将2S 切换到a ，读出电流表的示数为0I 安培．（2）闭合1S ，将2S 切换到b ，调节电阻箱3R 的阻值，当3R 的阻值是12Ω时，电流表的示数仍然为0I 安培． 则电阻1R =__________Ω．五、计算题（共32分）16．（8分）为了倡导低碳生活，太阳能热水器被广泛应用于现代生活．下表提供的是一装满初温为10C ︒水的太阳能热水器在太阳照射下的相关信息：（1）热水器中的水吸收的热量是多少．（4分） （2）此次热水器接收的太阳能为多少．（4分）17．（12分）在水平桌面上放置一空玻璃杯，它的底面积为20.01m ，它对桌面的压强为200Pa ．（1）（4分）求玻璃杯的重力．（2）（8分）在玻璃杯中装入1kg 水后，水对杯底产生压强为900Pa ．求水的深度；并通过计算推出玻璃杯的大致形状是图中甲、乙、丙的哪一种？（水的密度331.010kg /m ρ=⨯，取10N /kg g =）18．（12分）如图所示，灯泡的电阻L 12R =Ω，正常发光时的电压为12V ，212R Ω＝，当开关1S ，和2S 都闭合时，电流表的示数为1.2A ，这时灯泡正常发光．（1）（6分）求电源电压，求1R 的阻值．（2）（6分）当开关都断开时，求灯泡两端的电压．求2R 的电功率．。