第六章 正弦交流电路的功率

《电工技术》
知识点：正弦交流电路的功率
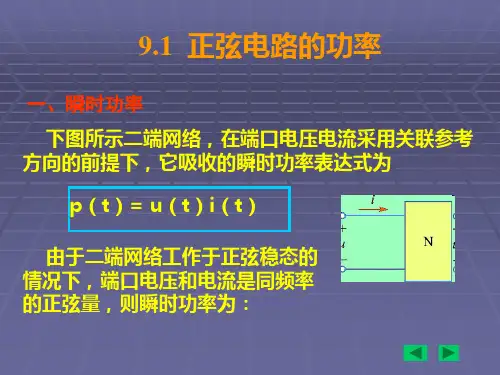
1. 瞬时功率
=⋅+ωωϕI U p t t sin sin()m m =-+ϕωϕI U t 2
[cos cos(2)m
m （设电感性电路）
=⋅p i u
2 . 平均功率（有功功率）P
u与i 的相
位差角
总电压总电流
1 UI
pdt ϕ
cos
T
P T =
=⎰
上述公式为有功功率的一般表达式，可推广到任何复杂交流电路，其有功功率等于电阻上消耗的功率。

===2
R R
P P U I I R
功率因数
ϕ
cos
=-=-=L C L C Q I X I X I U U IU 22sin ϕ
)(Q ＝Q L +（-Q C ） 3 . 无功功率 Q
单位：V A 、kV A
4. 视在功率 S。

电源（发电机、变压器等）可能提供的最大功率（额定电压×额定电流）
ϕ U U R U L -U C S=UI
---功率三角形
5 . 有功功率、无功功率与视在功率间的关系
=S U I
视在功率 =Q U I sin ϕ无功功率
=P U I cos ϕ有功功率
---功率三角形 S
Q P 功率三角形 U R
U
+ U U L C 电压三角形
阻抗
三角
形 R X L -X C ϕ
THE END。

正弦交流电路有功功率公式在我们学习电学知识的过程中，正弦交流电路有功功率公式可是个相当重要的角色。

这就好比是电学世界里的一把神奇钥匙，能帮我们打开很多难题的大门。

先来说说这个公式到底是啥。

正弦交流电路有功功率公式是 P = UIcosφ 。

这里的 P 代表有功功率，U 是电压的有效值，I 是电流的有效值，而cosφ 则是功率因数。

那这个公式到底有啥用呢？我给您举个例子吧。

有一次我去朋友家，他家的空调突然出了问题，制冷效果变得很差。

我就琢磨着是不是电路上出了啥毛病。

一检查，发现电压和电流好像不太对劲。

这时候，这个有功功率公式就派上用场啦！通过测量电压、电流以及计算功率因数，我发现原来是功率因数太低了，导致空调不能正常工作。

咱们再深入聊聊这个公式里的各个元素。

电压 U 就像是水流的压力，电流 I 就像是水流的速度，而功率因数cosφ 呢，就像是水流的顺畅程度。

如果水流压力大（电压高），速度快（电流大），而且流得顺畅（功率因数高），那输送的能量（有功功率）自然就多。

在实际生活中，很多电器的工作效率都和这个有功功率有关系。

比如说工厂里的大型机器，如果有功功率不足，生产效率就会大打折扣。

想象一下，一条生产线上的机器都慢悠悠地运转，那得耽误多少事儿啊！再比如说我们家里的电灯，如果有功功率不够，灯光就会变得昏暗，看书学习都不方便。

我记得有一次我在书房看书，灯光突然变得特别暗，原来是电路中的有功功率出了问题，搞得我眼睛都累得不行。

对于学习电学的同学们来说，理解和掌握这个公式可太重要了。

它不仅能帮助我们解决实际问题，还能让我们更深入地理解电的奥秘。

可别小看这个公式，它可是电学知识大厦的一块重要基石。

在解决实际电路问题的时候，我们要灵活运用这个公式。

有时候需要通过测量和计算来找到问题所在，有时候则要根据已知条件来优化电路，提高有功功率。

这就像是一个解谜的过程，充满了挑战和乐趣。

总之，正弦交流电路有功功率公式虽然看起来有点复杂，但只要我们用心去理解，多联系实际，就一定能掌握它的精髓，让它成为我们解决电学问题的有力武器。

正弦交流电路中的谐振、功率等相关概念在正弦交流电路中，谐振是指电路中电感（L）和电容（C）的阻抗对频率的变化呈现出共振现象的情况。

正弦交流电路中的谐振可以分为串联谐振和并联谐振两种情况。

1. 串联谐振：当电感和电容串联连接时，电路在特定的频率下，电感的感抗和电容的容抗大小相等且相互抵消，此时电路的总阻抗达到最小值，电路呈现出谐振现象。

2. 并联谐振：当电感和电容并联连接时，电路在特定的频率下，电感的感抗和电容的容抗大小相等且相互抵消，此时电路的总阻抗达到最大值，电路呈现出谐振现象。

谐振频率（Resonant Frequency）是指使电路达到谐振状态所需的频率，对于串联谐振和并联谐振电路而言，其谐振频率分别为：f=谐振电路在谐振频率下具有以下特性：1. 电流最大：在谐振频率下，电路中的电流达到最大值，而电压最小。

2. 总阻抗最小：在谐振频率下，电路的总阻抗达到最小值，等于电路中的纯电阻值（串联谐振）或者最大值（并联谐振）。

3. 功率因数为1：在谐振频率下，电路中的电感和电容的感抗和容抗大小相等且相互抵消，电路中只有纯电阻，功率因数为1，电路无功耗。

4. 能量传递效率最高：在谐振频率下，电路中的能量传递效率最高，能量传输损耗最小。

功率是交流电路中一个重要的参数，其计算方法是：P=VIcosϕ其中，V 为电压，I 为电流，ϕ为电压和电流的相位差， cosϕ为功率因数。

在谐振状态下，电路中的功率因数为1，因此电路的功率可以简化为：P=VI在串联谐振电路中，电压和电流同相位，功率为正数；在并联谐振电路中，电压和电流反相位，功率为负数，表示能量的吸收。

总之，在正弦交流电路中，谐振和功率是交流电路中的重要概念，对于电路的设计和分析具有重要意义。

2.4 交流电路的功率2.4.1 瞬时功率如图2-30所示，若通过阻抗Z的电流为i=I m sinωt，则Z两端的电压为u=U m sin（ωt+φ），在电流、电压关联参考方向下，瞬时功率为p=ui=U m sin（ωt+φ）×I m sinωt=UI cosφ-UI cos（2ωt+φ）（2-54）图2-30 正弦交流电路在式（2-54）中，第一项为不变的部分，总是大于等于零，是耗能元件上瞬时功率；第二项为变化的部分，是储能元件上瞬时功率。

由此可见，在每一瞬间，电源提供的功率一部分被耗能元件消耗，另一部分与储能元件进行能量交换。

2.4.2 有功功率与功率因数一个周期内瞬时功率的平均值称为平均功率，也称有功功率。

式中，λ=cosφ称为电路的功率因数。

可见，正弦交流电路中的有功功率不但与电压、电流有关，还与电压和电流相位差的余弦值有关。

可见，在正弦交流电路中，电感、电容元件实际不消耗电能，而电阻总是消耗电能的。

有功功率是电路实际消耗的功率，即二端网络中，各电阻所消耗的有功功率之和。

有功功率的单位是瓦特（W）。

2.4.3 无功功率电路中的电感元件与电容元件要与电源之间进行能量交换，根据电感元件、电容元件的无功功率，考虑到与相位相反，于是Q=（U L-U C）I=（X L-X C）I2=UI sinφ（2-56）单个电感元件，Q L=U L I L sinφ=U L I L>0单个电容元件，Q C=U C I C sinφ=-U C I C<0即电感的无功功率取正值，而电容的无功功率取负值，以便区别。

在既有电感又有电容的电路中，总的无功功率为Q L与Q C的代数和，即Q=Q L-Q C无功功率的单位是乏（var）。

2.4.4 视在功率在交流电路中，电压与电流有效值的乘积，只能表示电源可能提供的最大功率，叫视在功率，用字母S表示。

即S=UI=I2|Z| （2-57）视在功率的单位是伏安（V·A），常用来表示电气设备的容量。

电路分析基础100cos z P S ϕ==故减小无功功率Q 便可提高功率因数。

一般来说，负载大多是感性负载，我们通常在感性负载两端并联一个电容器，以提高电路的功率因数，这个电容器称为补偿电容。

采用并联电容以提高功率因数的方法，其实质是以电容的无功功率补偿电感的无功功率，从而减少了整个电路的无功功率，使功率因数得以提高。

但补偿电容超过一定数值时，电路将由感性转为容性，反而达不到提高功率因数的目的。

例 4.14 电路如图4-32所示，已知：80C X =Ω，90)V u t =+°，30)V C u t =−°。

求：平均功率P 、无功功率Q 和视在功率S 。

解 10090V U=∠°&8030(V)C U =∠−°& 8030160(A)j j80C C U I X ∠−°===∠°−−&&1009010030()160U Z I ∠°===∠°Ω∠°&&cos 1001cos30z P UI ϕ==××°= sin 1001sin 3050(Var)z Q UI ϕ==××°=100(V A)S UI ==图4-324.8.6 正弦交流电路中的最大功率负载电阻从具有内阻的直流电源获得最大功率的条件在第3章中讨论过。

本节将讨论在正弦交流电路中负载从电源获得最大功率的条件。

电路如图4-33所示，交流电源的电压为S U &，其内阻抗为S S Sj Z R X =+，负载阻抗为j L L L Z R X =+。