留数定义定理计算规则2

f
(z)
(4)
规则II 若z0是f (z)的m级极点
Re
s[
f
( z ),
z0]
1 (m 1)!
lim
z z0
d m1 dz m 1
{( z
z0 )m
f
( z )}
(5)
事实上，由条件 f (z) cm (z z0 )m c2 (z z0 )2 c1(z z0 )1
c0 c1(z z0 ) ,(cm 0)
得证！
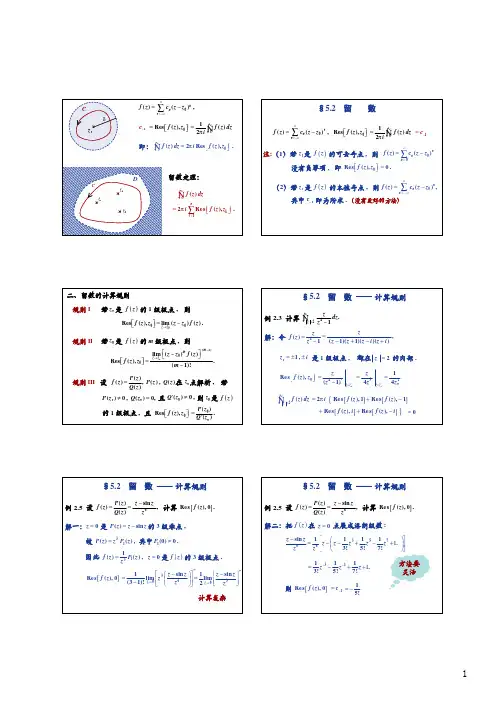
D
c
z1
z3
z2
zn
求沿闭曲线c的积分，归之为求在c中各孤立 奇点的留数。
3. 留数的计算规则
一般求Res[f (z), z0]是采用将f (z) 在 z0邻域内展开 成洛朗级数求系数c–1的方法,但如果能先知道奇点 的类型，对求留数更为有利。
以下就三类奇点进行讨论：
(i)若z z0为可去奇点 c1 0 Re s[ f (z), z0 ] 0
f (z)dz
c
(2)
2. 留数定理
定理 设c是一条简单闭曲线, f (z)在c内有有
限个弧立奇点z1, z2 , , zn ,除此以外, f (z)在c 内及c上解析
n
c f (z)dz 2i Re s[ f (z), zk ] (3) k 1
证明 用互不包含,互不相交的正向简单闭曲线ck
(k 1,2, n)，将c内的弧立奇点zk围绕,
z1
z
2
2
f (z)dz 2i Re s[ f (z),0] 2i Re s[ f (z),1] 0 z 2
例2
计算 z dz cz4 1
c : 正向z 2
解 f (z)有4个一级极点: 1,i都在圆周c内，
由规则
故
z c z4 1 dz
P(z) Q'(z)
z 4z3
1 4z2
2i{Res[ f (z),1] Re s[ f (z),1]
且g(z0 ) 0), 则z0为f (z)的 级极点,由规则
Re
s[
f
(z), z0
]
lim(z
zz0
z0
)
f
(z)
lim
zz0
p( z ) Q(z) Q(z0 )
p(z0 ) Q'(z0 )
(Q'
(z0
)
0)
得证！
z z0
例1
计算 :
5z 2 dz
z 2 z(z 1)2
解 f (z) 5z 2 在 z 2的内部有一个一级极点
2 z0
2
z
1
cos z3
z
dz
2i
Re
s[
f
(
z),0]
2i(
1 2
)
i
例4 计算 tan zdz (n N ) z n
解 tanz sinz 令 cosz 0 cosz
解 得z k 即, z k 1 (k 0,1,2, )
2
2

1 2
csc2 z
z
k
1 2
0
Re s[ f (z),i] Re s[ f (z),i]}
2i[1 1 1 1] 0
4444
例3
计算
cos z z 1 z3 dz
解
f
(z)
cos z3
z
有一个z
0的三级奇点
由 规 则
Re
s[
f
(
z ) ,0]
lim
z0
(3
1
1)!
d2 dz 2
[z
3
f
(
z)]
1 lim(cos z)'' 1
z k 1 为一级极点,由法则III得
2
Re s[tan z, k 1] sinz
1 (k 0,1, )
z(z 1)2
z 0和一个二级极点z 1
由 规 则
Re
s[
f
( z ),0]
lim
z0
zf
(
x)
lim
z0
5z 2 (z 1)2
2
由 规 则I I
Re
s[
f
( z ),1]
lim
z1
1 (2 1)!
d dz
{( z
1)2
5z 2 z(z 1)2
}
5z 2
2
lim( z1
z
)'
lim
由留数定义, Res[f (z), z0]= c–1
(1)
设f (z) cn (z z0 )n
n
(z0是f (z)的弧立奇点, c包含z0在其内部) 对 上 式 两 边 沿 简 单 闭 曲线c逐 项 积 分 得 ：
c f (z)dz c1
dz c z z0
2ic1
故
1
Re s[ f (z), z0 ] c1 2i
以(z z0 )m 乘上式两边, 得 (z z0 )m f (z) cm cm1(z z0 ) c1(z z0 )m1
c0(z z0 )m 两边求m 1阶导数得
d m1 dz m 1
{(z
z0 )m
f
(z)}
(m
1)!c1
m!(z
z0 )
lim
z z0
d m1 dz m 1
§2 留数(Residue)
1. 留数的定义 2. 留数定理 3. 留数的计算规则
1. 留数的定义
定义 设z0为f (z)的孤立奇点， f (z)在z0邻域内的 洛朗级数中负幂次项(z- z0)–1的系数c–1称为f (z)在z0
的留数，记作Res[f (z), z0] 或 Res f (z0)。
{( z
z0 )m
f
( z )}
(m 1)! c1 , 移项得(5)式.
当m=1时，式(5)即为式(4).
规则III
设f (z) p(z) Q(z)
p(z), Q(z)在z0处解析,
p(z0 ) 0, Q(z0 ) 0, Q'(z0 ) 0
z0是f
(z)的一级极点,且 Re s[
f
( z ),
展开
(ii)若z z0为本性奇点 f (z) cn(z z0 )n
Re s[ f (z), z0 ] c1
(iii)若z z0为极点时，求Re s[ f (z), z0 ]有以下几条 规则
规则I 若z0是f (z)的一级极点,
Re
s[
f
( z ),
z0 ]
lim(z
z z0
z0 )
z0 ]
p(z0 ) Q'(z0 )
(6)
事实上， Q(z0 ) 0及Q'(z0 ) 0
z0为Q(
z)的
一
级
零
点, 从
而z
为
0
1 Q(z
)
的
一
级
极
点,
因此, 1 Q(z)
z
1 z0
(z)( (z)在z0处解析且 (z0 )
0)
故f
(z)
z
1 z0
g(z)(g(z)
(z) p(z)在z0解析,
由复合闭路定理得：
f (z)dz f (z)dz f (z)dz f (z)dz
c
c1
c2
cn
用2i 除上式两边得:
1
n1
f (z)dz
f (z)dz
2i c
k 1 2i cn
n
Re s[ f (z), zk ] k 1
n
故 c f (z)dz 2i Re s[ f (z), zk ] k 1