中考数学课后自主训练第七单元：图形与变换

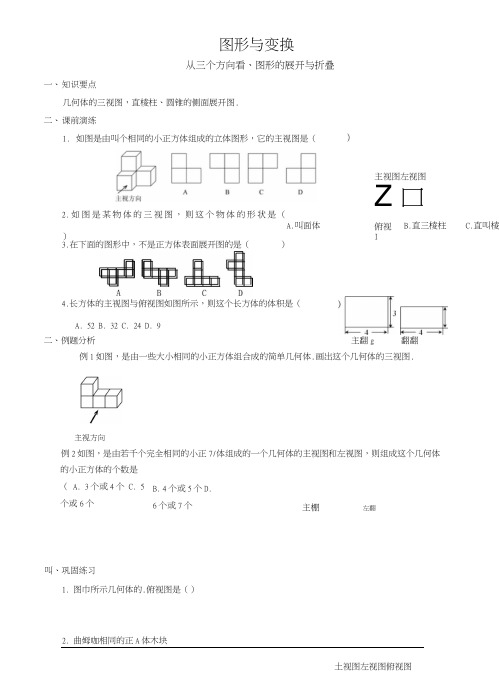
图形与变换从三个方向看、图形的展开与折叠一、知识要点几何体的三视图，直棱柱、圆锥的侧面展开图.二、课前演练1.如图是由叫个相同的小正方体组成的立体图形，它的主视图是（A.叫面体B.直三棱柱C.直叫棱二、例题分析主翻g 翻翻例1如图，是由一些大小相同的小正方体组合成的简单几何体.画出这个几何体的三视图.叫、巩固练习1.图巾所示几何体的.俯视图是（）2.曲姆咖相同的正A体木块土视图左视图俯视图主视图左视图Z口2.如图是某物体的三视图，则这个物体的形状是（）3.在下面的图形中，不是正方体表面展开图的是（）A. 52B. 32C. 24D. 94.长方体的主视图与俯视图如图所示，则这个长方体的体积是（主棚左翻俯视I主视方向例2如图，是由若千个完全相同的小正7/体组成的一个几何体的主视图和左视图，则组成这个几何体的小正方体的个数是（ A. 3个或4个 C. 5个或6个B. 4个或5个D.6个或7个所示，则该几何体中正方体木块的个数是（）① ② ③®4. 有一正方体木块，它的六个而分别标上数字1一一6,这是这个正方体木块从不同而所观察到的数字惜况.请问数字1和5对而的数字各是多少？1 // 46/2521 /4195. 如图所示的圆柱体中底面圆的半径是^,高为2,若一只小虫从A 点出发沿着圆柱体的侧面爬行到C 点，则小虫爬行的S 短 路程是 __________________ （结果保留根号）.A. 6个B. 5个C. 4个D. 3个3.右图是由四个相同的小立方体组成的立体图形的主视图和左视图，那么原立体图形可能是 _____________6.M出下面左边立体图的三视图.一、知识要点阁形的轴对称轴对称的概念，轴对称图形的基本性质，按要求作简单图形经过轴对称(两次以内)后的图形.二、课前演练1.下而的四个图案中，既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有( )A. 4个B. 3个C. 2个2.点八3, -5)关于x轴对称的点的坐标为( )A. (-3, -5)B. (5, 3)C. (-3, 5)D. (3, 5)3.如图给出了一个图案的一半，其中的虚线就是这个图案的对称轴，请画出这个图案的另一半.5.若等腰三角形一腰上的高与底边的夹角为35°.则这个三角形的顶角为三、例题分析例1如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是()A.①B.②C.⑤D.⑥D. 1个11•—■例2如图方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，AABC 的顶点均在格点上，0、M也在格点上.(1)画岀AABC关于直线0\1对称的⑵画出将AABC绕点0按顺时针方向旋转90n后所得的⑶△A I B I C I^AA2B2CJSJ^的图形是轴对称图形吗？如果是轴对称图形，请阃出对称轴.♦B*34?/\4?♦51-J MPP四、巩固练习1.以下环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形的是()A B C D2.如图，坐标平面内一点A(2, -1)，0为原点，P是x轴上的一个动点，如果以点P, 0, A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为（）A. 2 B. 3 C. 4 D. 5• >•（第3题图）（第4题图）（第2题图）3.在4X4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有_____________ 种.4.如图，将矩形ABCD沿CE折叠，点B恰好落在边八D的F处，如果AB 2那么tanZDCF的值是5.如图所示，AABC中，点E在AC上，点N在BC上，在AB上找一点F,使AENF的周长最小，并说明理由.6.（1）操作发现：如图①，D是等边AABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边ADCF，连接AF.你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论.（2）类比猜想：如图②，当动点D运动至等边AABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？（3）深入探究：1 .如图③，当动点D在等边AABC边BA上运动时（点D与点B不重合）连接DC,以DC 为边在BC上方、下方分别作等边ADCF和等边ADCF'，连接AF、BF',探究AF、BF'与AB有何数量关系？并证明你探究的结论.II.如图④，当动点D在等边△边BA的延长线上运动时，其他作法与图③相同，I中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论.图形的平移知识要点平移的基本性质，按要求作山简单的平而图形.课前演练1.如图，将AABC沿直线AB向右平移后到达ABDE的位置，若ZCAB=50°,ZABC=100°,则ZCBE的度数为 .（第2题图）例2如图，抛物线yF~|x2+l、y2=-|x2-l，求过点0），（2, 0）且平行于y轴的两条平行线与两抛2.如图，C、B、E分别是等边AADF三边的中点，则图中共有 _______ 个等边三角形.其中，有_______ 个是rflAABC平移得到的.3.如图，由2个边长为6的正方形拼成一个长方形，则阁屮阴影部分的而积为______________ .4.将图中三角形向右平移3格，作山平移后的图形.三、例题分析例1 一块长105m、宽60m的长方形土地，上而修了两条道路互相垂直的小路，宽都是5m，将阴影部分种上草坪，则草坪的而积是多少？叫、巩固练习6.已知：抛物线y=ax 2+bx+c 的图象如樹所示： （1） 求此抛物线的解析式；（2） 将抛物线作怎样的一次平移，才能使它与坐标轴仅有 两个交点,并写山此时抛物线的解析式.\J7B-2.V1.如图，当半径为30cm 的转动轮转过120"角时，传送带上的物体A 平移的距离为cm-（第1题图） A（第3题图）2. 如图在8X6的网格图（每个小正方形的边长均为1个单位长度）中，的半径为2个单位长度，的半径为1个单位长度，要使运动的O 及与静止的0/1内切，应将巾图示位置向左平移 _______________ 个单位长度.3. 如图，EF 是AABC 的中位线，将AAEF 沿AB 方向平移到△EBD 的位置，点D 在BC 上，己知AAEF 的而积为5,贝ij 图中阴影部分的而积为 ___________ .4. 如图，半圆AB 平移到半圆CD 的位置时所扫过的面积为__________ .5.如图，将RtAABC 沿射线BC 的方向平移得到ADEF.求图中阴影部分的而积.I阁形的旋转一、知识要点图形的旋转及其基本性质，作fli 简单的平而图形. 二、课前演练1. 将下列图形绕其对角线的交点逆时针旋转90"，所得图形一定与原图形重合的是（）A.平行四边形B.矩形C.菱形D.正方形2. 如图1,点A 、B 、C 、D 、0都在方格纸的格点上，若AC0D 是由AA0B 绕点0按逆时针方昀旋转而得, 则旋转的角度为（ ）3.如图 2, RtAABC 中，ZABC=90°，ZBAC=30°，AB=2#cm,将AABC 绕顶点 C 顺时针旋转至AA'BV 的位 置，且A 、C 、B'三点共线，则点A 经过的最短路线的长度是（ ）三、例题分析 例1如图，正方形网格屮每一个小正方形的边长都是1，四边形ABCD 的卩4个顶点都在格点上，0为AD 的中点，若把四边形ABCD 绕着点0顺时针旋转.试解决下列问题： （1） 画出四边形ABCD 旋转后的阁形； B （2） 求点C 旋转过程中所经过的路径长； O （3） 设点B 旋转后的对应点为B'，求tanZDAB'的值. cD例2平面内有一等腰直角三角板（ZACB=90° ）和一直线MN.过点C 作CE 丄MN 于点E ，过点B 作BF 丄MN 于点F.当点E 与点A 重合时（如图1）,易证：AF+BF=2CE.当三角板绕点A 顺时针旋转至图2、图3的位 置时，上述结论是否仍然成立？若成立，清给予证明；若不成立，线段AF 、BF 、CE 之间又有怎样的数量 关系，清直接写出你的猜想，不需证明.阁3A. 8cmB. 4-\/3cmC.32 T8 D. — cm4.如图3, AABC 的三个顶点都在5X5的网格海个小正方形的边长均为1个单位长度）的格点上，将么 ABC 绕点B 顺时针旋转到AA'BC'的位置，且点A'、C'仍落在格点上，则线段AB 扫过的图形的面积是 平方单位（结果保留n ）.D. 135°图1IS2 图3四.巩固练习1.如图，该图形围绕点0按下列角度旋转后，不能与其白身重合的是()A. 72B. 108阁1C 阁32.如图，等腰RtAABC的直角边AB的长为6cm，将AABC绕点A逆时针旋转15°后得到AABV,则图中阴影部分的面积等 ________ c m2.3.如图，在方格纸中的AABC经过变换得到ADEF,正确的变换是( )A.把AABC向右平移6格B.把AABC向右平移4格，再向上平移1格C.把AABC绕着点A顺时针旋转90°，再向右平移6格D.把AABC绕着点A逆时针旋转90Q4.按要求分别画出旋转图形：(1)画AABC绕0点顺时针方向旋转90° 后得到△A'B'C';(2)把四边形ABCD绕0点逆时针方向旋转90°后得四边形/VB'C'D'.再向右平移6格5.已知AABC，以AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.(1)利用旋转的观点，在此题中，AADC绕着_点旋转___________ 度可以得到△.(2)CD与BF相等吗?请说明理由.(3)CD与BF互相垂直吗？清说明理由.6.如图，点E为正方形ABCD的边CD上一点，AB=6,(1)旋转中心是哪一点？(2)旋转了多少度？(3)如果连接EF,那么ADEF是怎样的三角形？(4)求四边形DEBF的周长和面积？AE=2, ADAR旋转后能与ADCF重合.B C F。

广西贵港市2017届中考数学总复习第七单元图形变换单元测试（七）图形变换试题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（广西贵港市2017届中考数学总复习第七单元图形变换单元测试（七）图形变换试题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为广西贵港市2017届中考数学总复习第七单元图形变换单元测试（七）图形变换试题的全部内容。

贵港单元测试（七）图形与变换（时间：45分钟满分：100分）一、选择题（每小题3分，共24分)1．如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是（ B ）2．下列图案中既是中心对称图形，又是轴对称图形的是( C ）3．如图是一个正方体，则它的表面展开图可以是（ B ）4．如图，位似图形由三角尺与其灯光照射下的中心投影组成，相似比为2∶5。

且三角尺的一边长为8 cm，则投影三角尺的对应边长为（ B ）A．8 cm B．20 cm C．3。

2 cm D．10 cm 5．如图，已知△OAB是正三角形，OC⊥OB,OC＝OB，将△OAB绕点O按逆时针方向旋转，使得OA与OC重合,得到△OCD,则旋转的角度是（ A )A．150° B．120° C．90° D．60°6．如图，在△ABC中,BC＝5,∠A＝70°，∠B＝75°,把△ABC沿直线BC的方向平移到△DEF 的位置，若CF＝3，则下列结论中错误的是( C )A．BE＝3 B．∠F＝35° C．DF＝5 D．AB∥DE7．如图,在△ABC中，∠ACB＝90°，∠ABC＝30°，AB＝2。

D C B A 第1题图第6题图油加运奥京北第7题图第七章 图形与变换第一节 视图与投影习题精编1、如图摆放的正六棱柱的俯视图是（ ）2、如图，是某几何体的三视图，该几何体是（ ） A 、直棱柱 B 、圆柱 C 、圆锥 D 、球3、如图是由四个相同的小正方体组成的立体图形，它的左视图为（ ）4、如图是一个由6个大小相同、棱长为1的小正方体搭成的几何体，关于它的三视图下列说法中正确的是（ ）A 、主视图的面积为B 、左视图的面积为2C 、俯视图的面积为5D 、三种视图的面积都是55、如图，是一个由若干个相同的小正方体组成的几何体的三视图，则组成这个几何体的小正方体的个数是（ ）主视图 左视图 俯视图A 、9B 、8C 、7D 、6 6、如图是正方体的平面展开图，每个字上标有一个汉字，与“油”字相对的面上的字是（ ） A 、北 B 、京 C 、奥 D 、运7、某数学棵树的高刻，测得树的影长为4.8米，小明的C DBA俯视图321影长为1.2米，已知小明的身高为1.7米，则树的高度为________米。

8、有四个大小相同的正方体组成的几何体如图所示，那么它的俯视图是（）9、如图所示的几何体的左视图是（）10、一个几何体的三视图如图所示，那么这个几何体是（）DCBA11、如图，是由若干个同样大小的立方体搭成的几何体的俯视图，小正方形中的数字表示该位置立方体的个数，则这个几何体的主视图是（）A B C D第二节图形的对称、平移与旋转考点1 图形的对称1、轴对称与轴对称图形相平行；对应角2、中心对称与中心对称图形（1）中心对称：把一个图形绕着某一点旋转180°，如果它能与另一个图形完全重合，那么这两个图形成中心对称，该点叫做对称中心。

（2）中心对称图形：一个图形绕着某一点旋转180°后能与自身完全重合，这种图形叫中心对称图形，该点叫对称中心。

（3）性质：在中心对称的两个图形中，连接对称点的线段都经过对称中心，而且被对称中心平分。

全等变换:平移、对称、旋转30全等变换:平移、对称、旋转限时:30分钟夯实基础1.如图K30-1所示图形中,既是轴对称图形,又是中心对称图形的是 ( )图K30-12.若点A (-3,2)关于原点的对称点是点B ,点B 关于x 轴的对称点是点C ,则点C 的坐标是 ( )A .(3,2)B .(-3,2)C .(3,-2)D .(-2,3)3.[2018·绵阳] 在平面直角坐标系中,以原点为对称中心,把点A (3,4)逆时针旋转90°,得到点B ,则点B 的坐标为( )A .(4,-3)B .(-4,3)C .(-3,4)D .(-3,-4)4.[2018·聊城] 如图K30-2,将一张三角形纸片ABC 的一角折叠,使得点A 落在△ABC 外的一点A'处,折痕为DE.如果∠A=α,∠CEA'=β,∠BDA'=γ,那么下列式子正确的是 ( )图K30-2A .γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°-α-β5.如图K30-3,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC的度数为.图K30-36.如图K30-4,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为.图K30-47.如图K30-5,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE.若AB=3,BC=4,则BD= .图K30-58.如图K30-6,在△ABC中,∠ACB=90°,BC=1,AC=2,将△ABC绕点C按逆时针方向旋转90°得到△A1B1C,连接A1A,则△A1B1A的面积为.9.[2018·枣庄]如图K30-7,在4×4的方格纸中,△ABC的三个顶点都在格点上.(1)在图①中,画出一个与△ABC成中心对称的格点三角形;(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;(3)在图③中,画出△ABC绕点C按顺时针方向旋转90°后的三角形.图K30-7能力提升10.如图K30-8,在平面直角坐标系xOy中,△A'B'C'由△ABC绕点P旋转得到,则点P的坐标为()图K30-8A.(0,1)B.(1,-1)C.(0,-1)D.(1,0)11.[2018·天门]如图K30-9,在正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是()A.1B.1.5C.2D.2.512.如图K30-10,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的反射角等于入射角,进而可得∠6=∠1,∠3=∠5,∠2=∠4.如果∠1=55°,∠3=75°,那么∠2= 度.图K30-1013.如图K30-11,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分的面积为.图K30-1114.[2018·衢州]定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫做图形的γ(a,θ)变换.图K30-12如图K30-12,等边三角形ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC 经γ(1,180°)变换后所得的图形.若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推…,△A n-1B n-1C n-1经γ(n,180°)变换后得△A n B n C n,则点A1的坐标是,点A2018的坐标是.拓展练习15.[2018·德州]再读教材:宽与长的比是√5-1(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑为2取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形.(提示:MN=2)第一步,在矩形纸片一端,利用图K30-13①的方法折出一个正方形,然后把纸片展平.第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线AB,并把AB折到图③中所示的AD处.第四步,展平纸片,按照所得的点D折出DE,使DE⊥ND,则图④中就会出现黄金矩形.问题解决:(1)图③中AB= (保留根号);(2)如图③,判断四边形BADQ的形状,并说明理由;(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.实际操作:(4)结合图④,请在矩形BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.图K30-13参考答案1.D2.A3.B [解析] 如图,∴点B 的坐标为(-4,3).故选B .4.A [解析] 由折叠知∠A'=∠A=α,设A'D 交AC 于点F ,则∠BDA'=∠A+∠AFD=∠A+∠A'+∠A'EF.∵∠A=α,∠A'EF=β,∠BDA'=γ,∴γ=α+α+β=2α+β.5.17°6.107.58.19.解:(1)如图所示.(2)画出下列其中一个即可.(3)如图所示.10.B11.C [解析] 连接AE.易知AB=AD=AF ,∠D=∠AFE=90°,在Rt △AFE 和Rt △ADE 中,∵{AA =AA ,AA =AA ,∴Rt △AFE ≌Rt △ADE.∴EF=DE.设DE=FE=x ,则EC=6-x.∵G 为BC 的中点,BC=6,∴CG=BG=GF=3.在Rt △ECG 中,根据勾股定理,得(6-x )2+9=(x+3)2.解得x=2.∴DE=2.故选C . 12.6513.48 [解析] 根据题意,得DE=AB=10,BE=CF=6,CH ∥DF ,∴EH=10-4=6,易得S 阴影部分=S 梯形ABEH =12×(10+6)×6=48.14.-32,-√32-20172,√3215.解:(1)√5(2)四边形BADQ 是菱形. 理由如下:∵四边形ACBF 是矩形, ∴BQ ∥AD. ∴∠BQA=∠QAD.由折叠,得∠BAQ=∠QAD ,AB=AD , ∴∠BQA=∠BAQ. ∴BQ=AB.∴BQ=AD. 又∵BQ ∥AD ,∴四边形BADQ 是平行四边形. ∵AB=AD ,∴四边形BADQ 是菱形.(3)图④中的黄金矩形有矩形BCDE ,矩形MNDE , 以黄金矩形BCDE 为例,理由如下: ∵AD=√5,AN=AC=1, ∴CD=AD-AC=√5-1. 又∵BC=2,∴AA AA =√5-12.故矩形BCDE 是黄金矩形.(4)如图,在矩形BCDE 上添加线段GH ,使四边形GCDH 为正方形,此时四边形BGHE 为所要作的黄金矩形.长GH=√5-1,宽BG=3-√5.AA AA =√55-1=√5-12.。