层次分析法练习解答

层次分析法例题详解
例题：假设一家公司想要改善客户满意度，以下是几项建议：
A. 增加客户服务
B. 提高产品质量
C. 提高客户服务质量
层次分析法：
1.首先，将上述三项建议放入一个表格中，比较它们之间的关系。

建议 | 增加客户服务 | 提高产品质量 | 提高客户服务质量
------|-----------------|------------------|------------------------
关系 | 相关 | 相关 | 直接相关
2.然后，根据上表的关系，将建议分类：
A. 增加客户服务和提高客户服务质量：这两项建议直接相关，可以归为一类，即增加客户服务和提高客户服务质量。

B. 提高产品质量：这一项建议与其他两项建议相关，但不属
于同一类别，可以独立归类。

3.最后，根据分类的结果，提出有效的解决方案：
A. 增加客户服务和提高客户服务质量：可以采取措施增加客
户服务人员的数量，同时提高客户服务质量，如培训客服人员，
提升服务水平。

B. 提高产品质量：可以采取措施改善产品质量，如改进生产流程，提高材料质量，以及实施质量控制等。

黄廖版现代汉语练习题层次分析法划分结构（一）（后附答案）
1.静谧与清洁、优美与恬淡的景色。

2.她在不懈的努力下取得了好成绩。

3.为了实现我们的远大理想。

4.时代呼唤着研究者作出科学的说明。

5.班上今天多了一个人。

6.不断提高分析问题的能力。

7.生产出更多更好的产品。

8.下了一场非常大的雪。

9.潜心于生活海洋的作家。

10.我们的朋友是最值得信赖的人
参考答案
1. 【答案】
2. 【答案】
静 谧 与 清 洁 、 优 美 与 恬 淡 的 景 色
她 在 不 懈 的
努 力 下 取 了 好 成 绩
4. 【答案】
5. 【答案】
为 了 实 现 我 们 的 远 大 的 理 想
时 代 呼 唤 着 研 究 者 作 出 科 学 的 说 明
班 上 今 天
多 了 一 个 人
7. 【答案】
8. 【答案】
不 断 提 高 分 析 问 题 的 能 力
生 产 出 更 多 更 好 的 产 品
下 了 一 场 非
常 大 的 雪
10. 【答案】
潜 心 于 生 活 海 洋 的 作 家
我 们 的 朋 友 是 最 值 得 信 赖
的 人。

层次分析法（AHP ）作业解答供应商的选择作为目标层，总体服务价格、赔付率及可得性、交货周期、服务水准及信息传递作为准则层，可供选择的公司作为相应的方案层。

由此可以得出相应的供应商选择的层次图：从上述表格中可以得出一个矩阵A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1447/14/133/17/14/1317/17771 用根法求相应的数值：W1=4.304，W2=0.572, W3=0.330, W4=1.230. 再用归一法求得相应的向量 W=（0.683，0.089，0.051，0.177）T再一致性检验可以求得()706.4353.4213.4249.41411+++∑===n i Wi AWi n λ 求得λ=4.380CI=1--n nλ=0.127<1符合一致性检验所以得到额向量W=（0.683，0.089，0.051，0.177）T给每一中方案中的各个指标打分如下表：从上述表格中，可以的每一个指标下两两公司比较下的矩阵：总服务价格 赔付率及可得性⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡13/59/555/313/135/93195/13/19/11 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡124/38/32/112/34/33/43/212/13/83/421 A B C D交货周期 服务水准及信息传递⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡18/94/32/99/813/343/24/3139/24/13/11 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡14/18/17/1412/17/48217/874/78/71得到的上述四个指标矩阵。

由此可以得到在总服务价格下的向量M1 =（0.055，0.0.500，0.167，0.278）T用想相同的方法求得λ=4.023 得出相应的CI=1--n nλ=0.001<1符合一致性检验。

所以得到的向量是M1 =（0.055，0.0.500，0.167，0.278）T得到在赔付率及可得性下的向量M2 =（0.391，0.195，0.207，0.207）T用想相同的方法求得λ=4.247 得出相应的CI=1--n nλ=0.082<1符合一致性检验。

层次分析法例题详解，层次分析法题目层次分析法(AHP法)。

层次分析法是美国匹兹堡大学T.LSaaby 教授在20世纪70年代初提出的一种多目标决策分析方法。

这一方法的核心是对决策行为、决策方案及决策对象进行评价与选择，并对其进行优劣排序，从而为决策者提供定量形式的决策信息。

一致性检验，最后获取各评价指标重要性大小的排序系数，即评价指标的权重系数。

层次分析法确定权数的步骤如下。

①构造判断矩阵。

层次分析法运用层次分析法确定各评价指标的权数，首先是构造判断矩阵B,表示同一层次各个指标的相对重要性的判断值。

1.问题重述本文要求分析Y,Q两个旅游城市旅游业发展水平，并且给出了两个城市各方面因素的对比，如城市规模与密度，经济条件，交通条件，生态环境条件，宣传与监督，旅游规格，空气质量，城市规模，人口密度，人均GDP,人均住房面积，第三产业增加值占GDP比重，税收GDP,外贸依存度，市内外交通，人均拥有绿地面积，污水集中处理率，环境噪音，国内外旅游人数，理赔金额，立案数量，A级景点数量，旅行社数量，星级饭店数量。

建立数学模型进行求解。

2.问题分析本文要求分析y,Q两个旅游城市旅游业发展水平，在对y,Q两个城市的分析中，发现需要考虑因素较多。

第一、城市规模与度，包括城市规模与人口密度第二、经济条件，包括外贸依存度，人均GDP,人均住房面积，第二产业增加值占GDP比重，税收GDP.第三、交通条件，包括市内外交通。

第四，生态环境条件包括空气质量，人均绿地面积，污水处理能力，环境噪音。

第五、宣传与监督，包括国内外旅游人数，游客投诉立案件数。

第六、旅游规格，包括A级景点个数，旅行社个数，星级饭店个数，这就涉及到层次分析法来估算各个指标的权重，评出最优方案。

具体内容如下：(1)本文选择了对y,Q两个旅游城市旅游业发展水平有影响的19个指标作为评价要素，指标规定如下：城市规模：城市的人口数量人口密度：单位面积土地上居住的人口数。

用层次分析法分析下列句法结构
用层次分析法分析下列句法结构：
（1）这是一个鲜花盛开的村庄（2）非常热爱祖国和人民的英雄
解答一：
非常热爱祖国和人民的英雄A 非常热爱祖国和人民的| 英雄（偏正）非常热爱|祖国和人民（动宾）非常|热爱（偏正）祖国和人民（联合）B 非常热爱|祖国和人民的英雄（动宾）非常热爱（偏正）
分析说明:
本题比较突出的错误有两处:第一,第一层从“这是”切开,分出主谓关系,这是一个比较严重的错误。

第二,将“一个鲜花盛开的村庄”切分为“一个鲜花盛开的/村庄”,其中直接成分“一个鲜花盛开”是没有意义的单位,所以是错误切分。

黄廖版现代汉语练习题层次分析法划分结构（二）（后附答案）
1.我特别想得到朋友们的关怀。

2.在自己的工作岗位上做出应有的贡献。

3.结冰的水泥地特别滑。

4.栽种的是观赏的油菜花。

5.他在演讲中的一席话说得大家振奋起来。

6.思考如何加快改革进程。

7.全心全意为人民服务的精神。

8.对改革实践发挥了有效的指导作用。

9.唱得那么深沉而又动情。

10.我认真地看了两遍教材。

参考答案
1. 【答案】
2. 【答案】
3. 【答案】
我 特 别 想 得 到 朋 友 们 的 关 怀
在 自
己 的 工 作 岗 位 上 做 出 应
有 的 贡 献
结 冰 的
水 泥 地
特 别
滑
4. 【答案】
5. 【答案】
6. 【答案】
栽 种 的 是 观 赏 的 油 菜 花
他 在 演 讲 中 的
一 席 话 说 得 大 家 振 奋 起 来
思 考 如 何 加 快 改 革 进
程
7. 【答案】
8. 【答案】
9. 【答案】
全 心 全 意 为 人 民 服 务 的 精 神
对 改 革 实 践 发 挥 了 有 效
的 指 导 作 用
唱
得 那
么 深 沉 又 动 情
10.【答案】
我认真地看了两遍教材。

定 中 定 中
定 中
联 合
27、一股带着清凉与花香的微风
定 中
数 量 动 宾
定 中
联 合
28、在一片绿色背景中显得分外好瞧
29、公民有学习与使用国家通用语言文字的权利
9、
10、 发 明 能 打 出 乐 谱 的 打 字 机 的 人
11、 对 国 内 外 旅 游 者 有 着 极 大 的 吸 引 力
12、 气氛紧张的会议室里
13、
14、整个村庄沉浸在欢呼声与锣鼓声中
15、希望参加去海南的旅行团
16、首都北京的秋天景色十分宜人
主 谓
定 中 主 谓
同 位 状 中
17、最贵的一张值五千元
一、用层次分析法分析下列复杂短语,如果有歧义要作不同分析。
1、成为建设社会主义现代化强国的有用人才
2、当我走下台阶离开纪念碑的时候
3、 希望在人民中间加强法制教育
动 宾
状 中
介 词 动 宾定 中 定 中Fra bibliotek4、5、
6、 雨后的天空显得比平时晴朗
7、 把院子收拾得干净又整齐
8、语言要传递的信息无穷无尽且无法预测
A主 谓
“的” 字主 谓
状 中动 宾
数 量
B主 谓
定 中 动 宾
状 中数 量
18、
19、 比 较 了 解 中 文 系 的 学 生
20、一些国家领导人出席了会议
一些国家领导人出席了会议
21、访 问 美 国 归 来 的 科学家
22、关于批判继承问题的讨论 关于批判继承问题的讨论
介 词 定 中
定 中 介 词
定 中 定 中
联 合 联 合
23、 赞 扬 青 年 学 生 的 作 品 赞 扬 青 年 学 生 的 作 品

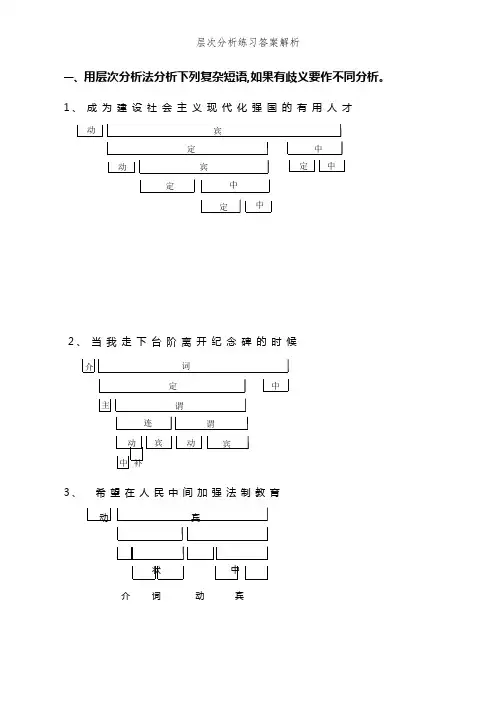
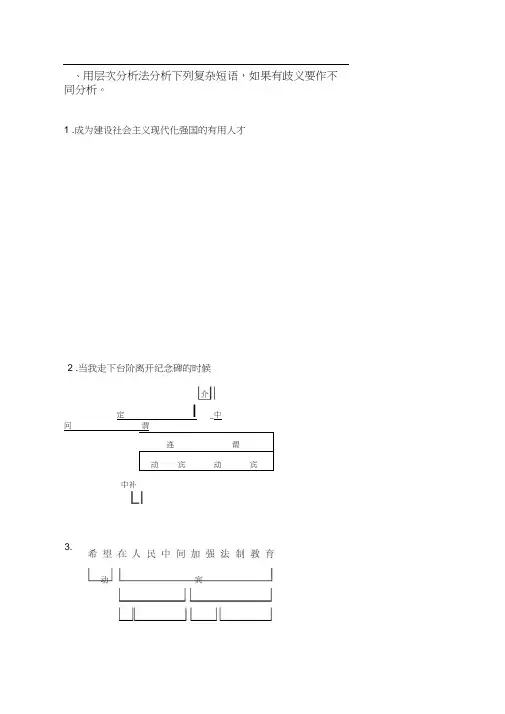
3.、用层次分析法分析下列复杂短语，如果有歧义要作不同分析。

1 .成为建设社会主义现代化强国的有用人才2 .当我走下台阶离开纪念碑的时候定I_中中补Ll状中3.介 词 动 宾定 中 定 中4.浓郁的充满乡土味的生活气息I 动丨I 宾I 5.I ⅞IligI I 定 I I Φ Il ¾ Il ⅞ I I状Il 中I I介Il 词I6.雨后的天空显得比平时晴朗一列从两山缝隙里冲出来的火车⅛ll φI I 定Il 中I⅛]∣⅛I 中II状I I 中、IydLJfLJ L⅛J I 补LSLl l⅛d7.把院子收拾得干净又整齐8 .语言要传递的信息无穷无尽且无法预测用中国乐器演奏的西洋乐曲旳I 词II 定I l_?J10.发明能打出乐定谱的打字机的人动宾I LJDM11.对国内外旅游者有着极大的吸引力I 状I I中I曲1I词I l⅛l」I 宾I 定Il中丨定I丨中I13.不知道他会不会答应让你去I动丨1 宾丨I状Il中Il壬I 谓II 状H 中II联Il合Il动H 宾IQgiffiJ ι⅛ι⅛ι匡）谊14.主谓疋中中补【I介___________ 词方11位II联I合丨12. 气氛紧张方的会议丨动丨1 宾Il-⅛JI _____ ≡______ II定I I中I型1宾I15. 希望参加去海南的旅行团16. 首都北京的秋天景色十分宜人17. 最贵的一张值五千元A I 主丨丨谓________Il I状中主状中动18.热情接待我们的進澳同胞 A I 折H 兵一I19.比较了解中文系的学生B I 动I I 一宜II状I I中I I 足I I ÷I20. 一些国家领导人出席了会议定中些国家领导人出席了会议I 主谓I定中I动I宾定I中21.访问美国归来的科学家I ⅞ Il ________ 昱 _______ II 定I I 中II ⅜⅞ ll中丨I 定I I中II 连I丨谓丨I动丨I宾I2 2.关于批判继承问题的讨论介词关于批判继承问题的讨论____________ 定____________ 中I23.赞扬青年学生的作品定中赞扬青年学生的作品疋I中动宾定中定中合疋中mil⅜ I I 宾II 主I I谓II定丨丨中I圈I ⅝ II 主I I谓II 定I I中I世I I中I丨主Il 谓丨LaJ I 宾I2 4. 厂长批评小李的意见不正确2 5.非常热爱祖国和人民的英雄状中非常热爱祖国和人民的英雄动宾√∖合疋中28 .在一片绿色背景中显得分外好看状I中汕词 I 动 宾I方11位I丨状丨丨中I27. 2 6.以法律的形式确认了公民对国家的权利和义务 联 合带着清凉 和花香中I 数Il 量H 定"中疋中29.公民有学习和使用国家通用语言文字的权利3 0.景泰蓝花瓶里插满了各种名贵的花 丨 主丨丨 谓 I方Il 位H 动丨丨宾I定11中I I 中丨丨补I I 定I中31.摆脱了香港上千影迷热情的围困夺路归来的李连杰32.钦佩小张说话的谨慎严密、小王做事的果敢决断、小李待人的热情和蔼动宾I。

你已经去过几家主要的摩托车商店，基本确定将从三种车型中选购一种。

你选择的标准主要有：价格，耗油量大小，舒适程度和外表美观情况。

经反复思考比较，构造了它们的成对比较矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1315518731315181517131 三种车型(记为a,b,c)关于价格，耗油量，舒适程度及你对他们外观喜欢程度的成对比较矩阵为（价格）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡121321213121 （耗油量）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡127151712151 （舒适程度）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡141531415131 （外观）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡171531713151 （1）根据上述矩阵可以看出这四项标准在你的心目中的比重是不同的，请按由大到小的顺序排出。

（2）哪辆车最便宜，哪辆车最省油，哪辆车最舒适，你认为哪辆车最漂亮？用层次分析法确定你对这三种车型的喜欢程度（用百分比表示）。

比建模过程如下：先构建成对比较矩阵1378111552311133751114853x x x x ⎡⎤⎢⎥⎢⎥ ⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥1⎢⎥⎣⎦A =列向量归一化，得到矩阵B=0.62450.68180.52500.47060.20820.22730.37500.29410.08920.04550.07500.17650.07810.04550.02500.0588⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，然后按行求和得到矩阵C =2.30191.10460.38620.2074⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，再对矩阵C = 2.30191.10460.38620.2074⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦归一化得到w =0.57530.27610.09650.0518⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，2.49401.20970.38940.2111*?A w ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=1/4 2.4940/0.5753 1.2097/0.27610.3894/0.09650.2111/0.0518 1.2068µ=⨯+++=（）同理，可求得下面四个比较矩阵权向量和最大特征根。

语法层次分析试题及答案一、选择题（每题2分，共10分）1. 下列句子中，动词“看”的宾语是：A. 我看了一本书。

B. 他看了我一眼。

C. 她看了电视。

D. 我们看了电影。

答案：A2. 以下句子中，哪个是被动句？A. 他被老师批评了。

B. 老师批评了他。

C. 他批评了老师。

D. 老师批评了学生。

答案：A3. 下列句子中，哪个使用了倒装句式？A. 只有努力学习，才能取得好成绩。

B. 他不仅学习好，而且体育也好。

C. 他学习好，体育也好。

D. 他不仅学习好，体育也好。

答案：A4. 下列句子中，哪个是复合句？A. 他去图书馆了。

B. 他去了图书馆，我也去了。

C. 他去了图书馆。

D. 他去图书馆了，我也去了。

答案：B5. 下列句子中，哪个使用了虚拟语气？A. 如果明天下雨，我们就不去公园了。

B. 他昨天去了公园。

C. 他去公园了。

D. 他去了公园。

答案：A二、填空题（每题2分，共10分）1. 句子“他昨天去了公园。

”中，“去了”是______。

答案：谓语2. 句子“他不仅学习好，而且体育也好。

”中，“不仅...而且...”是______。

答案：并列连词3. 句子“只有努力学习，才能取得好成绩。

”中，“只有...才能...”是______。

答案：条件状语4. 句子“他被老师批评了。

”中，“被”是______。

答案：被动标记5. 句子“如果明天下雨，我们就不去公园了。

”中，“如果”是______。

答案：条件状语从句引导词三、改错题（每题2分，共10分）1. 他昨天去图书馆了。

答案：他昨天去了图书馆。

2. 他不仅学习好，体育也好。

答案：他不仅学习好，而且体育也好。

3. 只有努力学习，才能取得好成绩。

答案：只有努力学习，我们才能取得好成绩。

4. 他被老师批评了。

答案：他被老师批评。

5. 如果明天下雨，我们就不去公园了。

答案：如果明天下雨，我们就不去了公园。

四、翻译题（每题5分，共20分）1. 请将“他昨天去了图书馆。

层次分析法练习练习一、市政工程项目建设决策问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案就是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。

除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即就是多准则决策问题,试运用层次分析法建模解决。

1、建立递阶层次结构在市政工程项目决策问题中,市政管理人员希望通过选择不同的市政工程项目,使综合效益最高,即决策目标就是“合理建设市政工程,使综合效益最高”。

为了实现这一目标,需要考虑的主要准则有三个,即经济效益、社会效益与环境效益。

但问题绝不这么简单。

通过深入思考,决策人员认为还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。

假设本问题只考虑这些准则,接下来需要明确为了实现决策目标、在上述准则下可以有哪些方案。

根据题中所述,本问题有两个解决方案,即建高速路或建地铁,这两个因素作为措施层元素放在递阶层次结构的最下层。

很明显,这两个方案于所有准则都相关。

将各个层次的因素按其上下关系摆放好位置,并将它们之间的关系用连线连接起来。

同时,为了方便后面的定量表示,一般从上到下用A 、B 、C 、D 。

代表不同层次,同一层次从左到右用1、2、3、4。

代表不同因素。

这样构成的递阶层次结构如下图。

目标层A准则层B准则层C措施层D2、构造判断矩阵并请专家填写 征求专家意见,填写后的判断矩阵如下:计算所得的权向量及检验结果见下:4、层次总排序及检验层次总排序及检验结果见下:表5 C层次总排序(CR = 0、0000)表5、结果分析从方案层总排序的结果瞧,建地铁(D2)的权重(0、6592)远远大于建高速路(D1)的权重(0、3408),因此,最终的决策方案就是建地铁。

根据层次排序过程分析决策思路。

层次分析法练习练习一、市政工程项目建设决策问题提出市政部门管理人员需要对修建一项市政工程项目进行决策，可选择的方案是修建通往旅游区的高速路（简称建高速路）或修建城区地铁（简称建地铁）。

除了考虑经济效益外，还要考虑社会效益、环境效益等因素，即是多准则决策问题，试运用层次分析法建模解决。

1、建立递阶层次结构在市政工程项目决策问题中，市政管理人员希望通过选择不同的市政工程项目，使综合效益最高，即决策目标是“合理建设市政工程，使综合效益最高”。

为了实现这一目标，需要考虑的主要准则有三个，即经济效益、社会效益和环境效益。

但问题绝不这么简单。

通过深入思考，决策人员认为还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素（准则），从相互关系上分析，这些因素隶属于主要准则，因此放在下一层次考虑，并且分属于不同准则。

假设本问题只考虑这些准则，接下来需要明确为了实现决策目标、在上述准则下可以有哪些方案。

根据题中所述，本问题有两个解决方案，即建高速路或建地铁，这两个因素作为措施层元素放在递阶层次结构的最下层。

很明显，这两个方案于所有准则都相关。

将各个层次的因素按其上下关系摆放好位置，并将它们之间的关系用连线连接起来。

同时，为了方便后面的定量表示，一般从上到下用A、B、C、D。

代表不同层次，同一层次从左到右用1、2、3、4。

代表不同因素。

这样构成的递阶层次结构如下图。

目标层A准则层C措施层D图1 递阶层次结构示意图2、构造判断矩阵并请专家填写征求专家意见，填写后的判断矩阵如下：表2 判断矩阵表3、计算权向量及检验计算所得的权向量及检验结果见下：表4 层次计算权向量及检验结果表4、层次总排序及检验层次总排序及检验结果见下：表5 C层次总排序(CR = 0.0000)表D层次总排序(CR = 0.0000)5、结果分析从方案层总排序的结果看，建地铁（D2）的权重（0.6592）远远大于建高速路（D1）的权重（0.3408），因此，最终的决策方案是建地铁。

24. 厂长批评小李的意见不正确
25.非常热爱祖国和人民的英雄
定 中
状 中
动 宾
联 合
非常热爱祖国和人民的英雄
动 宾
状 中 联 合
定 中
26.以法律的形式确认了公民对国家的权利和义务
状中
介词动宾
定中定中
Байду номын сангаас定中
联合
27.一股带着清凉和花香的微风
定 中
数 量 动 宾
定 中
联合
28.在一片绿色背景中显得分外好看
状 中数 量
18.
19. 比 较 了 解 中 文 系 的 学 生
20.一些国家领导人出席了会议
一些国家领导人出席了会议
21.访问美国归来的科学家
22.关于批判继承问题的讨论关于批判继承问题的讨论
介词定中
定中介词
定中定中
联合联合
23. 赞 扬 青 年 学 生 的 作 品 赞 扬 青 年 学 生 的 作 品
11. 对 国 内 外 旅 游 者 有 着 极 大 的 吸 引 力
12. 气氛紧张的会议室里
13.
14.整个村庄沉浸在欢呼声和锣鼓声中
15.希望参加去海南的旅行团
16.首都北京的秋天景色十分宜人
主谓
定中主谓
同位状中
17.最贵的一张值五千元
A主 谓
“的” 字主 谓
状 中动 宾
数 量
B主 谓
定 中 动 宾
一、用层次分析法分析下列复杂短语，如果有歧义要作不同分析。
1.成为建设社会主义现代化强国的有用人才
2.当我走下台阶离开纪念碑的时候
3. 希望在人民中间加强法制教育
动宾
状中
介词动宾

层次分析练习答案————————————————————————————————作者：————————————————————————————————日期：一、用层次分析法分析下列复杂短语，如果有歧义要作不同分析。

1.成为建设社会主义现代化强国的有用人才2.当我走下台阶离开纪念碑的时候3.希望在人民中间加强法制教育动宾状中介词动宾定中定中4.5.动词介定中主谓连谓动宾宾中补动宾定中动宾定中定定中中6. 雨后的天空显得比平时晴朗7.把院子收拾得干净又整齐8.语言要传递的信息无穷无尽且无法预测9.10. 发明能打出乐谱的打字机的人11. 对国内外旅游者有着极大的吸引力主谓定中合联主谓状中状中动宾定中中状动宾中补中定12. 气氛紧张的会议室里13.14. 整个村庄沉浸在欢呼声和锣鼓声中15.希望参加去海南的旅行团16.首都北京的秋天景色十分宜人主 谓 定 中 主 谓 同 位 状 中方 位中定 主 谓 方 主 谓 补定 中 中 介 词位 联 合17. 最贵的一张值五千元A主谓“的”字主谓状中动宾数量B主谓定中动宾状中数量18.19. 比较了解中文系的学生20. 一些国家领导人出席了会议一些国家领导人出席了会议主谓定定中中宾动主谓21. 访问美国归来的科学家22.关于批判继承问题的讨论关于批判继承问题的讨论介词定中定中介词定中定中联合联合23. 赞扬青年学生的作品赞扬青年学生的作品24.厂长批评小李的意见不正确25.非常热爱祖国和人民的英雄定中状中动宾联合动宾动宾定定中中中中定定非常热爱祖国和人民的英雄动 宾状 中 联 合定 中26.以法律的形式确认了公民对国家的权利和义务状 中 介 词 动 宾 定 中 定 中 定 中 联 合27. 一股带着清凉和花香的微风定 中数 量 动 宾定 中联 合28.在一片绿色背景中显得分外好看29.公民有学习和使用国家通用语言文字的权利主 谓 动宾 定宾 中动状词中 介 动 宾 状 中方 位 定 中 定 中数 量30.景泰蓝花瓶里插满了各种名贵的花31. 摆脱了香港上千影迷热情的围困夺路归来的李连杰 32.钦佩小张说话的谨慎严密、小王做事的果敢决断、小李待人的热情和蔼主 谓 方 位 定 定 定 中 中 中动 宾中 补定 定 定 定 定 中中中中 中 连 谓动宾 动宾联 合合合 合 联 联 联 定 定 定 中 中中 主 主 主 谓 谓 谓。

关于层次分析法的例题与解旅游发展水平评价摘要为了研究和比较两个旅游城市的旅游发展水平，建立了层次分析法[数学模型，对两个旅游城市的旅游发展水平进行了评价.首先，通过对本课题中图1和表1的分析和讨论，按照层次分析法，建立了四个层次:目标层a、准则层b、子准则层c和方案层d，通过比较同一层目标之间的重要度，得到判断矩阵，每个判断矩阵用MATLAB[1]编程求解。

其次，利用MATLAB软件计算决策组合向量，然后比较决策组合向量的大小。

以“最大决策组合向量”为目标，Y市的决策组合向量为0.4325，Q市的决策组合向量为0.5675。

最后，通过比较q市和y市旅游发展水平的决策组合向量，得出q市旅游发展水平较高的结论。

层次分析法MATLAB旅游发展水平；决策组合向量11.问题重述本文要求对Y和Q两个旅游城市的旅游发展水平进行分析，并对两个城市的各种因素进行比较，如城市规模和密度、经济条件、交通条件、生态环境条件、宣传监督、旅游规格、空气质量、城市规模、人口密度、人均国内生产总值、人均住房面积、第三产业增加值占国内生产总值的比重、税收国内生产总值、对外贸易依存度、城市内外交通、人均绿地等。

污水集中处理率、环境噪声、国内外游客数量、索赔金额、立案数量、甲级景区数量、旅行社数量、星级酒店数量。

建立数学模型来解决这个问题。

2.问题分析本文要求对Y、Q旅游城市的旅游业发展水平进行分析。

在对Y和Q 旅游城市的分析中，发现有许多因素需要考虑。

首先，城市规模和密度，包括城市规模和人口密度。

第二，经济条件，包括对外贸易依存度，人均国内生产总值，人均住房面积，第三产业增加值占国内生产总值的比重，税收占国内生产总值的比重。

第三，运输条件，包括内部运输和外部运输。

第四，生态环境条件包括空气质量、人均绿地面积、污水处理能力和环境噪声。

第五，宣传和监督，包括国内外游客人数，以及游客投诉的数量。

第六，旅游指标，包括甲类景区的数量、旅行社的数量、星级酒店的数量，用层次分析法来估计各指标的权重，并对最优方案进行评价。

旅游业发展水平评价问题摘要为了研究比较两个旅游城市Q、Y的旅游业发展水平，建立层次分析法]3[数学模型，对两个旅游城市Q、Y的旅游业发展水平进行了评价.首先，通过对题目中的图1、表1进行了分析与讨论，根据层次分析法，建立了目标层A、准则层B和子准则层C、方案层D四个层次，通过同一层目标之间的重要性的两两比较，得出判断矩阵,利用]1[MATLAB编程对每个判断矩阵进行求解.其次,用MATLAB软件算出决策组合向量，再比较决策组合向量的大小，由“决策组合向量最大”为目标,得出城市Y的决策组合向量为0.4325，城市Q组合向量为0.5675.最后，通过城市Q旅游业发展水平与旅游城市Y旅游业发展水平的决策组合向量比较，得出城市Q的旅游业发展水平较高.关键词层次分析法MATLAB旅游业发展水平决策组合向量1.问题重述本文要求分析QY,两个旅游城市旅游业发展水平,并且给出了两个城市各方面因素的对比，如城市规模与密度，经济条件，交通条件，生态环境条件，宣传与监督，旅游规格，空气质量，城市规模，人口密度，人均GDP，人均住房面积，第三产业增加值占GDP比重，税收GDP，外贸依存度，市内外交通，人均拥有绿地面积，污水集中处理率，环境噪音，国内外旅游人数，理赔金额，立案数量，A级景点数量，旅行社数量，星级饭店数量.建立数学模型进行求解.2.问题分析本文要求分析QY,两个城市的分析Y,两个旅游城市旅游业发展水平，在对Q中，发现需要考虑因素较多，第一、城市规模与密度，包括城市规模与人口密度.第二、经济条件，包括外贸依存度，人均GDP，人均住房面积，第三产业增加值占GDP比重，税收GDP.第三、交通条件，包括市内外交通.第四，生态环境条件包括空气质量，人均绿地面积，污水处理能力，环境噪音.第五、宣传与监督，包括国内外旅游人数，游客投诉立案件数.第六、旅游规格，包括A级景点个数，旅行社个数，星级饭店个数，这就涉及到层次分析法来估算各个指标的权重，评出最优方案.具体内容如下：（1）本文选择了对QY,两个旅游城市旅游业发展水平有影响的19个指标作为评价要素,指标规定如下：城市规模：城市的人口数量.人口密度：单位面积土地上居住的人口数.是反映某一地区范围内人口疏密程度的指标.人口影响城市规模.人口密度越大城市规模也就越大.人均GDP：即人均国内生产总值.人均城建资金：即用于城市建设的资金总投入.第三产业增加值：增加值率指在一定时期内单位产值的增加值.即第三产业增加值越高越能带动城市经济的发展.税收GDP：税收是国家为实现其职能，凭借政治权力，按照法律规定，通过税收工具强制地、无偿地征收参与国民收入和社会产品的分配和再分配取得财政收入的一种形式.外贸依存度：即城市对于外贸交易的依赖程度.市内交通：即城市市区交通情况.市外交通：即城市郊区交通情况.市内交通与市外交通对于城市交通条件具有同等的重要性.空气质量：即城市总体空气质量情况.空气质量越好对于城市生态环境就越好.人均绿地面积：即反应城市绿化面积以及人口密度的比值关系.污水处理能力：城市污水处理水平.环境噪音：城市环境噪音情况.国内外旅客人数：国内外来旅客一年总人数.人数越多说明宣传与监督就越好.理赔金额：即立案后需要赔付的资金数.立案件数：即在旅游时发生违法事件后公安部立案的件数.A 级景点数量：即A 级景点的个数.A 级景点越多,越能带动旅行社数量以及星级饭店数量,则旅游规格越大.旅行社数量：即旅行社的个数.星级饭店数量：即星级饭店在旅游景点的个数.（2）用层次分析法建立模型，根据判断矩阵，利用MATLAB 软件，算出每个判断矩阵的特征向量W 、最大特征根c 、一次性指标CI ，再结合随机一次性指标，得出每个指标的特征向量.（3）用（2）得出的数据，运用MATLAB 软件算出两个城市的决策组合向量，做比较.3.模型假设1.假设两个城市Q 、Y 的人口流动不大.2.假设两个城市Q 、Y 的各项指标短期内不会发生太大的改变.4.符号说明A : 表示目标层；j B : 表示准则层第j 个指标的名称)6,,2,1( =j ；i C : 表示子准则层第i 个指标的名称()19,,2,1 =i ； q D : 表示方案层第q 个指标的名称()2,1=q ；1w : 表示准则层对目标层的特征向量组成的矩阵； 2w : 表示子准则层对准则层的特征向量组成的矩阵； 3w : 表示方案层对子准则层的特征向量组成的矩阵；CI : 表示一次性指标；CR : 表示随机一次性指标； Z : 表示决策组合向量.5.模型建立与求解5.1 根据层次分析法分析以及题目中的图1可以建立如下表5-1的层次分析结构，并构造两两比较判断矩阵在递阶层次结构中，设上一层元素B 为准则层，所支配的下一层元素为1C ……19C ，要确定元素1C ……n C 对于准则层B 相对的重要性即权重，可分为两种情况：（1）如果1C 2C ……n C 对B 的重要性可定量，其权重可直接确定； （2）如果问题复杂，1C 2C ……n C 对B 的重要性无法直接定量，而是一些定性的，确定权重用两两比较方法.（3）其方法是，对于准则层C ，元素i C 和j C 哪一个更重要，重要多少，按1-9比例标度对重要性程度赋值.表5-2中列出了1-9标度的含义.对于准则B ，n 个元素之间相对重要性的比较得到一个两两比较判断矩阵P =()mxn ij P ，表示其中ij P 表示i P 和j P 对B 的影响之比，显然ij P >0，ij P =ijP 1，ij P =1，由ij P 的特点，P 称为正互反矩阵.通过两两判断矩阵用方根法求出他们的最大特征根和特征向量，求法如下： 1. 判断矩阵每一行元素的乘积，其中ij n1j 1p m =∏=，i =1,2…,n .2. 计算i m 的n 次方根_i w ，_i w =n i m .3. 对向量Tn w w w ⎪⎭⎫ ⎝⎛=__1,...,归一化，即∑==n j ji w 1__i w w ，则Tn w w w ⎪⎭⎫⎝⎛=__1,...,为所求的特征向量.4. 计算判断矩阵的最大特征跟m ax λ，()∑==n1max i iinw pw λ，式中()i pw 表示pw 的第i 个元素.5. 定义⎪⎭⎫ ⎝⎛--=1max n n CI CI λ为矩阵A 的一致性指标，为了确定A 的不一致性程度的容许范围，需要找出衡量A 的一致性指标CI 的标准.引入随机一致性指标RI .平均随机一致性指标RI 是这样得到的；对于固定的n ，随机构造正互反矩阵A ，其中ij a 是从1，2，……9,91......31,21中随机抽取的，这样的A 是最不一致的，取充分大的样子（500个样本）得到A 的最大特征跟的平均值m ax λ，定义⎪⎭⎫ ⎝⎛--=1max n n RI λ，对于不同的n 得出随机一致性指标RI 的数值如下表5-3表中n =1,2时RI =0，是因为1,2阶的正互反矩阵总是一致阵.令RICICR =，称CR 为一致性比率，当CR <0.1时，本文认为判断矩阵具有满意的一致性，否则就需要调整判断矩阵，使之具有满意的一致性.最后通过计算得出下表5-4（其中n B 表示准则层的特征向量中的第n 个数值，in C 表示指标层的特征向量第n 个准则对第j 个指标的数值）层次总排序一致性检验的方法j n1CI c CI j j ∑==j n 1c RI RI j j ∑==RICI CR =若1.0CR时，所以认为判断矩阵具有满意的一致性，否则就需要调整判断.矩阵，使之具有满意的一致性.5.2根据层次分析法求出各个指标的权重依据题目中的表1分析，对本题做出其中一种假设：（1）经济条件和交通条件重要性相当，生态环境条件最重要，旅游规格、宣传与监督、城市规模与密度依次次之.（2）在城市规模与密度中，城市人口比人口密度重要一点.（3）在经济条件中，第三产业增加值GDP第一重要，其次是人均GDP，税收GDP、外贸依存度、人均城建资金依次次之.（4）在交通条件中，市内交通和市外交通的重要性相当.（5）在生态环境条件中，空气质量第一重要，其次是人均绿地面积，污水处理能力、环境噪音依次次之.（6）在宣传与监督中，国内外旅游人数第一重要，理赔金额、游客投诉立案件数重要性相当.（7）在旅游规格中，A级景点个数第一重要，星级饭店个数、旅行社个数依次次之.（8）对于城市规模，城市Q比城市Y的重要性小一些；对于人口密度，城市Y比城市Q的重要性明显重要；对于人均GDP，城市Q比城市Y的重要性稍重要；对于人均城建资金，城市Q比城市Y的重要性稍微重要；对于第三产业增加值GDP，城市Q比城市Y的重要性小一些；对于税收GDP，城市Q比城市Y的重要性稍小一点；对于外贸依存度,城市Q比城市Y的重要性稍重要；对于市内交通，城市Y比城市Q的重要性稍重要一点；对于市外交通，城市Y比城市Q的重要性比稍重要小一点；归于空气质量，城市Q比城市Y的重要性相当；对于人均绿地面积，城市Y比城市Q的重要性稍重要；对于污水处理能力，城市Y比城市Q的重要性稍重要一些；对于环境噪音，城市Q比城市Y的重要性相当；对于国内外旅游人数，城市Q比城市Y的重要性稍重要；对于理赔金额，城市Q比城市Y的重要性稍重要一些；对于游客投诉立案件数，城市Q比城市Y的重要性稍重要；对于A级景点个数，城市Y比城市Q的重要性稍重要小一些；对于旅行社个数，城市Y比城市Q的重要性稍重要小一些；对于星级饭店个数，城市Q比城市Y的重要性相当.根据上述分析，按1-9比例标度对准则层对目标层、子准层对准则层、目标层对子准则层的重要程度进行赋值，构造准则层对目标层的判断矩阵、子准则层对准则层的判断矩阵、方案层对子准则层的判断矩阵.准则层()6,,2,1 =j B j 对目标层A 的判断矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=12312121321141313123412252321114232111431215141411A 利用MATLAB 软件(附录1)求得 最大特征值0719.6max =λ特征向量⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1219.00753.03422.02057.02057.00492.01w一致性检验比率1.00116.0<=CR所以矩阵满足一致性检验.子准则层21,C C 对准则层1B 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=131311B利用MATLAB 软件(附录2)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 子准则层76543,,,,C C C C C 对准则层2B 的判断矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=121412312131321431522131511413221412B 利用MATLAB 软件(附录3)求得 最大特征值0681.5max =λ特征向量⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0973.01599.04185.00618.02625.0w一致性检验比率1.00152.0<=CR所以矩阵满足一致性检验.子准则层98,C C 对准则层3B 的判断矩阵⎥⎦⎤⎢⎣⎡=11113B 利用MATLAB 软件(附录4)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 子准则层13121110,,,C C C C 对准则层4B 的判断矩阵⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=1121311121312212133214B 利用MATLAB 软件(附录5)求得最大特征值0104.4max =λ特征向量⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1409.01409.02628.04554.0w 一致性检验比率1.00038.0<=CR所以矩阵满足一致性检验.子准则层161514,,C C C 对准则层5B 的判断矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1221211212215B 利用MATLAB 软件(附录6)求得最大特征值0536.3max =λ特征向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3108.01958.04934.0w 一致性检验比率1.00462.0<=CR所以矩阵满足一致性检验.子准则层191817,,C C C 对准则层6B 的判断矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1221211312316B 利用MATLAB 软件(附录7)求得最大特征值0092.3max =λ特征向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2970.01634.05396.0w 一致性检验比率1.00079.0<=CR所以矩阵满足一致性检验.方案层对子准则层的判断矩阵 方案层21,D D 对子准则层1C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=122111C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层2C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=155112C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎢⎣=1667.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层3C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=133113C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层4C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=144114C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=8000.02000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层5C 的判断矩阵：⎥⎥⎦⎤⎢⎢⎣⎡=122115C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎢⎣=3333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层6C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=133116C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层7C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=141417C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=8000.02000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层8C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=155118C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎢⎣=8333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层9C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=122119C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层10C 的判断矩阵⎥⎦⎤⎢⎣⎡=111110C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层11C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1313111C利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=7500.02500.0w因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层12C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1414112C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2000.08000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层13C 的判断矩阵⎥⎦⎤⎢⎣⎡=111113C 利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层14C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1331114C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验.2115⎥⎥⎦⎤⎢⎢⎣⎡=1441115C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=8000.02000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层16C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1331116C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=2500.07500.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层17C 的判断矩阵⎥⎥⎦⎤⎢⎢⎣⎡=1331117C利用MATLAB 软件(附录8)求得最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验.2118⎥⎥⎦⎤⎢⎢⎣⎡=1221118C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=6667.03333.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 方案层21,D D 对子准则层19C 的判断矩阵：⎥⎦⎤⎢⎣⎡=111119C 利用MATLAB 软件(附录8)求得 最大特征值2max =λ特征向量为⎥⎦⎤⎢⎣⎡=5000.05000.0w 因为当2=n 时，0=RI ,2阶的正反矩阵总是一致性，所以满足一致性检验. 通过准则层()6,,2,1 =j B j 对目标层A 的判断矩阵、子准则层()19,,2,1 =i C i 对准则层()6,,2,1 =j B j 的判断矩阵得出特征向量，建立层次总表5-5层次总排序一致性检验如下:0073.061==∑=j j j CI B CI65274.0j 61j j ==∑=RI B RI0111.065274.00073.0===RI CI CR 由于1.00111.0<=CR ,所以认为层次总排序的结果具有满意的一致性，因此不需要重新调整判断矩阵的元素取值.5.3 利用MATLAB 进行决策组合向量的运算（附录9）⋅⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⋅⋅=Tw w w Z 2970.0001634.0000005396.00000003108.0000001958.0000004934.00000001409.0000001409.0000002628.0000004554.00000005000.0000005000.00000000973.000001599.0000004185.0000000618.0000002625.00000002500.0000007500.0132⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡5000.05000.06667.03333.06667.03333.02500.07500.08000.02000.02500.07500.05000.05000.02000.08000.07500.02500.05000.05000.06667.03333.01667.08333.08000.02000.02500.07500.06667.03333.02000.08000.02500.07500.08333.01667.03333.06667.0⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⋅1219.00753.03422.02057.02057.00492.0 Z ⎥⎦⎤⎢⎣⎡=5675.04325.0 比较Z 值大小可知，12Z Z >,表明城市Q 的旅游发展也水平最高，城市Y 的旅游业发展水平次之，所以城市Q 的旅游发展也水平高.6模型的评价优点：(1) 本文选择了计算比较简单的层次分析法，经过计算得到了相应的综合发展旅游业的估计值，为城市旅游业的发展提供了依据.(2) 使用了MATLAB 软件，减少了计算工作量，大大降低了运算的困难.缺点：判断的结果具有一定的主观性，不能比较切实的结合当地的具体情况，做出科学的决策方案.7参考文献[1] 姜启源等，数学建模（第四版）北京:高等教育出版社.2011年[2] 马莉，数学实验与建模，北京:清华大学出版2010年[3] 王莲芬，层次分析法引论，北京:中国人民大学出版社，1990年附录：附录1x=[1 1/4 1/4 1/5 1/2 1/3;4 1 1 1/2 3 2;4 1 1 1/2 3 2;5 2 2 1 4 3;2 1/3 1/3 1/4 1 1/2;3 1/2 1/2 1/3 2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-6)/5 %一致性指标CR=CI/1.24 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =6.0719W =0.04920.20570.20570.34220.07530.1219B =0.04670.21410.21410.29180.08810.1452CI =0.0144CR =0.0116C =0.2146附录2：>> x=[1 3;1/3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250附录3：x=[1 4 1/2 2 3;1/4 1 1/5 1/3 1/2;2 5 1 3 4;1/2 3 1/3 1 2;1/3 2 1/4 1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-5)/4 %一致性指标CR=CI/1.12 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =5.0681W =0.26250.06180.41850.15990.0973B =0.27340.05940.36640.18730.1135CI =0.0170CR =0.0152C =0.2698附录4：x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =CR =NaNC =0.5000附录5：x=[1 2 3 3;1/2 1 2 2;1/3 1/2 1 1;1/3 1/2 1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-4)/3 %一致性指标CR=CI/0.90 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =4.0104W =0.45540.26280.14090.1409B =0.43950.27870.14090.1409CI =0.0035CR =0.0038C =0.3131附录6：x=[1 2 2;1/2 1 1/2;1/2 2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-3)/2 %一致性指标CR=CI/0.58 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =3.0536W =0.49340.19580.3108B =0.46060.18790.3515CI =0.0268CR =0.0462C =0.3733附录7：x=[1 3 2;1/3 1 1/2;1/2 2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-3)/2 %一致性指标CR=CI/0.58 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =3.0092W =0.53960.16340.2970B =0.51990.16200.3181CI =0.0046CR =0.0079C =0.4015附录8：% 目标层Q,Y对子准则层C1的赋值>> x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C2的赋值x=[1 5;1/5 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.83330.1667B =0.83330.1667CI =CR =NaNC =0.7222End% 目标层Q,Y对子准则层C3的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C4的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.80000.2000B =0.80000.2000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C5的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.66670.3333B =0.66670.3333CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C6的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C7的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.20000.8000B =0.20000.8000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C8的赋值x=[1 5;1/5 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.16670.8333B =0.16670.8333CI =CR =NaNC =0.7222End% 目标层Q,Y对子准则层C9的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C10的赋值x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =NaNC =0.5000% 目标层Q,Y对子准则层C11的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.25000.7500B =0.25000.7500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C12的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =W =0.80000.2000B =0.80000.2000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C13的赋值x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =CR =NaNC =0.5000% 目标层Q,Y对子准则层C14的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C15的赋值x=[1 4;1/4 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.20000.8000B =0.20000.8000CI =CR =NaNC =0.6800End% 目标层Q,Y对子准则层C16的赋值x=[1 1/3;3 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.75000.2500B =0.75000.2500CI =CR =NaNC =0.6250End% 目标层Q,Y对子准则层C17的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C18的赋值x=[1 2;1/2 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.33330.6667B =0.33330.6667CI =CR =NaNC =0.5556End% 目标层Q,Y对子准则层C19的赋值x=[1 1;1 1];[V,D]=eig(x);%c=max(diag(D)) %最大特征根位置f=find(diag(D)==max(diag(D))); %求lamda（最大特征根）位置----其中:diag 为矩阵对角线上的元素W=V(:,f)/sum(V(:,f)) %归一特征向量B=x/sum(x) %计算权向量CI=(c-2)/1 %一致性指标CR=CI/0 %一致性比率，要小于0.1C=sum(B.*W) %组合权重运算结果：c =2W =0.50000.5000B =0.50000.5000CI =CR =NaNC =0.5000附录9：% 最终组合权向量：x=[0.75 0 0 0 0 0;0.25 0 0 0 0 0;0 0.2625 0 0 0 0;0 0.0618 0 0 0 0;0 0.4185 0 0 0 0;0 0.1599 0 0 0 0;0 0.0973 0 0 0 0;0 0 0.5 0 0 0;0 0 0.5 0 0 0;0 0 0 0.4554 0 0;0 0 0 0.2628 0 0;0 0 0 0.1409 0 0;0 0 0 0.1409 0 0;0 0 0 0 0.4934 0;0 0 0 0 0.1958 0;0 0 0 0 0.3108 0;0 0 0 0 0 0.5396;0 0 0 0 0 0.1634;0 0 0 0 0 0.2970]x =0.7500 0 0 0 0 00.2500 0 0 0 0 00 0.2625 0 0 0 00 0.0618 0 0 0 00 0.4185 0 0 0 00 0.1599 0 0 0 00 0.0973 0 0 0 00 0 0.5000 0 0 00 0 0.5000 0 0 00 0 0 0.4554 0 00 0 0 0.2628 0 00 0 0 0.1409 0 00 0 0 0.1409 0 00 0 0 0 0.4934 00 0 0 0 0.1958 00 0 0 0 0.3108 00 0 0 0 0 0.53960 0 0 0 0 0.16340 0 0 0 0 0.2970y=[0.0492;0.2057;0.2057;0.3422;0.0753;0.1219]y =0.04920.20570.20570.34220.07530.1219z=x*y运算结果：z =0.03690.01230.05400.01270.08610.03290.02000.10290.10290.15580.08990.04820.04820.03720.01470.02340.06580.01990.0362a=[0.3333 0.8333 0.75 0.2 0.3333 0.75 0.2 0.1667 0.3333 0.5 0.25 0.8 0.5 0.75 0.2 0.75 0.3333 0.3333 0.5;0.6667 0.1667 0.25 0.8 0.6667 0.250.8 0.8333 0.6667 0.5 0.75 0.2 0.5 0.25 0.8 0.25 0.6667 0.6667 0.5]a =Columns 1 through 70.3333 0.8333 0.7500 0.2000 0.3333 0.7500 0.20000.6667 0.1667 0.2500 0.8000 0.6667 0.2500 0.8000Columns 8 through 140.1667 0.3333 0.5000 0.2500 0.8000 0.5000 0.75000.8333 0.6667 0.5000 0.7500 0.2000 0.5000 0.2500Columns 15 through 190.2000 0.7500 0.3333 0.3333 0.50000.8000 0.2500 0.6667 0.6667 0.5000c=a*z运算结果：c =0.43250.5675。