层次分析法例题(1)
- 格式:doc
- 大小:200.50 KB
- 文档页数:6
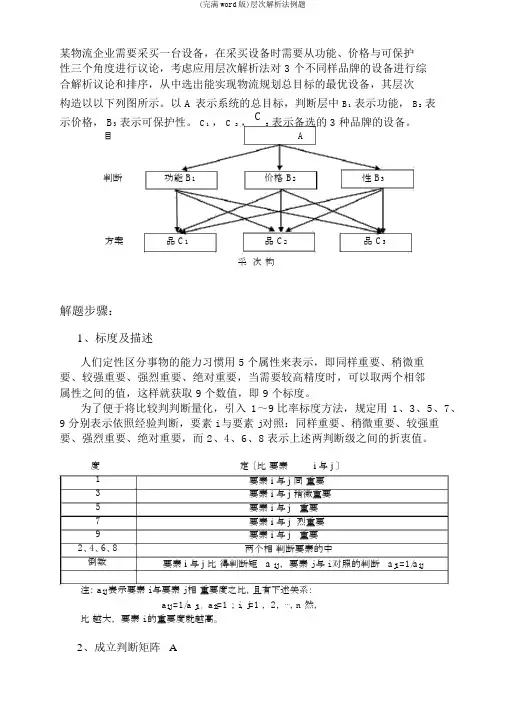
某物流企业需要采买一台设备,在采买设备时需要从功能、价格与可保护性三个角度进行议论,考虑应用层次解析法对 3 个不同样品牌的设备进行综合解析议论和排序,从中选出能实现物流规划总目标的最优设备,其层次构造以以下列图所示。
以 A 表示系统的总目标,判断层中B1表示功能,B2表示价格, B3表示可保护性。
C1,C2,C3表示备选的3种品牌的设备。
目A判断功能 B1价格B2性B3方案品 C1品C2品C3采次构解题步骤:1、标度及描述人们定性区分事物的能力习惯用 5个属性来表示,即同样重要、稍微重要、较强重要、强烈重要、绝对重要,当需要较高精度时,可以取两个相邻属性之间的值,这样就获取 9个数值,即 9个标度。
为了便于将比较判判断量化,引入1~9比率标度方法,规定用1、3、5、7、9分别表示依照经验判断,要素 i 与要素 j对照:同样重要、稍微重要、较强重要、强烈重要、绝对重要,而 2、4、6、8表示上述两判断级之间的折衷值。
度13579 2、4、6、8倒数定〔比要素i 与 j 〕要素 i 与 j 同重要要素 i 与 j 稍微重要要素 i 与 j 重要要素 i 与 j 烈重要要素 i 与 j 重要两个相判断要素的中要素 i 与 j 比得判断矩 a ij,要素j与i对照的判断 a ji=1/a ij注: a ij表示要素 i与要素 j 相重要度之比,且有下述关系:a ij =1/a ji; a ii=1 ; i,j=1 , 2,⋯,n然,比越大,要素 i 的重要度就越高。
2、成立判断矩阵A判断矩 是 次解析法的根本信息,也是 行 重 算的重要依照。
依照 构模型,将 中各要素两两 行判断与比 ,构造判断矩 :●判断矩 A比 )如表 1所示;●判断矩 B 1 ●判断矩 B 2 ●判断矩 B 3示。
B (即相 于物流系 目 ,判断 各要素相 重要性C (相 功能,各方案的相 重要性比 )如表 2 所示; C(相 价格,各方案的相 重要性比 )如表 3 所示;C(相 可 性,各方案的相 重要性比)如表 4 所表1判断矩 A BAB 1B 2 B 3B 1 1 1/3 2 B 2 3 1 5 B 31/21/51表 2 判断矩B1CB 1C 1C 2 C 3C 1 1 l/3 1/5 C 2 3 1 1/3 C 35 3 1表 3 判断矩 B 2-CB 2C 1C 2C3C 1 1 27 C 2 1/2 1 5 C 31/71/51表4 判断矩 B3CB 3C 1C 2 C 3C 1 1 3 l/7 C 2l/3 1 1/9 C 379 13、 算各判断矩 的特色 、特色向量及一致性 指一般来 ,在AHP 法中 算判断矩 的最大特色 与特色向量, 必不需要 高的精度,用求和法或求根法可以 算特色 的近似 。

层次分析法是一种决策分析方法,通常用于多个方案或因素之间进行比较和排序。
以下是一个使用层次分析法的现代汉语例题:
假设你是一名公司的采购主管,你需要从三个供应商(A、B、C)中选择一家供应商品质最好、价格最优、售后服务最好的供应商。
你将使用层次分析法来进行决策。
解题步骤:
制定目标层次:选择最优供应商
确定判断准则:商品质量、价格、售后服务
构建层次结构模型:将目标层次下的判断准则放在下一层,形成层次结构模型
刻画判断矩阵:采用1~9的比较尺度,对每两个判断准则进行比较,得到判断矩阵
求出权重向量:对判断矩阵进行归一化处理,计算出每个判断准则的权重
计算一致性指标:检查矩阵的一致性程度,得出一致性指标
计算最终权重:根据层次结构模型和权重向量,计算出每个供应商的最终权重
进行灵敏度分析:分析每个判断准则的变化对结果的影响程度
得出决策结果:综合考虑判断准则的权重和灵敏度分析的结果,得出选择最优供应商的决策结果
以上是一个基本的层次分析法的应用例题,具体细节需要根据实际情况进行调整和处理。

层次分析法例题详解
例题:假设一家公司想要改善客户满意度,以下是几项建议:
A. 增加客户服务
B. 提高产品质量
C. 提高客户服务质量
层次分析法:
1.首先,将上述三项建议放入一个表格中,比较它们之间的关系。
建议 | 增加客户服务 | 提高产品质量 | 提高客户服务质量
------|-----------------|------------------|------------------------
关系 | 相关 | 相关 | 直接相关
2.然后,根据上表的关系,将建议分类:
A. 增加客户服务和提高客户服务质量:这两项建议直接相关,可以归为一类,即增加客户服务和提高客户服务质量。
B. 提高产品质量:这一项建议与其他两项建议相关,但不属
于同一类别,可以独立归类。
3.最后,根据分类的结果,提出有效的解决方案:
A. 增加客户服务和提高客户服务质量:可以采取措施增加客
户服务人员的数量,同时提高客户服务质量,如培训客服人员,
提升服务水平。
B. 提高产品质量:可以采取措施改善产品质量,如改进生产流程,提高材料质量,以及实施质量控制等。
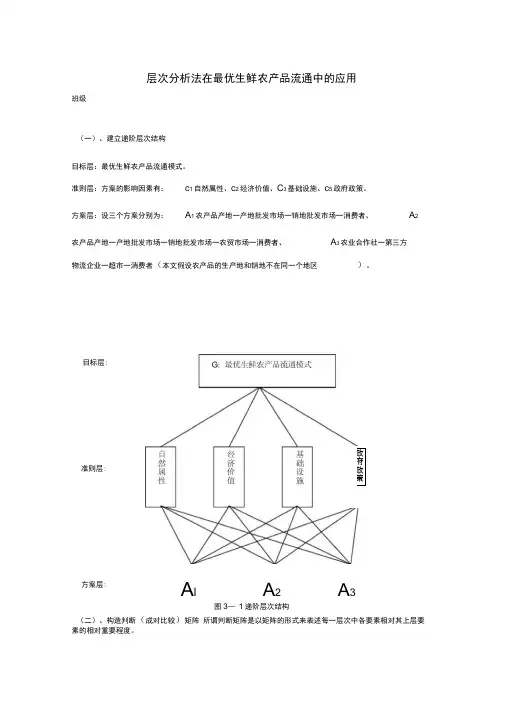
层次分析法在最优生鲜农产品流通中的应用班级(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:c 1自然属性、c 2经济价值、C 3基础设施、c 5政府政策。
方案层:设三个方案分别为:A 1农产品产地一产地批发市场一销地批发市场一消费者、A 2农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、A 3农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
图3— 1递阶层次结构(二)、构造判断(成对比较)矩阵 所谓判断矩阵是以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
目标层:准则层:政府政策方案层:A lA 2A 3了使各因素之间进行两两比较得到量化的判断矩阵,弓I入1〜9的标度,见表为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根入max的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
由于入连续的依赖于a j,则入比n大的越多,A 的不一致性越严重。
用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用入一n数值的大小来衡量A的不一致程度。
用一致性指标进行检验:CI 工 n。
其中max 是比较矩阵的最大特征值,n 是比较矩n 1阵的阶数。
CI 的值越小,判断矩阵越接近于完全一致。
反之,判断矩阵偏离完全一致的程 度越大。
(四)、层次总排序及其一致性检验1 8 5 30.603 0.470 0.526 0.667 2.266 A181 12 16列向量归一化0.075 0.059 0.053 0.037 按行求和0.224 15 2 1 1.30.121 0.118 0.105 0.074 0.418 1 3 6310.201 0.353 0.316 0.2221.0920.567归一化0.056 w (°)0.1040.2731 8530.567 2.354AW(0)18 1 1 21 6 0.056 0.225AW1 52 1 13 0.104 0.42213 6310.2731.110(0)1 2.3540.225 0.422 1.110max- -----------4.0734 0.5670.056 0.104 0.273⑼ 0.567,0.056,0.104,0.273 T同理可计算出判断矩阵1 1 3 1.91 391 291 13 1 9 B 3 1 1 8 ,B2 131 8 , B 31 2 1 7,B 4 3 1 17 981 1 9 1. 8 11 917 1971对应的最大特征值与特征向量依次为:0.0680.6400.595 (1)max3.111,(1)10.146 ;⑵max 3.216, (1)2 0.306; (3)max 3.024, (1)3 0.3470.786 0.0540.0580.069 ⑷ max 3.083(1)40.155 .0.776用一致性指标进行检验:CICRRImax nCIn 12 3 4 5 6 7 8 9 10 11 RI0 00.580.901.121.241.321.411.451.49 1.51(1)对于判断矩阵 A ,入0)max =4.O73, RI=0.90表示A 的不一致程度在容许范围内,此时可用 A 的特征向量代替权向量。


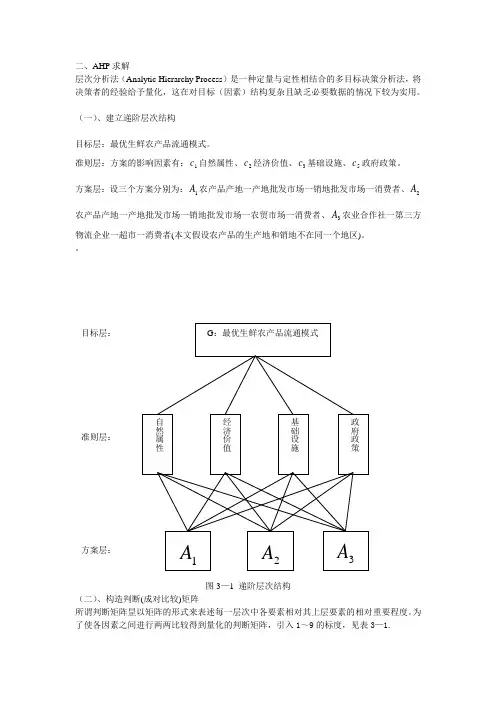
二、AHP 求解层次分析法(Analytic Hierarchy Process )是一种定量与定性相结合的多目标决策分析法,将决策者的经验给予量化,这在对目标(因素)结构复杂且缺乏必要数据的情况下较为实用。
(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层:设三个方案分别为:1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
图3—1 递阶层次结构(二)、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵,引入1~9的标度,见表3—1.目标层:准则层:方案层:表3—1 标度值为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
a,则λ比n 大的越多,A 的不一致性越严重。
用最大特征值对由于λ连续的依赖于ij应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用λ―n数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验:max 1nCI n λ-=-。
其中max λ是比较矩阵的最大特征值,n 是比较矩阵的阶数。
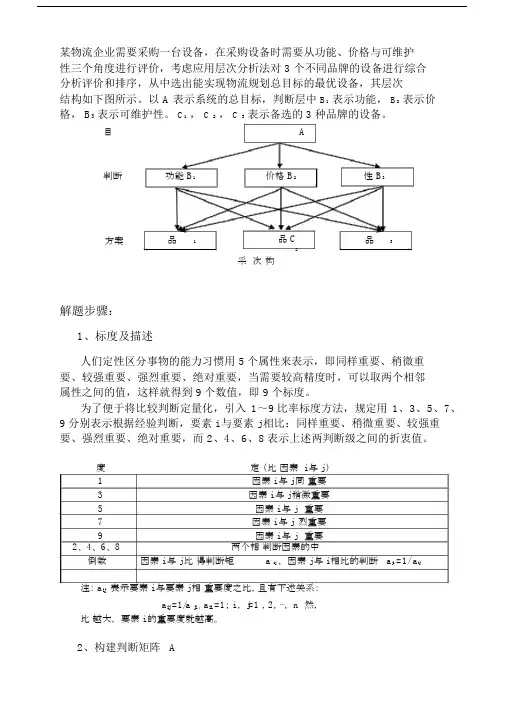
某物流企业需要采购一台设备,在采购设备时需要从功能、价格与可维护性三个角度进行评价,考虑应用层次分析法对 3 个不同品牌的设备进行综合分析评价和排序,从中选出能实现物流规划总目标的最优设备,其层次结构如下图所示。
以 A 表示系统的总目标,判断层中B1表示功能,B2表示价格, B3表示可维护性。
C1,C2,C3表示备选的3种品牌的设备。
目A判断功能 B1价格B2性B3方案品1品 C品3C2C采次构解题步骤:1、标度及描述人们定性区分事物的能力习惯用 5个属性来表示,即同样重要、稍微重要、较强重要、强烈重要、绝对重要,当需要较高精度时,可以取两个相邻属性之间的值,这样就得到 9个数值,即 9个标度。
为了便于将比较判断定量化,引入1~9比率标度方法,规定用1、3、5、7、9分别表示根据经验判断,要素 i 与要素 j 相比:同样重要、稍微重要、较强重要、强烈重要、绝对重要,而 2、4、6、8表示上述两判断级之间的折衷值。
度定(比因素 i 与 j )1因素 i 与 j 同重要3因素 i 与 j 稍微重要5因素 i 与 j 重要7因素 i 与 j 烈重要9因素 i 与 j 重要2、 4、 6、 8两个相判断因素的中倒数因素 i 与 j 比得判断矩 a ij,因素 j 与 i 相比的判断 a ji =1/ a ij注: a ij表示要素 i 与要素 j 相重要度之比,且有下述关系:a ij =1/a ji;a ii =1; i , j=1 ,2,⋯, n 然,比越大,要素 i 的重要度就越高。
2、构建判断矩阵A判断矩阵是层次分析法的基本信息,也是进行权重计算的重要依据。
根据结构模型,将图中各因素两两进行判断与比较,构造判断矩阵:●判断矩阵 A B( 即相对于物流系统总目标,判断层各因素相对重要性比较 ) 如表 1所示;●判断矩阵 B 1 C ( 相对功能,各方案的相对重要性比较 ) 如表 2 所示;●判断矩阵 B 2 C( 相对价格,各方案的相对重要性比较 ) 如表 3 所示;●判断矩阵 B 3 C( 相对可维护性, 各方案的相对重要性比较 ) 如表 4 所示。

层次分析法练习练习一、市政工程项目建设决策问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,试运用层次分析法建模解决。
1、建立递阶层次结构在市政工程项目决策问题中,市政管理人员希望通过选择不同的市政工程项目,使综合效益最高,即决策目标是“合理建设市政工程,使综合效益最高”。
为了实现这一目标,需要考虑的主要准则有三个,即经济效益、社会效益和环境效益。
但问题绝不这么简单。
通过深入思考,决策人员认为还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。
假设本问题只考虑这些准则,接下来需要明确为了实现决策目标、在上述准则下可以有哪些方案。
根据题中所述,本问题有两个解决方案,即建高速路或建地铁,这两个因素作为措施层元素放在递阶层次结构的最下层。
很明显,这两个方案于所有准则都相关。
将各个层次的因素按其上下关系摆放好位置,并将它们之间的关系用连线连接起来。
同时,为了方便后面的定量表示,一般从上到下用A、B、C、D。
代表不同层次,同一层次从左到右用1、2、3、4。
代表不同因素。
这样构成的递阶层次结构如下图。
目标层A准则层C措施层D图1 递阶层次结构示意图2、构造判断矩阵并请专家填写征求专家意见,填写后的判断矩阵如下:表2 判断矩阵表3、计算权向量及检验计算所得的权向量及检验结果见下:表4 层次计算权向量及检验结果表4、层次总排序及检验层次总排序及检验结果见下:表5 C层次总排序(CR = 0.0000)表D层次总排序(CR = 0.0000)5、结果分析从方案层总排序的结果看,建地铁(D2)的权重(0.6592)远远大于建高速路(D1)的权重(0.3408),因此,最终的决策方案是建地铁。

二、求解层次分析法()是一种定量与定性相结合的多目标决策分析法,将决策者的经验给予量化,这在对目标(因素)结构复杂且缺乏必要数据的情况下较为实用。
(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:c自然属性、2c经济价值、3c基础1设施、c政府政策。
5方案层:设三个方案分别为:A农产品产地一产地批发市场一销1地批发市场一消费者、A农产品产地一产地批发市场一销地批发2市场一农贸市场一消费者、A农业合作社一第三方物流企业一超3市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
图3—1 递阶层次结构(二)、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵,引入1~9的标度,见表3—1.表3—1 标度值目标准则方案为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λ的特征向量,经归一化(使向量中各元素之和等于1)后记为W 。
W 的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A 确定不一致的允许范围。
由于λ 连续的依赖于ij a ,则λ 比n 大的越多,A 的不一致性越严重。
用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用 λ―n 数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验:max 1nCI n λ-=-。
其中max λ是比较矩阵的最大特征值,n 是比较矩阵的阶数。
CI 的值越小,判断矩阵越接近于完全一致。
一件的确良衬衫的运费层次分析法例题一件的确良衬衫的运费层次分析法例题。
从图中可以很清楚地了解到,整个价格不会超过50元。
现在,先对第一层进行计算:原料及辅料100元;加工费60元(这是老师要求自己给加工费);运费、利润10元(做这样衣服用了1小时,当然需要利润)。
那么,所有的价格就变为170元。
如果超出成品20元的话,则由公司承担,也就是说,他只收了25元钱,所以该层次的加工成本为零元!第二层,包装,该环节总共产生5元费用(主要是塑料袋和胶带,其实按照“禁止”要求,也应该交消费者协会处理)。
第三层,货物运输,总共支付7元(这里按100元/件计算),最后,又减去利润2元(因为衣服是新鲜的活体动物,损耗率大约为30%左右),即160元,所以,此次加工全部价格最终为155元。
至于如何找到第四层,暂且不谈。
第四层,经销商赚取25元钱。
第五层,作为厂家或者经销商来说,他没必要将该衣服批量卖掉,而宁愿让它积压着,或者继续放在仓库里睡觉,但绝对不能打折,否则,将严重影响企业形象和效益。
第一层:运输和包装成本在200元以下。
他们之间相差40倍,明显属于高利润范围,而且还低于违反国家规定的幅度,故不得向消费者提供该种便宜货。
另外,按照市场惯例,每年夏季都会大量上架一些旧款式、滞销的夏装,有很多店铺并未开门营业,实际上他们都想趁机捞一把,因此你买到的衣服80%都被打折了,而且有的服装降价达3折,甚至更多。
再从上面看看我们发生的纠纷案例,大部分都涉嫌假冒伪劣商品。
首先,这种情况往往比较难举证,我认识几位淘宝网购买家都存在类似问题,即拿回商品质量与实际质量不符合,退换货的商家寥寥无几,更令人愤怒的是商家死皮赖脸不肯负责任,同时客服却推脱责任等。
这种情况下,消费者非常容易遭受损失。
第二点是在双方发生矛盾之后,无论是天猫、京东等电子商务平台还是各大 B2C 平台都会踢皮球,不管事情闹到哪里都没办法彻底解决,使得消费者维权十分困难。
专题:层次分析法一般情况下,物流系统的评价属于多目标、多判据的系统综合评价。
如果仅仅依靠评价者的定性分析和逻辑判断,缺乏定量分析依据来评价系统方案的优劣,显然是十分困难的。
尤其是物流系统的社会经济评价很难作出精确的定量分析。
层次分析法(Analytical Hierarchy Process )由美国著名运筹学家萨蒂(T .L .Saaty )于1982年提出,它综合了人们主观判断,是一种简明、实用的定性分析与定量分析相结合的系统分析与评价的方法。
目前,该方法在国内已得到广泛的推广应用,广泛应用于能源问题分析、科技成果评比、地区经济发展方案比较,尤其是投入产出分析、资源分配、方案选择及评比等方面。
它既是一种系统分析的好方法,也是一种新的、简洁的、实用的决策方法。
◆ 层次分析法的基本原理人们在日常生活中经常要从一堆同样大小的物品中挑选出最重的物品。
这时,一般是利用两两比较的方法来达到目的。
假设有n 个物品,其真实重量用w 1,w 2,…w n 表示。
要想知道w 1,w 2,…w n 的值,最简单的就是用秤称出它们的重量,但如果没有秤,可以将几个物品两两比较,得到它们的重量比矩阵A 。
如果用物品重量向量W =[w 1,w 2,…w n ]T右乘矩阵A ,则有:由上式可知,n 是A 的特征值,W 是A 的特征向量。
根据矩阵理论,n 是矩阵A 的唯一非零解,也是最大的特征值。
这就提示我们,可以利用求物品重量比判断矩阵的特征向量的方法来求得物品真实的重量向量W 。
从而确定最重的物品。
将上述n 个物品代表n 个指标(要素),物品的重量向量就表示各指标(要素)的相对重要性向量,即权重向量;可以通过两两因素的比较,建立判断矩阵,再求出其特征向量就可确定哪个因素最重要。
依此类推,如果n 个物品代表n 个方案,按照这种方法,就可以确定哪个方案最有价值。
◆ 应用层次分析法进行系统评价的主要步骤如下:(1)将复杂问题所涉及的因素分成若干层次,建立多级递阶的层次结构模型(目标层、判断层、方案层)。
层次分析法应用实例问题描述:通讯交流在当今社会显得尤其重要,手机便是一个例子,现在每个人手里都有至少一部手机。
但如今生产手机的厂家越来越多,品种五花八门,如何选购一款适合自己的手机这个问题困扰了许多人。
目标:选购一款合适的手机准则:选择手机的标准大体可以分成四个:实用性,功能性,外观,价格。
方案:由于手机厂家有几十家,我们不妨可以将其归类:○1欧美(iphone);○2亚洲(索爱);○3国产(华为).解决步骤:1.建立递阶层次结构模型图1 选购手机层次结构图2.设置标度人们定性区分事物的能力习惯用5个属性来表示,即同样重要、稍微重要、较强重要、强烈重要、绝对重要,当需要较高精度时,可以取两个相邻属性之间的值,这样就得到9个数值,即9个标度。
为了便于将比较判断定量化,引入1~9比率标度方法,规定用1、3、5、7、9分别表示根据经验判断,要素i与要素j相比:同样重要、稍微重要、较强重要、强烈重要、绝对重要,而2、4、6、8表示上述两判断级之间的折衷值。
注:aij表示要素i与要素j相对重要度之比,且有下述关系:aij=1/aji ;aii=1;i,j=1,2,…,n显然,比值越大,则要素i的重要度就越高。
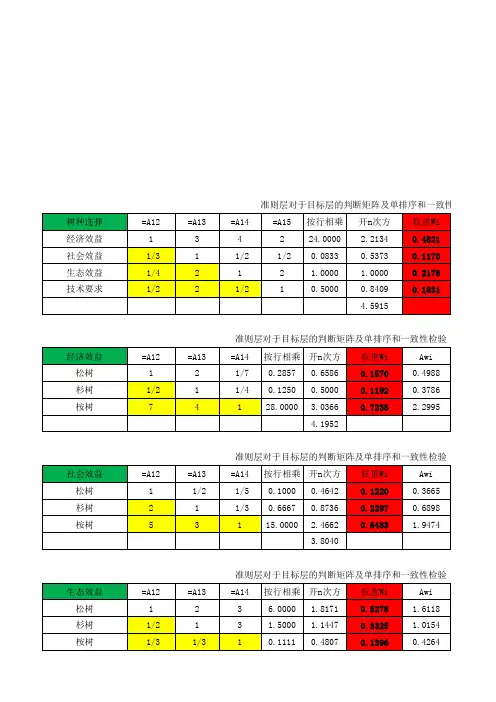
3.构造判断矩阵A B1 B2 B3 B4B1 1 3 5 1B2 1/3 1 3 1/3B3 1/5 1/3 1 1/5B4 1 3 5 1表1 判断矩阵A—BB1 C1 C2 C3C1 1 1/3 1/5C2 3 1 1/3C3 5 3 1表2 判断矩阵B1—CB2 C1 C2 C3C1 1 3 3C2 1/3 1 1C3 1/3 1 1表3 判断矩阵B2—CB3 C1 C2 C3C1 1 3 6C2 1/3 1 4 C31/61/41表4 判断矩阵B3—CB4 C1 C2 C3C1 1 1/41/6 C2 4 1 1/3 C3631表5 判断矩阵B4—C4.计算各判断矩阵的特征值,特征向量和一致性检验 用求和发计算特征值:○1将判断矩阵A 按列归一化(即列元素之和为1):bij= ai j /Σaij ; ○2将归一化的矩阵按行求和:ci=Σbij (i=1,2,3….n );○3将ci 归一化:得到特征向量W=(w1,w2,…wn )T ,wi=ci /Σci , W 即为A 的特征向量的近似值; ○4求特征向量W 对应的最大特征值:1).153111311131311531=A ,按列归一化后为381514522938153831412213833851432235391514522938152).按行求和并归一化后得()T389.0069.0153.0389.0=W3).计算特征根:()TAW 389.0069.0153.0389.015315111513131311531=582.1389.0*1069.0*5153.0*3389.0*11=+++=AW ,同理有 619.02=AW ,275.0AW 3=,582.1AW 4=4).计算最大特征根: 5).进行一致性检验:查同阶平均随机一致性指针(表6所示)知R.I=0.89,(一般认为CI<0.1、 CR<0.1时,判断矩阵的一致性可以接受,否则重新两两进行比较)。
层次分析法(Analytical Hierarchy Process,AHP)是美国运筹学家沙旦(T.L.Saaty)于20世纪70年代提出的,是一种定性与定量分析相结合的多目标决策方法。
AHP 通过对多准则决策问题构造层次结构模型,在每一层次上将决策者的主观判断进行数量化,然后进行逐层加权处理,最后得到各备选方案相对于总目标的权重,从而实现多准则(目标)下对备选方案的排序。
优点:AHP 具有思路清晰、方法简单、适用面广、便于推广应用等特点,是目前解决多准则决策问题有效的方法之一.层次分析法的基本步骤和要点结合一个具体例子,说明层次分析法的基本步骤和要点。
【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
1. 建立递阶层次结构应用AHP解决实际问题,首先明确要分析决策的问题,并把它条理化、层次化,理出递阶层次结构。
AHP要求的递阶层次结构一般由以下三个层次组成:●目标层(最高层):指问题的预定目标;●准则层(中间层):指影响目标实现的准则;●措施层(最低层):指促使目标实现的措施;通过对复杂问题的分析,首先明确决策的目标,将该目标作为目标层(最高层)的元素,这个目标要求是唯一的,即目标层只有一个元素。
然后找出影响目标实现的准则,作为目标层下的准则层因素,在复杂问题中,影响目标实现的准则可能有很多,这时要详细分析各准则因素间的相互关系,即有些是主要的准则,有些是隶属于主要准则的次准则,然后根据这些关系将准则元素分成不同的层次和组,不同层次元素间一般存在隶属关系,即上一层元素由下一层元素构成并对下一层元素起支配作用,同一层元素形成若干组,同组元素性质相近,一般隶属于同一个上一层元素(受上一层元素支配),不同组元素性质不同,一般隶属于不同的上一层元素。
(一)用层次分析法分析下列句子的结构层次,并标明每层的结构关系。
1、她很爱看香山的红叶。
|主|谓||状|中||动|宾||动|宾||定|中|2、这本书的再次出版是我们意料中的事情。
|主|谓||定|中||动|宾||定|中|状|中||定|中||量词|短语||定|中|3、暴虐的李逵杀了许多无辜的百姓。
|主|谓||定|中||动|宾||定|中||定|中|4、他是我们班成绩最优秀的学生。
|主|谓||动|宾||主|谓||定|中||状|中||主|谓||定|中||状|中||量词|短语||介词|短语|12、他青年时期积极投入文化运动。
|主|谓||状|中||定|中||状|中||动|宾||定|中|13.大家都在默默祈祷和平的到来。
|主|谓||状|中||状|中||状|中||动|宾||定|中|14、《说文解字》对于探究上古汉语词义系统具有极其重要的价值。
|主|谓||状|中||介词|短语||动|宾||动|宾||定|中||定|中||状|中||定|中|(注:上古汉语是固定短语)15、鲁迅在一篇文章里,主张打落水狗。
16、在世界各地,保护环境的呼声都很高。
17、举行国庆阅兵有助于提升中国的形象和扩大中国的影响。
18、铃木是我们班口语最好的学生|主||谓||动||宾||定||中||定||中||定||中||主||谓|19、那些科学家已经设计好了解决这个问题的方案。
|主||谓||定||中||状||中心语||动||宾||动||补||述||宾||定||中|20、我没见过这样勇敢的年轻人。
2122232425262728(二)分析下列多重复句。
用“│”、“‖”、“Ⅲ”等分别表示第一、二、三重,在切分线下面标明关系。
(在原句划分即可)1、成功的基础是奋斗,||奋斗的收获是成功,|所以,只有知艰而进和奋斗不已,||才能走上成功的高峰。
并列因果条件2、生活是一张网,‖哪里都觉得有约束和限制,|||同时哪里都觉得有漏洞和机会,│所以,我们应该学会戴着镣铐跳舞,‖而非解说并列因果并列奢望绝对的自由。
层次分析法在最优生鲜农产品流通中的应用 班级
(一)、建立递阶层次结构
目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层:设三个方案分别为:1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
目标层: 准则层:
方案层:
图3—1 递阶层次结构
(二)、构造判断(成对比较)矩阵
所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵,引入1~9的标度,见表
为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:
(三)、层次单排序及其一致性检验
层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax 的特征向量,经归一化(使向量中各元素之和等于1)后记为W 。
W 的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A 确定不一致的允许范围。
由于λ 连续的依赖于ij a ,则λ 比n 大的越多,A 的不一致性越严重。
用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用 λ―n 数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验:max 1
n
CI n λ-=
-。
其中max λ是比较矩阵的最大特征值,n 是比较矩
阵的阶数。
CI 的值越小,判断矩阵越接近于完全一致。
反之,判断矩阵偏离完全一致的程度越大。
(四)、层次总排序及其一致性检验 )0(273.0104.0056.0567.0092.1418.0224.0266.2222.0316.0353.0201
.0074.0105.0118.0121
.0037.0053.0059.0075
.0667.0526.0470.0603
.0136131121121113581
W
A =⎪⎪⎭
⎪⎪
⎬⎫
⎪⎪⎩⎪⎪⎨⎧−−−→−⎪⎪
⎭
⎪
⎪⎬
⎫
⎪⎪⎩⎪⎪⎨⎧−−−−→−⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨
⎧−−−−−−→−⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨
⎧=归一化按行求和列向量归一化
()T
AW 273.0,104.0,056.0,567.0073
.4273.0110.1104.0422.0056.0225.0567.0354.241110.1422.0225.0354.2273.0104.0056.0567.0136311121612118135
81)0(max )0()0(==⎪⎭
⎫
⎝⎛+++=⎪⎪⎭⎪
⎪⎬
⎫⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=ωλ
同理可计算出判断矩阵
⎪⎭⎪⎬
⎫
⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=179711391111117121921,1811811931,189811313114321B B B B ,
对应的最大特征值与特征向量依次为:
.
776.0155.0069.0,083.3;
058.0347.0595.0,024.3;054.0306.0640.0,216.3;786.0146.0068.0,111.34)1(max )4(3)1(max )3(2)1(max )2(1)1(max )1(⎪⎭
⎪
⎬⎫⎪⎩⎪⎨⎧==⎪⎭⎪
⎬⎫
⎪⎩⎪⎨⎧==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==ωλωλωλωλ用一致性指标进行检验:max 1
n
CI n λ-=-,
RI CI
CR =
(1)对于判断矩阵A ,λ
(0)
max
=,RI=
1
.0027.090.0024.0024.0144
073.4<====--=
RI CI CR CI 表示A 的不一致程度在容许范围内,此时可用A 的特征向量代替权向量。
(2)同理,对于判断矩阵B 1,B 2,B 3,B 4利用上述原理均通过一致性检验。
利用层次结构图绘出从目标层到方案层的计算结果:
⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧776.0155.0069.0,058.0347.0595.0,054.0306.0640.0,786.0146.0068.0
()
⎪⎭⎪⎬⎫
⎪⎩⎪⎨⎧==776.0058.0054.0786.0155.0347.0306.0146.0069.0595.0640.0068.0,,,4)1(3)1(2)1(1)1()1(ωωωωω
⎪
⎭
⎪⎬
⎫⎪⎩⎪⎨⎧=⎪⎪⎭⎪⎪⎬⎫
⎪⎪⎩⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==667.0178.0155.0273.0104.0056.0567.0776.0058.0054.0786.0155.0347.0306.0146.0069.0595.0640.0068.0)
0()1(ωωω
决策结果:是首选方案A 3,其次是方案A 2,再次是方案A 1.
目标层: 准则层:。