下载文档原格式
电子科技大学研究生试题《图论及其应用》(参考答案)考试时间：120分钟一．填空题(每题3分，共18分)1．4个顶点的不同构的简单图共有__11___个；2．设无向图G 中有12条边，已知G 中3度顶点有6个，其余顶点的度数均小于3。
则G 中顶点数至少有__9___个；3．设n 阶无向图是由k(k ?2)棵树构成的森林，则图G 的边数m= _n-k____;4．下图G 是否是平面图？答__是___; 是否可1-因子分解？答__是_.5．下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。
图G二．单项选择(每题3分，共21分)1．下面给出的序列中，是某简单图的度序列的是( A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2．已知图G 如图所示，则它的同构图是（ D ）3． 下列图中，是欧拉图的是（ D ）4． 下列图中，不是哈密尔顿图的是（B ）5． 下列图中，是可平面图的图的是（B ）AC DA B CD6．下列图中，不是偶图的是（ B ）7．下列图中，存在完美匹配的图是（B ）三．作图(6分)1．画出一个有欧拉闭迹和哈密尔顿圈的图；2．画出一个有欧拉闭迹但没有哈密尔顿圈的图；3．画出一个没有欧拉闭迹但有哈密尔顿圈的图；解： 四．(10分)求下图的最小生成树，并求其最小生成树的权值之和。
解：由克鲁斯克尔算法的其一最小生成树如下图：权和为：20.五．(8分)求下图G 的色多项式P k (G).解：用公式(G P k -G 的色多项式：)3)(3)()(45-++=k k k G P k 。
六．(10分) 22，n 3个顶点的度数为3，…，n k 个顶点的度数为k ，而其余顶点的度数为1，求1度顶点的个数。
解：设该树有n 1个1度顶点，树的边数为m.一方面：2m=n 1+2n 2+…+kn k另一方面：m= n 1+n 2+…+n k -1 v v 13图G由上面两式可得：n 1=n 2+2n 3+…+(k -1)n k七．证明：(8分) 设G 是具有二分类(X,Y)的偶图，证明(1)G 不含奇圈；（2）若|X |≠|Y |，则G 是非哈密尔顿图。
图论作业3一、填空题1. 完全图K2n共有个不同的完美匹配。
2. 超方体Q6的最小覆盖包含的点数为。
3. 图K m,n (m≤n)的最小覆盖包含的点数为。
4. 完全图K60能分解为个边不重的一因子之并。
5. 完全图K61能分解为个边不重的二因子之并。
6. 假设G是具有n个点、m条边、k个连通分支的无圈图，则G的荫度为。
7. 图G是由3个连通分支K1, K2, K4组成的平面图，则其共有个面。
8. 设图G与K5同胚，则至少从G中删掉条边才可能使其成为可平面图。
9. 设连通平面图G具有5个顶点，9条边，则其面数为。
10. 若图G是10阶极大平面图，则其面数等于。
11. 若图G是10阶极大外平面图，其内部面共有个。
二、不定项选择题1. 关于非平凡树T，下面说法错误的是( )(A) T至少包含一个完美匹配；(B) T至多包含一个完美匹配；(C) T的荫度大于1；(D) T是只有一个面的平面图；(E) T的对偶图是简单图。
2. 下列说法正确的是( )(A) 三正则的偶图存在完美匹配；(B) 无割边的三正则图一定存在完美匹配；(C) 有割边的三正则图一定没有完美匹配；(D) 有完美匹配的三正则图一定没有割边；(E) 三正则哈密尔顿图存在完美匹配。
3. 下列说法正确的是( )(A) 在偶图中，最大匹配包含的边数等于最小覆盖包含的点数；(B) 任一非平凡正则偶图包含完美匹配；(C) 任一非平凡正则偶图可以1-因子分解；(D) 偶度正则偶图可以2-因子分解；(E) 非平凡偶图的最大匹配是唯一的。
4. 下列说法中错误的是( )(A) 完全图K101包含1-因子；(B) 完全图K101包含2-因子；(C) 完全图K102包含1-因子；(D) 完全图K102包含2-因子；(E) 图G的一个完美匹配实际上就是它的一个1因子；(F) 图G的一个2-因子实际上就是它的一个哈密尔顿圈。
5. 下列说法正确的是( )(A) 方体Q n可以1-因子分解；(B) 非平凡树可以1-因子分解；(C) 无割边的3正则图可以1-因子分解；(D) 有割边的3正则图一定不可以1-因子分解；(E) 可1-因子分解的3正则图一定是哈密尔顿图。
图论期末考试试题和答案****一、单项选择题（每题2分，共20分）1. 图论中，图的基本元素不包括以下哪一项？A. 顶点B. 边C. 权重D. 节点答案：D2. 在图论中，一个图的路径是指什么？A. 一系列顶点B. 一系列边C. 一系列顶点和边的序列D. 一系列权重答案：C3. 有向图和无向图的主要区别是什么？A. 边的方向B. 顶点的数量C. 边的数量D. 图的颜色答案：A4. 在图论中，一个完全图是指什么？A. 所有顶点都相连的图B. 所有边都相连的图C. 所有顶点和边都相连的图D. 所有权重都相同的图答案：A5. 图论中的欧拉路径是指什么？A. 经过每条边恰好一次的路径B. 经过每个顶点恰好一次的路径C. 经过每条边恰好一次的回路D. 经过每个顶点恰好一次的回路答案：C6. 图论中的哈密顿路径是指什么？A. 经过每条边恰好一次的路径B. 经过每个顶点恰好一次的路径C. 经过每条边恰好一次的回路D. 经过每个顶点恰好一次的回路答案：B7. 在图论中，二分图是指什么？A. 图的顶点可以被分成两个不相交的集合B. 图的边可以被分成两个不相交的集合C. 图的顶点和边可以被分成两个不相交的集合D. 图的权重可以被分成两个不相交的集合答案：A8. 图论中的最短路径问题是指什么？A. 寻找从一个顶点到另一个顶点的最短路径B. 寻找从一个顶点到所有其他顶点的最短路径C. 寻找所有顶点之间的最短路径D. 寻找所有边之间的最短路径答案：A9. 图论中的最小生成树问题是指什么？A. 寻找一个图中所有顶点的最小生成树B. 寻找一个图中所有边的最小生成树C. 寻找一个连通图中所有顶点的最小生成树D. 寻找一个连通图中所有边的最小生成树答案：C10. 图论中的网络流问题是指什么？A. 在图中寻找最大流量B. 在图中寻找最小流量C. 在图中寻找最大流和最小割D. 在图中寻找最小流和最大割答案：C二、填空题（每题2分，共20分）1. 在图论中，如果一个图的任意两个顶点都由一条边连接，则称这个图为______图。
《图论》练习题(2014)1、利用Dijkstra 算法求下图中顶点0v 到其它各顶点的距离，并写出到顶点8v 的最短路。
2、1、列出色数3为的三个图： 。
2、p 阶完全图的色数为： 。
3、p 阶树的邻接多项式为： 。
4、p 阶完全图的邻接多项式为： 。
5、如下图所示的图的邻接矩阵为 ，关联矩阵为 。
6、度序列为(2,2,2,2,2,2)的简单图是 。
7、是否存在度序列为(2,2,3,4,5,6)，(1,2,3,4,4,5)的简单图？若存在，给出一个图；若不存在，请说明理由。
8、画出如下图的所有生成子图。
9、设图G 如下图所示，求该图的生成树个数)(G 。
v 2v 6v 4v 610、已知图G （V 、E ），画出G －V 5，G －v 3v 4，G[{v 2，v 3，v 5}]，G[{v 3v 4，v 4，v 6，v 7v 8}]G ：11、已知图G 的邻接矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2111102112011111A ，画出G ，并求出度序列。
12、证明：偶图G 的任意子图H 仍为偶图。
13、证明：设图G （V 、E ）的度序列为（p d d d ,,,21 ），边数为q ，则q i d pi 21==∑14、证明：在任何图中，奇顶点个数为偶数。
15、证明：整数序列（6，6，5，4，3，3，1）不可能为一个简单图的图序列。
16、证明顶点度数均为2的简单连通图是圈。
17、证明非平凡树T 的边连通度为'()1T κ=。
18、n 阶完全图n K 的连通度为()1T n κ=-。
19、设G 是一个p 阶图，且()()21,-≥∈∀p v d G V v ，则G 连通图。
20、若图G 是 不连通的，则其补图G C 是连通的。
21、证明：设G 是由1G 和2G 两个连通分支组成的图，则);();();(21x G P x G P x G P =。
v 1v 2v 3v 4v 5v 6v 8v 722、证明：设G 是由1G 和2G 两个连通分支组成的图，则)}(),(max{)(21G G G χχχ=。
离散数学图论部分期末复习辅导一、单项选择题 1．设图G ＝<V , E >，v V ，则下列结论成立的是 ( ) ．A ．deg(v )=2EB ．deg(v )=EC ．deg()2||v Vv E ∈=∑ D ．deg()||v Vv E ∈=∑解 根据握手定理（图中所有结点的度数之和等于边数的两倍）知，答案C 成立。
答 C2．设无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100100110， 则G 的边数为( )．A ．6B ．5C ．4D ．3解 由邻接矩阵的定义知，无向图的邻接矩阵是对称的．即当结点v i 与v j 相邻时，结点v j 与v i 也相邻，所以连接结点v i 与v j 的一条边在邻接矩阵的第i 行第j 列处和第j 行第i 列处各有一个1，题中给出的邻接矩阵中共有10个1，故有102=5条边。
答 B3．已知无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0111110101110001000111010，则G 有（ ）．A ．5点，8边B ．6点，7边C ．6点，8边D ．5点，7边解 由邻接矩阵的定义知，矩阵是5阶方阵，所以图G 有5个结点，矩阵元素有14个1，14÷2=7，图G 有7条边。
答 D4．如图一所示，以下说法正确的是 ( ) ． A ．{(a, e )}是割边 B ．{(a, e )}是边割集C ．{(a, e ) ,(b, c )}是边割集D ．{(d, e)}是边割集定义3.2.9 设无向图G =<V ,E >为连通图，若有边集E 1ÌE ，使图G 删除了E 1的所有边后，所得的子图是不连通图，而删除了E 1的任何真子集后，所得的子图仍是连通图，则称E 1是G 的一个边割集．若边割集为单元集{e }，则称边e 为割边（或桥）．解 割边首先是一条边，因为答案A 中的是边集，不可能是割边，因此答案A 是错误的．删除答案B 或C 中的边后，得到的图是还是连通图，因此答案B 、C 也是错误的．在图一中，删去(d , e )边，图就不连通了，所以答案D 正确． 答 D注：如果该题只给出图的结点和边，没有图示，大家也应该会做．如：若图G =<V , E >，其中V ={ a , b , c , d , e }，E ={ (a , b ), (a , c ) , (a , e ) , (b , c ) , (b , e ) , (c , e ) , (e , d )}，则该图中的割边是什么？5．图G 如图二所示，以下说法正确的是 ( )． A ．a 是割点 B ．{b, c}是点割集 C ．{b , d }是点割集 D ．{c }是点割集定义3.2.7 设无向图G =<V ,E >为连通图，若有点集V 1ÌV ，使图G 删除了V 1的所有结点后，所得的子图是不连通图，而删除了V 1的任何真子集后，所得的子图仍是连通图，则称V 1是G 的一个点割集．若点割集为单元集{v }，则称结点v 为割点．οοο ο a bc d图一 οe ο οο a b c d图二ο解 在图二中，删去结点a 或删去结点c 或删去结点b 和d 图还是连通的，所以答案A 、C 、D 是错误的．在图二中删除结点b 和c ，得到的子图是不连通图，而只删除结点b 或结点c ，得到的子图仍然是连通的，由定义可以知道，{b, c }是点割集．所以答案B 是正确的． 答 B6．图G 如图三所示，以下说法正确的是 ( ) ． A ．{(a, d )}是割边 B ．{(a, d )}是边割集C ．{(a, d) ,(b, d)}是边割集D ．{(b , d )}是边割集解 割边首先是一条边，{(a, d )}是边集，不可能是割边．在图三中，删除答案B 或D 中的边后，得到的图是还是连通图．因此答案A 、B 、D 是错误的．在图三中，删去(a,d )边和(b, d )边，图就不连通了，而只是删除(a, d )边或(b, d )边，图还是连通的，所以答案C 正确．7．设有向图（a ）、（b ）、（c ）与（d ）如图四所示，则下列结论成立的是( )．图四A ．（a ）是强连通的B ．（b ）是强连通的C ．（c ）是强连通的D ．（d ）是强连通的复习：定义3.2.5 在简单有向图中，若在任何结点偶对中，至少从一个结点到另一个结点可达的，则称图G 是单向（侧）连通的；若在任何结点偶对中，两结点对互相可达，则称图G 是强连通的；若图G 的底图，即在图G 中略去边的方向，得到的无向图是连通的，则称图G 是弱连ο ο ο a bcd图三ο通的．显然，强连通的一定是单向连通和弱连通的，单向连通的一定是弱连通，但其逆均不真．定理3.2.1一个有向图是强连通的，当且仅当G中有一个回路，其至少包含每个结点一次．单侧连通图判别法：若有向图G中存在一条经过每个结点至少一次的路，则G是单侧连通的。
电⼦科技⼤学《图论及其应⽤》复习总结--第四章欧拉图与哈密尔顿图第四章欧拉图与哈密尔顿图(⼀)、欧拉图及其性质(1)、问题背景---欧拉与哥尼斯堡七桥问题问题：对于图G，它在什么条件下满⾜从某点出发，经过每条边⼀次且仅⼀次，可以回到出发点？注：⼀笔画----中国古⽼的民间游戏（存在欧拉迹）要求：对于⼀个图G, 笔不离纸, ⼀笔画成.拓展：三笔画：在原图上添加三笔，可使其变为欧拉图。
定义1 对于连通图G，如果G中存在经过每条边的闭迹，则称G为欧拉图，简称G为E图。
欧拉闭迹⼜称为欧拉环游，或欧拉回路。
定理1 下列陈述对于⾮平凡连通图G是等价的：(1) G是欧拉图；(2) G的顶点度数为偶数；(3) G的边集合能划分为圈。
推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。
推论2 连通⾮欧拉图G存在欧拉迹当且仅当G中只有两个顶点度数为奇数。
证明：若G和H是欧拉图，则G×H是欧拉图。
若G是⾮平凡的欧拉图，则G的每个块也是欧拉图。
(⼆)、Fleury算法(欧拉图中求出⼀条具体欧拉环游的⽅法)⽅法是尽可能避割边⾏⾛(三)、中国邮路问题（最优欧拉环游，管梅⾕）定理2 若W是包含图G的每条边⾄少⼀次的闭途径，则W具有最⼩权值当且仅当下列两个条件被满⾜：(1) G的每条边在W中最多重复⼀次；(2) 对于G的每个圈上的边来说，在W中重复的边的总权值不超过该圈⾮重复边总权值。
(四)、哈密尔顿图的概念定义1 ：如果经过图G的每个顶点恰好⼀次后能够回到出发点，称这样的图为哈密尔顿图，简称H图。
所经过的闭途径是G的⼀个⽣成圈，称为G的哈密尔顿圈。
定义2: 如果存在经过G的每个顶点恰好⼀次的路，称该路为G的哈密尔顿路，简称H路。
(五)、哈密尔顿图性质与判定1、性质定理【必要条件】；定理1 (必要条件) 若G为H图，则对V(G)的任⼀⾮空顶点⼦集S，有：w(G−S)≤|S|注：不等式为G是H图的必要条件，即不等式不满⾜时，可断定对应图是⾮H、图。
1电子科技大学研究生试卷（考试时间： 至 ，共__2_小时）课程名称 图论及其应用 教师 学时 60 学分 教学方式 讲授 考核日期_2013__年_6__月__20__日 成绩 考核方式： （学生填写）一．填空题(每空2分，共20分)1． n 阶k 正则图G 的边数m =_____。
2．4个顶点的不同构单图的个数为________。
3．完全偶图,r s K (,2r s ≥且为偶数)，则在其欧拉环游中共含____条边。
4．高为h 的完全2元树至少有_______片树叶。
5. G 由3个连通分支124,,K K K 组成的平面图，则其共有_______个面。
6. 设图G 与5K 同胚，则至少从G 中删掉_______条边，才可能使其成为可平面图。
7. 设G 为偶图，其最小点覆盖数为α，则其最大匹配包含的边数为________。
8. 完全图6K 能分解为________个边不重合的一因子之并。
9. 奇圈的边色数为______。
10. 彼得森图的点色数为_______。
二．单项选择(每题3分，共15分) 1．下面说法错误的是( )学 号 姓 名 学 院…………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………2(A) 图G 中的一个点独立集，在其补图中的点导出子图必为一个完全子图；(B) 若图G 连通，则其补图必连通； (C) 存在5阶的自补图； (D) 4阶图的补图全是可平面图. 2．下列说法错误的是（ ） (A) 非平凡树是偶图；(B) 超立方体图(n 方体,1n ≥)是偶图； (C) 存在完美匹配的圈是偶图； (D) 偶图至少包含一条边。
3.下面说法正确的是( )(A) 2连通图一定没有割点（假定可以有自环）； (B) 没有割点的图一定没有割边；(C) 如果3阶及其以上的图G 是块，则G 中无环，且任意两点均位于同一圈上；(D) 有环的图一定不是块。
电子科技大学研究生试题《图论及其应用》(参考答案)考试时间：120分钟一.填空题(每题3分，共18分)1. 4个顶点的不同构的简单图共有__11—;2. 设无向图G中有12条边，已知G中3度顶点有6个，其余顶点的度数均小于3。
则G中顶点数至少有__9―;3. 设n阶无向图是由k(k 2)棵树构成的森林，则图G的边数m=_n-k _______4. 下图G是否是平面图？答—是___;是否可1-因子分解？答—是_.5. 下图G的点色数(G) __________ ,边色数(G) __5 ________ 。
图G二.单项选择(每题3分，共21分)1. 下面给出的序列中，是某简单图的度序列的是(A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2. 已知图G如图所示，贝卩它的同构图是(D )3. 下列图中，是欧拉图的是(D)4. 下列图中，不是哈密尔顿图的是(B )ABC5.下列图中，是可平面图的图的是(B )6. 下列图中，不是偶图的是(B )7. 下列图中，存在完美匹配的图是(B )三. 作图(6分)1. 画出一个有欧拉闭迹和哈密尔顿圈的图；2. 画出一个有欧拉闭迹但没有哈密尔顿圈的图;3. 画出一个没有欧拉闭迹但有哈密尔顿圈的图;四. (10分)求下图的最小生成树，并求其最小生成树的权值之和。
解：由克鲁斯克尔算法的其一最小生成树如下图：权和为：20.五. (8分)求下图G 的色多项式P k (G).解：用公式P k (G e) P k (G) P 「(G?eh 可得G 的色多项式：P k (G) (k )5 3(k )4 侏)3、k(k 1)2(k 2)(k 3)。
六. (10分)一棵树有n 图个顶点的度数为2, n a 个顶点的度数为3,…，m 个顶点的度数为k ，而其余顶点的度数为1,求1度顶点的个数。
解：设该树有n 1个1度顶点，树的边数为 m.一方面：2m=n+2n 2+…+kn k另一方面： m= m+n 2+…+n k -1 解:由上面两式可得：n 1=门2+2皿+…+(k-1)n k七证明：(8分)设G是具有二分类(X,Y)的偶图，证明(1)G不含奇圈；(2) 若|X |工| Y |，则G是非哈密尔顿图。
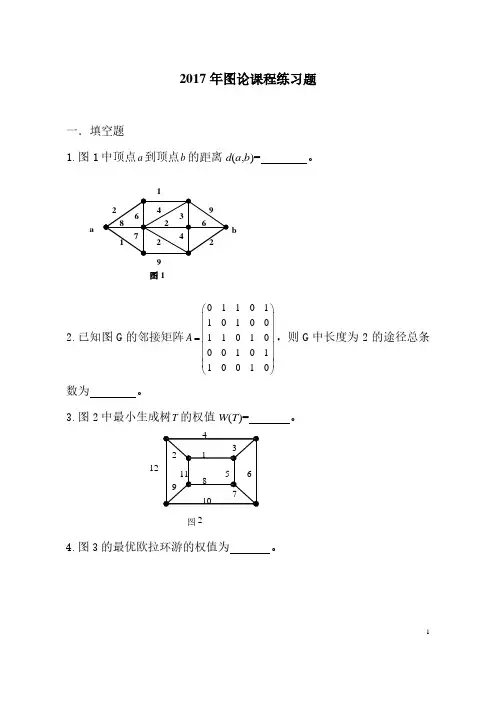
12017年图论课程练习题一．填空题1.图1中顶点a 到顶点b 的距离d (a ,b )= 。
ab9 图112.已知图G 的邻接矩阵0110110100110100010110010A=，则G 中长度为2的途径总条数为 。
3.图2中最小生成树T 的权值W (T )= 。
4.图3的最优欧拉环游的权值为 。
12 图 22图35.树叶带权分别为1,2,4,5,6,8的最优二元树权值为 。
二．单项选择1．关于图的度序列，下列说法正确的是( )(A) 对任意一个非负整数序列来说，它都是某图的度序列；(B) 若非负整数序列12(,,,)n d d d π= 满足1ni i d =∑为偶数，则它一定是图序列；(C) 若图G 度弱于图H ，则图G 的边数小于等于图H 的边数；(D) 如果图G 的顶点总度数大于或等于图H 的顶点总度数，则图G 度优 于图H 。
2．关于图的割点与割边，下列说法正确的是（ ） (A) 有割边的图一定有割点； (B) 有割点的图一定有割边； (C) 有割边的简单图一定有割点； (D) 割边不在图的任一圈中。
3.设()k G ，()G λ，()G δ分别表示图G 的点连通度，边连通度和最小度。
下面说法错误的是( )3(A) 存在图G ，使得()k G =()G δ=()G λ； (B) 存在图G ，使得()()()k G G G λδ<<；(C) 设G 是n 阶简单图，若()2n G δ≥，则G 连通，且()()G G λδ=；(D) 图G 是k 连通的，则G 的连通度为k 。
4.关于哈密尔顿图，下列命题错误的是( ) (A) 彼得森图是非哈密尔顿图；(B) 若图G 的闭包是哈密尔顿图，则其闭包一定是完全图； (C) 若图G 的阶数至少为3且闭包是完全图，则图G 是哈密尔顿图； (D) 设G 是三阶以上简单图，若G 中任意两个不邻接点u 与v ，满足()()d u d v n +≥，则G 是哈密尔顿图。
1 电子科技大学研究生试卷 （考试时间： 至 ，共__2_小时） 课程名称 图论及其应用 教师 学时 60 学分 教学方式 讲授 考核日期_2014__年_6__月__20__日 成绩 考核方式： （学生填写） 一．填空题(每空2分，共20分) 1． n 阶简单k 正则图G 的补图的边数为_____。
2．4个顶点的不同构树的个数为________。
3．具有m 条边的简单图的不同生成子图的个数为____。
4．彼得森图的点连通度为_______。
5. n 点圈的2—宽直径为_______。
6. 2n 阶完全图共有_______个不同的完美匹配。
7. 设G 的阶数为n ，点覆盖数为β，则其点独立数为________。
8. 完全图21n K +能分解为________个边不重合的二因子之并。
9. 拉姆齐数(3,3)R =______。
10. n 完全图的不同定向方式有_______种。
二．单项选择(每题3分，共15分) 1．下面说法错误的是( ) (A) 在正常点着色下，图G 中的一个色组，在其补图中的点导出子图必为一个完全子图； 学 号 姓 名 学 院 …………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………(B) 若图G不连通，则其补图必连通；(C) 存在14阶的自补图；(D) 6阶图的补图可能是可平面图.2．下列说法错误的是（）(A) 一个非平凡图是偶图，当且仅当它不含有奇圈；(B) 超立方体图(n方体,1n≥)是偶图；(C) 非平凡森林是偶图；(D) 不含三角形的图都是偶图。
3.下面说法正确的是( )(A) k连通图的连通度一定为k；(B) 完全图一定没有割边；(C) (3)n n≥阶图G是块，则G中无环，且任意两点均位于同一圈上；(D) 非平凡树一定有割点。
4.下列说法错误的是( )(A) 若图G是哈密尔顿图，则其闭包一定为完全图；(B) 设(3)n n≥阶单图的任意两个不邻接顶点u与v满足()()d u d v n+≥，则其闭包一定为完全图；(C)若(n,m)单图G的边数112nm-⎛⎫>+⎪⎝⎭，且3n≥，则G是哈密尔顿图；(D) 若G是3n≥的非H单图，则G度弱于某个,m nC图。
1图论及其应用研究生试卷一．填空题(每空3分，共30分)1.若n 阶图G 是自补图，则其边数为______________。
2．若简单图G 的边数为m ，则其所有不同生成子图(包括G 和空图)的个数为________。
3.设1G 是11(,)n m 图，设2G 是22(,)n m 图，且它们不相交，则它们的联图12G G G =∨的边数为__________。
4.设图G 的邻接矩阵()ij n n A a ⨯=，则图中从顶点i v 到顶点j v 中长度为k的途径条数为__________________。
5.设G 是一个9阶简单图，且不含有完全子图4K ，则G 能够达到的最多边数为________________。
6.图1中树的中心为_______________。
7.图2中最大生成树的权值为____________。
168 13147105 129172431116 15图 11 244 3 33 4 5 12图2图3u x1 4 52 12 3 26 3 2y wz图 428.图3中，割点数为____，割边数为____，块数为_____. 9.设图G 的顶点数为n 且5连通，则其边数至少为_________。
10.图4的最优欧拉环游的总权值为_______。
二．单项选择(每题3分，共15分) 1．下列说法错误的是( )(A) 若一个图中存在闭途径，则一定存在圈； (B) 偶图中不存在奇圈；(C) 无向图的顶点之间的连通关系一定是等价关系； (D). 存在非平凡简单图G ，使得每个顶点的度数互不相同。
2．设图G 是一个非平凡块，下列说法错误的是（ ） (A) G 中一定有圈；(B) 若G 的阶数大于等于3，则G 中任意两点必位于某一圈上； (C) 若G 的阶数大于等于3，则G 中任意两条边必位于某一圈上； (D) 若G 的阶数大于等于3，则G 中没有割边。
3. 关于欧拉图，下面说法错误的是( ) (A) 欧拉图中每个顶点度数一定为偶数； (B) 顶点度数为偶数的图一定是欧拉图； (C) 有向欧拉图中每个顶点的入度一定等于出度； (D) 有向欧拉图的边集合可以划分为有向圈。
《图论》期末考试模拟题（答案） ⼀、选择题 1、给定⽆向图如图所⽰，下⾯给出的顶点集⼦集中，是点割集的为（A,B,C,D）。
A. {b, d} B. {d} C. {a, c} D. {g, e} bf 内容需要下载⽂档才能查看 2、设V＝{a,b,c,d},与V能构成强连通图的边集E＝（ A ）。
A. {,,,,} B. {,,,,} C. {,,,,} {,,,,} 3、⼀个连通的⽆向图G，如果它的所有结点的度数都是偶数，那么它具有⼀条（ B ）。
A. 哈密尔顿回路 B. 欧拉回路 C. 哈密尔顿通路 D. 欧拉通路 4、如图所⽰各图，其中存在哈密顿回路的图是（ A, C ）。
内容需要下载⽂档才能查看 第 1 页共 5 页 图论期末考试题⽬参考 《图论》 5. 下图中既是欧拉图，⼜是哈密尔顿图的有（D）。
5、设G是有5个顶点的完全图，则G（ B ）。
D. ⽆哈密尔顿路 E. 可以⼀笔画出 F. 不能⼀笔画出 G. 是平⾯图 6、设G是连通简单平⾯图，G中有11个顶点5个⾯，则G中的边是（ D ）。
A. 10 B. 12 C. 16 D. 14 ⼆、填空题 1、完全图K8具有（ 28 ）条边。
2、图G如图所⽰， ab fc 那么图G的割点是（ a, f ）。
e d 3、⽆向图G为欧拉图，当且仅当G是连通的，且G中⽆（奇数度）结点。
第 2 页共 5 页 图论期末考试题⽬参考 《图论》 4、连通有向图D含有欧拉回路的充分必要条件是（ D中每个结点的⼊度＝出度）。
5、 n个结点、m条边的⽆向连通图是树当且仅当m=__（3）___。
(1) n+1 (2) n (3) n-1 (4)2n-1 三、 1、设图G=(P,E) 中有12条边，6个度数为3的顶点，其余顶点的度数均⼩于3，求G⾄少有多少个顶点。
解答：设G有n个顶点，由定理1， ∑d i=1nG(vi)=2m=24 (|E|=m) 由题设 24<3×6+3(n?6) ∴ 3n>24 即 n>8 因此，G中⾄少有9个顶点。
图论期末考试题库及答案一、单项选择题1. 图论的创始人是（）。
A. 欧拉B. 莱布尼茨C. 牛顿D. 高斯答案：A2. 在图论中，一个图的顶点集合为空，但边集合不为空的图称为（）。
A. 空图B. 完全图C. 树D. 多重图答案：A3. 如果一个图的任意两个顶点之间都存在一条路径，则称该图为（）。
A. 连通图B. 强连通图C. 弱连通图D. 无环图答案：A4. 在图论中，一个图的边的集合可以划分为若干个不相交的路径，使得图中的每个顶点恰好属于其中一条路径，这样的图称为（）。
A. 欧拉图B. 哈密顿图C. 树答案：C5. 图论中，一个图的边的集合可以划分为若干个不相交的回路，使得图中的每个顶点恰好属于其中一条回路，这样的图称为（）。
A. 欧拉图B. 哈密顿图C. 树D. 环答案：A二、多项选择题1. 下列哪些是图论中的基本术语（）。
A. 顶点B. 边D. 权重答案：ABCD2. 在图论中，以下哪些图是无向图（）。
A. 完全图B. 树C. 多重图D. 有向图答案：ABC3. 图论中，以下哪些图是连通图（）。
A. 完全图B. 树C. 多重图D. 空图答案：ABC三、填空题1. 图论中，一个图的顶点集合为V，边集合为E，那么图可以表示为G=（）。
答案：(V, E)2. 如果一个图的任意两个顶点之间都存在一条路径，则称该图为（）。
答案：连通图3. 在图论中，一个图的边的集合可以划分为若干个不相交的路径，使得图中的每个顶点恰好属于其中一条路径，这样的图称为（）。
答案：树四、简答题1. 请解释什么是图论中的“完全图”？答案：完全图是指图中每一对不同的顶点之间都恰好有一条边相连的图。
在完全图Kn中，n个顶点两两相连，共有n(n-1)/2条边。
2. 请解释什么是图论中的“欧拉路径”和“欧拉回路”？答案：欧拉路径是指图中存在一条路径，该路径恰好经过每条边一次。
欧拉回路是指图中存在一条回路，该回路恰好经过每条边一次。
五、计算题1. 给定一个图G=(V, E)，其中V={A, B, C, D, E}，E={(A, B), (B, C), (C, D), (D, E), (E, A), (A, C)}，请判断该图是否为连通图，并说明理由。
2015电子科技大学 图论考试复习题关于图论中的图，以下叙述不正确的是A ．图中点表示研究对象，边或有向边表示研究对象之间的特定关系。
B ．图论中的图，画边时长短曲直无所谓。
C ．图中的边表示研究对象，点表示研究对象之间的特定关系。
D ．图论中的图，可以改变点与点的相互位置，只要不改变点与点的连接关系。
一个图中最长的边一定不包含在最优生成树内。
下面哪个图形不与完全二分图K 3,3同构？ A ．B ．C ．D ．有10条边的5顶单图必与K 5同构。
完全二分图K m ,n 的边数是 A ．m B ．n C ．m +n D ．mn无向完全图K n 的边数为 A ．n B ．n 2C ．n (n -1)D ．n (n -1)/2若一个无向图有5个顶点，如果它的补图是连通图，那么这个无向图最多有 条边。
对于两个图，如果顶点数目相等，边数相等，次数相等的顶点数目也相等，则这两个图同构。
有15个顶的单图的边数最多是 A ．105B ．210C ．21D ．45图G 如右，则dacbeb A ．是G 中的一条道路B ．是G 中的一条道路但不是行迹C ．是G 中的一条行迹但不是轨道D ．不是G 的一条道路图G 如右，则befcdefA ．是G 的一个圈B ．是G 的一条道路但不是行迹C ．是G 的一条行迹但不是轨道D ．是G 的一条轨道但不是圈v367图G如右图所示，则ω (G)=A．1 B．2C．7 D．8下列图形中与其补图同构的是A．B．C．D．求下图中顶u0到其余各顶点的最短轨长度。
u0v1=8，u0v2=1，u0v3=4，u0v4=2，u0v5=7，v1v2=7，v1v3=2，v1v6=4，v2v4=2，v2v7=3，v3v5=3，v3v6=6，v4v5=5，v4v7=1，v5v6=4，v5v7=3，v6v7=6，请画出6阶3正则图。
请画出4个顶，3条边的所有非同构的无向简单图。
设图G={V(G)，E(G)}其中V={a1, a2, a3, a4, a5}，E(G)={(a1, a2)，(a2, a4)，(a3, a1)，(a4, a5)，(a5, a2)}，试给出G的图形表示并画出其补图的图形。
电⼦科技⼤学《图论及其应⽤》复习总结--第⼀章图的基本概念⼀、重要概念图、简单图、图的同构、度序列与图序列、偶图、补图与⾃补图、两个图的联图、两个图的积图1.1 图⼀个图G定义为⼀个有序对(V, E)，记为G = (V, E)，其中（1）V是⼀个有限⾮空集合，称为顶点集或边集，其元素称为顶点或点；（2）E是由V中的点组成的⽆序点对构成的集合，称为边集，其元素称为边，且同⼀点对在E中可出现多次。
注：图G的顶点数（或阶数）和边数可分别⽤符号n(G) 和m(G)表⽰。
连接两个相同顶点的边的条数，叫做边的重数。
重数⼤于1的边称为重边。
端点重合为⼀点的边称为环。
1.2 简单图⽆环⽆重边的图称为简单图。
（除此之外全部都是复合图）注： 1.顶点集和边集都有限的图称为有限图。
只有⼀个顶点⽽⽆边的图称为平凡图。
其他所有的图都称为⾮平凡图。
边集为空的图称为空图。
2.n阶图：顶点数为n的图，称为n阶图。
3.(n, m) 图：顶点数为n的图，边数为m的图称为(n, m) 图1.3 邻接与关联：顶点u与v相邻接：顶点u与v间有边相连接(u adj v)；其中u与v称为该边的两个端点。
注：1.规定⼀个顶点与⾃⾝是邻接的。
2.顶点u与边e相关联：顶点u是边e的端点。
3.边e1与边e2相邻接：边e1与边e2有公共端点。
1.4 图的同构设有两个图G1=(V1,E1)和G2=(V2,E2),若在其顶点集合间存在双射，使得边之间存在如下关系：u1,v1∈V1,u2,v2∈ V2 ，设u1↔u2，v1↔v2,; u1v1∈E1 当且仅当u2v2∈E2,且u1v1与u2v2的重数相同。
称G1与G2同构，记为：G1≌G2注：1、图同构的两个必要条件： (1) 顶点数相同；(2) 边数相同。
2、⾃⼰空间的理解：通过空间的旋转折叠可以进⾏形态转换1.5 完全图、偶图1、在图论中，完全图是⼀个简单图，且任意⼀个顶点都与其它每个顶点有且只有⼀条边相连接。
效无题院学答内名姓以线封号学密电子科技大学研究生试卷（考试时间：至，共__2_小时）课程名称图论及其应用教师学时60学分教学方式讲授考核日期_2015__年_6__月__26__日成绩考核方式：（学生填写）一．填空题 (每空 3 分，共 15 分)1.不同构的 3 阶简单图的个数为 _____。
2．图 1 中的最小生成树的权值为________。
3.基于图 2 的最优欧拉环游的总权值为__________ 。
4.图 3 中块的个数为_______。
61546321262227433833216图 1图 3图 25.图 4 中强连通分支的个数为________。
图41二．单项选择 (每题 3 分，共 15 分)1．关于图的度序列，下列命题错误的是( ) (A)同构的两个图的度序列相同；(B) 非负整数序列( d1, d2,n, d n ) 是图的度序列当且仅当d i是偶数；i1(C)如果非负整数序列 (d1 , d2 , , d n ) (n 2)是一棵树的度序列，那么序列中至少有两个整数的值为 1；(D). 如果非负整数序列(d1, d2,,d n ) 是简单图的度序列，那么在同构意义下只能确定一个图。
2．关于n阶简单图的邻接矩阵 A (a ij )n n，下列说法错误的是（）(A)矩阵 A 的行和等于该行对应顶点的度数；(B)矩阵所有元素之和等于该图边数的 2 倍；(C)不同构的两个图，它们的邻接矩阵特征谱一定不同；(D)非连通图的邻接矩阵一定可以表示为准对角矩阵形式。
3.关于欧拉图，下面说法正确的是()(A)欧拉图存在唯一的欧拉环游；(B)非平凡欧拉图中一定有圈；(C)欧拉图中一定没有割点；(D)度数为偶数的图一定是欧拉图。
4.关于哈密尔顿图，下列命题错误的是()(A)设G是n3的简单图，若其闭包是完全图，则G 是哈密尔顿图；(B)若 n 阶单图的闭包不是完全图，则它一定是非哈密尔顿图；2(C) 若G 是哈密尔顿图，则对于V 的每个非空顶点子集S ，均有(G S) S ；(D)若 G 是n 3的非 H 单图，则 G 度弱于某个C m,n图。
