轮齿弯曲强度计算公式

三、蜗杆传动的强度计算1、蜗轮齿面接触疲劳强度计算，由赫其公式（Hertz ）按主平面内斜齿轮与齿条啮合进行强度计算H n E H L KF Z ][σρσ≤=∑Fn ——法向载荷（N ）；L ——接触线长度（注意蜗杆蜗轮接触线是倾斜的，并计入重合度）；∑ρ——综合曲率半径；Z E ——材料弹性线数，对钢蜗杆↔配青铜蜗轮αMP Z E 160=，代入蜗杆传动有关参数，并化简得 校核公式：H P E H a KT Z Z ][/32σσ≤⋅= Mpa式中，Z E ——材料的弹性系数，钢蜗杆配青铜蜗轮αMP Z E 160=Z P ——接触系数，Z P 为反映蜗杆传动接触线长度和曲率半径对接触强度的影响系数 βK K K K V A ⋅⋅=——载荷系数K A ——工况系数βK ——齿面载荷分布系数：1=βK ——载荷平稳6.1~3.1=βK ——载荷变化较大，或有冲击、振动时 K V ——动载荷系数 s m V K V /3,1.1~0.12≤=——精制蜗杆s m V K V /3,2.1~1.12>=——一般蜗杆设计公式：322][⎪⎪⎭⎫ ⎝⎛≥H P E Z Z KT a σmm ⇒定m,q ，H ][σ——蜗轮齿面许用接触应力（1）当蜗轮材料为铸铁或高强度青铜，ασMP B 300≥——失效形式为胶合（不属于疲劳失效），∴许用应力H ][σ与应力循环次数N 无关。

（2）若蜗轮材料ασMP B 300<（锡青铜）——失效形式为点蚀，H ][σ与应力循环次数N 有关。

OH HN H K ][][σσ=OH ][σ——基本许用接触应力HN K ——接触强度寿命系数，8710NK HN =，N 为应力循环次数，h L jn N 260=，n 2为蜗轮转速（r/min ），L h 为蜗轮总工作时数h ，j 为每转一圈每个轮齿啮合次数。

2、蜗轮齿根弯曲疲劳强度计算齿根折断一般发生在Z 2>90，及开式传动中，∴在闭式传动中弯曲强度计算作为校核计算对于重载传动，通过计算还可差别由于轮齿的弯曲变形量引起的轮齿弹性变形量是否过大而影响蜗杆传动的平稳性。

差速器齿轮的强度计算
差速器齿轮的尺寸受结构限制，而且承受的载荷较大，它不像主减速器齿轮那样经常处于啮合状态，只有当汽车转弯或左右轮行驶不同的路程时，或一侧车轮打滑而滑转时，差速器齿轮才能有啮合传动的相对运动。

因此对于差速器齿轮主要应进行弯曲强度校核。

轮齿弯曲强度w σ为
w σ=J
m bz K K K TK v m s 2203102⨯ MPa (3.6)
式中：T ——差速器一个行星齿轮传给一个半轴齿轮的转矩,在此T 为1006
N ·m ；
n ——差速器的行星齿轮数；
2z ——半轴齿轮齿数；
0K 、v K 、s K 、m K ——见式（2.9）下的说明；
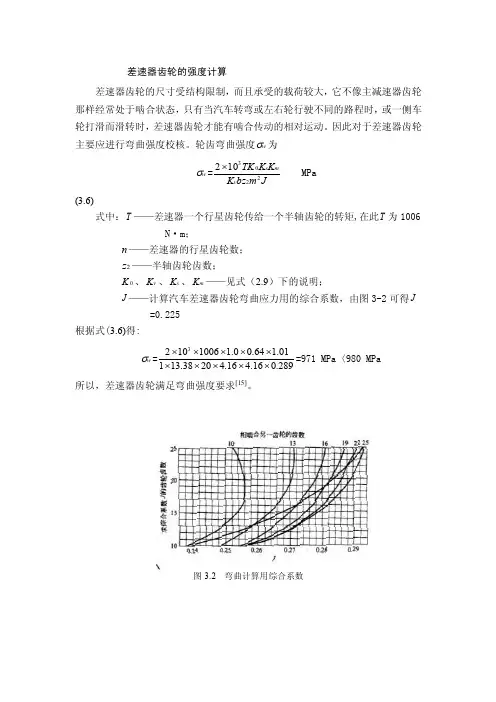
J ——计算汽车差速器齿轮弯曲应力用的综合系数，由图3-2可得J
=0.225
根据式(3.6)得:
w σ=32101006 1.00.64 1.01113.3820 4.16 4.160.289
⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=971 MPa 〈980 MPa 所以，差速器齿轮满足弯曲强度要求[15]。

图3.2 弯曲计算用综合系数。

11-4直齿圆柱‎齿轮传动的‎作用力及计‎算载荷：一、齿轮上的作‎用力：为了计算齿‎轮的强度，设计轴和选‎用轴承，有必要分析‎轮齿上的作‎用力。

当不计齿面‎的摩擦力时‎，作用在主动‎轮齿上的总‎压力将垂直‎于齿面，（因为齿轮传‎动一般都加‎以润滑，齿轮在齿啮‎合时，摩擦系数很‎小，齿面所受的‎摩擦力相对‎载荷很小，所以不必考‎虑），即为P17‎5图11-5b所示的‎F n（沿其啮合线‎方向），Fn可分解‎为两个分力‎：圆周力：Ft=2T1/d1 N径向力：Fr=Fttgα‎ N而法向力：Fn=Ft/cosα NT1：小齿轮上的‎扭矩 T1=95500‎00p/n1 n·mmP：传递的功率‎（KW） d1：小齿轮分度‎圆直径 mmα：压力角 n1：小齿轮的转‎速(r·p·m)Ft1：与主动轮运‎动方向相反‎；Ft2与从‎动轮运动方‎向一致。

各力的方向‎ Fr：分别由作用‎点指向各轮‎轮心。

Fn：通过节点与‎基圆相切（由法切互为‎性质）。

根据作用力‎与反作用力‎的关系，主从动轮上‎各对的应力‎应大小相等‎，方向相反。

二、计算载荷：Fn是根据‎名义功率求‎得的法向力‎，称为名义载‎荷，理论上Fn‎沿齿宽均匀‎分布，但由于轴和‎轴承的变形‎，传动装置的‎制造安装误‎差等原因，载荷沿齿宽‎的分布并不‎均匀，即出现载荷‎集中现象（如P176‎图11-6所示，齿轮相对轴‎承不对称布‎置，由于轴的弯‎曲变形，齿轮将相互‎倾斜，这时，轮齿左端载‎荷增大，轴和轴承刚‎度越小，b越宽，载荷集中越‎严重。

此外，由于各种原‎动机和工作‎机的特性不‎同，齿轮制造误‎差以及轮齿‎变形等原因‎，还会引起附‎加动载荷。

精度越低，圆周速度V‎越大，附加载荷越‎大。

因此在计算‎强度时，通常以计算‎载荷K·Fn代替名‎义载荷Fn‎，以考虑上两‎因素的影响‎。

K—载荷系数表达式11‎-311-5 直齿圆柱齿‎轮的齿面接‎触强度计算‎：一、设计准则：齿轮强度计‎算是根据齿‎轮失效形式‎来决定的，在闭式传动‎中，轮齿的失效‎形式主要是‎齿面点蚀，开式传动中‎，是齿轮折断‎，在高速变截‎的齿轮传动‎中，还会出现胶‎合破坏，因胶合破坏‎的计算方法‎有待进一步‎验证和完善‎。

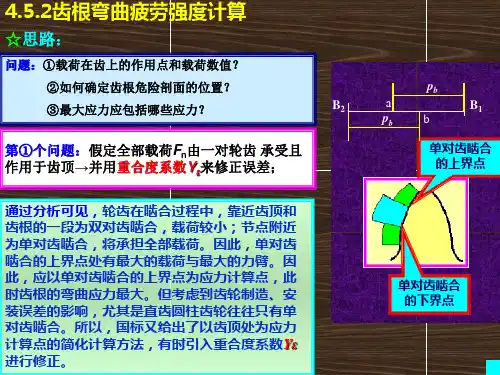
一、轮齿的接触应力ζj 的计算：ζj=0.418√FE(1/ρz+1/ρb )/bF=F1/(cos αcos β)F1=2Tg/dd 为节圆的直径Tg 为计算载荷ρz 、ρb 分别为主从动齿轮节点处的曲率半径：直齿轮：ρz=r z sin α ρb= r b sin α斜齿轮：ρz=（r z sin α）/cos 2β ρb=（ r b sin α）/cos 2βr z r b为主，从动齿轮节圆半径 二、轮齿弯曲应力ζw 的计算：直齿轮：ζw=F1K ζK f /bty=2TgK ζK f /πm 3ZK c y斜齿轮：ζw=2Tgcos βK ζ/∏m 3n ZK c yK εK ε为重合度系数，一般取K ε=2.0K ζ集中应力系数，一般直齿轮取K ζ=1.65，斜齿轮取K ζ=1.50y 为齿形系数，一般在0.16---0.18之间K c 为齿宽系数，一般在4.5---8.0之间K f 为摩擦力系数，主动轮取1.1，从动轮取0.9 A B δf Fa LbX一、初选轴的直径已知中心距A。

第二轴与中间轴中部直径：d≈0.45A，轴的最大直径d和支承间距离L的比值：d/L=0.16--0.18；对二轴：d/L=0.18--0.21；第一轴花键部分直径d可按下试初选：d=K 3√T emax式中，K为经验系数，K=4.0---4.6；T emax为发动机最大转矩（N.m）二、轴的强度计算1.轴的刚度计算：轴在垂直面内绕度：f c=F1a2b2/3EIL轴在水平面内绕度：f s=F2a2b2/3EIL轴在水平面内转角: δ=F1ab（b-a）/3EIL式中，F1为齿轮齿宽中间平面上的径向力（N）,F2为齿轮齿宽中间平面上的圆周力（N），E为弹性模量，E=2.1×105MPa；I为惯性矩（mm4），对于实心轴，I=πd4/64;d为轴的直径（mm），花键外按平均直径计算；a，b为齿轮上的作用力矩A,B的距离（mm），L为支座间的距离（mm）。

§8-5 标准直齿圆柱齿轮传动的强度计算一．齿轮传动承载能力计算依据轮辐、轮缘、轮毂等设计时，由经验公式确定尺寸。

若设计新齿，可参《工程手册》20、22篇，用有限元法进行设计。

轮齿的强度计算：1．齿根弯曲强度计算：应用材料力学弯曲强度公式WMb =σ进行计算。

数学模型：将轮齿看成悬臂梁，对齿根进行计算，针对齿根折断失效。

因为齿轮轮缘刚性较大，所以可将齿看成宽度为的悬臂梁，并以此作为推导齿根弯曲应力计算公式的力学模型。

1）危险剖面及其位置 受载齿的危险剖面是一在轮齿根部的平剖面，位置在与齿廓对称中线各成300的二直线与齿根过渡曲线相切处。

2）载荷及其作用位置1≥ε的齿轮传动，当载荷作用于齿顶时，（力一定）力臂最大，但此时相邻的一对齿仍在啮合，载荷由两对齿分担，齿根弯矩不一定最大。

当轮齿在节线附近啮合时，只有一对齿啮合，但此时力臂不是最大，齿根弯矩不一定最大。

齿根所受最大弯矩发生在轮齿啮合点位于单对齿啮合区最高点。

进行弯曲疲劳强度计算时，对于制造精度较低（7级及以下）的齿轮传动，因为制造误差较大，可认为载荷的大部分甚至全部由在齿顶啮合的轮齿承受，轮齿根部产生最大弯矩。

为简化计算，对于制造精度较低（7级及7级以下）的齿轮传动，常将齿顶作为齿根弯曲强度计算时的载荷作用位置，并按全部载荷作用于一对轮齿进行计算。

对制造精度较高（6级及以上）的齿轮传动，应考虑重合度的影响，其计算方法参GB3480-83或有关资料。

3）齿根弯曲应力计算公式 将ca p 分解成γγsin cos ca ca p p 和，并将其简化到危险截面上，γcos ca p --产生剪应力τ，γsin ca p 产生压应力σc ，γcos .h p M ca =产生弯曲应力σF 。

分析表明，σF 起主要作用，若只用σF 计算齿根弯曲疲劳强度，误差很小（<5%），在工程计算允许范围内，所以危险剖面上只考虑σF 。

单位齿宽（b=1）时齿根危险截面的理论弯曲应力为220cos .66*1cos .S h p S h p W M ca ca F γγσ===令αcos ,,b KF L KF p m K S m K h tn ca S h ====，代入上式，得()αγαγσcos cos 6.cos cos ..6220S h t S h t F K K bm KF m K b m K KF ==令 αγcos cos 62S h Fa K K Y =Fa Y --齿形系数，表示齿轮齿形对σF 的影响。

齿轮弯曲强度计算齿轮弯曲强度计算是齿轮设计的重要环节，它直接关系到齿轮的耐用性和可靠性。

本文将详细介绍齿轮弯曲强度的计算方法，包括对齿轮的基本参数、弯曲力矩、弯曲应力等方面的讨论。

一、齿轮的基本参数在进行齿轮弯曲强度计算之前，我们需要了解齿轮的基本参数，包括模数、齿数、压力角、齿宽等。

模数是齿轮设计和制造中的基本单位，它表示齿轮的轮齿尺寸和强度。

齿数是齿轮的齿数，它直接影响到齿轮的传动能力和弯曲强度。

压力角是指齿轮轮齿上的齿廓与分度圆交点的切线与齿廓方向之间的夹角，它对齿轮的传动性能和强度有一定的影响。

齿宽是指齿轮轮齿的宽度，它对齿轮的弯曲强度和稳定性有一定的影响。

二、弯曲力矩的计算弯曲力矩是导致齿轮弯曲的主要因素，它的大小直接影响到齿轮的弯曲强度。

根据弯曲力矩的计算公式，可以得出弯曲力矩与齿轮的基本参数之间的关系。

一般来说，弯曲力矩的计算公式如下：M = F * d其中，M是弯曲力矩，F是作用在齿轮上的名义应力，d是齿轮的分度圆直径。

根据这个公式，我们可以得出以下结论：1.弯曲力矩与名义应力成正比，与分度圆直径成反比。

因此，在设计齿轮时，可以通过降低名义应力和增加分度圆直径来提高齿轮的弯曲强度。

2.在相同的名义应力和分度圆直径下，齿数越少，弯曲力矩越大。

因此，在保证齿轮传动能力和强度的前提下，可以适当减少齿数来降低弯曲力矩的影响。

三、弯曲应力的计算弯曲应力是衡量齿轮弯曲强度的关键指标，它的大小直接影响到齿轮的使用寿命和可靠性。

根据材料力学的基本理论，可以得出弯曲应力的计算公式：σ = M / W其中，σ是弯曲应力，M是弯曲力矩，W是抗弯截面系数。

根据这个公式，我们可以得出以下结论：1.弯曲应力与弯曲力矩成正比，与抗弯截面系数成反比。

因此，在设计齿轮时，可以通过增加材料的抗弯截面系数来提高齿轮的弯曲强度。

常用的增加抗弯截面系数的措施包括增加齿高、增加齿宽等。

2.在相同的弯曲力矩和抗弯截面系数下，模数越小，弯曲应力越大。

塑料齿轮强度校核方法马瑞伍，余毅，张光彦（深圳市创晶辉精密塑胶模具有限公司，广东省深圳市518000）【摘要】随着动力传递型塑料齿轮应用领域的不断拓展，如何评估或校核塑料齿轮的强度成为设计者不得不考虑的难题。

由于塑料材料种类繁多，且不同种类的塑料性能指标差异很大，所以迄今为止有关塑料齿轮的强度算法还未形成统一的标准。

目前，具有代表性的塑料齿轮强度算法主要四种：①尼曼&温特尔法；②VDI 2545标准法；③KISSsoft软件基于VDI 2545标准修正法；④宝理“Duracon”法。

由于第②种算法已经废止，第③种算法主要以软件形式发布，因此本文将主要介绍第①和第④种算法，以期能为塑料齿轮的设计起到一定的借鉴意义。

【关键词】塑料齿轮强度设计1引言在国内，塑料齿轮起步于20世纪70年代。

在发展初期，塑料齿轮主要应用集中在水电气三表的计数器、定时器、石英闹钟、电动玩具等小型产品中。

这时期的塑料齿轮的多为直径一般不大于25mm，传递功率一般不超过0.2KW的直齿轮。

换言之，早期的塑料齿轮主要用于小空间内的运动传递，属于运动传递型齿轮。

随着注塑模具技术与注塑装备及注塑工艺水平的不断提高，模塑成型尺寸更大、强度更高的塑料齿轮成为可能。

现在，塑料齿轮传递动力可达 1.5KW，直径已超过150mm。

动力型塑料齿轮已经成为众多产品动力传递系统的重要组成部分。

虽然动力型塑料齿轮的应用越来越广泛，但相应的塑料齿轮强度计算理论或标准却比较匮乏。

目前，塑料齿轮的强度计算多以金属齿轮的强度计算方法为参考，通过修正或修改某些系数来计算或评估塑料齿轮的强度是否满足使用要求，然后再通过实验方法验证强度是否满足使用要求。

下面，本文将介绍具有代表性的塑料齿轮强度的计算方法或观点，以期能够为塑料齿轮的强度设计提供借鉴。

2塑料齿轮强度计算方法从查阅到的相关文献资料看，塑料齿轮的强度计算方法基本上沿用了金属齿轮的强度校核理论及计算公式。