推求Gardner-Russo持水曲线模型参数的简单入渗法

土壤水分特征曲线（研究）综述卢常磊（学号：1001064113）（系别：农学系专业：种子科学与工程班级：一班）前言：土壤水的基质势（或土壤水吸力）随土壤含水量而变化，其关系曲线称为土壤水分特征曲线。

该曲线反映了土壤水分能量和数量之间的关系，是研究土壤水动力学性质比不可少的重要参数，在生产实践中具有重要意义。

几十年来，人们投入了大量的精力来发展确定该曲线的方法，这些方法归纳起来可分为两大类：一类是直接测定法，另一类是间接推算法（或参数估计法）。

这些方法各有优缺点，而在生产实践中有的方法几乎没有实际应用价值。

基于这一点，本文针对这些方法以及近年来发展的新方法进行了比较和综述。

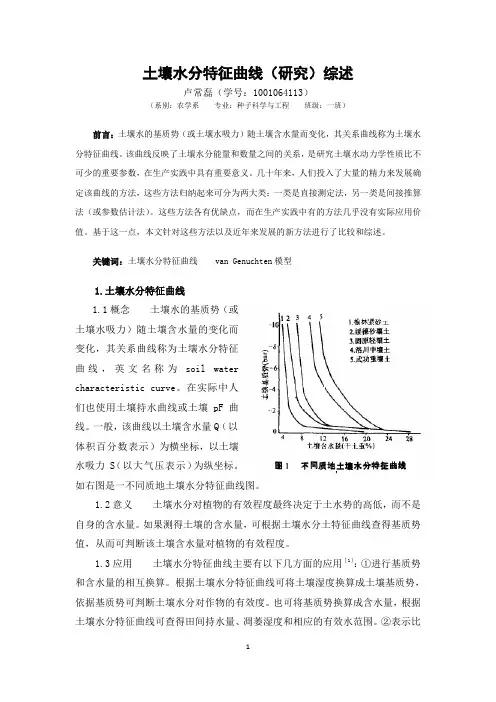
关键词：土壤水分特征曲线 van Genuchten模型1.土壤水分特征曲线1.1概念土壤水的基质势（或土壤水吸力）随土壤含水量的变化而变化，其关系曲线称为土壤水分特征曲线，英文名称为soil watercharacteristic curve。

在实际中人们也使用土壤持水曲线或土壤pF曲线。

一般，该曲线以土壤含水量Q（以体积百分数表示）为横坐标，以土壤水吸力 S（以大气压表示）为纵坐标。

如右图是一不同质地土壤水分特征曲线图。

1.2意义土壤水分对植物的有效程度最终决定于土水势的高低，而不是自身的含水量。

如果测得土壤的含水量，可根据土壤水分土特征曲线查得基质势值，从而可判断该土壤含水量对植物的有效程度。

1.3应用土壤水分特征曲线主要有以下几方面的应用［1］：①进行基质势和含水量的相互换算。

根据土壤水分特征曲线可将土壤湿度换算成土壤基质势，依据基质势可判断土壤水分对作物的有效度。

也可将基质势换算成含水量，根据土壤水分特征曲线可查得田间持水量、凋萎湿度和相应的有效水范围。

②表示比水容重。

土壤水分特征曲线斜率的倒数，即单位基质势变化所引起含水量的变化，称之为比水容重，是衡量土壤水分对植物的有效性和反映土壤持水性能的一个重要重要指标。

③可以间接反映土壤孔隙的分布。

*国家自然科学基金项目(No.40101005,No.50609022)资助作者简介:刘贤赵(1970~),男,湖南隆回人,教授,博士,主要从事区域水土资源高效利用研究。

E -mail:xianz haoliu@ 收稿日期:2006-09-21;收到修改稿日期:2007-03-23土壤持水曲线van Genuchten 模型求参的一种新方法*刘贤赵 李嘉竹 张振华(鲁东大学地理与规划学院,山东烟台 264025)A NEW METHOD TO ES TIMATING PARAMETERS OF VAN GENUCHTEN MODEL FORSOIL WATER RETENTIONLiu Xianzhao Li Jiazhu Zhang Zhe nhua(Colleg e o f Geogra ph y a n d Pla nn in g ,Lu don g U ni versit y ,Yan tai,Shan don g 264025,Chin a )关键词 土壤持水曲线;van Genuchten 模型;DPS 数据处理系统;Marquardt 方法中图分类号 S15217 文献标识码 A土壤持水曲线是研究土壤水动力学性质必不可少的重要参数。

在已经建立的众多数学模型中,van Genuchten 模型以其与实测数据拟合程度好而得到广泛的应用,而运用该模型的关键是如何获得其中的4个参数。

仅就我国而言,不少学者投入大量的精力发展了确定van Genuchten 模型参数的方法。

邵明安等[1~3]基于一维土壤水分运动的Richards 方程提出了推求土壤van Genuchten 模型和Brooks -Corey 模型参数的简单入渗法;王金生等[4]将最小二乘法和非线性单纯形法相结合拟合了van Genuchten 模型参数;徐绍辉等[5]也借助最小二乘法并结合P-i card 迭代法拟合了砂质黏壤土的van Genuchten 模型参数;李春友等[6]也利用单纯形调优法拟合van Genuchten 模型的参数;魏义长等[7]运用Matlab 编程软件对辽西淋溶褐土van Genuchten 模型的参数进行了推导估算。

摘要土壤水分运动特征及其参数确定学科名称: 水文学及水资源答辩日期：2003.3作者: 来剑斌作者签名：导师: 王全九教授导师签名：摘要在总结国内外有关土壤水分运动特征及参数确定方法研究成果的基础上，采取理论分析与室内试验相结合的方法，研究了四种不同质地土壤水平一维入渗、垂直一维入渗、点源自由积水入渗及负压盘式吸渗等的入渗模型及土壤水分运动参数的确定方法,获得以下研究结果。

1. 对常用的土壤水分特征曲线公式特点和相互关系进行了分析,获得了土壤质地与水分特征曲线常用表达式中参数之间的相关关系。

研究表明土壤质地与分形理论预测土壤水分特征曲线结果较好。

采用积分方法与入渗特性法确定的土壤水分特征曲线，在土壤低吸力段，与实测值吻合良好。

2. 由水平一维入渗资料计算土壤水分扩散率，结果表明，扩散率与含水率间符合指数函数变化关系，扩散率系数D0随土壤粘性增加而减小。

采用Burdine模式和Mualem模式计算的土壤水分扩散率表达式中的系数和指数随着土壤质地由细变粗而逐渐变大。

3. 利用实测资料分析Philip入渗公式与Kostiakov经验公式间的关系表明，二者在某种程度上具有一致性。

分析获得了Green-Ampt入渗模型与Philip模型参数间的相关关系表达式。

利用垂直一维入渗资料分别计算了四种不同质地土壤的导水率，结果表明，土壤导水率与含水率间关系符合乘幂函数变化关系。

比较分析了不同方法确定饱和导水率K s。

4. 对负压盘吸渗的稳定性分析表明，用改进的盘式吸渗仪进行土壤吸渗实验具有一定的稳定性和可靠度。

入渗时间相同时，不同负压水头下的累积入渗量随着负压的增大而减小。

利用负压盘式入渗资料，采用不同方法，分别计算并对比分析西安理工大学硕士学位论文了四种不同质地土壤的吸湿率及导水率。

结果表明，负水头越大土壤吸湿率及导水率越小。

对于同一个负压值，土壤吸湿率与导水率随土壤粘性增加而减小。

5. 除榆林土外，其余三种不同质地的土，渗透仪与点源入渗确定的土壤导水率接近，而一维入渗与盘式吸渗确定的土壤导水率接近，且比渗透仪及点源入渗测定值大。

间接推求非饱和土壤导水参数的方法【摘要】本文介绍了四种间接推求非饱和土壤导水参数的方法，包括土壤水分再分布过程法、土壤水分特征曲线拟合模型法、简单入渗法和土壤转换函数法，并对四种方法出归纳，提出了进一步研究的方向。

【关键词】非饱和土壤导水参数；水分再分布；水分特征曲线；简单入渗法；PTFs确定非饱和土壤导水参数的方法有两大类：直接法和间接法。

鉴于直接法，耗时多，价格昂贵，所得精度难以保证，空间差异性大，间接法成为许多专家学者研究的焦点。

本文通过介绍推求非饱和土壤导水参数的主要几种间接方法，做出归纳，以期为非饱和土壤导水参数间接法的进一步研究起到推动作用。

1.土壤水分再分布过程法邵明安[1]提出的一种土壤导水参数模型，将一维垂直和水平土壤水分再分布过程结合起来，根据土壤湿润锋湿度与湿润剖面平均湿度之间的函数关系，推出非饱和导水率K(θ)的解析表达式。

这样，只要利用土壤水分再分布的湿润过程，确定表达式中的常数，就可直接算出土壤的非饱和导水率。

根据湿润锋湿度与平均湿度拟合关系的不同，推出K(θ)有不同的表达式，本文采用湿润锋湿度与平均湿度为幂函数关系：K(θ)=（θ-θinm■■-Z■■-n■m■■■-X■■）上式：θ为体积含水率，θi为初始含水率，H为水深，Z、X分别为垂直和水平方向水分运移的距离，Z■和X■为所加其水面刚刚消失时初始湿润深度，m、n、m1、n1、a、b均为拟合参数。

2.土壤水分特征曲线拟合模型法2.1 Mualem模型Mualem模型关于相对导水率的表达式如下：Kr(Θ)=Θ1/2■■/■■■（1）式中：Kr为相对导水率，即K/Ks，h为水头值，Θ为无量纲含水量。

无量纲含水量表达式Θ=■（2）求解方程（1）时需要建立无量纲含水量与水头值的关系式，采用幂函数形式：Θ=（ａｈ）－ｂ（3）将（3）式代入方程（1）积分得：Kr(Θ)＝Θ５／２＋２／ｂ（4）2.2 Burdine模型Burdine建立的相对导水率表达式如下：Kr(Θ)＝Θ２■■／■■（5）将（3）式代入方程（5）积分得：Kr(Θ)＝Θ３＋２／ｂ（6）2.3 Van Genuchten模型[2]Van Genuchten水分特征曲线模型为：Θ＝［１＋（ａｈ）ｎ］－ｍ（7）式中：α是标定参数，与土壤平均孔隙半径成正比，n和m是土壤水分特征曲线的形状参数或孔隙分布指数,且有m=1-1/n。

>>专门水文地质学>>教材>>专门水文地质学§6.2渗透系数和导水系数渗透系数又称水力传导系数，是描述介质渗透能力的重要水文地质参数。

根据达西公式，渗透系数代表当水力坡度为1时，水在介质中的渗流速度，单位是m/d 或cm/s 。

渗透系数大小与介质的结构（颗粒大小、排列、空隙充填等）和水的物理性质（液体的粘滞性、容重等）有关。

导水系数即含水层的渗透系数与其厚度的乘积。

其理论意义为水力梯度为1时，通过含水层的单宽流量，常用单位是m 2/d 。

导水系数只适用于平面二维流和一维流，而在三维流及剖面二维流中无意义。

利用抽水试验资料求取含水层的渗透系数及导水系数方法视具体的抽水试验情况而定，下面就各种情况下的计算公式加以简述，其原理及具体计算步骤可参考地下水动力学相关教材。

一、单孔稳定流抽水试验抽水孔水位下降资料求渗透系数1. 当Q ～s （或2h ∆）关系曲线呈直线时， （1）承压水完整孔：rR sMQ K ln 2π= (6-9)（2）承压水非完整孔： 当M ﹥150r ，l /M ﹥0.1时， )12.1ln (ln2rMl l M r R sMQ K ππ-+=(6-10) 当过滤器位于含水层的顶部或底部时，)]2.01ln([ln 2rM llM r R sMQ K +-+=π(6-11)（3）潜水完整孔：rR h HQK ln )(22-=π (6-12)（4）潜水非完整孔：当h ﹥150r ，l /h ﹥0.1时，)12.1ln(ln)(22rhll h rR h HQK ππ⋅-+-=(6-13)当过滤器位于含水层的顶部或底部时，)]2.01ln([ln )(22rh ll h rR h HQK +-+-=π图6-2 土壤含水率变化曲线-14)式中 K —渗透系数（m/d ）； Q —出水量（m 3/d ）； s —水位下降值（m ）；M —承压水含水层的厚度（m ）； H —自然情况下潜水含水层的厚度（m ）；h —潜水含水层在自然情况下和抽水试验时的厚度的平均值（m ）； h —潜水含水层在抽水试验时的厚度（m ）； l —过滤器的长度（m ）； r —抽水孔过滤器的半径（m ）； R —影响半径（m ）。

2011年1月农业机械学报第42卷第1期用水平土柱估算土壤入渗性能和水分布简化模型方法*毛丽丽 雷廷武(中国农业大学水利与土木工程学院,北京100083)摘要 在对G reen Ampt 修正模型研究的基础上,根据水量平衡原理,提出了在水平土柱试验供水量、土壤初始与饱和含水率、土壤含水率线性分布假定的基础上计算土壤入渗性能的简化模型方法。

用本研究提出的简化算法计算得到的土壤入渗性能与其他方法得到的结果非常接近。

将该简化方法计算得到的土壤含水率分布与实测值进行比较表明,平均误差为4 18%,证明该方法估算的土壤含水率分布与实测值非常接近。

结果表明该方法可以较为准确地估算土壤入渗性能在时间上及含水率在空间上的分布,能方便地应用到相关研究与应用中。

关键词:水平土柱 G reen Ampt 入渗模型 土壤含水率 修正模型中图分类号:S152 7+2文献标识码:A文章编号:1000 1298(2011)01 0049 05Si m plifiedM ethod for SoilW ater D istributi on and I nfiltrability Esti m ationsM ao Lili Le iT i n g wu(College of H ydraulic and C ivil Eng ineering,China A gricu ltural University,Beijing 100083,China )Abst ractA si m p lified m athe m atic m odel w as for m ed to esti m ate the so il infiltrab ility fro m the tota l w ater supply ,the i n iti a l and sat u ra ted soilw ater con tent and the li n ear assumpti o n o f the so ilw ater distribution based on the study o f m od ified Green Ampt mode l and the m ass/w ater balance pri n c i p le .The so il i n filtrability esti m ated w ith t h is ne w si m p lified m e t h od is ver y close to the values calcu lated w it h the other m ethods .Co m parisons w ere m ade bet w een the predicted and m easured so il w ater d istri b u ti o n .The average relati v e err o r w as 4 18%w hich verified that the predicted one w as ver y close to the m easured val u es .The results sho w ed that the ne w l y suggested m odel cou l d pred ict the soilw ater distri b ution a l o ng the horizontal so il co l u m n as a function of ti m e very accurate l y .This ne w m ode l i s read il y applicab le to the re lated stud i e s and applicati o ns .It has g reat i m po rtance for the study o f hydrolog ic circulationstud ies .K ey w ords H orizontal so il co l u m n ,G reen Am pt infiltration m ode,l So ilw ater con ten,t M od ifiedm ode l收稿日期:2009 12 10 修回日期:2010 01 06*国家自然科学基金资助项目(40635027)作者简介:毛丽丽,博士生,主要从事农业水土工程研究,E ma i :l l eoa m@126.co m通讯作者:雷廷武,教授,博士生导师,主要从事农业水土工程研究,E m ai:l dd ragon @pub li c3.b ta .net .cn引言土壤入渗过程是水文循环中的重要环节。