降雨强度与稳定入渗率关系的公式化分析

降雨入渗对非饱和土边坡稳定性的影响摘要：降雨往往是引起边坡失稳的主要促发因素。

本文采用极限平衡分析方法，并结合算例，讨论了降雨入渗对边坡稳定性的影响。

计算结果表明，土体的初始体积含水率，降雨的强度和时间对边坡稳定性有重要的影响。

关键词：降雨入渗非饱和土坡边坡稳定性斜坡失稳是山区常见的自然地质灾害。

滑坡的发生与降雨的关系密切是早为人知的事实。

我国南方以及中南、西南地区广泛分布着粘性土，这些地区的山地或人工边坡经常在雨季发生滑坡，而且以浅层滑坡最为多见；在对基坑失稳事故的统计中，由于降雨诱发的就占很大比重。

这些都表明了土体边坡的稳定性与土体含水量的变化有很大的关系。

雨季边坡容易发生浅层滑坡，是由于近地表浅层土多为非饱和粘性土，雨水入渗使其饱和度增加，基质吸力降低，而基质吸力对表部边坡稳定性特别重要。

在降雨期间，随着含水量的增大，粘土的抗剪参数降低，从而土体本身的稳定性也降低。

此外，持续降雨还可引起地下水位上升或在相对隔水层以上出现暂时性地下水。

当持续降雨的历时和强度超过某种限度时，可导致土坡失稳。

浅层土的物理、力学性状因受气象因素影响随时都发生变化，而且滑坡常常给国民经济和人民生命财产造成巨大的损失，加上浅层滑坡的发生常带有突发性，且常常发生在强降雨期间。

如果在临时边坡或基坑工程设计、施工及防护中充分利用非饱和土的性质特点，不仅可以带来可观的经济效益，也可保证工程建设的安全进行。

因此研究降雨入渗对非饱和土稳定性的影响具有重要的工程意义。

1非饱和土边坡稳定性分析基本理论在土坡稳定性分析中，目前大都采用极限平衡法进行分析。

极限平衡法是根据土体沿着假设滑动面上的极限平衡条件进行，将潜在滑动面上可利用的抗剪强度除以安全系数而予以降低，使包围在滑动面和自出表面以内的土体处于极限平衡状态。

该方法已历经70年的应用和发展，人们在使用这类方法方面积累了相当多的经验，使得这类方法在计算分析方面有相当的精度。

同时，它能给出土坡的整体安全系数，另外，这类方法判别标准简单、明了、直观、使用方便，故极限平衡方法为工程界所广泛采用。

第六章流域产汇流分析本章要点本章的主要内容包括如下部分：1）介绍流域产流的机制，重点讨论蓄满产流与超渗产流；2）介绍流域产流计算的基本原理和方法；3）介绍流域汇流的基本概念和计算方法。

6.1 概述径流是自然水文循环过程中非常重要的一个环节，径流的产生和发展过程是水文学研究的重要内容。

河道任何一点的径流过程可以通过流量曲线的变化反映，而任意一点的径流过程都是流域上游径流过程综合之后得到的结果，是对整个流域降雨、融雪和其他水量输入的响应。

因此径流产生和发展过程并不是局部空间的水文现象，而是应该在流域尺度下进行研究。

径流的产生和形成是流域尺度上的综合问题，需要综合考虑其他水文过程，如降雨、入渗、饱和及非饱和土壤中的水流运动等。

尽管对这些水文过程单独加以研究已经有了相对成熟的方法，但是如何把这些理论加以综合得到解释流域产流机理的理论尚未取得令人满意的结果，其中一个很重要的原因是流域空间中的变异性太大，各个流域在很多方面都具有差异性。

研究径流的产生和发展过程，人为的可以把整个过程概化为产流阶段和汇流阶段两个阶段。

产流（流域蓄渗）指降雨经植物（树冠）截留、下渗和填洼等过程，形成地表和地下径流的过程。

产生的径流可以分为3种形式：地表径流（坡面流 Overland flow）、壤中流（Interflow / unsaturated flow）和地下径流（Groundwater flow）。

汇流则是指降落在流域上的雨水，从流域各处向流域出口断面汇集的过程。

汇流又可以分为山坡汇流和河网汇流两个阶段。

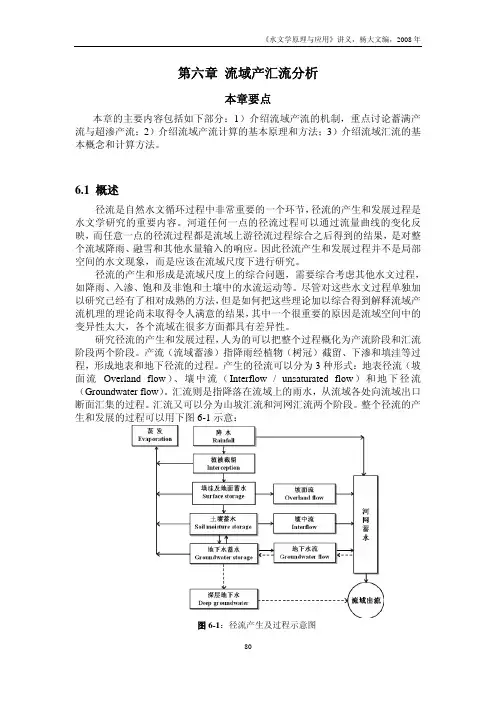
整个径流的产生和发展的过程可以用下图6-1示意：图6-1：径流产生及过程示意图本章主要研究的内容是地表径流的产流机理和汇流原理。

6.2 流域产流机理流域产流过程实质上就是流域中各种径流成分的生成过程，其实质就是水分经过流域下垫面（包括地面和包气带）作用之后对降水的再分配的过程。

因此不同的下垫面条件对应不同的流域产流机制（Streamflow Generation Mechanisms ），从而进一步影响到整个流域径流发展的过程也不相同。

N = 0.84 F
0 .2
N——洪峰流量时刻到直 ——洪峰流量时刻到直 接径流终止点的时间 ——流域面积 F——流域面积
（3）地面地下径流深的计算 地面、地下径流分割后， 地面、地下径流分割后，分割线上面的部分即地面 径流WS，下面的部分即地下径流 径流 ，下面的部分即地下径流Wg，其地面径流 ， 分别除以流域面积F即可得到 深RS、地下径流深 分别除以流域面积 即可得到。 、地下径流深Rg分别除以流域面积 即可得到。
二.
g e
f
a
b
则有： 则有：
流域蓄水曲线用B次抛物线表示后： 流域蓄水曲线用B次抛物线表示后： 流域蓄水容量WM WM为 流域蓄水容量WM为：
W =∫ M
w'mm 0
[1−ϕ(w )]dW = ∫
' m ' m
w'mm
0
W' ' W' m 1− 'm dW = m （1） ） W m 1+ B m m
【算例】 算例】 已知：Wm=100mm，k=0.96，6月1日至6月12日的 已知： =100mm，k=0.96， 日至6 12日的 流域平均降雨系列。 流域平均降雨系列。
第三节 流域产流分析
一.包气带对降雨的再分配作用 (Redistribution of rainfall by unsaturated zone) (1) 包气带对降雨的再分配作用： 已知：降雨强度为i ; 土壤的下渗能力（容量）为fp ①若i > fp ，则实际的下渗率为f = fp 则在某时段T内降雨形成的地表径流量（超渗雨） 为 T
第二节 降雨径流要素计算
一.
流域降雨分析

S 0 = sinθ,θ 为坡面倾角 ; n 为 Manning 糙率
9u 9u 9h ur ( 8) + + g = g ( i 0 - if ) 9 x 9t 9x h
式中 : q 为单宽流量 , m2 / s ; h 为水深 , m ; u 为 流速 , m/ s ; i 0 为坡面坡降 ; if 为阻力坡降 ; r 为净降雨量 , mm/ h ; x 、 t 为距离与时间 ; g 为 重力加速度 , m/ s 。 坡面产流研究已有很长历史 ,但对它的数 学求解还只有 30 多年 。20 世纪 60 年代后期 Woolhjiser 和 ligget ( 1967 ) 将运动波模型引入 坡面水流研究 , 大简化了计算工作 , 促进了研 究的发展 。运动波模型是从一维圣维南方程 简化而来 , 其基本假设是水流的坡面坡降 i 0 和阻力坡降 if 相等 , 并借助 Chezy 阻力公式 得到流量和水深的关系 。Woolhiser 和 Ligget 的研究结果表明在运动波波数 k > 10 时 , 运 动波 模 型 可 以 很 好 地 描 述 坡 面 水 流 运 动 。 而实际 坡 面 流 的 运 动 波 数 一 般 远 大 于 10 (沈 冰等 ,1996 ) 。因此 , 运动波近似是一种 较好的数学描述方式 。其后 ,又有对运动波理 论的修正 ( Ponce , 1978 ; Govindaraju , 1988 ) 保 留了水深的沿程变化项 , 相当于压力梯度 , 被 称为扩散波模型 。该模型扩展了适用的参数 范围 ,但并无实质性改进 。因此 , 实际应用仍 以运动波为主 。也有使用完整圣维南方程求 解实际问题的 ( 戚隆溪 ,1997) [ 3～8 ] 。 坡面产流是非常复杂的 ,目前主要采用运 动波理论 、 扩散波或完整圣维南方程进行描 述 。正如上文所述 ,运动波近似理论在大多数 情况下可以很好地描述坡面流运动过程 ,且计 算简单 [ 3 ] 。因此本文仍 采 用 一 维 运 动 波 理 论 ,即坡面流基本方程为 9q 9 h 连续方程 + = r 9 x 9t 1 . ∀ 动量方程 q = h & S 0−

福建省推理公式计算设计洪水手册一、基本公式：推理公式是无资料地区由暴雨推求洪水比较常用的方法，我省中小型水利工程设计洪水的计算也通常采用这种方法（一般在流域面积200km 2以下采用）。

它是假定汇流时间内降雨强度是均匀，并将汇形面积曲线概化为矩形，导出如下计算公式：当τ≥c t 时，即全面汇流情况下，F R Q m ττ278.0= (1)当τ<c t 时，即部分汇流情况下，F R F tc R Q tctc tc m τ278.0278.0==……..(2) 式中：m Q 为地表净峰流量(m 3/s )，F 为流域面积（km 2），tc F 为成峰的产流面积（即与tc 相应的部份面积中最大的一块，km 2）；τ为流域汇流历时（小时）；tc 为地表产流历时（小时）；τR 为汇流历时内的最大地表净雨量（毫米）；tc R 为产流历时内的地表净雨量（毫米）；0.278为换算系数。

二、设计暴雨的计算 1、查图法计算设计暴雨（1）查算设计流域各种历时的暴雨参数：根据设计流域所在地点，应用年最大各种历时的降雨量均值等值线图和变差系数等值线图，按地理内插法读取流域中心点的暴雨参数值，如果流域内有两条以上等值线通过，可按面积加权法计算。

（2）计算设计频率的各种历时降雨量：根据上步查算的各种历时降雨量的变差系数Cv 值，从皮尔逊Ⅲ型曲线的模比系数K P 值表中（Cs/Cv=3.5）分别读取设计频率P 的K P 值，乘以相应的历时降雨量均值即得。

（3）计算各种历时的面雨量：根据设计流域的面积和降雨历时，查读暴雨点面关系表（附表1），得暴雨点面折算系数α，乘以相应的点雨量即得（流域面积在10km 2以下直接采用点雨量，不打折扣）。

（4）推求设计雨量的时程分配：把上面所求的设计降雨量代入24小时（或三天）的设计雨型表（附表3），即得设计雨量的时程分配。

（5）设计净雨的计算：24小时的设计雨量不扣损，直接用设计雨量过程作为设计净雨过程。

经河网汇流形成流域出口的径流过程的计算称之为 汇流计算。
第四章 流域产汇流计算
二. 流域产汇流计算基本流程和思路 产流与汇流之间的联系可简明地表示成图4.1所示的流程图。
图4.1
基本思路:先从实际降雨径流资料出发，分析产流或汇流的规律；然后， 用于设计条件时，则可由设计暴雨推求设计洪水，用于预报时，则由实际 暴雨预报洪水。
降降雨雨PP((tt)) 蒸蒸发发EE((tt))
产流计算
数量上相等
净雨R(t)
汇流计算
流域出口断面 径流过程Q(t)
第四章 流域产汇流计算
一. 流域产汇流计算基本内容 由流域降雨推求流域出口的河川径流，大体上分为
两个步骤： ①产流计算：降雨扣除截留、填洼、下渗、蒸发等损
失之后，转化为净雨的计算称为产流计算。 ②汇流计算：净雨沿着坡度汇入地面和地下河网，并
第一节 降雨径流要素的分析计算
2、降雨深—面积关系
降雨深—面积关系曲线，是反映同一场降雨过程中，降 雨深与面积之间对应关系的曲线，一般规律是面积越大， 降雨深越小。
3、降雨深与面积和历时关系曲线
一般规律是：面积一定时，历时 越长平均雨深越大；历时一定时，则 面积越大，平均雨深越小。
面积
雨深—面积—历时示意图
包气带含水量达到田间持水量时的蓄水容量称该包气带 的最大蓄水容量，记为W'm,包气带含水量达到田间持水 量时,习惯上称为“蓄满”。当包气带未蓄满时，下渗水 量将滞留在土壤中；当蓄满后，再渗入的水量在重力作用 下产生壤中流RG1和浅层地下径流RG2。
综上所述，在包气带的调节、分配作用下，降雨有两种 产流方式：包气带未蓄满产流方式和包气带蓄满产流方式， 包气带未蓄满产流方式称为超渗产流方式。

福建省推理公式计算设计洪水手册一、基本公式：推理公式是无资料地区由暴雨推求洪水比较常用的方法，我省中小型水利工程设计洪水的计算也通常采用这种方法（一般在流域面积200km 2以下采用）。

它是假定汇流时间内降雨强度是均匀，并将汇形面积曲线概化为矩形，导出如下计算公式：当τ≥c t 时，即全面汇流情况下，F R Q m ττ278.0= (1)当τ<c t 时，即部分汇流情况下，F R F tc R Q tctc tc m τ278.0278.0==……..(2) 式中：m Q 为地表净峰流量(m 3/s )，F 为流域面积（km 2），tc F 为成峰的产流面积（即与tc 相应的部份面积中最大的一块，km 2）；τ为流域汇流历时（小时）；tc 为地表产流历时（小时）；τR 为汇流历时内的最大地表净雨量（毫米）；tc R 为产流历时内的地表净雨量（毫米）；0.278为换算系数。

二、设计暴雨的计算 1、查图法计算设计暴雨（1）查算设计流域各种历时的暴雨参数：根据设计流域所在地点，应用年最大各种历时的降雨量均值等值线图和变差系数等值线图，按地理内插法读取流域中心点的暴雨参数值，如果流域内有两条以上等值线通过，可按面积加权法计算。

（2）计算设计频率的各种历时降雨量：根据上步查算的各种历时降雨量的变差系数Cv 值，从皮尔逊Ⅲ型曲线的模比系数K P 值表中（Cs/Cv=3.5）分别读取设计频率P 的K P 值，乘以相应的历时降雨量均值即得。

（3）计算各种历时的面雨量：根据设计流域的面积和降雨历时，查读暴雨点面关系表（附表1），得暴雨点面折算系数α，乘以相应的点雨量即得（流域面积在10km 2以下直接采用点雨量，不打折扣）。

（4）推求设计雨量的时程分配：把上面所求的设计降雨量代入24小时（或三天）的设计雨型表（附表3），即得设计雨量的时程分配。

（5）设计净雨的计算：24小时的设计雨量不扣损，直接用设计雨量过程作为设计净雨过程。

四川建筑 第29卷2期 2009 04降雨强度对黄土边坡入渗性能影响的研究李守升,张俊云(西南交通大学土木工程学院,四川成都610031)摘 要 降雨入渗使得非饱和土边坡内含水量增大,进而令土的抗剪强度降低,这是降雨诱发浅层边坡失稳的重要原因之一。

通过有限元方法计算三种不同降雨强度下边坡内瞬态渗流场分析降雨入渗性能,数值计算结果表明:在历时3h 降雨以内,大于或等于土体饱和渗透性能的雨强条件下湿润锋深度相差不大,但饱和度明显不同;雨强越大,边界瞬时入渗量越大,稳定入渗量越大;在降雨期间,雨水不会以饱和入渗速度入渗,而是随时间呈非线性变化。

关键词 雨强; 边坡; 最大负孔隙水压; 瞬态渗流; 相对入渗量 中图分类号 P642 2 文献标识码 A近年来,国内外边坡地质灾害比较严重,如泥石流、滑坡等,这给经济建设造成了巨大的损失。

灾害发生的主要原因是降雨。

而边坡降雨的水文过程极其复杂,主要受土壤性质、降雨性质、地面形态和地貌等因素影响。

目前,国内外已有许多关于边坡降雨入渗规律的研究[1]~[3],但多侧重于坡体内孔隙水压变化来进行边坡稳定性分析。

关于黄土区边坡降雨向土壤水转化及运动规律方面仍需深入探讨。

1 二维瞬态渗流方程水在非饱和土中的流动同样服从D arcy 定律,与在饱和土中流动不同之处在于非饱和土中的渗透系数不是常量,而是饱和度或者基质吸力的函数。

D arcy 定律是多孔介质中流体的运动方程;质量守恒是物质运动和变化普遍遵循的原理,将质量守恒定律应用于多孔介质中的流体即为连续方程。

D arcy 定律和连续方程结合便可导出水分在多孔介质中的运动方程,见式(1)。

x k x h w x +y k y h w y= g m w 2h w t (1)式中:k x ,k y 分别为水平和垂直方向的渗透系数; 为水的密度;g 为重力加速度;m w 2为与基质吸力变化相关的含水量体积变化系数,即:m w 2=- w(u a -u w )(2)图1 非饱和边坡几何模型从式(2)看出m w 2也是土水特征曲线的斜率。

利用动态分析法分析降水入渗补给系数的变化规律姚建【摘要】Precipitation is the main recharge sources of regional water resources.In hydrology and water resources evaluation,especially the groundwater resources evaluation,the precipitation infiltration recharge isa very important recharge,so that in the mountain area,the quantity of groundwater resources is the precipitation infiltrationrecharge.Precipitation infiltration coefficient is a key parameter for calculating the infiltration recharge.This paper discusses on the change law of permeability in precipitation recharge coefficient by using the dynamic analysis method.%降水是区域水资源最主要的补给来源。

在水文水资源评价特别是地下水资源的评价中，降水入渗补给量是一个非常重要的补给量，以至于在山丘区，其地下水资源量就是降水入渗补给量。

降水入渗补给系数是计算降水入渗补给量的关键参数。

文章利用动态分析法对降水入渗补给系数的变化规律作了一些探讨。

【期刊名称】《黑龙江水利科技》【年(卷),期】2015(000)003【总页数】3页(P1-3)【关键词】降水入渗补给系数;动态分析法;规律【作者】姚建【作者单位】辽宁省营口水文局，辽宁营口 115000【正文语种】中文【中图分类】P641.21.1 降水入渗补给量降水通过地面进入土中的那部分水量，即下渗的水量，首先在土壤吸力作用下被土壤颗粒吸附保持，成为土壤持水量的一部分，其中一些还要以蒸散发形式返回大气，剩余的部分水量才可成为自由水补给到地下水中，即为降水入渗补给量。

降雨强度与稳定入渗率关系的公式化分析作者：刘正风来源：《海峡科学》2010年第10期[摘要]稳定入渗率在设计洪水的计算中起着将一次净雨过程分割为地表净雨过程与地下净雨过程的作用,以前稳定入渗率fc的确定是由i～fc经验关系曲线人工读出的,对工程计算带来诸多不便,该文拟合了某地区i～fc经验关系曲线的一个表达式,并对此表达式与经验关系曲线的符合效果进行分析。

[关键词]稳定入渗率降雨强度经验关系曲线公式化1降雨强度i与稳定入渗率fc的经验关系稳定入渗率fc在设计洪水的计算中起着将一次净雨过程分割为地表净雨过程与地下净雨过程的作用,通常我们将各站各次洪水以次净雨平均强度i为纵坐标,以稳定入渗率fc为横坐标,点绘相关图进行综合分析。

相关点子数据见表1,相关点子图如图1所示(本文示例数据采为某地区的50次洪水的统计数据)。

表 1实测降雨强度i与稳定入渗率fc的关系表单位:mm/h项目 i～fc关系数据i(测) 0.0 4.0 4.0 4.4 4.4 4.6 4.8 5.0 5.0 5.5fc(测) 0.00 2.00 3.98 3.20 5.00 2.20 2.10 3.40 4.80 4.80i(测) 5.6 5.7 5.8 6.7 6.8 7.2 7.4 7.9 8.2 8.5fc(测) 3.10 5.20 1.70 4.60 2.80 7.80 6.30 2.90 3.40 2.10i(测) 8.8 9.0 9.1 9.2 9.3 9.5 9.8 9.9 10.2 10.5fc(测) 4.10 4.70 3.80 5.20 2.70 6.90 2.40 8.30 4.90 3.90i(测) 11.0 11.3 11.7 11.8 12.5 13.8 15.1 16.1 16.5 16.6fc(测) 5.70 6.20 4.70 7.10 7.70 9.60 12.50 4.90 4.50 9.70i(测) 17.4 18.2 18.6 19.0 28.2 31.0 35.0 40.0 50.0 60.0fc(测) 8.10 9.30 8.70 12.00 7.90 8.80 9.60 10.40 11.80 12.90图1净雨平均强度i与稳定入渗率fc相关点子图稳定下渗率fc是由地下径流分析得来,往往稳定下渗率fc大地下径流也大,在分割地表与地下径流时,退水段第二拐点位置的确定带来一定的任意性,所以i～fc的相关点在小洪水时比较散乱。

降雨条件下边坡渗流及稳定性数值模拟分析苏恒宇【摘要】为了研究苏北某高速公路旁边坡在降雨条件下的渗流和稳定性,通过Geo-studio软件的seep/w和slope模块,对边坡进行了不同工况(特大暴雨、暴雨、大雨、小雨)条件下的数值模拟,研究不同降雨强度、不同时间下孔隙水压力及安全系数的变化规律.结果表明:孔隙水压力随着降雨时间的增长呈上升趋势,安全系数呈下降趋势;降雨强度越大,孔隙水压力增大的越快,较易饱和形成表面径流;安全系数在降雨前中期降低较快,后期趋于平缓.【期刊名称】《江苏建筑职业技术学院学报》【年(卷),期】2019(019)001【总页数】4页(P28-31)【关键词】Geo-studio;降雨类型;边坡稳定;数值模拟;孔隙水压力;安全系数【作者】苏恒宇【作者单位】江苏建筑职业技术学院建筑管理学院,江苏徐州221116【正文语种】中文【中图分类】TV223.6降雨使得边坡土体强度锐减,下滑力加剧,大量的边坡失稳事故都发生在降雨的天气条件下.因此,国内外学者在对降雨条件下边坡稳定进行了分析,做了很多研究工作[1].本文针对这个问题,利用Geostudio边坡渗流及稳定计算软件,以苏北某高速公路边坡为例,研究降雨条件变化对边坡渗流和稳定性的影响.1 计算原理1.1 非饱和渗流理论非饱和土体渗流分析,一般采用Richards来描述,方程如下：其中：式中,u w为孔隙水压力,k Pa;θ为表征土体的体积含水率,%;γw为水重度,kg/m2;t 为时间,h;T x、T y 分别代表为x 和y 方向的渗透系数,m/h;H 是基质吸力的函数. 土体体积含水量可由水土特征曲线获得[2],方程如下：其中：式中：θw 为土体的体积含水量,%;Cφ为修正值;θs 为土体饱和体积含水量,%;λ为土体体积含水量的拐点,%;m 为残余含水量,%;n 为土水特征曲线的斜率;φ为基质吸力,kPa;e为自然对数的底;s为拐点处斜率.渗透系数函数采用Geo-studio自带函数[3].1.2 稳定性分析边坡稳定性分析一般采用极限平衡法,常用的极限平法计算方法有很多,本文采用的是Morgenstern-Price法,并引入Fredlund的土体非饱和双应力变量强度理论：式中：σn 为土体破坏时其破坏面上的净法向应力,N/m2;s a-s w 为土体破坏时的基质吸力,k Pa;c′为有效内聚力,k Pa;φ′为有效内摩擦角,rad;φb为基质吸力的内摩擦角,rad.2 降雨模拟计算2.1 分析模型建立边坡模型如图1所示,山坡高为50 m,长为95 m,边坡前后缘高差为40 m,ab为初始地下水位线,边坡倾斜角为14°,节点14为本研究分析节点,各层的土体物理力学计算参数见表1.土体水工特征曲线,如图2所示.图1 初始边坡模型Fig.1 Initial slope model表1 土体物理力学计算参数Tab.1 Calculation parameters of soil physical mechanics层号土质 (k N重·度m/-3)______粘_k聚Pa力/_________内___摩(°擦)角_/_________饱_和(m渗·透h-系1)数/___________饱__和__含%水__率__/_____________残__余_含%水__率__/______L1 粉质黏土18.8 20 12 0.012 0.3 0.03 L2 黏土 19.1 26 30 0.011 0.22 0.011__L3 黏土19.8____________________29_________________2_9_________________0_._0_0_7__2__ _________________0__.1____________________0__.0_1_______2.2 边界条件建立边坡下边界为竖直约束边界,左右为水平设置边界.其中,左右水头高度分别为28 m 和5 m,表面为降雨边界,降雨共4种工况,见表2.模型网格如图3所示.共剖分为1 006节点,944单元.图2 土体水土特征曲线Fig.2 Curve of soil and water characteristics图3 边界条件模型Fig.3 Boundary condition model表2 工况参数Tab.2 Duty parameter____工况___________降雨类型___降雨强度/__(_m_·__h__-_1_)____降__雨__时__间__/_h_工况1 特大暴雨0.008 3工况2 暴雨0.005 4工况3 大雨 0.003 24____工况4__________小__雨___________0.0004____________________4_8______3 计算结果分析3.1 渗流结果分析本分析采用Geo-studio种的seep/w 模块对模型进行渗流分析,不同工况的渗流分析即孔隙水压力随时间的变化规律,如图4所示.由图可知,孔隙水压力在不同降雨条件下的值,会随降雨时间的增加而不断升高,负孔隙水压力会减小,基质吸力减小[4].且高强度的孔隙水压力值较低强度的孔隙水压力值增长的更快.以2 d末的数值为例,孔隙水压力的数值由大到小的工况依次是特大暴雨、暴雨、大雨、小雨.因为,在同一时间段下,高强度的工况降雨量更大,孔隙水压力增长更快.此时,土体更快且更易达到饱和.但是,图4中未见负隙水压力值增至0 kPa,证明这几种常见的工况均未能使土体达到饱和状态,边坡暂时不会出现表面渗流现象.以工况1 为例,增加降雨时间,可得出降雨时间对孔隙水压力的影响,如图5所示.前期孔隙水压力增长较快,在0.5 d时,孔隙水压力为0,当时间到达1 d时,土体近似达到饱和状态,后期速率降低且趋于平缓,这与现场观测的结果相吻合.说明降雨入渗随着时间的增长,入渗能力减弱,孔隙水压力增长变缓慢.当土体被水充满达到饱和状态时,雨水不能继续入渗,孔隙水压力基本不变,土体会产生坡面径流.雨水入渗会削弱土体的抗剪强度,改变土体天然重度,对土体稳定性产生影响[5].此外,由于高强度降雨持续时间短,土体蒸发与入渗时间有限,极易在表面形成径流,需采取相应改善措施.图4 不同工况下孔隙水压力与降雨时间关系Fig.4 Relationship between pore water pressure and rainfall time under different working conditions图5 特大暴雨条件下孔隙水压力与时间关系Fig.5 Relationship between pore water pressure and time under rainstorm图6 安全系数与时间关系Fig.6 Relationship between safety factor and time 3.2 稳定性分析根据地质灾害防治规范规定,由表3中的稳定系数可知,边坡在自然工况下最稳定,安全系数可达到1.161,其余各种工况下,工况1、2安全系数较低,但都能保持稳定.总体来说,高强度降雨工况稳定系数略低于低强度的稳定系数.以3 h末时间为例,从工况1至工况4,安全系数分别为工况1＞工况2＞工况3＞工况4.说明降雨强度对边坡的稳定性具有一定影响,降雨强度越大,安全系数降低的时间越短.分析其原因,在降雨强度大的情况下,同一时间内总降雨量大,在降雨本身冲击力下迅速入渗,土体易形成饱和土质,基质吸力减小,入渗能力减弱,土体抗剪强度和重度降低,从而削弱边坡的稳定性,与上面所讨论的孔隙水压力的变化相对应.表3 降雨类型对安全系数的削弱程度Tab.3 The degree to which the type of rainfall weakens the safety factor工况降雨强度/(mm·d-1) 安全系数削弱程度/%1 190 1.062 8.5 2 120 1.069 7.9 3 80 1.092 5.9 4 10 1.157 3.4 5 0 1.161—降雨时间对安全系数的影响.以特大暴雨为例,模拟暴雨75 h 降雨条件,如图6 所示.由图可知,安全系数的变化可分为3段,即降雨前期(0～50 h)、降雨中期(50～62 h)和降雨后期(62～75 h).总体来说,安全系数随着降雨时间的增加而降低,即边坡越不安全.且在降雨前期,虽然土体的基质吸力较大,但是此时降雨量小,土体渗透系数大于雨水渗透速度,雨水可以迅速向下渗流.所以,对土体的稳定影响不大,安全系数下降较缓慢.降雨中期,安全系数近似趋于直线下降.是因为较高的基质吸力及土体高渗透性,使得雨水迅速入渗.此时降雨量增加,土体空隙被越来越多的雨水所填满,基质吸力减弱,土体抗剪强度迅速下降,加大边坡的下滑力,影响边坡的稳定性.到降雨后期会发现,中期时土体空隙迅速增长的雨水使得土体趋于饱和,土体渗透能力降低,雨水入渗困难,土体变化情况趋于稳定.所以,安全系数变化微小.综上所述,降雨强度及降雨时间对边坡稳定性的影响有着共同的机理,两者会影响边坡的稳定性,研究时需要全面看待各种影响因素.4 结论1)随着降雨时间的增加,孔隙水压力不断上升.降雨初期孔隙水压力增长速率快,降雨时间越长,后期增长速率越慢,总体呈正比关系.2)相同时间不同工况下,高强度的孔隙水压力较低强度的孔隙水压力增长的更快,安全系数降低时间短.3)苏北某高速公路边坡根据江苏气象资料,在几种常见的工况条件下整体呈稳定状态,且土体暂未达到饱和状态,不会出现土体表面径流现象.4)随着降雨时间的增加,安全系数整体呈下降趋势,即反比关系.在特大暴雨情况下降雨初期安全系数降低缓慢,中期降低速率增大,后期雨水入渗困难,安全系数又趋于稳定.【相关文献】[1] 俞新,李红英.降雨条件下边坡稳定性研究[J].山西建筑,2017,43(33)：61-63.[2] 刘淑燕.降雨强度对不同渗透性土质高边坡稳定性数值分析[J].湖南交通科技,2017,43(4)：15-19.[3] 吴宏伟,陈守义,庞宇威.雨水入渗对非饱和土坡稳定性影响的参数研究[J].岩土力学,1999,20(1)：1-14.[4] 罗林,徐颖,左昌群,等.降雨对类土质滑坡微观结构及稳定性的影响分析[J].水电能源科学,2015,33(1)：119-123.[5] 石振明,沈丹祎,彭铭,等.考虑多层非饱和土降雨入渗的边坡稳定性分析[J].水利学报,2016,47(8)：977-985.。

降雨入渗深度对土质边坡稳定性影响的有限元分析杨宇杰【摘要】采用有限元分析分析方法，计算了土质边坡在不同的降雨重现期、降雨强度、降雨持时情况下的入渗深度，提出了合理的降雨入渗深度的计算公式；在所得出的入渗深度的基础上，运用渗流有限元法对土质边坡进行了稳定分析，得出实际土质边坡的降雨入渗很难超过2.0 m，在边坡的地下水深度逐渐增加，降雨入渗深度不变的情况下，边坡的稳定安全系数逐渐减小；在边坡的地下水深度相同，降雨入渗深度逐渐变大，边坡的稳定安全系数同样逐渐减小，但减小的幅度较小；这说明降雨对边坡体的影响集中在地表附近；在地下水位与降雨入渗深度较大时，滑坡体稳定性不足。

%The finite element analysis method is used in this paper,calculated soil slope in differ-ent rainfall return period,rainfall intensity,rainfall duration,the infiltration depth,and puts forward the reasonable rainfall infiltration depth calculation formula;in income based on the depth of infiltration and seepage finite element method on soil slope the stability analysis,obtained the actual soil slope rainfall infiltration is difficult to more than 2.0 m,A gradual increase in the slope of the groundwater depth,con-stant depth of rainfall infiltration,the stability safety factor of the slope decreases gradually.In the same slope groundwater depth,the depth of rainfall infiltration gradually become larger,and stability safety factor of the slope is also gradually decreased,but decreases the amplitude is smaller.This shows that effect of rainfall on slope near the surface;in the underground water level andrainfall in infiltration depth is larger,the landslide body stability is insufficient.【期刊名称】《公路工程》【年(卷),期】2016(041)005【总页数】5页(P226-229,262)【关键词】降雨入渗;土质边坡;稳定性;有限元【作者】杨宇杰【作者单位】长春建筑学院，吉林长春 130604【正文语种】中文【中图分类】U416.1+4降雨是引起边坡失稳，影响边坡稳定性的主要因素之一。

计算过程中 得到传播与放大’ 使计算结果可靠性大为降低。
３ ｉ ｃ ～ｆ 经验关系 曲线模 拟公式 的提出 与检 验
虽 然 ｉ ｃ 验 关 系 曲 线 轨 迹 很 难 用 简 单 的 函 数 公 式 表 ～ｆ经
达 ，但我们相信该函数表达式是客观存在的。随着计 算机的 发展和计算方法 的改进，借助一些 达 式 的 特 性 进行 了分 析 。 示 例 数 据 采
用 某地 区 ５ 次 洪 水 的 统 计数 据 ，相 关 点 子 数 据 见表 １ ～ｆ ０ ，ｉ ｃ 经 验关 系 曲线 见 图 １ ～ｆ经 验 关 系 曲线 读 出 数 据 见 表 ２ 。ｉ ｃ 。
结 果 表 明 ，ｉ ｃ 拟 公 式 计 算 的 ｆ（ ） 比 ｉ ｃ 验 关 系 曲线 插 值 计 算 的 ｆ 插） 更 合 理 ， 即 ｉ ～ｆ 模 ｃ计 值 ～ｆ 经 ｃ 值 （
～
ｆ 拟 公 式 计 算 方 法 合 理 、 简单 、 高效 。 ｃ模
关键 词 ：稳 定 下渗 率 ；降雨强度 ；经验 关 系曲线
一｝ ’ ’ ｝ ’ 一‘
１ ．０ ００
： ：
：
一
。 ‘ ‘ ‘
｝－ ： 一－ … ： ・ ・－
－ －
０ｏ ．０ Ｏ ０ ２ ０ ４．０ ６ ０ ８ ｏ ｌ ０ １ ． ０ １ ｏ ０ ．０ ０ ．０ ．ｏ Ｏ．０ ２ ｏ ４．０
中图分类号 ： Ｖ１ １ Ｔ ２
文献标识码 ： Ｂ
文章编号 ：０ ２ ０ １ ２ １ ）２ ０ ０ ３ １ ０ —３ １ （０ ０ ０ —０ ３ —０
１ 降雨强度 ｉ 与稳 定 入 渗率 ｆ ｃ的经 验 关 系
在 设 计 洪 水 计 算 中， 稳 定 下 渗 率 ｆ 起 着 将 一 次 净 雨 过 ｃ 程分 割 为 地 表 净 雨 过 程与 地 下 净 雨 过 程 的作 用 。通 常 将 各 站 各 次 洪 水 以次 净 雨 平 均强 度 ｉ 纵 坐 标 。 以稳 定 下 渗 率 ｆ 为 为 ｃ 横 坐标 ，点 绘 相 关 图 进行 综 合 分 析 。 稳定 下 渗 率 ｆ ｃ由地 下径 流 分 析 得来 ，往 往 稳 定下 渗 率 ｆ ｃ

土壤初始含水率和降雨强度对黏黄土入渗性能的影响2009年4月7(2):卜6中国水土保持科学ScienceofSoilandWaterConservationV o1.7No.2Apr.2009土壤初始含水率和降雨强度对黏黄土入渗性能的影响刘汗,雷廷武,赵军(1.中国农业大学水利与土木工程学院现代精细农业系统综合研究重点实验室,100083,北京;2.中国科学院水利部水土保持研究所黄土高原土壤侵蚀与早地农业国家重点实验室,712100,陕西杨凌)摘要为研究初始含水率和降雨强度对土壤入渗性能的影响,采用径流一人流一出流法和双环入渗法测量比较,采用不同降雨强度(20,40和60mm/h)和3种土壤含水率(2.60%,10.4%和19.5%)进行试验比较.结果表明:土壤入渗性能随着降雨强度的增加而降低,随着初始含水率的增加而降低;双环法测量的土壤初始入渗率随着含水率增加而增加,稳定人渗率则随着含水率的增加而降低.同时,通过Kostiakov,Ho~on和Philip入渗模型对试验结果进行回归分析,径流一人流一出流法测量结果均优于双环法测量结果,而且Ho~on入渗模型回归结果优于其他人渗模型.关键词土壤含水率;人渗性能;降雨;双环入渗法;地表结皮EffectsofinitialsoilwatercontentandrainfallintensityonLoessinfiltrationcapacityLiuHan,LeiTingwul-,ZhaoJun(1.KeyLaboratoryofModemPrecisionAgricultureSystemIntegrationResearch,Collegeo fWaterConservancyandCM1Engineering,ChinaAgriculturalUniversity,100083,Beijing;2.StateKeyLaboratoryofSoilErosionand DrylandFanningontheLoessPlateau, InstituteofSoilandWaterConservation,CAS&amp;MWR,712100,Yani"g,Shaanxi:Chin a)AbstractTheRun—off-on?out(ROOO)methodwasusedtomeasuresoilinfiltrabilityinordertoresearchthe effectsofrainfallintensityandsoilwatercontentonsoilinfihrabilitycomparedwithDoubleR ing(DR)method.Theexperimentsinvolved3soilmoisturecontents(2.6%,10.4%and19.5%)and3rai nfallinten-sities(20,40and60mm/h).SoilinfihrabilitymeasuredbytheROOOmethoddecreasedwithh igherinitialsoilwatercontentandrainfallintensity.However,theinitialsoilinfihrabilityobtainedbyDR methodin—creasedwithhighersoilwatercontent,aswellasthestableinfiltrabilitydecreasedwithhigher soilwatercon—tent.ThesoilinfihrabilityprocessesmeasuredwiththeROOOmethodgivebetterfittingswit hKostiakov,Hor—tonandPhilipinfihrationmodels,thanthosemeasuredwithdouble—ringinfiltrometer.Moreover,theHorton infiltrationmodelgivesthebestfittingresultscomparingwithothermodels. Keywordssoilwatercontent;infiltrability;rainfall;doubleringmethod;surfacecrust土壤人渗是地表水转化过程中的重要环节,在水循环过程中具有重要的作用.土壤入渗性能对于水资源高效利用,农业灌溉和水文环境等领域具有重要的意义.土壤水分人渗是水分在土壤内部分布的一个动态过程,因此,土壤初始含水率的变化必然影响土壤入渗过程.随着土壤初始含水率的增加,非稳渗阶段的入渗速率迅速降低,趋于稳定人渗速率的时间收稿日期:2008-06—30修回日期:2oo8—1卜11项目名称:国家自然科学基金"黄土区多尺度小流域土壤水蚀动态过程模拟研究"(40635027);天水籍河重点支流治理项目(二期)水土保持监测体系建设第一作者简介:刘汗(1981一),男,博士研究生.主要研究方向:土壤侵蚀及水土保持.E—mail:lylblh@.十责任作者简介:雷廷武(1958一),男,博士,教授,博士生导师.主要研究方向:土壤侵蚀及水土保持.E—mail:ddragon@pub—.an2中国水土保持科学2009矩缩短….G.B.Bodman等Ⅲ2认为,在人渗初期,随着土壤含水率的增加,土壤入渗速率减小,随着时间的延续,含水率对入渗的影响变小,最终可以忽略.J.D.Eigle等_3的研究表明,土壤结皮对裸地入渗的影响大大超过其他因素的影响,其减少人渗量可达80%.降雨动能与降雨强度密切相关,因此,降雨强度也是影响土壤降雨人渗性能的重要因素.J.Rubin_4和A.0.Aken等5J的研究表明,不同降雨强度下,入渗曲线形式是相同的,如果降雨历时足够长,均质土壤的稳定入渗率,人渗总量与降雨强度无关,但瞬时人渗速率受降雨强度大小和时间变化影响较大.国内也有一些不同的研究结果:随着降雨强度增大,土壤入渗率和稳定入渗率均有增大的趋势¨6,但大部分研究都是针对土壤实际人渗率与降雨强度之间的关系,而对于土壤入渗性能(最大入渗能力)与降雨强度关系的研究非常少.双环入渗是常用的土壤入渗测量仪器,可以方便快速地测量土壤人渗率,具有结构简单,操作简便和移动方便等特点_8j.由于双环入渗法测量过程中需要保持环内水位高度稳定一致,因此不适用于坡地土壤测量.人工降雨法也是较为广泛使用测量土壤入渗的方法之一.通过模拟天然降雨,测量降雨量与产流量随时间变化过程,即可计算土壤人渗率变化过程,具有不受地形限制适应性强的特点,而且综合考虑了降雨引起土壤侵蚀对土壤人渗过程的影响;但人工降雨法测量土壤入渗率受降雨强度限制,只能测量土壤人渗性能小于降雨强度部分.雷廷武等¨lo_研究了一种测量土壤人渗性能的径流一人流一出流法,可以方便测量模拟天然降雨条件下,土壤人渗性能变化全过程.笔者主要采用径流一人流一出流法,以双环人渗仪测量结果作为对照,.研究不同土壤含水率和降雨强度对土壤入渗性能的影响,并通过传统入渗计算模型回归分析比较研究结果的合理性.1材料与方法试验在中国科学院水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室的人工降雨大厅进行.试验土壤为陕西杨凌的黏黄土,土样采自地表20～30cm土层,土壤颗粒组成如表1所示.表1试验土壤颗粒组成Tab.1Particlesizedistributionoftheexperimentalsoil试验所需初始土壤含水率按田间持水量的百分比配置,分别为自然风干土,体积含水率为10.4%(约等于田间持水量的30%)和体积含水率为19.5%(约等于田间持水量的60%)的土壤.土壤含水率按要求配置后均用塑料薄膜覆盖密封处理7～10d,一方面防止土壤表层水分散失,另一方面使土壤充分熟化,含水率进一步均匀.实验用水平土槽尺寸为8m×3m×0.5m,按照5cm厚度分层装土,土层总厚度为25cm,密度为1.3g/cm3,装土时采用自制钢钉插实,避免传统方法表面打压夯实,破坏表层土壤结构.装土后用塑料薄膜覆盖进行密闭处理,翌日进行试验,以使土壤水分进一步均匀,试验前再次现场快速测定土壤含水率,以确保所配置含水率符合试验要求.采用产渗流土壤人渗性能测量仪_10_测定不同土壤含水率下土壤入渗变化过程,该仪器装置如图1所示,包括人工模拟降雨装置(图1(a))和下垫面设置(图1(b)),其中,下垫面分隔设计3个相同尺寸土槽,相当于3次重复试验.实验过程中记录径(a】人工降雨装置(b)F垫面设置图1径流一入流一出流法测量系统Fig.1Schematicsystemofthe13in—off-on—outmethod流在地表随时间推进的过程,代人计算模型得出土壤人渗性能随时间变化规律.本研究设计了3种不同的降雨强度,分别为20,40和60mm/h,研究稳定降雨强度下,不同含水率对土壤入渗性能的影响.同时采用传统双环入渗法作为对照,双环入渗仪内第2期刘汗等:土壤初始含水率和降雨强度对黏黄土人渗性能的影响外环直径分别为28和53cm,采用马氏瓶补给内环水量维持稳定水位,3次重复实验.2结果与分析2.1降雨强度对土壤入渗性能影响在稳定降雨强度下,径流一人流一出流法测量的土壤入渗性能大于双环入渗法(图2～4),特别是试验开始阶段的初始入渗性能.如图2所示,径流一人流一出流法测量的稳定入渗率远大于双环入渗法,是双环法测量数值的2—4倍,而随着降雨强度的增大(图3～4),稳定人渗率之间的差别逐渐缩小.原因在于雨滴动能随着降雨强度的增加而增加,而雨滴动能是土壤表面结皮的重要影响因素,降雨强度增加使得结皮发育更成熟,导致稳定入渗率大幅下降, 与双环入渗法的差异随之缩小.表2为不同降雨强度下降雨动能计算列表,对于不同研究地区的不同计算公式结果均表明,随着降雨强度增大,降雨动能逐渐增大,但增加趋势逐渐变缓,也就是说降雨动能增加的趋势小于降雨强度增加趋势.这与不同降雨强度下土壤入渗性能变化曲线趋势是一致的(图2 ～4),即降雨强度20mm/h与40mm/h的入渗性能曲线之间的差异大于降雨强度40mm/h与60mm/h 入渗性能曲线之间的差异,一定程度上说明了径流一人流一出流法测量结果的合理性.三l瓣&lt;图2降雨强度20min/h下土壤入渗性能曲线与Fig.2Comparisonofinfiltrabilitycurvesunder20mm/h withdoubleringmethod因此,径流一人流一出流法测量土壤入渗性能随着降雨强度的增加而逐渐降低,并逐渐趋于稳定;原因在于随着降雨强度的增加,降雨动能增加趋势变缓,雨滴对地表的打击扰动能力逐渐达到相对稳定值,不再随降雨强度增大而线性递增,地表结皮程度也相应达到稳定.在试验过程中,20mm/h降雨强度下一直未见有径流出流,说明此工况下土壤稳定入渗率大于降雨强度,所有降雨及径流完全入渗,而传统的降雨入渗测量方法对于未产流的情况,很难测量土壤人渗性能变化过程.,皇喜斛斑&lt;时间/l1图3降雨强度40mm/h下土壤入渗性能曲线与双环法测量比较Fig.3Comparisonofinfiltrabilitycurvesunder40mm/h withdoubleringmethod昌.1;{L&lt;时间/l1图4降雨强度60mm/h下土壤入渗性能曲线与Fig.4Comparisonofinfiltrabilitycurvesunder60mm/hwith doubleringmethod双环入渗法测量土壤入渗性能小于径流一人流一出流法测量结果,可能的原因如下:一方面双环人渗法在测量开始时,需要向内外环迅速加水造成土壤快速湿润,土壤颗粒迅速崩解分散,堵塞土壤孔隙通道,很短时间内就引起土壤表面结皮,土壤人渗性能随之迅速降低,并且由于双环入渗法为积水人渗在土壤表面形成水封,使得土壤中的气体无法及时排出,阻碍了水分的正常人渗;另一方面双环法测量试验开始阶段,土壤初始人渗性能很高,马氏瓶供水能力受限于出水口直径和管径,未能及时补给双环入渗所需水量,为非充分供水人渗.4中国水土保持科学2009年K=11.87+8.731ogiK=29(1—0.72exp(一0.051))K=36.8(1一O.69exp(一O.0381))K=28.3(1一O.52exp(一O.0421))K=27.83+11.551oglK=32.98+12.131ogl23.2321.3224.9321.9542-8648.7625.8626.1731.2525.5646.3352.4127.39W.H.Wischmeier等【"J27.96L.C.Brown等lJ34.20A.W.Jayawardena等[]27.12A.M.VanDiik【j48.37江忠善等[15针对中国西北地区普通雨型54.55江忠善等[]针对中国西北地区矩阵型雨型2.2含水率对土壤入渗性能影响图2～4径流一人流一出流法测量结果表明,土壤初始含水率增加时,土壤入渗性能降低速度更快. 对于40mm/h(图3)和60mm/h(图4)降雨强度,随着降雨强度的增大,土壤含水率对土壤入渗性能的影响逐渐缩小,土壤入渗性能曲线趋于一致.径流一人流一出流法土壤初始含水率增加时,土壤入渗性能降低速度更快,可能的原因是随着土壤含水率增加,初始土壤水吸力降低,水力梯度逐渐减小,土壤入渗性能降低速度加快.随着降雨强度的增大,土壤含水率对土壤入渗性能的影响逐渐缩小, 土壤入渗性能曲线趋于一致.可能的原因是,在较大降雨强度时,土壤表面结皮对入渗性能的影响占据主要作用,而含水率对入渗的影响相对处于次要位置.说明随着降雨强度的增加,含水率的变化对土壤入渗性能的影响逐渐降低.用图2～4双环入渗法测量的结果表明,试验初始阶段土壤初始入渗率随着土壤含水率增加而增加,稳定人渗率随着土壤含水率的增加而减小.可能的原因是:双环人渗法开始测量时,需要向内外环同时加水,土壤颗粒快速湿润分散,堵塞土壤孔隙引起地表结皮,严重影响土壤人渗,掩盖了土壤含水率对入渗性能的影响;因此,在双环人渗初始阶段,地表结皮状况对入渗的影响大于含水率变化对初始入渗的影响,尤其是对于含水率较低的干燥土壤(2.60%),地表快速湿润时更容易形成结皮.所以,用双环入渗法测得的土壤初始入渗率随着初始含水率的降低而降低.对于初始含水率较高的土壤(10.4%与19.5%),地表结皮敏感度降低,初始入渗率之间的差异逐渐缩小.当地表结皮程度相对稳定后,水力梯度逐渐成为影响人渗的主导因素,初始含水率较低的土壤水力梯度越大,有利于增加土壤入渗,双环入渗法测量的稳定入渗率随着含水率降低而增加.2.3土壤累积入渗量比较图5～7比较了双环入渗法和径流一人流一出流法不同试验状况下的累积人渗量.径流一人流一出流法的累积入渗量均大于双环法的累积入渗量,特别是较小降雨强度20mm/h时,径流一人流一出流法累积入渗量约为同时段双环累积入渗量的2～4倍.可能的原因是,双环入渗法和径流一入流一出流法测量过程中不同的湿润速度,引起地表不同程度的结皮直接影响土壤入渗.双环人渗法在测量开始时,快速湿润会引起严重的地表结皮,而径流一人流一出流法对地表土壤颗粒而言,降雨首先起到了预湿润的作用,而随后的径流逐步湿润;因此,湿润速度与双环人渗相比较慢,并且土壤孔隙通道中空气随着降雨持续而逐渐被排出,不会瞬间被压缩形成气泡直至破裂,从而破坏土壤结构.第2期刘汗等:土壤初始含水率和降雨强度对黏黄土入渗性能的影响5 300I200&lt;鼬{5100●2.6O%,40mm/h◆lO-4%,40mrn/h▲19.5%40mm/ho2.60%,双环人渗法◇10.4%,双环人渗法△19.5%,双环入渗法象22宝0_20.40.6081.0时间/h图6降雨强度40mm/h累积入渗与双环法累积入渗量比较Fig.6Comparisonofcumulativeinfiltrationunder40mm/h withdoubleringmethod300目200&lt;100●2.6O%.60mm/h◆10.4%.60mm/h▲19.5%.60mm/hO2.60%,双环入渗法o10.4%,双环人渗法△19.5%,双环人渗法罢是窘盒222宝2时f目/h图7降雨强度60mm/h累积入渗与双环累积人渗量比较Fig.7Comparisonofcumulativeinfiltrationunder60mm/h withdoubleringmethod线性增加.可能的原因是,由于降雨强度较小,影响入渗的主导因素为水力梯度,累积入渗量随着土壤含水率的增加而逐渐降低_1.对于40mm/h(图6)和60mm/h(图7)较大降雨强度时,降雨动能增加的同时地表湿润速度加快,由此引起的地表结皮会显着降低土壤人渗性能,而随着降雨强度递增,地表结皮程度达到相对稳定状态;因此,随着降雨强度的增加,含水率对累积人渗量的影响逐渐变小.图5～7不同降雨强度累积人渗量比较表明,20mm/h降雨强度累积入渗量远大于40和60mm/h降雨强度,主要原因是降雨强度增加,雨滴对地表打击夯实能力增强,使得地表结皮状况更严重,产流转化率迅速提高,土壤人渗性能降低.尽管20mm/h降雨强度相比40和60mm/h更小,相同时间内降雨量更少,但径流一人流一出流法中降雨产流面的上方来水,能够满足20mm/h降雨强度下为充分供水人渗,表现土壤的真实人渗性能.不同含水率状况下,双环人渗法测量累积人渗量曲线均非常接近(图5),可能的原因是双环人渗法测量开始向内外环注水时,快速一致的湿润速度决定了地表结皮状况的相似性,进一步决定土壤累积入渗曲线的相似性.当试验后期水力梯度逐渐对入渗起主导作用时,双环法测量累积入渗量结果表明,随着土壤含水率的增加而减少.2.4土壤入渗计算模型回归比较传统入渗计算模型对不同测量方法试验结果回归分析(表3)表明,径流一人流～出流法测量数据的回归计算结果均显着优于双环入渗法测量数据的回归计算结果,一定程度上说明了径流一人流一出流法测量不同含水率对土壤入渗性能影响的合理性,均能够很好的满足经典入渗理论模型描述土壤入渗性能变化过程.其中,径流一人流一出流法测量结果入渗模型回归决定系数R为0.940.99.而对于双环入渗法测量结果,Horton入渗模型回归分析结果是最好的,回归决定系数为0.97—0.99,明显优于A.N.K0stiakov['](0.86&lt;R&lt;0.93)和J.R.Philip_l副(0.76&lt;R&lt;0.84)入渗模型回归计算结果, 这与M.K.Shukla等_19¨的研究结果是一致的.3结论与讨论1)径流一人流一出流法测量结果表明,土壤人渗性能随着降雨强度的增加而降低,随着含水率的增加而降低,而且随着降雨强度的增加,含水率变化对土壤人渗性能的影响逐渐降低.双环入渗法测量结果表明,初始人渗率随着土壤含水率增加而增加,稳定人渗率随着土壤含水率的增加而减小;主要原因是双环人渗仪测量初期地表结皮是影响初始入渗的主要因素,之后含水率变化引起的水力梯度才逐渐成为影响人渗的主要因素.解文艳等_20_通过双环入渗仪野外实验研究土壤含水量对土壤人渗能力的影响也得出相似的结论.2)径流一人流一出流法测量的稳定入渗率大于双环人渗法,20mm/h较小降雨强度时约为双环测量数值的2～4倍,而随着降雨强度的增大,稳定人渗率之间的差别逐渐缩小.3)通过Kostiakov,Horton和Philip入渗计算模型回归拟合,径流一人流一出流法测量结果回归分析优于双环入渗法测量结果,Horton入渗模型回归决定系数优于其他人渗模型.由于该研究在室内条件下进行实验比较,进一步可以考虑更为广泛的野外应用研究,为水文水资源,灌溉管理及土壤侵蚀等相关学科提供参考.6中国水土保持科学2009年4参考文献[1]HiHelD.CrustFormationinLassiessoils.InternationalSoil Science,1960,29(5):330-337[2]BodmanGB,ColmanEA.MoistureandEnergyCondition DuringDownwardEntryofWaterintosoil.SoilScience SocietyofAmericaJournal,1994,8(2):166—182[3]EigleJD,MooreID.Effectofrainfallenergyoninfiltration intoabaresoil.JRANS.OfASAE,1983,26(6):189—199 [4]RubinJ.Theoryofrainfalluptakebysoilinitiallydriverthan theirfieldcapacityanditsapplications.WaterResource Research,1966,2(4):739-749[5]AkenAO,YenBC.Effectofrmnfallintensitynoinfiltration andsurfacerunoffrates.JournalofHydraulicResearch, 1984,21(2):324—331[6]王玉宽.黄土高原坡地降雨产流过程的试验分析.水土保持,1991,5(2):25-29[7]李毅,邵明安.雨强对黄土坡面土壤水分人渗及再分布的影响.应用生态,2006,17(12):2271-2276[8]BouwerH.Intakerate:Cylinderinfiltrometer∥KluteA. Methodsofsoilanalysis.Part1.2nded.AgronMonogNo.9.MadisonWI:ASAandSSSA,1986:825—843[9]袁建平,蒋定生,文妙霞.坡地土壤降雨入渗试验装置研究.水土保持通报,1999,19(1):24—27[10]LeiTW,"uH,PanYH,eta1.Runoff-on—outMethod andModelsforSoilInfiltrabilityonHill—slopeunderRainfall Conditions.ScienceinChinaSeriesD,2006,49(2):193—201[11]WischmeierWH,Smi山DD.Predictingrainfallerosion DAAgriculturalResearchServiceHandbook,1978:537l12』BrownLC,FosterGR.Stromerosivityusingidealized intensitydistributions.TransactionsoftheAmericanSocietyof AgriculturalEngineers,1987,30(2):379—386l13JJayawardenaAW,RezaurRB.Dropsizedistributionand kineticenergyloadofrainstormsinHongKong.Hydrological Processes,20O0,14(6):1069—1082l14JVanDijkAM,Rainfallintensity—kineticenergyrelationships: acriticalliteratureappraisa1.JournalofHydrology,2002,261(1.4):卜23[15]江忠善,宋文径,李秀英.黄土地区天然降雨雨滴特性研究.中国水土保持,1983(3):32-36[16]陈洪松,邵明安,王克林.初始含水率对坡面降雨入渗及土壤水分再分布的影响.农业工程,2006,22(1):44-47[17jKostiakovAN.Onthedynamicsofthecoefficientofwater- percolationinsoilsandonthenecessityforstudyingitfroma dynamicpointofviewforpurposesofamelioration. TransactionsofSixthCongressofInter-nationalSocietyofSoil Science,Moscow,Russian,1932:17—21[18]PhilipJR.Thetheoryofinfil~ation:1.Theinfiltrationequationanditssolution.SoilScience,1957,83(5):345—357[19]ShuklaMK,R.UnkeferPE.Experimentalevaluationof infiltrationmodelsfordifferentlanduseandsoilmanagement systems.SoilScience,2003,168(3):178—191[2O]解文艳,樊贵盛.土壤含水量对土壤入渗能力的影响. 太原理工大学,2004,35(3):272—275(责任编辑:程云)。

坡面降雨入渗产流规律的数值模拟研究摘要：本文采用运动波理论和两次改进后的Green-Ampt入渗模型建立了坡面降雨入渗产流的动力学模型，并得到了实验资料的良好验证。

运用该模型研究了简单坡面上降雨入渗产流的动力学规律，分析了雨强、土壤初始含水量、渗透系数、坡面阻力，以及坡长、坡度等因素对坡面产流过程的影响规律，得出了一些有益的结论。

关键词：入渗产流坡面动力学1 概述雨水降落在坡面上将产生雨水的聚集并形成坡面水流。

坡面水流是土壤水蚀过程的主要动力，搞清产流的动力学特点是进一步研究侵蚀过程规律的基础。

坡面水流不同于一般明渠流动，其水深极浅(一般只有几毫米)，沿程不断有质量源和动量源加入，使其随时间和空间有较大的变化。

且坡面流的坡度较一般河渠陡得多，边界条件也更为复杂。

这些特点使得对坡面水流的研究有相当的难度。

坡面产流研究已有很长历史，但对它的数学求解还只有三十多年。

60年代后期Woolhiser和Ligget(1967)将运动波模型引入坡面水流研究，大大简化了计算工作，促进了研究的发展。

运动波模型是从一维圣维南方程简化而来，其基本假设是水流的能坡和底坡相等，并借助Chezy阻力公式得到流量和水深的关系。

Woolhiser和Ligget的研究结果表明在运动波波数k>10时，运动波模型可以很好地描述坡面水流运动。

而实际坡面流的运动波波数一般远大于10(沈冰等，1996)。

因此，运动波近似是一种较好的数学描述方式。

其后，又有对运动波理论的修正(Ponce,1978,Govindaraju,1988)，保留了水深的沿程变化项，相当于压力梯度，被称为扩散波模型。

该模型扩展了适用的参数范围，但并无实质性改进，因此实际应用仍以运动波为主。

也有使用完整圣维南方程求解实际问题的(戚隆溪，1997)。

土壤入渗过程的研究也有很长历史，从1911年提出概念明确形式简单的Green-Ampt积水入渗模型开始，相继有Horton(1940),Philip(1957)等模型出现，但G-A模型仍以其简单的形式，明晰的物理概念，良好的扩展性和可信的应用效果受到广泛重视，特别是经过Mein & Larson(1973)和Chu(1978)的两次改进，使其可应用于不均匀降雨的入渗计算，更使它成为最有效和应用最广泛的模型。

边坡在降雨作用下易发生滑坡，目前大量的学者对降雨作用下的边坡饱和一非饱土渗流及强度进行了较深入的分析研究。

现有的研究多将降雨入渗面作为同一土层进行了分析研究，对入渗面为不同土层进行分析研究的较少。

本文以半填方半挖方挡土墙作为研究对象，通过有限元法分析了降雨作用下挡土墙后回填土体、原状土体的雨水下渗的饱和一非饱和渗流状态，研究了该挡土墙在不同降雨持时，挡土墙的整体稳定性，为挡土墙的设计提供必要的参考。

1、降雨入渗模型1.1 降雨入渗挡土墙模型降雨入渗过程一般受降雨强度q.地面以上水层厚度、土层表面的含水率、土层饱和渗透系数KW有关，当降雨持续时间较长时，土层的入渗强度近似等于土层饱和渗透系数。

本文中挡土墙形式及渗流模型如图1所示。

降雨量假设原状土饱和渗透系数为KW 一回填土饱和渗透系数为Kwz, 挡土墙渗透系数为KW3。

此处回填土考虑采取砂质回填土，渗透 性大于原状土，考虑到一般挡土墙泄水孔质量较差，假设其渗透 性系数大于原状土，故有：Kw2>Kw ∖>Kw3.假设原状土体宽Ll , 回填土体宽L 2o 挡土墙后降雨入渗的过程分为如下过程及行为。

(1 )当4<Kw ∣,此时地表径流不会发生，降雨将全部入渗， 此时地表入渗强度i = q.(2 )当KQq> K~回填土部分的降水全部下渗，但原状 土部分降雨发生径流，径流将全部径流至回填土区，此时，原状 土入渗强度为：iι = Kw2 ；回填土入渗强度为/2 = (/+ ( q-Kw ∖ ) L ∖∕Lι 和i 2 = K w 2中的大值0(3 )当q>Kw2 ,由于降雨强度大于土壤的入渗率，故部分降 雨并不入渗，形成地表径流，原状土入渗强度为Zi = ∕C w ι /回填土 入渗强度为Z2 = ∕C W 2O1.2 饱和一非饱和渗流的控制方程及定解条件饱和一非饱和渗流的控制方程表示为：式中：Kw 为渗透系数(cm/s ) ； 〃W 为水的密度；m?w 为土水特征曲线斜率的绝对值；人为总水头；〃W 为压力水头(非饱和区 为负值，饱和区为正值)，/2 = /?w+ Z o(1 )初始条件：ah 、 a 「一)+『(&, ∂x ∂y c)h(1)(2 )边界条件。

降雨条件下土质边坡稳定性分析发布时间：2021-07-07T07:24:16.032Z 来源：《防护工程》2021年7期作者：王秋其[导读] 我国滑坡灾害相当严重，降雨更会导致土质边坡力学性能下降，稳定性降低，诱发滑坡。

因此研究降雨条件下的土质边坡失稳具有重要意义。

本文先介绍降雨入渗与渗流理论以期明确土体内部渗流规律，并根据非饱和土体强度理论确定边坡最危险滑弧。

并阐述现今用于土质边坡稳定性分析的多种方法，最后总结降雨条件下土质边坡稳定性分析过程，及其发展方向。

王秋其重庆交通大学河海学院重庆 400041摘要：我国滑坡灾害相当严重，降雨更会导致土质边坡力学性能下降，稳定性降低，诱发滑坡。

因此研究降雨条件下的土质边坡失稳具有重要意义。

本文先介绍降雨入渗与渗流理论以期明确土体内部渗流规律，并根据非饱和土体强度理论确定边坡最危险滑弧。

并阐述现今用于土质边坡稳定性分析的多种方法，最后总结降雨条件下土质边坡稳定性分析过程，及其发展方向。

关键词：土质边坡；稳定性分析；降雨；渗流中国是世界上滑坡灾害最严重的地区之一，而 95%以上的滑坡均与降雨或地下水渗流有密切关系[1]。

国内外学者采用了许多方法对雨水入渗后的土坡稳定性作了详细的探讨。

1降雨对边坡稳定的影响降雨会带来大量的地下水体渗流，而渗流会导致边坡稳定性的下降，具体表现在物理力学和物理化学两个方面，前者表现在地下水压力使有效正应力减小,后者表现在降雨带来的软化使岩土的粘结力和摩擦力减小。

具体来说，有以下方面。

降雨使得地下水产生与边坡压应力方向相反的水压力,使边坡有效压应力减小,边坡稳定性减弱。

坡顶或破面上的张裂缝充水后,还会增大滑动力。

降雨带来地下水,使边坡滑动面之间的摩擦系数、粘结力减小。

降雨加强地下水的渗流引起对地表土和裂隙充填物的侵蚀,这种侵蚀不仅会降低边坡稳定性,而且还会淤塞排水系统。

2 饱和土体的渗流降雨条件下的水体渗流与边坡失稳有很大的相关性，因为渗流运动与土质边坡稳定性分析时考虑的孔隙水压力息息相关。