初中数学动点最值问题解法探析

专题01 动点问题中的最值、最短路径问题动点问题是初中数学阶段的难点，它贯穿于整个初中数学，自数轴起始，至几何图形的存在性、几何图形的长度及面积的最值，函数的综合类题目，无不包含其中.其中尤以几何图形的长度及面积的最值、最短路径问题的求解最为繁琐且灵活多变，而其中又有一些技巧性很强的数学思想（转化思想），本专题以几个基本的知识点为经，以历年来中考真题为纬，由浅入深探讨此类题目的求解技巧及方法.一、基础知识点综述1. 两点之间，线段最短；2. 垂线段最短；3. 若A 、B 是平面直角坐标系两定点，P 是某直线上一动点，当P 、A 、B 在一条直线上时，PA PB 最大，最大值为线段AB 的长（如下图所示）；（1）单动点模型作图方法：作已知点关于动点所在直线的对称点，连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示，P 是x 轴上一动点，求PA +PB 的最小值的作图.（2）双动点模型P是∠AOB一点，M、N分别是边OA、OB上动点，求作△PMN周长最小值.作图方法：作已知点P关于动点所在直线OA、OB的对称点P’、P’’，连接P’P’’与动点所在直线的交点M、N即为所求.OBPP'P''MN5. 二次函数的最大（小）值()2y a x h k=-+，当a>0时，y有最小值k；当a<0时，y有最大值k.二、主要思想方法利用勾股定理、三角函数、相似性质等转化为以上基本图形解答. （详见精品例题解析）三、精品例题解析例1. （2019·凉山州）如图，正方形ABCD中，AB=12，AE=3，点P在BC上运动（不与B、C重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为例2.（2019·凉山州）如图，已知A、B两点的坐标分别为（8,0），（0,8）. 点C、F分别是直线x=－5和x轴上的动点，CF=10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取最小值时，tan∠BAD=（）x y A B C F D EO x=-5A .817B . 717C . 49D . 59例3.（2019·）如图，矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动，顶点B 在x 轴的正半轴及原点上滑动，点E 为AB 的中点，AB =24,BC =5,给出结论：①点A 从点O 出发，到点B 运动至点O 为止，点E 经过的路径长为12π；②△OAB 的面积的最大值为144；③当OD 最大时，点D 的坐标为)2626125,262625(，其中正确的结论是（填写序号）.例4.（2019·XX ）已知抛物线2y x bx c =-+（b 、c 为常数，b >0）经过点A (－1,0)，点M (m ,0)是x 轴正半轴上的动点，若点Q （1,2Q b y +22AM QM +332时，求b 的值.例5. （2019·）如图，一副含30°和45°角的三角板ABC 和EDF 拼合在个平面上，边AC 与EF 重合，12AC cm ．当点E 从点A 出发沿AC 方向滑动时，点F 同时从点C 出发沿射线BC 方向滑动．当点E 从点A 滑动到点C 时，点D 运动的路径长为cm ；连接BD ，则△ABD 的面积最大值为2cm ．例6. （2019·）如图，在菱形ABCD 中，连接BD 、AC 交于点O ，过点O 作OH ⊥BC 于点H ，以O 为圆心，OH 为半径的半圆交AC 于点M .（1）求证：DC 是圆O 的切线；（2）若AC =4MC ，且AC =8，求图中阴影部分面积；（3）在（2）的前提下，P 是线段BD 上的一动点，当PD 为何值时，PH +PM 的值最小，并求出最小值. ABC DH O M N专题01 动点问题中的最值、最短路径问题（解析）例1. （2019·凉山州）如图，正方形ABCD中，AB=12，AE=3，点P在BC上运动（不与B、C重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为【答案】4.【解析】解：∵PQ⊥EP，∴∠EPQ=90°，即∠EPB+∠QPC=90°，∵四边形ABCD是正方形，∴∠B=∠C=90°，∠EPB+∠BEP=90°，∴∠BEP=∠QPC，∴△BEP∽△CPQ，∴BE BP CP CQ=，∵AB=12，AE=3，∴BE=9，设CQ=y，BP=x，CP=12－x，（0<x<12）∴912xx y=-，即()()21216499x xy x-==--+，∴当x=6时，y有最大值为4，即CQ的最大值为4.【点睛】此题为“一线三直角模型”，解题方法为相似三角形性质求解，综合利用二次函数的性质求解最值问题.例2.（2019·）如图，已知A、B两点的坐标分别为（8,0），（0,8）. 点C、F分别是直线x=－5和x轴上的动点，CF=10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取最小值时，tan∠BAD=（）A . 817B . 717C . 49D . 59【答案】B .【解析】解：S △ABE =142BE OA BE ⨯⨯=,当BE 取最小值时，△ABE 面积为最小值.设x =－5与x 轴交于点G ，连接DG ，因为D 为CF 中点，△CFG 为直角三角形，所以DG =152CD =,∴D 点的运动轨迹为以G 为圆心，以5半径的圆上，如图所示 xyABD E O x=-5G由图可知：当AD 与圆G 相切时，BE 的长度最小，如下图，xyABD E O x=-5G H过点E 作EH ⊥AB 于H ，∵OG =5，OA =8，DG =5，在Rt △ADG 中，由勾股定理得：AD =12，△AOE ∽△ADG ， ∴AO AD OE DG =, 求得：OE =103， 由OB =OA=8，得：BE =143，∠B =45°，AB =82 ∴EH =BH =27223BE =,AH =AB -BH =1723， ∴tan ∠BAD =727317172EH AH ==, 故答案为B .【点睛】此题解题的关键是找到△ABE 面积最小时即是AD 与D 的远动轨迹圆相切的时刻. 进而构造以∠BAD 为角的直角三角形，利用勾股定理求出边长，代入三角函数定义求解.例3.（2019·）如图，矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动，顶点B 在x 轴的正半轴及原点上滑动，点E 为AB 的中点，AB =24,BC =5,给出结论：①点A 从点O 出发，到点B 运动至点O 为止，点E 经过的路径长为12π；②△OAB 的面积的最大值为144；③当OD 最大时，点D 的坐标为)2626125,262625(，其中正确的结论是（填写序号）.【答案】②③.【解析】解：根据题意可知：OE =12AB =12,即E 的轨迹为以O 为圆心以12为半径的四分之一圆（第一象限的部分），根据弧长公式，得点E 的路径长为：9012180π⨯⨯=6π，故①错误； 因为AB =24,当斜边AB 上的高取最大值时，△OAB 的面积取最大值，点O 在以AB 为直径的圆上（圆心为E ），当OE ⊥AB 时，斜边AB 上的高最大， 所以△OAB 的面积取最大值为：124122⨯⨯=144，故②正确；连接OE 、DE ，得：OD ≤OE +DE ，当O 、E 、D 三点共线时取等号，即OD 的最大值为25，如图，过点D 作DF ⊥y 轴于F ，过点E 作EG ⊥y 轴于G ,25DF OD 即：1225EG DF =，512AF AD EG AE ==, 即：51125AF EG DF ==,设DF =x ，在Rt △ADF 中，由勾股定理得：221255x x ⎛⎫+= ⎪⎝⎭，解得：x =26，在Rt △ODF 中，由勾股定理得：OF =26，即点D 的坐标为)2626125,262625(，故③正确.综上所述，答案为：②③. 例4.（2019·XX ）已知抛物线2y x bx c =-+（b 、c 为常数，b >0）经过点A (－1,0)，点M (m ,0)是x 轴正半轴上的动点.若点Q （1,2Q b y +）在抛物线上，当22AM QM +的最小值为3324时，求b 的值. 【答案】见解析. 【解析】解：∵2y x bx c =-+经过点A (－1,0)，∴1+b +c =0，即21y x bx b =--- ∵点Q （1,2Q b y +）在抛物线2y x bx c =-+上， ∴324Q b y =--， 即13,224b Q b ⎛⎫+-- ⎪⎝⎭， ∵b >0，∴Q 点在第四象限，2222AM QM AM QM ⎛⎫+=+ ⎪⎝⎭所以只要构造出22AM QM ⎛⎫+ ⎪⎝⎭即可得到22AM QM +的最小值取N （1,0），连接AN ，过M 作MG ⊥AN 于G ，连接QM ，如图所示，△AGM 为等腰直角三角形，GM =22AM ，即当G 、M 、Q 三点共线时，GM +MQ 22QM +取最小值， 此时△MQH 为等腰直角三角形，∴QM=2QH=3224b⎛⎫+⎪⎝⎭，GM=22AM=()212m+∴()223332222=21222244bAM QM AM QM m⎛⎫⎡⎤⎛⎫+=++++=⎪⎢⎥⎪⎝⎭⎝⎭⎣⎦①∵QH=MH，∴324b+=12b m+-，解得：m=124b-②联立①②得：m=74，b=4.即当22AM QM+的最小值为3324时，b=4.【点睛】此题需要利用等腰直角三角形将22AM QM+转化为222AM QM⎛⎫+⎪⎝⎭，进而根据两点之间线段最短及等腰三角形性质求解.例5. （2019·）如图，一副含30°和45°角的三角板ABC和EDF拼合在个平面上，边AC与EF重合，12AC cm=．当点E从点A出发沿AC方向滑动时，点F同时从点C出发沿射线BC方向滑动．当点E从点A滑动到点C时，点D运动的路径长为cm；连接BD，则△ABD的面积最大值为2cm．【答案】24-1223623126；【解析】解：如图1所示，当E运动至E’，F滑动到F’时，DD'E'G图1过D ’作D ’G ⊥AC 于G ，D ’H ⊥BC 交BC 延长线于点H ，可得∠E ’D ’G =∠F ’D ’H ，D ’E ’=D ’F ’，∴Rt △E ’D ’G ≌Rt △F ’D ’H ，∴D ’G =G ’H ,∴D ’在∠ACH 的角平分线上，即C ，D ，D ’三点共线.通过分析可知，当D ’E ’⊥AC 时，DD ’的长度最大，随后返回初始D 点，如图2所示，D 点的运动路径为D →D ’→D ，行走路线长度为2DD ’；BD'图2∵∠BAC =30°，AC =12，DE =CD∴BC =CD =DE=由图知：四边形E ’CF ’D ’为正方形，CD ’=EF =12，∴DD ’=CD ’-CD =12-D 点运动路程为2DD ’=24-D'图3如图3所示，当点D 运动至D ’时，△ABD ’的面积最大，最大面积为：'''''''ABC AE D BD F E CF D S S S S ++-△△△正方形=(((211112222⨯+⨯--⨯+⨯=【点睛】准确利用全等、角平分线判定得到D 点的运动轨迹是关键，利用三角函数及勾股定理求解，计算较为繁琐，尤其是利用割补法求解三角形的面积时对学生计算能力要求较高，此题难度较大，新颖不失难度.例6. （2019·）如图，在菱形ABCD 中，连接BD 、AC 交于点O ，过点O 作OH ⊥BC 于点H ，以O 为圆心，OH 为半径的半圆交AC 于点M .（1）求证：DC 是圆O 的切线；（2）若AC =4MC ，且AC =8，求图中阴影部分面积；（3）在（2）的前提下，P 是线段BD 上的一动点，当PD 为何值时，PH +PM 的值最小，并求出最小值.BD【答案】见解析.【解析】（1）证明：过点O 作ON ⊥CD 于N ， AC 是菱形ABCD 的对角线，∴AC 平分∠BCD ，∵OH ⊥BC ，ON ⊥CD ，∴OH =ON ，又OH 为圆O 的半径，∴ON 为圆O 的半径，即CD 是圆O 的切线.（2）由题意知：OC =2MC =4，MC =OM =2，即OH =2，在Rt △OHC 中，OC =2OH ，可得：∠OCH =30°，∠COH =60°，由勾股定理得：CH==23OCH OMHS S S π-=-△阴影扇形（3）作点M 关于直线BD 的对称点M ’，连接M ’H 交BD 于点P ， 可知：PM =PM ’即PH +PM =PH +PM ’=HM ’，由两点之间线段最短，知此时PH +PM 最小， ∵OM ’=OM =OH ，∠MOH =60°，∴∠MM ’H =30°=∠HCM ，∴HM ’=HC=即PH +PM的最小值为在Rt △M ’PO 及Rt △COD 中，OP =OM ’ tan 30°=3，OD =OCtan 30°=3， 即PD =OP +OD=B D。

动点与最值问题解题技巧
1. 确定问题类型：动点与最值问题是指在一定条件下，寻找某个动点的位置或数值达到最大或最小值的问题。

可以通过数学建模、图形分析、函数求导等方法解决。

2. 建立数学模型：根据问题的描述，将问题抽象为一个数学模型。

常见的方法包括建立函数关系式、约束条件和目标函数等。

3. 分析特殊情况：在解题过程中，可以通过分析极端情况或特殊情况来确定动点的位置或数值的最值。

这可以帮助我们更好地理解问题，并推导出一般情况下的解答方法。

4. 使用图形分析：如果问题涉及到几何图形，可以通过绘制图形来分析问题。

通过观察图形的形状、相交关系、对称性等特点，可以得出一些有用的信息，帮助解决动点与最值问题。

5. 求解最值：根据问题的具体要求，可以使用函数求导、代数方法、几何方法等多种方法求解最值问题。

通过求导可以找到函数的极值点，通过代数方法可以消去变量，通过几何方法可以利用几何性质得出最值。

6. 检查答案：在得到最值之后，需要对答案进行检查。

检查的方法可以是代入原问题进行验证，或者在图形上进行观察，是否符合题目的条件。

7. 总结归纳：在解决动点与最值问题时，可以总结出一些经验
和规律，并将其归纳为一般的解题技巧。

这样可以帮助我们更快地解答类似的问题，并提高解题的效率。

动点最值问题永远都是中考最难的压轴类题目，很多同学都反应不知道该怎么下手寻找思路。

其实这类题目的题型有限，全部总结归纳就是这19种，希望同学们对每一种都能掌握技巧，再遇见类似的就能及时找到思路。

PS：可下载电子版打印高清版本，链接文末获取！
1、将军饮马模型（对称点模型）
2、利用三角形两边差求最值
3、手拉手全等取最值
4、手拉手相似取最值
5、平移构造平行四边形求最小
6、两点对称勺子型连接两端求最小
7、两点对称折线连两端求最小
8、时钟模型，中点两定边求最小值
9、时钟模型，相似两定边求最小值
10、转化构造两定边求最值
11、面积转化法求最值
12、相似转化法求最值
13、相似系数化一法求最值
14、三角函数化一求最值
15、轨迹最值
16、三动点的垂直三角形
17、旋转最值
18、隐圆最值-定角动弦
19、隐圆最值-动角定弦。

动点最值题精讲动点最值问题是数学中一个非常重要的问题，它表示了在动态变化中，某个参数随时间而变化时可能取到的最大或最小值。

在这个过程中，我们需要找到这个参数随时间变化的规律，并且计算出这个参数的最大最小值，这需要我们掌握动点最值问题的方法和技巧。

在本文中，我们将更深入地探讨这个问题，并提供几个常见的例子和解决方案。

1. 动点最值问题的基本原理动点最值问题在数学中的表现形式是，一个点 P 在过程中不断变化，变化规律可以表示为：X=f(t), Y=g(t)。

其中 X，Y 分别表示点 P 的横坐标和纵坐标，t 表示时间。

我们需要确定 t 的范围，然后求出 X 和 Y 的最小值和最大值。

解决这个问题的基本方法是通过求导数，在函数的关键点处判断函数的值。

由于我们要求的是最大最小值，所以我们需要找到 f(t) 和 g(t) 的导数。

求导可能比较复杂，但是十分必要。

我们将在下文中讨论如何求解动点最值问题的各个方面。

2. 解决动点最值问题的技巧我们将解决动点最值问题分为以下几个步骤。

第一步，使用物理学的方法。

从物理学（运动学）的角度分析问题，求出变化过程中的速度和加速度等参数。

这种方法适用于解决一个物体在直线或平面上运动的问题。

我们可以将问题抽象为一个物理学问题，然后使用速度和加速度的公式来解决问题。

第二步，使用数学方法。

这是更为常见的方法，也是本文的核心部分。

在这种情况下，我们需要找到一个函数来表示参数的变化过程，然后对该函数求导，找到关键点，最终确定最大最小值。

第三步，使用计算机方法。

现代计算机很擅长解决动点最值问题，因为它们能够计算复杂的函数和大量的数据。

我们可以使用计算机做出模拟，然后找到最大或最小点。

这种方法往往需要程序员或科学家具备一定的计算机技能。

第四步，使用统计学方法。

在某些情况下，使用统计学方法可能更好。

例如，当我们面对大量数据时，我们可以用统计方法来确定数据变化的趋势。

在这种情况下，我们可能使用回归方法或其他统计学方法来找到变化过程的规律，最终决定最大最小值。

A动点问题最值最值问题有四种情形：定点到动点的最值，动点在圆上或直线上，就是点到圆的最近距离，和点到直线的最近距离；三角形两边之和大于第三边的问题，当两边成一直线最大；几条线段之和构成一条线段最小；还有就是对称点最小问题。

一、定点到动点所在圆的最大或最小值，动点在一个定圆上运动，其实质是圆外一点到圆的最大或最小距离，就是定点与圆心所在直线与圆的交点的两个距离。

方法：证明动点在圆上或者去找不变的特殊三角形，证明两个三角形相似，求出某些边的值。

1．如图，△ABC 、△EFG 均是边长为2的等边三角形，点D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ．当△EFG 绕点D 旋转时，线段BM 长的最小值是〔〕 A ．32-B ．13+C ．2D ．13-提示：点M 在以AC 为直径的圆上2．〔2015•XX 〕如图，已知正方形ABCD 的边长为2，E 是边BC 上的动点，BF ⊥AE 交CD 于点F ，垂足为G ，连结CG ．下列说法：①AG ＞GE ；②AE =BF ；③点G 运动的路径长为π；④CG 的最小值为﹣1．其中正确的说法是②③．〔把你认为正确的说法的序号都填上〕提示：G 在以AB 为直径的圆上：正确答案是：②④3、如图，正方形ABCD 的边长为4cm,正方形AEFG 的边长为1cm ，如果正方形AEFG 绕点A旋转，那么C 、F 两点之间的最小距离为ABC4、如图，在边长为2的菱形ABCD中，∠A=60°,M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是5、如图，等腰直角△ACB，AC=BC=5，等腰直角△CDP，且PB=2，将△CDP绕C点旋转. 〔1〕求证：AD=PB〔2〕若∠CPB=135°，求BD；〔3〕∠PBC=时，BD∠PBC=时，BD有最小值，并画图说明.分析：在△ABD中有：BD≤AB+AD，当BD=AB+AD时BD最大，此时AB与AD在一条直线上，且AD在BA的延长线上，又△ACB是等腰直角三角形，∠CAB=45°，由〔1〕知∠PBC=∠CAD=180°-45°=135°BD≥AB-AD，当BD=AB-AD时BD最小，此时，AB与AD在一条直线上，且AD在线段AB上，此时∠CAD=45°，所以∠PBC=∠CAD=45°6、如图，△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°,∠BAE=135°,AD=1，，F为BE中点.〔1〕求CF的长〔2〕将△ADE绕A旋转一周，求点F运动的路径长；〔3〕△ADE绕点A旋转一周，求线段CF的X围.A BAACCAGDAGDA提示：本题根据中点构造三角形相似，△BOF∽△BAE,且12OF AE==7、如图，AB=4，O为AB中点，⊙O的半径为1，点P是⊙O上一动点，以点P为直角顶点的等腰△PBC〔点P，B，C按逆时针方向排列〕则线段AC的取值X提示：发现定等腰直角△AOC与等腰直角△OBE，从而得到相似。

动点最值问题19大模型+例题详解，彻底解决压轴难题动点最值问题永远都是中考最难的压轴类题目，很多同学都反应不知道该怎么下手寻找思路。

其实这类题目的题型有限，全部总结归纳就是这19种，希望同学们对每一种都能掌握技巧，再遇见类似的就能及时找到思路。

1、将军饮马模型（对称点模型）
2、利用三角形两边差求最值
3、手拉手全等取最值
4、手拉手相似取最值
5、平移构造平行四边形求最小
6、两点对称勺子型连接两端求最小
7、两点对称折线连两端求最小
8、时钟模型，中点两定边求最小值
9、时钟模型，相似两定边求最小值
10、转化构造两定边求最值
11、面积转化法求最值
12、相似转化法求最值
13、相似系数化一法求最值
14、三角函数化一求最值
15、轨迹最值
16、三动点的垂直三角形
17、旋转最值
18、隐圆最值-定角动弦
19、隐圆最值-动角定弦。

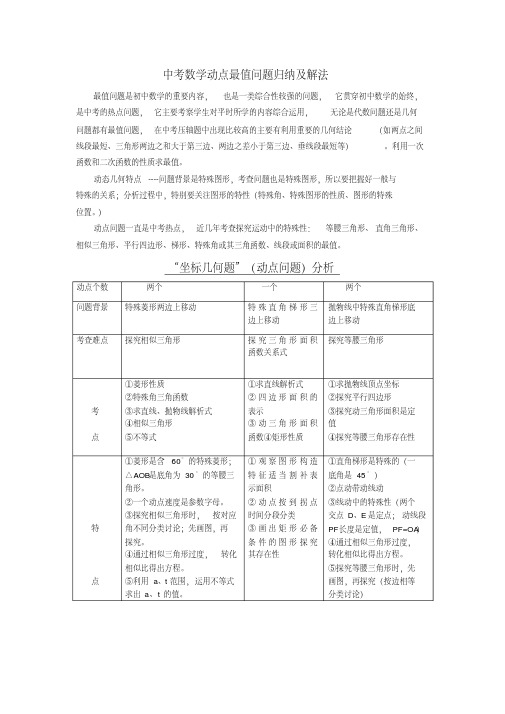
中考数学动点最值问题归纳及解法最值问题是初中数学的重要内容，也是一类综合性较强的问题，它贯穿初中数学的始终，是中考的热点问题，它主要考察学生对平时所学的内容综合运用，无论是代数问题还是几何问题都有最值问题，在中考压轴题中出现比较高的主要有利用重要的几何结论（如两点之间线段最短、三角形两边之和大于第三边、两边之差小于第三边、垂线段最短等）。

利用一次函数和二次函数的性质求最值。

动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

“坐标几何题”（动点问题）分析动点个数两个一个两个问题背景特殊菱形两边上移动特殊直角梯形三边上移动抛物线中特殊直角梯形底边上移动考查难点探究相似三角形探究三角形面积函数关系式探究等腰三角形考点①菱形性质②特殊角三角函数③求直线、抛物线解析式④相似三角形⑤不等式①求直线解析式②四边形面积的表示③动三角形面积函数④矩形性质①求抛物线顶点坐标②探究平行四边形③探究动三角形面积是定值④探究等腰三角形存在性特点①菱形是含60°的特殊菱形；△AOB是底角为30°的等腰三角形。

②一个动点速度是参数字母。

③探究相似三角形时，按对应角不同分类讨论；先画图，再探究。

④通过相似三角形过度，转化相似比得出方程。

⑤利用a、t范围，运用不等式求出a、t的值。

①观察图形构造特征适当割补表示面积②动点按到拐点时间分段分类③画出矩形必备条件的图形探究其存在性①直角梯形是特殊的（一底角是45°）②点动带动线动③线动中的特殊性（两个交点D、E是定点；动线段PF长度是定值，PF=OA）④通过相似三角形过度，转化相似比得出方程。

⑤探究等腰三角形时，先画图，再探究（按边相等分类讨论）近几年共同点：①特殊四边形为背景；②点动带线动得出动三角形；③探究动三角形问题（相似、等腰三角形、面积函数关系式）；④求直线、抛物线解析式；⑤探究存在性问题时，先画出图形，再根据图形性质探究答案。

动点问题求最小值的做法思路
1、化动为静：将动点问题转化为静态的几何问题，简化问题，使解题过程更加直观和易于操作。

这种方法适用于多种动点问题，包括但不限于求最值问题。

2、构造比例线段：在某些特定的动点问题中，通过构造比例线段来求解是最直接有效的方法。

这种方法在解决阿氏圆最值模型等题目时尤为常见。

3、利用轴对称性质：初中数学中，利用轴对称的性质可以实现“搬点移线”，从而求解几何图形中的最值问题。

这种方法依赖于基本定理，如两点之间线段最短、三角形任意两边之和大于第三边等。

4、寻找线段的“替身”或“等比替身”：在解决双动点线段问题时，找到一个与原线段长度相等或成比例的线段作为替代，是解题的关键。

这种方法有助于简化问题，找到解决问题的突破口。

5、分类讨论：当动点问题存在多种可能性时，需要进行分类讨论，以确保不遗漏任何可能的情况。

这种方法适用于那些情况复杂、可能存在多种解法的问题。

6、建立直角三角形模型：在某些情况下，通过建立直角三角形模型并利用其性质（如勾股定理）来求解是最有效的策略之一。

这种方法特别适用于涉及圆和直线的问题。

7、动态规划：虽然动态规划主要用于解决算法问题，但其思想也可以应用于某些特定的动点最值问题中。

通过定义状态、计算转移方程和确定终止条件，可以有效地求解这类问题。

动点与最值问题解题技巧【实用版4篇】篇1 目录1.动点与最值问题概述2.动点与最值问题的解题技巧3.动点与最值问题的应用篇1正文一、动点与最值问题概述动点与最值问题是数学中的一类常见问题，主要涉及到点在平面直角坐标系中的运动以及函数的最值求解。

这类问题通常需要结合几何知识、函数知识以及代数知识进行求解。

二、动点与最值问题的解题技巧1.理解问题：仔细阅读题目，理解问题的含义和限制条件，明确求解的目标。

2.建立模型：根据问题建立合适的数学模型，可以使用函数、方程、几何图形等方法。

3.求解模型：使用数学工具和方法求解模型，得到结果。

4.验证结果：验证所得结果是否符合问题要求，是否具有实际意义。

三、动点与最值问题的应用动点与最值问题在生活和工程中有着广泛的应用。

例如，在建筑设计、桥梁设计、道路设计等领域中，需要考虑动点的运动和最值问题，以保证设计的合理性和可行性。

篇2 目录1.动点与最值问题概述2.动点与最值问题的解题技巧3.动点与最值问题的应用篇2正文一、动点与最值问题概述动点与最值问题是数学中的常见问题，涉及到的知识点包括几何、函数、导数等。

这类问题具有综合性强、难度较大的特点，需要学生具备扎实的基础知识和灵活的解题技巧。

二、动点与最值问题的解题技巧1.理解问题本质：首先需要仔细阅读题目，理解问题的本质，确定动点的运动方式和约束条件。

2.建立数学模型：根据题目中的几何关系和函数关系，建立数学模型，使用几何或函数的方法描述问题。

3.寻找解题方法：根据具体问题选择合适的方法，如代数方法、几何方法、微积分方法等。

4.优化解题过程：在解题过程中，要善于利用各种技巧，如配方、拆项、代入数值等，使解题过程更加简洁。

三、动点与最值问题的应用动点与最值问题在日常生活和工程中都有广泛的应用，如建筑工程中的最短路径问题、交通规划中的最优路径问题等。

篇3 目录1.动点与最值问题的联系与区别2.动点问题的解题技巧3.最值问题的解题技巧篇3正文一、动点与最值问题的联系与区别动点问题与最值问题都是中学数学中常见的几何问题，它们在解题思路上有许多相似之处，但也有一些区别。

初中数学动点最值问题解法探析最值问题是初中数学中一个基本的概念，是用来求解某些特定的函数在连续的区间上的最大值或最小值的问题。

本文就初中数学动点最值问题解法进行探析。

一、初中数学动点最值问题涉及到的内容1、动点问题中涉及到的数学概念：动点最值问题是关于数学中的泰勒展开式、微分等概念的应用，它要求计算函数在给定范围内某一点处最大值或最小值。

2、动点问题中涉及到的方法：解动点问题时，要求用到微分求导、求极限、对函数的最值后进行判断等方法。

二、初中数学动点最值问题的解法1、根据设定的条件，计算函数的导数，再求函数的极限；2、将求极限的结果带入原函数，根据结果判断函数的最值，保存相应的数据（一般保存此处的极大值和极小值）；3、将原函数从一定的范围内，扩大或缩小至限定范围，重复上述操作；4、将所求出来在改变范围中找出的最大值和最小值整理到同一个表格中，最后判断函数最值的情况。

三、初中数学动点最值问题的解法案例以函数f(x) = x² + 3x - 4为例，求f(x)在区间[-2, 2]内的动点最值。

1、计算函数的导数：f'(x) = 2x + 3；2、求函数的极限：对f'(x)的极限进行计算，就可以求得函数f(x)的极限解；3、将求极限的结果带到原函数，得到函数f(x)在区间[-2, 2]内的最大值和最小值：f(-2) = -8，f(2) = 8；4、将得到的数据整理成表格：| f(x) | 区间 | 最值 ||:--------:|:------:|:----:|| f(-2) | [-2,2] | -8 || f(2) | [-2,2] | 8 |最后，可以得到函数f(x)在区间[-2, 2]内的最大值为f(2) = 8，最小值为f(-2) = -8。

综上所述，本文就初中数学动点最值问题解法的探析完成。

文中所述的解法，可以用来进行解答动点最值问题，让学生有办法针对动点最值问题给出算式解决方案，也能够去领会要解决动点最值问题之前要掌握的基础概念和技术，让学生在解决动点最值问题方面更有质的提高。

几何动点最值问题解题技巧1. 理解动点问题的本质同学们啊，几何动点最值问题呢，就像是一群调皮的小蚂蚁在图形里跑来跑去，我们要找到它们跑到哪里会让某个量最大或者最小。

比如说，有一个点在一条线段上动，那我们得想想这个点在什么位置的时候，它到另外一个点或者一条直线的距离是最长或者最短的呢。

这就像是我们在操场上玩捉迷藏，你要找到那个最隐蔽或者最容易被发现的角落一样。

像在三角形里，有个点在边上动，那这个点到三角形另外两个顶点的距离之和什么时候最小呢？这时候我们可能就会想到一些特殊的点，像三角形的费马点之类的。

再打个比方，假如有一个圆，圆上有个动点，那这个动点到圆外一个定点的距离，那肯定是这个动点在过定点和圆心的直线与圆的交点的时候，距离最大或者最小呀。

就好像你在一个圆形的池塘边跑步，池塘外有个小亭子，你跑到哪里离那个亭子最近或者最远呢，肯定是在特定的位置嘛。

2. 利用图形的性质对于三角形，我们都知道三角形两边之和大于第三边，两边之差小于第三边。

这在动点最值问题里可太有用了。

比如说，有个动点在三角形的一条边上，要找这个动点到另外两个顶点距离之差的最大值，那肯定是当这个动点在这条边的端点的时候，距离之差最大呀。

因为这时候就等于三角形另外两条边的差。

在四边形里呢，如果是平行四边形，对角线互相平分这个性质有时候就能帮我们解决动点问题。

假设平行四边形里有个动点，我们要找这个动点到四个顶点距离之和的最小值，我们就可以利用对角线的性质来转化问题。

对于圆来说，圆的切线性质也很关键。

如果有个动点是圆的切点，那它和圆心的连线就垂直于切线。

这时候要是涉及到求这个动点到圆外一点距离的最小值，我们就可以通过圆心到圆外点的距离减去圆的半径来得到。

3. 转化思想的运用很多时候啊，我们看到的动点最值问题的样子很复杂，就像一团乱麻。

这时候我们就要学会转化。

比如说，有个动点在一条曲线（不是圆）上，要找它到一个定点的距离的最值。

我们可能要通过建立坐标系，把这个曲线的方程写出来，然后把距离公式表示出来，这样就把几何问题转化成了代数问题。

动点最值问题解法探析一、问题原型：（人教版八年级上册第42页探究）如图1-1，要在燃气管道上修建一个泵站，分别向、两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？这个“确定最短路线”问题，是一个利用轴对称解决极值的经典问题。

解这类问题二、基本解法：对称共线法。

利用轴对称变换，将线路中各线段映射到同一直线上（线路长度不变），确定动点位置，计算线路最短长度。

三、一般结论：(在线段上时取等号)（如图1-2）线段和最小，常见有三种类型：（一）“|定动|+|定动|”型：两定点到一动点的距离和最小通过轴对称，将动点所在直线同侧的两个定点中的其中一个，映射到直线的另一侧，当动点在这个定点的对称点及另一定点的线段上时，由“两点之间线段最短”可知线段和的最小值，最小值为定点线段的长。

1.两个定点+一个动点。

如图1-3，作一定点关于动点所在直线的对称点，线段（是另一定点）与的交点即为距离和最小时动点位置，最小距离和。

例1（2006年河南省中考题）如图2，正方形的边长为，是的中点，是对角线上一动点，则的最小值是。

解析：与关于直线对称，连结，则。

连结,在中，，，则故的最小值为例2（2009年济南市中考题）如图3，已知：抛物线的对称轴为，与轴交于、两点，与轴交于点，其中，。

（1）求这条抛物线的函数表达式；（2）已知在对称轴上存在一点，使得的周长最小，请求出点的坐标。

解析：（1）对称轴为，，由对称性可知：。

根据、、三点坐标，利用待定系数法，可求得抛物线为：（2）与关于对称轴对称，连结，与对称轴交点即为所求点。

设直线解析式为：。

把、代入得，。

当时，，则2.两个定点+两个动点。

两动点，其中一个随另一个动（一个主动，一个从动），并且两动点间的距离保持不变。

用平移方法，可把两动点变成一个动点，转化为“两个定点和一个动点”类型来解。

例3如图4，河岸两侧有、两个村庄，为了村民出行方便，计划在河上修一座桥，桥修在何处才能两村村民来往路程最短？解析：设桥端两动点为、，那么点随点而动，等于河宽，且垂直于河岸。

探究动点背景下的线段最值问题【专题综述】图形运动问题是中考数学命题的热点题型，其中有一类动点背景下线段长度的最值问题，常常使学生感到比较为难.本文谈谈破解这类问题的方法. 动点背景下线段长度的最值问题一般有两种解法:1、代数解法.通过设未知量，建立函数关系或列方程列不等式等，用函数最值、二次方程判别式、解不等式来求解.2、几何方法.常通取特殊点，如线段中点、端点;与动点的特殊位置相关的特殊线段，如三角形的高、中线、圆的直径等;特殊图形，如直角三角形、等边三角形、矩形等，用几何公理、定理来求解. 一般而言，用几何方法抓住特殊情形处理，比代数方法更有独特魅力. 【方法解读】一、从动点所在特殊位置入手图形中动点的运动有一定的范围，其较为特殊的位置有:线段上动点的两端点、线段中点等;若点在线段外运动，则与某线段共线就是特殊位置.这些特殊位置正是产生最值的关键点.例1 如图1，在四边形ABCD 中，90A ∠=︒，33AB =，3AD =，点M ，N 分别为线段BC ，AB 上的动点(含端点，但点M 不与点B 重合)，点E ，F 分别为DM ，MN 的中点，则EF 长度的最大值为. 分析 DM ，MN 的长度随点M ，N 分别在线段BC ，AB 上运动而变化，点E ，F 分别为DM ，MN 的中点却保持不变.题设中EF 与不变量A ∠，AB ，AD 无直接数量关系，但连结DN ，则由三角形的中位线定理可知12EF DN =，如图1所示，从而可知DN 最大时，EF 最大.因为N 在线段AB 上，当点N 与其端点B 重合时DN 最大，如图2所示.此时，由勾股定理知6BD =，所以EF 长度的最大值为3.例2 如图3，在⊙O 中，直径6AB =，BC 是弦，30ABC ∠=︒，点P 是BC 上的一个动点，点Q 在⊙O 上，且OP PQ ⊥.求PQ 长的最大值.分析 点P 在BC 运动时，OP ，PQ 的位置和大小都变化，但OP PQ ⊥，圆的半径不变，连结OQ ，则OPQ ∆保持直角三角形不变.在Rt OPQ ∆中，22223PQ OQ OP OP =-=-,所以OP 最小时PQ 的长的最大.由垂径定理知，此时点P 正好是CB 的中点，如图4所示，Q 点与C 点重合.分析 连结OQ . ∵OP PQ ⊥，∴OPQ ∆为直角三角形. 又∵OP CB ⊥，132OB AB ==，30ABC ∠=︒， ∴32OP =由勾股定理，得223333()22PQ =-=即PQ 长的最大值332. 二、从动点产生的特殊线段入手在图形中，点的运动会引起相应线段位置和长度大小的变化，位置的变化会使线段成为具有某种特殊性质抓住这些线段变化的特殊性:如三角形的高、中线、圆的直径等，往往会找到最值的答案.例3 如图5，在直角ABC ∆中，90C ∠=︒，3AC =，4BC =，P 为AB 上(不与AB 重合)一动点，过点P 分别作PE AC ⊥于点E ，PF BC ⊥与F ，则EF 的最小值 .分析 因为点P 在AB 上运动时，PE AC ⊥于点E ，PF BC ⊥与F ，90C ∠=︒，所以四边形CFDE 是矩形，且这些关系不变.连结PC ，则EF CP =，要求EF 的最小值，就是求CP 的最小值.显然当CD AB ⊥，即CD 是斜边AB 的高时，CD 最小.又由勾股定理，得5AB =，根据三角形面积不变，得AC BC CD AB ⨯=⨯，解得125CP =，所以EF 的最小值为125. 例4 如图6，在圆O 上有定点C 和动点P 位于直径AB 的异侧，过点C 作CP 的垂线，与PB 的延长线交于点G .已知:圆O 半径为52，4tan 3ABC ∠=，则CG 的最大值是(). (A)5 (B)154(C)253(D)203分析 点P 在AB 上运动时，PC 的位置和大小会随之变化，但CAB CPG ∠=∠，90ACB PCG ∠=∠=︒保持不变，故有ABCPGC ∆∆，∴BC AC CG PC =，即BC CG PC AC=，由3tan 4AC ABC PC ∠==，知43CG PC =，当PC 最大时，CQ 取到最大值易知，当PC 经过圆心，即PC 为圆O 的直径时，PC 最大(此时CG 是圆O 的切线). ∵圆O 半径为52， ∴PC 的最大值为5,∴315544CG =⨯=. ∴CG 的最大值154，故选B.三、抓住动点问题的特性，从构造特殊图形入手某些动点问题中，难以找到图形变化时与相关线段最值的特殊情形若要用几何解法，应联系整个问题所含条件添加辅助线，构造特殊图形，然后借助特殊图形的性质将问题进行有效转化.例5 如图7，ABC ∆中，45B ∠=︒，60BAC ∠=︒，22AB =. D 是BC 上的一个动点以AD 为直径画圆与AB ，AC 相交于E ，F 两点，求EF 的最小值.分析 点D 在BC 上运动，AD 的位置改变引起圆O 的位置和大小变化，而所求EF 的 值与不变量B ∠，BAC ∠以及AB 的关系不明显.连结OE ，OF ，构造含120︒角的特殊等腰三角形，如图8所示，过O 点作OH EF ⊥垂足为H ，由圆周角定理可知1602EOH EOF BAC ∠=∠=∠=︒.在Rt EOH ∆中，由垂径定理可知23EF EH OE ==.所以当OE 最小时，EF 的值最小，而12OE AD =，由垂线段的性质可知，当AD 为ABC ∆的边BC 上的高时，直径AD 最短，此时线段EF 最小.在Rt ADB ∆中，45ABC ∠=︒，22AB =∴2AD BD ==，即此时圆的直径为2. 在Rt EOH ∆中，33sin 122EH OE EOH =∠=⨯= ∴23EF EH ==， 即EF 的最小值为3.四、从图形运动中相对保持不动的点入手若图形中的动点不止一个，这种情形相对单一动点问题要复杂一般会引起变化的量增加或整个图形发生运动，难以找到原图中保存不变的量，这时可着眼于图中的相对不变量.相对不变量是指在整个图形运动变化中，保持某种特性不变的量与动点下线段最值所对应的仍是图中特殊相对不变量透过图形运动的整体，抓住特殊相对不变量才是解题的关键.例6 如图9，在ABC ∆中，90ACB ∠=︒，3BC =，8AC =，点A ，C 分别在x 轴、y 轴的正半轴上.当点A 在x 轴上运动时，点C 随之在y 轴上运动，在运动中OB 的最大值是多少?分析 当点A 在x 轴上运动时，点C 随之在y 轴上运动，这样改变了ABC ∆的位置，点B 的位置也随之改变，OB 的长度随之发生变化.虽然BC 、AC 的长度不变，但些相对不变的量与OB 没有直接的关系. 仔细观察图9，AC 是Rt COA ∆的斜边，AC 长度不变，则点O 与其中点D 的连线段OD 的长度保持不变，这个隐含的相对不变的特殊量与OB 有关. 于是，连结DB ，则OB DB OD <+,所以，当O 、D 、B 三点共线时OB 值最大，即BO OD DB =+. 在Rt BCA ∆中，4CD =，3CB =，5DB =. 则OB 的最大值为549+=:.综上可知，解决动点背景下线段长度的最值问题时，一般可用几何方法从特殊情形出发考虑.1、在分析动点位置变化的同时，重点抓住图形中不变的量，不变的关系和性质，以不变应万变，动中求静.2、线段的最大值和最小值，常与下列知识相关:两点之间线段最短，垂线段最短，直径是圆中最大的弦，三角形中任意两边之和大于第三边，任意两边之差小于第三边等等.所以要抓住特殊情形，联系与问题相关的结论进行有效转化.【强化训练】1.（2017四川省内江市）如图，已知直线l1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=430，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且P A+AB+BQ 最小，此时P A+BQ= ．2.（2017山东省东营市）如图，已知菱形ABCD的周长为16，面积为83，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为．3．（2017山东省威海市）如图，△ABC为等边三角形，AB=2．若P为△ABC内一动点，且满足∠P AB=∠ACP，则线段PB长度的最小值为．4. （2017甘肃省天水市）如图所示，正方形ABCD的边长为4，E是边BC上的一点，且BE=1，P是对角线AC上的一动点，连接PB、PE，当点P在AC上运动时，△PBE周长的最小值是．5．（2017贵州省贵阳市）如图，在矩形纸片ABCD 中，AB =2，AD =3，点E 是AB 的中点，点F 是AD 边上的一个动点，将△AEF 沿EF 所在直线翻折，得到△A ′EF ，则A ′C 的长的最小值是 ．6.（2016山东省枣庄市）如图，把△EFP 放置在菱形ABCD 中，使得顶点E ，F ，P 分别在线段AB ，AD ，AC 上，已知EP =FP =6，EF =63，∠BAD =60°，且AB ＞63． （1）求∠EPF 的大小；（2）若AP =10，求AE +AF 的值；（3）若△E FP 的三个顶点E 、F 、P 分别在线段AB 、AD 、AC 上运动，请直接写出AP 长的最大值和最小值．7．（2016山东省枣庄市）如图，已知抛物线2y ax bx c =++（a ≠0）的对称轴为直线x =﹣1，且抛物线经过A （1，0），C （0，3）两点，与x 轴交于点B ．（1）若直线y =mx +n 经过B 、C 两点，求直线BC 和抛物线的解析式；（2）在抛物线的对称轴x =﹣1上找一点M ，使点M 到点A 的距离与到点C 的距离之和最小，求出点M 的坐标；（3）设点P 为抛物线的对称轴x =﹣1上的一个动点，求使△BPC 为直角三角形的点P 的坐标．8.（2017山东省烟台市）如图1，抛物线22y ax bx =++与x 轴交于A ，B 两点，与y 轴交于点C ，AB =4，矩形OBDC 的边CD =1，延长DC 交抛物线于点E ． （1）求抛物线的解析式；（2）如图2，点P 是直线EO 上方抛物线上的一个动点，过点P 作y 轴的平行线交直线EO 于点G ，作PH ⊥EO ，垂足为H ．设PH 的长为l ，点P 的横坐标为m ，求l 与m 的函数关系式（不必写出m 的取值范围），并求出l 的最大值；（3）如果点N 是抛物线对称轴上的一点，抛物线上是否存在点M ，使得以M ，A ，C ，N 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M 的坐标；若不存在，请说明理由．9.（2016四川省眉山市）已知如图，在平面直角坐标系xOy 中，点A 、B 、C 分别为坐标轴上上的三个点，且OA =1，OB =3，OC =4．（1）求经过A 、B 、C 三点的抛物线的解析式；（2）在平面直角坐标系xOy 中是否存在一点P ，使得以以点A 、B 、C 、P 为顶点的四边形为菱形？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）若点M 为该抛物线上一动点，在（2）的条件下，请求出当|PM ﹣AM |的最大值时点M 的坐标，并直接写出|PM ﹣AM |的最大值．10. （2016广西梧州市）如图，抛物线24y ax bx =+-（a ≠0）与x 轴交于A （4，0）、B （﹣1，0）两点，过点A 的直线y =﹣x +4交抛物线于点C ． （1）求此抛物线的解析式；（2）在直线AC 上有一动点E ，当点E 在某个位置时，使△BDE 的周长最小，求此时E 点坐标； （3）当动点E 在直线AC 与抛物线围成的封闭线A →C →B →D →A 上运动时，是否存在使△BDE 为直角三角形的情况，若存在，请直接写出符合要求的E 点的坐标；若不存在，请说明理由．。

函数的动点最值问题探析函数和最值问题是初中数学重点内容之一，将函数的动点问题与最值问题相结合更是近年来中考试题的热点，这类题目探索性强、综合性高，对培养学生的思维品质和各种能力有很大的促进作用。

它往往能考查学生的数学建模、数形结合、归纳猜想和分类讨论等能力，常常以一道中高档的解答题或者压轴题出现。

本文就近两年中考数学压轴题中有关函数的动点最值问题进行剖析，从中寻找解决该类问题的基本方法。

一、运用几何性质解函数的动点最值问题利用几何性质解函数的动点最值问题，常考虑的性质有：①三角形的三边关系：两边之和大于第三边，两边之差小于第三边；②两点之间，线段最短；③连结直线外一点和直线上各点的所有线段中，垂线段最短；④定圆的所有弦中，直径最长。

例1．如图，抛物线2124y x x =--+的顶点为A ，与y 轴交于点B ． （1）求点A 、点B 的坐标．（2）若点P 是x 轴上任意一点，求证：PA PB AB -≤． （3）当PB PA -最大时，求点P 的坐标． 解：（1）A （—2，3），B （0，2） （2）当点P 是AB 的延长线与x 轴交点时，AB PB PA =-当点P 是x 轴上又异于AB 的延长线与x 轴的交点时， 在点P 、A 、B 构成的三角形中，AB PB PA <- 综上所述： PA PB AB -≤（3）作直线AB 交x 轴于点P ，由（2）可知这时PA-PB 最大，点P 就是所求的点. 作AH⊥OP 于H ∵△BOP∽△AHP ∴AH HP BO OP= ∴OP=4，故P （4，0）评注：解决本题的关键是利用三角形任意两边之差小于第三边这一性质，得出PA-PB ＜AB ，结合P 是AB 的延长线与x 轴交点时PA-PB=AB ，从而知道当点P 是AB 的延长线与x 轴交点时，PA-PB 最大，最后利用三角形相似使问题得解。

二、运用代数证法解函数的动点最值问题一元二次方程根的判别式已不再列入中考考试内容，因此利用代数证法解函数的动点最值问题时，常考虑的方法有：①02≥a ，②0≥a ，③0≥a ，④运用配方法求二次三项式的最值。

初中数学动点问题解析与思路探讨摘要：新课改背景下，提高学生的解题能力，培养数学思维已经成为教学工作中的一大重点。

数学这门课程对于很多学生来说难度都很高，尤其是在解决高难度问题时，学生既要有扎实的基础功底，又要能运用个人思维灵活解决这些高难度问题。

本文将以初中数学中的动点问题为例，探讨解决相关问题的思路与方法。

关键词：初中数学；动点问题；解题思路前言：初中阶段有几个知识点具有比较高的难度，比如中考压轴题中经常出现的动点问题，这种问题需要学生发挥较强的逻辑思维和发散性思维，既考验基础知识的扎实掌握，又需要学生能运用个人数学素养大胆尝试各种解题思路。

也正是由于动点问题的高难度，教师有必要就此问题带领学生探讨动点问题解题技巧。

一、先分析动点问题的考察方向初中阶段动点问题属于难度比较高的一类问题，一般来说，这种题目广泛出现在毕业年级的日常练习题或中考压轴题中，综合分析近年来的中考试题，教师就会发现动点问题一直是考察中的难点，得分率不高，学生对这类问题也缺乏必要的做题信心。

在这种背景下，教师首先要带着学生认清动点问题的真面目，只有把握了动点问题的本质，学生才会明白这种问题并非洪水猛兽，只要细心作答，认真分析就可以做出来。

首先，教师要带领学生分析动点问题的若干种考察方向，就要让学生了解动点问题，一共有几种出题题型。

一般来讲，初中阶段学生常用的动点类问题有以下三种，其一是函数图像动点问题，一般是将函数图像和动点问题相结合，在一个函数图像上存在动点，引起未知量和已知量之间的某种变化关系，让学生根据这种变化关系探究函数关系式。

其二是动态几何型题目，主要是将动点和几何图形结合起来，问题的背景是一个特殊图形，考察的问题也多半和特殊图形有关，在这类问题中，等腰三角形直角三角形等图形出现的频率较高，一般也是让求三角形的周长或面积的最值，所以又称为最值问题。

其三是双动点问题，这是最近几年中考数学压轴题中的常考题型，双动点问题。

初中数学动点最值问题解题技巧总结示例文章篇一：哎呀呀，同学们，你们有没有被初中数学里的动点最值问题难倒过呀？反正我之前是被搞得晕头转向的！不过呢，经过我一番苦苦摸索，还真总结出了一些超有用的解题技巧，今天就来和大家分享分享。

咱们先来说说啥是动点最值问题。

就好比有个小调皮的点，在图形里到处乱跑，然后让咱们找它跑到啥位置的时候能得到最大或者最小的值。

这可不像找藏起来的糖果那么简单哟！那怎么解决呢？首先，咱们得学会用“两点之间线段最短”这个宝贝定理。

比如说，有A、B 两个点，那连接这两个点的线段AB 不就是最短的距离嘛。

这就像从家到学校，咱们走直线肯定是最近的路呀，难道还能绕个大圈子？再说说“垂线段最短”。

假如有一条直线l，还有一个点P，那从点P 向直线l 作垂线，垂足为Q，线段PQ 就是点P 到直线l 最短的距离。

这就好比你站在河边，要到河里打水，肯定是垂直下去打水最近，要是斜着走，那不是多走冤枉路嘛！还有一种常见的方法是利用三角形的三边关系。

两边之和大于第三边，两边之差小于第三边。

比如说有三角形ABC，AB 边长是5，AC 边长是3，那BC 的长度就在2 到8 之间。

这就好像三个人手拉手，两边的人胳膊加起来肯定要比中间那个人的胳膊长呀！有一次，我和同桌一起做一道动点最值问题。

题目说在一个直角三角形里，有一个动点P，让咱们找P 点在啥位置的时候，PA + PB 的值最小。

我一开始毫无头绪，急得直抓脑袋，嘴里嘟囔着：“这可咋办呀？”同桌倒是挺冷静，他说：“咱们想想刚刚学的那些方法呀！”然后我俩就一起琢磨，突然我灵光一闪：“哎呀，这不就可以用两点之间线段最短嘛！”最后我们成功解出了这道题，那种喜悦，简直没法形容！还有一次，数学老师在课堂上讲一道特别难的动点最值问题，好多同学都听得云里雾里的。

老师就耐心地一遍又一遍解释，还说：“同学们，别着急，咱们慢慢理清楚思路。

”最后大家终于明白了，都忍不住欢呼起来。

所以呀，同学们，动点最值问题虽然看起来很难很可怕，但只要咱们掌握了这些解题技巧，再加上多做练习，多和同学老师讨论，就一定能把它拿下！你们说是不是呀？我相信，只要咱们肯努力，就没有解决不了的数学难题！示例文章篇二：哎呀呀，同学们，你们是不是一碰到初中数学里的动点最值问题就头疼得要命呀？反正我之前是这样的！但是后来我发现，只要掌握了一些小技巧，这类题也没那么可怕啦！就拿那种在三角形里找动点最值的题来说吧。

初二动点最值问题的常用解法
初二动点最值问题是数学中常见的一类问题，常用的解法包括
几何法、代数法和微积分法。

首先，我们来看看几何法。

对于动点最值问题，我们可以通过
几何方法来解决。

例如，如果问题涉及到平面几何中的最短路径或
最大面积等问题，我们可以通过画图、利用几何性质和相似三角形
等方法来求解动点的最值问题。

这种方法相对直观，适用于一些简
单的动点最值问题。

其次，代数法也是常用的解法之一。

对于一些动点问题，我们
可以建立坐标系，引入变量，列方程，然后通过代数运算来求解动
点的最值问题。

例如，对于直线上的动点问题，我们可以设定动点
的坐标，列出相关方程，然后通过代数运算来求解最值。

这种方法
适用于一些需要进行坐标计算的动点最值问题。

最后，微积分法也是解决动点最值问题的常用方法。

通过对动
点轨迹的函数进行微分，找到函数的极值点，可以求得动点的最值。

这种方法适用于一些需要利用导数性质和极值定理的动点最值问题。

综上所述，初二动点最值问题的常用解法包括几何法、代数法和微积分法。

针对不同的问题，我们可以灵活运用这些方法来求解动点的最值问题。

希望这些解法对你有所帮助。

动点求最值方法总结一、引言动点求最值是一类经典数学问题，在各个学科领域中都有广泛的应用。

它可以通过将问题转化为数学模型，通过解析方法或数值计算方法求解。

本文将对动点求最值的方法进行总结和探讨，深入探究这类问题的解决思路和技巧。

二、常见的动点求最值问题2.1 直线上的动点问题在一条直线上，给定两个固定点A和B，求动点P到A点和B点的距离之和的最小值或最大值。

这类问题可以通过求解P点的坐标来实现。

2.2 平面内的动点问题在平面内，给定固定点A、B和C，求动点P到点A、B、C的距离之和的最小值或最大值。

这类问题涉及到平面几何和三角函数的运用。

2.3 空间内的动点问题在三维空间中，给定固定点A、B和C，求动点P到点A、B、C的距离之和的最小值或最大值。

这类问题需要运用空间几何和向量的知识。

三、解决动点求最值问题的方法3.1 几何解法几何解法是通过绘制几何图形，利用几何性质和定理来解决问题。

在直线上的动点问题中，可以通过绘制线段和圆等图形来分析，确定最值点的位置。

在平面内和空间内的动点问题中，可以借助几何图形的相似性和对称性来求解。

3.2 代数解法代数解法是通过建立方程或运用代数方法来求解问题。

在直线上的动点问题中，可以通过设定P点的坐标，利用距离公式建立相应的方程，并通过求导或配方法求解。

在平面内和空间内的动点问题中，可以利用向量运算和三角函数关系建立方程，然后通过求解方程组来得到最值点的坐标。

3.3 数值计算方法如果问题比较复杂，无法通过几何或代数的方法得到解析解，可以使用数值计算方法进行近似求解。

常用的数值计算方法包括最优化算法、数值优化算法和遗传算法等。

这些方法通过迭代计算，逐步逼近最值点的位置。

四、案例分析4.1 直线上的动点问题案例假设直线上有两个点A(1, 2)和B(3, 4)，求动点P到A点和B点的距离之和的最小值。

通过建立P点的坐标(x, y)，利用距离公式可得：d=√(x−1)2+(y−2)2+√(x−3)2+(y−4)2通过求导可以得到最小值点的坐标：∂d=0∂x∂d=0∂y解得最小值点为P(2, 3)。